In silico studies of plant primary cell walls – structure and mechanics
ABSTRACT
Primary plant cell wall (PCW) is a highly organized network, its performance is dependent on cellulose, hemicellulose and pectic polysaccharides, their properties, interactions and assemblies. Their mutual relationships and functions in the cell wall can be better understood by means of conceptual models of their higher-order structures. Knowledge unified in the form of a conceptual model allows predictions to be made about the properties and behaviour of the system under study. Ongoing research in this field has resulted in a number of conceptual models of the cell wall. However, due to the currently limited research methods, the community of cell wall researchers have not reached a consensus favouring one model over another. Herein we present yet another research technique – numerical modelling – which is capable of resolving this issue. Even at the current stage of development of numerical techniques, due to their complexity, the in silico reconstruction of PCW remains a challenge for computational simulations. However, some difficulties have been overcome, thereby making it possible to produce advanced approximations of PCW structure and mechanics. This review summarizes the results concerning the simulation of polysaccharide interactions in PCW with regard to network fine structure, supramolecular properties and polysaccharide binding affinity. The in silico mechanical models presented herein incorporate certain physical and biomechanical aspects of cell wall architecture for the purposes of undertaking critical testing to bring about advances in our understanding of the mechanisms controlling cells and limiting cell wall expansion.
I. INTRODUCTION
The primary plant cell wall (PCW) is a highly ordered and specialized network that developed to protect the cell and manage the mechanical responses, strengths and flexibility of both the individual cell and the plant as a whole (O'Neill & York, 2018). PCW is formed mainly of polysaccharides (up to 90% dry mass), glycoproteins (threonine and hydroxyproline-rich glycoproteins, up to 10% dry mass), phenolic compounds, minerals and enzymes (endo- and exoglycanases, transglycosylases, peroxidases) (Carpita & Gibeaut, 1993). In the wet state, water makes up to 60–65% by volume of the PCW (Jackman & Stanley, 1995; Pettolino et al., 2012). The dry matter generally contains 15–40% by mass cellulose, 30–50% pectins and 20–30% hemicelluloses (Cosgrove & Jarvis, 2012). The most abundant hemicelluloses are xyloglucan (XG), xylan and glucomannan, while galactoglucomannan (GGM) and arabinoxylan (AX) are much less common and only occur in particular types of PCW and specific tissues. The structure of pectic polysaccharides is based on three main polymers, homogalacturonan (HG), rhamnogalacturonan I (RGI) and rhamnogalacturonan II (RGII). The main unit comprising approximately 70% of all pectin is D-galacturonic acid (GalA), while the remaining 30% consists of a rich family of neutral sugars (O'Neill & York, 2018). With regard to hemicellulose in the PCW, there are two main types of primary walls: Type I (containing XG and/or GGM and pectin), and Type II (rich in AX and pectin) (Carpita & Gibeaut, 1993; Carpita, 1996). Mannan-rich walls with a low pectin content are classified as Type III walls (Silva et al., 2011).
Cellulose and hemicellulose are considered to be key compartments forming the mechanical scaffold of the PCW. To date, a number of idealized models of cell wall structure have been proposed to enhance our understanding of the mechanics of this system (Probine & Barber, 1966; Keegstra et al., 1973; Talbott & Ray, 1992; Ha, Apperley & Jarvis, 1997; Park & Cosgrove, 2012a,b). Various concepts of cell wall structure raise specific questions about the role of hemicellulose and pectin in determining its structure. In some models, hemicellulose chains crosslink cellulose fibres, hypothetically separating them from each other. However, it is unknown if hemicellulose is stiff enough mechanically to separate cellulose or whether it acts as a space filler. Another open question concerns the structure, nature and strength of cellulose–hemicellulose bonds and whether their collective contribution is sufficient to maintain the integrity of the turgor-exposed cell wall. Although the role of inter-fibre links in PCWs is commonly recognized, direct measurements of the adhesive forces between nanoscale cellulose fibres have only been reported recently (Dolan et al., 2019). Even for well-established conceptual models of the interactions of PCW basic components such as hemicellulose and cellulose, recent discoveries have led to new conceptions of PCW polysaccharide assemblies (Park & Cosgrove, 2012a).
Studies concerning PCWs in their intact state encounter a number of difficulties which make it almost impossible to provide clear estimations of the individual contributions of specific PCW compounds to the various mechanical properties in planta. An alternative approach to solving this problem is to provide in silico representations of biological systems by means of numerical methods. Numerical modelling uses a wide range of methods, from classical mechanics to quantum-field theories to resolve the current state of the simulated system and its evolution over time under the influence of changing environmental conditions (Zhao et al., 2014; Berglund et al., 2016, 2019). In this context, revision of current PCW conceptual models may be achieved via a new approach based on multiscale robust computational modelling tools.
The aim of this review is to provide a brief overview of the most significant achievements in the field of the numerical modelling of PCW mechanics. In this review we assign importance to the cellulose–hemicellulose complex as the main component of the primary PCW mechanical system. We begin with a summary of the current knowledge concerning basic PCW polysaccharides and their structure and properties. Next we briefly discuss both historical and current conceptual views on their spatial assemblies in PCW. We present various PCW conceptual models that have been developed based on experimental data.
The final section presents both the historical and the latest advances in numerical modelling of wall-like structures. It should be emphasized that only a handful of PCW numerical models have been developed to date. Therefore we expand our overview to include models of random fibre networks. This decision was motivated by the fact that these systems share many similarities in terms of their structure–mechanics relationships. Moreover, the random fibre networks developed much earlier laid the conceptual foundations for the PCW models described below.
II. PCW LOAD-BEARING POLYSACCHARIDES
Cellulose is the main building block of PCWs. It is a para-crystalline array of two to three dozen polymer chains, made up of 7000–15,000 β-D-glucosyl-(1→4) units, which oscillate at an angle of 180°, with a twofold screw conformation (Carpita, 2011; Berglund et al., 2019). Equatorial β-(1→4)-linkages and surface hydroxyl groups lead to the formation of cellulose–cellulose and cellulose–water hydrogen bonds, in turn causing microfibrils to organize themselves into a ribbon-like structure (Martínez-Sanz et al., 2017). Cellulose biosynthesis is carried out in terminal complexes and facilitated by complex cellulose synthase (CESA) proteins (Endler & Persson, 2011; Fernandes et al., 2011; Pauly et al., 2013; Braidwood, Breuer & Sugimoto, 2014). CESA proteins move along fibrils on the plasma membrane and deposit fibrils onto the cell wall (McFarlane, Döring & Persson, 2014).
Separate cellulose units (18 according to modern predictions, 24 and 36 according to earlier references) may become coordinated to create microfibrils, which can form crystalline, para-crystalline, and non-crystalline domains (Martínez-Sanz et al., 2017; Purushotham, Ho & Zimmer, 2020; Yang & Kubicki, 2020). Different diameters of cellulose microfibrils have been reported, ranging from 2–5 nm in the case of plant fibrils, 4–8 nm for bacterial cellulose, greater than 15 nm for algal cellulose, and up to 40 nm in the case of wood fibrils (Newman, Hill & Harris, 2013; Thomas et al., 2013). The native crystallographic form of plant cellulose (cellulose I) exhibits structural heterogeneity with two different para-crystalline forms – a triclinic system with one chain per unit cell (cellulose Iα) and a more stable monoclinic system with two chains per unit cell (cellulose Iβ) – the distribution of which, within the cell wall, remains unclear (Matthews et al., 2006). Other cellulose crystal formations are formed after cellulose mercerization (cellulose II) or treatment with hot liquid ammonia or amines (cellulose III). Cellulose microfibrils have regularly distributed definite hydrophilic and hydrophobic surfaces, making it possible for them to interact with other polysaccharides such as hemicelluloses (Martínez-Sanz et al., 2017; Broxterman & Schols, 2018).
Hemicelluloses are a chemically heterogeneous class of polysaccharides of medium chain length, with glucose, mannose and xylose β-(1→4)-linked backbones (Uhlin, Atalla & Thompson, 1995; Scheller & Ulvskov, 2010). Although hemicelluloses have different component sugars, their backbones are structurally similar (York et al., 1990; Tuomivaara et al., 2015). All hemicelluloses have straight β-(1→4)-linked backbones with an equatorial configuration at C1 and C4. The three main families of hemicellulose polysaccharides (XG, AX and GGMs) can be found in the cell walls of fruit and vegetables, hardwood, annual plants, cereals, and herbs (Spiridon & Popa, 2008; Ren & Sun, 2010; Scheller & Ulvskov, 2010; Yu et al., 2022). Among these, XG is the most abundant primary cell wall hemicellulose, with AX and GGM generally present in significantly smaller proportions according to the species in question. XG represents about 20–25% of the primary wall (Lima, Loh & Buckeridge, 2004). XG consists of β-D-glucosyl-(1→4) units ramified at O-6 by α-D-xylosyl monomers, regularly organized into blocks. It can be further extended by galactose, fucose, arabinose, xylose or uronic acid residues as sidechains. However, the side chains attached to the backbone are short – usually just one sugar long – and protrude from the sides of the backbone. GGM consists of β-D-glucosyl-(1→4) and β-D-mannosyl-(1→4) residues either alternating or as blocks more or less ramified at the O-6 of glucose or mannose by galactose and di-galactose (Melton et al., 2009). GGM is particularly prominent in tomato fruit (about 6% of the cell wall dry mass) (Prakash et al., 2012) and is a minor hemicellulose in other fruits, such as kiwi, apple and banana (Schröder et al., 2001; Cheng et al., 2009; Ray et al., 2014; Colodel, Vriesmann & de Oliveira Petkowicz, 2018). AX is a common hemicellulose present in the flesh and peel of fruit and vegetables (Marcelin, Williams & Brillouet, 1993). It consists of β-D-xylosyl-(1→4) units substituted at O-2 and O-3 by α-L-arabinosyl units, and at O-2 by α-D-glucuronic acid which also occurs as its 4-O methyl ether derivative (Hao & Mohnen, 2014; Chen et al., 2019). Apart from some reports on mannan (Mackie & Preston, 1968), there is no evidence for self-aggregation of hemicelluloses into long, close-packed crystalline fibrils in the manner of cellulose. However, hemicellulose polysaccharide chains can form significant hydrogen-bonded associations with each other in the cell wall, particularly between regions of the chains with few side branches or axial hydroxyl groups (McNiel et al., 1975). Importantly, the structural similarity to cellulose facilitates a close, non-covalent association of hemicellulose with cellulose microfibrils, resulting in the formation of a cellulose–hemicellulose network which is believed to play a major role PCW mechanics (Scheller & Ulvskov, 2010).
III. CONCEPTS OF PCW POLYSACCHARIDE INTERACTIONS
Several models of PCW structure have been established according to cellulose–cellulose and cellulose–hemicellulose physicochemical and mechanical interactions. These models were designed to explain how the cell wall maintains its integrity under turgor pressure, and most importantly, how such rigid structures allow plant cells to grow (Cosgrove, 2000, 2014; Thompson, 2005; Cosgrove & Jarvis, 2012). The first theory proposed visualized PCW as a template of cellulose fibrils, loosely incorporated into the amorphous wall matrix (the ‘multinet model’) (Probine & Barber, 1966). The model assumed that about 10% of the PCW volume is occupied by cellulose, which has long fibrils that cause many contact and adhesion points with neighbouring fibrils or they may even twist around each other (Roelofsen, 1958). Matrix polysaccharides (hemicellulose and pectin) were considered to be partly immobilized, and partly arranged in fibrils.
In the cell wall structure proposed by Keegstra et al. (1973) hemicelluloses coat the microfibrils and interact with other fibrils via covalently linked matrix polymers and PCW proteins (Fig. 1A). In this case, XGs are attached to the galactan side chains of pectic polysaccharides (RGs), while pectic polysaccharides are attached to the wall proteins through arabinogalactan chains (Albersheim et al., 2011). The proposed structure was supported in part by the observed degradation of cell walls during the selective enzymatic hydrolysis of matrix polysaccharides. However, the lack of evidence for the presence of other key hypothetical linkages predicted by this model finally led to the rejection of this concept.
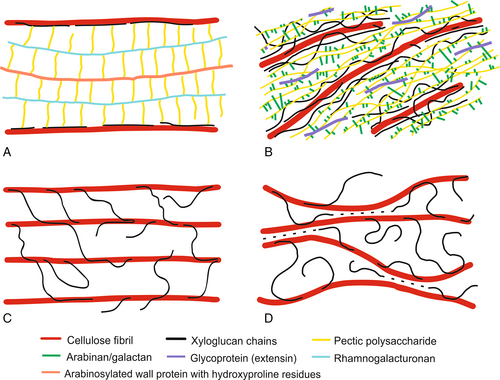
Talbott & Ray (1992) proposed a multi-coat cell wall model in which cellulose microfibrils are covered with XG, followed by successive layers of less closely bound pectic polysaccharides (Fig. 1B). In their concept, XG does not form crosslinks between the cellulose molecules, therefore cleavage of XG is not a necessary condition for wall expansion. The PCW structure is held together by interactions between the matrix polymers. Other authors modified this multi-coat model to include structures in which layers of cellulose are crosslinked by XG and separated by lamellae of pectic polysaccharides (Ha et al., 1997).
A simplified view of PCW structure was proposed in the tethered network model (Carpita & Gibeaut, 1993). In this model the cellulose fibrils are separated from each other by XG chains, which crosslink fibrils into a load-bearing network via 20–40 nm long tethers (Fig. 1C). According to this hypothesis, XG is a key component of PCW, providing mechanical strength and integrity. Pectic polysaccharides and structural proteins, although physically entangled with the cellulose–XG network, create separate networks which are not covalently bound. The loosening of the cell wall structure and its growth can be achieved through the hydrolysis of hemicellulose connections. This model was supported by a series of studies confirming the affinity of XG to cellulose and the presence of relatively long XG chains, of sufficient length to pass through neighbouring cellulose fibrils (Hayashi, Marsden & Delmer, 1987; Hayashi, Ogawa & Mitsuishi, 1994; Fry, 1989; Hayashi, 1989; McCann, Wells & Roberts, 1990; Fry et al., 1992; Hayashi & Kaida, 2011).
Despite being widely supported and accepted by many researchers, some experimental results have challenged the concept of the tethered network model. Experiments on primary PCWs using enzymes targeting XG tethers showed no wall extension or mechanical weakening, while enzymes with the ability to cut both XG and cellulose were effective at loosening the wall (Park & Cosgrove, 2012a,b). At the same time, research with XG-deficient Arabidopsis mutants showed that XG is not necessary to maintain PCW mechanical integrity, which would be expected for a critical load-bearing component of the expanding cell wall (Cavalier et al., 2008; Park & Cosgrove, 2012b; Uluisik et al., 2016). Based on data that contradicted the assumptions of the tethered model, a new cell wall model was conceived where tethers, although present, do not play a significant role in PCW mechanics. Instead of crosslinking tethers, mechanically important XGs are located in close proximity to two adjacent cellulose fibrils, forming lateral tight load-bearing junctions called biomechanical hotspots (Fig. 1D) (Park & Cosgrove, 2012a,b; Zhang et al., 2014; Cosgrove, 2018). According to this model, the mechanical load is transmitted between fibrils not through the XG backbone but rather due to lateral interactions generated by the contact surfaces of XG sandwiched between cellulose fibrils. The biomechanical hotspot concept has the implication that wall extensibility is controlled by limited, specific junctions between microfibrils rather than by the bulk viscoelasticity of the matrix. Despite promising results there remain questions to be answered with regard to the formation, density, location and strength of these cellulose–hemicellulose junctions as well as the nature of the role of other PCW polysaccharides.
In order to achieve this goal, in silico mechanical models of cell walls need to incorporate physical and biomechanical aspects of cell wall architecture before critical testing and refinement by a combination of numerical approaches in order to improve our understanding of the mechanisms controlling cells and limiting cell wall expansion.
IV. COMPUTATIONAL MODELS OF PCWS
(1) Random fibre networks – precursors of cell wall models
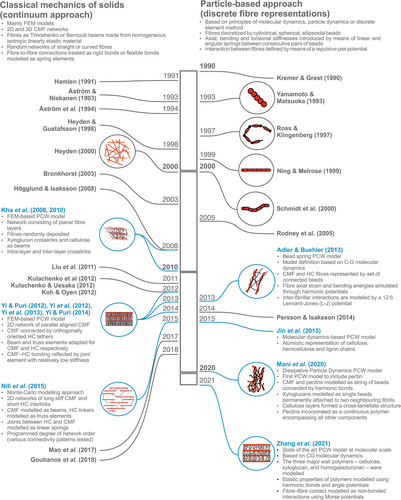
The first studies dedicated to the simulation of wall-like cellulose networks involved two-dimensional (2D) paper structures with a random fibre length and distribution (Rigdahl, Westerlind & Hollmark, 1984; Åström et al., 1994). Although these models were initially simple and designed for industrial use, they provided valuable insights into the structure–mechanics relationships of fibre-based networks. Subsequently, many publications have modelled cellulose networks as 2D and three-dimensional (3D) random fibre networks. In these models, all fibres are straight, with the same diameter and length, and randomly distributed in 2D or 3D. The interspace between the fibres is considered as an empty void that cannot dissipate strain energy. Fibre-to-fibre connections are treated as rigid or flexible bonds modelled as spring elements (Rigdahl et al., 1984; Åström et al., 1994; Heyden, 2000; Bronkhorst, 2003; Hägglund & Isaksson, 2008; Liu et al., 2011; Koh & Oyen, 2012; Kulachenko & Uesaka, 2012; Kulachenko et al., 2012; Mao et al., 2017; Deogekar & Picu, 2018; Goutianos, Mao & Peijs, 2018) (see Fig. 2).
Heyden (2000) summarized the results of simulations of the mechanical properties of cellulose fibre fluff. 2D and 3D finite element method network models were used to determine the relationship between network stiffness and fibre and bond stiffness, network density, fibre curl and length. Networks were generated by placing fibres randomly in space. Single fibres were modelled using a Bernoulli beam, while fibre–fibre interactions were approximated using an artificial spring element connecting fibres. Bonds were designed to exhibit non-linear stick–slip fracture behaviour.
The models showed that the elastic modulus of the network rises rapidly with increases in its density and number of inter-fibre contacts, while Poisson's ratio showed a weaker response, being less affected by network structural changes. Networks consisting of curled fibres were less stiff due to the lower axial stiffness of the curled beam segments. Long fibres resulted in stiffer networks, with stiffer responses along the preferred fibre orientation.
An interesting observation was that the overall network fracture mechanism was more sensitive to fibre failure than to bond disruption. In the case of fibre failure, the load-bearing path was completely interrupted. However, due to the possibility of the fibre being entangled with other fibres or connected by more than two bonds, bond disruption results in a lower decrease in network strength. These conclusions may be applied to PCW growth, where structural expansion requires its partial loosening, but not complete disintegration. According to both the tethered network and biomechanical hotspot models, loosening is achieved by the degradation of the hemicellulose connections, which corresponds to elastic bonds between fibres in the model used by Heyden (2000). Results showed that the partial degradation of the cellulose–hemicellulose network would allow the cell wall to expand without the risk of damaging its integrity. Moreover, simulation results showed that structural loosening progressed much faster when the cellulose fibres were interrupted, which corresponds with the hotspot hypothesis, assuming the simultaneous degradation of cellulose and hemicelluloses (Park & Cosgrove, 2012b).
Nevertheless, the model had several limitations that distinguished it from conceptual PCW models. Bonds were modelled as contact points rather than crosslinks, suggesting that this approach should rather be interpreted as a representation of a biomechanical hotspot model. Moreover, potential slippage of inter-fibre bonds was limited. Once broken, they did not form new connections, which is a departure from the previously discussed models of hemicellulose adsorption.
Heyden's (2000) modelling approach was further explored with variations of 2D or 3D models of cellulose networks. Kulachenko & Uesaka (2012) and Kulachenko et al. (2012) used a 2D and 3D nano-paper finite element model (FEM) and found generally similar conclusions to those of Heyden (2000). The elastic modulus of the network, strength and strain-to-failure were mainly influenced by fibre length. Bond stiffness had a negligible impact on network stiffness if it varied within a reasonable range. Similar findings had been reported by Rigdahl et al. (1984) who noted that bond stiffness did not play a role in stress transfer, unless it was below some critical value indicating rapid deterioration. Mao et al. (2017) developed a 2D FEM of a fibrous network to investigate the impact of network structural properties on its elastic modulus. Their 2D modelling approach used fibres in the form of linear elastic Timoshenko beam elements and point-wise fibre–fibre bonds that could not slide or separate under strain; thus this is an example of an idealized biomechanical hotspot PCW model. A simulation showed that the network elastic modulus increases with fibre length (thereby enhancing stress-transfer capability and number of contacts), fibre modulus, bond density and network density (multiple contacts). However, it decreases with increasing fibre diameter (due to the decreasing number of fibres but with an overall constant fibril volume) and with fibre waviness. Goutianos et al. (2018) developed a 3D extension of this model to examine the effects of inter-fibre bonds. Bonds were assumed to be damageable non-linear springs, which only carry axial loads (truss elements). The spring damage was irreversible – once broken, the bonds neither carry a load nor re-establish connections. It was found that the Young's modulus of the network increased with the growing number and strength of inter-fibre bonds. On the other hand, both parameters only had a minor effect on the cellulose network strain-to-failure relationship.
(2) PCW models with classical beam theory representations of fibres
Despite intensive research concerning the mechanics of random fibre networks, the value of numerical simulations as a research tool has only been recognized by the PCW community relatively recently (see Fig. 2). Conceptual models have had a profound influence on the way numerical models of cell walls were constructed. All models to a greater or lesser degree have attempted to recreate one of the idealized concepts of PCW. Major findings and limitations of PCW models can be found in Table 1.
| Reference | Technique | Major findings | Limitations |
|---|---|---|---|
| Finite element method |
|
|
|
| Yi & Puri (2012, 2014); Yi et al. (2012, 2013) | Finite element method |
|
|
| Nili et al. (2015) | Finite element method |
|
|
| Jin et al. (2015) | Molecular dynamics/atomistic model |
|
|
| Adler & Buehler (2013) | Coarse-grained molecular dynamics |
|
|
| Mani et al. (2020) | Dissipative particle dynamics |
|
|
| Zhang et al. (2021) | Coarse-grained particle dynamics |
|
One of the first structural models designed exclusively to simulate PCW mechanical behaviour was presented by Kha et al. (2008, 2010). This novel modelling approach was aimed at the reconstruction of multilayered cellulose–hemicellulose networks, resembling a fine-structure, interlinked tethered PCW model. The FEM-based model fibrils were organized into separate flat and parallel layers of cellulose networks. Randomly deposited cellulose fibres were crosslinked by XG chains, which were also modelled as beams. XG chains, which were inserted into the cellulose network were constrained to crosslinking with only two cellulose fibrils each. As for the previously described random fibre networks, simulations showed that structures with a higher number of, or longer, cellulose fibres were stiffer. Cell wall stiffness was positively correlated with XG stiffness. The structures were stiffer in the direction parallel to cellulose alignment, as compared to the perpendicular direction or a random orientation. Despite its novelty, this approach suffered from several limitations. The models were designed to simulate relatively small cell wall deformations with the thickness of the structure being limited to 100 nm. More importantly, the cellulose–hemicellulose connections were designed to act as permanent crosslinks with no bonding–debonding mechanism, which is crucial for the reproduction of PCW viscoelastic properties.
This approach was extended by Yi & Puri (2012, 2014) and Yi, Zamil & Puri (2012, 2013) who developed a tethered network computational model to explore the PCW hydrogen-bond hypothesis. The 2D representation of the PCW network consisted of cellulose microfibrils in a parallel alignment which were connected by orthogonally oriented hemicellulose tethers. Classical beam theory was adapted to reflect the physical properties of both PCW components. Two-node beam elements were used to describe the capabilities of cellulose microfibrils to resist axial and lateral loading, while truss elements were used to model the single molecular backbone of hemicellulose, which were considered to be too weak to resist lateral forces. In order to consider the effect on cellulose–hemicellulose of hydrogen bonding between cellulose and hemicellulose, both structures were connected indirectly via intermediate linearly elastic joint elements, with a spring constant equivalent to the stiffness of a hydrogen bond. The results showed that cellulose–hemicellulose hydrogen bonds experienced the highest value of strain energy, being the weakest structural component. Cellulose–hemicellulose interactions via hydrogen bond equivalent structures were recognized as crucial components of cell wall network mechanics. Model sensitivity analysis showed that the stiffness of these structures contributed up to 75% of the overall stiffness of the PCW, while hemicellulose stiffness alone contributed ~25% overall. Variations in cellulose microfibril (CMF) stiffness showed a marginal impact (1%) on overall cell wall mechanical performance. The results were explained by the possibility of CMF–hemicellulose bonds acting as growth regulators. Based on the theoretical hydrogen bond energy and strain energies of the cellulose–hemicellulose links, it was concluded that at 1% cell wall strain hydrogen bonding was not strong enough to maintain the integrity of the cell wall. The necessity for other, and more importantly, stronger load-bearing mechanisms was postulated to maintain the overall shape of the cell. Among various possibilities, the authors identified the biomechanical hotspot concept of Park & Cosgrove (2012b), as well as additional interactions with the pectin matrix.
The same model-building concept was used by Nili et al. (2015), who examined the biomechanical hotspot cell wall model with an almost in silico duplication of Park & Cosgrove (2012a). Simulations of uniaxial tensile tests were carried out with a decreasing number of linkers per fibril, showing that disorder in cellulose distribution had a greater impact on PCW stiffness than the degree of disorder in the cellulose–hemicellulose crosslinks. PCW integrity decay was also disorder dependent, so that the highly disordered networks required more links per fibre to maintain the same level of stiffness as the ordered network. The simulation showed 3.75 XG links per cellulose fibril to be a critical value for system integrity, which correlates with the Park & Cosgrove (2012a) predictions for the mass fraction of biomechanical hotspots in PCW (≈0.3%). However, the corresponding PCW network stiffness was not enough to maintain its structural integrity under loads generated by turgor pressure. Similar to the theories of Yi & Puri (2014), the authors hypothesized another mechanism governing cell wall stiffness (a more important role of pectin, or a different nature of the hotspot linkage).
(3) PCW models with particle-based representation of fibres
Early PCW models and random fibre networks, which were based on classical continuum mechanics, shared the same limitations. For instance, certain modelling approaches take into account adhesion and failure between cellulose nanofibrils but do not include self-healing induced by reformation bonds, which is an important phenomenon in cell walls. Awareness of these issues led to the development of an alternative approach based on the principles of particle dynamics (Fig. 2). In this approach, fibres were represented using modified bead–spring models adopted from particle dynamics simulations (Rodney, Fivel & Dendievel, 2005; Persson & Isaksson, 2014). In the bead–spring model, fibres were discretized by nodes, whose number was equal to a fibre aspect ratio. Axial and bending stiffnesses were introduced by means of linear and angular springs between consecutive pairs of nodes. Interaction between the fibres was defined by means of a repulsive pair potential. Other variations of the bead–spring technique included various bead–bead interaction potentials (Yamamoto & Matsuoka, 1993) or spring potentials (Kremer & Grest, 1990). Bead–spring models also allowed for modifications to bead shape from spherical to prolate spheroids (Ross & Klingenberg, 1997), cylindrical (Ning & Melrose, 1999) or cylindrical with hemispherical end caps (Schmid, Switzer & Klingenberg, 2000).
A milestone in the field of PCW modelling was the work of Adler & Buehler (2013), who described a mesoscale bead–spring model of the wall mechanics of various wood species. Their model included cellulose and hemicellulose only, thus providing a universal representation of cellulose–hemicellulose networks, similar to the tethered PCW model. Cellulose and hemicellulose chains were divided into segments, approximated by spherical beads – a simplified representation of large number of connected molecules. Harmonic bond potentials between beads were established to simulate the axial strain and bending energies of the fibres. Inter-fibrillar interactions were modelled by means of Lennard-Jones (LJ) potentials. The application of LJ interaction potentials made this model the first to allow users to simulate the process of desorption and adsorption of hemicelluloses freely during the deformation of the cell wall; this is significant because it had a key influence on the shape of the force–strain characteristics obtained during uniaxial tensile experiments. The authors reported so-called ‘slip–stick’ behaviour between the cellulose and hemicellulose, which was indicated by three regimes of tensile behaviour of the deformed cell wall: (i) initial elastic deformation, (ii) yielding of the matrix polysaccharides and (iii) plastic deformation caused by the sliding of the matrix along the cellulose. The resulting binomial stress–strain curve is characteristic for plant materials and was observed on larger scales for wood and plant tissues (Spatz, Köhler & Niklas, 1999; Köhler, 2000; Keunecke et al., 2008). The cell wall yield and the resulting plastic deformation was explained by the continuous process of cellulose–hemicellulose bonding and debonding. After exceeding the critical values of shear strain, the locally overloaded hydrogen bonds broke, allowing for short-term fibre slippage and relaxation. During the slip event the hemicellulose re-attached in a new location along the cellulose, thereby creating a new bond which again contributed to overall PCW stiffness. The implementation of structural self-healing allowed for the reconstruction of the general behaviour of the PCW material, and also reproduced the trend of increasing stiffness with decreases in the microfibril angle. This mechanism was further explored and confirmed at the molecular level with a wood cell wall model approximated by a ‘cellulose-xylan-lignin-xylan-cellulose’ double sandwich-like structure (Jin, Qin & Buehler, 2015).
Another coarse-grained (CG) model based on dissipative particle dynamics (DPD) principles was developed by Mani, Cosgrove & Voth (2020) to investigate changes in the arrangement and spatial distribution of basic PCW polysaccharides during the initial phase of forced deformation. The cell wall included cellulose (in the form of bead–spring chains) and hemicelluloses (single bead, interconnecting with two fibrils). Unlike the previous models, pectin molecules were also included in the PCW molecular structure. The cellulose was arranged into separate layers which varied according to fibril orientation, all of which was submerged in the pectin matrix. XGs were modelled as linkers between two neighbouring cellulose fibres, connected by permanent bonds. All of the PCW constituents showed a collective response to forced stretching, with the mode of deformation varying with respect to orientation, which in general followed the diverse range of motions under a series of well-defined extensions observed in experiments (Zhang et al., 2017). Fibres aligned with the stretching direction exhibited mainly angular reorientations. Fibres with a transverse direction predominantly showed a kinking movement due to the existence of compressive loads in a direction orthogonal to the stretching vector. The mesoscale phenomenological model developed was one of the first to recognize explicitly the presence of pectin. Simulations of chains with a wide range of lengths had almost no impact on the fibril motions. These findings suggested that the interactions between pectin and fibrils are limited to weak non-covalent interactions. The negligible effects of pectin on fibril motion is in line with indirect observations of a lower binding affinity of pectin to cellulose fibrils compared to that of XGs for cell wall analogues, as well as cucumber hypocotyl walls in which mechanics predominantly was determined by contacts involving XGs and cellulose (Whitney et al., 1995; Chanliaud & Gidley, 1999; Park & Cosgrove, 2012a). However, it should be emphasized that the adopted force field works exclusively by means of repulsive potentials. Therefore, the results obtained were specific to certain simulation conditions, which are only capable of reflecting a limited range of interactions. The developed simulation affirmed roles for XG and pectin as a cellulose fibril coating and background matrix, respectively.
Recently a state-of-the-art research process developed a CG model based on polymer physics which aimed to simulate the mechanics of epidermal cell walls at a nanoscale level (Zhang et al., 2021). The methodology used shared a conceptual basis with the model developed by Adler & Buehler (2013), and belongs to the same category as the bead–spring models derived from CG molecular dynamics (CGMD), with the elastic properties of PCW polysaccharides being modelled using harmonic bonds and angle potentials between beads, and fibre-to-fibre contacts modelled as non-bonded interactions using Morse potentials.
The onion epidermal cell wall was modelled as a polylamellate structure of cellulose microfibrils (four lamellae) with varied orientation angles, mimicking surface deposition by synthase complexes, and embedded in matrix polysaccharides (XG and HG). Both matrix polysaccharides were initially randomly dispersed in a simulation domain, following which the whole system was dynamically equilibrated, resulting in structures resembling PCW in terms of organization as observed using an atomic force microscope.
Simulations showed that cellulose fibrils support most cell wall stress, highly dependent on fibril length and density; there was little response to XG and HG length and HG crosslinking, in line with previous experimental studies (Park & Cosgrove, 2012a; Zhang et al., 2019). The modulus of the uniaxially stretched PCW model showed a non-linear response to applied strain, being constant up to ≈1% strain, and increasing up to ≈8% with a further drop due to the plastic deformation of selected wall components. An analysis of tensile stress distribution showed the highest values for lamellae aligned most closely to the stretching direction and decreasing with alignment angle. The simulations provided unprecedented insight into structural changes in the deformation system, thereby allowing three main microfibril movements associated with epidermis stretching to be distinguished. Straightening was observed at low CMF orientation angles (0–30°) and low strains, then this ceased and was replaced by sliding at high strains, marking the beginning of the plastic yield point. Bending was observed for 60–90° orientation angles irrespective of the strain rate, due to cell wall compression in the transverse direction. For lamellae with intermediate CMF orientation angles, reorientation was observed due to increased microfibril bundling at higher strains. Modelling of the cyclic extension of the wall showed irreversible deformation for the first cycle, whereas subsequent loading was reversible. Fibril sliding made a major contribution to irreversible extension, which increased with strain and CMF alignment in the stretching direction. The breakage and reforming of non-covalent bonding between cell wall polysaccharides was considered to govern cell wall elastic behaviour under subsequent loading. Despite some simplifications in the representation of PCW polysaccharides (CGMD representation, pectin was modelled as a HG due to the lack of other PCW constituents), this model is the most detailed depiction of supramolecular morphology and the tensile behaviour of PCWs to date.
Despite these successes and promising results, the current models are far from complete. The next challenge is to incorporate pectic polysaccharides into future computational models of the PCW. A number of recent studies have indicated an important role of pectin on the mechanical performance and growth of the PCW (Peaucelle, Braybrook & Höfte, 2012; Wolf & Greiner, 2012). Liu, Talbot & Llewellyn (2013) showed that some of the specific polymethyl esterase isoforms were expressed throughout rapid cotton fibre elongation and so may be contributing to cell wall loosening by lowering wall pH and assisting turgor-driven wall extension. The growth enhancement reported for the low-MW Arabidopsis thaliana mutant with a lower molecular weight of HG chains was correlated with increased esterification, reduced crosslinking, and increased aggregation of interfibrillar pectins and weaker HG–CMF interactions (Phyo et al., 2017). Another study with an arabinan-deficient Arabidopsis thaliana mutant indicated an influence of arabinan structures on responsiveness of PCW to an imposed mechanical stress (Verhertbruggen et al., 2013). Haas et al. (2020) reported the presence of pectin nanofilaments in cell walls that possess an intrinsic expansion capacity. Using growth models containing such structures it was shown that a complex plant cell shape can arise from chemically induced local and polarized expansion of the pectin nanofilaments without turgor-driven growth. To take this complexity into account, future models must consider not only the pectin structure itself in unprecedented detail, but also the dynamics of changes in its structure over time. Current cell wall models take into account the presence of only HG at best, thus ignoring the true diversity of pectin. One possible solution to this problem is the application of multiscale and multi-physics modelling (Fish, Wagner & Keten, 2021). With multiscale modelling, the target system is described simultaneously by multiple models at different scales. On the other hand, multi-physics simulations allow capturing different aspects of a physical system such as mechanical stress and fluid dynamics at the same time. Both modelling techniques allow the formulation of models that couple together different scales and modelling techniques, offering new possibilities for modelling complex systems with reasonable accuracy and efficiency. Regardless of the strategy adopted, the initial path has been set and awaits researchers ready to take on this challenge.
V. CONCLUSIONS
- (1)
The primary plant cell wall (PCW) is a complex system whose structure and functions are the subject of ongoing studies. The available and currently widely recognized conceptual models of PCWs facilitate the idealization of this biological system and the interpretation of experimental results. However, their experimental validation is hindered due to a lack of techniques to enable the assessment of individual mechanical contributions of PCW components in planta.
- (2)
The first models of PCW were based on the experience gained by researchers with random fibre networks. Despite achieving considerable successes, their development was ultimately limited by the conceptual assumptions imposed by the applied methodology. An alternative methodology developed at the same time was based on particle dynamics, and due to its flexibility and relatively straightforward implementation, this has led to far more accurate PCW modelling.
- (3)
The role of major wall polysaccharides and mechanisms of hemicellulose and pectin incorporation should be investigated using modern computational methods. Modelling allows for the exploration of conditions that it may not be possible to measure experimentally. Further developments in this field await the extension of current PCW numerical models or approaches that include the molecular backgrounds of cell wall plasticity, elasticity, softening, loosening and the key mechanical and regulatory molecules in order to understand the nature of PCW processes. However, the exploration of spatiotemporal organization, the mechanisms of wall polymer synthesis as well as degradation and cell wall constituent assembly remain a challenge even with the most sophisticated modelling techniques.
ACKNOWLEDGEMENTS
This study was supported by the National Science Centre, Poland (Project no. 2019/35/D/NZ9/00555).




