Bulletin of Economic Research
Early View
RESEARCH ARTICLE
Open Access

How Can Inflation Contracts Discipline Central Bankers When Agents Are Learning?

Marine Charlotte André, 

Marine Charlotte André

CNRS, BETA, Université de Strasbourg, Université de Lorraine, Strasbourg, France

Search for more papers by this author
Meixing Dai, 

Corresponding Author

Meixing Dai

CNRS, BETA, Université de Strasbourg, Université de Lorraine, Strasbourg, France

Search for more papers by this author
First published: 06 June 2025
https://doi.org/10.1111/boer.12503

ABSTRACT

This paper studies, in a new Keynesian model with a positive optimal output gap, how to design linear inflation contracts to shape the central bank's incentive structure when private expectations are based on adaptive learning. In this model, under rational expectations, inflation contracts could only partially deal with the time-inconsistency problem arising from incentives for the central bank to exploit the inflation-output trade-off induced by an “overambitious” output-gap target. This is true even if the government incurs no cost related to such contracts, unlike in the Barro–Gordon framework. When agents are learning, their design should reflect the intertemporal trade-off due to learning such that the optimal inflation penalty rate decreases from the high-level set under optimal discretion and rational expectations and then approaches gradually, but does not equal, the low-level set under optimal limited commitment and rational expectations as the learning gain tends to unity.

1 Introduction

Many empirical studies show that beliefs based on learning, in particular adaptive learning, not only help explain patterns in standard macroeconomic time series but are also consistent with a range of survey data measuring expectations and displaying low-frequency drift.

Most of the theoretical learning literature has focused on evaluating the robustness of rational expectations (RE) policy prescriptions to learning dynamics. Some recent studies have paid attention to the design of optimal monetary policy conditional on such belief structures and explore how learning affects it compared to RE (Gaspar et al. 2006; Molnár and Santoro 2014; André and Dai 2017, 2018, 2023; Eusepi et al. 2018; Mele et al. 2020). Except for Eusepi et al. (2018), they share a common implicit assumption: absent disturbances to the economy, price stability defined as zero inflation is optimal in the long run, meaning that conditional inflation expectations converge to price stability as the forecast horizon extends to the indefinite future. Using a micro-founded loss function affected by steady-state distortions arising from Calvo rigidities and monopolistic competition as in Woodford (1999a, 2003), Eusepi et al. (2018) find that optimal monetary policy delivers a positive inflation rate in the long run, even when the central bank's (CB's) inflation target is set to zero.

This paper revisits the prescriptions for designing optimal linear inflation contracts through the lens of adaptive learning in a theoretical framework built on Molnár and Santoro (2014) and Eusepi et al. (2018). As in Eusepi et al. (2018), due to distortions, price stability is generally not optimal in the long run, even when the CB has a zero inflation target, and both the CB and private agents form RE. Learning dynamics implies that beliefs are slow-moving state variables and constrain what can be achieved by monetary policy, so that commitment and discretion yield the same equilibrium. Thus, we cannot mention the inflation bias when comparing inflation rates under these two policy regimes when agents are learning. The positive inflation rate under learning represents the best the CB can do. However, optimal policy under learning suffers, less than optimal discretionary policy under RE but more than the optimal commitment policy under RE, from an “inflation bias” compared to the inflation target.

Among different settings in which the inflation bias can be addressed, we choose to follow Candel-Sánchez and Campoy-Miñarro (2004). We consider a class of linear inflation contracts where Walsh's (1995) contract is a particular case and assume that the government is able to impose a transfer that cannot be rejected by the CB. The government designs a punishment (or transfer) mechanism, called an inflation contract, to achieve the efficient equilibrium but has to bear a cost due to the transfer payment. This mechanism aims to fight against the inflation bias by providing an incentive, that is, an inflation penalty for missing the inflation goal, for the central banker to limit his short-run opportunism.

As Molnár and Santoro (2014); Eusepi and Preston (2018a), and Eusepi et al. (2018) point out, monetary policy anchoring agents' beliefs based on learning can improve equilibrium outcomes. Policy internalizing the effects of such beliefs induces drifts into the latter and can generate further fluctuations in output and inflation. This requires the CB to act more aggressively against inflation compared to what would be required under the standard RE hypothesis. For García-Cicco (2022), learning behaviors capture the CB's limited credibility. Therefore, when designing optimal inflation contracts, the government should take into account these consequences.

Our main findings are (1) under RE, optimal linear inflation contracts in the new Keynesian model depend on the discount factor and the policy regime (discretion or limited commitment) and cannot fully eliminate the inflation bias when the social welfare loss function displays an “overambitious” output-gap target; (2) adaptive learning significantly affects the design of linear inflation contracts. Departing from the highest penalty rate set under discretion and RE, the government should penalize increasingly less the central banker as belief revisions become more responsive to new data. Inflation penalty gradually approaches, but does not equal, the low optimal level obtained under optimal limited commitment and RE as the learning gain approaches unity.

The underlying mechanism is that learning gives rise to an intertemporal trade-off. It is optimal for the CB to somehow sacrifice stabilizing the output gap in the present in exchange for smaller fluctuations in future expectations to ease agents' learning and hence facilitate future intratemporal trade-offs. The more sensitive private beliefs are to new information (higher learning gain), the less can they be exploited through surprise inflation to achieve the “overambitious” output gap target. This gives a motive for the government to less punish the CB for overshooting the inflation target than under discretion and RE.

Relationship to the literature on time inconsistency

This research is related to a vast literature on time inconsistency pioneered by Kydland and Prescott (1977) and the one on monetary policy delegation initiated by Thompson (1981), Barro and Gordon (1983), and Rogoff (1985). In the early literature, delegation is a way to remove distortions and hence eliminate the average inflation bias, arising from the fact that the CB targets a level of output higher than the socially desirable one. In Lockwood (1997) and Svensson (1997), the state-contingent inflation bias occurs when a lagged term appears in the supply function to capture output (employment) persistence. In such backward-looking models, there is a stabilization bias that refers to the suboptimal reaction to supply shocks in the discretionary equilibrium. Various delegation schemes have been proposed that exactly implement the commitment optimum when the CB operates under discretion. They include the appointment of an independent and conservative central banker (Rogoff 1985; Lohmann 1992), performance contracts (Walsh 1995; Persson and Tabellini 1993), inflation targeting (Svensson 1997), and nominal income growth targeting (Beetsma and Jensen 1999).

This paper contributes to a recent and growing literature studying, under RE, the virtues of such a delegation in forward-looking new Keynesian models. The stabilization bias in such models pertains most prominently to the lack of inertia induced by discretionary policy in response to persistent cost-push shocks. A variety of delegation schemes such as interest-rate smoothing (Woodford 1999a, 2003), nominal income growth (Jensen 2002), output-gap growth (Walsh 2003a), inflation-targeting regimes with the government penalizing the CB for deviating from targets (Walsh 2003b), and price-level targeting (Vestin 2006) can induce inertia and hence improve upon the discretionary equilibrium. When the discretionary CB is delegated with an appropriate objective function different from that of society, it is possible to exactly implement the timeless optimal commitment policy under various delegation schemes, hence completely eliminating the stabilization bias (Bilbiie 2014). An inflation forecast contract, which makes the central banker' remunerations contingent on the precision of his forecasts, may enable the CB to influence inflation expectations more effectively, thus facilitating inflation stabilization (Gersbach and Hahn 2014). In contrast, when agents are adaptively learning, appointing a liberal central banker would be optimal (André and Dai 2017, 2023).

More specifically, our paper belongs to the strand of literature that treats monetary policy delegation as a principal–agent problem and proposes a linear inflation contract to reconcile inflation reduction and stabilization policy while eliminating the inflation bias (Persson and Tabellini 1993; Walsh 1995). The basic idea is that the government, as the principal, designs an optimal incentive scheme for the independent central banker while aiming at obtaining monetary policy outcomes equivalent to those under credible commitment. Generally, such a scheme includes an efficient punishment mechanism that, by sufficiently raising the welfare costs of surprise inflation, counteracts the central banker's tendency to conduct a more accommodative policy under discretion.

Fratianni et al. (1997) compare various institutional arrangements designed to eliminate inflation and stabilization biases and find that CB independence and inflation contracts work best. Candel-Sánchez and Campoy-Miñarro (2004) and Chortareas and Miller (2007) discuss the implications for such contracts when distorting the CB's objective function induces a cost for the government. Several studies examine how inflation contracts are affected by uncertainty about the CB's output target (Muscatelli 1999), its preference weights put on inflation and output stabilization (Beetsma and Jensen 1998; Muscatelli 1998, 1999), its responsiveness to incentive schemes (Chortareas and Miller 2003), or its preference for model robustness (Dai and Spyromitros 2012). Additionally, Chortareas and Miller (2004), Campoy and Negrete (2008), and Ciccarone and Marchetti (2012) explore the issue of common agency when the CB is offered an incentive scheme by an interest group, in addition to the inflation contract. Ewald and Geißler (2017) find that allowing the CB to sell inflation-linked calls provides a mechanism to implement linear inflation contracts. Nakata and Schmidt (2019) find that the linear inflation contract performs quite well compared to the conservatism regime facing an occasionally binding zero lower bound.

Insofar this principal–agent literature is built on the RE hypothesis. Our study differs from previous research by considering that agents are learning. Compared to RE, learning fundamentally changes the way optimal monetary policy is conducted and induces a dependence of optimal inflation contracts on learning gain. The presence of an “overambitious” output-gap target implies that the optimal inflation penalty rate is positive under discretion and RE as well as under learning. The difference is that the intertemporal trade-off introduced by learning pushes the CB to focus more on expectations management to improve future intratemporal trade-offs. This reduces the government's incentive to punish the CB and hence the optimal inflation penalty rate as the learning gain rises. This effect also plays in André and Dai (2017, 2023) who consider the optimal degree of CB conservatism or the design of optimal nonlinear inflation contracts in a framework where there is not an “overambitious” output gap target. Given that the output-gap target is zero, the optimal degree of CB conservatism (inflation penalty rate) is zero under discretion and RE. Learning leads the government to appoint a liberal central banker (negative degree of CB conservatism) or implements nonlinear inflation contracts with a negative inflation penalty rate, and more so as the learning gain rises.

The rest of the paper is organized as follows. The next section sets up the model. Section 3 derives the closed-form RE equilibrium solutions. Section 4 gives the equilibrium solution under constant-gain learning. Section 5 examines the design of optimal inflation contracts while take account learning. Section 6 discusses some extensions. The last section concludes.

2 The Model

This section recapitulates a simple new Keynesian model similar to the standard sticky-price new Keynesian model that has been extensively used in the recent literature on monetary policy (Clarida et al. 1999). The main difference is that we do not introduce labor subsidy to eliminate the distortions due to monopolistic competition.

A representative household maximizes utility
U ( C , N ) = E t ∗ ∑ i = 0 + ∞ β k ϱ t + i C t + i 1 − σ 1 − σ − η N t + i 1 + φ 1 + φ , $$\begin{equation} U(C,N)=E_{t}^{*}\sum _{i=0}^{+\infty }\beta ^{k}{\left[\frac{{\left(\varrho _{t+i}C_{t+i}\right)}^{1-\sigma }}{1-\sigma }-\eta \frac{N_{t+i}^{1+\varphi }}{1+\varphi }\right]},\end{equation}$$ (1)
where β ∈ ( 0 , 1 ) $\beta \in (0,1)$ denotes the subjective intertemporal discount factor, C t $C_{t}$ is the composite consumption, N t $N_{t}$ is the working time, 1 − N t $\left(1-N_{t}\right)$ is the leisure time, σ $\sigma$ is the coefficient of relative risk aversion, and φ > 0 $\varphi >0$ is the inverse of the steady-state Frisch elasticity of labor supply. E t ∗ $E_{t}^{*}$ is the expectation operator, where the asterisk indicates that agents form adaptive learning expectations and its absence signals that they form RE. ϱ t + i $\varrho _{t+i}$ is a stochastic preference parameter with the steady-state value ϱ ¯ = 1 $\overline{\varrho }=1$ .

The composite consumption good C t $C_{t}$ consists of differentiated products of measure 1, that is, C t ≡ ∫ 0 1 C j t ( ε − 1 ) / ε d j ε / ( ε − 1 ) $C_{t}\equiv \left[\int _{0}^{1}C_{jt}^{(\epsilon -1)/\epsilon }dj\right]^{\epsilon /(\epsilon -1)}$ , with good C j $C_{j}$ selling at price P j t $P_{jt}$ . The aggregate price index is given by P t ≡ ∫ 0 1 P j t − ( ε − 1 ) d j 1 / ( 1 − ε ) $P_{t}\equiv \left[\int _{0}^{1}\left(P_{jt}\right)^{-(\epsilon -1)}dj\right]^{1/(1-\epsilon)}$ .

Minimizing the cost of buying C t $C_{t}$ subject to ∫ 0 1 C j t ( ε − 1 ) / ε d j ε / ( ε − 1 ) ≥ C t $\left[\int _{0}^{1}C_{jt}^{(\epsilon -1)/\epsilon }dj\right]^{\epsilon /(\epsilon -1)}\ge C_{t}$ yields
C j t = P j t P t − ε C t , $$\begin{equation} C_{jt}={\left(\frac{P_{jt}}{P_{t}}\right)}^{-\epsilon }C_{t}, \end{equation}$$ (2)
where ε > 1 $\epsilon >1$ stands for the elasticity of substitution between any two varieties of goods.
Given the cost of the composite good, the household optimally chooses C t $C_{t}$ and N t $N_{t}$ by maximizing (1) subject to the budget constraint:
C t + B t P t + T t P t ≤ W t P t N t + 1 + i t − 1 B t − 1 P t + Π t , $$\begin{equation} C_{t}+\frac{B_{t}}{P_{t}}+\frac{T_{t}}{P_{t}}\le \frac{W_{t}}{P_{t}}N_{t}+{\left(1+i_{t-1}\right)}\frac{B_{t-1}}{P_{t}}+\varPi _{t}, \end{equation}$$ (3)
where B t $B_{t}$ is the government bond, i t ${i}_{t}$ is the interest rate and T t $T_{t}$ is lump sum taxes. The household earns nominal wages, W t $W_{t}$ , from working in the productive sector and receives real profits, Π t $\varPi _{t}$ , from firms.
The first-order conditions of the household's maximization problem imply the following Euler equations:
− U N U C = η N t φ ϱ t 1 − σ C t − σ = W t P t . $$\begin{equation} -\frac{U_{N}}{U_{C}}=\frac{\eta N_{t}^{\varphi }}{\varrho _{t}^{1-\sigma }C_{t}^{-\sigma }}=\frac{W_{t}}{P_{t}}. \end{equation}$$ (4)
F t , t + 1 ≡ 1 1 + i t = β E t ∗ ϱ t + 1 ϱ t 1 − σ P t P t + 1 C t + 1 C t − σ . $$\begin{equation} \mathcal {F}_{t,t+1}\equiv \frac{1}{{\left(1+i_{t}\right)}}=\beta E_{t}^{*}{\left[{\left(\frac{\varrho _{t+1}}{\varrho _{t}}\right)}^{1-\sigma }\frac{P_{t}}{P_{t+1}}{\left(\frac{C_{t+1}}{C_{t}}\right)}^{-\sigma }\right]}. \end{equation}$$ (5)
The optimal decision of the household must be consistent with the non-Ponzi game (transversality) condition, that is, lim i → ∞ E t ∗ F t , t + k B t + k = 0 $\underset{i\rightarrow \infty }{\lim }E_{t}^{*}\left(\mathcal {F}_{t,t+k}B_{t+k}\right)=0$ , with F t , t + k = E t ∗ ϱ t + k ϱ t 1 − σ β k P t P t + k C t + k C t − σ $\mathcal {F}_{t,t+k}=E_{t}^{*}\left[\left(\frac{\varrho _{t+k}}{\varrho _{t}}\right)^{1-\sigma }\frac{\beta ^{k}P_{t}}{P_{t+k}}\left(\frac{C_{t+k}}{C_{t}}\right)^{-\sigma }\right]$ . Equation (4) is the intratemporal optimality condition with respect to consumption and leisure that equals the marginal substitution rate between consumption and leisure to real wage. Equation (5) represents the intertemporal condition with respect to bonds and defines the stochastic discount factor F t , t + 1 $\mathcal {F}_{t,t+1}$ .

The supply side of the economy is composed of a continuum of monopolistically competitive firms uniformly distributed over the unit interval and indexed by j ∈ 0 , 1 $j\in \left[0,\thinspace 1\right]$ . The production sector is characterized by nominal rigidities in price setting. The aggregate production is Y t = ∫ 0 1 Y j t ( ε − 1 ) / ε d j ε / ( ε − 1 ) $Y_{t}=\left[\int _{0}^{1}Y_{jt}^{(\epsilon -1)/\epsilon }dj\right]^{\epsilon /(\epsilon -1)}$ , and the production of good j $j$ is given by Y j t = C j t = P j t P t − ε Y t $Y_{jt}=C_{jt}=\left(\frac{P_{jt}}{P_{t}}\right)^{-\epsilon }Y_{t}$ . For simplicity, capital is ignored, so the output is a function solely of labor input N j t $N_{jt}$ and an aggregate stochastic productivity disturbance Z t $Z_{t}$ such that Y j t = Z t N j t $Y_{jt}=Z_{t}N_{jt}$ , with the steady-state value of Z t $Z_{t}$ , that is, Z ¯ $\overline{Z}$ , equal to unity. Aggregating across firms yields Z t N t = Y t ∫ 0 1 P j t P t − ε d j ≡ Y t Ξ t $Z_{t}N_{t}=Y_{t}\int _{0}^{1}\left(\frac{P_{jt}}{P_{t}}\right)^{-\epsilon }dj\equiv Y_{t}\Xi _{t}$ , where N t = ∫ 0 1 N j t d j $N_{t}=\int _{0}^{1}N_{jt}dj$ is the aggregate level of hours worked and Ξ t = ∫ 0 1 P j t P t − ε d j $\Xi _{t}=\int _{0}^{1}\left(\frac{P_{jt}}{P_{t}}\right)^{-\epsilon }dj$ an index of price dispersion over all firms.

Each firm chooses the optimal level of labor demand and enters the labor market. It seeks to minimize total real costs subject to the technological constraint Y j t = Z t N j t $Y_{jt}=Z_{t}N_{jt}$ ,
min N j t δ t 1 − l W t P t N j t + ϕ t Y j t − Z t N j t , $$\begin{equation*} \underset{N_{jt}}{\min }\frac{\delta _{t}{\left(1-l\right)}W_{t}}{P_{t}}N_{jt}+\phi _{t}{\left(Y_{jt}-Z_{t}N_{jt}\right)}, \end{equation*}$$
where l $l$ is the rate at which the government subsidizes the employment and δ t $\delta _{t}$ is a disturbance to the flexible wage. The first-order condition implies the equilibrium real marginal cost M C t $MC_{t}$
ϕ t = δ t 1 − l W t Z t P t ≡ M C t . $$\begin{equation} \phi _{t}=\frac{\delta _{t}{\left(1-l\right)}W_{t}}{Z_{t}P_{t}}\equiv MC_{t}. \end{equation}$$ (6)

In the new Keynesian literature, it is standard to assume that the labor subsidy is set to equate the real wage to the marginal productivity of labor in the steady state, that is, W ¯ P ¯ = 1 $\frac{_{\overline{W}}}{\overline{P}}=1$ . This implies l = ε − 1 $l=\epsilon ^{-1}$ . This rather standard assumption eliminates also the effects of distortions due to monopolistic competition on the micro-founded social welfare function.

To keep the effect of distortions on the micro-founded social welfare function and hence the equilibrium, we assume that the government's labor subsidy is set to zero in this paper.

Nominal rigidities are introduced via Calvo's (1983) staggered price setting where opportunities to adjust occur following an exogenous Poisson process. Each firm optimally updates its price with probability ( 1 − θ ) $(1-\theta)$ in any given period t $t$ by maximizing the expected present discounted value of profits.

When able to set prices optimally, each firm seeks to maximize the expected stream of future dividends, taking into consideration that the chosen price will have to be charged until period t + k $t+k$ with probability θ k $\theta ^{k}$ .

Given the demand curve Y j t = C j t = P j t P t − ε Y t $Y_{jt}=C_{jt}=\left(\frac{P_{jt}}{P_{t}}\right)^{-\epsilon }Y_{t}$ , the j th $j{\rm th}$ firm sets the optimal price P j t ∗ $P_{jt}^{*}$ to maximize the present value of its present and future nominal profits
max P j t ∗ E t ∗ ∑ k = 0 ∞ θ k F t , t + k P j t ∗ P t + k − ε P j t ∗ − P t + k M C t + k Y t + k . $$\begin{equation} \underset{P_{jt}^{*}}{\max }E_{t}^{*}\sum _{k=0}^{\infty }\theta ^{k}\mathcal {F}_{t,t+k}{\left(\frac{P_{jt}^{*}}{P_{t+k}}\right)}^{-\epsilon }{\left(P_{jt}^{*}-P_{t+k}MC_{t+k}\right)}Y_{t+k}. \end{equation}$$ (7)

The larger is the elasticity of substitution ε $\epsilon$ , the smaller the market power for monopolistically competitive firms. For ε → + ∞ $\epsilon \rightarrow +\infty$ , all firms that have the opportunity to update their price will set the same price, that is, P j t ∗ = P t ∗ $P_{jt}^{*}=P_{t}^{*}$ .

Solving (7) while using (5), and the good market clearing condition, that is, C t + k = Y t + k $C_{t+k}=Y_{t+k}$ , we obtain
P j t ∗ P t = ε E t ∗ ∑ k = 0 ∞ θ k β k ϱ t + k ϱ t 1 − σ C t + k 1 − σ M C t + k P t + k P t ε ε − 1 E t ∗ ∑ k = 0 ∞ θ k β k ϱ t + k ϱ t 1 − σ C t + k 1 − σ P t + k P t ε − 1 , $$\begin{equation} \frac{P_{jt}^{*}}{P_{t}}=\frac{\epsilon E_{t}^{*}\sum _{k=0}^{\infty }\theta ^{k}\beta ^{k}{\left(\frac{\varrho _{t+k}}{\varrho _{t}}\right)}^{1-\sigma }{\left(C_{t+k}\right)}^{1-\sigma }MC_{t+k}{\left(\frac{P_{t+k}}{P_{t}}\right)}^{\epsilon }}{{\left(\epsilon -1\right)}E_{t}^{*}\sum _{k=0}^{\infty }\theta ^{k}\beta ^{k}{\left(\frac{\varrho _{t+k}}{\varrho _{t}}\right)}^{1-\sigma }{\left(C_{t+k}\right)}^{1-\sigma }{\left(\frac{P_{t+k}}{P_{t}}\right)}^{\epsilon -1}}, \end{equation}$$ (8)
where ε ε − 1 ≡ μ $\frac{\epsilon }{\epsilon -1}\equiv \mu$ is the steady-state gross markup.
In the limiting case of full price flexibility ( θ = 0 $\theta =0$ ), all firms set their price as a constant markup over nominal marginal costs, that is, P j t ∗ = μ P t M C t > P t M C t $P_{jt}^{*}=\mu P_{t}MC_{t}>P_{t}MC_{t}$ . A standard result in the model of monopolistic competition holds: each firm sets its price P j t ∗ $P_{jt}^{*}$ equal to a markup μ > 1 $\mu >1$ over its nominal marginal cost P t M C t $P_{t}MC_{t}$ . Because price exceeds marginal cost, output will be inefficiently low. When prices are flexible, all firms charge the same price. In this case, P j t ∗ = P t $P_{jt}^{*}=P_{t}$ . As a consequence, under full price flexibility, real marginal costs are constant at their steady-state level M C t = M C ¯ = ε − 1 ε 1 − l $MC_{t}=\overline{MC}=\frac{\epsilon -1}{\epsilon \left(1-l\right)}$ . Using this result in (6) while letting δ t = 1 $\delta _{t}=1$ , and then equaling W t P t $\frac{W_{t}}{P_{t}}$ in (6) and (4), we obtain
W t P t = η N t φ ϱ t 1 − σ C t − σ = ε − 1 ε 1 − l Z t . $$\begin{equation} \frac{W_{t}}{P_{t}}=\frac{\eta N_{t}^{\varphi }}{\varrho _{t}^{1-\sigma }C_{t}^{-\sigma }}=\frac{{\left(\epsilon -1\right)}}{\epsilon {\left(1-l\right)}}Z_{t}. \end{equation}$$ (9)
Substituting C t = Y t $C_{t}=Y_{t}$ and N t = Y t Z t $N_{t}=\frac{Y_{t}}{Z_{t}}$ in the latter and letting Y t f $Y_{t}^{f}$ denote equilibrium output under flexible prices, we obtain
Y t f = 1 η ε − 1 ε 1 − l 1 σ + φ ϱ t 1 − σ σ + φ Z t 1 + δ σ + φ . $$\begin{equation} Y_{t}^{f}=\frac{1}{\eta }{\left[\frac{\epsilon -1}{\epsilon {\left(1-l\right)}}\right]}^{\frac{1}{\sigma +\varphi }}\varrho _{t}^{\frac{1-\sigma }{\sigma +\varphi }}Z_{t}^{\frac{1+\delta }{\sigma +\varphi }}. \end{equation}$$ (10)

When prices are sticky ( θ > 0 $\theta >0$ ), the output can differ from the flexible-price equilibrium level. Equation (8) shows that, whenever a firm has an opportunity to adjust its price, it has to take into account expected future marginal cost as well as current marginal cost.

The aggregate price index is a weighted average of the price charged by the fraction 1 − θ $1-\theta$ of firms setting their price in period t $t$ and the average price of the remaining fraction θ $\theta$ of all firms that do not change their price in period t $t$ . The average price of the nonadjusters is just the aggregate price index of all firms that prevailed in period t − 1 $t-1$ , that is, P t − 1 ≡ ∫ 0 1 P j t − 1 − ( ε − 1 ) d j 1 / ( 1 − ε ) $P_{t-1}\equiv \left[\int _{0}^{1}\left(P_{jt-1}\right)^{-(\epsilon -1)}dj\right]^{1/(1-\epsilon)}$ , given that the adjusting firms were selected randomly among all firms. Hence, the aggregate price index in period t $t$ is
P t 1 − ε = 1 − θ P t ∗ 1 − ε + θ P t − 1 1 − ε . $$\begin{equation} P_{t}^{1-\epsilon }={\left(1-\theta \right)}{\left(P_{t}^{*}\right)}^{1-\epsilon }+\theta P_{t-1}^{1-\epsilon }. \end{equation}$$ (11)
The new Keynesian Phillips curve is obtained by log-linearizing (4), (6), (8), and (11) in the neighborhood of a zero-inflation steady state
π t = β E t ∗ π t + 1 + κ x t + e t , $$\begin{equation} \pi _{t}=\beta E_{t}^{*}\pi _{t+1}+\kappa x_{t}+e_{t}, \end{equation}$$ (12)
where κ = 1 − θ 1 − θ β θ σ + φ $\kappa =\frac{\left(1-\theta \right)\left(1-\theta \beta \right)}{\theta }\left(\sigma +\varphi \right)$ and x t ≡ y ̂ t − y ̂ t f $x_{t}\equiv \hat{y}_{t}-\hat{y}_{t}^{f}$ with y ̂ t f = 1 − σ ϱ ̂ t + 1 + φ z ̂ t σ + φ $\hat{y}_{t}^{f}=\frac{\left(1-\sigma \right)\hat{\varrho }_{t}+\left(1+\varphi \right)\hat{z}_{t}}{\sigma +\varphi }$ . Here, lower case letters with a hat denote percentage deviations of the original variable from its respective steady-state value, for example, y ̂ t = log Y t / Y ¯ $\hat{y}_{t}=\log \left(Y_{t}/\overline{Y}\right)$ , where Y ¯ $\overline{Y}$ is the steady-state value of Y t $Y_{t}$ . This implies that x t ≡ y ̂ t − y ̂ t f = log ( Y t Y ¯ ) − log ( Y t f Y ¯ ) = log ( Y t Y t f ) $x_{t}\equiv \hat{y}_{t}-\hat{y}_{t}^{f}=\log (\frac{Y_{t}}{\overline{Y}})-\log (\frac{Y_{t}^{f}}{\overline{Y}})=\log (\frac{Y_{t}}{Y_{t}^{f}})$ is an output gap that represents the percentage deviation of the current output gap ( Y t $Y_{t}$ ) from the flexible-price equilibrium output ( Y t f $Y_{t}^{f}$ ). The noise e t ≡ δ ̂ t $e_{t}\equiv \hat{\delta }_{t}$ is an independently and identically distributed cost-push shock characterized by e t ∼ N ( 0 , σ e 2 ) $e_{t}\sim \mathcal {N}(0,\,\sigma _{e}^{2})$ . When agents are learning, assuming serially uncorrelated cost-push shocks not only makes the model tractable but is also justified because learning could represent the main cause of inflation persistence (Milani 2007). Moreover, this assumption allows considering the boundary effect of learning on monetary policy since persistent shocks would make inflation and inflation expectations more persistent and would increase the importance of stabilizing inflation expectations (Molnár and Santoro 2014).

As in the literature on inflation contracts, we focus only on the Phillips curve and omit the IS equation in the description of the structural model. We assume that the CB can fully offset the shock in the IS equation by optimally controlling the policy interest rate.

Society's preferences are captured by a quadratic loss function that is a weighted sum of variances of inflation and the output gap and is obtained through a second-order Taylor series approximation to the exact welfare measure (expected household utility)
L t s = 1 2 E t ∑ i = 0 + ∞ β i π t + i 2 + α x t + i − x ∼ 2 , $$\begin{equation} L_{t}^{s}=\frac{1}{2}E_{t}{\textstyle {\textstyle {\displaystyle \sum _{i=0}^{+\infty }}}}\beta ^{i}{\left[\pi _{t+i}^{2}+\alpha {\left(x_{t+i}-\widetilde{x}\right)}^{2}\right]}, \end{equation}$$ (13)
where α = 1 − θ 1 − θ β θ σ + φ ε 1 + ε φ $\alpha =\frac{\left(1-\theta \right)\left(1-\theta \beta \right)}{\theta }\frac{\left(\sigma +\varphi \right)}{\epsilon \left(1+\epsilon \varphi \right)}$ stands for the relative weight placed on output-gap versus inflation stabilization and x ∼ $\widetilde{x}$ is the optimal output gap defined by x ∼ ≡ log Y ¯ ∗ Y ¯ = Ψ σ + φ > 0 $\widetilde{x}\equiv \log \frac{\overline{Y}^{*}}{\overline{Y}}=\frac{\varPsi }{\sigma +\varphi }>0$ with Ψ = 1 − ε l ε 1 − l $\varPsi =\frac{1-\epsilon l}{\epsilon \left(1-l\right)}$ . Here, Y ¯ ∗ $\overline{Y}^{*}$ denotes the efficient level of output. A positive x ∼ $\widetilde{x}$ is equivalent to assume that Y ¯ ∗ $\overline{Y}^{*}$ is at all times a certain number of percentage points above Y ¯ $\overline{Y}$ . Indeed, this makes sense since equilibrium output is smaller than Y ¯ ∗ $\overline{Y}^{*}$ given the distortions resulting from a constant level of market power that the producers of differentiated goods are assumed to have, if an offsetting output subsidy, that is, l = ε − 1 $l=\epsilon ^{-1}$ , is not in place (Woodford 1999a). If the government sets l = ε − 1 $l=\epsilon ^{-1}$ , then we have x ∼ = Ψ σ + φ = 0 $\widetilde{x}=\frac{\varPsi }{\sigma +\varphi }=0$ . Notice that a positive x ∼ $\widetilde{x}$ has the same implications for optimal monetary policy as an overambitious output-gap target in the literature on time inconsistency.
Therefore, an independent CB conducting discretionary policy, as it cares about social welfare, would not avoid the time-inconsistency problem and the associated inflation bias. To mitigate this bias, the government imposes on the CB an inflation contract. The latter stipulates that the CB receives a monetary transfer payment, F $F$ , from the government:
F = τ 0 − τ π t , $$\begin{equation} F=\tau _{0}-\tau \pi _{t},\end{equation}$$ (14)
where τ 0 $\tau _{0}$ is fixed to ensure the CB's participation and τ $\tau$ is the penalty rate the CB would face if it failed to control inflation (Walsh 1995). Such a payment can be considered as either the direct income of the central banker or the CB's budget. The weak aspect of this theoretical scheme emerges with issues induced by its implementation, for example, there is a potential public relations problem if the central banker's income rises following a deflationary recession. For Chortareas and Miller (2010), criticism about its effectiveness and implementability can emerge only under a narrow interpretation of inflation contracts. Indeed, the behavior of central bankers may also be determined by other motives such as altruism towards society, for example, their interest in reducing social welfare losses, and the prestige and possible career opportunities that come with holding office. The results obtained with an inflation contract can be achieved if other components of central bankers' utility such as the chance to be reappointed or the public's perception of their competence depend on inflation performance. Finally, the fact that this institutional arrangement bears little resemblance to policy regimes observed in practice is not a serious theoretical problem because it can serve as a useful tool for better understanding how delegation can affect monetary policy (Bilbiie 2014).
The delegation through the transfer mechanism (14) allows the government to regain some control over how the CB operates, but concurrently, the CB can escape from the government's heavy-handed control that might interfere with the proper conduct of monetary policy (Chortareas and Miller 2010). The CB conducts policy to maximize
U t C B = − 1 2 E t ∑ i = 0 + ∞ β i π t + i 2 + α x t + i − x ∼ 2 − ξ τ 0 − τ π t + i , $$\begin{equation} U_{t}^{CB}=-\frac{1}{2}E_{t}{\textstyle {\textstyle {\displaystyle \sum _{i=0}^{+\infty }}}}\beta ^{i}{\left[\pi _{t+i}^{2}+\alpha {\left(x_{t+i}-\widetilde{x}\right)}^{2}-\xi {\left(\tau _{0}-\tau \pi _{t+i}\right)}\right]}, \end{equation}$$ (15)
subject to (12). The parameter ξ $\xi$ indicates the extent to which the CB cares about the incentive scheme versus social welfare loss. The value of τ 0 $\tau _{0}$ is set such that the participation constraint, u t + i C B ≡ π t + i 2 + α x t + i − x ∼ 2 − ξ τ 0 − τ π t + i ≥ u 0 C B $u_{t+i}^{CB}\equiv \pi _{t+i}^{2}+\alpha \left(x_{t+i}-\widetilde{x}\right)^{2}-\xi \left(\tau _{0}-\tau \pi _{t+i}\right)\ge u_{0}^{CB}$ with u 0 C B $u_{0}^{CB}$ being the reservation utility of the CB, is satisfied. Thus, the CB accepts the inflation contract, which is designed in a way that the higher the penalty rate, the costlier it is for the CB to adjust inflation to achieve the “overambitious” output-gap target. In this paper, we focus on the case where the participation constraint is not binding, that is, u t C B > u 0 C B $u_{t}^{CB}>u_{0}^{CB}$ . The case where this constraint is binding, that is, u t + i C B = u 0 C B $u_{t+i}^{CB}=u_{0}^{CB}$ , implies that the central banker is not offered an additional incentive to accept the contract. Even though the central banker may accept the contract because of the prestige, nonpecuniary benefits or large future pecuniary benefits from serving as a central banker, there is no reason to expect her/him to perform (optimize) with respect to the contract (Chortareas and Miller 2007). Therefore, the binding participation constraint should only be considered as a limit case, showing to which extent the government can reduce τ 0 $\tau _{0}$ .
The government cares about both social welfare and the transfer it pays to the CB. Its utility function is modeled following Candel-Sánchez and Campoy-Miñarro (2004):
U t G = − 1 2 E t ∑ i = 0 + ∞ β i π t + i 2 + α x t + i − x ∼ 2 + ς τ 0 − τ π t + i , $$\begin{equation} U_{t}^{G}=-\frac{1}{2}E_{t}{\textstyle {\textstyle {\displaystyle \sum _{i=0}^{+\infty }}}}\beta ^{i}{\left[\pi _{t+i}^{2}+\alpha {\left(x_{t+i}-\widetilde{x}\right)}^{2}+\varsigma {\left(\tau _{0}-\tau \pi _{t+i}\right)}\right]}, \end{equation}$$ (16)
where ς $\varsigma$ denotes the weight of the transfer payment, considered by the government as a cost. To simplify the modeling, we assume that public expenditures are null. The government is subject to the following budget constraint:
B t = τ 0 − τ t π t + 1 + i t − 1 B t − 1 − T t . $$\begin{equation} {B}_{t}={\tau}_{0}-{\tau}_{t}{\pi}_{t}+\left(1+{i}_{t-1}\right){B}_{t-1}-{T}_{t}. \end{equation}$$ (17)
where the terms τ 0 − τ t π t ${\tau}_{0}-{\tau}_{t} {\pi}_{t}$ represent the transfer to the central banker to give an incentive to the latter to fulfill the objectives defined in the inflation contract.

We assume that the government and the CB form RE. As remarked by Eusepi et al. (2018), such an assumption emphasizes the degree to which imperfect knowledge of households and firms constrains what can be achieved by optimal monetary policy.

The sequence of events is as follows: (1) The government designs a linear inflation contract, taking into account the CB's response to any penalty it may impose. (2) Private agents form expectations. (3) The realization of shocks is known. (4) The CB conducts optimal policy.

3 Rational Expectations Equilibrium

This section provides benchmark equilibria and optimal inflation contracts when the private sector forms RE conditional on information available at time t $t$ . Whether the main results about linear inflation contracts obtained in the Barro–Gordon framework are valid in new Keynesian models is not evident and deserves an investigation.

3.1 Optimal Discretion

Under discretion, the CB does not seek to shape private expectations and maximizes its utility function (15) subject to (12). This gives the optimal inflation-targeting rule:
π t = − α κ x t − x ∼ − 1 2 ξ τ . $$\begin{equation} \pi _{t}=-\frac{\alpha }{\kappa }{\left(x_{t}-\widetilde{x}\right)}-\frac{1}{2}\xi \tau . \end{equation}$$ (18)
The rule (18) yields a “leaning against the wind” policy, that is, the CB should contract demand below capacity to disinflate the economy whenever inflation is above its target. In addition, a positive (instead of zero) penalty rate, by making it more costly for the CB to adjust inflation to achieve the output-gap target, implies a lower output gap.
Under RE, denote the expectation operator by E t $E_{t}$ instead of E t ∗ $E_{t}^{*}$ . For given E t π t + 1 $E_{t}\pi _{t+1}$ , solving (12) and (18) yields the actual laws of motion (ALM) that govern the evolution of π t $\pi _{t}$ and x t $x_{t}$ :
π t = α β α + κ 2 E t π t + 1 + α κ α + κ 2 x ∼ − 1 2 κ 2 α + κ 2 ξ τ + α α + κ 2 e t , $$\begin{eqnarray} \pi _{t} & = & \frac{\alpha \beta }{\alpha +\kappa ^{2}}E_{t}\pi _{t+1}+\frac{\alpha \kappa }{\alpha +\kappa ^{2}}\widetilde{x}-\frac{1}{2}\frac{\kappa ^{2}}{\alpha +\kappa ^{2}}\xi \tau +\frac{\alpha }{\alpha +\kappa ^{2}}e_{t},\end{eqnarray}$$ (19)
x t = − β κ α + κ 2 E t π t + 1 + α α + κ 2 x ∼ − 1 2 κ α + κ 2 ξ τ − κ α + κ 2 e t . $$\begin{eqnarray} x_{t} & = & -\frac{\beta \kappa }{\alpha +\kappa ^{2}}E_{t}\pi _{t+1}+\frac{\alpha }{\alpha +\kappa ^{2}}\widetilde{x}-\frac{1}{2}\frac{\kappa }{\alpha +\kappa ^{2}}\xi \tau -\frac{\kappa }{\alpha +\kappa ^{2}}e_{t}. \end{eqnarray}$$ (20)

The system of Equations (12) and (18) has a unique nonexplosive RE equilibrium solution, called the “minimal state variable” (MSV) solution (McCallum 1983), in terms of state variables e t $e_{t}$ , τ $\tau$ , and x ∼ $\widetilde{x}$ . The solution of π t $\pi _{t}$ takes the form: π t = ζ 0 + ζ 1 e t $\pi _{t}=\zeta _{0}+\zeta _{1}e_{t}$ . Given that e t $e_{t}$ is a serially uncorrelated cost-push shock, it follows that E t e t + 1 = 0 $E_{t}e_{t+1}=0$ and hence E t π t + 1 = ζ 0 + ζ 1 E t e t + 1 = ζ 0 $E_{t}\pi _{t+1}=\zeta _{0}+\zeta _{1}E_{t}e_{t+1}=\zeta _{0}$ . Using the method of undetermined coefficients yields ζ 0 = α κ α ( 1 − β ) + κ 2 x ∼ − 1 2 κ 2 α ( 1 − β ) + κ 2 ξ τ $\zeta _{0}=\frac{\alpha \kappa }{\alpha (1-\beta)+\kappa ^{2}}\widetilde{x}-\frac{1}{2}\frac{\kappa ^{2}}{\alpha (1-\beta)+\kappa ^{2}}\xi \tau$ and ζ 1 = α α + κ 2 $\zeta _{1}=\frac{\alpha }{\alpha +\kappa ^{2}}$ .

Replacing the solution of E t π t + 1 $E_{t}\pi _{t+1}$ into (19) and (20) leads to the RE equilibrium solutions:
π t = α κ α ( 1 − β ) + κ 2 x ∼ − 1 2 κ 2 α ( 1 − β ) + κ 2 ξ τ + α α + κ 2 e t , $$\begin{eqnarray} \pi _{t} & = & \frac{\alpha \kappa }{\alpha (1-\beta)+\kappa ^{2}}\widetilde{x}-\frac{1}{2}\frac{\kappa ^{2}}{\alpha (1-\beta)+\kappa ^{2}}\xi \tau +\frac{\alpha }{\alpha +\kappa ^{2}}e_{t},\end{eqnarray}$$ (21)
x t = α ( 1 − β ) α ( 1 − β ) + κ 2 x ∼ − 1 2 ( 1 − β ) κ α ( 1 − β ) + κ 2 ξ τ − κ α + κ 2 e t . $$\begin{eqnarray} x_{t} & = & \frac{\alpha (1-\beta)}{\alpha (1-\beta)+\kappa ^{2}}\widetilde{x}-\frac{1}{2}\frac{(1-\beta)\kappa }{\alpha (1-\beta)+\kappa ^{2}}\xi \tau -\frac{\kappa }{\alpha +\kappa ^{2}}e_{t}. \end{eqnarray}$$ (22)
These solutions suffer from the classic inflation bias, first identified by Kydland and Prescott (1977). For τ = 0 $\tau =0$ , the long-run inflation rate is not only positive but also substantially higher than under optimal limited commitment and RE (see below). Thus, the inflation-targeting regime is not effective in dealing with the inflation bias caused by the “overambitious” output-gap target.
Under discretion and RE, the inflation bias can be reduced by implementing an optimal inflation contract. Minimizing (16) subject to (21) and (22) yields the optimal inflation penalty rate that positively depends on the “overambitious” output-gap target:
τ | d R E = 2 α β ξ κ 2 + ς α ( 1 − β ) + κ 2 κ ξ ξ α ( 1 − β ) 2 + κ 2 + 2 ς α ( 1 − β ) + κ 2 x ∼ . $$\begin{equation} \tau |_{d}^{RE}=\frac{2\alpha {\left\lbrace \beta \xi \kappa ^{2}+\varsigma {\left[\alpha (1-\beta)+\kappa ^{2}\right]}\right\rbrace} }{\kappa \xi {\left\lbrace \xi {\left[\alpha (1-\beta)^{2}+\kappa ^{2}\right]}+2\varsigma {\left[\alpha (1-\beta)+\kappa ^{2}\right]}\right\rbrace} }\widetilde{x}. \end{equation}$$ (23)
Inserting the optimal τ $\tau$ obtained in (23) into (21) and (22) yields
π t = α κ ( 1 − β ) ξ + ς ξ α ( 1 − β ) 2 + κ 2 + 2 ς α ( 1 − β ) + κ 2 x ∼ + α α + κ 2 e t , $$\begin{eqnarray} \pi _{t} & = & \frac{\alpha \kappa {\left[(1-\beta)\xi +\varsigma \right]}}{\xi {\left[\alpha (1-\beta)^{2}+\kappa ^{2}\right]}+2\varsigma {\left[\alpha (1-\beta)+\kappa ^{2}\right]}}\widetilde{x}+\frac{\alpha }{\alpha +\kappa ^{2}}e_{t},\end{eqnarray}$$ (24)
x t = α ( 1 − β ) ξ ( 1 − β ) + ς ξ α ( 1 − β ) 2 + κ 2 + 2 ς α ( 1 − β ) + κ 2 x ∼ − κ α + κ 2 e t . $$\begin{eqnarray} x_{t} & = & \frac{\alpha (1-\beta){\left[\xi (1-\beta)+\varsigma \right]}}{\xi {\left[\alpha (1-\beta)^{2}+\kappa ^{2}\right]}+2\varsigma {\left[\alpha (1-\beta)+\kappa ^{2}\right]}}\widetilde{x}-\frac{\kappa }{\alpha +\kappa ^{2}}e_{t}. \end{eqnarray}$$ (25)

Thus, under discretion and RE, even an optimal inflation contract cannot fully neutralize the effects of the “overambitious” output-gap target on the equilibrium. This is due to the impatience of agents reflected by a discount factor smaller than unity ( β < 1 $\beta <1$ ) and the fact that the transfer payment enters the government's utility function with a weight ς > 0 $\varsigma >0$ . The impatience of agents is the key to explain why the optimal inflation contract cannot fully offset the effects of distortions on the equilibrium in this new Keynesian model even if ς = 0 $\varsigma =0$ , contrary to what happens in the Barro–Gordon framework. Indeed, a lower β $\beta$ leads the CB to pay less attention to inflation expectations that are a function of steady-state distortions and to be more focused on current inflation stabilization in response to cost-push shock. To avoid an excessive contraction in the output, the government should design an optimal inflation contract that only partially eliminates the inflation bias.

3.2 Optimal Limited Commitment

The equilibrium under optimal discretion is suboptimal compared to the equilibrium under optimal limited commitment. As the commitment in the Barro–Gordon model, the optimal limited commitment is interpreted as commitment to a policy rule that is a linear function of the state variables. More precisely, the CB considers a rule contingent on x ∼ $\widetilde{x}$ , τ $\tau$ , and e t $e_{t}$ for the target variable x t $x_{t}$ :
x t = a x x ∼ + b x τ + c x e t , $$\begin{equation} x_{t}=a_{x}\widetilde{x}+b_{x}\tau +c{}_{x}e_{t}, \end{equation}$$ (26)
where a x $a_{x}$ , b x $b_{x}$ , and c x $c_{x}$ are undetermined coefficients on state variables. Inserting (26) into (12) and iterating forwardly to eliminate inflation expectations yields a solution of π t $\pi _{t}$ with undetermined coefficients. Inserting the assumed solutions of π t $\pi _{t}$ and x t $x_{t}$ into (15) and minimizing the resulting function with respect to a x $a_{x}$ , b x $b_{x}$ , and c x $c_{x}$ . Solving the first-order conditions with the method of undetermined coefficients gives the equilibrium solutions for a given τ $\tau$ :
π t = α κ ( 1 − β ) α ( 1 − β ) 2 + κ 2 x ∼ − 1 2 κ 2 α ( 1 − β ) 2 + κ 2 ξ τ + α α + κ 2 e t , $$\begin{eqnarray} \pi _{t} & = & \frac{\alpha \kappa (1-\beta)}{\alpha (1-\beta)^{2}+\kappa ^{2}}\widetilde{x}-\frac{1}{2}\frac{\kappa ^{2}}{\alpha (1-\beta)^{2}+\kappa ^{2}}\xi \tau +\frac{\alpha }{\alpha +\kappa ^{2}}e_{t},\end{eqnarray}$$ (27)
x t = α ( 1 − β ) 2 α ( 1 − β ) 2 + κ 2 x ∼ − 1 2 κ ( 1 − β ) α ( 1 − β ) 2 + κ 2 ξ τ − κ α + κ 2 e t . $$\begin{eqnarray} x_{t} & = & \frac{\alpha (1-\beta)^{2}}{\alpha (1-\beta)^{2}+\kappa ^{2}}\widetilde{x}-\frac{1}{2}\frac{\kappa (1-\beta)}{\alpha (1-\beta)^{2}+\kappa ^{2}}\xi \tau -\frac{\kappa }{\alpha +\kappa ^{2}}e_{t}. \end{eqnarray}$$ (28)
Substituting these solutions into (16), we find that the government should optimally set
τ | l c R E = 2 α ς 1 − β κ ξ ξ + 2 ς x ∼ . $$\begin{equation} \tau |_{lc}^{RE}=\frac{2\alpha \varsigma {\left(1-\beta \right)}}{\kappa \xi {\left(\xi +2\varsigma \right)}}\text{$\widetilde{x}$.} \end{equation}$$ (29)
Inserting τ $\tau$ given by (29) into (27) and (28) yields
π t = α κ ( 1 − β ) α ( 1 − β ) 2 + κ 2 ξ + ς ξ + 2 ς x ∼ + α α + κ 2 e t , $$\begin{eqnarray} \pi _{t} & = & \frac{\alpha \kappa (1-\beta)}{\alpha (1-\beta)^{2}+\kappa ^{2}}{\left(\frac{\xi +\varsigma }{\xi +2\varsigma }\right)}\widetilde{x}+\frac{\alpha }{\alpha +\kappa ^{2}}e_{t},\end{eqnarray}$$ (30)
x t = α ( 1 − β ) 2 α ( 1 − β ) 2 + κ 2 ξ + ς ξ + 2 ς x ∼ − κ α + κ 2 e t . $$\begin{eqnarray} x_{t} & = & \frac{\alpha (1-\beta)^{2}}{\alpha (1-\beta)^{2}+\kappa ^{2}}{\left(\frac{\xi +\varsigma }{\xi +2\varsigma }\right)}\widetilde{x}-\frac{\kappa }{\alpha +\kappa ^{2}}e_{t}. \end{eqnarray}$$ (31)

Examining the above equilibrium solutions under discretion and these under optimal limited commitment, we can make four observations. First, the optimal long-run inflation rate is positive, as shown in (24) and (30), implying that there are inflation biases compared to the inflation target under both policy regimes. This is due to the “overambitious” output-gap target and the impatience of agents. Moreover, even if the optimal inflation contract is implemented, the best response of the CB given the constraints it faces cannot bring the average inflation to its target under optimal limited commitment according to (30).

Second, the average inflation implied by (21) is higher than that implied by (27) when the penalty rate is zero. Their difference is α β κ 3 α ( 1 − β ) + κ 2 α ( 1 − β ) 2 + κ 2 x ∼ ≡ ϖ x ∼ > 0 $\frac{\alpha \beta \kappa ^{3}}{\left[\alpha (1-\beta)+\kappa ^{2}\right]\left[\alpha (1-\beta)^{2}+\kappa ^{2}\right]}\widetilde{x}\equiv \varpi \widetilde{x}>0$ . To get an idea about the value of ϖ $\varpi$ , we consider the baseline parameter values as follows. Taking one period in the model as a quarter, we set the intertemporal discount factor β $\beta$ equal to 0.99. The inverse of the Frisch elasticity of labor supply, φ $\varphi$ , is set to 0.25, implying an elasticity equal to 4, which is common in the macro-labor literature (Imai and Keane 2004). The relative risk aversion σ $\sigma$ is set to 1 given that it must be close to 1 according to Levy (2025). We set the elasticity of substitution across differentiated goods ε = 2.3 $\epsilon =2.3$ , which is the midpoint estimate between the median elasticity values, 2.5 and 2.1, respectively, obtained by Broda and Weinstein (2006) for the pre-1990 and post-1990 samples on sectoral U.S. data. This calibration of ε $\epsilon$ gives a considerable degree of market power to monopolistically competitive firms. The Calvo probability of price rigidity is set at θ = 0.875 $\theta =0.875$ . Our baseline calibration implies κ = 0.0239 $\kappa =0.0239$ , α = 0.0066 $\alpha =0.0066$ , x ∼ = 0.3478 $\widetilde{x}=0.3478$ , and ϖ = 0.2447 $\varpi =0.2447$ .

Third, if the transfer is not a cost for the government, that is, ς = 0 $\varsigma =0$ , the optimal penalty rate is positive and increases with x ∼ $\widetilde{x}$ under discretion and RE, that is, τ | d R E > 0 $\tau |_{d}^{RE}>0$ , while it is zero under optimal limited commitment and RE, that is, τ | l c R E = 0 $\tau |_{lc}^{RE}=0$ .

Finally, when the discount factor β $\beta$ goes to unity (that is, the Barro–Gordon case), price stability, with an average inflation equal to zero, is optimal in the long run under optimal commitment and RE without the need of implementing an optimal inflation contract given that the optimal penalty rate is τ | l c R E = 0 $\tau |_{lc}^{RE}=0$ for any ς $\varsigma$ , while there is an inflation bias under discretion and RE as shown in (24), implying τ | d R E > 0 $\tau |_{d}^{RE}>0$ for any ς $\varsigma$ .

Proposition 1.In the new Keynesian model, optimal inflation penalty rates given by (23) under optimal discretion and (29) under optimal limited commitment cannot fully eliminate the inflation bias induced by an “overambitious” output-gap target even if ς = 0 $\varsigma =0$ . The inflation bias and the optimal inflation penalty rate depend on the intertemporal discount factor and policy regimes.

Proof.Comparing average inflation rates obtained using (24) and (30) with the zero inflation target yields strictly positive inflation biases for ς ≥ 0 $\varsigma \ge 0$ , that is, α κ ( 1 − β ) ξ + ς ξ α ( 1 − β ) 2 + κ 2 + 2 ς α ( 1 − β ) + κ 2 x ∼ > 0 $\frac{\alpha \kappa \left[(1-\beta)\xi +\varsigma \right]}{\xi \left[\alpha (1-\beta)^{2}+\kappa ^{2}\right]+2\varsigma \left[\alpha (1-\beta)+\kappa ^{2}\right]}\widetilde{x}>0$ under optimal discretion and α κ ( 1 − β ) α ( 1 − β ) 2 + κ 2 ξ + ς ξ + 2 ς x ∼ > 0 $\frac{\alpha \kappa (1-\beta)}{\alpha (1-\beta)^{2}+\kappa ^{2}}\left(\frac{\xi +\varsigma }{\xi +2\varsigma }\right)\widetilde{x}>0$ under optimal limited commitment. Setting β = 1 $\beta =1$ in (23) and (29) leads to the optimal inflation penalty rate in the static Barro–Gordon framework, that is, τ = 2 α ξ + ς κ ξ ξ + 2 ς x ∼ $\tau =\frac{2\alpha \left(\xi +\varsigma \right)}{\kappa \xi \left(\xi +2\varsigma \right)}\widetilde{x}$ under discretion, which fully eliminates the inflation bias only if ς = 0 $\varsigma =0$ , or τ = 0 $\tau =0$ under optimal (limited) commitment, meaning that inflation contracts are not necessary. □ $\Box$

The analysis of this section shows that the results of Candel-Sánchez and Campoy-Miñarro (2004) and Chortareas and Miller (2007) obtained in the Barro–Gordon framework are only partially valid in the new Keynesian model with a positive optimal output gap.

For Candel-Sánchez and Campoy-Miñarro (2004), the Walsh (linear inflation) contract is not the best choice for the government when the payment to the CB represents a cost for it and the fixed part of the transfer scheme ( τ 0 $\tau _{0}$ ) is a given constant ensuring that the participation constraint is not binding. However, if τ 0 $\tau _{0}$ is chosen as in Chortareas and Miller (2007), the Walsh's contracts are optimal after all in the Barro–Gordon framework. The discussions in Section 6 show that this is not true in the new Keynesian model under RE or adaptive learning expectations.

4 Equilibrium With Constant-Gain Learning

Private agents use more likely constant-gain (CG) learning algorithms if they believe in possible future structural changes (Evans and Honkapohja 2009). From the perspective of the CB, there are no forward-looking variables in the constraints imposed on its policy as beliefs become low-frequency variables. Therefore, the commitment is useless because private agents ignore any forward guidance that is effective in anchoring RE under commitment. As the learning equilibrium without an “overambitious” output-gap target is extensively studied by Molnár and Santoro (2014), we focus here on the difference introduced by the “overambitious” output-gap target and linear inflation contracts.

4.1 Learning Algorithm

Forming RE requires a massive amount of information that would be beyond the information-processing capacity of private agents. Based on the idea that they have limited rationality, we adopt here a more realistic assumption considering that they operate as econometricians and produce forecasts using a learning algorithm as in Marcet and Nicolini (2003) and Molnár and Santoro (2014). Ignoring both the market mechanisms determining the equilibrium aggregate prices and quantities and the prevailing policy regime, they have a limited knowledge of the process governing the evolution of endogenous variables. They focus only on their own objectives and constraints, and the realization of aggregate variables that are exogenous to their decision problems. To improve their decisions under learning, they estimate and recursively use a perceived law of motion (PLM) of aggregate variables in the terminology of Evans and Honkapohja (2001), which is consistent with the law of motion that the CB would implement under RE, by using the following algorithm:
E t ∗ π t + 1 ≡ a t = a t − 1 + γ t π t − 1 − a t − 1 , $$\begin{eqnarray} E_{t}^{*}\pi _{t+1} & \equiv & a_{t}=a_{t-1}+\gamma _{t}{\left(\pi _{t-1}-a_{t-1}\right)}, \end{eqnarray}$$ (32)
where γ t ∈ ( 0 , 1 ) $\gamma _{t}\in (0,1)$ is the learning gain or the weight on past inflation. The higher is γ t $\gamma _{t}$ , the more beliefs are revised in response to short-run forecast errors. The algorithm (32) implies that, when agents are learning, they do not believe in the CB's announcements. We can assume that private agents use a learning algorithm similar to Equation (32) to form output-gap expectations. However, the latter do not explicitly appear in the equilibrium solution given that we adopt the Euler equation approach as Molnár and Santoro (2014) and do not explicitly derive the optimal interest rate rule.

The Euler equation approach starts from the log-linearized equations obtained under RE. It posits that only one-period-ahead expectations matter for spending and pricing decision rules. Under this approach, the optimal policy delivers divine coincidence, that is, disturbances to the IS equation are fully stabilized.

4.2 Optimal Monetary Policy Rule

Learning dynamics gives rise to an intertemporal trade-off between current and future inflation stabilization that is absent under discretion and RE, making it possible for the CB to manipulate private expectations in the sense of Molnár and Santoro (2014). The CB exactly knows the learning algorithm (32) and rationally takes into account its own ability to affect the evolution of private beliefs. This assumption, despite being quite strong, allows assessing how the CB's policy decision could change if agents depart from full rationality.

The Lagrangian of the CB's optimization problem is
L t C B = E t ∑ i = 0 + ∞ β i 1 2 α x t + i − x ∼ 2 + π t + i 2 − ξ τ 0 − τ π t + i − λ 1 , t + i π t + i − β a t + i − κ x t + i − e t + i − λ 2 , t + i a t + i + 1 − a t + i − γ t + i + 1 ( π t + i − a t + i ) , $$\begin{eqnarray*} \mathcal {L}_{t}^{CB} & = & E_{t}{\textstyle {\textstyle {\displaystyle \sum _{i=0}^{+\infty }}}\beta ^{i}{\left\lbrace \frac{1}{2}{\left[\alpha {\left(x_{t+i}-\widetilde{x}\right)}^{2}+\pi _{t+i}^{2}-\xi {\left(\tau _{0}-\tau \pi _{t+i}\right)}\right]}\right.}}\\ & & -\lambda _{1,t+i}{\left[\pi _{t+i}-\beta a_{t+i}-\kappa x_{t+i}-e_{t+i}\right]}\\ & & {\left.-\lambda _{2,t+i}{\left[a_{t+i+1}-a_{t+i}-\gamma _{t+i+1}(\pi _{t+i}-a_{t+i})\right]}\right\rbrace}, \end{eqnarray*}$$
where λ i , t $\lambda _{i,t}$ with i = 1 , 2 $i=1,\nobreakspace 2$ are Lagrange multipliers associated with (12) and (32), respectively. Compared to the RE benchmark, the CB has to derive an additional first-order condition with respect to inflation expectations. Differentiating the Lagrangian with respect to x t $x_{t}$ , a t + 1 $a_{t+1}$ and π t $\pi _{t}$ yields:
α x t − x ∼ + κ λ 1 , t = 0 , $$\begin{eqnarray} & & \alpha {\left(x_{t}-\widetilde{x}\right)}+\kappa \lambda _{1,t}=0,\end{eqnarray}$$ (33)
λ 2 , t − β β λ 1 , t + 1 + 1 − γ t + 2 λ 2 , t + 1 = 0 , $$\begin{eqnarray} & & \lambda _{2,t}-\beta {\left[\beta \lambda _{1,t+1}+{\left(1-\gamma _{t+2}\right)}\lambda _{2,t+1}\right]}=0,\end{eqnarray}$$ (34)
π t + 1 2 ξ τ − λ 1 , t + γ t + 1 λ 2 , t = 0 . $$\begin{eqnarray} & & \pi _{t}+\frac{1}{2}\xi \tau -\lambda _{1,t}+\gamma _{t+1}\lambda _{2,t}=0. \end{eqnarray}$$ (35)
Substituting λ 1 , t $\lambda _{1,t}$ given by (33) and γ t + 1 $\gamma _{t+1}$ by γ $\gamma$ into (35), we get the optimal inflation targeting rule under the CG learning:
π t = − α κ x t − x ∼ − 1 2 ξ τ − γ λ 2 , t . $$\begin{equation} \pi _{t}=-\frac{\alpha }{\kappa }{\left(x_{t}-\widetilde{x}\right)}-\frac{1}{2}\xi \tau -\gamma \lambda _{2,t}. \end{equation}$$ (36)
In rule (36), the Lagrange multiplier on (32), that is, λ 2 , t $\lambda _{2,t}$ , determines the CB's choice when addressing the intertemporal trade-off. When γ = 0 $\gamma =0$ , private expectations are not updated so that the CB cannot influence them and the rule (36) turns out to be identical to (18), which is the optimality condition for setting monetary policy under discretion and RE.

The rule (36) reconciles the intratemporal trade-off between stabilizing inflation versus the output gap already present under RE and the intertemporal trade-off due to learning. The term γ λ 2 , t $\gamma \lambda _{2,t}$ in (36), capturing the policy implication of learning inflation expectations ( a t $a_{t}$ ), distinguishes the optimal discretionary policy under learning from its counterpart under RE. According to (32) and (34), γ $\gamma$ captures the marginal effect of π t $\pi _{t}$ on a t + 1 $a_{t+1}$ , and λ 2 , t $\lambda _{2,t}$ the marginal welfare effect of a t + 1 $a_{t+1}$ . For γ > 0 $\gamma >0$ , the sign of λ 2 , t $\lambda _{2,t}$ depends on the value of a t + 1 $a_{t+1}$ . The “overambitious” output-gap target implies that the steady-state inflation under CG optimal policy is positive, that is, π ¯ > 0 $\overline{\pi }>0$ , even though the inflation target is zero. However, a t $a_{t}$ could be positive or negative, depending on the nature of past shocks, although an “overambitious” output-gap target makes a t $a_{t}$ more likely to be positive than negative. An increase in a t $a_{t}$ , if a t > π ¯ $a_{t}>\overline{\pi }$ , drives a t $a_{t}$ further away from the steady-state inflation and hence reduces social welfare, implying that λ 2 , t $\lambda _{2,t}$ is positive, and, if a t < π ¯ $a_{t}<\overline{\pi }$ , has the opposite effects. An increase in π t $\pi _{t}$ raises a t + 1 $a_{t+1}$ with its welfare effects depending on the sign of λ 2 , t $\lambda _{2,t}$ . Thus, the term γ λ 2 , t $\gamma \lambda _{2,t}$ in (36) shows how the CB exploits the intertemporal trade-off to steer future inflation expectations via the learning algorithm (32) by influencing π t $\pi _{t}$ .

As the rule (18), the rule (36) also yields a “leaning against the wind” policy. Its stance can be reinforced or attenuated by learning, depending on the sign of λ 2 , t $\lambda _{2,t}$ . For γ > 0 $\gamma >0$ , when inflation expectations are positive such so that a t > π ¯ $a_{t}>\overline{\pi }$ and hence λ 2 , t > 0 $\lambda _{2,t}>0$ , the CB responds by an optimal contraction of x t $x_{t}$ that is harsher than under discretion and RE.

Substituting λ 2 , t $\lambda _{2,t}$ and λ 2 , t + 1 $\lambda _{2,t+1}$ determined by (36) and λ 1 , t + 1 $\lambda _{1,t+1}$ deduced from (33) into (34) yields the optimal policy rule exploiting both intratemporal and intertemporal trade-offs:
π t + α κ x t − x ∼ = β 1 − γ ( 1 − β ) E t π t + 1 + α κ E t x t + 1 − x ∼ − γ β 2 E t π t + 1 − 1 2 1 − β 1 − γ ξ τ = − ∑ k = 1 + ∞ γ β 2 β 1 − γ ( 1 − β ) k − 1 E t π t + k − 1 2 1 − β 1 − γ 1 − β 1 − γ ( 1 − β ) ξ τ , $$\begin{eqnarray} \pi _{t}+\frac{\alpha }{\kappa }{\left(x_{t}-\widetilde{x}\right)} & = & \beta {\left[1-\gamma (1-\beta)\right]}{\left[E_{t}\pi _{t+1}+\frac{\alpha }{\kappa }{\left(E_{t}x_{t+1}-\widetilde{x}\right)}\right]} \nonumber\\ && -\,\gamma \beta ^{2}E_{t}\pi _{t+1}-\frac{1}{2}{\left[1-\beta {\left(1-\gamma \right)}\right]}\xi \tau \nonumber \\ & = & -\sum _{k=1}^{+\infty }\gamma \beta ^{2}{\left\lbrace \beta {\left[1-\gamma (1-\beta)\right]}\right\rbrace} ^{k-1}E_{t}\pi _{t+k}\nonumber \\ && -\, \frac{1}{2}\frac{1-\beta {\left(1-\gamma \right)}}{1-\beta {\left[1-\gamma (1-\beta)\right]}}\xi \tau, \end{eqnarray}$$ (37)
where two transversality conditions are imposed, that is, lim k → + ∞ β 1 − γ ( 1 − β ) k E t π t + k = 0 $\underset{k\rightarrow +\infty }{\lim }\left\lbrace \beta \left[1-\gamma (1-\beta)\right]\right\rbrace ^{k}E_{t}\pi _{t+k}=0$ and lim k → + ∞ β 1 − γ ( 1 − β ) k E t x t + k = 0 $\underset{k\rightarrow +\infty }{\lim }\left\lbrace \beta \left[1-\gamma (1-\beta)\right]\right\rbrace ^{k} E_{t}x_{t+k}=0$ . In other words, if the steady-state value of E t π t + k $E_{t}\pi _{t+k}$ and E t x t + k $E_{t}x_{t+k}$ for k → + ∞ $k\rightarrow +\infty$ is different from zero, we assume that it is not exceedingly large. The absence of E t x t + k $E_{t}x_{t+k}$ for k > 1 $k>1$ in the sum at the right of (37) means that the CB does not have to specifically care about managing future output-gap expectations. The success of CG optimal policy only depends on the CB's success in managing future inflation expectations.

The rule (37) shows that the more sensitive are agents' beliefs to new information (higher γ $\gamma$ ), the less their beliefs can be exploited to improve current macroeconomic performance, because surprise inflation induces larger adverse shifts in future intratemporal inflation-output trade-offs, that is, the coefficient on E t π t + i $E_{t}\pi _{t+i}$ in the sum at the right of (37) becomes larger as γ $\gamma$ rises. The implied intertemporal trade-off pushes the CB to focus more on managing future inflation beliefs to improve future intratemporal trade-offs at the price of deteriorating the current intratemporal trade-off.

Proposition 2.A rise in γ $\gamma$ deteriorates the current intratemporal inflation-output trade-off and makes the inflation penalty more effective in improving current inflation stabilization.

Proof.The optimal intratemporal trade-off condition is π t + α κ x t − x ∼ = 0 $\pi _{t}+\frac{\alpha }{\kappa }\left(x_{t}-\widetilde{x}\right)=0$ under discretion and RE. According to (37), learning induces a deviation from the previous rule measured by H ≡ − ∑ i = 1 + ∞ γ β 2 β 1 − γ ( 1 − β ) i − 1 E t π t + i − 1 − β 1 − γ 2 1 − β 1 − γ ( 1 − β ) ξ τ $\mathcal {H}\equiv -\sum _{i=1}^{+\infty }\gamma \beta ^{2}\left\lbrace \beta \left[1-\gamma (1-\beta)\right]\right\rbrace ^{i-1}E_{t}\pi _{t+i}-\frac{1-\beta \left(1-\gamma \right)}{2\left\lbrace 1-\beta \left[1-\gamma (1-\beta)\right]\right\rbrace }\xi \tau$ . For constant E t π t + i $E_{t}\pi _{t+i}$ , ∀ i $\forall i$ , and τ $\tau$ , we get H ≡ − γ β 2 1 − β 1 − γ ( 1 − β ) E t π t + i − 1 − β 1 − γ 2 1 − β 1 − γ ( 1 − β ) ξ τ $\mathcal {H}\equiv -\frac{\gamma \beta ^{2}}{1-\beta \left[1-\gamma (1-\beta)\right]}E_{t}\pi _{t+i}-\frac{1-\beta \left(1-\gamma \right)}{2\left\lbrace 1-\beta \left[1-\gamma (1-\beta)\right]\right\rbrace }\xi \tau$ , and ∂ H ∂ E t π t + i ∂ γ = − β 2 1 − β 1 − β 1 − γ ( 1 − β ) 2 < 0 $\frac{\partial \mathcal {H}}{\partial E_{t}\pi _{t+i}\partial \gamma }=\frac{-\beta ^{2}\left(1-\beta \right)}{\left\lbrace 1-\beta \left[1-\gamma (1-\beta)\right]\right\rbrace ^{2}}<0$ and ∂ 2 H ∂ τ ∂ γ = − β 2 1 − β 2 1 − β 1 − γ ( 1 − β ) 2 < 0 $\frac{\partial ^{2}\mathcal {H}}{\partial \tau \partial \gamma }=\frac{-\beta ^{2}\left(1-\beta \right)}{2\left\lbrace 1-\beta \left[1-\gamma (1-\beta)\right]\right\rbrace ^{2}}<0$ . Thus, a rise in γ $\gamma$ for constant E t π t + i $E_{t}\pi _{t+i}$ and τ $\tau$ implies a greater deviation from the optimal intratemporal trade-off condition under discretion and RE, deteriorating thus the current intratemporal trade-off. □ $\Box$

For an equal rise in E t π t + i $E_{t}\pi _{t+i}$ for any i $i$ , denoted by ▵ E t π t + i $\triangle E_{t}\pi _{t+i}$ , the change in the first term at the right side of (37) is − γ β 2 1 − β 1 − γ ( 1 − β ) ▵ E t π t + i $\frac{-\gamma \beta ^{2}}{1-\beta \left[1-\gamma (1-\beta)\right]}\triangle E_{t}\pi _{t+i}$ . Thus current inflation or/and output gap must be reduced to ensure that the rule (37) is respected. Since the composite coefficient on ▵ E t π t + i $\triangle E_{t}\pi _{t+i}$ , that is, − γ β 2 1 − β 1 − γ ( 1 − β ) < 0 $\frac{-\gamma \beta ^{2}}{1-\beta \left[1-\gamma (1-\beta)\right]}<0$ , decreases with γ $\gamma$ , a higher γ $\gamma$ implies a further deterioration in the current intratemporal trade-off. As it becomes more difficult to exploit private beliefs for a better current macroeconomic performance, the CB would focus more on managing expectations to ease future intratemporal trade-offs.

The composite coefficient on τ $\tau$ in (37), that is, − 1 2 1 − β 1 − γ 1 − β 1 − γ ( 1 − β ) < 0 $-\frac{1}{2}\tfrac{1-\beta \left(1-\gamma \right)}{1-\beta \left[1-\gamma (1-\beta)\right]}<0$ , decreases with γ $\gamma$ , meaning that learning with higher gains reinforces the effect of inflation penalty on the CB's incentive to fight inflation.

The Phillips curve (12), the learning algorithms (32), and the targeting rule (37) fully characterize the CG learning equilibrium.

4.3 The ALMs for Endogenous Variables

Equations (12), (32), and (37) are solved following the methodology of Molnár and Santoro (2014). There are four relevant state variables, that is, a t $a_{t}$ , x ∼ $\widetilde{x}$ , τ $\tau$ , and e t $e_{t}$ . Under CG learning, inflation expectations ( a t $a_{t}$ ) become state variables because they depend on past values of inflation and hence on past cost-push shocks. Looking for the MSV solution while excluding bubbles and sunspots, we find that there exists a unique nonexplosive (E-stable and learnable) equilibrium solution to the CB's control problem (Appendix B.1).

The ALM for inflation corresponding to the E-stable equilibrium is given by
π t = c π c g a t + Ω π c g x ∼ + 𝛩 π c g ξ τ + d π c g e t , $$\begin{equation} \pi _{t}=c_{\pi }^{cg}a_{t}+\varOmega _{\pi }^{cg}\widetilde{x}+\varTheta _{\pi }^{cg}\xi \tau +d_{\pi }^{cg}e_{t}, \end{equation}$$ (38)
where c π c g $c_{\pi }^{cg}$ verifies p 1 c π c g + p 2 ( c π c g ) 2 = − p 0 $p_{1}c_{\pi }^{cg}+p_{2}(c_{\pi }^{cg})^{2}=-p_{0}$ , and
c π c g = c π c g γ = − p 1 − p 1 2 − 4 p 2 p 0 2 p 2 > 0 , $$\begin{eqnarray} c_{\pi }^{cg} & = & c_{\pi }^{cg}{\left(\gamma \right)}=\frac{-p_{1}-\sqrt {p_{1}^{2}-4p_{2}p_{0}}}{2p_{2}}>0,\end{eqnarray}$$ (39)
d π c g = d π c g γ = α Φ ( γ ) + β α 1 − γ ( 1 − β ) + κ 2 1 − γ > 0 , $$\begin{eqnarray} d_{\pi }^{cg} & = & d_{\pi }^{cg}{\left(\gamma \right)}=\dfrac{\alpha }{\varPhi (\gamma)+\beta {\left\lbrace \alpha {\left[1-\gamma (1-\beta)\right]}+\kappa ^{2}{\left(1-\gamma \right)}\right\rbrace} }>0,\end{eqnarray}$$ (40)
Ω π c g = Ω π c g γ = α κ 1 − β 1 − γ 1 − β Φ ( γ ) > 0 , $$\begin{eqnarray} \varOmega _{\pi }^{cg} & = & \varOmega _{\pi }^{cg}{\left(\gamma \right)}=\frac{\alpha \kappa {\left\lbrace 1-\beta {\left[1-\gamma {\left(1-\beta \right)}\right]}\right\rbrace} }{\varPhi (\gamma)}>0,\end{eqnarray}$$ (41)
𝛩 π c g = 𝛩 π c g γ = − 1 2 κ 2 1 − β 1 − γ Φ ( γ ) < 0 . $$\begin{eqnarray} \varTheta _{\pi }^{cg} & = & \varTheta _{\pi }^{cg}{\left(\gamma \right)}=-\frac{1}{2}\frac{\kappa ^{2}{\left[1-\beta {\left(1-\gamma \right)}\right]}}{\varPhi (\gamma)}<0. \end{eqnarray}$$ (42)
Composite coefficients in (39)–(42) are defined as
Φ ( γ ) = α 1 − β 1 − γ ( 1 − β ) 1 − γ β − c π c g + κ 2 1 − β 1 − γ 1 + γ c π c g > 0 , p 0 = α β 1 − β ( 1 − γ ) 1 − γ ( 1 − β ) > 0 , p 1 = − κ 2 1 − β ( 1 − γ ) − α ( 1 − β ) 1 − β 1 − γ ( 1 − β ) − p 0 − p 2 < 0 , p 2 = γ β α 1 − γ ( 1 − β ) + κ 2 1 − γ > 0 . $$\begin{eqnarray*} \varPhi (\gamma) & = & \alpha {\left\lbrace 1-\beta {\left[1-\gamma (1-\beta)\right]}{\left[1-\gamma {\left(\beta -c_{\pi }^{cg}\right)}\right]}\right\rbrace} \\&& +\,\kappa ^{2}{\left\lbrace 1-\beta {\left(1-\gamma \right)}{\left(1+\gamma c_{\pi }^{cg}\right)}\right\rbrace} >0,\\ p_{0} & = & \alpha \beta {\left\lbrace 1-\beta (1-\gamma){\left[1-\gamma (1-\beta)\right]}\right\rbrace} >0,\\ p_{1} & = & -\kappa ^{2}{\left[1-\beta (1-\gamma)\right]}-\alpha (1-\beta){\left\lbrace 1-\beta {\left[1-\gamma (1-\beta)\right]}\right\rbrace}\\ && -\, p_{0}-p_{2}<0,\\ p_{2} & = & \gamma \beta {\left\lbrace \alpha {\left[1-\gamma (1-\beta)\right]}+\kappa ^{2}{\left(1-\gamma \right)}\right\rbrace} >0. \end{eqnarray*}$$
If γ = 0 $\gamma =0$ , inflation expectations are not revised ( a t = a t − 1 $a_{t}=a_{t-1}$ ) and inflation persistence disappears. We have
c π c g 0 = α β α + κ 2 , d π c g 0 = α α + κ 2 , Ω π c g 0 = α κ α + κ 2 , 𝛩 π c g 0 = − 1 2 κ 2 α + κ 2 . $$\begin{eqnarray} c_{\pi }^{cg}{\left(0\right)} &=& \dfrac{\alpha \beta }{\alpha +\kappa ^{2}},\,\,\,\,d_{\pi }^{cg}{\left(0\right)}=\dfrac{\alpha }{\alpha +\kappa ^{2}},\,\,\,\,\varOmega _{\pi }^{cg}{\left(0\right)}=\frac{\alpha \kappa }{\alpha +\kappa ^{2}},\,\,\,\,\varTheta _{\pi }^{cg}{\left(0\right)}\nonumber\\ && =-\frac{1}{2}\frac{\kappa ^{2}}{\alpha +\kappa ^{2}}. \end{eqnarray}$$ (43)
When the learning gain goes to zero, the feedback coefficients in the ALM for inflation are given in (43) and equal their corresponding ones in (19) obtained under discretion and RE. When the learning gain goes to zero, the learning equilibrium just makes a one-shot adjustment following a shock and does not exhibit inflation and output-gap persistence. This is because, as inflation expectations are not adjusted, their initial value should be set to the level in the RE equilibrium. Otherwise, the economy will not converge to its steady-state equilibrium. In this case, the CB's best policy is not to implement the limited commitment equilibrium under RE, not even asymptotically, but instead to help people find the discretionary RE equilibrium. Thus, the learning equilibrium with a learning gain equal to zero could suffer from similar problems as the discretionary RE equilibrium.
As γ $\gamma$ deviates from zero, inertia in inflation arises and the learning equilibrium is increasingly closer, in the steady state, to the RE equilibrium under limited commitment. For γ = 1 $\gamma =1$ , that is, inflation expectations are static with a t = π t − 1 $a_{t}=\pi _{t-1}$ , meaning that past inflation becomes the only determinant of private inflation expectations. The feedback coefficients in (38) become
c π c g 1 = κ 2 + α + α β 3 − κ 2 + α + α β 3 2 − 4 α 2 β 3 2 α β 2 , $$\begin{eqnarray} c_{\pi }^{cg}{\left(1\right)} & = & \frac{\kappa ^{2}+\alpha +\alpha \beta ^{3}-\sqrt {{\left(\kappa ^{2}+\alpha +\alpha \beta ^{3}\right)}^{2}-4\alpha ^{2}\beta ^{3}}}{2\alpha \beta ^{2}},\end{eqnarray}$$ (44)
d π c g 1 = α α + κ 2 − α β 2 1 − β − c π c g 1 , $$\begin{eqnarray} d_{\pi }^{cg}{\left(1\right)} & = & \dfrac{\alpha }{\alpha +\kappa ^{2}-\alpha \beta ^{2}{\left\lbrace 1-{\left[\beta -c_{\pi }^{cg}{\left(1\right)}\right]}\right\rbrace} },\end{eqnarray}$$ (45)
Ω π c g 1 = α κ 1 − β 2 α + κ 2 − α β 2 1 − β − c π c g 1 , $$\begin{eqnarray} \varOmega _{\pi }^{cg}{\left(1\right)} & = & \frac{\alpha \kappa {\left(1-\beta ^{2}\right)}}{\alpha +\kappa ^{2}-\alpha \beta ^{2}{\left\lbrace 1-{\left[\beta -c_{\pi }^{cg}{\left(1\right)}\right]}\right\rbrace} },\end{eqnarray}$$ (46)
𝛩 π c g 1 = − 1 2 κ 2 α + κ 2 − α β 2 1 − β − c π c g 1 . $$\begin{eqnarray} \varTheta _{\pi }^{cg}{\left(1\right)} & = & -\frac{1}{2}\frac{\kappa ^{2}}{\alpha +\kappa ^{2}-\alpha \beta ^{2}{\left\lbrace 1-{\left[\beta -c_{\pi }^{cg}{\left(1\right)}\right]}\right\rbrace} }. \end{eqnarray}$$ (47)

The feedback coefficients given by (44)–(47) imply a steady-state equilibrium that is only very close, but not identical, to the one obtained under optimal commitment and RE. Indeed, as γ → 1 $\gamma \rightarrow 1$ , for the baseline parameter values, the feedback coefficient on x ∼ $\widetilde{x}$ in the ALM for inflation (38) in the steady state, that is, Ω π c g 1 − c π c g $\frac{\varOmega _{\pi }^{cg}}{1-c_{\pi }^{cg}}$ , equals 0.0055, compared to 0.0028 under limited commitment and RE.

Replacing π t $\pi _{t}$ given by (38) and E t ∗ π t + 1 ≡ a t $E_{t}^{*}\pi _{t+1}\equiv a_{t}$ into (12) yields the ALM for the output gap:
x t = c x c g a t + Ω x c g x ∼ + 𝛩 x c g ξ τ + d x c g e t , $$\begin{equation} x_{t}=c_{x}^{cg}a_{t}+\varOmega _{x}^{cg}\widetilde{x}+\varTheta _{x}^{cg}\xi \tau +d_{x}^{cg}e_{t}, \end{equation}$$ (48)
where c x c g = − 1 κ β − c π c g $c_{x}^{cg}=-\frac{1}{\kappa }\left(\beta -c_{\pi }^{cg}\right)$ , d x c g = − 1 κ 1 − d π c g $d_{x}^{cg}=-\frac{1}{\kappa }\left(1-d_{\pi }^{cg}\right)$ , Ω x c g = 1 κ Ω π c g $\varOmega _{x}^{cg}=\frac{1}{\kappa }\varOmega _{\pi }^{cg}$ , and 𝛩 x c g = 1 κ 𝛩 π c g $\varTheta _{x}^{cg}=\frac{1}{\kappa }\varTheta _{\pi }^{cg}$ .

It emerges from the comparison of the feedback coefficients in the ALMs under discretion and RE given by (19) and (20), with those in the ALMs under learning given by (38) and (48), that learning weakens (reinforces) the effect of out-of-equilibrium inflation expectations and noisy cost-push shocks in the ALM for inflation (the output gap), that is, 0 < c π c g < α β α + κ 2 $0<c_{\pi }^{cg}<\tfrac{\alpha \beta }{\alpha +\kappa ^{2}}$ and 0 < d π c g < α α + κ 2 < 1 $0<d_{\pi }^{cg}<\frac{\alpha }{\alpha +\kappa ^{2}}<1$ ( c x c g < − β κ α + κ 2 < 0 $c_{x}^{cg}<-\tfrac{\beta \kappa }{\alpha +\kappa ^{2}}<0$ and d x c g < − κ α + κ 2 < 0 $d_{x}^{cg}<-\frac{\kappa }{\alpha +\kappa ^{2}}<0$ , respectively).

We notice that linear inflation contracts do not modify the structural parameters of the model or the CB's preferences. Consequently, they do not affect the way the CB responds to exogenous shocks. Hence, all feedback coefficients in the ALMs for inflation and the output gap, given in (39)–(42), (43), or (44)–(47), are independent of τ $\tau$ .

In comparison, under nonlinear inflation contracts, the feedback coefficients on inflation expectations and cost-push shocks are a function of the penalty rate or the degree of CB conservatism (André and Dai 2017, 2023). Indeed, the latter modifies the weight the CB puts on stabilizing inflation relative to stabilizing the output gap. This has a multiplicative effect on the ALMs by affecting how the CB responds to changes in inflation expectations and cost-push shocks.

4.4 The Steady-State Equilibrium

To obtain elegant steady-state learning equilibrium solutions, we first use the definition of Φ $\varPhi$ , p 0 $p_{0}$ , p 1 $p_{1}$ , and p 2 $p_{2}$ , and the condition p 1 c π c g + p 2 ( c π c g ) 2 = − p 0 $p_{1}c_{\pi }^{cg}+p_{2}(c_{\pi }^{cg})^{2}=-p_{0}$ to obtain 1 − c π c g Φ = α 1 − β 1 − β 1 − γ ( 1 − β ) + κ 2 1 − β 1 − γ $\left(1-c_{\pi }^{cg}\right)\varPhi =\alpha \left(1-\beta \right)\left\lbrace 1-\beta \left[1-\gamma (1-\beta)\right]\right\rbrace +\kappa ^{2}\left[1-\beta \left(1-\gamma \right)\right]$ . Using this result, c x c g = − 1 κ ( β − c π c g ) $c_{x}^{cg}=-\frac{1}{\kappa }(\beta -c_{\pi }^{cg})$ , Ω x c g = 1 κ Ω π c g $\varOmega _{x}^{cg}=\frac{1}{\kappa }\varOmega _{\pi }^{cg}$ , and 𝛩 x c g = 1 κ 𝛩 π c g $\varTheta _{x}^{cg}=\frac{1}{\kappa }\varTheta _{\pi }^{cg}$ , and substituting a t = π t $a_{t}=\pi _{t}$ and e t = 0 $e_{t}=0$ into (19) and (20) while omitting the time index, we obtain
π ¯ = α κ 1 − Γ κ 2 + α ( 1 − β ) 1 − Γ x ∼ − 1 2 κ 2 κ 2 + α ( 1 − β ) 1 − Γ ξ τ , $$\begin{eqnarray} \overline{\pi } = \frac{\alpha \kappa {\left(1-\varGamma \right)}}{\kappa ^{2}+\alpha (1-\beta){\left(1-\varGamma \right)}}\widetilde{x}-\frac{1}{2}\frac{\kappa ^{2}}{\kappa ^{2}+\alpha (1-\beta){\left(1-\varGamma \right)}}\xi \tau,\qquad \end{eqnarray}$$ (49)
x ¯ = α 1 − β 1 − Γ κ 2 + α ( 1 − β ) 1 − Γ x ∼ − 1 2 1 − β κ κ 2 + α ( 1 − β ) 1 − Γ ξ τ . $$\begin{eqnarray} \overline{x} & = & \frac{\alpha {\left(1-\beta \right)}{\left(1-\varGamma \right)}}{\kappa ^{2}+\alpha (1-\beta){\left(1-\varGamma \right)}}\widetilde{x}-\frac{1}{2}{\left[\frac{{\left(1-\beta \right)}\kappa }{\kappa ^{2}+\alpha (1-\beta){\left(1-\varGamma \right)}}\right]}\xi \tau .\qquad \end{eqnarray}$$ (50)
where Γ ≡ γ β 2 1 − β 1 − γ > 0 $\varGamma \equiv \frac{\gamma \beta ^{2}}{1-\beta \left(1-\gamma \right)}>0$ and 1 − Γ = 1 − β 1 − γ ( 1 − β ) 1 − β 1 − γ > 0 $1-\varGamma =\frac{1-\beta \left[1-\gamma (1-\beta)\right]}{1-\beta \left(1-\gamma \right)}>0$ . When γ → 0 $\gamma \rightarrow 0$ , it follows that 1 − Γ = 1 $1-\varGamma =1$ and the steady-state equilibrium solutions given by (49) and (50) tend to be identical to those given by (21) and (22), obtained under optimal discretion and RE. When γ → 1 $\gamma \rightarrow 1$ and hence 1 − Γ → 1 − β 2 $1-\varGamma \rightarrow 1-\beta ^{2}$ , the solutions (49) and (50) approach very closely but are not equal to the ones obtained under optimal limited commitment and RE and given in (27) and (28).

As we follow the Euler equation approach of Molnár and Santoro (2014), the learning steady-state equilibrium would be identical to the one they obtained under CG optimal policy in the absence of both an optimal inflation contract and a positive output gap target (i.e., x ∼ = τ = 0 $\widetilde{x}=\tau =0$ ).

In the absence of inflation contracts ( τ = 0 $\tau =0$ ), the existence of a positive output-gap target makes our steady-state equilibrium comparable to those obtained by Eusepi et al. (2018). In their approach that solves for optimal decisions conditional on the belief structure, the CB can, through managing both output-gap and inflation expectations, achieve better stabilization than under the Euler equation approach. Their steady-state equilibrium solution can be written as π b s = α κ 1 − Γ b s κ 2 + α ( 1 − β ) 1 − Γ b s x ∼ $\pi ^{bs}=\frac{\alpha \kappa \left(1-\varGamma ^{bs}\right)}{\kappa ^{2}+\alpha (1-\beta)\left(1-\varGamma ^{bs}\right)}\widetilde{x}$ and x b s = α 1 − β 1 − Γ b s κ 2 + α ( 1 − β ) 1 − Γ b s x ∼ $x^{bs}=\frac{\alpha \left(1-\beta \right)\left(1-\varGamma ^{bs}\right)}{\kappa ^{2}+\alpha (1-\beta)\left(1-\varGamma ^{bs}\right)}\widetilde{x}$ , where Γ b s ≡ γ β 2 1 − β 1 − γ − 1 − β θ β $\varGamma ^{bs}\equiv \frac{\gamma \beta ^{2}}{1-\beta \left(1-\gamma \right)-\left(1-\beta \right)\theta \beta }$ , which is greater than Γ $\varGamma$ , meaning that π b s $\pi ^{bs}$ and x b s $x^{bs}$ are, respectively, lower than π $\pi$ and x $x$ obtained from (49) and (50) when τ $\tau$ is set to zero.

4.5 The Effects of Learning

The solutions (43) and (44)–(47) show that feedback coefficients on state variables ( a t $a_{t}$ , x ∼ $\widetilde{x}$ , τ $\tau$ , and e t $e_{t}$ ) in the ALMs under learning are identical to the ones obtained under discretion and RE when γ = 0 $\gamma =0$ and are close to the ones obtained under limited commitment and RE when γ = 1 $\gamma =1$ . These results do not tell us about how these coefficients behave as γ $\gamma$ evolves between 0 and 1.

In the following, we first summarize the effects of learning on the feedback coefficients on inflation expectations and cost-push shocks that are extensively studied in Molnár and Santoro (2014) and André and Dai (2017, 2023). Then, we derive some results regarding the effects of learning on the feedback coefficients on the output-gap target and inflation penalty rate. The summary and the new analysis are useful for understanding the dynamics of cumulative welfare loss and endogenous variables that we analyze in the following under learning or when there are interactions between learning and inflation contracts.

Inflation expectations ( a t $a_{t}$ ) are related to past inflation through the learning algorithm (32) and hence to past cost-push shocks through the Phillips curve (12). Current inflation depends on the CB's responses to a t $a_{t}$ and thus these shocks. A higher γ $\gamma$ has two opposite effects on c π c g $c_{\pi }^{cg}$ . Molnár and Santoro (2014) have discussed how the relationship between c π c g $c_{\pi }^{cg}$ and γ $\gamma$ could be nonlinear when τ = 0 $\tau =0$ . First, if agents are learning with a higher gain (i.e., paying greater attention to recent data), the CB would be more cautious about engineering surprise inflation to avoid higher inflation expectations. Indeed, according to (32), a rise in γ $\gamma$ increases the positive effect of π t $\pi _{t}$ on a t + 1 $a_{t+1}$ and hence the risk of future inflation and leads the CB to be more aggressive against inflation, implying a lower c π c g $c_{\pi }^{cg}$ in (38). Second, a higher γ $\gamma$ dampens the effect of a t $a_{t}$ on a t + 1 $a_{t+1}$ , creating policy space for the CB to engineer surprise inflation and yielding a higher c π c g $c_{\pi }^{cg}$ . In Molnár and Santoro (2014), the net effect depends on the calibration, and for most realistic parameters, the first effect dominates, that is, ∂ c π c g ∂ γ < 0 $\frac{\partial c_{\pi }^{cg}}{\partial \gamma }<0$ . For these authors, the second effect will be dominant only for high learning gains: the CB is more willing to engineer higher inflation in response to current inflation expectations because future inflation expectations are less responsive to current inflation when learning gains are high. Pushing further the algebraic analysis, we find that c π c g $c_{\pi }^{cg}$ would be nonmonotonic if κ 2 > α β 1 − β 2 $\kappa ^{2}>\alpha \beta \left(1-\beta ^{2}\right)$ .

Learning has a direct and an indirect effect on the feedback coefficient on the cost-push shock in the ALM for inflation, d π c g $d_{\pi }^{cg}$ . The first effect represents, for a given c π c g $c_{\pi }^{cg}$ , how the intertemporal trade-off leads the CB to reduce its focus on the conventional intratemporal trade-off. In other words, as the learning gain rises, the CB is more likely to conduct a more aggressive policy in response to the cost-push shock to keep inflation closer to its target at the price of amplifying variations in the output gap. The indirect effect captures the fact that the CB assesses how the learning gain γ $\gamma$ affects d π c g $d_{\pi }^{cg}$ , via its marginal effect on c π c g $c_{\pi }^{cg}$ that spreads in the complex linkage between current inflation that depends on d π c g $d_{\pi }^{cg}$ , future inflation expectations and future inflation that depends on c π c g $c_{\pi }^{cg}$ , implying that the CB should set d π c g $d_{\pi }^{cg}$ conditional on c π c g $c_{\pi }^{cg}$ . As a result, d π c g $d_{\pi }^{cg}$ is indirectly affected by learning via c π c g $c_{\pi }^{cg}$ . The feedback coefficients d π c g $d_{\pi }^{cg}$ is monotonic if ∂ c π c g ∂ γ < 0 $\frac{\partial c_{\pi }^{cg}}{\partial \gamma }<0$ or is likely to be still monotonic even if ∂ c π c g ∂ γ > 0 $\frac{\partial c_{\pi }^{cg}}{\partial \gamma }>0$ or κ 2 < α β 1 − β 2 $\kappa ^{2}<\alpha \beta \left(1-\beta ^{2}\right)$ .

Given the relationship between the feedback coefficients in the ALM for inflation and those in the ALM for the output gap, it is easy to deduce the effects on c x c g $c_{x}^{cg}$ and d x c g $d_{x}^{cg}$ .

The “overambitious” output-gap target x ∼ $\widetilde{x}$ , due to the distortions induced by the monopolistic competition, affects the equilibrium values of endogenous variables like an exogenous shock and appears as a part of an additive term in the ALMs for inflation and the output gap. The inflation penalty rate, depending on x ∼ $\widetilde{x}$ , also appears as a part of an additive term in these ALMs: it is set by the government to (partially) offset the effect of x ∼ $\widetilde{x}$ on the equilibrium inflation.

Proposition 3.An increase in learning gain weakens the effects of the “overambitious” output-gap target on inflation, and the output gap if the sufficient condition κ 2 < α β 1 − β 2 $\kappa ^{2}<\alpha \beta \left(1-\beta ^{2}\right)$ is verified.

Proof.We have Ω π c g > 0 $\varOmega _{\pi }^{cg}>0$ and Ω x c g > 0 $\varOmega _{x}^{cg}>0$ . We obtain ∂ Ω x c g ∂ γ = 1 κ ∂ Ω π c g ∂ γ < < 0 $\frac{\partial \varOmega _{x}^{cg}}{\partial \gamma }=\frac{1}{\kappa }\frac{\partial \varOmega _{\pi }^{cg}}{\partial \gamma }<<0$ if κ 2 < α β 1 − β 2 $\kappa ^{2}<\alpha \beta \left(1-\beta ^{2}\right)$ (Appendix B.2). To show if a higher γ $\gamma$ reinforces or not the sensitiveness of π t $\pi _{t}$ and x t $x_{t}$ to x ∼ $\widetilde{x}$ , we compare the sign of feedback coefficients on x ∼ $\widetilde{x}$ with that of their corresponding partial derivative with respect to γ $\gamma$ . □ $\Box$

A higher output-gap target leads the CB to sacrifice inflation stabilization according to (37), implying that Ω π c g > 0 $\varOmega _{\pi }^{cg}>0$ . For κ 2 < α β 1 − β 2 $\kappa ^{2}<\alpha \beta \left(1-\beta ^{2}\right)$ , an increase in γ $\gamma$ makes it less possible to exploit private beliefs via surprise inflation to achieve a given x ∼ $\widetilde{x}$ , such that ∂ Ω π c g ∂ γ < < 0 $\frac{\partial \varOmega _{\pi }^{cg}}{\partial \gamma }<<0$ . On the one hand, for a given c π c g $c_{\pi }^{cg}$ , the intertemporal trade-off due to learning leads the CB to reduce its focus on the conventional intratemporal trade-off induced by the “overambitious” output gap target. As γ $\gamma$ rises, the CB is more likely to conduct a less accommodative policy, making the realized output gap increasingly lower than the equilibrium output gap under discretion and RE. On the other hand, the CB assesses how the “overambitious” output-gap target affects current inflation, future inflation expectations, and future inflation, implying that the CB should set Ω π c g $\varOmega _{\pi }^{cg}$ conditional on c π c g $c_{\pi }^{cg}$ as in the case of the feedback coefficient on the cost-push shock.

A result related to Proposition 3 is about the effect of learning on the feedback coefficient of the inflation penalty rate. Inflation penalty pushes the CB to contract output to reduce inflation, that is, 𝛩 π c g < 0 $\varTheta _{\pi }^{cg}<0$ and 𝛩 x c g < 0 $\varTheta _{x}^{cg}<0$ . The way the inflation penalty reduces inflation depends on how much it impacts on inflation expectations and how it affects current inflation through this channel, meaning that the feedback coefficients 𝛩 π c g $\varTheta _{\pi }^{cg}$ and 𝛩 x c g $\varTheta _{x}^{cg}$ depend on c π c g $c_{\pi }^{cg}$ . As the learning gain rises, a given inflation penalty becomes more effective in reducing current inflation, implying thus a decrease in the absolute value of 𝛩 π c g $\varTheta _{\pi }^{cg}$ and 𝛩 x c g $\varTheta _{x}^{cg}$ for a given c π c g $c_{\pi }^{cg}$ . On the other hand, as γ $\gamma$ rises, c π c g $c_{\pi }^{cg}$ tends to be generally lower and the monetary policy more aggressive, making the inflation penalty rate an instrument less useful in fighting inflation. This implies that the values of 𝛩 π c g $\varTheta _{\pi }^{cg}$ and 𝛩 x c g $\varTheta _{x}^{cg}$ would be smaller in absolute value. To assess the net effect of learning on 𝛩 π c g $\varTheta _{\pi }^{cg}$ and 𝛩 x c g $\varTheta _{x}^{cg}$ , we undertake a numerical exercise and find that for the baseline parameter values, a rise in γ $\gamma$ reinforces the negative effect of inflation penalty on inflation and the output gap, that is, ∂ 𝛩 x c g ∂ γ = 1 κ ∂ 𝛩 π c g ∂ γ < 0 $\frac{\partial \varTheta _{x}^{cg}}{\partial \gamma }=\frac{1}{\kappa }\frac{\partial \varTheta _{\pi }^{cg}}{\partial \gamma }<0$ , for γ < 0.42 $\gamma <0.42$ , because the first effect dominates.

5 Optimal Inflation Contracts Under Learning

In the steady state, as γ → 1 $\gamma \rightarrow 1$ , the learning equilibrium approaches increasingly the optimal limited commitment RE equilibrium. Lack of commitment implies higher “inflation bias,” but this effect is compensated by the CB's expectations management when agents are learning. To optimally reduce the bias, the government should rationally anticipate the learning behavior and integrate its equilibrium effect into the design of linear inflation contracts.

5.1 The Government's Expected Utility

The government forms RE, based on information including the distribution of cost-push shocks, e t ∼ N ( 0 , σ e 2 ) $e_{t}\sim \mathbb {\mathit {\mathcal {N}}}(0,\sigma _{e}^{2})$ , the learning algorithm (32), and the ALM for inflation (38).

5.1.1 The Expected Equilibria Based on the Government's Estimation of Private Expectations

The government's estimation for private inflation expectations verifies (32) and (38) such that
E t + i a t + i + 1 = 1 − γ ( 1 − c π c g ) a t + i + γ ( Ω π c g x ∼ + 𝛩 π c g ξ τ + d π c g e t + i ) . $$\begin{equation} E_{t+i}a_{t+i+1}={\left[1-\gamma (1-c_{\pi }^{cg})\right]}a_{t+i}+\gamma (\varOmega _{\pi }^{cg}\widetilde{x}+\varTheta _{\pi }^{cg}\xi \tau +d_{\pi }^{cg}e_{t+i}). \end{equation}$$ (51)
In other words, it takes account of the backward-looking nature of learning equation (51), which is a stationary AR(1) with 0 < [ 1 − γ ( 1 − c π cg ) ] < 1 $0<[1-\gamma (1-{c}_{\pi}^{\textit{cg}})]<1$ . As the literature on adaptive learning has already shown, the updating algorithm with CG cannot make the expectations asymptotically converging to a precise value when shocks are random. Replacing Ω π c g $\varOmega _{\pi }^{cg}$ and 𝛩 π c g $\varTheta _{\pi }^{cg}$ by their definition, we obtain the solution of a t + i $a_{t+i}$ as a function of state variables such as x ∼ $\widetilde{x}$ and τ $\tau$ and a weighted sum of past cost-push shocks. Using the definition of Ω π c g $\varOmega _{\pi }^{cg}$ and 𝛩 π c g $\varTheta _{\pi }^{cg}$ into (38) and (48) and using the expression 1 − c π c g Φ ( γ ) = α 1 − β 1 − β 1 − γ ( 1 − β ) + κ 2 1 − β 1 − γ $\left(1-c_{\pi }^{cg}\right)\varPhi (\gamma)=\alpha \left(1-\beta \right)\left\lbrace 1-\beta \left[1-\gamma (1-\beta)\right]\right\rbrace +\kappa ^{2}\left[1-\beta \left(1-\gamma \right)\right]$ , the solution can be written as
a t + i = α κ 1 − Γ α 1 − β 1 − Γ + κ 2 x ∼ − 1 2 κ 2 α 1 − β 1 − Γ + κ 2 ξ τ + γ d π c g ∑ j = 1 ∞ 1 − γ 1 − c π c g j − 1 e t − j , $$\begin{eqnarray} a_{t+i} &=& \frac{\alpha \kappa {\left(1-\varGamma \right)}}{\alpha {\left(1-\beta \right)}{\left(1-\varGamma \right)}+\kappa ^{2}}\widetilde{x}-\frac{1}{2}\frac{\kappa ^{2}}{\alpha {\left(1-\beta \right)}{\left(1-\varGamma \right)}+\kappa ^{2}}\xi \tau \nonumber\\ && +\,\gamma d_{\pi }^{cg}\sum _{j=1}^{\infty }{\left[1-\gamma {\left(1-c_{\pi }^{cg}\right)}\right]}^{j-1}e_{t-j}, \end{eqnarray}$$ (52)
where a t + i $a_{t+i}$ has a mean equal to α κ 1 − Γ x ∼ − 1 2 κ 2 ξ τ α 1 − β 1 − Γ + κ 2 $\frac{\alpha \kappa \left(1-\varGamma \right)\widetilde{x}-\frac{1}{2}\kappa ^{2}\xi \tau }{\alpha \left(1-\beta \right)\left(1-\varGamma \right)+\kappa ^{2}}$ and a variance equal to σ a 2 = γ 2 d π c g 2 1 − 1 − γ 1 − c π c g 2 σ e 2 $\sigma _{a}^{2}=\frac{\gamma ^{2}\left(d_{\pi }^{cg}\right)^{2}}{1-\left[1-\gamma \left(1-c_{\pi }^{cg}\right)\right]^{2}}\sigma _{e}^{2}$ . It is numerically shown by Molnár and Santoro (2014) that σ a 2 $\sigma _{a}^{2}$ is increasing in γ $\gamma$ (see their Figure 2). Inserting the solution of a t + i $a_{t+i}$ given by (52) into (38) and (48) leads to
π t + i = α κ 1 − Γ x ∼ − 1 2 κ 2 ξ τ α 1 − β 1 − Γ + κ 2 + d π c g e t + γ c π c g d π c g ∑ j = 1 ∞ 1 − γ 1 − c π c g j − 1 e t − j , $$\begin{eqnarray} \pi _{t+i} & = & \frac{\alpha \kappa {\left(1-\varGamma \right)}\widetilde{x}-\frac{1}{2}\kappa ^{2}\xi \tau }{\alpha {\left(1-\beta \right)}{\left(1-\varGamma \right)}+\kappa ^{2}}+d_{\pi }^{cg}e_{t}\nonumber\\ & & +\,\gamma c_{\pi }^{cg}d_{\pi }^{cg}\sum _{j=1}^{\infty }{\left[1-\gamma {\left(1-c_{\pi }^{cg}\right)}\right]}^{j-1}e_{t-j},\end{eqnarray}$$ (53)
x t + i = 1 − β α 1 − Γ x ∼ − 1 2 κ ξ τ α 1 − β 1 − Γ + κ 2 + d x c g e t + γ c x c g d π c g ∑ j = 1 ∞ 1 − γ 1 − c π c g j − 1 e t − j . $$\begin{eqnarray} x_{t+i} & = & \frac{{\left(1-\beta \right)}{\left[\alpha {\left(1-\varGamma \right)}\widetilde{x}-\frac{1}{2}\kappa \xi \tau \right]}}{\alpha {\left(1-\beta \right)}{\left(1-\varGamma \right)}+\kappa ^{2}}+d_{x}^{cg}e_{t}\nonumber\\ && +\,\gamma c_{x}^{cg}d_{\pi }^{cg}\sum _{j=1}^{\infty }{\left[1-\gamma {\left(1-c_{\pi }^{cg}\right)}\right]}^{j-1}e_{t-j}. \end{eqnarray}$$ (54)

5.1.2 Plotting the Government's Expected Utility

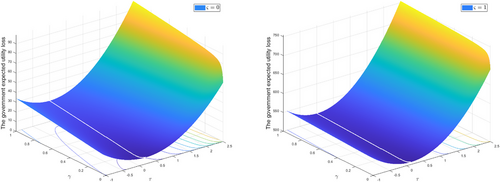
Using the baseline parameter values and setting ξ = 1 $\xi =1$ and a quarterly variance of 0.1452 for the cost-push shock, we plot the government's unconditional expected utility function (16) with π t + i $\pi _{t+i}$ and x t + i $x_{t+i}$ given by (53) and (54).

To illustrate the effect of the weight that the government puts on the transfer, we compare the expected utility loss plotted with ς = 0 $\varsigma =0$ , and ς = 1 $\varsigma =1$ respectively. The white lines in Figure 1 represent optimal penalty rates, which are increasing in the learning gain.

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
The government's expected utility loss and the optimal inflation penalty rate under learning for ς = 0 $\varsigma =0$ or 1. [Colour figure can be viewed at wileyonlinelibrary.com]

5.2 Determination of the Optimal Inflation Penalty Rate

The inflation contract to be embedded into the institutional arrangement of the CB is time-invariant under learning. The optimal penalty rate is solved by maximizing the government's unconditional expected utility subject to short-run equilibrium solutions of inflation and the output gap (53) and (54).

5.2.1 An Analytical Solution to the Government's Optimization Problem

Inserting π t + i $\pi _{t+i}$ and x t + i $x_{t+i}$ given by (53) and (54) into the government's utility function (16) and deriving the first-order condition relative to τ $\tau$ leads to
τ | c g = 2 α ( β − Γ ) ξ κ 2 + ς α ( 1 − β ) 1 − Γ + κ 2 1 − Γ κ ξ ξ α ( 1 − β ) 2 + κ 2 + 2 ς α ( 1 − β ) 1 − Γ + κ 2 x ∼ > 0 . $$\begin{equation} \tau |^{cg}=\frac{2\alpha {\left\lbrace (\beta -\varGamma)\xi \kappa ^{2}+\varsigma {\left[\alpha (1-\beta){\left(1-\varGamma \right)}+\kappa ^{2}\right]}{\left(1-\varGamma \right)}\right\rbrace} }{\kappa \xi {\left\lbrace \xi {\left[\alpha (1-\beta)^{2}+\kappa ^{2}\right]}+2\varsigma {\left[\alpha (1-\beta){\left(1-\varGamma \right)}+\kappa ^{2}\right]}\right\rbrace} }\widetilde{x}>0. \end{equation}$$ (55)

The characteristics of the optimal inflation contract are time invariant and only related to the government's steady-state utility and the steady-state equilibrium solutions of π t $\pi _{t}$ and x t $x_{t}$ . The latter, independent of the system's eigenvalues, can be solved using the system composed of (12) and (33)–(35) while removing the time index. The optimal penalty rate (55) could be alternatively solved by maximizing (16) using the steady-state solutions of π t $\pi _{t}$ and x t $x_{t}$ .

The optimal inflation penalty rate decreases with the learning gain ( ∂ τ ∂ γ < 0 $\frac{\partial \tau }{\partial \gamma }<0$ ) because a higher γ $\gamma$ improves the integration of information about past inflation and hence the effect of inflation penalty into private expectations, making penalty more effective in reducing current inflation. The solution (55) is consistent with the graphic solutions (white lines) in Figure 1.

We notice that the optimal penalty rate τ | c g $\tau |^{cg}$ is decreasing in the weight placed on the incentive scheme ( ∂ τ ∂ ξ < 0 ) $\frac{\partial \tau }{\partial \xi }<0)$ and increasing in the relative weight placed on output-gap stabilization ( ∂ τ ∂ α > 0 $\frac{\partial \tau }{\partial \alpha }>0$ ) and the output-gap elasticity of inflation ( ∂ τ ∂ κ < 0 $\frac{\partial \tau }{\partial \kappa }<0$ ). Furthermore, τ | c g $\tau |^{cg}$ decreases with the weight put on the transfer in the government's utility, ∂ τ ∂ ς < 0 $\frac{\partial \tau }{\partial \varsigma }<0$ if γ < 2 κ 2 α ( 1 − β ) 2 + κ 2 − 1 β $\gamma <\frac{2\kappa ^{2}}{\alpha (1-\beta)^{2}+\kappa ^{2}}-\frac{1}{\beta }$ or γ < 0.9876 $\gamma <0.9876$ for the baseline parameter values, and with the discount factor, that is, ∂ τ ∂ β < 0 $\frac{\partial \tau }{\partial \beta }<0$ if κ 2 < α 1 − β 2 $\kappa ^{2}<\alpha \left(1-\beta \right)^{2}$ when ς = 0 $\varsigma =0$ .

A higher β $\beta$ amplifies the impact of a t $a_{t}$ on π t $\pi _{t}$ through the Phillips curve, making managing inflation expectations less easier and leading the CB to be more aggressive against inflation. Furthermore, there is an indirect effect of β $\beta$ through κ $\kappa$ as a higher β $\beta$ implies a lower κ $\kappa$ , meaning that a percentage decrease in the output gap would reduce less inflation. This reduces the effectiveness of inflation management by the CB and more so if γ $\gamma$ is high, implying an even more aggressive policy. In general, the government lowers τ | c g $\tau |^{cg}$ as β $\beta$ and γ $\gamma$  increase.

5.2.2 Comparing Optimal Penalty Rates: Learning Versus RE

For τ = 0 $\tau =0$ , when beliefs are invariant to short-run forecast errors (i.e., γ → 0 $\gamma \rightarrow 0$ ), the long-run optimal inflation and output gap deduced from (53) and (54) coincide with those obtained under optimal discretion and RE using (27) and (28). Optimal policy and the equilibrium under CG learning, as γ → 1 $\gamma \rightarrow 1$ are increasingly closer to those under optimal limited commitment and RE. The optimal long-run inflation under learning is bounded by the ones obtained under discretion and limited commitment, respectively, using (21) and (27), when agents form RE.

For γ → 0 $\gamma \rightarrow 0$ , we have Γ = 0 $\varGamma =0$ such that the optimal penalty rate given by (55) is reduced to
τ | γ → 0 c g = 2 α β ξ κ 2 + ς α ( 1 − β ) + κ 2 κ ξ ξ α ( 1 − β ) 2 + κ 2 + 2 ς α ( 1 − β ) + κ 2 x ∼ > 0 , $$\begin{equation} \tau |_{\gamma \rightarrow 0}^{cg}=\frac{2\alpha {\left\lbrace \beta \xi \kappa ^{2}+\varsigma {\left[\alpha (1-\beta)+\kappa ^{2}\right]}\right\rbrace} }{\kappa \xi {\left\lbrace \xi {\left[\alpha (1-\beta)^{2}+\kappa ^{2}\right]}+2\varsigma {\left[\alpha (1-\beta)+\kappa ^{2}\right]}\right\rbrace} }\widetilde{x}>0, \end{equation}$$ (56)
which is identical to the optimal solution of τ $\tau$ under discretion and RE, τ | d R E $\tau |_{d}^{RE}$ , given in (23).
Setting γ = 1 $\gamma =1$ implies Γ = β 2 $\varGamma =\beta ^{2}$ and substituting this result into (55) leads to
τ | γ → 1 c g = 2 α ( 1 − β ) κ 2 ξ β + ς 1 + β κ 2 + α ( 1 − β ) 2 1 + β κ ξ ξ α ( 1 − β ) 2 + κ 2 + 2 ς κ 2 + α ( 1 − β ) 2 1 + β x ∼ > 0 , $$\begin{equation} \tau |_{\gamma \rightarrow 1}^{cg}=\frac{2\alpha (1-\beta){\left\lbrace \kappa ^{2}\xi \beta +\varsigma {\left(1+\beta \right)}{\left[\kappa ^{2}+\alpha (1-\beta)^{2}{\left(1+\beta \right)}\right]}\right\rbrace} }{\kappa \xi {\left\lbrace \xi {\left[\alpha (1-\beta)^{2}+\kappa ^{2}\right]}+2\varsigma {\left[\kappa ^{2}+\alpha (1-\beta)^{2}{\left(1+\beta \right)}\right]}\right\rbrace} }\widetilde{x}>0, \end{equation}$$ (57)
which is above the one obtained under optimal limited commitment and RE, τ | c c R E $\tau |_{cc}^{RE}$ , given in (29).

Regardless of policy regimes and types of expectations, the optimal penalty rate decreases with ξ $\xi$ , that is, the more the CB cares about the incentive scheme versus social welfare loss, the less it is necessary to penalize the CB.

Under limited commitment and RE, the transfer payment drives the government to reduce inflation below its optimal level under discretion and RE by setting a positive penalty rate, which increases with ς $\varsigma$ . The reason is that for ς > 0 $\varsigma >0$ , the transfer to the CB represents a cost to be taken into account by the government. More inflation increases the social welfare loss, but the transfer is also reduced, so that the marginal cost of generating inflation is thus smaller (Candel-Sánchez and Campoy-Miñarro 2004).

Under learning, as under discretion and RE, inflation contracts are effective in fighting inflation. A rise in ς $\varsigma$ decreases the incentive for the government to offset the inflation bias and leads it to set a lower τ $\tau$ . As ς → 0 $\varsigma \rightarrow 0$ , the optimal penalty rate under learning becomes
τ | ς → 0 c g = 2 α κ β − Γ ξ κ 2 + α ( 1 − β ) 2 x ∼ . $$\begin{equation} \tau |_{\varsigma \rightarrow 0}^{cg}=\frac{2\alpha \kappa {\left(\beta -\varGamma \right)}}{\xi {\left[\kappa ^{2}+\alpha (1-\beta)^{2}\right]}}\widetilde{x} .\end{equation}$$ (58)
This is to be compared with the corresponding rate under optimal discretion and RE, that is, τ = 2 α κ β ξ κ 2 + α ( 1 − β ) 2 x ∼ $\tau =\frac{2\alpha \kappa \beta }{\xi \left[\kappa ^{2}+\alpha (1-\beta)^{2}\right]}\widetilde{x}$ , and under optimal limited commitment and RE, that is, τ = 0 $\tau =0$ .

Using the baseline parameter values and ξ = 1 $\xi =1$ , Figure 2 plots the optimal penalty rate given by (55) as a function of the learning gain and compares it with those obtained under discretion and RE, (23) and under limited commitment and RE, (29). In the case where ς = 1 $\varsigma =1$ , the optimal penalty rate equals 0.125 under discretion and RE, and 0.00064 under limited commitment and RE, while the one set under adaptive learning decreases from 0.125 to 0.00191 as γ $\gamma$ increases from zero to unity. Given that estimated learning gains are usually quite low and not higher than 0.2 (Milani 2007, 2014, 2017; Molnár and Ormeño 2015), the optimal inflation contract under limited commitment and RE will not be replicated under learning but will be approached if the learning gain is near to 0.2, which would correspond in practice to more backward-looking agents. If the inflation contract does not represent a cost for the government, ς = 0 $\varsigma =0$ , the latter is free to optimally set higher inflation penalty rates under discretion and RE as well as under learning for small learning gains compared to the case where ς = 1 $\varsigma =1$ .

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Optimal inflation penalty rate, policy regimes, and expectations for ς = 0 $\varsigma =0$ or 1. [Colour figure can be viewed at wileyonlinelibrary.com]

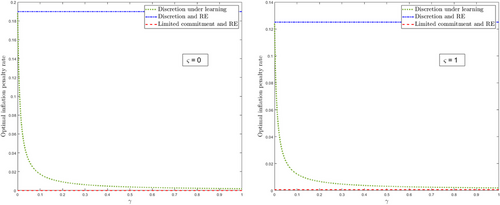
Optimal inflation contracts under learning could approach those under limited commitment and RE but their underlying mechanisms are different. Under RE, a credible CB anchors private expectations by committing to a policy rule for its future actions, making an inflation contract less useful or useless. In contrast, under adaptive learning, such a commitment device cannot be used because agents' beliefs are revised only based on past shocks.

Proposition 4.The optimal inflation penalty rate is positively related to the output-gap target and decreases with the learning gain. It converges (is close) to the rate set under optimal discretion (limited commitment) and RE if the learning gain approaches zero (unity).

Proof.Differentiating τ | c g $\tau |^{cg}$ given by (55) with respect to x ∼ $\widetilde{x}$ and γ $\gamma$ and summarizing the above discussion in the limit cases lead straightforwardly to Proposition 4. □ $\Box$

5.3 Welfare Loss Analysis

To obtain a quantitative measure of the welfare effects of internalizing the intertemporal trade-off and implementing the optimal linear inflation contract, we present a numerical welfare loss analysis. We use the baseline parameter values defined previously and ς = ξ = 1 $\varsigma =\xi =1$ . We perform a Monte Carlo with a simulation length of 10,000 periods and a cross-sectional sample size of 1000. Cost-push shocks are drawn from a normal distribution with 0 mean and variance 0.1452.

Unlike Molnár and Santoro (2014) who compared the CG learning equilibrium, in which the CB conducts optimal policy to manage beliefs, with a benchmark equilibrium in which the CB conducts anticipated utility (AU) policy taking private learning expectations as given, we compare the optimal CG learning equilibrium with the discretionary RE equilibrium. The case of limited commitment is not considered as a benchmark or compared to other equilibria given that the variances of inflation and the output gap are insignificant under this policy regime and the optimal inflation penalty rate is negligible (Figure 2).

Figure 3 plots the transition path of cumulative welfare loss under CG learning divided by the one corresponding to the discretionary RE equilibrium. The left and right graphs compare welfare losses when the government does not implement any inflation contract (i.e., τ = 0 $\tau =0$ ) and implements the optimal inflation contract defined in (55), respectively. We can make two observations: (1) Starting from the steady state, the ratios of welfare loss under learning compared to that measured in the discretionary RE equilibrium are under 1 when shocks begin to impact the economy for small learning gains. The higher is the learning gain, the lower is the ratio in the first periods. (2) An optimal inflation contract raises these ratios, making them exceed 1 even earlier.

Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
The dynamics of cumulative welfare loss under CG learning relative to that under discretion and RE. Initial conditions: a 0 $a_{0}$ , π 0 $\pi _{0}$ , and x 0 $x_{0}$ are set to their respective steady-state equilibrium value according to policy regimes, inflation contracts, and types of expectations. [Colour figure can be viewed at wileyonlinelibrary.com]

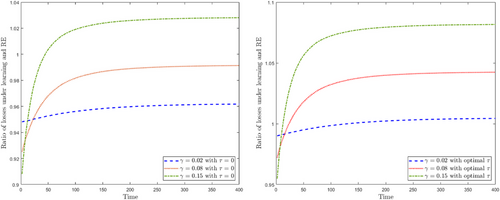
The first observation is explained by the intertemporal trade-off. The latter implies an aggressive optimal policy in response to cost-push shocks, and hence lower inflation variations at the cost of larger output-gap variations in the short run, reducing thus the welfare loss. The higher is the learning gain, the more aggressive the CG optimal policy and hence the stronger this initial effect. On the other hand, despite the CB's effort in managing private beliefs, inflation expectations and hence inflation and the output gap are volatile and persistent during the transition to the steady state. But as long as γ $\gamma$ is small enough, the CG optimal policy implies a smaller welfare loss than the discretionary RE policy. As γ $\gamma$ rises, another effect can become dominant over time: starting from a steady state, random shocks make no impact on inflation expectations under RE, but under learning, their effect on the variance of backward-looking inflation expectations increases as γ $\gamma$ rises. Hence, when γ $\gamma$ is high enough and as time moves on, the ratio of welfare loss can rise well over 1.

The second observation does not mean that the optimal inflation contract does not reduce welfare loss under learning. On the contrary, it does reduce the welfare loss under learning, but less than under discretion and RE. Furthermore, as γ $\gamma$ rises, the government sets lower inflation penalty rates, reducing further the welfare gain due to the optimal inflation contract under learning. This makes it possible for the ratios of welfare loss to rise above 1 for lower learning gains or makes it happen earlier for higher learning gains.

Another way to gauge what the effects of intertemporal trade-off and the optimal inflation contract on social welfare is to calculate separately the measure of welfare loss caused by inflation or output gap variations. Figure 4 shows that optimal inflation contracts significantly reduce (insignificantly increase) the welfare loss due to inflation (output-gap) variations under discretion and RE. The invisible effect on the cumulative welfare loss due to output-gap variations is explained by the combined effects of a low output-gap elasticity of inflation ( κ $\kappa$ ) and a low relative weight on stabilizing the output gap ( α $\alpha$ ) in the CB's loss function in our calibration. Indeed, a lower κ $\kappa$ makes managing inflation beliefs more costly in terms of output-gap variations while a lower α $\alpha$ means that output-gap variations generate smaller welfare loss.

Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
Decomposition of cumulative welfare loss under CG learning. Initial conditions: a 0 $a_{0}$ , π 0 $\pi _{0}$ , and x 0 $x_{0}$ are set to their respective steady-state equilibrium value according to policy regimes, inflation contracts, and types of expectations. [Colour figure can be viewed at wileyonlinelibrary.com]

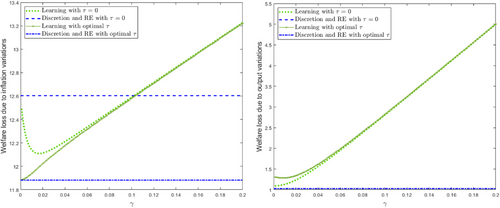
Under learning, similar effects of inflation contracts on both components of welfare loss could be quite strong but only for low learning gains. This result is explained by the effect of intratemporal trade-off but, as γ $\gamma$ rises, this effect is offset more and more by the effect of learning gain via the optimal inflation penalty rate. When γ $\gamma$ is higher, the welfare-improving effect of inflation contracts decreases as the government sets lower inflation penalty rates while the effect of learning on the variance of inflation expectations becomes the dominant factor in increasing both inflation and output-gap variations under CG optimal policy.

5.4 Optimal Penalty Rate and Short-Run Dynamics of Inflation and the Output Gap

To understand the dynamic effects of inflation contracts, we compare the dynamic paths of inflation and the output gap under learning and those under RE.

Figure 5 displays, for baseline parameter values and ς = ξ = 1 $\varsigma =\xi =1$ , the impulse responses of inflation and the output gap under various policy regimes to an initial positive cost-push shock when private agents form RE or are learning in the absence of inflation contracts ( τ = 0 $\tau =0$ ) or when optimal inflation contracts are implemented.

The equilibrium solutions under optimal limited commitment and RE, that is, (27) and (28), with the optimal inflation contract given by (29) or without it ( τ = 0 $\tau =0$ ) almost coincide.

Under both discretion and limited commitment when agents form RE, inflation rises on the arrival of the shock and immediately reverts to the steady state once the independently and identically distributed shock disappears. The transition dynamics of inflation and the output gap under these two policy regimes is absent and is represented by a horizontal line. This is explained by the fact that under RE, inflation, and output-gap expectations are forward looking and not responding to any random shock. The optimal inflation contract induces a large (small) downward shift in the path of inflation (the output gap) under discretion and RE, while the impact of the optimal inflation penalty rate on the paths of inflation and the output gap under limited commitment and RE is undetectable.

The intertemporal trade-off due to learning induces the CB to engineer a smaller initial response of inflation to cost-push shocks to manage inflation beliefs. In subsequent periods, inflation gradually converges to its steady-state value. For a given inflation penalty rate, the dynamic path of inflation under CG optimal policy is bounded at the top by its steady-state value in the discretionary RE equilibrium and at the bottom by the one corresponding to optimal limited commitment under RE. The management of inflation beliefs under learning is done at the cost of a large fall in the output gap in the first period, which goes well below the bounds defined by the output gap paths in the two policy regimes under RE.

A higher γ $\gamma$ implies faster learning and leads the CB to conduct a more aggressive policy against changes in inflation expectations and the cost-push shock in the present to reduce future macroeconomic volatility around the steady state. When γ $\gamma$ is high (i.e., the case γ = 0.9 $\gamma =0.9$ represented in Figure 5), as the optimal monetary policy has already led to a severe contraction of the output gap, it is only possible for the government to impose a low penalty rate as given by (55), meaning that the optimal inflation contract better stabilizes inflation under discretion and RE than under learning during the first periods before the management of inflation expectations under learning improves enough macroeconomic performance.

Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
Impulse response of π t $\pi _{t}$ and x t $x_{t}$ to an initial cost-push shock e = 0.1 $e=0.1$ . Private agents are learning with a high learning gain, that is, γ = 0.9 $\gamma =0.9$ . Initial conditions: a 0 $a_{0}$ , π 0 $\pi _{0}$ , and x 0 $x_{0}$ are set to their respective steady-state equilibrium value according to policy regimes, inflation contracts, and types of expectations. [Colour figure can be viewed at wileyonlinelibrary.com]

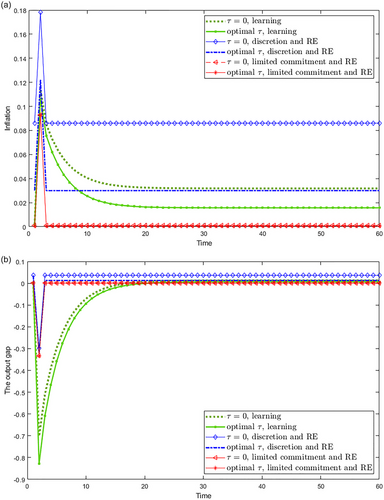
Under learning, the optimal linear inflation contract induces inflation and the output gap to a downward jump in the first period and then accelerates the adjustment of inflation and the output gap in intermediate periods compared to the case without an inflation contract. Its effect on the speed of adjustment of inflation and the output is diminishing as the latter approaches their steady-state values. The initial downward shift in both variables is due to the direct effect of the inflation penalty rate that depends on the “overambitious” output-gap target. Without changing the way the CB responds to out-of-equilibrium inflation expectations and noisy cost-push shocks, it can nevertheless make a time-varying impact (or indirect effect) on inflation and output-gap dynamics through its downward effect on the revision of inflation beliefs over time.

In comparison, optimal nonlinear inflation contracts considered in André and Dai (2017, 2023) would similarly have nonlinear effects on the dynamic paths of endogenous variables. There is a new channel through which such effects happen: the penalty rate defined by an optimal nonlinear inflation contract or the optimal degree of CB conservatism modifies the CB's incentive, that is, the weight put on stabilizing inflation relative to stabilizing the output gap. This has a multiplicative effect on the short- and long-run equilibrium by affecting the CB's response to out-of-equilibrium inflation expectations and noisy cost-push shocks. It directly affects feedback coefficients in the ALMs and hence the curvature of the adjustment paths of inflation and the output gap.

6 Discussion

The previous results are limited by the assumption of CG learning. The latter is a more suitable description of private agents' learning behavior in a time-varying environment given that frequent structural changes rationalize a continuous learning effort when revising their beliefs. As the economic environment does not represent a source of uncertainty for private agents as it is stabilizing, a more pertinent assumption would be that they revise their beliefs using a DG algorithm. This is because a steady state does not need a sustained learning effort. Another appealing feature of DG learning is that it reflects the fact that as time goes by, private agents increasingly gain learning experiences and hence confidence in their expectations. Following Molnár and Santoro (2014), it is easy to show that under DG learning, our main results are still valid. As time goes on, to accommodate the fact that the economy jumps from one dynamic trajectory with a higher learning gain onto another one with a lower one, the government has to increase the optimal inflation penalty rate accordingly. In other words, the optimal inflation contract is contingent on the learning gain. This could reduce the usefulness of inflation contracts if one agrees with Lohmann (1992, 274) who pointed out: “In practice, it is infeasible for a policy-maker to commit to a state-contingent policy rule.” Indeed, it is impossible or prohibitively costly to specify all possible contingencies in advance. Therefore, the policymaker is constrained to make simple commitments, which are invariant to the state of the world. However, this remark does not fully apply to the case of DG learning and its implications could be nuanced because the evolution of learning gain is generally a low-frequency event such that the government does not have to anticipate but just observe its evolution and adapt the inflation contract.

Previously, the participation constraint for the CB is assumed to be not binding. This can be justified on the ground that the central banker may have some negotiating power or the government may want to give him/her an incentive to optimize with respect to the inflation contract. However, the government has an incentive to lower the cost of the contract by reducing τ 0 $\tau _{0}$ and can impose inflation contracts with a participation constraint that is almost binding. To study this limit case, we follow Candel-Sánchez and Campoy-Miñarro (2004) and Chortareas and Miller (2007) by defining the CB's iso-utility when this constraint is binding:
τ 0 = 1 ξ π t + i 2 + α x t + i − x ∼ 2 − u 0 C B + τ π t + i . $$\begin{equation} \tau _{0}=\frac{1}{\xi }{\left[\pi _{t+i}^{2}+\alpha {\left(x_{t+i}-\widetilde{x}\right)}^{2}-u_{0}^{CB}\right]}+\tau \pi _{t+i}. \end{equation}$$ (59)
Substituting τ 0 $\tau _{0}$ given by (59) into the government's utility function (16) yields
U t G = − 1 2 E t ∑ i = 0 + ∞ β i 1 + ς ξ π t + i 2 + α x t + i − x ∼ 2 − u 0 C B , $$\begin{equation} U_{t}^{G}=-\frac{1}{2}E_{t}{\textstyle {\textstyle {\displaystyle \sum _{i=0}^{+\infty }}}}\beta ^{i}{\left\lbrace {\left(1+\frac{\varsigma }{\xi }\right)}{\left[\pi _{t+i}^{2}+\alpha {\left(x_{t+i}-\widetilde{x}\right)}^{2}-u_{0}^{CB}\right]}\right\rbrace}, \end{equation}$$ (60)
The government's new utility function (60) is homothetic to the society's loss function (13), implying that a government imposing a binding participation constraint can ignore the costs due to inflation contracts when setting the optimal penalty rate, and hence the Walsh's contracts are optimal after all (Chortareas and Miller 2007). This is equivalent to assume that ς = 0 $\varsigma =0$ . However, setting ς = 0 $\varsigma =0$ does not eliminate inflation bias under RE as well as under learning in the new Keynesian model with a positive optimal output gap.

Finally, our results are limited by the adoption of a specific adaptive learning algorithm. By focusing on such an algorithm, one might run the risk of exaggerating the degree to which a more rational policy analyst can predict and thus exploit the forecasting errors resulting from a particular manner of extrapolating from past observations (Woodford 2010). It would be interesting to reexamine inflation contracts by considering alternative approaches to non-RE surveyed in Woodford (2013). On the other hand, a model with only learning agents makes the CB's communication useless for anchoring private expectations and ignores the fact that some agents are more sophisticated than others. Therefore, a hybrid model with some private agents forming RE and others learning adaptively would provide further insights. One would expect two significant changes to our analysis: (1) The effect of learning under discretion is attenuated, depending on the proportion of agents forming RE; and (2) it would be possible to distinguish commitment from discretion when some agents are learning.

7 Conclusion

This paper studies how the fact that private agents are adaptively learning dramatically changes the logic in the design of linear inflation contracts in the new Keynesian model with a positive optimal output gap.

The results derived in the RE benchmark reveal that optimal inflation contracts could almost, but less than fully, deal with the time-inconsistency problem in the new Keynesian model. The residual inflation bias, relative to the inflation target, is a function of the intertemporal discount factor and depends on policy regimes. For comparison, an optimal linear inflation contract fully eliminates the inflation bias under optimal discretion while such a contract is not needed under optimal commitment to achieve the inflation target in the Barro–Gordon framework.

Under learning, given the ineffectiveness of the CB's announcements, discretion, and commitment yield the same equilibrium. As the learning gain tends to zero (unity), the learning equilibrium makes agents to learn asymptotically the equilibrium under optimal discretion (limited commitment) and RE.

The “inflation bias” exhibited by the learning equilibrium, compared to the zero inflation target, is decreasing with the learning gain. To deal with this bias, the government should design optimal inflation contracts with the penalty rate negatively varying with the learning gain, accounting for inflation persistence. The optimal penalty rates for different learning gains are included in the range having as the upper bound the optimal rate obtained under discretion and RE, and as the lower bound (but not attained) the one set under limited commitment and RE, which is close to zero. Optimal inflation contracts, which represent a cost for the government, are reduced to the Walsh contract when the participation constraint for the central bank is binding.

Acknowledgments

We are especially grateful to two anonymous referees as well as Dmitry Matveev for their very helpful comments. Any errors are our own.

    Endnotes

  1. 1 Such drifts could be induced by adaptive learning; see, for example, Branch and Evans (2006), Milani (2007, 2011), Slobodyan and Wouters (2012), Molnár and Ormeño (2015), Malmendier and Nagel (2016), Altavilla et al. (2017), Eusepi and Preston (2011, 2018b), Armantier et al. (2021), Mangapuram (2022), and Banerjee and Mehrotra (2023).
  2. 2 For surveys, see Evans and Honkapohja (2009) and Eusepi and Preston (2018a).
  3. 3 The stabilization bias means that the inflation volatility is higher out of steady state under discretion than under commitment.
  4. 4 Commitment, by reducing the response of inflation to such shocks to subdue expected inflation, makes stabilizing inflation less costly in terms of future output contraction, while under discretion, the CB takes expected inflation as given.
  5. 5 This “contracting” approach is not directly related to the literature on CB independence that seeks to explain why the government accepts the CB's independence (see, for example, de Haan and Eijffinger 2016).
  6. 6 For more details on the microfoundations, one can refer to Woodford (2003, chap. 6) and Walsh (2003c, chap. 8).
  7. 7 This condition is sufficient to warrant the existence of an optimal path under the usual assumptions imposed on a time-varying utility function.
  8. 8 By introducing δ t $\delta _{t}$ , we adopt an approach similar to the one of Benigno and Woodford (2005) who introduce an exogenous markup factor ( μ w $\mu ^{w}$ ) in the labor market such that W t P t = − μ t w U N U C $\frac{W_{t}}{P_{t}}=-\mu _{t}^{w}\frac{U_{N}}{U_{C}}$ is the wage for wage-taker firms. Such an approach allows to include the possibility of “pure cost-push shocks” that affect equilibrium pricing behavior while implying no change in the efficient allocation of resources.
  9. 9 In the new Keynesian model, under RE, assuming serially uncorrelated cost-push shocks avoids that discretionary policy suffers from a stabilization bias, compared to commitment to a policy rule.
  10. 10 Following Woodford (2003, chap. 6) and Walsh (2003c, chap. 8), we have derived such a welfare loss function in Appendix A.
  11. 11 A subclass of inflation contracts is adopted in practice and takes a simple form called inflation band targeting regimes where central bankers are accountable for their inflation achievement (Mishkin and Westelius 2008). For example, the Reserve Bank of New Zealand is required to keep inflation within the range of 1–3% and in case of failure the Governor is subject to dismissal. The Bank of England has a target range of ± 1 % $\pm 1\%$ around a 2% inflation target, and if it fails the Governor is required to publicly explain why.
  12. 12 The assumption according to which the government and the CB share society's preferences can be relaxed in two ways. First, the government and the CB might have different relative weights on output-gap stabilization, raising the question of the optimal degree of Rogoff's CB conservatism. Second, the government sets an overambitious output-gap target that differs from the optimal output gap for electoral reasons. This does not change fundamentally our results regarding optimal inflation contracts.
  13. 13 In a new Keynesian model with a positive output-gap target under RE, André and Dai (2022) have considered in addition a nonzero inflation target and the timeless perspective commitment.
  14. 14 The distinction between limited commitment and timeless perspective commitment (Woodford 1999b) could be made in new Keynesian dynamic stochastic general equilibrium (DSGE) models but not in the static Barro–Gordon model.
  15. 15 The term “forward guidance” becomes popular after the global financial crisis of 2008 and is notably used to signal that future short-term nominal interest rates will be kept low for longer, meaning a commitment for loose monetary policy. In this paper, “forward guidance” is used in its general sense and refers to the CB's communication about the state of the economy and likely future course of monetary policy.
  16. 16 Solving for optimal decisions under learning are very complex since agents are required to assess anticipated future revisions to beliefs when making current decisions. The learning literature avoids this problem by adopting the “anticipated utility” approach to individual optimization (Kreps 1998; Preston 2005). The “divine coincidence” result obtained in the Euler equation approach emerges as a special case but fails to hold more generally in the anticipated-utility framework (Eusepi et al. 2018).
  17. 17 As noticed by Eusepi et al. (2018), in their model with drifting beliefs structure, the aggregate supply curve has a short-run trade-off between inflation and the output gap that shifts in response to movements in both inflation and output-gap beliefs. While in the Euler equation approach of Molnár and Santoro (2014) that we adopt in this paper, the short-run trade-off depends only on inflation beliefs. The optimal policy problem in Eusepi et al., therefore, has an additional constraint but also one additional channel to influence inflation outcomes.
  18. 18 As t → + ∞ $t\rightarrow +\infty$ , we have π t = a t $\pi _{t}=a_{t}$ and the ALM for inflation (38) becomes π t = Ω π c g 1 − c π c g x ∼ + Θ π c g 1 − c π c g ξ τ + d π c g 1 − c π c g e t $\pi _{t}=\frac{\varOmega _{\pi }^{cg}}{1-c_{\pi }^{cg}}\widetilde{x}+\frac{\Theta _{\pi }^{cg}}{1-c_{\pi }^{cg}}\xi \tau +\frac{d_{\pi }^{cg}}{1-c_{\pi }^{cg}}e_{t}$ . Here, we compare Ω π c g 1 − c π c g $\tfrac{\varOmega _{\pi }^{cg}}{1-c_{\pi }^{cg}}$ with its counterpart in (21) and (27). In the short run, under learning, the effect of x ∼ $\widetilde{x}$ on inflation is smaller, with Ω π c g = 0.0014 $\varOmega _{\pi }^{cg}=0.0014$ . In the steady state, it includes an indirect effect of x ∼ $\widetilde{x}$ through variations in beliefs ( a t $a_{t}$ ). Notice that under optimal discretion and RE, the coefficient on x ∼ $\widetilde{x}$ in (21) equals 0.022.
  19. 19 We first rearrange terms in Φ $\varPhi$ while using the definition of p 1 $p_{1}$ and p 2 $p_{2}$ to obtain Φ = Φ + p 1 − p 1 = − p 1 − p 2 − p 2 c π c g $\varPhi =\varPhi +p_{1}-p_{1}=-p_{1}-p_{2}-p_{2}c_{\pi }^{cg}$ . Then, we use the relationship p 1 c π c g + p 2 ( c π c g ) 2 = − p 0 $p_{1}c_{\pi }^{cg}+p_{2}(c_{\pi }^{cg})^{2}=-p_{0}$ and substitute p 0 $p_{0}$ and p 2 $p_{2}$ by their definition to obtain the expression of 1 − c π c g Φ $\left(1-c_{\pi }^{cg}\right)\varPhi$ .
  20. 20 Checking with parameterizations characterized by a higher κ $\kappa$ and a lower α $\alpha$ , they found that the relationship would be nonmonotonic, that is, c π c g $c_{\pi }^{cg}$ decreases (increases) with γ $\gamma$ for smaller (larger) values of γ $\gamma$ .
  21. 21 See Appendix B.2 for the derivation of this condition and the analysis of the sensitiveness of c π c g $c_{\pi }^{cg}$ , d π c g $d_{\pi }^{cg}$ , Θ π c g $\Theta _{\pi }^{cg}$ , and Ω π c g $\varOmega _{\pi }^{cg}$ to γ $\gamma$ . A similar condition is derived in André and Dai (2023). (See the latter for a discussion about the interactions between the effects of learning and deep parameters such as θ $\theta$ , ε $\epsilon$ , β $\beta$ , and φ $\varphi$ .)
  22. 22 Using U.S. monthly data 1960:M1 to 2007:M8, Milani (2017) has estimated that the cost-push shock has a standard deviation of 0.22 or a variance of 0.0484. To match the model using quarterly data, we approximate the quarterly variance of the cost-push shock by multiplying the monthly variance by 3.
  23. 23 The effects of α $\alpha$ , β $\beta$ , and ς $\varsigma$ on τ $\tau$ differ across policy regimes and types of expectations. The effect of ς $\varsigma$ on τ $\tau$ under learning is as under discretion and RE. For ς > 0 $\varsigma >0$ , we would have ∂ τ ∂ β > 0 $\frac{\partial \tau }{\partial \beta }>0$ for very small learning gains, that is, when the learning equilibrium asymptotically approaches the discretionary RE equilibrium. Otherwise, the effects of α $\alpha$ and β $\beta$ on τ $\tau$ under learning are similar to those observed under optimal limited commitment and RE.
  24. 24 Molnár and Santoro show that the long-run gains of CG learning in containing inflation expectations come at a cost in the short run compared to the AU policy.
  25. 25 See Figure 2 in Molnár and Santoro (2014).
  26. 26 In practice, agents can shift from CG learning to decreasing-gain (DG) learning. As shown by Milani (2014), they seem to have often switched to CG learning, with a high gain, during most of the 1970s and until the early 1980s, before reverting to DG learning.

    27. Appendix A: Social Welfare Loss Function as a Second-Order Approximation of the Utility

    The analysis of the appropriate social welfare objective function consistent with the fully micro-founded new Keynesian model is based on Woodford (2003) and Walsh (2003c). Following them, we redefine the period utility of the representative agent (1) using C j , t = Y j , t $C_{j,t}=Y_{j,t}$ and N j , t = Y j , t Z t = C j , t Z t $N_{j,t}=\frac{Y_{j,t}}{Z_{t}}=\frac{C_{j,t}}{Z_{t}}$ as
    V t = U Y t , ϱ t − ∫ 0 1 υ C j t , Z t d j , $$\begin{equation} V_{t}=U{\left(Y_{t},\varrho _{t}\right)}-\int _{0}^{1}\upsilon {\left(C_{jt},Z_{t}\right)}dj,\end{equation}$$ (A.1)
    where U Y t , v t = ϱ t 1 − σ Y t 1 − σ 1 − σ $U\left(Y_{t},v_{t}\right)=\frac{\varrho _{t}^{1-\sigma }Y_{t}^{1-\sigma }}{1-\sigma }$ is the utility derived from consuming goods and υ C j , t , Z t = η 1 + φ C j , t Z t 1 + φ $\upsilon \left(C_{j,t},Z_{t}\right)=\frac{\eta }{1+\varphi }\left(\frac{C_{j,t}}{Z_{t}}\right)^{1+\varphi }$ is the disutility of producing good C j t $C_{jt}$ . To derive an approximation to the aggregate utility, it is necessary to introduce some additional notations. For any variable X t $X_{t}$ , let X ¯ $\overline{X}$ be its steady-state value, X t ∗ $X_{t}^{*}$ its efficient level, and X ∼ t = X t − X ¯ $\widetilde{X}_{t}=X_{t}-\overline{X}$ the deviation of X t $X_{t}$ around the steady state. Let x ̂ t = log X t / X ¯ $\hat{x}_{t}=\log \left(X_{t}/\overline{X}\right)$ be the log deviation of X t $X_{t}$ around its steady-state value. Using a second-order Taylor approximation, the variables X ∼ t $\widetilde{X}_{t}$ and x ̂ t $\hat{x}_{t}$ can be related to
    X ∼ t = X t − X ¯ = X ¯ X t X ¯ − 1 ≈ X ¯ x ̂ t + 1 2 x ̂ t 2 . $$\begin{equation} \widetilde{X}_{t}=X_{t}-\overline{X}=\overline{X}{\left(\frac{X_{t}}{\overline{X}}-1\right)}\approx \overline{X}{\left(\hat{x}_{t}+\frac{1}{2}\hat{x}_{t}^{2}\right)}. \end{equation}$$ (A.2)

    A.1 Approximating the Utility of Consumption

    The first term on the right side of (A.1) can be approximated around the steady state as
    U ( Y t , ϱ t ) ≈ U ( Y ¯ , 0 ) + U Y Y ∼ t + 1 2 U Y Y Y ∼ t 2 + U Y ϱ ϱ ∼ t Y ∼ t + 1 2 U ϱ ϱ ϱ ∼ t 2 + t . i . p . , $$\begin{equation} U(Y_{t},\varrho _{t})\approx U(\overline{Y},0)+U_{Y}\widetilde{Y}_{t}+\frac{1}{2}U_{YY}\widetilde{Y}_{t}^{2}+U_{Y\varrho }\widetilde{\varrho }_{t}\widetilde{Y}_{t}+\frac{1}{2}U_{\varrho \varrho }\widetilde{\varrho }_{t}^{2}+\mathrm{t.i.p.}, \end{equation}$$ (A.3)
    where t.i.p. are terms independent of policy. The choice of terms to include in t.i.p. is based on the idea that, in the new Keynesian model, the steady state is independent of monetary policy.
    Using Y ∼ t ≈ Y ¯ y ̂ t + 1 2 y ̂ t 2 $\widetilde{Y}_{t}\approx \overline{Y}\left(\hat{y}_{t}+\frac{1}{2}\hat{y}_{t}^{2}\right)$ and ϱ ∼ t ≈ ϱ ¯ ϱ ̂ t + 1 2 ϱ ̂ t 2 = ϱ ̂ t + 1 2 ϱ ̂ t 2 $\tilde{\varrho }_{t}\approx \overline{\varrho }\left(\hat{\varrho }_{t}+\frac{1}{2}\hat{\varrho }_{t}^{2}\right)=\hat{\varrho }_{t}+\frac{1}{2}\hat{\varrho }_{t}^{2}$ following the rule defined in (A.2), putting U ( Y ¯ , 0 ) $U(\overline{Y},0)$ and U ϱ ϱ ϱ ∼ t 2 $U_{\varrho \varrho }\widetilde{\varrho }_{t}^{2}$ into t . i . p . $\mathrm{t.i.p.}$ , while ignoring terms of order 3 or higher, such as y ̂ t i $\hat{y}_{t}^{i}$ for i > 2 $i>2$ , ϱ ̂ t y ̂ t 2 $\hat{\varrho }_{t}\hat{y}_{t}^{2}$ , ϱ ̂ t 2 y ̂ t $\hat{\varrho }_{t}^{2}\hat{y}_{t}$ , and ϱ ̂ t 2 y ̂ t 2 $\hat{\varrho }_{t}^{2}\hat{y}_{t}^{2}$ , we rewrite (A.3) as
    U ( Y t , v t ) ≈ U Y Y ¯ y ̂ t + 1 2 y ̂ t 2 + 1 2 U Y Y Y ¯ 2 y ̂ t + 1 2 y ̂ t 2 2 + U Y ϱ ϱ ∼ t Y ¯ y ̂ t + 1 2 y ̂ t 2 + 1 2 U ϱ ϱ ϱ ∼ t 2 + t . i . p . = U Y Y ¯ y ̂ t + 1 2 1 + U Y Y U Y Y ¯ y ̂ t 2 + U Y Y Y ¯ U Y Y Y ¯ U Y ϱ U Y ϱ ̂ t y ̂ t + t . i . p . $$\begin{eqnarray*} U(Y_{t},v_{t}) & \approx & U_{Y}\overline{Y}{\left(\hat{y}_{t}+\frac{1}{2}\hat{y}_{t}^{2}\right)}+\frac{1}{2}U_{YY}\overline{Y}^{2}{\left(\hat{y}_{t}+\frac{1}{2}\hat{y}_{t}^{2}\right)}^{2}\\ &&+\, U_{Y\varrho }\widetilde{\varrho }_{t}\overline{Y}{\left(\hat{y}_{t}+\frac{1}{2}\hat{y}_{t}^{2}\right)} +\frac{1}{2}U_{\varrho \varrho }\widetilde{\varrho }_{t}^{2}\mathrm{+}\,\mathrm{t.i.p.}\\ & = & U_{Y}\overline{Y}{\left[\hat{y}_{t}+\frac{1}{2}{\left(1+\frac{U_{YY}}{U_{Y}}\overline{Y}\right)}\hat{y}_{t}^{2}+\frac{U_{YY}\overline{Y}}{U_{YY}\overline{Y}}\frac{U_{Y\varrho }}{U_{Y}}\hat{\varrho }_{t}\hat{y}_{t}\right]}\mathrm{+}\,\mathrm{t.i.p.} \end{eqnarray*}$$
    Differentiating U Y t , ϱ t $U\left(Y_{t},\varrho _{t}\right)$ , for ϱ ¯ = 1 $\overline{\varrho }=1$ , yields U Y Y ¯ , 1 = Y ¯ − σ $U_{Y}\left(\overline{Y},1\right)=\overline{Y}^{-\sigma }$ , U Y Y Y ¯ , 1 = − σ Y ¯ − σ − 1 $U_{YY}\left(\overline{Y},1\right)=-\sigma \overline{Y}^{-\sigma -1}$ and U Y ϱ Y ¯ , 1 = 1 − σ Y ¯ − σ $U_{Y\varrho }\left(\overline{Y},1\right)=\left(1-\sigma \right)\left(\overline{Y}\right)^{-\sigma }$ . We get − U Y Y U Y Y ¯ = σ $-\frac{U_{YY}}{U_{Y}}\overline{Y}=\sigma$ , which implies that σ $\sigma$ can be interpreted as the coefficient of relative risk aversion, and − U Y v U Y Y Y ¯ ϱ ̂ t = 1 − σ σ ϱ ̂ t $-\frac{U_{Yv}}{U_{YY}\overline{Y}}\hat{\varrho }_{t}=\frac{\left(1-\sigma \right)}{\sigma }\hat{\varrho }_{t}$ . Then the approximation for U ( Y t , ϱ t ) $U(Y_{t},\varrho _{t})$ becomes
    U ( Y t , ϱ t ) ≈ U Y Y ¯ 1 + 1 − σ ϱ ̂ t y ̂ t + 1 2 1 − σ y ̂ t 2 + t . i . p . , $$\begin{eqnarray} U(Y_{t},\varrho _{t}) & \approx & U_{Y}\overline{Y}{\left\lbrace {\left[1+{\left(1-\sigma \right)}\hat{\varrho }_{t}\right]}\hat{y}_{t}+\frac{1}{2}{\left(1-\sigma \right)}\hat{y}_{t}^{2}\right\rbrace} \mathrm{+}\,\mathrm{t.i.p.}, \end{eqnarray}$$ (A.4)
    where U Y Y ¯ , 1 = U C Y ¯ , 1 $U_{Y}\left(\overline{Y},1\right)=U_{C}\left(\overline{Y},1\right)$ given the goods market equilibrium condition Y t = C t $Y_{t}=C_{t}$ .

    A.2 Approximating the Disutility of Work

    We analyze now the second term on the right-hand side in (A.1), which arises from the disutility of work. Expanding it around the steady state yields
    υ ( C j t , Z t ) ≈ υ ( Y ¯ , 1 ) + υ C C ∼ j t + υ v v t + 1 2 υ C C C ∼ j t 2 + υ C v Z ∼ t C ∼ j t + 1 2 υ Z Z Z ∼ t 2 + t . i . p . $$\begin{equation*} \upsilon (C_{jt},Z_{t})\approx \upsilon (\overline{Y},1)+\upsilon _{C}\widetilde{C}_{jt}+\upsilon _{v}v_{t}+\frac{1}{2}\upsilon _{CC}\widetilde{C}_{jt}^{2}+\upsilon _{Cv}\widetilde{Z}_{t}\widetilde{C}_{jt}+\frac{1}{2}\upsilon _{ZZ}\widetilde{Z}_{t}^{2}+\mathrm{t.i.p.} \end{equation*}$$
    By approximating C ∼ j t $\widetilde{C}_{jt}$ with Y ¯ c ̂ j t + 1 2 c ̂ j t 2 $\overline{Y}\left(\hat{c}_{jt}+\frac{1}{2}\hat{c}_{jt}^{2}\right)$ and putting terms such as υ ( Y ¯ , 1 ) $\upsilon (\overline{Y},1)$ and υ Z Z Z ∼ t 2 $\upsilon _{ZZ}\widetilde{Z}_{t}^{2}$ in t.i.p., one obtains
    υ ( C j t , Z t ) ≈ υ C Y ¯ c ̂ j t + 1 2 1 + υ C C υ C Y ¯ c ̂ j t 2 + υ C C Y ¯ υ C υ C Z υ C C Y ¯ z ̂ t c ̂ j t + t . i . p . $$\begin{eqnarray} \upsilon (C_{jt},Z_{t}) & \approx & \upsilon _{C}\overline{Y}{\left[\hat{c}_{jt}+\frac{1}{2}{\left(1+\frac{\upsilon _{CC}}{\upsilon _{C}}\overline{Y}\right)}\hat{c}_{jt}^{2}+\frac{\upsilon _{CC}\overline{Y}}{\upsilon _{C}}\frac{\upsilon _{CZ}}{\upsilon _{CC}\overline{Y}}\hat{z}_{t}\hat{c}_{jt}\right]}\nonumber\\ &&+\mathrm{t.i.p.} \end{eqnarray}$$ (A.5)
    Differentiating υ C j , t , Z t = η 1 + φ C j , t Z t 1 + φ $\upsilon \left(C_{j,t},Z_{t}\right)=\frac{\eta }{1+\varphi }\left(\frac{C_{j,t}}{Z_{t}}\right)^{1+\varphi }$ yields υ C Y ¯ , 1 = υ C C ¯ , 1 = η C ¯ φ $\upsilon _{C}\left(\overline{Y},1\right)=\upsilon _{C}\left(\overline{C},1\right)=\eta \overline{C}^{\varphi }$ , υ C C Y ¯ , 1 = υ C C C ¯ , 1 = η φ C ¯ φ − 1 $\upsilon _{CC}\left(\overline{Y},1\right)=\upsilon _{CC}\left(\overline{C},1\right)=\eta \varphi \overline{C}^{\varphi -1}$ , and υ C Z Y ¯ , 1 = υ C Z C ¯ , 1 = − ( 1 + φ ) η C ¯ φ $\upsilon _{CZ}\left(\overline{Y},1\right)=\upsilon _{CZ}\left(\overline{C},1\right)=-(1+\varphi)\eta \overline{C}^{\varphi }$ . Thus, we have
    υ C C υ C Y ¯ = φ $\frac{\upsilon _{CC}}{\upsilon _{C}}\overline{Y}=\varphi$ , and − υ C Z υ C C Y ¯ = ( 1 + φ ) φ $-\frac{\upsilon _{CZ}}{\upsilon _{CC}\overline{Y}}=\frac{(1+\varphi)}{\varphi }$ . Equation (A.5) can be rewritten as
    υ ( C j t , v t ) = υ C Y ¯ c ̂ j t + 1 2 1 + φ c ̂ j t 2 − ( 1 + φ ) z ̂ t c ̂ j t + t . i . p . $$\begin{eqnarray} \upsilon (C_{jt},v_{t}) & = & \upsilon _{C}\overline{Y}{\left[\hat{c}_{jt}+\frac{1}{2}{\left(1+\varphi \right)}\hat{c}_{jt}^{2}-(1+\varphi)\hat{z}_{t}\hat{c}_{jt}\right]}+\mathrm{t.i.p.} \end{eqnarray}$$ (A.6)
    In a model of perfect competition, the household producer of good j $j$ would equate the marginal rate of substitution between leisure and consumption to the real wage, or υ c / U Y = 1 $\upsilon _{c}/U_{Y}=1$ , given the implicit production function C j , t = N j , t $C_{j,t}=N_{j,t}$ . The ratio υ c / U Y $\upsilon _{c}/U_{Y}$ is equivalent to − U N U C = W P $-\frac{U_{N}}{U_{C}}=\frac{W}{P}$ implied by the first-order conditions of the household's optimization problem. Equation (9) implies that, given that Z ¯ = 1 $\overline{Z}=1$ , we have in the steady state
    υ c U Y = − U N U C = W ¯ P ¯ = ε − 1 ε 1 − l Z ¯ = ε − 1 ε 1 − l . $$\begin{equation} \frac{\upsilon _{c}}{U_{Y}}=-\frac{U_{N}}{U_{C}}=\frac{\overline{W}}{\overline{P}}=\frac{\epsilon -1}{\epsilon {\left(1-l\right)}}\overline{Z}=\frac{\epsilon -1}{\epsilon {\left(1-l\right)}}. \end{equation}$$ (A.7)
    In the presence of monopolistic competition, υ c U Y $\frac{\upsilon _{c}}{U_{Y}}$ = ε − 1 ε 1 − l $=\frac{\epsilon -1}{\epsilon \left(1-l\right)}$ is 1 over the markup μ ≡ ε ε − 1 $\mu \equiv \frac{\epsilon }{\epsilon -1}$ if the distortion is not compensated by the labor subsidy l $l$ . We define Ψ = 1 − ε l ε 1 − l $\varPsi =\frac{1-\epsilon l}{\epsilon \left(1-l\right)}$ , yielding υ c U Y $\frac{\upsilon _{c}}{U_{Y}}$ = 1 − Ψ $=1-\varPsi$ . When the distortion generated by monopolistic competition is small and the labor subsidy is close to zero, terms such as Ψ c ̂ j , t 2 $\varPsi \hat{c}_{j,t}^{2}$ and Ψ ( 1 + φ ) z ̂ t c ̂ j , t $\varPsi (1+\varphi)\hat{z}_{t}\hat{c}_{j,t}$ will be of the third order, and
    υ ( C j t , Z t ) ≈ U Y Y ¯ υ C U Y c ̂ j t + 1 2 υ C U Y 1 + φ c ̂ j t 2 − υ C U Y ( 1 + φ ) z ̂ t c ̂ j t + t . i . p . = U Y Y ¯ 1 − Ψ c ̂ j t + 1 2 1 + φ c ̂ j t 2 − ( 1 + φ ) z ̂ t c ̂ j t + t . i . p . $$\begin{eqnarray} \upsilon (C_{jt},Z_{t}) & \approx & U_{Y}\overline{Y}{\left[\frac{\upsilon _{C}}{U_{Y}}\hat{c}_{jt}+\frac{1}{2}\frac{\upsilon _{C}}{U_{Y}}{\left(1+\varphi \right)}\hat{c}_{jt}^{2}-\frac{\upsilon _{C}}{U_{Y}}(1+\varphi)\hat{z}_{t}\hat{c}_{jt}\right]}+\mathrm{t.i.p.}\nonumber \\ & = & U_{Y}\overline{Y}{\left[{\left(1-\varPsi \right)}\hat{c}_{jt}+\frac{1}{2}{\left(1+\varphi \right)}\hat{c}_{jt}^{2}-(1+\varphi)\hat{z}_{t}\hat{c}_{jt}\right]}+\mathrm{t.i.p.} \end{eqnarray}$$ (A.8)
    On the other hand, we express the log deviation of aggregate revenue and consumption Y t = C t = ∫ 0 1 C j t ( ε − 1 ) / ε d j ε / ( ε − 1 ) $Y_{t}=C_{t}=\left(\int _{0}^{1}C_{jt}^{(\epsilon -1)/\epsilon }dj\right)^{\epsilon /(\epsilon -1)}$ as a function of first- and second-order log deviations of the consumption of good j $j$ :
    y t ̂ = c ̂ ≈ E j c ̂ j t + 1 2 1 − 1 ε v a r j c ̂ j t . $$\begin{eqnarray} \hat{y_{t}}=\hat{c} & \approx & E_{j}\hat{c}_{jt}+\frac{1}{2}{\left(1-\frac{1}{\epsilon }\right)}var_{j}\hat{c}_{jt} .\end{eqnarray}$$ (A.9)
    The last relationship implies
    E j c ̂ j t = y t ̂ − 1 2 1 − 1 ε v a r j c ̂ j t . $$\begin{equation} E_{j}\hat{c}_{jt}=\hat{y_{t}}-\frac{1}{2}{\left(1-\frac{1}{\epsilon }\right)}var_{j}\hat{c}_{jt}. \end{equation}$$ (A.10)

    The term E j c ̂ j t $E_{j}\hat{c}_{jt}$ in (A.9) is the average log deviation of consumption of individual good, and the term v a r j c ̂ j t $var_{j}\hat{c}_{jt}$ captures the dispersion in the average consumption of the household.

    The dispersion of consumption across goods ( v a r j c ̂ j t $var_{j}\hat{c}_{jt}$ ) can also be defined as
    v a r j c ̂ j t = E j c ̂ j t − E j c ̂ j t 2 = E j c ̂ j t 2 − E j c ̂ j , t 2 , $$\begin{eqnarray*} var_{j}\hat{c}_{jt} & = & E_{j}{\left(\hat{c}_{jt}-E_{j}\hat{c}_{jt}\right)}^{2}=E_{j}{\left(\hat{c}_{jt}^{2}\right)}-{\left[E_{j}\hat{c}_{j,t}\right]}^{2}, \end{eqnarray*}$$
    meaning that
    E j c ̂ j t 2 = E j c ̂ j , t 2 + v a r j c ̂ j t . $$\begin{eqnarray} E_{j}{\left(\hat{c}_{jt}^{2}\right)} & = & {\left(E_{j}\hat{c}_{j,t}\right)}^{2}+var_{j}\hat{c}_{jt}. \end{eqnarray}$$ (A.11)
    Integrating υ ( C j t , z t ) $\upsilon (C_{jt},z_{t})$ given by (A.8) over all goods, and using the relationships (A.10) and (A.11), we obtain
    ∫ 0 1 υ ( c ̂ j t , z t ) d j = U Y Y ¯ 1 − Ψ − ( 1 + φ ) z ̂ t y ̂ t + 1 2 1 + φ y ̂ t 2 + 1 2 φ + 1 ε v a r j c ̂ j t + t . i . p . , $$\begin{eqnarray} &&\int _{0}^{1}\upsilon (\hat{c}_{jt},z_{t})dj\nonumber\\ &&= U_{Y}\overline{Y}{\left\lbrace {\left[1-\varPsi -(1+\varphi)\hat{z}_{t}\right]}\hat{y}_{t}+\frac{1}{2}{\left(1+\varphi \right)}\hat{y}_{t}^{2}+\frac{1}{2}{\left(\varphi +\frac{1}{\epsilon }\right)}var_{j}\hat{c}_{jt}\right\rbrace} \nonumber \\ & & +\mathrm{t.i.p.,} \end{eqnarray}$$ (A.12)
    where terms like y ̂ t v a r j c ̂ j t $\hat{y}_{t}var_{j}\hat{c}_{jt}$ and v a r j c ̂ j t 2 $\left(var_{j}\hat{c}_{jt}\right)^{2}$ are set equal to zero and, as before, the terms such as ε − 1 v a r j c ̂ j t $\epsilon ^{-1}var_{j}\hat{c}_{jt}$ and ( 1 + φ ) z ̂ t v a r j c ̂ j t $(1+\varphi)\hat{z}_{t}var_{j}\hat{c}_{jt}$ will be considered as of third order.

    A.3 Combining Approximated Utility of Consumption and Disutility of Work

    Bringing together the approximation results for the utility of consumption (A.4) and the disutility of work (A.12), we obtain
    V t ≈ U Y Y ¯ Ψ + 1 − σ ϱ ̂ t + ( 1 + φ ) z ̂ t y ̂ t − 1 2 σ + φ y ̂ t 2 − 1 2 φ + 1 ε v a r j c ̂ j t + t . i . p . $$\begin{eqnarray} V_{t} & \approx & U_{Y}\overline{Y}{\left\lbrace {\left[\varPsi +{\left(1-\sigma \right)}\hat{\varrho }_{t}+(1+\varphi)\hat{z}_{t}\right]}\hat{y}_{t}-\frac{1}{2}{\left(\sigma +\varphi \right)}\hat{y}_{t}^{2}\right.}\nonumber \\ & &{\left.-\frac{1}{2}{\left(\varphi +\frac{1}{\epsilon }\right)}var_{j}\hat{c}_{jt}\right\rbrace} +\mathrm{t.i.p.} \end{eqnarray}$$ (A.13)
    Using the definition (10), we get
    y ̂ t f = 1 − σ ϱ ̂ t + ( 1 + φ ) z ̂ t σ + φ . $$\begin{eqnarray} \hat{y}_{t}^{f} & = & \frac{{\left(1-\sigma \right)}\hat{\varrho }_{t}+(1+\varphi)\hat{z}_{t}}{\sigma +\varphi } .\end{eqnarray}$$ (A.14)
    The utility's approximation (A.13) can now be rewritten while using U Y = U C $U_{Y}=U_{C}$ , as
    V t ≈ − 1 2 σ + φ U C Y ¯ x t − x ∼ 2 + φ + 1 ε σ + φ v a r j c ̂ j t + t . i . p . , $$\begin{eqnarray} V_{t} & \approx & -\frac{1}{2}{\left(\sigma +\varphi \right)}U_{C}\overline{Y}{\left[{\left(x_{t}-\widetilde{x}\right)}^{2}+\frac{\varphi +\frac{1}{\epsilon }}{\sigma +\varphi }var_{j}\hat{c}_{jt}\right]}+\mathrm{t.i.p.,} \end{eqnarray}$$ (A.15)
    where the term Ψ σ + φ + y ̂ t f 2 enters $\left(\frac{\varPsi }{\sigma +\varphi }+\hat{y}_{t}^{f}\right)^{2} {\rm enters}$ t.i.p., x t = y t ̂ − y ̂ t f $x_{t}=\hat{y_{t}}-\hat{y}_{t}^{f}$ is defined as the gap between the current output and the flexible-price equilibrium output, and
    x ∼ = Ψ σ + φ . $$\begin{equation} \widetilde{x}=\frac{\varPsi }{\sigma +\varphi } .\end{equation}$$ (A.16)

    Denote by Y ¯ ∗ $\overline{Y}^{*}$ the steady-state efficient level of output. Then, x ∼ $\widetilde{x}$ is equal to log Y ¯ ∗ Y ¯ $\log \frac{\overline{Y}^{*}}{\overline{Y}}$ and is a measure of the distortion generated by the monopolistic competition. We obtain x ∼ = 0 $\widetilde{x}=0$ in the case of perfect competition where ε → + ∞ $\epsilon \rightarrow +\infty$ .

    A.4 Expressing the Variance of Consumption of Individual Good in Terms of Price Dispersion

    To express the variance of c ̂ j t $\hat{c}_{jt}$ in terms of the dispersion of prices across individual firms, we use C t = Y t $C_{t}=Y_{t}$ in (2) to write C j t = P j t P t − ε C t = P j t P t − ε Y t $C_{jt}=\left(\frac{P_{jt}}{P_{t}}\right)^{-\epsilon }C_{t}=\left(\frac{P_{jt}}{P_{t}}\right)^{-\epsilon }Y_{t}$ . Log-linearizing the latter gives
    c ̂ j t = y ̂ t − ε p ̂ j t − p ̂ t . $$\begin{equation*} \hat{c}_{jt}=\hat{y}_{t}-\epsilon {\left(\hat{p}_{jt}-\hat{p}_{t}\right)}. \end{equation*}$$
    Evaluating the variance across all goods j $j$ and all firms j $j$ , we get
    v a r j c ̂ j t = ε 2 v a r j p ̂ j t . $$\begin{equation} var_{j}\hat{c}_{jt}=\epsilon ^{2}var_{j}\hat{p}_{jt}. \end{equation}$$ (A.17)
    Rewriting (A.15) leads to the following welfare criterion:
    V t = − 1 2 U C Y ¯ σ + φ x t − x ∼ 2 + φ + 1 ε ε 2 v a r j p ̂ j t + t . i . p . . $$\begin{eqnarray} V_{t} & = & -\frac{1}{2}U_{C}\overline{Y}{\left[{\left(\sigma +\varphi \right)}{\left(x_{t}-\widetilde{x}\right)}^{2}+{\left(\varphi +\frac{1}{\epsilon }\right)}\epsilon ^{2}var_{j}\hat{p}_{jt}\right]}+\mathrm{t.i.p.}. \end{eqnarray}$$ (A.18)

    A.5 The Derivation of Price Dispersion

    We now relate v a r j p ̂ j t = v a r j log P j t ≡ ▵ t $var_{j}\hat{p}_{jt}=var_{j}\log P_{jt}\equiv \triangle _{t}$ to the average inflation rate across all firms P ¯ t ≡ E j log P j t $\overline{P}_{t}\equiv E_{j}\log P_{jt}$ . Recall that in the price adjustment mechanism based on Calvo (1983), a randomly chosen fraction 1 − θ $1-\theta$ of all firms can optimally adjust price each period. Since v a r j log P j t − 1 = v a r j P ¯ t − 1 = 0 $var_{j}\log P_{jt-1}=var_{j}\overline{P}_{t-1}=0$ , we obtain:
    ▵ t = v a r j log P j t − P ¯ t − 1 = E j log P j t − P ¯ t − 1 2 − E j log P j t − P ¯ t − 1 2 = θ E j log P j , t − 1 − P ¯ t − 1 2 + ( 1 − θ ) E j log P j t ∗ − P ¯ t − 1 2 − P ¯ t − P ¯ t − 1 2 , $$\begin{eqnarray} \triangle _{t} & = & var_{j}{\left[\log P_{jt}-\overline{P}_{t-1}\right]}=E_{j}{\left[\log P_{jt}-\overline{P}_{t-1}\right]}^{2}-{\left[E_{j}\log P_{jt}-\overline{P}_{t-1}\right]}^{2}\nonumber \\ & = & \theta E_{j}{\left[\log P_{j,t-1}-\overline{P}_{t-1}\right]}^{2}+(1-\theta)E_{j}{\left[\log P_{jt}^{*}-\overline{P}_{t-1}\right]}^{2} {-} {\left[\overline{P}_{t}-\overline{P}_{t-1}\right]}^{2},\nonumber \\ \end{eqnarray}$$ (A.19)
    where P j t ∗ $P_{jt}^{*}$ is the price set at time t $t$ by the fraction 1 − θ $1-\theta$ of firms that reset their price. Given that P ¯ t = ( 1 − θ ) log P j t ∗ + θ P ¯ t − 1 $\overline{P}_{t}=(1-\theta)\log P_{jt}^{*}+\theta \overline{P}_{t-1}$ , it follows that
    log P j t ∗ − P ¯ t − 1 = 1 1 − θ P ¯ t − P ¯ t − 1 . $$\begin{equation} \log P_{jt}^{*}-\overline{P}_{t-1}=\frac{1}{1-\theta }{\left(\overline{P}_{t}-\overline{P}_{t-1}\right)}. \end{equation}$$ (A.20)
    Using the result (A.20) in (A.19), we get
    ▵ t = θ E j log p j t − 1 − P ¯ t − 1 2 + ( 1 − θ ) 1 1 − θ P ¯ t − P ¯ t − 1 2 − P ¯ t − P ¯ t − 1 2 = θ ▵ t − 1 + θ 1 − θ P ¯ t − P ¯ t − 1 2 ≈ θ ▵ t − 1 + θ 1 − θ π t 2 . $$\begin{eqnarray*} \triangle _{t} & = & \theta E_{j}{\left[\log p_{jt-1}-\overline{P}_{t-1}\right]}^{2}+(1-\theta){\left[\frac{1}{1-\theta }{\left(\overline{P}_{t}-\overline{P}_{t-1}\right)}\right]}^{2}-{\left(\overline{P}_{t}-\overline{P}_{t-1}\right)}^{2}\\ & = & \theta \triangle _{t-1}+\frac{\theta }{1-\theta }{\left(\overline{P}_{t}-\overline{P}_{t-1}\right)}^{2}\\ & \approx & \theta \triangle _{t-1}+\frac{\theta }{1-\theta }\pi _{t}^{2}. \end{eqnarray*}$$
    Taking the sum of discounted values of each term and making iterative substitutions imply
    E t ∑ i = 0 + ∞ β i ▵ t + i ≈ θ 1 − θ 1 − θ β E t ∑ i = 0 + ∞ β i π t + i 2 + t . i . p . $$\begin{eqnarray} E_{t}\sum _{i=0}^{+\infty }\beta ^{i}\triangle _{t+i} & \approx & {\left[\frac{\theta }{{\left(1-\theta \right)}{\left(1-\theta \beta \right)}}\right]}E_{t}\sum _{i=0}^{+\infty }\beta ^{i}\pi _{t+i}^{2}+\mathrm{t.i.p}. \end{eqnarray}$$ (A.21)

    Taking the sum of discounted values of V t + i $V_{t+i}$ given by (A.18), then using ▵ t ≡ v a r j p ̂ j t $\triangle _{t}\equiv var_{j}\hat{p}_{jt}$ and (A.21) yields L t s = − E t ∑ i = 0 + ∞ β i V t + i Λ $L_{t}^{s}=-\frac{E_{t}\sum _{i=0}^{+\infty }\beta ^{i}V_{t+i}}{\varLambda }$ with Λ = 1 2 U C Y ¯ θ 1 − θ 1 − θ β ε 1 + ε φ $\varLambda =\frac{1}{2}U_{C}\overline{Y}\left[\frac{\theta }{\left(1-\theta \right)\left(1-\theta \beta \right)}\epsilon \left(1+\epsilon \varphi \right)\right]$ , which is reported in (13).

    Appendix B: The Effect of Learning on the Equilibrium

    In Subsection B.1, we closely follow Molnár and Santoro (2014) to find the equilibrium solution. In Subsection B.2, we develop original techniques to analyze the effects of learning.

    B.1 Equilibrium Solution of Inflation When Agents Are Learning

    Using (12) and (32), we obtain
    x t = 1 κ π t − β 1 κ a t − 1 κ e t , $$\begin{eqnarray} x_{t} & = & \frac{1}{\kappa }\pi _{t}-\beta \frac{1}{\kappa }a_{t}-\frac{1}{\kappa }e_{t},\end{eqnarray}$$ (B.1)
    x t + 1 = 1 κ π t + 1 − β κ a t + γ ( π t − a t ) − 1 κ e t + 1 . $$\begin{eqnarray} x_{t+1} & = & \frac{1}{\kappa }\pi _{t+1}-\frac{\beta }{\kappa }{\left[a_{t}+\gamma (\pi _{t}-a_{t})\right]}-\frac{1}{\kappa }e_{t+1}. \end{eqnarray}$$ (B.2)
    Substituting x t $x_{t}$ and x t + 1 $x_{t+1}$ given by (B.1) and (B.2) into (37) and arranging terms yield
    E t π t + 1 = A 11 π t + A 12 a t + A 13 x ∼ + A 14 ξ τ + P 1 e t , $$\begin{equation} E_{t}\pi _{t+1}=A_{11}\pi _{t}+A_{12}a_{t}+A_{13}\widetilde{x}+A_{14}\xi \tau +P_{1}e_{t}, \end{equation}$$ (B.3)
    with
    A 11 ≡ α + κ 2 + α γ β 2 1 − γ ( 1 − β ) β α 1 − γ ( 1 − β ) + κ 2 1 − γ , $$\begin{eqnarray} A_{11} & \equiv & \frac{\alpha +\kappa ^{2}+\alpha \gamma \beta ^{2}{\left[1-\gamma (1-\beta)\right]}}{\beta {\left\lbrace \alpha {\left[1-\gamma (1-\beta)\right]}+\kappa ^{2}{\left(1-\gamma \right)}\right\rbrace} },\end{eqnarray}$$ (B.4)
    A 12 ≡ − α β 1 − β 1 − γ 1 − γ ( 1 − β ) β α 1 − γ ( 1 − β ) + κ 2 1 − γ , $$\begin{eqnarray} A_{12} & \equiv & -\frac{\alpha \beta {\left\lbrace 1-\beta {\left(1-\gamma \right)}{\left[1-\gamma (1-\beta)\right]}\right\rbrace} }{\beta {\left\lbrace \alpha {\left[1-\gamma (1-\beta)\right]}+\kappa ^{2}{\left(1-\gamma \right)}\right\rbrace} },\end{eqnarray}$$ (B.5)
    A 13 ≡ − α κ 1 − β 1 − γ 1 − β β α 1 − γ ( 1 − β ) + κ 2 1 − γ , $$\begin{eqnarray} A_{13} & \equiv & -\frac{\alpha \kappa {\left\lbrace 1-\beta {\left[1-\gamma {\left(1-\beta \right)}\right]}\right\rbrace} }{\beta {\left\lbrace \alpha {\left[1-\gamma (1-\beta)\right]}+\kappa ^{2}{\left(1-\gamma \right)}\right\rbrace} },\end{eqnarray}$$ (B.6)
    A 14 ≡ κ 2 1 − β 1 − γ 2 β α 1 − γ ( 1 − β ) + κ 2 1 − γ , $$\begin{eqnarray} A_{14} & \equiv & \frac{\kappa ^{2}{\left[1-\beta {\left(1-\gamma \right)}\right]}}{2\beta {\left\lbrace \alpha {\left[1-\gamma (1-\beta)\right]}+\kappa ^{2}{\left(1-\gamma \right)}\right\rbrace} },\end{eqnarray}$$ (B.7)
    P 1 ≡ − α β α 1 − γ ( 1 − β ) + κ 2 1 − γ . $$\begin{eqnarray} P_{1} & \equiv & -\frac{\alpha }{\beta {\left\lbrace \alpha {\left[1-\gamma (1-\beta)\right]}+\kappa ^{2}{\left(1-\gamma \right)}\right\rbrace} }. \end{eqnarray}$$ (B.8)
    Proposition 1 from Blanchard and Kahn (1980) implies that the ALM for inflation takes the following form:
    π t = c π c g a t + Ω π c g x ∼ + Θ π c g ξ τ + d π c g e t . $$\begin{equation} \pi _{t}=c_{\pi }^{cg}a_{t}+\varOmega _{\pi }^{cg}\widetilde{x}+\Theta _{\pi }^{cg}\xi \tau +d_{\pi }^{cg}e_{t}. \end{equation}$$ (B.9)
    Combining (32) and (B.9) gives: E t π t + 1 = c π c g ( 1 − γ ) a t + γ π t + Θ π c g ξ τ + Ω π c g x ∼ $E_{t}\pi _{t+1}=c_{\pi }^{cg}\left[(1-\gamma)a_{t}+\gamma \pi _{t}\right]+\Theta _{\pi }^{cg}\xi \tau +\varOmega _{\pi }^{cg}\widetilde{x}$ . Substituting the latter into (B.3) and arranging terms yield
    π t = A 12 − c π c g ( 1 − γ ) c π c g γ − A 11 a t + A 14 − Ω π c g γ c π c g − A 11 x ∼ + A 13 − Θ π c g c π c g γ − A 11 ξ τ + P 1 c π c g γ − A 11 e t . $$\begin{eqnarray} \pi _{t}&=&\frac{{\left[A_{12}-c_{\pi }^{cg}(1-\gamma)\right]}}{c_{\pi }^{cg}\gamma -A_{11}}a_{t}+\frac{A_{14}-\varOmega _{\pi }^{cg}}{\gamma c_{\pi }^{cg}-A_{11}}\widetilde{x}+\frac{A_{13}-\Theta _{\pi }^{cg}}{c_{\pi }^{cg}\gamma -A_{11}}\xi \tau \nonumber\\ &&+\frac{P_{1}}{c_{\pi }^{cg}\gamma -A_{11}}e_{t}. \end{eqnarray}$$ (B.10)
    To determine the undetermined coefficients, we compare (B.9) with (B.10) to get
    c π c g = A 12 − c π c g ( 1 − γ ) γ c π c g − A 11 , $$\begin{eqnarray} c_{\pi }^{cg} & = & \dfrac{A_{12}-c_{\pi }^{cg}(1-\gamma)}{\gamma c_{\pi }^{cg}-A_{11}},\end{eqnarray}$$ (B.11)
    d π c g = P 1 γ c π c g − A 11 , $$\begin{eqnarray} d_{\pi }^{cg} & = & \dfrac{P_{1}}{\gamma c_{\pi }^{cg}-A_{11}},\end{eqnarray}$$ (B.12)
    Ω π c g = A 13 1 + γ c π c g − A 11 $$\begin{eqnarray} \varOmega _{\pi }^{cg} & = & \frac{A_{13}}{1+\gamma c_{\pi }^{cg}-A_{11}}\end{eqnarray}$$ (B.13)
    Θ π c g = A 14 1 + c π c g γ − A 11 , $$\begin{eqnarray} \Theta _{\pi }^{cg} & = & \frac{A_{14}}{1+c_{\pi }^{cg}\gamma -A_{11}}, \end{eqnarray}$$ (B.14)
    Gathering (32) and (B.3), while using (B.1) to substitute x t $x_{t}$ , we obtain
    E t y t + 1 = Z + A y t + P e t , $$\begin{equation*} E_{t}y_{t+1}=Z+Ay_{t}+Pe_{t}, \end{equation*}$$
    where y t ≡ π t , a t , Z ≡ A 13 ξ τ + A 14 x ∼ 0 , A ≡ A 11 A 12 γ 1 − γ , and P ≡ P 1 0 $y_{t}\equiv \left[\pi _{t},\,a_{t}\right],\thinspace Z\equiv \left[ \def\eqcellsep{&}\begin{array}{c}A_{13}\xi \tau +A_{14}\widetilde{x}\\ 0 \end{array} \right],\,A\equiv \def\eqcellsep{&}\begin{bmatrix} A_{11} & A_{12}\\ \gamma & 1-\gamma \end{bmatrix},\thinspace \mathrm{and}\,P\equiv \def\eqcellsep{&}\begin{bmatrix} P_{1}\\ 0 \end{bmatrix}$ . This system is subject to two boundary conditions: a 0 $a_{0}$ and lim s → ∞ | E t π t + s | < ∞ $\underset{s\rightarrow \infty }{\lim }|E_{t}\pi _{t+s}|<\infty$ .

    Among infinite stochastic sequences of c π c g $c_{\pi }^{cg}$ satisfying (B.11), we focus on a nonexplosive solution, that is, the eigenvalue of A $A$ inside the unit circle. Indeed, the policymaker would not choose an explosive solution because it would generate very high welfare losses.

    The discriminant of the characteristic polynomial of A $A$ is strictly positive, that is, ▵ = A 11 − 1 − γ 2 + 4 γ A 12 > 0 $\triangle =\left[A_{11}-\left(1-\gamma \right)\right]^{2}+4\gamma A_{12}>0$ , meaning that A $A$ has two real eigenvalues ( μ 1 $\mu _{1}$ , μ 2 $\mu _{2}$ ). To show that one is inside and one outside the unit circle, it is sufficient to show that ( 1 − μ 1 ) ( 1 − μ 2 ) < 0 $(1-\mu _{1})(1-\mu _{2})<0$ or equivalently μ 1 + μ 2 > 1 + μ 1 μ 2 $\mu _{1}+\mu _{2}>1+\mu _{1}\mu _{2}$ . Notice that μ 1 + μ 2 $\mu _{1}+\mu _{2}$ equals the trace of A $A$ and μ 1 μ 2 $\mu _{1}\mu _{2}$ its determinant. Using these equivalences and substituting A 11 $A_{11}$ and A 12 $A_{12}$ using (B.4) and (B.5) and rearranging the terms, we find that the inequality μ 1 + μ 2 > 1 + μ 1 μ 2 $\mu _{1}+\mu _{2}>1+\mu _{1}\mu _{2}$ is true if α 1 − β 1 − β 1 − γ ( 1 − β ) + κ 2 1 − β 1 − γ > 0 $\alpha \left(1-\beta \right)\left\lbrace 1-\beta \left[1-\gamma (1-\beta)\right]\right\rbrace +\kappa ^{2}\left[1-\beta \left(1-\gamma \right)\right]>0$ , which is always verified.

    Rewriting (B.11) as γ ( c π c g ) 2 + ( 1 − γ − A 11 ) c π c g − A 12 = 0 $\gamma (c_{\pi }^{cg})^{2}+(1-\gamma -A_{11})c_{\pi }^{cg}-A_{12}=0$ and substituting A 11 $A_{11}$ and A 12 $A_{12}$ by their expression given in (B.4) and (B.5) yield
    p 2 ( c π c g ) 2 + p 1 c π c g + p 0 = 0 . $$\begin{equation} p_{2}(c_{\pi }^{cg})^{2}+p_{1}c_{\pi }^{cg}+p_{0}=0. \end{equation}$$ (B.15)
    with
    p 0 = α β 1 − β ( 1 − γ ) 1 − γ ( 1 − β ) > 0 , p 1 = β 1 − γ κ 2 ( 1 − γ ) + α 1 − γ ( 1 − β ) − α γ β 2 1 − γ ( 1 − β ) − α − κ 2 , p 2 = γ β α 1 − γ ( 1 − β ) + κ 2 1 − γ > 0 . $$\begin{eqnarray*} p_{0} & = & \alpha \beta {\left\lbrace 1-\beta (1-\gamma){\left[1-\gamma (1-\beta)\right]}\right\rbrace} >0,\\ p_{1} & = & \beta {\left(1-\gamma \right)}{\left\lbrace \kappa ^{2}(1-\gamma)+\alpha {\left[1-\gamma (1-\beta)\right]}\right\rbrace} \\ && -\alpha \gamma \beta ^{2}{\left[1-\gamma (1-\beta)\right]}-\alpha -\kappa ^{2},\\ p_{2} & = & \gamma \beta {\left\lbrace \alpha {\left[1-\gamma (1-\beta)\right]}+\kappa ^{2}{\left(1-\gamma \right)}\right\rbrace} >0. \end{eqnarray*}$$
    We rewrite p 1 $p_{1}$ as p 1 = − κ 2 1 − β ( 1 − γ ) − α ( 1 − β ) 1 − β 1 − γ ( 1 − β ) − p 0 − p 2 < 0 $p_{1}=-\kappa ^{2}\left[1-\beta (1-\gamma)\right]-\alpha (1-\beta)\left\lbrace 1-\beta \left[1-\gamma (1-\beta)\right]\right\rbrace -p_{0}-p_{2}<0$ . Then, it is straightforward to show that the polynomial (B.15) has a positive discriminant and thus two real roots. To characterize the solutions of c π c g $c_{\pi }^{cg}$ , we write (B.15) as
    c π c g = − p 0 + p 2 c π c g 2 p 1 ≡ f ( c π c g ) . $$\begin{equation} c_{\pi }^{cg}=-\dfrac{p_{0}+p_{2}{\left(c_{\pi }^{cg}\right)}^{2}}{p_{1}}\equiv f(c_{\pi }^{cg}).\end{equation}$$ (B.16)
    As f ( c π c g ) $f(c_{\pi }^{cg})$ is strictly increasing for c π c g ∈ 0 , 1 $c_{\pi }^{cg}\in \left[0,1\right]$ with f ′ ( c π c g ) = − 2 p 2 p 1 c π c g > 0 $f^{\prime }(c_{\pi }^{cg})=-\dfrac{2p_{2}}{p_{1}}c_{\pi }^{cg}>0$ for c π c g ∈ 0 , 1 $c_{\pi }^{cg}\in \left[0,1\right]$ , to prove f ( c π c g ) : 0 , 1 → ( 0 , 1 ) $f(c_{\pi }^{cg}):\left[0,1\right]\rightarrow (0,1)$ , it is sufficient to show that f ( 0 ) > 0 $f(0)>0$ and that f ( 1 ) < 1 $f(1)<1$ . The signs of p 0 $p_{0}$ , p 1 $p_{1}$ , and p 2 $p_{2}$ imply that f ( 0 ) = − p 0 p 1 > 0 $f(0)=-\dfrac{p_{0}}{p_{1}}>0$ and
    f ( 1 ) = p 0 + p 2 κ 2 1 − β ( 1 − γ ) + α ( 1 − β ) 1 − β 1 − γ ( 1 − β ) + p 0 + p 2 < 1 . $$\begin{eqnarray*} f(1) & = & \dfrac{p_{0}+p_{2}}{\kappa ^{2}{\left[1-\beta (1-\gamma)\right]}+\alpha (1-\beta){\left\lbrace 1-\beta {\left[1-\gamma (1-\beta)\right]}\right\rbrace} +p_{0}+p_{2}}<1. \end{eqnarray*}$$

    Since f ( c π c g ) : 0 , 1 → ( 0 , 1 ) $f(c_{\pi }^{cg}):\left[0,1\right]\rightarrow (0,1)$ and f ( c π c g ) $f(c_{\pi }^{cg})$ is strictly increasing, it follows from the theorem of Brouwer that there exists one unique solution of c π c g $c_{\pi }^{cg}$ in the interval (0,1), given in (39).

    The other possible solution, c π c g = − p 1 + p 1 2 − 4 p 2 p 0 2 p 2 $c_{\pi }^{cg}=\frac{-p_{1}+\sqrt {p_{1}^{2}-4p_{2}p_{0}}}{2p_{2}}$ , is larger than unity, which is excluded to avoid explosive inflation dynamics. Replacing A 11 $A_{11}$ , A 13 $A_{13}$ , A 14 $A_{14}$ , and P 1 $P_{1}$ given by (B.4), (B.6), (B.7) and (B.8) into (B.12), (B.13) and (B.14) leads to the solutions of d π c g $d_{\pi }^{cg}$ , Ω π c g $\varOmega _{\pi }^{cg}$ , and Θ π c g $\Theta _{\pi }^{cg}$ reported in (40)–(42).

    The feedback coefficient on E t π t + 1 $E_{t}\pi _{t+1}$ in the ALM for inflation under discretion and RE, α β α + κ 2 $\frac{\alpha \beta }{\alpha +\kappa ^{2}}$ could be shown to be the upper bound for the nonexplosive solution of c π c g $c_{\pi }^{cg}$ such that f ( c π c g ) : [ 0 , α β α + κ 2 ] → ( 0 , α β α + κ 2 ) $f(c_{\pi }^{cg}):[0,\tfrac{\alpha \beta }{\alpha +\kappa ^{2}}]\rightarrow (0,\tfrac{\alpha \beta }{\alpha +\kappa ^{2}})$ . Substituting c π c g $c_{\pi }^{cg}$ by α β α + κ 2 $\tfrac{\alpha \beta }{\alpha +\kappa ^{2}}$ into f ( c π c g ) $f(c_{\pi }^{cg})$ defined by (B.16), we find
    f ( α β α + κ 2 ) = − p 0 + p 2 α β α + κ 2 2 p 1 = α β α + κ 2 α + κ 2 α β p 0 + α β α + κ 2 p 2 − p 1 . $$\begin{eqnarray} f(\dfrac{\alpha \beta }{\alpha +\kappa ^{2}}) & = & -\dfrac{p_{0}+p_{2}{\left(\tfrac{\alpha \beta }{\alpha +\kappa ^{2}}\right)}^{2}}{p_{1}}=\dfrac{\tfrac{\alpha \beta }{\alpha +\kappa ^{2}}{\left(\tfrac{\alpha +\kappa ^{2}}{\alpha \beta }p_{0}+\tfrac{\alpha \beta }{\alpha +\kappa ^{2}}p_{2}\right)}}{-p_{1}}.\quad \end{eqnarray}$$ (B.17)
    Using p 0 = − α ( 1 − β ) + κ 2 α β p 0 + α + κ 2 α β p 0 $p_{0}=-\tfrac{\alpha (1-\beta)+\kappa ^{2}}{\alpha \beta }p_{0}+\tfrac{\alpha +\kappa ^{2}}{\alpha \beta }p_{0}$ and the definition of p 0 $p_{0}$ , p 1 $p_{1}$ , and p 2 $p_{2}$ , we rewrite the denominator in (B.17) as
    − p 1 = κ 2 1 − β ( 1 − γ ) + α ( 1 − β ) 1 − β 1 − γ ( 1 − β ) − α ( 1 − β ) + κ 2 α β p 0 + α + κ 2 α β p 0 + p 2 = − ( 1 − β ) p 2 + α + κ 2 α β p 0 + p 2 = β p 2 + α + κ 2 α β p 0 . $$\begin{eqnarray} -p_{1} & = & \kappa ^{2}{\left[1-\beta (1-\gamma)\right]}+\alpha (1-\beta){\left\lbrace 1-\beta {\left[1-\gamma (1-\beta)\right]}\right\rbrace}\nonumber \\ &&-\tfrac{\alpha (1-\beta)+\kappa ^{2}}{\alpha \beta }p_{0}+\tfrac{\alpha +\kappa ^{2}}{\alpha \beta }p_{0}+p_{2}\nonumber \\ & = & -(1-\beta)p_{2}+\tfrac{\alpha +\kappa ^{2}}{\alpha \beta }p_{0}+p_{2}=\beta p_{2}+\tfrac{\alpha +\kappa ^{2}}{\alpha \beta }p_{0}. \end{eqnarray}$$ (B.18)
    Substituting the final expression of − p 1 $-p_{1}$ into (B.17), we obtain
    f ( α β α + κ 2 ) = α β α + κ 2 α + κ 2 α β p 0 + α β α + κ 2 p 2 β κ 2 α + κ 2 p 2 + α + κ 2 α β p 0 + α β α + κ 2 p 2 < α β α + κ 2 . $$\begin{eqnarray*} f(\dfrac{\alpha \beta }{\alpha +\kappa ^{2}}) & = & \dfrac{\tfrac{\alpha \beta }{\alpha +\kappa ^{2}}{\left(\tfrac{\alpha +\kappa ^{2}}{\alpha \beta }p_{0}+\tfrac{\alpha \beta }{\alpha +\kappa ^{2}}p_{2}\right)}}{\tfrac{\beta \kappa ^{2}}{\alpha +\kappa ^{2}}p_{2}+\tfrac{\alpha +\kappa ^{2}}{\alpha \beta }p_{0}+\tfrac{\alpha \beta }{\alpha +\kappa ^{2}}p_{2}}<\dfrac{\alpha \beta }{\alpha +\kappa ^{2}}. \end{eqnarray*}$$
    Given that f ( 0 ) > 0 $f(0)>0$ and f ′ ( c π c g ) = − 2 p 2 p 1 c π c g > 0 $f^{\prime }(c_{\pi }^{cg})=-\dfrac{2p_{2}}{p_{1}}c_{\pi }^{cg}>0$ for c π c g ∈ ( 0 , 1 ) $c_{\pi }^{cg}\in (0,1)$ , f ( c π c g ) $f(c_{\pi }^{cg})$ is strictly increasing in the interval ( 0 , α β α + κ 2 ) $(0,\ \tfrac{\alpha \beta }{\alpha +\kappa ^{2}})$ . This property and the fact that f ( c π c g ) : [ 0 , α β α + κ 2 ] → ( 0 , α β α + κ 2 ) $f(c_{\pi }^{cg}):\ [0,\ \tfrac{\alpha \beta }{\alpha +\kappa ^{2}}]\rightarrow (0,\ \tfrac{\alpha \beta }{\alpha +\kappa ^{2}})$ imply that c π c g $c_{\pi }^{cg}$ has a unique solution verifying 0 < c π c g < α β α + κ 2 < β $0<c_{\pi }^{cg}<\tfrac{\alpha \beta }{\alpha +\kappa ^{2}}<\beta$ . Replacing Φ ( γ ) $\varPhi (\gamma)$ by its expression into d π c g $d_{\pi }^{cg}$ and rearranging, we get d π c g = α α + α β γ 1 − γ ( 1 − β ) β − c π c g + β κ 2 1 − γ + κ 2 1 − β 1 − γ 1 + γ c π c g $d_{\pi }^{cg}=\tfrac{\alpha }{\alpha +\alpha \beta \gamma \left[1-\gamma (1-\beta)\right]\left(\beta -c_{\pi }^{cg}\right)+\beta \kappa ^{2}\left(1-\gamma \right)+\kappa ^{2}\left\lbrace 1-\beta \left(1-\gamma \right)\left(1+\gamma c_{\pi }^{cg}\right)\right\rbrace }$ . Given that c π c g < β $c_{\pi }^{cg}<\beta$ , it follows that 0 < d π c g < 1 $0<d_{\pi }^{cg}<1$ .

    B.2 The Effect of an Increase in Learning Gain

    Differentiating p 0 $p_{0}$ , p 1 $p_{1}$ , and p 2 $p_{2}$ with respect to γ $\gamma$ and using (B.18) yield
    ∂ p 2 ∂ γ = β α 1 − 2 γ ( 1 − β ) + κ 2 1 − 2 γ , ∂ p 0 ∂ γ = α β 2 ( 2 − β ) ( 1 − γ ) + γ β > 0 , ∂ p 1 ∂ γ = − β ∂ p 2 ∂ γ − α + κ 2 α β ∂ p 0 ∂ γ . $$\begin{eqnarray*} \frac{\partial p_{2}}{\partial \gamma } & = & \beta {\left\lbrace \alpha {\left[1-2\gamma (1-\beta)\right]}+\kappa ^{2}{\left(1-2\gamma \right)}\right\rbrace},\\ \frac{\partial p_{0}}{\partial \gamma } & = & \alpha \beta ^{2}{\left[(2-\beta)(1-\gamma)+\gamma \beta \right]}>0,\\ \frac{\partial p_{1}}{\partial \gamma } & =- & \beta \frac{\partial p_{2}}{\partial \gamma }-\frac{\alpha +\kappa ^{2}}{\alpha \beta }\frac{\partial p_{0}}{\partial \gamma }. \end{eqnarray*}$$
    Differentiating c π c g $c_{\pi }^{cg}$ given by (39) with respect to γ $\gamma$ , we obtain
    ∂ c π c g ∂ γ = − p 2 − p 1 p 2 p 1 2 − 4 p 2 p 0 ∂ p 1 ∂ γ + 2 p 2 p 2 p 1 2 − 4 p 2 p 0 ∂ p 0 ∂ γ + p 1 + p 1 2 − 2 p 2 p 0 p 1 2 − 4 p 2 p 0 ∂ p 2 ∂ γ 2 p 2 2 , $$\begin{equation*} \frac{\partial c_{\pi }^{cg}}{\partial \gamma }=\frac{{\left(-p_{2}-\frac{p_{1}p_{2}}{\sqrt {p_{1}^{2}-4p_{2}p_{0}}}\right)}\frac{\partial p_{1}}{\partial \gamma }+\frac{2p_{2}p_{2}}{\sqrt {p_{1}^{2}-4p_{2}p_{0}}}\frac{\partial p_{0}}{\partial \gamma }+{\left(p_{1}+\frac{p_{1}^{2}-2p_{2}p_{0}}{\sqrt {p_{1}^{2}-4p_{2}p_{0}}}\right)}\frac{\partial p_{2}}{\partial \gamma }}{2p_{2}^{2}}, \end{equation*}$$
    which, incorporating ∂ p 2 ∂ γ = − 1 β ∂ p 1 ∂ γ − α + κ 2 α β 2 ∂ p 0 ∂ γ $\frac{\partial p_{2}}{\partial \gamma }=-\frac{1}{\beta }\frac{\partial p_{1}}{\partial \gamma }-\tfrac{\alpha +\kappa ^{2}}{\alpha \beta ^{2}}\frac{\partial p_{0}}{\partial \gamma }$ deduced from (B.18), becomes
    ∂ c π c g ∂ γ = 1 2 p 2 2 F ∂ p 1 ∂ γ + G ∂ p 2 ∂ γ , $$\begin{equation*} \frac{\partial c_{\pi }^{cg}}{\partial \gamma }=\frac{1}{2p_{2}^{2}}{\left(F\frac{\partial p_{1}}{\partial \gamma }+G\frac{\partial p_{2}}{\partial \gamma }\right)}, \end{equation*}$$
    where F = − p 2 + − p 1 p 2 p 1 2 − 4 p 2 p 0 − 1 β p 1 − 1 β p 1 2 − 2 p 2 p 0 p 1 2 − 4 p 2 p 0 $F=-p_{2}+\tfrac{-p_{1}p_{2}}{\sqrt {p_{1}^{2}-4p_{2}p_{0}}}-\frac{1}{\beta }p_{1}-\frac{1}{\beta }\tfrac{p_{1}^{2}-2p_{2}p_{0}}{\sqrt {p_{1}^{2}-4p_{2}p_{0}}}$ and G = 2 p 2 p 2 p 1 2 − 4 p 2 p 0 − p 1 + p 1 2 − 2 p 2 p 0 p 1 2 − 4 p 2 p 0 α + κ 2 α β 2 $G=\tfrac{2p_{2}p_{2}}{\sqrt {p_{1}^{2}-4p_{2}p_{0}}}-\left(p_{1}+\tfrac{p_{1}^{2}-2p_{2}p_{0}}{\sqrt {p_{1}^{2}-4p_{2}p_{0}}}\right)\tfrac{\alpha +\kappa ^{2}}{\alpha \beta ^{2}}$ .
    Using (B.18), we get after fastidious arrangements of terms:
    ∂ c π c g ∂ γ = 1 − α + κ 2 α β c π c g H β p 2 p 1 2 − 4 p 2 p 0 , $$\begin{equation*} \frac{\partial c_{\pi }^{cg}}{\partial \gamma }=\frac{{\left(1-\tfrac{\alpha +\kappa ^{2}}{\alpha \beta }c_{\pi }^{cg}\right)}H}{\beta p_{2}\sqrt {p_{1}^{2}-4p_{2}p_{0}}}, \end{equation*}$$
    where H ≡ p 0 ∂ p 1 ∂ γ − p 1 ∂ p 0 ∂ γ $H\equiv p_{0}\frac{\partial p_{1}}{\partial \gamma }-p_{1}\frac{\partial p_{0}}{\partial \gamma }$ . Using c π c g < α β α + κ 2 $c_{\pi }^{cg}<\tfrac{\alpha \beta }{\alpha +\kappa ^{2}}$ , we find 1 − α + κ 2 α β c π c g > 1 − α + κ 2 α β α β α + κ 2 = 0 $1-\tfrac{\alpha +\kappa ^{2}}{\alpha \beta }c_{\pi }^{cg}>1-\tfrac{\alpha +\kappa ^{2}}{\alpha \beta }\tfrac{\alpha \beta }{\alpha +\kappa ^{2}}=0$ . To determine the sign of H $H$ , we first check its value for γ = 1 $\gamma =1$ and then the sign of its derivative with respect to γ $\gamma$ . For γ = 1 $\gamma =1$ , we get: ∂ p 0 ∂ γ = α β 3 > 0 $\frac{\partial p_{0}}{\partial \gamma }=\alpha \beta ^{3}>0$ , ∂ p 1 ∂ γ = − β 2 α ( 1 + β ) < 0 $\frac{\partial p_{1}}{\partial \gamma }=-\beta ^{2}\alpha (1+\beta)<0$ , p 1 = − κ 2 + α + α β 3 $p_{1}=-\left(\kappa ^{2}+\alpha +\alpha \beta ^{3}\right)$ , and p 0 = α β $p_{0}=\alpha \beta$ , and hence
    H 1 ≡ α β 3 κ 2 − α β 1 − β 2 . $$\begin{equation*} H{\left(1\right)}\equiv \alpha \beta ^{3}{\left[\kappa ^{2}-\alpha \beta {\left(1-\beta ^{2}\right)}\right]}. \end{equation*}$$
    We have H ( 1 ) < 0 $H(1)<0$ if
    κ 2 < α β 1 − β 2 . $$\begin{equation} \kappa ^{2}<\alpha \beta {\left(1-\beta ^{2}\right)}. \end{equation}$$ (B.19)
    Differentiating once H $H$ and twice p 0 $p_{0}$ and p 1 $p_{1}$ with respect to γ $\gamma$ yields
    ∂ H ∂ γ = ∂ p 0 ∂ γ ∂ p 1 ∂ γ + p 0 ∂ 2 p 1 ∂ 2 γ − ∂ p 1 ∂ γ ∂ p 0 ∂ γ − p 1 ∂ 2 p 0 ∂ 2 γ = p 0 ∂ 2 p 1 ∂ 2 γ − p 1 ∂ 2 p 0 ∂ 2 γ , ∂ 2 p 0 ∂ 2 γ = − 2 α β 2 ( 1 − β ) < 0 , ∂ 2 p 1 ∂ 2 γ = 2 β α ( 1 − β 2 ) + κ 2 > 0 . $$\begin{align*} \frac{\partial H}{\partial \gamma } & =\frac{\partial p_{0}}{\partial \gamma }\frac{\partial p_{1}}{\partial \gamma }+p_{0}\frac{\partial ^{2}p_{1}}{\partial ^{2}\gamma }-\frac{\partial p_{1}}{\partial \gamma }\frac{\partial p_{0}}{\partial \gamma }-p_{1}\frac{\partial ^{2}p_{0}}{\partial ^{2}\gamma }=p_{0}\frac{\partial ^{2}p_{1}}{\partial ^{2}\gamma }-p_{1}\frac{\partial ^{2}p_{0}}{\partial ^{2}\gamma },\\ \frac{\partial ^{2}p_{0}}{\partial ^{2}\gamma } & =-2\alpha \beta ^{2}(1-\beta)<0,\\ \frac{\partial ^{2}p_{1}}{\partial ^{2}\gamma } & =2\beta {\left[\alpha (1-\beta ^{2})+\kappa ^{2}\right]}>0. \end{align*}$$
    Substituting these second-order derivatives into the expression of ∂ H ∂ γ $\frac{\partial H}{\partial \gamma }$ yields
    ∂ H ∂ γ = 2 α 2 β 3 ( 1 − β ) 1 − β 1 − γ ( 1 − β ) + 2 α β 3 1 − β ( 1 − γ ) κ 2 > 0 . $$\begin{eqnarray*} \frac{\partial H}{\partial \gamma } & = & 2\alpha ^{2}\beta ^{3}(1-\beta){\left\lbrace 1-\beta {\left[1-\gamma (1-\beta)\right]}\right\rbrace} +2\alpha \beta ^{3}{\left[1-\beta (1-\gamma)\right]}\kappa ^{2}>0. \end{eqnarray*}$$

    Since H γ < 0 $H\left(\gamma \right)<0$ for γ = 1 $\gamma =1$ and ∂ H ∂ γ > 0 $\frac{\partial H}{\partial \gamma }>0$ for γ ∈ ( 0 , 1 ) $\gamma \in (0,1)$ , we conclude that ∂ c π c g ∂ γ < 0 $\frac{\partial c_{\pi }^{cg}}{\partial \gamma }<0$ . If the condition (B.19) was not verified, we would have ∂ c π c g ∂ γ > 0 $\frac{\partial c_{\pi }^{cg}}{\partial \gamma }>0$ for γ < 1 $\gamma <1$ .

    Differentiating d π c g $d_{\pi }^{cg}$ with respect to γ $\gamma$ yields
    ∂ d π c g ∂ γ = − α β Υ − γ α β γ + ( 1 − γ ) α + κ 2 ∂ c π c g ∂ γ κ 2 + α + α β 2 γ 2 ( β − c π c g ) + β γ ( 1 − γ ) α β − α + κ 2 c π c g 2 . $$\begin{equation*} \frac{\partial d_{\pi }^{cg}}{\partial \gamma }=\dfrac{-\alpha \beta {\left\lbrace \Upsilon -\gamma {\left[\alpha \beta \gamma +(1-\gamma){\left(\alpha +\kappa ^{2}\right)}\right]}\frac{\partial c_{\pi }^{cg}}{\partial \gamma }\right\rbrace} }{{\left\lbrace \kappa ^{2}+\alpha +\alpha \beta ^{2}\gamma ^{2}(\beta -c_{\pi }^{cg})+\beta \gamma (1-\gamma){\left[\alpha \beta -{\left(\alpha +\kappa ^{2}\right)}c_{\pi }^{cg}\right]}\right\rbrace} ^{2}}. \end{equation*}$$

    Using c π c g < α β α + κ 2 $c_{\pi }^{cg}<\tfrac{\alpha \beta }{\alpha +\kappa ^{2}}$ , we find that Υ ≡ 2 α β γ ( β − c π c g ) + ( 1 − 2 γ ) α β − ( α + κ 2 ) c π c g > 2 α β γ ( β − c π c g ) > 0 $\Upsilon \equiv 2\alpha \beta \gamma (\beta -c_{\pi }^{cg})+(1-2\gamma)\left[\alpha \beta -(\alpha +\kappa ^{2})c_{\pi }^{cg}\right]>2\alpha \beta \gamma (\beta -c_{\pi }^{cg})>0$ . It follows that ∂ d π c g ∂ γ < < 0 $\frac{\partial d_{\pi }^{cg}}{\partial \gamma }<<0$ if ∂ c π c g ∂ γ < 0 $\frac{\partial c_{\pi }^{cg}}{\partial \gamma }<0$ or if the condition (B.19) holds.

    Differentiating (41) with respect to γ $\gamma$ and using c π c g < α β α + κ 2 $c_{\pi }^{cg}<\tfrac{\alpha \beta }{\alpha +\kappa ^{2}}$ allow us to show that
    ∂ Ω π c g ∂ γ = − α β κ 1 − β Φ 2 β κ 2 + α β 2 γ κ 2 2 + β γ α + κ 2 − γ ( 1 + β γ ) ( α + κ 2 ) 1 − γ + α β γ ∂ c π c g ∂ γ . $$\begin{eqnarray*} \frac{\partial \varOmega _{\pi }^{cg}}{\partial \gamma }&=&-\frac{\alpha \beta \kappa {\left(1-\beta \right)}}{\Phi ^{2}}\\ &&{\left\lbrace \beta \kappa ^{2}+\tfrac{\alpha \beta ^{2}\gamma \kappa ^{2}{\left(2+\beta \gamma \right)}}{\alpha +\kappa ^{2}}-\gamma (1+\beta \gamma){\left[(\alpha +\kappa ^{2}){\left(1-\gamma \right)}+\alpha \beta \gamma \right]}\frac{\partial c_{\pi }^{cg}}{\partial \gamma }\right\rbrace} . \end{eqnarray*}$$

    We have ∂ Ω π c g ∂ γ < < 0 $\frac{\partial \varOmega _{\pi }^{cg}}{\partial \gamma }<<0$ if ∂ c π c g ∂ γ < 0 $\frac{\partial c_{\pi }^{cg}}{\partial \gamma }<0$ , that is, the condition (B.19) holds.

    Differentiating (42) with respect to γ $\gamma$ gives
    ∂ Θ π c g ∂ γ = − β κ 2 2 Φ 2 α β 1 − β + κ 2 + α ( 1 − β ) 1 − γ 1 − β ( 1 − γ ) − γ c π c g + α γ β ( 1 − β ) 2 ( 1 − β ) + β γ + γ 1 − β 1 − γ 1 − γ α ( 1 − β ) + κ 2 + α β ∂ c π c g ∂ γ . $$\begin{eqnarray*} \frac{\partial \Theta _{\pi }^{cg}}{\partial \gamma } & = & -\frac{\beta \kappa ^{2}}{2\Phi ^{2}}{\left\lbrace {\left\lbrace \alpha \beta {\left(1-\beta \right)}+{\left[\kappa ^{2}+\alpha (1-\beta)\right]}{\left[{\left(1-\gamma \right)}{\left[1-\beta (1-\gamma)\right]}-\gamma \right]}\right\rbrace} c_{\pi }^{cg}\right.}\\ & & +\,\alpha \gamma \beta (1-\beta){\left[2(1-\beta)+\beta \gamma \right]}+\gamma {\left[1-\beta {\left(1-\gamma \right)}\right]} \\ &&\left. {\left\lbrace {\left(1-\gamma \right)}{\left[\alpha (1-\beta)+\kappa ^{2}\right]}+\alpha \beta \right\rbrace}\tfrac{\partial c_{\pi }^{cg}}{\partial \gamma }\right\rbrace . \end{eqnarray*}$$

    Here, it is impossible to analytically determine the sign of ∂ Θ π c g ∂ γ $\frac{\partial \Theta _{\pi }^{cg}}{\partial \gamma }$ . We have checked that ∂ Θ π c g ∂ γ < 0 $\frac{\partial \Theta _{\pi }^{cg}}{\partial \gamma }<0$ for γ < 0.45 $\gamma <0.45$ , using the baseline parameter values.

    Knowing that c x c g = − 1 κ ( β − c π c g ) $c_{x}^{cg}=-\frac{1}{\kappa }(\beta -c_{\pi }^{cg})$ , d x c g = − 1 κ ( 1 − d π c g ) $d_{x}^{cg}=-\frac{1}{\kappa }(1-d_{\pi }^{cg})$ , Ω x c g = 1 κ Ω π c g $\varOmega _{x}^{cg}=\frac{1}{\kappa }\varOmega _{\pi }^{cg}$ and 𝛩 x c g = 1 κ 𝛩 π c g $\varTheta _{x}^{cg}=\frac{1}{\kappa }\varTheta _{\pi }^{cg}$ , it is straightforward to show the sign of their partial derivative with respect to γ $\gamma$ .

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.