Bulletin of Economic Research
Volume 77, Issue 1 pp. 47-66
RESEARCH ARTICLE
Open Access

Learning at university

Gervas Huxley, 

Gervas Huxley

School of Economics, University of Bristol, Bristol, UK

Search for more papers by this author
Mike W. Peacey, 

Corresponding Author

Mike W. Peacey

School of Economics, University of Bristol, Bristol, UK

Correspondence

Mike W. Peacey, School of Economics, University of Bristol, Bristol, UK.

Email: [email protected]

Search for more papers by this author
First published: 21 August 2024
https://doi.org/10.1111/boer.12470

Abstract

Much of the economic literature on education models the process of acquiring human capital as a “black box.” While such models have many interesting uses, they are of little use when a student is considering how much teaching she needs and how her time at university is allocated between study and attending class. Considering such questions requires us to “open up” the black box. Our paper shows what one such model would look like by explicitly modeling how students choose to learn. We believe that this framework can inform the current debate about teaching in higher education.

1 INTRODUCTION

In this paper, we develop a model of how individuals invest in human capital and the nature of the choices we face when we make these investments.

The theoretical literature on human capital treats the process of acquiring education as a “black box” (starting with Becker, 1962, and Ben-Porath, 1967). The inputs provided by schools, colleges, or parents (teachers, study materials, reading at home, etc.) are often lumped together into a single input (“effort,” “investment,” or “expenditure”), which is assumed to affect educational outcomes. Meanwhile students vary according to a single parameter (usually called “ability”) that determines their responsiveness to the learning input. In these models, the only decision that students have to make is how much human capital to acquire; in practice this usually comes down to years of schooling. If human capital is produced with one input, “expenditure,” then in this literature students have no meaningful choice about how they learn.

A one input model assumes that students only vary in one dimension “ability.” As long ago as 1972, Grossman combined Becker's work on human capital and time allocation (Becker, 1962; Becker, 1965), to produce a two input model of health human capital (Grossman, 1972). In his model, time is allocated between three goods: leisure, work, and time spent investing in health (e.g., exercise). In our two input model, since teaching is paid for through earnings, which requires time, the choice is ultimately one about the allocation of time between three goods: study, tuition, and work.

We develop a model where students produce human capital by combining two inputs: time spent on study ( S ) $(S)$ and time being taught by an instructor ( T ) $(T)$ , with the S–T ratio playing a similar role to the capital–labor ratio in producer theory. In producer theory, firms must decide on how capital intensive the production process should be, in our model students must decide how teaching intensive their investment in human capital should be.

There is a small theoretical literature covering how students divide their time between independent study and formal instruction (Bratti & Staffolani, 2013, Bolli & Johnes, 2015, Beneito et al., 2018), which relies heavily on the Cobb–Douglas production function. In this function, cross-price elasticity is zero, and it is therefore not possible to explore complementarities between class time and private study. The main contribution of our model is to use a constant elasticity of substitution (CES) production function, which enables us to overcome this limitation. Our model provides a framework for understanding the results of the related empirical literature (Babcock & Marks, 2011, Dolton et al., 2003, Stinebrickner & Stinebrickner, 2008, Silva, 2024).

In any model where students have meaningful choices about how they learn, dimensions other than ability become important. Cunha and Heckman (2007), like us, use a CES production function to consider complementarities between investment periods over the lifecycle. We are interested in the within-period complementarities between inputs S $S$ and T $T$ .

In this paper, we define two personality traits, independence and flexibility, that explain how students respond to the inputs in our model. Independence is a measure of how important it is for a student to engage in study. Candy (1991) characterizes independent learning as the acquisition of knowledge by the student's own efforts, with some freedom of choice in determining learning objectives and a degree of responsibility resting on the student for achieving those objectives. We interpret this idea as the share parameter in a CES production function, so that a more independent learner (IL) has a higher marginal product from study.

Flexibility is a measure of a student's willingness to consider study and teaching as interchangeable. This allows us to consider the possibility that independent learning might be a poor substitute for face-to-face teaching (HEA, 2014, Rosenblit, 2018). This naturally leads us to consider the extent to which study and teaching are substitutes or complements. If there are complementarities between teaching and study, this will reduce the extent to which substitutability is possible. We are able to model the relationship between study and teaching as anywhere from perfect substitutes to perfect complements, using the substitution parameter in a CES production.

Innovations in pedagogy represent technological change and have implications for how students should learn and cost minimize (Pea, 2004). For example, Powerpoint might increase lecture quality and therefore the productivity of instructional time; e-learning, which promotes user generated content (e.g., blogs or wikis), might increase the productivity of study. Thus, changes in pedagogy can be teaching-augmenting, or study-augmenting, or both. The introduction of recorded lectures has increased the direct productivity of both teaching and study and the complementarity between the two. The discussion about “flipped classrooms” (Abeysekera & Dawson, 2015, Bishop & Verleger, 2013) is about the type of activity that takes place inside (and outside) of the classroom, and is therefore implicitly about how the inputs in our production function should be best combined for student learning.

Educationists and economists have increasingly come to understand that students are heterogeneous across a variety of personality and noncognitive dimensions (Heckman et al., 2006). We are interested in the heterogeneous ways students combine two inputs, teaching and study, to acquire education. The cognitive psychologist Jerome Bruner emphasizes the role that teaching has when children learn tasks (Bruner, 1974, Bruner, 1997). In a classic study, in which children were tasked with building pyramids from blocks of wood, Wood et al. (1976), demonstrated the crucial role of a tutor in solving problems “beyond [the child's] unassisted efforts.” In our framework the complementarity between teacher and student emphasized in Wood et al. (1976) is similar to the complementarity we emphasize between study and teaching.

This paper has three key results. Result 1: Heterogeneity in how students learn results in different benefits from a given amount of teaching. Therefore, for a student of a given ability, the Graduate Premium will depend on how they learn and the constraints that they face. Result 2: The compulsory classes at a traditional university may impose large costs on students who are ILs. Result 3: The current “one size fits all” model is inefficient. We characterize the welfare gains that would arise from unbundling study and teaching. Although these results are relatively obvious once the model has been set out, they highlight the possibility that under the current system, students may learn inefficiently and the market failures that will result.

2 THE MODEL

In this paper, we use a CES production function, which contrasts to the earlier literature, which uses a Cobb–Douglas production function (Bratti & Staffolani, 2013, Bolli & Johnes, 2015). This allows us to derive a number of important and interesting results that these earlier models were unable to address.

In this two period model, individual i $i$ first attends university, and later enjoys the financial rewards. In the first period, it is possible to obtain education in a number of ways according to her CES education production function:
e i ( S , T ) = ( α i S ρ i + ( 1 − α i ) ( T ) ρ i ) 1 ρ i , $$\begin{equation} e_i (S,T)=(\alpha _i S^{\rho _i}+(1-\alpha _i) (T)^{\rho _i})^\frac{1}{\rho _i}, \end{equation}$$ (1)
where S $S$ and T $T$ are the time spent studying and being taught. In the CES production function α $\alpha$ is referred to as the share parameter and ρ $\rho$ as the substitution parameter. We interpret these as a measure of the student's independence and flexibility.
In the second period the realized wage, w 2 $w_2$ , will depend on the education obtained in the first period. In particular, we assume a nongraduate wage ( w ̲ = w 1 $\underline{w}=w_1$ ), and a graduate wage ( w ¯ $\overline{w}$ ). i $i$ obtains the latter if e i $e_i$ is above the threshold standard ( e ∗ $e^*$ ) required to justify the award of a degree:
w 2 ( e ( S , T ) ) = w ¯ if e ≥ e ∗ w ̲ otherwise. $$\begin{equation} w_2(e(S,T))= {\begin{cases} \overline{w} &\text{if } e \ge e^*\\ \underline{w} & \text{otherwise.} \end{cases}} \end{equation}$$ (2)

Utility maximization involves deciding whether or not to graduate from university ( e ∈ { 0 , e ∗ } $e\in \lbrace 0,e^*\rbrace$ ). We highlight those features of traditional universities that constrain students, and show how relaxing these gives students more choice about how they learn. Assumption 1 and Assumption 2 capture these features of our traditional university.

Assumption 1.A university provides a fixed amount of teaching, T ¯ $\overline{T}$ , with compulsory attendance.

Given this provision, students choose how much study to undertake ( S ∗ $S^*$ ). The student is subject to two constraints: an intratemporal time constraint (3) and an intertemporal money constraint (4). The first implies a fixed endowment of time, Ω $\Omega$ , in each period:
Ω = S + T ¯ + H , $$\begin{equation} \Omega =S+\overline{T}+H, \end{equation}$$ (3)
where H $H$ are the hours of paid work undertaken in the first period. In the second period, H = Ω $H=\Omega$ , since there will be no investment in education.

Assumption 2.A university charges a lump sum “tuition fee,” p ¯ $\overline{p}$ .

The second constraint implies that lifetime expenditure (on teaching or consumption of a composite good, m $m$ , which we treat as numéraire) cannot exceed lifetime income:
m 1 + m 2 + p ¯ ≤ w 2 ( e ( S , T ) ) Ω + w 1 H . $$\begin{equation} m_1+m_2+\overline{p} \le w_2 (e(S,T))\Omega +w_1H. \end{equation}$$ (4)

3 RESULTS

In this section, we start by considering how much studying students must undertake and the implications for who will chose to attend university (Section 3.1). We then relax the assumptions to consider situations where students are given progressively more choice about how they learn; first by assuming class attendance is optional (Section 3.2), and second by allowing full optimization in a world where students can choose how much teaching they purchase (Section 3.3). The welfare implications of this unbundling are considered in Section 3.4. Finally in Section 3.6, we show that the definition of ability introduced by Becker (1962) must be modified for a two input production function.

3.1 Traditional university

A number of authors have pointed out that higher education is bundled and that this results in inefficiencies (Norton, 2013; Wang, 1975). However, the concept of bundling being used is not clearly defined. In Assumption 1 and Assumption 2, we provide a precise definition of what it means for universities to bundle. Under these assumptions, students must choose S $S$ given T = T ¯ $T=\overline{T}$ . A student who attends university will choose to Study S ∗ $S^*$ :
S ∗ = e ∗ ρ i − ( 1 − α i ) ( T ¯ ) ρ i α i 1 ρ i . $$\begin{equation} S^*= \left(\frac{e^{*{\rho _i}} - (1-\alpha _i) (\overline{T})^{\rho _i}}{\alpha _i}\right)^{\frac{1}{\rho _i}}. \end{equation}$$ (5)

For all learners, if a higher standard ( e ∗ $(e^*$ ) is required they will need to study more. How much more depends on the marginal productivity of study, and this will depend on T ¯ $\overline{T}$ . In a situation where T ¯ $\overline{T}$ is fixed, some students will receive less teaching, and others more, than they would like. If T ¯ $\overline{T}$ is low, then ILs (i.e. those with larger α $\alpha$ ) will be at an advantage relative to directed learners (DLs), but the reverse is true if T ¯ $\overline{T}$ is higher. Moreover, the identity of the dissatisfied students will change as T ¯ $\overline{T}$  varies.

The existing literature suggests that how much studying a student must undertake depends on their ability, but in our model it is determined by how well suited they are to the particular provision (i.e., T ¯ $\overline{T}$ ) that is offered by the university.

We define the “Graduate Premium” (GP) as the net increase in consumption achieved through education. This is clearly maximized when the lowest amount of study required to graduate is undertaken:
G P ( S ∗ , T ¯ ) = Ω w ¯ + w ̲ Ω − e ∗ ρ i − ( 1 − α i ) ( T ¯ ) ρ i α i 1 ρ i − T ¯ − p ¯ − ( 2 Ω w ̲ ) . $$\begin{equation} GP(S^*,\overline{T})= \left(\Omega \overline{w}+\underline{w} \left(\Omega - \left(\frac{e^{*{\rho _i}} - (1-\alpha _i) (\overline{T})^{\rho _i}}{\alpha _i}\right)^{\frac{1}{\rho _i}}-\overline{T}\right)-\overline{p}\right)-(2\Omega \underline{w}). \end{equation}$$ (6)

If S ∗ $S^*$ (Equation 5) generates a negative Graduate Premium, a student should not attend university. This can happen if the price ( p ¯ $\overline{p}$ ) is too high, the standard ( e ∗ $e^*$ ) is too high, the difference between graduate and nongraduate wages ( w ¯ − w ̲ $\overline{w}-\underline{w}$ ) is too small, or the student is not well suited to the teaching provision provided ( T ¯ $\overline{T}$ ). A lower T ¯ $\overline{T}$ will not necessarily decrease the number of students choosing to attend university, as we might expect. This is because for ILs (even if p ¯ $\overline{p}$ is constant) a lower T ¯ $\overline{T}$ might be preferred.

Result 1.Heterogeneity in how students learn results in different benefits from a given amount of teaching. Therefore, for a student of a given ability, the Graduate Premium will depend on how they learn and the constraints that they face.

3.2 Optional class attendance

The literature on whether or not class attendance should be compulsory directly addresses one element of our model (see, e.g., Romer, 1993, Marburger, 2006, Dobkin et al., 2010, Arulampalam et al., 2012, and Bratti & Staffolani, 2013). All five of these studies find that, after controlling for motivation and ability, attendance in class is positively correlated with performance. Romer (1993) generated an unusually large correspondence (JEP 1994), with many noting that Romer ignores the opportunity cost associated with attending class, which is at the core of our paper.

In this section, we relax Assumption 1. The amount of teaching offered by the university remains fixed ( T ¯ $\overline{T}$ ), but now students are able to choose whether or not they attend classes (i.e., students can choose T ≤ T ¯ $T \le \overline{T}$ ). Assumption 2 remains unchanged, so that whether or not students attend class, the same fixed fee is paid ( p ¯ $\overline{p}$ ).

With optional attendance students will choose:
T ∗ = min e ∗ ( α w ̲ ( 1 − α ) w ̲ ) ρ ρ − 1 α + ( 1 − α ) ( α w ̲ ( 1 − α ) w ̲ ) ρ ρ − 1 1 ρ , T ¯ . $$\begin{equation} T^*={\rm min}{\left\lbrace \frac{e^* (\frac{\alpha \underline{w}}{(1-\alpha)\underline{w}})^{\frac{\rho }{\rho -1}}}{\left(\alpha +(1-\alpha) (\frac{\alpha \underline{w}}{(1-\alpha)\underline{w}})^{\frac{\rho }{\rho -1}}\right)^{\frac{1}{\rho }}},\overline{T}\right\rbrace}. \end{equation}$$ (7)

The Graduate Premium is now determined by the cheapest combination (of S $S$ and T $T$ ) needed to reach the required education level, subject to T ∗ < T ¯ $T^*<\overline{T}$ . Since university is paid via a fixed fee (Assumption 2), the marginal cost of both inputs is equal to the forgone wage ( w ̲ $\underline{w}$ ). In general, students will benefit from the freedom to choose their optimal bundle ( S ∗ $S^*$ and T ∗ $T^*$ ) because they can now replace T with S if the marginal benefit of the latter is greater than the former. If S ∗ $S^*$ was previously 0 (i.e., T ¯ $\overline{T}$ was more than sufficient to acquire e ∗ $e^*$ on its own), the student now benefits by skipping some of the “unnecessary” classes.

Result 2.Students generally have greater Graduate Premiums when class attendance is optional than when class is compulsory.

For ILs, the increase in the Graduate Premium will be large because for these students compulsory classes impose a high cost. Figure 1 illustrates these asymmetric effects. In Figure 1, the DL would choose to attend more classes than T ¯ $\bar{T}$ and is therefore indifferent between optional or compulsory classes (the cost associated with Figure 1L point a is the same as the cost associated with Figure 1R point a). The IL is made better off by the move to optional classes because she now acquires the same level of education with a different optimal bundle (the cost associated with 1R point b1 is higher than the cost associated with 1L point b0).

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Optimal inputs under fixed fee with (L) optional classes and (R) compulsory classes. [Colour figure can be viewed at wileyonlinelibrary.com]

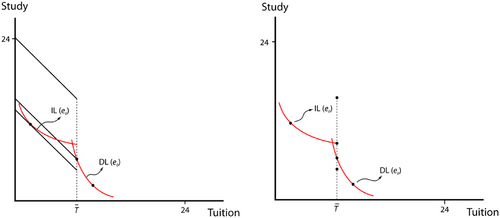
These effects are ameliorated by flexibility—when teaching is compulsory, the benefits of being flexible outweigh the advantages that can accrue from complementarity. Inflexible learners cannot use the “extra” teaching to substitute for study, while flexible learners can do so.

This result depends on the assumption that students are fully rational. For example, they do not suffer from self-control problems (see Huxley & Peacey, 2016; Hopkins, 2019). However a contribution of this paper is to show that students must fully understand the nature of the complementarity between Study and Teaching if they are to achieve their potential.

Arulampalam et al. (2012) find that the cost of missing class is higher for high-ability students. They find this counterintuitive because “these students would be better able to compensate for missing class through, for example, private study.”, however, as our model demonstrates, attendance in class can be especially productive for students who “prepare for class and who participate fully in class discussion.”

3.3 An unbundled university

We now relax both Assumption 1 and Assumption 2 so that students can choose how many classes to attend and pay for. In this world, where students are free to choose any combination of inputs, the complementaries in their education production function become critical.

Students will choose:
S ∗ ∗ = e ∗ α + ( 1 − α ) α ( w ̲ + p ) ( 1 − α ) w ̲ ρ ρ − 1 1 ρ , $$\begin{equation} S^{**}=\frac{e^*}{\left(\alpha + (1-\alpha) \left(\frac{\alpha (\underline{w}+p)}{(1-\alpha)\underline{w}}\right)^{\frac{\rho }{\rho -1}}\right)^{\frac{1}{\rho }}}, \end{equation}$$ (8)
T ∗ = e ∗ α ( w ̲ + p ) ( 1 − α ) w ̲ ρ ρ − 1 α + ( 1 − α ) α ( w ̲ + p ) ( 1 − α ) w ̲ ρ ρ − 1 1 ρ . $$\begin{equation} T^*=\frac{e^*\left(\frac{\alpha (\underline{w}+p)}{(1-\alpha)\underline{w}}\right)^{\frac{\rho }{\rho -1}}}{\left(\alpha +(1-\alpha) \left(\frac{\alpha (\underline{w}+p)}{(1-\alpha)\underline{w}}\right)^{\frac{\rho }{\rho -1}}\right)^{\frac{1}{\rho }}}. \end{equation}$$ (9)
This results in the unconstrained student receiving the following GP:
G P ( S ∗ ∗ , T ∗ ) = ( Ω w ¯ + w ̲ ( Ω − S ∗ ∗ − T ∗ ) − p ¯ ) − ( 2 Ω w ̲ ) . $$\begin{equation} GP(S^{**},T^*)=(\Omega \overline{w}+\underline{w}(\Omega -S^{**}-T^*)-\overline{p})-(2\Omega \underline{w}). \end{equation}$$ (10)

The Graduate Premium depends on how students learn. There is a widely held view that being more independent is beneficial, but this is no longer true if the relative price of teaching falls below the level required to makes it “the input of choice” (i.e., ∂ G P ∂ α > 0 $\frac{\partial GP}{\partial \alpha }>0$ iff w ̲ w ̲ + p < α 1 − α $\frac{\underline{w}}{\underline{w}+p}<\frac{\alpha }{1-\alpha }$ ). This shows the potential advantage of being a DL. In this case, the relative return to teaching is what matters. For example, a prospective MBA student who is highly paid will wish to minimize the time spent out of the labor force and therefore find a teaching-intensive course attractive.

In our model, flexibility ( ρ $\rho$ ) confers an unambiguous advantage ( ∂ G P ∂ ρ > 0 $\frac{\partial GP}{\partial \rho }>0$ ). This is because where there are significant complementaries between S $S$ and T $T$ , students will be especially particular about the bundle they use. This means they are at the mercy of the inputs' relative prices, and will be disadvantaged if they receive the “wrong” bundle.

It is obvious that increases in p $p$ will reduce the Graduate Premium for all students (i.e., ∂ G P ∂ p < 0 $\frac{\partial GP}{\partial p}<0$ ). One contribution of our model is to emphasize that, when students are unconstrained, the reduction in the Graduate Premium will depend on how students learn. To illustrate how differences in learning can determine the Graduate Premium, consider the special case where, apart from opportunity cost, education is free and unlimited ( p = 0 $p=0$ ). In this case, we might expect all individuals to obtain the same Graduate Premium. However, individuals with different learning parameters will use inputs differently and therefore have different opportunity costs.

When students pay for teaching, their choice of S $S$ and T $T$ will change and this has differential effects on the Graduate Premium. Independence mitigates the reduction in the Graduate Premium that results from an increase in p $p$ (i.e., ∂ 2 c ∂ p ∂ α < 0 $\frac{\partial ^2 c}{\partial p\partial \alpha }<0$ ). The individuals who lose most are DLs because of their heavy reliance on teaching. When w ̲ w ̲ + p > α 1 − α $\frac{\underline{w}}{\underline{w}+p}>\frac{\alpha }{1-\alpha }$ , flexibility mitigates the reduction in the Graduate Premium (i.e., ∂ 2 c ∂ p ∂ ρ < 0 $\frac{\partial ^2 c}{\partial p\partial \rho }<0$ ). This is because higher complementarity between S $S$ and T $T$ means that when price increases, substitution away from T $T$ is increasingly expensive.

3.4 Welfare implications of unbundling

In this section, we investigate the welfare implications of the bundling of teaching and study and show that if there is any heterogeneity in how students learn, then some students must be purchasing a suboptimal bundle.

To compare the welfare effects of variable fees relative to fixed fees, we set the price of teaching equal to p = f i x e d f e e T ¯ $p=\frac{fixed\text{}fee}{\overline{T}}$ . This means any bundle available under the fixed fee is available under the variable fee (although for a university this change is unlikely to be resource neutral). Figure 2 shows how unbundling expands the budget set.

Result 3.Unbundling benefits everyone, with the most distorted learners benefiting most.

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Unbundling relaxes the constraint.

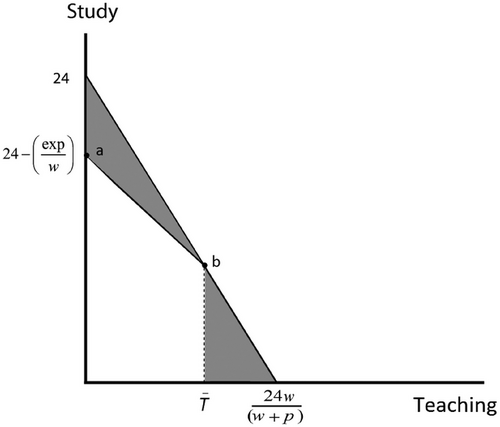
Unbundling gives rise to both price and wealth effects. These depend on the student's initial bundle, how distorted she was, and her learning parameters.

Distorted learners who choose zero teaching (Figure 2, point a) will not change their behavior when price increases, and only benefit from a wealth effect. Inframarginal learners who choose an interior solution will change their behavior when unbundling occurs.

Distorted learners who made full use of the bundled tuition (Figure 2, point b) will change their behavior depending on α $\alpha$ and ρ $\rho$ . After unbundling, the increased price of T $T$ leads ILs to substitute S $S$ for T $T$ , moving to a point in the region c. Replacing x $x$ hours of study (opportunity cost w ̲ x $\underline{w}x$ ) with y $y$ hours of teaching (cost y ( w ̲ + p ) $y(\underline{w} + p)$ ) will generate a benefit of y ( w ̲ + p ) − w ̲ $y(\underline{w} + p) - \underline{w}$ . How much study is required for this substitution will determine the size of the gain—and thus the size of the gain will be increasing in flexibility.

DLs will increase T $T$ and reduce S $S$ , moving to a point in the region d. The benefit arises because the constraint on T ¯ $\overline{T}$ has been relaxed (in contrast to the gains made by ILs that arise because of the change in price).

3.5 Signaling and the wage function

Human capital is the only variable in our wage function. This has two important implications:
  • (1) The wage function is independent of ability.
  • (2) The wage function is independent of the choice of inputs.
  • (1) assumes that ability only affects the wage indirectly via its influence on educational attainment. Becker (1962) does not make this assumption, at least in principle, he allows the wage to depend on both ability and education. It turns out that this assumption also has implications for the discussion of ability (see Section 3.6).
  • (2) becomes relevant in a two input model and implies employers have no preferences about how human capital is acquired. For example, how an individual learns a language does not matter, what matters is whether she can speak it. For this reason, we assume that study and teaching affect the wage only through education. Hence, choices about study and teaching will depend on both the wage elasticity of education and how students learn.
In neoclassical theories of production, consumers have no preferences over how goods are produced. There are good reasons to believe that this assumption may not hold in the case of education. If employers want workers to replenish their human capital on the job they will seek out “life long learners,” in which case, employers might have preferences over both the level of education and how that education was acquired. However, we think it is unlikely that either of the parameters in the education production function are readily observable, and so employers will make inferences on what can be observed. If it was common knowledge that different universities (providing the same E $E$ ) offer different T $T$ , employers might be able to infer how a graduate learns from the choice of university.

For example, if employers are willing to pay an IL a higher wage but α $\alpha$ is not observable, there would be a separating equilibrium where ILs choose a university that offers very little teaching, and DLs choose a university where more teaching is offered. In these circumstances an employer would offer a wage that is increasing in E $E$ but decreasing in T $T$ . Students will now need to signal how they learn in addition to ability, and this will increase the total cost of the signal, therefore increasing the welfare loss relative to perfect information.

The signaling hypothesis is notoriously hard to test because the predictions of the model are hard to distinguish from the human capital story. A recent empirical literature on what happens when there are unexpected changes in college duration has provided some helpful evidence (Arteaga, 2018; Seah et al., 2020). However, while these papers show the impact of a reduction in the level of education required to graduate, they do not show how a student might have responded by changing the mix of S $S$ and T $T$ to achieve this outcome.

3.6 Ability

Becker (1962) defined ability by the ratio of output to input in his one input production function. As he acknowledged, when considering more than one input this definition is no longer straightforward: “The i t h $i^{th}$ person has more ability if f i > f j $f_i>f_j$ … If sometimes f i > f j $f_i>f_j$ and sometimes f j > f i $f_j>f_i$ , there is no unique ranking of their abilities”(Becker, 1975, p. 110, footnote 107).

In order to calculate ability, inputs must be aggregated and thus weighted by price. Because we allow marginal returns for each input to vary between individuals, the focus shifts to relative price, and who can make better use of the cheaper input.

Definition 1.(Ability) Where two individuals choose to produce e ∗ $e^*$ , if individual i $i$ has a lower cost than j $j$ , then i $i$ is said to be of higher ability.

e i ( T ∗ i , S ∗ i ) = e j ( T ∗ j , S ∗ j ) $$\begin{equation} e_i (T^{*i},S^{*i})=e_j (T^{*j},S^{*j}) \end{equation}$$ (11)
and
c ( T ∗ i , S ∗ i ) < c ( T ∗ j , S ∗ j ) . $$\begin{equation} c(T^{*i},S^{*i})<c(T^{*j},S^{*j}). \end{equation}$$ (12)

This is equivalent to saying that if the cost is the same for the two individuals, then the individual with the higher ability will acquire more education. We believe this definition of ability is intuitive and more consistent with the evidence that cognitive ability is multidimensional (Carroll, 1993).

In our two input model, Ability depends on the price of teaching. Figure 3 illustrates this result. At p = 0 $p=0$ , IL and DL have the same ability. At a higher price, DL is lower ability than IL because the increase in cost for DL exceeds the increase in cost for IL.

Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
The impact of independence on cost minimization. [Colour figure can be viewed at wileyonlinelibrary.com]

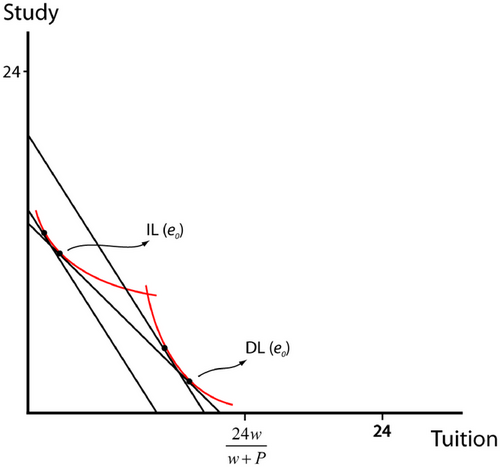
In this respect Heckman's two period, one input model is similar to our one period, two input model. It follows that the same ambiguity must arise. The cost of investment I 0 $I_0$ is the opportunity cost of investment in the next period, ( 1 + r ) I 1 $(1+r)I_1$ . If the interest rate changes, the relative price of the two investments will change. The higher ability individual is now whoever makes better use of the cheaper investment.

In our model, the monotonic relationship between ability and optimum expenditure on human capital (Becker, 1962) is broken. If ability is positively correlated with independence, a low-ability student might require a larger expenditure on education than a higher ability student. This would reverse the usual relationship between ability and expenditure on education. Even in a one input model, this problem can arise if individuals face different opportunity costs. This is because opportunity cost does not enter into the standard definition of ability. Comparing ability between individuals requires considering the difference in the input/output ratio, and if the same input has different costs to different individuals this cost will influence ability rankings.

4 CONCLUSION

In this paper, we have developed a model that is based on assumptions that will be familiar to any economist but the results we derive are novel. If study and teaching are inputs in an education production function it is natural to ask questions about the interaction between these inputs. We are able to address some important questions about how students learn and therefore how higher education should be delivered.

Using this framework, we are able to show how the Graduate Premium depends on the interaction between how students learn and how higher education is delivered. We have provided a formal analysis of what is implied by unbundling in higher education, and showed that unbundling teaching and study can benefit all learners. Our framework also allows for new perspectives on questions such as whether class attendance should be compulsory and how higher education should be priced.

These results hold because we specify a price for each type of investment: The price of study comes in the form of an opportunity cost whereas the price students pay for teaching is a market price. ILs should pay less for their education even if they are high ability and make large overall investments in human capital.

This provides us a new perspective on the structure and regulation of higher education markets. For example, if higher ability students are more independent than lower ability students, it is possible that those universities that recruit the highest ability students should charge lower fees (and offer less teaching) than universities that recruit lower ability students, at least to achieve a given level of education. However, if there are complementarities between study and teaching the paradox that prestigious universities should charge less than lower ranked universities is reversed. Consider a parallel with sport: Talented athletes make large investments in exercise (study). However because of complementarities, it is worth their while to purchase large amounts of training (teaching).

Our paper raises questions about the amount of teaching students receive relative to the amount of study they undertake. In the United Kingdom, recent cuts in funding, which have reduced teaching intensity (see Huxley et al., 2018; Ambler et al., 2023), have resulted in students needing to compensate with additional study. If there are strong complementaries, then this solution may be inefficient. When policy makers are trying to improve incentives it is important to focus on the right margin, and this implies a focus on teaching. In the United Kingdom, the Teaching Excellence Framework has unfortunately moved away from teaching toward an emphasis on the bundle of goods that make up the student experience.

The model we present in this paper is exclusively focused on student heterogeneity in terms of their learning parameters. We therefore do not consider here how this heterogeneity may be influenced by the other dimensions in which students are heterogeneous. For example a student's socioeconomic background can result in home environments that are more or less conducive to study. Although these socioeconomic differences have not been modeled it should be clear that the parameters in our model will be influenced by them. This means that the model has implications for equity at least as much as it does for efficiency.

Furthermore, while our framework is applicable to any field of study, the appropriate ratio between study and teaching will vary by discipline. For example, in chemistry, some learning must take place inside a lab—and it is virtually impossible to substitute this with study at home. Although our results hold for all disciplines, the learning parameter values (particularly flexibility) will be discipline specific, as well as individual specific.

As different pedagogic techniques are increasingly being subjected to rigorous, controlled trials, and the quantitative literature regarding different educational inputs (class sizes, teacher quality, etc.) continues to grow, we provide a framework for integrating some of these findings into a broader model of teaching and learning. Such a framework will hopefully lay the groundwork for increasingly fruitful interaction between developmental psychologists and educational economists, helping to translate findings from psychological and pedagogical research more directly into concrete policy developments.

ACKNOWLEDGMENTS

We are grateful to Ken Binmore, Partha Dasgupta, Nigel Duck, Miriam Gensowski, Bill Geoff, Paul Grout, Ian Jewitt, Ali Muriel, In-Uck Park, Helen Simpson, Alasdair Smith, and Anna Vignoles for comments on earlier drafts. This research was supported by the Economics and Social Research Council.

    APPENDIX A

    A.1 Algebraic results

    The results of the model are found by solving the following Lagrangian equation:
    L = w S + ( w + P ) T + λ ( α S ρ + ( 1 − α ) T ρ ) 1 ρ − e ∗ , $$\begin{equation} L=wS+(w+P) T+\lambda \left((\alpha S^\rho +(1-\alpha) T^\rho)^\frac{1}{\rho }-e^*\right), \end{equation}$$ (A.1)
    where w has been replaced with w for brevity. Assuming the individual chooses to graduate, then the following first-order conditions hold:
    ∂ L ∂ S = w + λ α S 1 − ρ ( α S ρ + ( 1 − α ) T ρ ) 1 − ρ ρ , $$\begin{equation} \frac{\partial L}{\partial S}=w+\lambda \alpha S^{1-\rho } (\alpha S^\rho +(1-\alpha) T^\rho)^\frac{1-\rho }{\rho }, \end{equation}$$ (A.2)
    ∂ L ∂ T = ( w + p ) + λ ( 1 − α ) T ρ − 1 ( α S ρ + ( 1 − α ) T ρ ) 1 − ρ ρ , $$\begin{equation} \frac{\partial L}{\partial T}=(w+p)+\lambda (1-\alpha)T^{\rho -1} (\alpha S^\rho +(1-\alpha) T^\rho)^\frac{1-\rho }{\rho }, \end{equation}$$ (A.3)
    ∂ L ∂ λ = ( α S ρ + ( 1 − α ) T ρ ) 1 ρ − e ∗ . $$\begin{equation} \frac{\partial L}{\partial \lambda }=(\alpha S^\rho +(1-\alpha) T^\rho)^\frac{1}{\rho }-e^*. \end{equation}$$ (A.4)
    Solving:
    S ∗ ∗ = e ∗ α + ( 1 − α ) ( α ( w + p ) ( 1 − α ) w ) ρ ρ − 1 1 ρ , $$\begin{equation} S^{**}=\frac{e^*}{\left(\alpha +(1-\alpha) (\frac{\alpha (w+p)}{(1-\alpha)w})^{\frac{\rho }{\rho -1}}\right)^{\frac{1}{\rho }}}, \end{equation}$$ (A.5)
    T ∗ = e ∗ ( α ( w + p ) ( 1 − α ) w ) ρ ρ − 1 α + ( 1 − α ) ( α ( w + p ) ( 1 − α ) w ) ρ ρ − 1 1 ρ . $$\begin{equation} T^*=\frac{e^*(\frac{\alpha (w+p)}{(1-\alpha)w})^{\frac{\rho }{\rho -1}}}{ \left(\alpha +(1-\alpha) (\frac{\alpha (w+p)}{(1-\alpha)w})^{\frac{\rho }{\rho -1}}\right)^{\frac{1}{\rho }}}. \end{equation}$$ (A.6)

    A.2 Proofs of statements in paper

    For simplicity in this appendix, we express equations in terms of the elasticity of substitution ( σ $\sigma$ ) rather than ρ $\rho$ . The relationship is given by σ = 1 1 − ρ $\sigma =\frac{1}{1-\rho }$ . We also replace w with w for brevity.

    A.2.1      

    • ∂ G P ∂ α > 0 $\frac{\partial GP}{\partial \alpha }>0$ iff w w + p < α 1 − α $\frac{w}{w+p}<\frac{\alpha }{1-\alpha }$ .

    Proof.

    ∂ l n ( c ( w , w + p , e ∗ ) ) ∂ α = σ ( − w ( w + P ) σ α σ − 1 + w 1 + σ ( 1 − α ) σ − 1 + w σ ( 1 − α ) σ − 1 p ) ( σ − 1 ) ( α σ w ( w + p ) σ + ( 1 − α ) σ w 1 + σ + ( 1 − α ) σ p w σ ) . $$\begin{equation} \frac{\partial ln(c(w,w+p,e^*))}{\partial \alpha }=\frac{\sigma (-w(w+P)^\sigma \alpha ^{\sigma -1}+w^{1+\sigma }(1-\alpha)^{\sigma -1}+w^\sigma (1-\alpha)^{\sigma -1}p)}{(\sigma -1)(\alpha ^\sigma w (w+p)^\sigma +(1-\alpha)^\sigma w^{1+\sigma } +(1-\alpha)^\sigma p w^\sigma)}. \end{equation}$$ (A.7)
    The denominator has the sign of σ − 1 $\sigma -1$ , since the rest is clearly positive. Since σ > 0 $\sigma >0$ , the numerator takes the sign of:
    − w ( w + P ) σ α σ − 1 + w 1 + σ ( 1 − α ) σ − 1 + w σ ( 1 − α ) σ − 1 p . $$\begin{equation} -w(w+P)^\sigma \alpha ^{\sigma -1}+w^{1+\sigma }(1-\alpha)^{\sigma -1}+w^\sigma (1-\alpha)^{\sigma -1}p. \end{equation}$$ (A.8)
    This is negative iff:
    w σ − 1 ( 1 − α ) σ − 1 < ( w + p ) σ − 1 α σ − 1 . $$\begin{equation} w^{\sigma -1}(1-\alpha)^{\sigma -1}<(w+p)^{\sigma -1} \alpha ^{\sigma -1}. \end{equation}$$ (A.9)
    If σ − 1 > 0 $\sigma -1>0$ , then w ( w + p ) < α ( 1 − α ) $\frac{w}{(w+p)}<\frac{\alpha }{(1-\alpha)}$ . If σ − 1 < 0 $\sigma -1<0$ , then w ( w + p ) > α ( 1 − α ) $\frac{w}{(w+p)}>\frac{\alpha }{(1-\alpha)}$ .

    Hence, in either case, ∂ c ( w , w + p , e ∗ ) ∂ α < 0 $\frac{\partial c(w,w+p,e^*)}{\partial \alpha }<0$ iff w ( w + p ) < α ( 1 − α ) $\frac{w}{(w+p)}<\frac{\alpha }{(1-\alpha)}$ . □ $\Box$

    A.2.2      

    • ∂ G P ∂ ρ > 0 $\frac{\partial GP}{\partial \rho }>0$ .

    Proof.

    ∂ c ( w , w + p , e ∗ ) ∂ σ = ( α 1 − σ w σ + ( 1 − α ) 1 − σ ( w + p ) σ ) σ − 1 ( A + B ) , $$\begin{equation} \frac{\partial c(w,w+p,e^*)}{\partial \sigma }=(\alpha ^{1-\sigma }w^{\sigma }+(1-\alpha)^{1-\sigma } (w+p)^{\sigma })^{\sigma ^{-1}}(A+B), \end{equation}$$ (A.10)
    where
    A = − ln ( α 1 − σ w σ + ( 1 − α ) 1 − σ ( w + p ) σ ) σ 2 $$\begin{equation} A=-{\frac{\ln ({\alpha }^{1-\sigma }{w}^{\sigma }+(1-\alpha)^{1-\sigma }(w+p)^{\sigma })}{{\sigma }^{2}}} \end{equation}$$ (A.11)
    and
    B = α 1 − σ w σ ( ln ( w ) − ln ( α ) ) + ( 1 − α ) 1 − σ ( w + p ) σ ( ln ( w + p ) − ln ( 1 − α ) ) σ ( α 1 − σ w σ + ( 1 − α ) 1 − σ ( w + p ) σ ) , $$\begin{equation} B={\frac{{\alpha }^{1-\sigma }{w}^{\sigma }(\ln (w)-\ln (\alpha)) + (1-\alpha) ^{1-\sigma }(w+p) ^{\sigma }(\ln (w+p)-\ln (1-\alpha))}{\sigma ({\alpha }^{1-\sigma }{w}^{\sigma }+(1-\alpha) ^{1-\sigma }(w+p)^{\sigma })}}, \end{equation}$$ (A.12)
    which simplifies to
    ∂ c ( w , w + p , e ∗ ) ∂ σ = − Q R P , $$\begin{equation} \frac{\partial c(w,w+p,e^*)}{\partial \sigma }=-\frac{QR}{P}, \end{equation}$$ (A.13)
    where
    Q = ( α 1 − σ w σ + ( w + p ) σ ( 1 − α ) − σ − ( w + p ) σ ( 1 − α ) − σ α ) σ − 1 , $$\begin{equation} Q=(\alpha ^{1-\sigma }w^{\sigma }+(w+p)^{\sigma }(1-\alpha)^{-\sigma }-(w+p)^{\sigma }(1-\alpha)^{-\sigma }\alpha)^{{\sigma }^{-1}}, \end{equation}$$ (A.14)
    R = ( 1 − α ) σ w σ α ( σ ( l n ( α ) − l n ( w ) ) + l n ( z ) ) + ( 1 − α ) ( w + p ) σ α σ ( σ ( l n ( 1 − α ) − l n ( w + p ) ) + l n ( z ) ) , $$\begin{eqnarray} R & = & (1-\alpha)^\sigma w^\sigma \alpha (\sigma (ln(\alpha)-ln(w))+ln(z)) \nonumber\\[-2pt] && + \ (1-\alpha)(w + p)^\sigma \alpha ^\sigma (\sigma (ln(1-\alpha)-ln(w+p))+ln(z)),\end{eqnarray}$$ (A.15)
    where z = α 1 − σ w σ + ( 1 − α ) 1 − σ ( w + p ) σ $z=\alpha ^{1-\sigma }w^\sigma +(1-\alpha)^{1-\sigma }(w+p)^\sigma$ , and
    P = σ 2 ( α w σ ( 1 − α ) σ + ( w + p ) σ α σ − ( w + p ) σ α 1 + σ ) . $$\begin{equation} P=\sigma ^{2}(\alpha w^{\sigma }(1-\alpha)^{\sigma }+(w+p)^{\sigma }\alpha ^{\sigma }-(w+p)^{\sigma }\alpha ^{1+\sigma }). \end{equation}$$ (A.16)
    Since P > 0 $P>0$ and Q > 0 $Q>0$ , ∂ c ( w , w + p , e ∗ ) ∂ σ $\frac{\partial c(w,w+p,e^*)}{\partial \sigma }$ clearly has the opposite sign to R $R$ . R is always negative if w > 1 $w>1$ (verified by computer).

    Note the sign of ∂ c ( w , w + p , e ∗ ) ∂ ρ $\frac{\partial c(w,w+p,e^*)}{\partial \rho }$ is the same as ∂ c ( w , w + p , e ∗ ) ∂ σ $\frac{\partial c(w,w+p,e^*)}{\partial \sigma }$ since σ = 1 1 − ρ $\sigma =\frac{1}{1-\rho }$ and ρ ≤ 1 $\rho \le 1$ . □ $\Box$

    A.2.3      

    • ∂ c ∂ p > 0 $\frac{\partial c}{\partial p}>0$ .

    Proof.

    ∂ l n ( c ) ∂ p = ( 1 − α ) σ ( w + p ) 1 − σ ( w + p ) ( α σ w 1 − σ + ( 1 − α ) σ ( w + p ) 1 − σ ) , $$\begin{equation} \frac{\partial ln(c)}{\partial p}=\frac{(1-\alpha)^\sigma (w+p)^{1-\sigma }}{(w+p)(\alpha ^\sigma w^{1-\sigma }+(1-\alpha)^\sigma (w+p)^{1-\sigma })}, \end{equation}$$ (A.17)
    which is clearly positive for everyone. □ $\Box$

    A.2.4      

    • ∂ 2 c ∂ p ∂ α < 0 $\frac{\partial ^2 c}{\partial p\partial \alpha }<0$ .

    Proof.

    ∂ ∂ l n ( c ) ∂ p ∂ α = − ( A + B ) , $$\begin{equation} \frac{\partial \frac{\partial ln(c)}{\partial p}}{\partial \alpha }=-(A+B), \end{equation}$$ (A.18)
    where A = ( 1 − α ) 1 − σ ( 1 − σ ) ( w + p ) σ ( 1 − α ) ( w + p ) ( α 1 − σ w σ + ( 1 − α ) 1 − σ ( w + p ) σ ) ${\frac{(1-\alpha) ^{1-\sigma }(1-\sigma)(w+p)^{\sigma }}{(1-\alpha)(w+p)({\alpha }^{1-\sigma }{w}^{\sigma }+(1-\alpha)^{1-\sigma }(w+p) ^{\sigma })}}$ , and B = ( α 1 − σ ( 1 − σ ) w σ α − ( 1 − α ) 1 − σ ( 1 − σ ) ( w + p ) σ 1 − α ) ( 1 − α ) 1 − σ ( w + p ) σ ( α 1 − σ w σ + ( 1 − α ) 1 − σ ( w + p ) σ ) 2 ( w + p ) $B= \frac{({\frac{{\alpha }^{1-\sigma }(1-\sigma){w}^{\sigma }}{\alpha }}-{\frac{(1-\alpha)^{1-\sigma }(1-\sigma)(w+p)^{\sigma }}{1-\alpha }})(1-\alpha)^{1-\sigma }(w+p)^{\sigma }}{({\alpha }^{1-\sigma }{w}^{\sigma }+(1-\alpha)^{1-\sigma }(w+p) ^{\sigma }) ^{2}(w+p)}$ .

    Multiplying out, to give a (positive) common denominator of ( α 1 − σ w σ + ( 1 − α ) 1 − σ ( w + p ) σ ) 2 ( w + p ) ( 1 − α ) $({\alpha }^{1-\sigma }{w}^{\sigma }+(1-\alpha)^{1-\sigma }(w+p)^{\sigma })^{2}(w+p)(1-\alpha)$ , gives a numerator:

    − ( ( 1 − α ) 1 − σ ( 1 − σ ) ( w + p ) σ ) α 1 − σ w σ + ( 1 − α ) 1 − σ ( w + p ) σ α 1 − σ ( 1 − σ ) w σ α − ( 1 − α ) 1 − σ ( 1 − σ ) ( w + p ) σ 1 − α ( 1 − α ) 1 − σ ( w + p ) σ − ( 1 − α ) α 1 − σ ( 1 − σ ) w σ α − ( 1 − α ) 1 − σ ( 1 − σ ) ( w + p ) σ 1 − α ( 1 − α ) 1 − σ ( w + p ) σ , $$\begin{multline} {-}((1-\alpha) ^{1-\sigma }(1-\sigma)(w+p)^{\sigma }) \left( \left({\alpha }^{1-\sigma }{w}^{\sigma }+(1-\alpha)^{1-\sigma }(w+p) ^{\sigma }\right){\vphantom{\left(\left({\frac{{\alpha }^{1-\sigma }(1-\sigma){w}^{\sigma }}{\alpha }}-{\frac{(1-\alpha) ^{1-\sigma }(1-\sigma)(w+p)^{\sigma }}{1-\alpha }}\right)(1-\alpha)^{1-\sigma }(w+p)^{\sigma } \right)}}\right.\\ \quad\left. - \ (1-\alpha) \left(\left({\frac{{\alpha }^{1-\sigma }(1-\sigma){w}^{\sigma }}{\alpha }}-{\frac{(1-\alpha) ^{1-\sigma }(1-\sigma)(w+p)^{\sigma }}{1-\alpha }}\right)(1-\alpha)^{1-\sigma }(w+p)^{\sigma } \right)\right),\end{multline}$$ (A.19)
    which can be rewritten as:
    − ( 1 − α ) 1 − σ ( 1 − σ ) ( w + p ) σ α 1 − σ w σ + ( 1 − α ) 1 − σ ( w + p ) σ + ( 1 − α ) α 1 − σ w σ α − ( w + p ) σ ( 1 − α ) σ , $$\begin{eqnarray} -(1-\alpha)^{1-\sigma }(1-\sigma)(w+p)^\sigma \left(\alpha ^{1-\sigma }w^\sigma + (1-\alpha)^{1-\sigma } (w+p)^\sigma +(1-\alpha) \left(\frac{\alpha ^{1-\sigma }w^\sigma }{\alpha }-\frac{(w+p)^\sigma }{(1-\alpha)^\sigma }\right)\right), \qquad \end{eqnarray}$$ (A.20)
    which simplifies to:
    − ( 1 − α ) 1 − σ ( 1 − σ ) ( w + p ) σ α − 1 α 1 − σ w σ , $$\begin{equation} -(1-\alpha)^{1-\sigma }(1-\sigma)(w+p)^\sigma \alpha ^{-1}\alpha ^{1-\sigma }w^\sigma, \end{equation}$$ (A.21)
    which is clearly negative. □ $\Box$

    A.2.5      

    • ∂ 2 c ∂ p ∂ ρ < 0 $\frac{\partial ^2 c}{\partial p\partial \rho }<0$ iff w w + p < α 1 − α $\frac{w}{w+p}<\frac{\alpha }{1-\alpha }$ .

    Proof.

    ∂ 2 l n ( c ) ∂ p ∂ σ = − ( 1 − α ) 1 − σ ln ( 1 − α ) ( w + p ) σ ( w + p ) ( α 1 − σ w σ + ( 1 − α ) 1 − σ ( w + p ) σ ) + ( 1 − α ) 1 − σ ( w + p ) σ ln ( w + p ) ( w + p ) ( α 1 − σ w σ + ( 1 − α ) 1 − σ ( w + p ) σ ) − ( 1 − α ) 1 − σ ( w + p ) σ ( − α 1 − σ ln ( α ) w σ + α 1 − σ w σ ln ( w ) ) ( α 1 − σ w σ + 1 − α 1 − σ ( w + p ) σ ) 2 ( w + p ) − ( 1 − α ) 1 − σ ( w + p ) σ ( − ( 1 − α ) 1 − σ ln ( 1 − α ) ( w + p ) σ + ( 1 − α ) 1 − σ ( w + p ) σ ln ( w + p ) ) ( α 1 − σ w σ + 1 − α 1 − σ ( w + p ) σ ) 2 ( w + p ) , $$\begin{eqnarray} \frac{\partial ^2 ln(c)}{\partial p\partial \sigma }&=& -{\frac{(1-\alpha)^{1-\sigma }\ln (1-\alpha)(w+p)^{\sigma }}{(w+p)({\alpha }^{1-\sigma }{w}^{\sigma }+ (1-\alpha)^{1-\sigma }(w+p)^{\sigma })}}+{\frac{(1-\alpha)^{1-\sigma }(w+p)^{\sigma }\ln (w+p)}{(w+p)({\alpha }^{1-\sigma }{w}^{\sigma }+(1-\alpha)^{1-\sigma }(w+p)^{\sigma })}}\nonumber\\ && - \ {\frac{(1-\alpha)^{1-\sigma }(w+p)^{\sigma }(-{\alpha }^{1-\sigma }\ln (\alpha){w}^{\sigma }+{\alpha }^{1-\sigma }{w}^{\sigma }\ln (w))}{({\alpha }^{1-\sigma }{w}^{\sigma }+ {\left(1-\alpha \right)} ^{1-\sigma }(w+p)^{\sigma })^{2}(w+p)}}\nonumber\\ && - \ {\frac{(1-\alpha)^{1-\sigma }(w+p)^{\sigma }(-(1-\alpha)^{1-\sigma }\ln (1-\alpha)(w+p)^{\sigma }+(1-\alpha) ^{1-\sigma }(w+p)^{\sigma }\ln (w+p)) }{({\alpha }^{1-\sigma }{w}^{\sigma }+ {\left(1-\alpha \right)} ^{1-\sigma }(w+p)^{\sigma })^{2}(w+p)}},\nonumber\\ \end{eqnarray}$$ (A.22)
    which can be simplified and then factorized as:
    ∂ 2 l n ( c ) ∂ p ∂ σ = [ A + B ] [ l n ( α ) − l n ( w ) − l n ( 1 − α ) + l n ( w + p ) ] , $$\begin{equation} \frac{\partial ^2 ln(c)}{\partial p\partial \sigma }=[A+B][ln(\alpha)-ln(w)-ln(1-\alpha)+ln(w+p)], \end{equation}$$ (A.23)
    where A = ( w + p ) σ α σ ( 1 − α ) 2 σ w 2 σ − 1 ( p 2 + 2 w p + w 2 ) $A=(w+p)^\sigma \alpha ^\sigma (1-\alpha)^{2\sigma }w^{2\sigma -1}(p^2+2wp+w^2)$ and B = w σ + 2 ( w + p ) 2 σ ( 1 − α ) σ α 2 σ ( w + p ) $B=w^{\sigma +2}(w+p)^{2\sigma }(1-\alpha)^\sigma \alpha ^{2\sigma } (w+p)$ .

    Since A $A$ and B $B$ are both > 0 $>0$ , the sign of ∂ 2 l n ( c ) ∂ p ∂ σ $\frac{\partial ^2ln(c)}{\partial p\partial \sigma }$ is given by [ l n ( α ) − l n ( w ) − l n ( 1 − α ) + l n ( w + p ) ] $[ln(\alpha)-ln(w)-ln(1-\alpha)+ln(w+p)]$ , which is just a log transformation of α 1 − α − w w + p $\frac{\alpha }{1-\alpha }-\frac{w}{w+p}$ .

    Note the sign of ∂ 2 l n ( c ) ∂ p ∂ ρ $\frac{\partial ^2ln(c)}{\partial p\partial \rho }$ is the same as ∂ 2 l n ( c ) ∂ p ∂ σ $\frac{\partial ^2ln(c)}{\partial p\partial \sigma }$ since σ = 1 1 − ρ $\sigma =\frac{1}{1-\rho }$ and ρ ≤ 1 $\rho \le 1$ . □ $\Box$

    A.3 N period model

    An individual i $i$ lives for N $N$ periods. Her lifetime utility, U $U$ , is increasing in consumption of a numéraire good, m t $m_t$ :
    U = ∑ t = 1 N u ( m t ) . $$\begin{equation} U=\sum \limits _{t=1}^Nu(m_t). \end{equation}$$ (A.24)
    In any period, t $t$ , it is possible to obtain e t $e_t$ education in a number of ways according to her education production function:
    e i , t ( S t , T t ) , $$\begin{equation} e_{i,t}(S_t,T_t), \end{equation}$$ (A.25)
    where S t $S_t$ is time spent on study in period t $t$ and T t $T_t$ is time spent being taught in period t $t$ . Education is strictly increasing in both S t $S_t$ and T t $T_t$ .
    ∂ e i , t ∂ S t > 0 , ∂ e i , t ∂ T t > 0 . $$\begin{equation} \frac{\partial e_{i,t}}{\partial S_t}>0, \quad \frac{\partial e_{i,t}}{\partial T_t}>0. \end{equation}$$ (A.26)
    In period t $t$ it is possible to obtain a “level t diploma” subject to:
    • (1) meeting the prerequisite (having a level t−1 diploma).
    • (2) attaining a level of education of at least e t ∗ $e_t^*$ in this period (a single diploma cannot be obtained over multiple periods).
    Education is cumulative and as such i's stock of education in period t $t$ is given by:
    E i , t = ∑ s = 1 t 1 ( e i , s ∗ ) , $$\begin{equation} E_{i,t}=\sum \limits _{s=1}^{t} \mathbb{1}(e_{i,s}^*), \end{equation}$$ (A.27)
    where 1 ( e s ∗ ) $\mathbb{1}(e_s^*)$ denotes if a diploma was acquired in period s $s$ .
    The wage, w t $w_t$ , is an increasing function of this education stock:
    w t = W ( E t − 1 ) . $$\begin{equation} w_t=W(E_{t-1}). \end{equation}$$ (A.28)
    The individual's decision problem is to choose a stream of education and work to maximize consumption. She is subject to an intertemporal money constraint (A.29), and N $N$ intratemporal time constraints (A.30). The first constraint implies that the lifetime value of the stream of expenditure (on teaching or consumption) cannot exceed the lifetime value of the stream of earned income:
    ∑ t = 1 N ( w t H t − m t − p T t ) = 0 , $$\begin{equation} \sum \limits _{t=1}^N(w_tH_t-m_t-pT_t)=0, \end{equation}$$ (A.29)
    where H t $H_t$ is hours worked in period t $t$ and p $p$ is the hourly price of teaching. p $p$ is assumed to be an exogenous positive constant. The second set of constraints implies the amount of time devoted to each activity must add up to the endowment of time, Ω $\Omega$ , in each period:
    Ω = S t + T t + H t t = 1 … N . $$\begin{equation} \Omega =S_t+T_t+H_t \quad \quad \quad \quad \quad t=1\ldots N. \end{equation}$$ (A.30)
    Since U $U$ is increasing in m $m$ , maximizing utility is achieved through maximizing consumption. Assuming the individual chooses to graduate with a k-diploma, her graduate consumption is given by:
    m E k = ( N − k ) Ω w k + ∑ j = 1 k ( ( Ω − T j − S j ) w j − p T j ) . $$\begin{equation} m^{Ek}=(N-k)\Omega w_k+\sum \limits _{j=1}^k((\Omega -T_j-S_j)w_j-pT_j). \end{equation}$$ (A.31)
    If she chooses no education and becomes a nongraduate, her consumption is:
    m E 0 = N Ω w 0 . $$\begin{equation} m^{E0}=N\Omega w_0. \end{equation}$$ (A.32)
    The Graduate Premium is G = ( m E k − m E 0 ) $G=(m^{Ek}-m^{E0})$ . The individual maximizes G $G$ subject to:
    • (1) the education production function (Equations A.25 and A.27),
    • (2) the wage function (Equation A.28),
    • (3) time constraints (Equation A.30).

    We note there is an equivalent cost minimization problem: Minimize C k = ∑ j = 1 k c j ( T j , S j ) = ∑ j = 1 k ( ( T j + S j ) w j − p T j ) $C^k=\sum \limits _{j=1}^kc_j(T_j,S_j)=\sum \limits _{j=1}^k((T_j+S_j)w_j-pT_j)$ , subject to the same constraints.

    Lemma A.1.The individual would always minimize the cost of whatever education is undertaken in each period.

    Proof.It is clear that the education levels chosen in each period will either be 0 or e i ∗ $e_i^*$ . This is because, for 0 < e i < e i ∗ $0<e_i<e_i^*$ , the marginal benefit from education is zero and the individual would be wasting resources (which could be used to increase her Graduate Premium) by not choosing e i = 0 $e_i=0$ . If e i > e i ∗ $e_i>e_i^*$ , then the gain would come from decreasing education to e i ∗ $e_i^*$ .

    Moreover, if it is optimal to choose no education in period i $i$ , then for j = i + 1 $j=i+1$ , it will also be optimal to choose no education. In both periods the education production function and forgone wage are identical and the individual faces a similar decision. However, in period j $j$ the benefit of the increased wage would last for one fewer period.

    Suppose that S 1 ∗ , S 2 ∗ , … , S N ∗ $S_1^*,S_2^*,\ldots, S_N^*$ and T 1 ∗ , T 2 ∗ , … , T N ∗ $T_1^*,T_2^*,\ldots,T_N^*$ are the amounts of study and teaching undertaken in each period to maximize the Graduate Premium. Since ∂ e i S i > 0 $\frac{\partial e_i}{S_i}>0$ and ∂ e i T i > 0 $\frac{\partial e_i}{T_i}>0$ , it is clear that there is only one way to produce e i = 0 $e_i=0$ , which is to use S i = T i = 0 $S_i=T_i=0$ . Hence S i ∗ $S_i^*$ and T i ∗ $T_i^*$ are also the cost minimizing inputs.

    If e i = e i ∗ $e_i=e_i^*$ , we use proof by contradiction to show that S i ∗ $S_i^*$ and T i ∗ $T_i^*$ satisfy this period's cost minimization problem. Suppose using ( S i ′ , T i ′ ) ≠ ( S i ∗ , T i ∗ ) $(S_i^{\prime },T_i^{\prime })\ne (S_i^*,T_i^*)$ is the least costly way for an individual to produce e i ∗ $e_i^*$ in period i $i$ .

    A change to S ′ $S^{\prime }$ and T ′ $T^{\prime }$ in period i $i$ , holding S $S$ and T $T$ unchanged in all other periods, only results in a change to the period i $i$ payoff (since e i ∗ $e_i^*$ is still produced). This switch to ( S i ′ , T i ′ ) $(S_i^{\prime },T_i^{\prime })$ would decrease cost by ( p + w i ) ( T i ∗ − T i ′ ) + w i ( S i ∗ − S i ′ ) > 0 $(p+w_i)(T_i^*-T_i^{\prime })+w_i(S_i^*-S_i^{\prime })>0$ , and hence increase the Graduate Premium by this amount. □ $\Box$

    • 1 The term “learning” is often used in reference to information processing using, for example, Bayesian updating. In this paper, we use the term “learning” to mean the acquisition of human capital.
    • 2 The comparative statics we are interested in are not explored by Grossman.
    • 3 Biddle and Hamermesh (1990) also consider a three good model, with time spent investing in sleep replacing health investment
    • 4 For example, study lays the groundwork for understanding concepts independently, while teaching serves to reinforce and deepen this understanding (and can also motivate individuals to engage in study). Thus creating a positive feedback loop.
    • 5 Our paper moves away from the usual focus on intertemporal questions, and concerns itself with how a student learns. This means we can omit discounting of utility, depreciation of education, and the role of interest rates. See Appendix A3 for an N period extension.
    • 6 Since the choice about education investment is restricted to the first period, time subscripts have been removed for brevity.
    • 7 In the CES production function, the parameters are interdependent and must be carefully interpreted (see Temple, 2012). Data on S $S$ are hard to observe, and so α $\alpha$ and ρ $\rho$ are hard to identify. However, the CES production function we use has been identified in many contexts and we believe that with a rich enough data set our model can be tested (see Klump et al., 2012).
    • 8 See Section 3.5 for a discussion of this wage function.
    • 9 p ¯ $\overline{p}$ can also be interpreted as a travel cost of attending class. This interpretation does not affect any of our results and, while it might seem natural, it shifts the focus away from questions we wish to address.
    • 10 The literature on returns to education considers tuition fees relative to the wage differential of graduates. It is apparent from our focus on time, that if S + T $S+T$ is different to the hours worked in a nongraduate job, then estimated returns may be biased.
    • 11 For proof, see Appendix A.1
    • 12 For proof, see Appendix A.2.1
    • 13 For proof, see Appendix A.2.2
    • 14 For proof, see Appendix A.2.3
    • 15 Individuals only obtain the same Graduate Premium if they are all forced to use bundles, which are symmetric. This is the only case where Graduate Premium is independent of learning parameters.
    • 16 For proof, see Appendix A.2.4
    • 17 For proof, see Appendix A.2.5
    • 18 A distorted learner is a student for whom, in equilibrium, ∂ e / ∂ S ∂ e / ∂ T ≠ w w + p $\frac{\partial e/\partial S}{\partial e/\partial T}\ne \frac{w}{w+p}$ . This is because they either choose to only make use of one input, or they face a restriction on the amount of one input.
    • 19 For example, if individuals i $i$ and j $j$ both undertake the same number of years schooling (at a cost n w ̲ $n\underline{w}$ ) but achieve different levels of education ( e i > e j $e_i>e_j$ ), then, because n w ̲ e i < n w ̲ e j $\frac{n\underline{w}}{e_i}<\frac{n\underline{w}}{e_j}$ , i $i$ is higher ability than j $j$ . However, heterogeneous opportunity costs (e.g., w i ̲ > w j ̲ $\underline{w_i}>\underline{w_j}$ ) may reverse such a ranking (i.e., n w i ̲ e i > n w j ̲ e j $\frac{n\underline{w_i}}{e_i}>\frac{n\underline{w_j}}{e_j}$ ).
    • 20 To give one example, if we include high- and low-income students, an IL from a low-income background (whose marginal product of study was reduced by their home environment) would appear to less independent than an identical student from a high-income family. This approach could be generalized by replacing each of the inputs with functions that adjust the inputs for dimensions such as socioeconomic background.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.