Measurement of the concentration of nutrients in grapevine petioles by attenuated total reflectance Fourier transform infrared spectroscopy and chemometrics
Abstract
Background and Aims
We determined the effectiveness of attenuated total reflectance Fourier transform infrared spectroscopy as a rapid and low-cost method for measuring the concentration of nutrients in grapevine petioles.
Methods and Results
Attenuated total reflectance Fourier transform infrared spectra were recorded for 392 dried and ground petiole samples collected from Chardonnay, Semillon and Shiraz vineyards in the Riverina between 2003 and 2010. Predictive models of nutrient concentration obtained with standard reference methods were developed using partial least squares regression. Good predictive models were produced for all macronutrients, with R2 values for nitrogen (N), phosphorus (P), potassium (K), magnesium (Mg), calcium (Ca) and sulfur (S) of 0.945, 0.915, 0.951, 0.961, 0.940 and 0.849, respectively. For sodium (Na) and the micronutrients iron (Fe), manganese (Mn), boron (B), copper (Cu) and zinc (Zn), R2 values were 0.773, 0.750, 0.743, 0.630, 0.612 and 0.835, respectively. When ranked according to the residual predictive deviation, expressed as the ratio of the standard error of performance to the calibration set standard deviation, values of 5.4, 3.8, 3.1, 3.8 and 3.5 were obtained for N, P, K, Mg and Ca, respectively; intermediate values of 2.4, 2.0 and 1.8 were obtained for S, Zn and Na, while Fe, Mn, B, Cu had a value of 1.3 or below.
Conclusion
All macronutrients in grapevine petiole tissue can be determined by attenuated total reflectance Fourier transform infrared spectroscopy with sufficient accuracy to assess grapevine nutritional status against standard interpretive ranges. Certain micronutrients can also be determined, although the predictive models for these elements were not as robust as models for the macronutrients.
Significance of Study
The study presents a rapid, low-cost and easy-to-implement technique suited to the widespread adoption and routine analysis of plant tissue for the management of grapevine nutrition in the Australian winegrape vineyards.
Introduction
Plant tissue analysis is widely used in agriculture to assist with managing crop nutrition, and plant sampling techniques together with corresponding interpretative ranges are available for many species. The objective of such analysis is to obtain a representative and integrated measure of plant nutritional status, which can then act as a guide for seasonal fertiliser requirements or managing longer term issues with mineral nutrient deficiency or toxicity. Various methods for assessing grapevine nutritional status have been investigated, but the most widely used interpretive standards in Australia relate to petiole nutrient concentration at flowering (Robinson et al. 1997). These are based on research undertaken in California and subsequently refined for Australian conditions (Cook 1966, Christensen et al. 1978, Robinson and McCarthy 1985). Interpretive standards have also been published for petioles at veraison, and for leaf lamina nutrient concentration at flowering and veraison (Weir and Cresswell 1993, Bavaresco et al. 2010). The petioles are always collected from a basal position on the shoot opposite an inflorescence or bunch, and would typically be sent as fresh samples to a commercial laboratory for analysis.
The most common analytical method for total N is based on the Dumas combustion method, whereby samples are oxidised at 900–1000°C, and the released gaseous nitrogen-containing products are reduced to N2 and quantified. The other macronutrients P, K, Ca, Mg and S, and the micronutrients Mn, Fe, Cu, B, Zn and Cu, Na, Ni and Mo, are commonly measured by inductively coupled plasma (ICP) spectrometry following acid digestion (Zarcinas et al. 1987). Vibrational spectroscopy combined with chemometric modelling offers an alternative means for the determination of multiple analytes in intact or ground samples, and near infrared (NIR) spectroscopy in particular has become a widely accepted method for the analysis of plant materials (Batten 1998, International Organization for Standardization 2010). This process involves collecting NIR spectra of samples with a known concentration of analytes and developing predictive models to determine the concentration of the same analytes from the NIR spectra of subsequent unknown samples. The more recognised applications include protein content of grain and animal feedstuffs, moisture content, starch, and total N concentration (Batten 1998). The mineral plant-based elements required by plants do not directly absorb in the IR region, but when present as components of organic or inorganic molecules, through influence on hydrogen bonding, and interaction or association with other matrix components, spectral information can be obtained about their concentration in solid or liquid samples. In previous studies, this information has been used to develop calibrations for IR-based measurements of the concentration of elemental nutrients in a range of plant tissues (e.g. Ruano-Ramos et al. 1999, Morón and Cozzolino 2002, Petisco et al. 2008, Cozzolino et al. 2011), including a robust NIR calibration for K concentration of grapevine leaf and petioles (Ciavarella et al. 1998).
Attenuated total reflectance Fourier transform infrared (ATR-FT-IR) spectroscopy is an alternative infrared (IR) spectroscopy technique where the sample is placed in contact with a crystal or diamond sensing element, and IR absorbance information obtained after internal reflection of an IR beam from the sensing element and sample interface. The technique has advantages over NIR spectroscopy in that absorbance bands in the mid-IR region provide more structural information about unknown compounds, samples require limited or no preparation, and once appropriate calibrations are developed the technique can be used for routine analysis with minimal expertise and training. Previous research has demonstrated the application of ATR-FT-IR spectroscopy for juice and wine analysis (Edelmann et al. 2003, Shah et al. 2010), and the measurement of total N and starch concentration in grapevine wood and root tissues (Schmidtke et al. 2012). The aim of the present study was to test the effectiveness of the same technique for predicting the concentration of several nutrients in grapevine petiole tissue.
Materials and methods
Petiole collection and nutrient analysis
The petiole samples utilised for the study originated from a collection of grapevine material sampled between November 2003 and January 2010 from research trial sites in the Riverina grapegrowing region of New South Wales, Australia. The collection comprised 392 samples from commercial Chardonnay, Semillon or Shiraz vineyards which were collected at flowering, veraison or harvest. Details of the Chardonnay vineyards and trial layout have been published previously (Barlow et al. 2009); briefly, these consisted of three drip- and three furrow-irrigated blocks with planting dates ranging from 1994 to 2002. Four of the vineyards were grafted on Ramsey (Vitis champinii), one was grafted on 140 Ruggeri (V. berlandieri × V. rupestris) and one was grown on own roots. Samples were collected from four locations within the drip-irrigated vineyards, and from eight locations in the furrow-irrigated vineyards. The Semillon and Shiraz petioles were collected from single, own-rooted, drip-irrigated vineyards. These were located near Hanwood (34°19′ S, 145°49′ E) or Wagga Wagga (35°03′ S, 147°21′ E), and planted in 1995 and 1998, respectively. Details of these studies have not been published previously, but both included a range of deficit irrigation and N fertiliser timing treatments.
Each sample consisted of 25 petioles that were collected from opposite an inflorescence or bunch from random shoots along panels of six to ten vines. The petioles were washed in phosphate-free detergent, rinsed twice with deionised water and then oven-dried at 70°C. These were then ground to approximately 0.12 mm in an ultracentrifugal mill (Restch ZM100 or Restch ZM200, Haan, Germany), and stored in air-tight containers prior to analysis. Total N concentration was determined on a 50-mg subsample with a Carlo Erba model NA-1500 combustion gas chromatograph (Milan, Italy) for petioles collected to 2005. For petioles collected from 2006 to 2010, N analysis was undertaken with an Elementar vario MAX (Elementar Analysensysteme GmbH, Hanau, Germany). Total concentration of P, K, Mg, Ca and S was determined on a 400–600 mg subsample by ICP following nitric acid digestion (Zarcinas et al. 1987). An ARL model 3580 B (Applied Research Laboratories S.A., Ecublens, Switzerland) inductively coupled plasma optical emission spectrometer (ICP-OES) was used for the 2003/04 season petioles, and a Spectro CIROS (SPECTRO Analytical Instruments GmbH, Kleve, Germany) radial ICP-OES subsequently. Data for N, P, K, Mg and Ca concentration are reported on a percentage dry mass basis, while Fe, Mn, B, Cu and Zn are reported as mg/kg dry mass. Reference method variance was estimated from the reported concentration values of repeated sample controls run concurrently with the analysis of the petiole samples. For total N, the method variance was estimated from 50 repeated analyses of a specific control sample, and from 38 for ICP-OES elemental analysis.
Collection of ATR-FT-IR spectra
Infrared spectra of dried and powdered petiole samples were collected using Opus software (version 7, Bruker, Ettlingen, Germany) and an Alpha ATR-FT-IR spectrophotometer (Bruker) with a diamond internal reflection element and sample temperature at 40°C. An ATR spectra for each sample was prepared by averaging 64 scans on a single sample over the wavenumber range 375–7500 cm−1. A background scan against air was conducted approximately every ten samples. Data were converted to ascii format at a resolution of 1.4 cm−1 and imported into Matlab version 7.4.0.287 R2007a (The Mathworks, Natick, MA, USA).
Exploratory data analysis
For the purposes of exploratory data and regression analysis, ATR data between 400 and 4000 cm−1 were extracted from each spectra and converted to absorbance to correct for differences in sample penetration of the beam at different wavelengths. Spectra from all samples and the 95% confidence interval for absorbance were plotted to identify regions that may contain information relating to compositional differences between samples. A principal component analysis (PCA) of the standard normal variate (SNV) scaled and mean centred spectra between the regions 375 and 1800 cm−1 was conducted using the singular value decomposition algorithm with principal components (PC) 1 and 2, and associated loadings plotted to identify specific sample groupings based upon cultivar, growing season and sampling time.
Outlier samples were identified from the PCA model of the spectral data using six PCs by plotting Q residuals and Hotelling T2 values (data not shown) using previously described methods (Schmidtke et al. 2012). High Hotelling T2 values indicate samples that deviate considerably from the mean and possess disproportionate leverage over the model, and high Q residuals indicate poorly modelled samples with the chosen number of principal components (Westerhuis et al. 2000, Brereton 2009, Ferrer-Riquelme 2009). For the purposes of further modelling, samples with high Hotelling T2 and/or Q residuals from the PCA of spectral data were excluded. Of the remaining samples within the data set, 240 were then allocated to a ‘calibration’ data set and 122 to a ‘test’ data set using the D-optimal criteria (Table 1). The D-optimal approach seeks to choose samples that maximise the determinant of the association matrix of the calibration samples (Ferré and Rius 1997); thus, samples are chosen for the calibration set that span the greatest area of spectral variations.
| Calibration set | Test set | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Season | Cultivar | Flowering | Veraison | Harvest | Total | Flowering | Veraison | Harvest | Total |
| 2003/04 | Chardonnay | 13 | 18 | 20 | 51 | 6 | 7 | 8 | 21 |
| 2004/05 | Chardonnay | 24 | 16 | 23 | 63 | 11 | 9 | 11 | 31 |
| 2005/06 | Chardonnay | 21 | 19 | 16 | 56 | 11 | 8 | 15 | 34 |
| 2006/07 | Chardonnay | 12 | — | — | 12 | 10 | — | — | 10 |
| 2007/08 | Semillon | 15 | — | — | 15 | 9 | — | — | 9 |
| 2008/09 | Semillon | 14 | — | — | 14 | 10 | — | — | 10 |
| 2009/10 | Shiraz | 14 | — | 15 | 29 | 4 | — | 3 | 7 |
| Total | 113 | 53 | 74 | 240 | 61 | 24 | 37 | 122 | |
- —, No samples collected.
Data pre-processing and regression modelling
Calibration and test data were pre-processed using SNV scaling followed by calculating the first or second derivative with a Savitzky–Golay (Savitzky and Golay 1964) filter prior to variable selection. Data smoothing for the Savitzky–Golay derivation used a 15-point curve and second-order polynomial. Alternatively, multiplicative scatter correction (MSC) or extended multiplicative scatter correction (EMSC) using reference spectra for water and carbon dioxide vapour were applied to the calibration data set using a second-order polynomial filter in accordance with described procedures (Martens et al. 2003, Gallagher et al. 2005, Rinnan et al. 2009) prior to variable selection. Spectra at a resolution of 0.1 cm−1 for carbon dioxide were obtained from an online database (Sharpe et al. 2002), and de-resolved and re-sampled to match the reflectance spectra of samples. For the purposes of applying MSC and EMSC, the mean spectra of the calibration samples were used as the reference spectra. Orthogonal signal correction was applied to spectra to remove structured noise that was not correlated to the analytical values (Wold et al. 1998). Variable selection within the calibration block was conducted using the forward interval partial least squares regression for each analyte and model combination (Norgaard et al. 2000).
Predictive models of the macro- and micronutrient concentration values were constructed from the spectra using PLS regression (PLS1 and PLS2) using the SIMPLS algorithm. The models of the concentration of multiple nutrients were not improved by PLS2 regression over that achieved with PLS1 (results not shown), and final models were therefore constructed using the PLS1 algorithm. Cross-validation was conducted using random sample subsets with ten data splits of the calibration samples. The number of latent variables chosen for each model was determined from eigenvalues and minima of the root mean square errors of calibration and cross-validation. Principal component analysis, sample allocation, Hotelling T2, Q residuals and regression modelling were conducted with Matlab and PLS Toolbox version 7.0.2 (Eigenvector Research Inc., Wenatchee, WA, USA).
To estimate the ‘pure component’ spectra, a linear rotation of the regression coefficients was undertaken in accordance with the method of Trygg (2004). To visualise the influence of each region of the normalised spectra upon the regression model, the selectivity ratio was also plotted (Kvalheim and Karstang 1989). The selectivity ratio is calculated as the ratio of the explained to residual variance for each variable used in the model, and enables the identification of regions of the spectra used for regression that are most strongly associated with the component of interest (Rajalahti et al. 2009). As an interpretive tool, it can assist with calibration refinement, removal of non-relevant spectral variables, and allow information about potential sample composition or regions of interest to be obtained from spectra of a complex sample matrix.
Evaluation of the predictive models was conducted by determining the predictive uncertainty, at the set level, of the independent test sample set by calculating the root mean square error of prediction (RMSEP). The RMSEP value describes the average difference between the measured and predicted values for each sample, and is expressed in the same units as in the reference method analysis (e.g. %DM). It is well documented that multivariate regression predictive errors are compounded by the model and reference method errors, and consequently RMSEP will overestimate the true predictive error (Faber and Bro 2002, Faber et al. 2003, Fernández Pierna et al. 2003, Bro et al. 2005). A corrected test set prediction error (RMSEPCORR) of each model RMSEP was, therefore, calculated by correcting for reference method variance using the method described by Faber and Kowalski (1997). To determine the usefulness of the predictive models, the ratio of standard error of performance (SEP) to standard deviation (RPD) statistic was calculated (Fearn 2002); this statistic compares the RMSEPCORR with the standard deviation of the reference values (Williams 2001). This ratio is used to compare the predictive model with alternative methods of analysis, and generally models with an RPD above 2.5 are considered acceptable (Lomborg et al. 2009).
Results and discussion
Concentration of petiole macronutrients
The variation associated with season, growth stage, cultivar, vineyard and research trial treatment generated a petiole macronutrient data set with a four- to 14-fold difference in concentration between the minimum and maximum values for each element (Figure 1). The highest individual sample concentration for N, P, K and S was observed at flowering, and the lowest at either the veraison or harvest sampling dates. Conversely, the lowest concentration of Mg and Ca was observed at flowering and the highest at harvest. These contrasting patterns of nutrient accumulation and mobilisation are consistent with results of previous studies, with the concentration of Mg and Ca commonly increasing with leaf age, and that of N, P and K stable or declining (Christensen 1969, Conradie 1981, Romero et al. 2010).
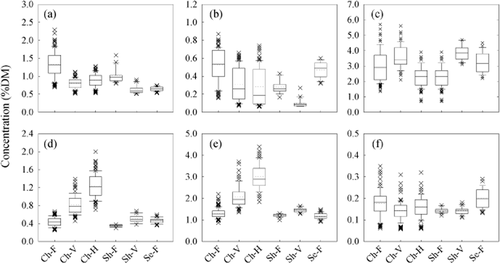
Concentration ranges of petiole macronutrients (a) nitrogen, (b) phosphorus, (c) potassium, (d) magnesium, (e) calcium and (f) sulfur according to cultivar and growth stage. For x-axis labels, Ch, Sh and Se indicate Chardonnay, Shiraz and Semillon, respectively, and F, V and H represent flowering, veraison and harvest, respectively (n = 392).
Relative to interpretative standards used in Australia for petiole analysis at flowering (Table 2, Robinson et al. 1997), the concentration ranges for the macronutrients N, P, K, Mg and Ca spanned from deficient or marginal through to above that necessary for maintaining optimal nutritional status (Figure 1, Table 3). Sulfur deficiency is rarely observed in grapevines due to the common use of S-containing N, P or K fertilisers and of elemental S fungicide sprays; as samples are not always washed prior to commercial analysis, contamination from spray residues would be expected. The concentration ranges, however, observed in the present study are consistent with general plant tissue requirements for optimal growth of 0.1–0.5% on a dry mass basis (Hawkesford et al. 2012). The concentration distributions and lack of outliers above this range also suggest that the washing procedure effectively removed residual surface S prior to analysis. For N, P, K and S, the lower values from the veraison or harvest dates extended the concentration ranges spanned by the sample set, but the variability associated with growth stage was largely encompassed by the variability within the flowering sampling dates. In contrast, the concentration range for Mg and Ca was extended towards the higher end due to the concentration increasing between growth stages, and all values above 0.68 and 2.2 %DM for each nutrient, respectively, were derived from petioles collected at either veraison or harvest.
| Element | Units | Deficient | Marginal | Adequate | High | Toxic/excessive |
|---|---|---|---|---|---|---|
| N | %DM | — | — | 0.8–1.1† | — | — |
| P | %DM | <0.2 | 0.2–0.24 | 0.25–0.50 | >0.50 | — |
| K | %DM | <1.0 | 1.0–1.7 | 1.8–3.0 | — | — |
| Mg | %DM | <0.3 | 0.3–0.39 | >0.4 | — | — |
| Ca | %DM | — | — | 1.2–2.5 | — | — |
| Fe | mg/kg | — | — | >30 | — | — |
| Mn | mg/kg | <20 | 20–29 | 30–60 | — | >500 |
| B | mg/kg | <25 | 26–34 | 35–70 | 71–100 | >100 |
| Cu | mg/kg | <3 | 3–5 | 6–11 | — | — |
| Zn | mg/kg | <15 | 16–25 | >26 | — | — |
| Na | mg/kg | — | — | — | — | >5000 |
- †0.9–1.25 for vines grafted on Ramsey. DM, dry mass; —, Ranges not reported.
| Calibration set | Test set | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Element | Units | Min. | Max. | Mean | SD | Min. | Max. | Mean | SD |
| n = 240 | n = 122 | ||||||||
| N | %DM | 0.52 | 2.29 | 0.95 | 0.35 | 0.52 | 2.02 | 0.96 | 0.34 |
| P | %DM | 0.06 | 0.80 | 0.37 | 0.21 | 0.07 | 0.81 | 0.39 | 0.20 |
| K | %DM | 0.75 | 5.10 | 3.08 | 0.89 | 0.69 | 5.60 | 3.11 | 0.96 |
| Mg | %DM | 0.25 | 1.79 | 0.70 | 0.36 | 0.28 | 1.75 | 0.71 | 0.35 |
| Ca | %DM | 0.87 | 4.40 | 1.85 | 0.80 | 0.99 | 4.20 | 1.83 | 0.78 |
| S | %DM | 0.06 | 0.35 | 0.16 | 0.05 | 0.06 | 0.33 | 0.17 | 0.06 |
| n = 238 | n = 121 | ||||||||
| Fe | mg/kg | 14 | 101 | 33 | 14 | 17 | 77 | 33 | 12 |
| Mn | mg/kg | 22 | 1800 | 196 | 243 | 18 | 1400 | 221 | 280 |
| B | mg/kg | 32 | 198 | 69 | 33 | 30 | 194 | 74 | 33 |
| Cu | mg/kg | 3 | 133 | 20 | 21 | 5 | 147 | 22 | 24 |
| Zn | mg/kg | 15 | 153 | 72 | 34 | 23 | 151 | 75 | 30 |
| Na | mg/kg | 79 | 6800 | 1115 | 1436 | 70 | 7600 | 1015 | 1337 |
- SD, standard deviation; DM, dry mass.
Concentration of petiole micronutrients
For the micronutrients Fe, Mn, B, Cu and Zn, the average concentration for the flowering sample dates was within the adequate nutritional range as defined by Australian petiole standards, and individual values ranged from marginal through to high (Figure 2, Table 3). For Na, with a maximum concentration of 730 mg/kg at flowering, all values were well below the 5000 mg/kg or 0.5%DM threshold considered toxic and indicative of excessive salt uptake. Concentration increased with each sampling date, but at harvest only 14 of the 392 samples had values exceeding this threshold.
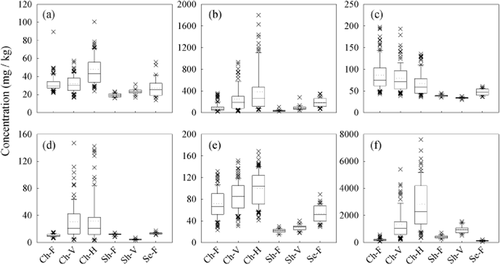
Concentration ranges of petiole micronutrients (a) iron, (b) manganese, (c) boron, (d) copper, (e) zinc and (f) sodium according to cultivar and growth stage. For x-axis labels, Ch, Sh and Se indicate Chardonnay, Shiraz and Semillon, respectively, and F, V and H represent flowering, veraison and harvest, respectively (n = 392).
The concentration values for Fe contained several outliers that suggested contamination from metal grinder parts; three values above 230 mg/kg were removed along with spectra outliers identified from the PCA Hotelling T2 and Q residual values. Although it is possible that some of the higher values retained in the calibration and test data set may still reflect contamination from the grinding process, a concentration above 100 mg/kg was not inconsistent with published data (e.g. Christensen 1969). Likewise, while all petiole samples were washed with detergent and rinsed twice with deionised water, it cannot be ruled out that the high Mn and Cu at veraison and harvest were a reflection of accumulated fungicide spray residue. For Chardonnay, the high Cu concentration was mostly associated with two vineyards, and pronounced increases in concentration between collection dates suggest that this was because of the application of Cu-based fungicides. The higher Mn value within each sampling date, and progressive skewing of the sample distribution through the season, were related to the consistently high Mn status of a third Chardonnay vineyard. Maximum Mn concentration at flowering at this site ranged from 137 to 360 mg/kg, which is higher than values previously attributed to spray contamination or soils with high, readily available Mn (Robinson and McCarthy 1985). Other tissue analysis undertaken at the site (not reported here) showed that the higher Mn concentration was also reflected in 1-year-old wood tissue. As the bark was removed prior to analysis, spray contamination is unlikely, so the Mn values at this site may reflect natural soil abundance and the progressive accumulation during the season of the phloem-immobile nutrient.
For the remaining micronutrients B and Zn, which were similar in this regard to N, P, K and S, the variability at the flowering date encompassed most of the range spanned by the subsequent veraison and harvest sampling dates. The concentration ranges of B at the Chardonnay vineyards was skewed somewhat by generally higher values through the 2005/06 season, but the population distribution of five of the remaining nine sampling date groups for B and Zn did not differ significantly from normal. One high outlier of 290 mg/kg was observed for Zn, which like high Mn and Cu values may indicate the presence of fungicide residue. The gradual increase in concentration through the season, however, is consistent with previous reports (e.g. Christensen 1984, Romero et al. 2010). The otherwise uniform sample distributions and lack of extreme outliers suggest that the Zn petiole concentration may more reliably reflect uptake by the roots than the concentration of Cu and Mn. Similarly, for B and Na, contamination from the vineyard or processing stage would be considered unlikely.
ATR-FT-IR spectra
The mean ATR-FT-IR spectra of dried ground petiole samples was characterised by a broad peak at 3000–3500 cm−1, and dominant peaks between 375 and 800, and between 875 and 1800 cm−1. The broad absorbance band between 3000 and 3500 cm−1 is characteristic of the O-H stretch and may be related to the presence of carbohydrates or residual moisture (Dufour 2009). The region with the largest variation occurs between 375 and 1800 cm−1 (Figure 3). The spectral bands characterising carbohydrates are typically observed in the 2800–3600 cm−1, 1200–1500 cm−1, 950–1200 cm−1 and 700–950 cm−1 regions, corresponding to O-H and C-H bond stretching, bending of symmetric HCH bonds, C-O and C-C bond stretching, and COH, CCH and OCH bond bending (Dufour 2009). The region between 1200 and 1800 cm−1 includes IR bands associated with amino acids and nitrate (Barth 2000, Larkin 2011). The petiole IR absorbance spectra were similar to that reported for grapevine wood and root tissue (Schmidtke et al. 2012), except that absorbance peaks for petiole samples were higher in the 1200–1800 cm−1 region and lower in the 875–1200 cm−1 region. Principal component analysis of the spectra between 375 and 1800 cm−1 clearly separated the samples according to cultivar and growth stage, with the first two PCs capturing approximately 83% of the variation in this region (Figure 4a,b). No obvious grouping for growing season was evident in the first two PCs (Figure 4c).
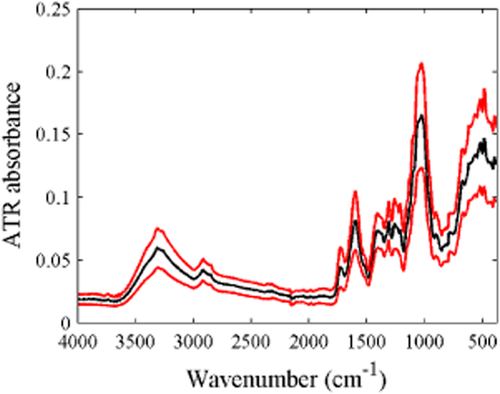
Mean attenuated total reflectance (ATR) Fourier transform infrared spectra ( ) and 95% confidence interval (
) and 95% confidence interval ( ) of all petiole samples prior to outlier deletion.
) of all petiole samples prior to outlier deletion.
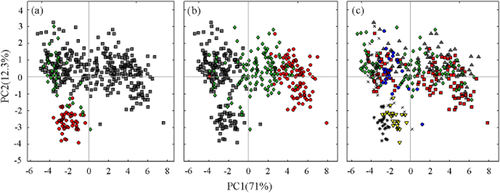
Identification of sample groupings by PCA of petiole attenuated total reflectance Fourier transform infrared spectra (375–1800 cm−1): (a) cultivar, Chardonnay ( ), Semillon (
), Semillon ( ) and Shiraz (
) and Shiraz ( ); (b) growth stage, flowering (
); (b) growth stage, flowering ( ), veraison (
), veraison ( ) and harvest (
) and harvest ( ); and (c) season, 2003/04 (
); and (c) season, 2003/04 ( ), 2004/05 (
), 2004/05 ( ), 2005/06 (
), 2005/06 ( ), 2006/07 (
), 2006/07 ( ), 2007/08 (
), 2007/08 ( ), 2008/09 (
), 2008/09 ( ) and 2009/10 (
) and 2009/10 ( ).
).
The identification and removal of spectral outliers from the data set prior to fitting regression models is an important first step for multivariate predictions (Brereton 2003, Zeaiter and Rutledge 2009). Various methods can be used for this purpose, and an acceptable approach is to determine the sample Hotelling T2 and Q residuals from a PCA with an appropriate number of PCs. In the present study, six PCs were used for this purpose based upon the variance captured for each PC and a cumulative variance of approximately 95%. Reference method outlier samples in the present study, however, were not identified in this manner, as samples with suspected contamination with inorganic ions or non-plant-derived elements did not exhibit increased or unusual spectral absorbance characteristics. This was not unexpected given the lack of infrared absorbance by most elements, and as previously described a small number of samples that could be identified as most likely possessing Fe contaminants were manually removed from the data set when modelling micronutrients.
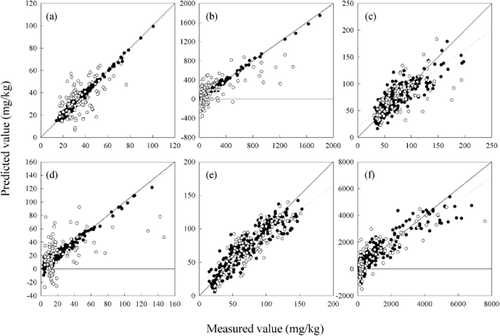
Macronutrient calibration models
Predictive models utilising PLS regression were successfully constructed for all macronutrients (Figure 5), with the coefficient of determination (R2) ranging between 0.849 for S and 0.961 for Mg (Table 4). The selectivity ratio plots for each element showed that the macronutrient regressions utilised spectral variability in the 460–1870 cm−1 region, and to a lesser extent in regions between 2870–3700 cm−1 (Figure 6a-f) . Although the petiole samples used in the study represent a complex matrix of organic and inorganic compounds, several key regions of interest could be identified based on the contribution to the regression models for each element. For N, the selectivity ratio indicated a high level of spectral variability associated with the concentration measured at 1030, 1613 and 1726 cm−1 with additional information used at wavenumbers between 2800 and 3717 cm−1. These correspond to regions associated with IR absorbance by C-H, C-N and C-N-H bonds of primary and secondary amine groups, and may be indicative of the concentration of amino acids. The IR absorbance bands of inorganic N also overlap with some of these regions (Larkin 2011). For P, compounds containing P-O-C, P-O-P and P-O-H bonds have strong IR absorbance bands in the region between 870 and 1090 cm−1, while P=O bonds have a strong absorbance band between 1140 and 1350 cm−1. The highest selectivity ratios for P in the present study were consistent with these frequencies, with peaks observed at 923, 958 and 1358 cm−1. For the other macronutrients, K exhibited the highest selectivity ratios around 1413–1467 cm−1, Mg at 951 and 1661 cm−1, Ca at 785 and 1308 cm−1, and S at 621 and 1557–1649 cm−1.

Regression plots for the prediction of petiole macronutrients: (a) nitrogen, (b) phosphorus, (c) potassium, (d) magnesium, (e) calcium and (f) sulfur by attenuated total reflectance Fourier transform infrared spectroscopy. R2 value, corrected test set prediction error (RMSEPCORR) and adequate concentration [%dry mass (DM)]: (a) 0.945, 0.078 and 0.8–1.1; (b) 0.915, 0.056 and 0.25–0.5; (c) 0.951, 0.305 and 1.8–3.0; (d) 0.961, 0.093 and >0.4; (e) 0.940, 0.226 and 1.2–2.5; and (f) 0.849 and 0.023. Calibration data (●) and test data (○); calibration fit (· · · · ·) and 1:1 (—).
| Element | Units | Reference method variance | R2 | RMSEP | RMSEPCORR | SEP | Bias | LV | RPD | RER |
|---|---|---|---|---|---|---|---|---|---|---|
| N | %DM | 0.35 × 10−3 | 0.945 | 0.081 | 0.078 | 0.081 | 0.000 | 6 | 5.4 | 22 |
| P | %DM | 0.23 × 10−4 | 0.915 | 0.056 | 0.056 | 0.056 | 0.000 | 5 | 3.8 | 13 |
| K | %DM | 3.3 × 10−3 | 0.951 | 0.311 | 0.305 | 0.310 | 0.037 | 7 | 3.1 | 14 |
| Mg | %DM | 0.69 × 10−4 | 0.961 | 0.094 | 0.093 | 0.092 | −0.012 | 7 | 3.8 | 5 |
| Ca | %DM | 2.6 × 10−3 | 0.940 | 0.232 | 0.226 | 0.233 | −0.016 | 5 | 3.5 | 6 |
| S | %DM | 0.39 × 10−4 | 0.849 | 0.024 | 0.023 | 0.024 | −0.004 | 6 | 2.4 | 12 |
| Fe | mg/kg | 193 | 0.750 | 11 | 11 | 11 | −0.226 | 5 | 1.2 | 7 |
| Mn | mg/kg | 24 | 0.743 | 222 | 222 | 220 | −35.5 | 6 | 1.3 | 2 |
| B | mg/kg | 0.308 | 0.630 | 25 | 25 | 25 | −1.0 | 7 | 1.3 | 6 |
| Cu | mg/kg | 0.108 | 0.612 | 24 | 24 | 24 | −1.1 | 5 | 1.0 | 0.5 |
| Zn | mg/kg | 2.81 | 0.835 | 16 | 16 | 16 | −2.3 | 3 | 2.0 | 17 |
| Na | mg/kg | 7529 | 0.773 | 800 | 795 | 803 | −11.0 | 3 | 1.8 | 1 |
- DM, dry mass; Bias, systematic error; R2, coefficient of determination; RER, range error ratio (here calculated as SEP to flowering sample date concentration range); RMSEP, root mean square error of prediction; RMSEPCORR, root mean square error of prediction corrected for reference method variance; LV, number of latent variables used in each model; RPD, residual predictive deviation; SEP, standard error of prediction.
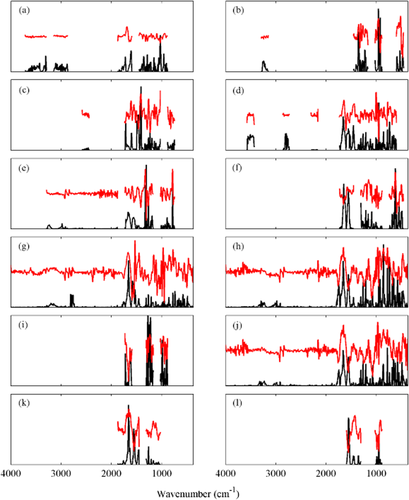
Estimate of pure spectral profiles ( ) and selectivity ratios (
) and selectivity ratios ( ) for (a) nitrogen, (b) phosphorus, (c) potassium, (d) magnesium, (e) calcium, (f) sulfur, (g) iron, (h) manganese, (i) boron, (j) copper, (k) zinc and (l) sodium as calculated from the partial least squares regression according to Trygg (2004) and Rajalahti et al. (2009).
) for (a) nitrogen, (b) phosphorus, (c) potassium, (d) magnesium, (e) calcium, (f) sulfur, (g) iron, (h) manganese, (i) boron, (j) copper, (k) zinc and (l) sodium as calculated from the partial least squares regression according to Trygg (2004) and Rajalahti et al. (2009).
In previous studies, NIR spectroscopy has been widely employed for the analysis of mineral elements in plant tissue (Clark et al. 1987, Ruano-Ramos et al. 1999, Morón and Cozzolino 2002, Cozzolino et al. 2011), but the present work appears to be the first to report the application of ATR-based mid-IR spectroscopy for measurement of the full range of macronutrients in the vegetative tissue of grapevines or in any other plant species. A comparison of NIR prediction errors with the SEP values for the ATR-FT-IR calibrations suggests that more robust calibrations for individual elements may be possible with NIR spectroscopy, with Ciavarella et al. (1998), for example, reporting a prediction error as low as 0.179 %DM for petiole K concentration compared with 0.311 %DM in the present study. Similarly, Petisco et al. (2005) reported an SEP value of 0.060 %DM for a Ca calibration across multiple species compared with 0.232 %DM reported here. In the few NIR studies, however, that have examined the complete (Morón and Cozzolino 2002) or near complete macronutrient range (Menesatti et al. 2010), satisfactory calibrations were not able to be developed for all elements.
The ratio of SEP to standard deviation (RPD) is a commonly used statistic that provides a measure of concentration variability of a sample set in relation to the accuracy of concentration predictions from calibration models. As a ratio, the RPD value has no units, and therefore provides a common metric by which the general performance and potential applications of different calibration models can be compared (Fearn 2002). For example, there is general agreement that calibrations with an RPD below about 1.5 have limited application, while values between 2 and 5 are regarded as acceptable and well suited for screening or analysis purposes (Chang et al. 2001, Williams 2001, Lomborg et al. 2009). The RPD values in the present study ranged between 2.4 for S and 5.4 for N (Table 4), which are comparable to the ranges reported for plant tissue NIR calibrations, but consistently good across all of the macronutrients.
An alternative statistic, the range error ratio (RER), can also be used to relate the predictive accuracy of a model. It is calculated as the ratio of the sample concentration range (max–min) to the SEP (Fearn 2002), and relates the predictive error of a method to the concentration range over which it will be applied. In the present study, we used a calibration and test set spanning three growth stages, but petiole nutrient analysis and corresponding interpretative standards are most commonly based on concentration at flowering (Robinson 1992). As the higher values of Mg and Ca from veraison and harvest increased the concentration span well beyond what would normally be observed at flowering, the RER values presented here have been calculated using the subset of flowering samples rather than full data set. For N, P, K and S, the RER effectively resolves the accuracy of the ATR-FT-IR-based analysis method into a minimum of 12 categories or intervals across the concentration range at flowering (Table 4). For Mg and Ca, which have a lower concentration early in the season, the RER values were 5 and 6, respectively. These values indicate that ATR-FT-IR spectroscopy is sufficiently accurate to estimate the concentration of all macronutrients in grapevine petioles, and identify where these values lie within the standard interpretive ranges.
Micronutrient calibration models
The performance of the micronutrient models was variable, and for the micronutrients Mn and Cu, concentration could not be estimated with the same accuracy of the macronutrients (Table 4, Figure 7). The contrasting fit of the predicted values for the calibration and test data sets suggests that the PLS regression was not successfully modelling spectral variation associated with the plant-derived concentration of these elements. This is supported by the selectivity plots which show utilisation of most of the spectra by the PLS regression (Figure 6f,h), and a lack of dominant IR regions. Calibration performance for Fe was similar to that of Mn and Cu, and for all of these nutrients this may reflect the influence of elemental contamination from metal grinder parts or from fungicide sprays that can be quantified by the ICP reference method, but not with IR spectroscopy. The calibration and test data set fits for B, Zn and Na were similar, and selectivity ratio plots indicated that the concentration of the elements was associated with absorbance bands in specific regions of the IR spectra. The potential of NIR for micronutrient analysis has previously been demonstrated (Cozzolino and Moron 2004), with calibrations developed for legume B, Cu, Mn and Zn concentration with sufficient accuracy for application as a screening tool. The elements Na and S were also well predicted. Aside from issues with suspected contamination for Cu and Mn, the results of the present study are consistent with this earlier work. Performance for Zn was sufficient to provide a reasonably predictive value with RPD and RER values of 2.0 and 17, respectively. For B and Na, although not sufficient for analytical purposes, the calibrations could be potentially used to determine if the concentration of these elements was in the excessive or toxic range.
Regression plots for the prediction of petiole micronutrients: (a) iron, (b) manganese, (c) boron, (d) copper, (e) zinc and (f) sodium by attenuated total reflectance Fourier transform infrared spectroscopy. R2 value, corrected test set prediction error (RMSEPCORR) and adequate concentration (mg/kg): (a) 0.750, 11 and >30; (b) 0.743, 0.743 and 30–60; (c) 0.630, 25 and 35–70; (d) 0.612, 0.612 and 6–11; (e) 0.835, 0.835 and >26; and (f) 0.773, and 0.773 and toxic >5000. Calibration data (●) and test data (○); calibration fit (· · · · ·) and 1:1 (—).
Grapevine petiole nutrient analysis with ATR-FT-IR spectroscopy
The small surface area of the diamond internal reflection element and relatively shallow penetration of the IR evanescent wave necessitates the use of dried and finely ground homogenous samples with bench top ATR-FT-IR instruments. The same initial sample preparation, however, would be required if nutrient concentration was to be determined by ICP and combustion analysis. The average time required for loading and scanning each sample in the present study was approximately 2 min, which could reduce analysis turnaround time to as little as 2 days for oven-dried samples. Although not tested here, microwave drying has been used successfully for IR-based applications and could further reduce sample preparation times. The calibration and test data sets consisted mainly of Chardonnay petioles, but sufficient Semillon and Shiraz samples were included to suggest that specific models would not be required for each cultivar if future work was undertaken to expand the calibrations. Similarly, the variation in the concentration of individual elements associated with sample collection over three growth stages, eight vineyards and seven growing seasons could be well modelled with a single calibration.
The error variance of the combustion and of ICP analysis was an order of magnitude lower than that of the ATR-FT-IR instrument for all elements except Fe, and the calibrations presented here would not be viewed as a replacement for these reference methods when high analytical precision is required. Several micronutrients (Fe, Mn and Cu) could be quantified only with low accuracy, and confirmation of analysis results would be recommended before management decisions are made on the basis of the mid-IR predictions for these elements. Calibration performance for all macronutrients, however, was sufficiently robust for assessing vine nutrient status against standard interpretative ranges, and indicative values could also be obtained for several micronutrients (B, Zn and Na). The trade-off for lower method accuracy is that expedited turnaround times and low analysis costs provide an opportunity to improve the precision and efficiency of grapevine nutrition management through increasing the frequency and spatial resolution of petiole sample collection.
Conclusion
The work undertaken in the current study took the opportunity presented by a large database of petiole samples to test the effectivenes of ATR-FT-IR spectroscopy as a rapid and low-cost method of plant tissue analysis for grapevines. With interpretative standards based on petiole nutrient concentration already widely used in Australia, and ATR-FT-IR instruments increasingly common in winery laboratories, the technique could be readily adapted for industry use. Previous studies demonstrating the effectiveness of IR spectroscopy for measurement of grapevine leaf K concentration (Ciavarella et al. 1998), or perennial tissue reserve carbohydrate and N status (Schmidtke et al. 2012), suggest that future applications would not be limited just to petiole analysis. Where the amount of stored nutrient and carbohydrate reserves is also of interest, or the nutrient status of other tissues or growth stages is regarded as more useful diagnostic tools, there is scope to develop a wider suite of viticultural applications for ATR-FT-IR spectroscopy.
Acknowledgements
This work was supported by Australia's grapegrowers and winemakers through their investment body, the Grape and Wine Research and Development Corporation, with matching funds from the Australian Government, and by the Commonwealth Cooperative Research Centre for Viticulture Program. Elemental analysis was undertaken by Waite Analytical Services, School of Agriculture and Wine, The University of Adelaide.




