Does news travel slowly before a market crash? The role of margin traders
Abstract
We investigate how investor overconfidence and attention affect market efficiency around the 2015 Chinese stock market crash. We find that the price delay before the crash is about twice the price delay after the crash. Investors become more sensitive to market movements after the crash. Price delays are larger on market down-days than on up-days before the crash, but the differences are insignificant between up- and down-days after the crash, indicating that negative information travels slowly only when investors are overconfident. Margin traders follow market trends and intensify the pyramiding and de-pyramiding effects caused by market sentiment change.
1 Introduction
Financial market crises are preceded by excessive optimism and investor overconfidence. For example, the Federal Reserve Chairman Alan Greenspan described investor behaviour before the technology stock bubble burst in March 2000 as ‘irrational exuberance’. Peicuti (2014) indicates that the close similarities between the decades preceding the Great Depression in 1929 and the US subprime mortgage crisis in 2009 are rapid growth without major contractions, which prolonged the life of bad debtors, postponed defaults, and caused investors to have greater confidence in a future without crises.1 In contrast, after financial crises and other extreme negative events, investors update their beliefs and react to market information differently (Kuhnen, 2015). The seminal paper by Peng and Xiong (2006) indicates that constrained investors allocate more or all of their attention to market information, whereas overconfident investors neglect useful public information and rely on their information (also see Kaustia and Knupfer, 2008; Chiang et al., 2011).
- Hypothesis 1: price delay is larger in the pre-crash period than in the post-crash period.
This hypothesis is also supported by both psychology theory and empirical evidence in behavioural finance. The psychology literature shows that individuals exhibit attribution bias. They attribute events that confirm the validity of their actions to their high ability and events that disconfirm their actions to external noise or sabotage (Hastorf et al., 1970). Similarly, the financial literature finds that investors credit high-market returns in bull markets to their trading skills (Thaler and Johnson, 1990; Odean, 1998; Gervais and Odean, 2001; Statman et al., 2006), which is why Wall Street analysts frequently warn investors not to confuse brains with a bull market (Odean, 1998; Statman et al., 2006). Studies further indicate that overconfident investors rely more on their own information and experience and ignore potentially useful information embedded in the markets (Peng and Xiong, 2006; Kaustia and Knupfer, 2008; Chiang et al., 2011). Thus, the combined effects of attribution and information biases lead to slow price discovery in pre-crash periods when investors are overconfident.2
- Hypothesis 2: predicts that changes in price delay after the market crash are more pronounced for high-margin trade stocks than for low-margin trade stocks.
- Hypothesis 3: bad news travels slowly only when market sentiment is high.
We test these three hypotheses using Chinese stocks during a 6-month pre-crash period from December 2014 to May 2015 and a 6-month post-crash period from July 2015 to December 2015. Using this sample during these periods has several distinctive advantages. First, these periods provide a clean test environment with a dramatic shift in investor sentiment. During the 6-month period from December 2014 to May 2015, the two main stock indices in China, the Shanghai Stock Exchange (SHSE) index and the Shenzhen Stock Exchange (SZSE) index, increased about 92.8 and 99.0 percent, respectively, and the Investor Sentiment Index (ISI) in China increased more than 48.5 percent. This is undoubtedly evidence of irrational exuberance. After the market crash in June 2015, the main stock market indices declined by approximately 50 percent and the ISI declined more than 55 percent during the rest of 2015.3 Second, individual Chinese investors are in general sentiment traders. They rely more on rumours and sentiment than on fundamental analysis for their trading (Kang et al., 2002). Thus, this provides an ideal setting for testing sentiment effects on market efficiency. Finally, our dataset has detailed daily and monthly margin trade information for individual stocks in our sample. This information cannot be captured by the commonly used broad market sentiment indices, and the detailed margin trade data are unavailable in many other markets. This unique information provides additional insight regarding investor sentiment for individual stocks.
We use price delay as an inverse measure of price discovery (Hou and Moskowitz, 2005; Boehmer and Wu, 2013) and obtain the following main results. First, the price delay in the pre-crash period is about twice the delay in the post-crash period. The magnitude of the decrease in the price delay after the crash is larger for high-margin trade stocks than for low-margin trade stocks. This supports our main hypothesis that investor overconfidence during the pre-crash period impedes price discovery. After extreme events such as stock market crises, investors become more vigilant and pay closer attention to market information, facilitating price discovery and reducing price delay. Second, the price delay on market down-days is about 19 percent to 30 percent larger than that on market up-days in the pre-crash period. In contrast, no apparent difference exists in price delay between the up- and down-days in the post-crash period. This indicates that bad news travels slower only when market sentiment is high due to investor overconfidence associated with attribution and confirmation biases.
To provide supplemental evidence that the reduction in price delay after the market crash can indeed be attributed to investor attention, we investigate the changes in price synchronicity and the sensitivity to the market movement before and after the crash. Our results show that price synchronicity almost doubles after a crash. The average increases in price synchronicity for the high-margin trade stocks after the crash range from 97 to 122 percent, which are significantly larger than the increases (49–82 percent) in price synchronicity for the low-margin trade stocks. In addition, the average increases in the sensitivity to market movement range from 27 to 63 percent for low-margin trade stocks, compared with increases of 78–101 percent for high-margin trade stocks. This additional evidence provides strong support for the investor attention argument, which suggests that after extreme attention-grabbing events, investors update their beliefs (Kuhnen, 2015) and that constrained investors allocate more attention to market-wide information (Peng and Xiong, 2006). This is also consistent with Seybert and Yang's (2012) finding that investors react more strongly to negative surprises following high-sentiment periods.4
One may also argue that margin trades are possibly driven by informed investors rather than by sentiment traders because under information asymmetry, informed investors trade strategically by taking advantage of their private information (Kyle, 1985; Foster and Viswanathan, 1996). We use two different ways to investigate this issue. First, we compare abnormal returns (ARs) and cumulative abnormal returns (CARs) in the pre- and post-crash periods for stocks in different margin trade groups. If margin trades reflect informed traders’ private information rather than investor overconfidence or noise, the decline in abnormal returns of high-margin trade stocks would be smaller than that of low-margin trade stocks after the crash. However, if margin trades mainly reflect investor overconfidence and are driven by sentiment traders, high-margin stocks would suffer more than low-margin stocks after the market crash. Our analyses support the latter. As an example, for stocks in the low-margin trade group measured by the ratio of monthly margin balance to monthly total trading volume (MG bal./TRD), the change in CAR0,2 is −3.81 percent from the pre-crash to the post-crash periods, whereas the change in CAR0,2 for the high MG bal./TRD group is −8.68 percent. The difference is −4.87 percent and significant both economically and statistically.
Second, if margin trades reflect private information, the informed investors would buy undervalued stocks on market down-days and sell overvalued stocks on market up-days. Thus, margin trades predict future price movement. However, if margin trades reflect investor sentiment and overconfidence, more (less) margin trades are expected on up (down) days. Our results show that the net margin trade to total trade ratio ranges from 2.11 to 2.40 on up-days, whereas the ratio ranges from −0.29 to −1.64 on down-days. Also, the reductions in margin positions are substantially larger on down-days in the post-crash period than in the pre-crash period. Furthermore, the net margin trade to total trade ratio on extreme down-days (up-days) is always negative (positive) regardless of whether the following day is a reversal, continuation, or overshot. These results suggest that margin traders are sentiment investors rather than informed traders.
Our study makes several contributions to the literature. First, many studies have investigated the effect of financial crises on market liquidity after the crises; however, we show that both investor attention and overconfidence affect market efficiency. Overconfidence impedes price discovery before a market crash, and investors become more vigilant and highly sensitive to market movement after crises. Second, prior studies using margin requirements at the macro level find mixed results on how the changes in margin level requirement affect market volatility (Hardouvelis, 1990; Hsieh and Miller, 1990; Seguin, 1990; Alexander et al., 2004). We overcome the weakness of previous studies by using detailed stock level margin trade information and show that margin traders follow market trends, create more pressure in the market, and intensify the pyramiding and de-pyramiding effects. Third, existing studies indicate that bad news travels slowly, but our results suggest this to be the case only when investor sentiment is high due to attribution bias. Finally, this study has important implications for policy makers and other markets, as Baker et al. (2012) indicate that sentiment spreads across markets and forms global sentiment.
2 Literature review
In this section, we provide brief literature reviews on investor overconfidence and attribution biases, which are pertinent to our hypotheses. We also discuss briefly studies related to margin restrictions in the United States and China, respectively.
2.1 Attribution bias and investor overconfidence
The psychology literature finds the existence of pervasive attribution bias. People attribute success to their own dispositions and failure to external forces (Hastorf et al., 1970). Gervais and Odean (2001) indicate that traders become more overconfident and trade more actively after the market increases because they attribute returns from the overall market increases to their own acumen when assessing their trading ability. Daniel et al. (1998) show that when individuals observe the outcomes of their actions, they update their confidence in their own ability in a biased manner. They attribute events that confirm the validity of their actions to their high ability and events that disconfirm the action to external noise or sabotage. Investors adjust their beliefs and seek support for their past investment decisions to reduce psychological costs and cognitive dissonance (Shefrin and Statman, 1985; Goetzmann and Peles, 1997). While existing studies reveal the causes of investor overconfidence and attribution bias, the current study contributes to the literature by showing the effects of overconfidence and attribution bias on price discovery, especially during market rallies.
2.2 Investor overconfidence and trade behaviour
Daniel et al. (1998) show that investors tend to be overconfident about the information they have generated but not about public information. Although prior studies indicate that momentum occurs because the market is slow to react to news (Jegadeesh and Titman, 1993), Daniel et al. (1998) argue that overreaction can also cause momentum because public information can trigger further overreaction, and continuing overreaction causes momentum in security prices. Daniel and Titman (1999) also show that investor overconfidence generates momentum in stock returns, and the momentum effect is likely to be strongest in stocks whose valuations require the interpretation of ambiguous information. Odean (1998) shows that overconfident traders cause markets to underreact to the information of rational traders. They underreact to abstract, statistical, and highly relevant information, and overreact to information that is salient, anecdotal, and less relevant. Positive (negative) return serial correlation occurs when investors underweight (overweight) new information. Griffin and Tversky (1992) indicate that individuals overreact to a prolonged record of salient performance but underreact to intermittent news.
Hong and Stein (1999) show that one group of traders (news watchers) underreact to private information gradually, then a second group of traders (arbitrageurs) try to exploit this underreaction and create an excessive momentum in prices, leading to overreaction. The existence of underreaction sows the seeds for overreaction by making it profitable for momentum traders to enter the market. Mendel and Shleifer (2012) analyse the interaction of insiders, noise traders, and outsiders. Noise traders are vulnerable to sentiment shocks and trade on them; outsiders who possess no information trade rationally by learning from prices. Outsiders are also prone to chasing price increases caused by insiders with private information. However, as long as there are sufficiently few noise traders, outsiders may get confused and chase noise as if it were information, thereby suppressing the possible impact of informed trading on prices, amplifying sentiment shocks and moving prices away from fundamentals.
Stambaugh et al. (2012) show that overpricing is more prevalent when market-wide sentiment is high. Yu and Yuan (2011) find that the market is less rational during high-sentiment periods due to high participation by noise traders in such periods. Similarly, Antoniou et al. (2010) indicate that sentiment has an asymmetric effect on prices, with optimism producing greater mispricing (overvaluation) than pessimism (underpricing). Adebambo and Yan (2016) find that stocks held by more overconfident managers experience greater momentum profits and stronger return reversals than stocks held by less overconfident managers. Cooper et al. (2004) show that momentum profits exist only in the subsequent periods after prolonged market gains. Chui et al. (2010) further show that momentum profits are higher in countries with stronger individualism. Differing from these studies, we add to the literature by investigating and documenting that overconfidence reduces price discovery, which is a more direct measure of market efficiency.
2.3 Background information on margin trades in the US and in China and the related studies
After the Securities and Exchange Act of 1934, the US Federal Reserve System (Fed) was responsible for setting the margin requirement, which was set initially at 45 percent in October 1934 and adjusted 23 times between 1934 and 1974. The margin requirement reached the highest rate of 100 percent (i.e., 0 percent borrowing) during January 1946 and February 1947 and remained at 50 percent after January 1974 (Hsieh and Miller, 1990; Alexander et al., 2004). Before January 1999, the Fed published a quarterly list of newly margin-eligible securities. After January 1999, the Fed ceased publishing its list and abandoned the vetting process in favour of an automatic rule whereby all domestic securities became margin-eligible once they were listed on the market (Alexander et al., 2004).
Starting on 31 March 2010, the China Securities Regulatory Commission (CSRC) launched a pilot programme and allowed margin trading and short selling for the first time in China. Initially, only 90 stocks listed on the Shanghai Stock Exchange and the Shenzhen Stock Exchange were eligible for margin trading and short selling (see Figure 1). After the pilot programme, the number of stocks eligible for margin trading and short selling increased four times in November 2011, January 2013, September 2013, and September 2014. There are about 900 stocks and 16 exchange-traded funds (ETFs) available for margin trading since the most recent addition in September 2014.
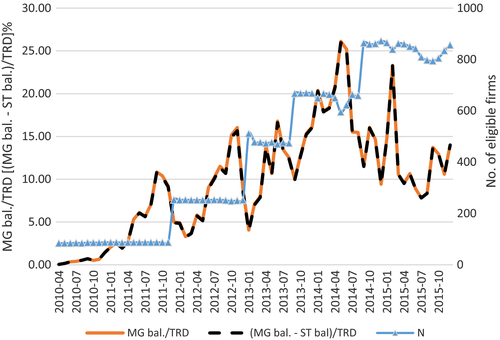
Due to limited availability of detailed margin trade information at stock level, many studies use the changes in margin level requirement in the US before 1999 to investigate the effects of margin requirement on market volatility, and find mixed results. For example, Seguin (1990) finds that share prices increase and volatility decreases when a firm is added to the eligible list, implying that margin trading reduces volatility. The author argues that reducing trader wealth constraints enhances liquidity (also see Conrad, 1989). Hsieh and Miller (1990) find a weak negative association between the level of margin requirements and the level of volatility during the late 1930s and early 1940s. They also indicate that changes in margin requirements tended to follow rather than lead changes in volatility because the Fed tended to raise margins when the market was booming and cut them after markets fell, and volatility normally rises when a market falls; thus, apparently a negative relationship exists between margin requirements and volatility.
Alexander et al. (2004) show that trading volume increases and that market liquidity and volatility do not change after stocks become eligible for margin trading. They suggest that the information content of trading, informational environment, and the efficiency of a firm's share price improves when the margin level is lowered. However, Hardouvelis (1990) shows that higher or increasing margin requirements are associated with lower stock price volatility and smaller deviations of stock prices from their fundamental values. This result indicates that margin trading increases volatility. Hardouvelis and Theodossiou (2002) show that an inverse relationship between margin levels and volatility exists only during bull and normal markets, and that no relationship exists during bear markets. We use detailed margin trade information of individual stocks and overcome the weakness of the existing studies that rely on margin-level requirement for all eligible stocks. More importantly, our results indicate that margin traders are sentiment investors. They rely on market sentiment and generate more pressure in the market, which slows down price discovery.
3 Data and sample selection
We collect daily stock margin trade information and firm financial data from the China Stock Market & Accounting Research (CSMAR) database distributed by GTA in China. The CSMAR is one of the most widely used databases for financial research on Chinese markets. Our initial sample includes 837 margin-eligible stocks that have non-missing margin trade data from the CSMAR dataset during a 12-month test period from December 2014 to December 2015, excluding June 2015.
We choose the 6-month period from December 2014 to May 2015 as the pre-crash period and the 6-month period from July to December 2015 as the post-crash period because the Chinese stock markets experienced an unpreceded flash boom-and-bust surrounding June 2015. As shown by Figure 2a, the SHSE index remained around 2,000–2,500 points in 2013 and 2014. Starting in November 2014, it soared from 2,430 points on 3 November 2014 to 5,166 points on 12 June 2015, an increase of about 112 percent. Then, it plunged continuously during June, July and August 2015, and the market recovered slightly and closed at approximately 3,500 points at the end of December 2015. The SZSE index shows a similar pattern (Figure 2b). It skyrocketed from 8,240 points on 3 November 2014 to a historic high point of 18,098 on 12 June 2015, an increase of about 120 percent in 6 months. It then plunged to 9,290 points on 15 September 2015. We exclude June 2015 in the test period because of the extreme volatility during that month.
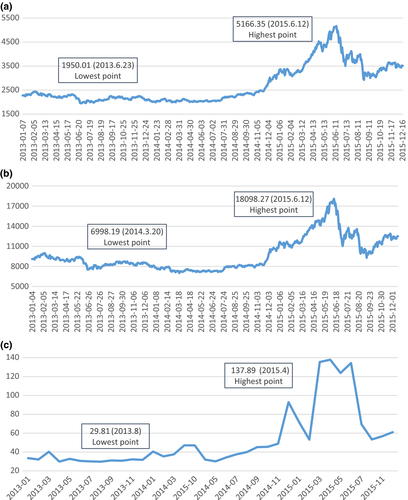
Unsurprisingly, the investor sentiment shows a dramatic shift after June 2015. The ISI remained in the range of 30–50 points during 2013 and 2014. Starting from November 2014, the ISI picked up steam and reached the highest level of 137 points in April 2015, just about 2 months prior to the market crash on 12 June 2015 (Figure 2c). The increase in ISI from January 2013 to April 2015 is more than 360 percent (137/30 − 1) and the increase from November 2014 to April 2015 is about 180 percent (137/49 − 1). Once the financial crisis started in June 2015, the ISI plunged more than 50 percent in a month, from 134.4 in June to 69.5 in July 2015. This evidence clearly supports our argument of investor overconfidence in the pre-crash period and changes in sentiment after the crisis.5
Table 1 reports the summary statistics of the entire sample. The average monthly closing price is 19.35 yuan (Chinese currency), ranging from 3.53 yuan (minimum) to 197.50 yuan (maximum) during the test periods. The average value of the logarithm of total assets scaled by millions is 4.09 (equivalent to approximately 12.3 billion yuan). The earnings per share to price (E/P) ratio ranges from −0.02 to 0.04, and both the mean and median values are close to zero. We use the E/P instead of the P/E ratio to avoid extreme numbers when earnings are close to zero. The mean and median values of the Herfindahl index of the top 10 shareholders (HHI-Top10) are 0.17 and 0.14, respectively. The stock turnover ratio computed as the monthly number of shares traded to the number of shares outstanding at the end of a given year ranges from 0.07 to 3.40, confirming the highly speculative trading behaviour of Chinese investors (Allen et al., 2005; Mei et al., 2009; Jun et al., 2014).
| Variable | N | Mean | Min | 25th percentile | Median | 75th percentile | Max |
|---|---|---|---|---|---|---|---|
| Price | 837 | 19.35 | 3.53 | 10.34 | 15.49 | 23.88 | 197.50 |
| Log (TA) | 837 | 4.09 | 2.77 | 3.63 | 3.98 | 4.41 | 6.69 |
| E/P | 837 | 0.00 | −0.02 | 0.00 | 0.00 | 0.00 | 0.04 |
| HHI-Top10 | 837 | 0.17 | 0.00 | 0.07 | 0.14 | 0.25 | 0.65 |
| Turnover | 837 | 0.75 | 0.07 | 0.45 | 0.69 | 0.94 | 3.40 |
| MG bal./TRD(%) | 837 | 11.78 | 2.40 | 9.31 | 11.54 | 13.71 | 33.85 |
| (MG bal. – ST bal.)/TRD (%) | 837 | 11.76 | 2.40 | 9.29 | 11.54 | 13.71 | 33.83 |
| MG bal./TA (%) | 837 | 14.27 | 0.04 | 3.71 | 9.49 | 19.02 | 91.77 |
| (MG bal. – ST bal.)/TA (%) | 837 | 14.25 | 0.04 | 3.70 | 9.47 | 19.01 | 91.77 |
- This table reports the summary statistics of the 837 stocks that are eligible for margin trading and short selling and have non-missing data during the test period from December 2014 to May 2015 and from July to December 2015. June 2015 is not included in the sample period since the Chinese stock markets experienced extreme volatility during that month. Price is the closing price at the end of a month. Log (TA) is the log transformation of a firm's total assets (TA) measured in millions of Chinese currency (yuan, or RMB). E/P is the ratio of earnings per share to price. HHI-Top10 is Herfindahl index of top 10 shareholders. Turnover is a stocks’ monthly turnover ratio computed as the total number of shares traded to the number of shares outstanding in a month. MG bal./TRD is the ratio of monthly margin trade balance to monthly total trading amount, and (MG bal. – ST bal.)/TRD is the ratio of difference in monthly margin trade balance and short selling balance to monthly trading amount. MG bal./TA and (MG bal. – ST bal.)/TA are the ratios of monthly margin trade balance, and the differences in the monthly margin trade balance and short selling balance to total assets.
Our main interest is in margin trade activity, which is measured by four different methods: (i) the ratio of monthly margin trade balance to monthly trading volume (MG bal./TRD), (ii) the ratio of the difference in the monthly margin balance and short selling balance to the monthly total trading amount ((MG bal. – ST bal.)/TRD); (iii) the ratio of monthly margin trade balance to total assets (MG bal./TA); and (iv) the ratio of the difference in the monthly margin balance and short selling balance to total assets (MG bal. – ST bal.)/TA. The MG bal./TRD ratios range from 2.4 to 33.85 percent, with mean and median values of 11.78 and 11.54 percent, respectively. The (MG bal. – ST bal.)/TRD ratio is identical to MG bal./TRD, indicating that short selling is not active (also see Figure 2). The MG bal./TA ranges from 0.04 to 91.77 percent, and the (MG bal. – ST bal.)/TA ratio shows a similar pattern.
The low short-selling activity is consistent with previous studies, which show that short selling is expensive and that traders are reluctant to take short positions. For example, Barber and Odean (2008) and Stambaugh et al. (2012) show that less than 0.3 percent of individual investor positions are short positions. Informed or institutional investors who believe that prices are too high may also be reluctant to take short positions because they face the risk that prices go up before they go down (DeLong et al., 1990; Shleifer and Vishny, 1997). Given the small amount of short selling, our analyses in the rest of this paper focus mainly on margin trades.
4 Test methods and empirical results
 (1)
(1)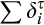 ) is restricted to be zero, and the model is specified as:
) is restricted to be zero, and the model is specified as:
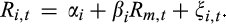 (2)
(2)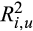 and
and 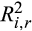 , respectively. To make the estimations more reliable, we exclude stocks with fewer than 15 daily returns in a given month. The price delay for each stock in each month is computed by:
, respectively. To make the estimations more reliable, we exclude stocks with fewer than 15 daily returns in a given month. The price delay for each stock in each month is computed by:
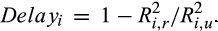 (3)
(3)The larger the 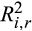 is relative to
is relative to 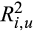 , the more rapidly the current market information is incorporated into the price and the smaller the price delay.6
, the more rapidly the current market information is incorporated into the price and the smaller the price delay.6
4.1 Univariate analysis of price delay
As an initial test of how price delay is different before and after the market crash, we conduct univariate analyses and compare price delay between the pre- and post-crash periods. To analyse how margin trades affect price delay differently in the pre- and post-crash periods, we divide the stocks in our sample into three groups based on their margin trade ratios in the pre-crash period. Stocks ranked at the bottom (top) third based on the monthly MG bal./TRD ratio are included in the Low (High) group, and the rest of all other stocks are included in the Medium group. Similarly, we also classify stocks into Low, Medium, and High groups based on the ratios of monthly net margin trade to total trading amount (i.e., non-margin trade amount), MG/TRD, and the monthly MG bal./TA, which are defined in Section 33. Note that we intentionally do not reclassify stocks based on the margin trade ratios in the post-crash period because our primary focus is how investor sentiment for a stock, as measured by margin trade ratios, affects price delay and how the changes in price delay are different for stocks in different sentiment categories. This design reduces the sample to 627 stocks that have margin trade data in both the pre- and post-crash periods.
Table 2 reports the results, and we observe two clear patterns. First, the price delay in the pre-crash period is about twice the delay in the post-crash period, and the differences are significant both statistically and economically regardless of margin trade classification. For example, the price delays of the Low, Medium, and High groups based on the MG bal./TRD ratio (the first two columns) are 0.41, 0.43, and 0.44, respectively, in the pre-crash period. In sharp contrast, the delays are only 0.19, 0.18, and 0.20, respectively, in the post-crash period. The changes from the pre- to the post-crash periods are −0.21, −0.25, and −0.25, respectively. All these changes are significant both economically and statistically at the 0.01 level. The results based on MG/TRD (the middle two columns) and MG bal./TA ratios (the last two columns) are similar.
| Margin class | Period | MG bal./TRD | MG/TRD | MG bal./TA | |||
|---|---|---|---|---|---|---|---|
| Mean | T-stat | Mean | T-stat | Mean | T-stat | ||
| Low (n = 157) | Pre-crash | 0.41 | 31.54*** | 0.42 | 32.14*** | 0.33 | 31.61*** |
| Post-crash | 0.19 | 23.27*** | 0.20 | 21.48*** | 0.19 | 23.13*** | |
| Diff 1 = Post - Pre | −0.21 | −13.94*** | −0.22 | −14.05*** | −0.14 | −10.64*** | |
| (Paired T-test) | |||||||
| Medium (n = 313) | Pre-crash | 0.43 | 49.23*** | 0.42 | 47.87*** | 0.45 | 53.99*** |
| Post-crash | 0.18 | 25.40*** | 0.19 | 27.12*** | 0.17 | 29.20*** | |
| Diff 1 = Post - Pre | −0.25 | −21.97*** | −0.23 | −20.37*** | −0.27 | −26.65*** | |
| (Paired T-test) | |||||||
| High (n = 157) | Pre-crash | 0.44 | 35.94*** | 0.45 | 37.53*** | 0.48 | 37.96*** |
| Post-crash | 0.20 | 22.57*** | 0.18 | 21.25*** | 0.21 | 18.41*** | |
| Diff 1 = Post - Pre | −0.25 | −16.43*** | −0.28 | −18.91*** | −0.27 | −15.78*** | |
| (Paired T-test) | |||||||
| High – Low | Diff 3 - Diff 1 | −0.03 | −1.76* | −0.05 | −2.73** | −0.13 | −6.55*** |
| (Grand Diff) | (Pooled T-test) | ||||||
-
This table reports price delay for stocks in different margin trade groups in the pre- and post-crash periods. Price delay is computed as
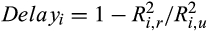 based on the method of Hou and Moskowitz (2005), where
based on the method of Hou and Moskowitz (2005), where 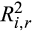 and
and 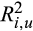 are estimated from a restricted market model (i.e., the coefficients on the lagged market returns are restricted to be zero) and an unrestricted market model, respectively. Stocks ranked at the bottom (top) third based on the monthly margin trade ratios of MG bal./TRD, MG/TRD, and MG bal./TA in the pre-crash period are included in the Low (High) group, and the other stocks are included in the Medium group. The pre-crash period is from 1 December 2014 to 31 May 2015, and the post-crash period is from 1 July to 31 December 2015. We drop June 2015 since the Chinese stock markets were extremely volatile during that month. We conduct paired T-tests for the differences in the price delay between the pre- and post-crash periods for each margin trade group. The differences in the changes of price delay between the Low and High groups (Diff 3 – Diff 1) are based on pooled T-tests. ***, **, and * indicate significance levels of 0.01, 0.05, and 0.1, respectively.
are estimated from a restricted market model (i.e., the coefficients on the lagged market returns are restricted to be zero) and an unrestricted market model, respectively. Stocks ranked at the bottom (top) third based on the monthly margin trade ratios of MG bal./TRD, MG/TRD, and MG bal./TA in the pre-crash period are included in the Low (High) group, and the other stocks are included in the Medium group. The pre-crash period is from 1 December 2014 to 31 May 2015, and the post-crash period is from 1 July to 31 December 2015. We drop June 2015 since the Chinese stock markets were extremely volatile during that month. We conduct paired T-tests for the differences in the price delay between the pre- and post-crash periods for each margin trade group. The differences in the changes of price delay between the Low and High groups (Diff 3 – Diff 1) are based on pooled T-tests. ***, **, and * indicate significance levels of 0.01, 0.05, and 0.1, respectively.
Second, the magnitude of the decrease in price delay is positively related to the margin trade ratios. For example, the change in price delay for the Low MG bal./TRD ratio group is −0.21, which is equivalent to a decrease of 51 percent (−0.21/0.41); whereas the change in the price delay for the High MG bal./TRD ratio group is −0.25, which is a decrease of 57 percent (−0.25/0.44). The difference in the changes between the Low and High groups (Diff 3 – Diff 1) is −0.03 and significant at the 0.1 level. When stocks are classified by the MG/TRD ratio, the changes in price delay for the Low and the High ratio groups are −0.22 (or a decline of 52 percent) and −0.28 (or a decline of 62 percent), respectively. The difference in the decreases between the High and Low groups (Diff 3 – Diff 1) is −0.05, which is significant at the 0.05 level. The changes in the price delay are more pronounced when margin trade is measured by the MG bal./TA ratio (the last two columns). The decrease in price delay for the Low MG bal./TA group is −0.14, which is equivalent to a 42 percent decline, but it is −0.27, or a 56 percent decline, for the High MG bal./TA group. The difference in the declines between the Low and High groups is −0.13 and significant at the 0.01 level.
The large price delay in the pre-crash period combined with the more pronounced decrease in price delay for the high-margin trade stocks indicate an adverse effect of investor sentiment and overconfidence on price discovery. This is consistent with the findings of Seybert and Yang (2012) and Coulton et al. (2016), which indicate that investor sentiment impacts their decision-making process and consequently the timeliness of price discovery. Walther and Willis (2013) further show that even financial analysts are more optimistic and least accurate in the presence of high sentiment.7
4.2 Regression analysis and control of firm characteristics
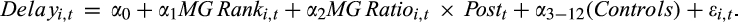 (4)
(4)where the dependent variable Delayi,t is the price delay for firm i in month t. MG Ranki,t is a ranking score (on a 1–3 scale) of firm i's margin trade ratio in month t. Instead of using the actual value of margin trade ratios, we use the ranking score to reduce potential noise. Specifically, we rank stocks in each month based on their margin trade ratios. Stocks that are ranked at the bottom (top) third take a value of 1 (3) and the other stocks take a value of 2. To capture the asymmetric effect of margin trade on price delay in the pre- and post-crash periods, we use an interaction variable MG Ranki,t × Postt, where Postt takes a value of 1 if month t is in the post-crash period and 0 otherwise. Firm control variables include stock price (Log(Pricei,t)); total assets (Log(TAi,t)); earnings to price ratio (E/Pi,t) and lagged E/P ratio (E/Pi,t−1); Herfindahl index of top 10 shareholders (HHI_TOP10i,t); monthly stock turnover ratio (Turnoveri,t); stock return (Returni,t), and lagged return (Returni,t−1); and stock risk (βi,t) estimated using the monthly returns from t−12 to t−1. We also include market return (Rm,t) and lagged market return (Rm,t−1) to control for market conditions.
Table 3 reports the regression results. In the first model (columns 1–2), the MG Rank is the ranking score of MG bal./TRD ratio, and the coefficient on MG bal./TRD is positive (0.006) but not significant at the 0.1 level. The coefficient on the interaction variable MG × Post is negative (−0.056) and significant at the 0.01 level. In terms of economic significance, this implies that the average declines in price delay after the market crash are about 0.168 (−0.056 × 3) for high-margin stocks ranked in the top third based on MG bal./TRD ratio, and the decline in price delay is only about 0.056 (−0.056 × 1) for the low-margin stocks ranked in the bottom third based on MG bal./TRD ratio. This is largely consistent with the univariate results reported in Table 2. Among the firm control variables, price, stock turnover, and the current and lagged stock returns are positively related to price delay. The coefficients on both the total asset (Log(TA)) and stock risk (β) are negative and significant at the 0.01 level. The coefficient on Rm,t is 0.625 and significant at the 0.01 level, whereas the coefficient on Rm,t−1 is −0.379 and also significant at the 0.01 level.
| Variables | Coefficient | T-stat | Coefficient | T-stat | Coefficient | T-stat |
|---|---|---|---|---|---|---|
| Intercept | 0.435 | (13.16)*** | 0.361 | (11.99)*** | 0.376 | (9.43)*** |
| MG bal./TRD i,t | 0.006 | (1.13) | ||||
| MG/TRD i,t | 0.030 | (6.53)*** | ||||
| MG bal./TA i,t | 0.036 | (5.45)*** | ||||
| MG × Postt | −0.056 | (−14.04)*** | −0.054 | (−13.58)*** | −0.072 | (−17.51)*** |
| Log(Price i,t ) | 0.036 | (3.28)*** | 0.046 | (4.22)*** | 0.045 | (4.05)*** |
| Log (TA i,t ) | −0.028 | (−4.90)*** | −0.028 | (−5.01)*** | −0.033 | (−4.63)*** |
| E/P i,t | −1.187 | (−0.96) | −1.016 | (−0.82) | −1.135 | (−0.92) |
| E/P i,t−1 | 0.906 | (0.76) | 0.501 | (0.42) | 1.061 | (0.90) |
| HHI_Top10 i,t | −0.007 | (−0.27) | 0.020 | (0.82) | 0.025 | (1.01) |
| Turnover i,t | 0.015 | (2.24)** | 0.032 | (4.90)*** | 0.034 | (5.24)*** |
| Return i,t | 0.208 | (11.42)*** | 0.195 | (10.47)*** | 0.201 | (11.19)*** |
| Return i,t−1 | 0.126 | (6.94)*** | 0.128 | (7.06)*** | 0.135 | (7.52)*** |
| β i,t | −0.048 | (−10.09)*** | −0.049 | (−10.65)*** | −0.035 | (−7.41)*** |
| R m,t | 0.625 | (17.47)*** | 0.640 | (18.02)*** | 0.571 | (16.18)*** |
| R m,t−1 | −0.397 | (−11.25)*** | −0.393 | (−11.17)*** | −0.451 | (−12.89)*** |
| Adjusted R2 | 0.299 | 0.295 | 0.308 | |||
| Durbin–Watson | 1.743 | 1.735 | 1.758 | |||
| Obs. | 6,530 | 6,530 | 6,530 | |||
| 1st Order Autocorrelation | 0.128 | 0.132 | 0.121 | |||
| Max VIF | 3.02 | 3.03 | 3.02 |
- This table reports the panel data regression of price delay on margin trade ratios. The dependent variable is Delayi,t, which is computed based on the method of Hou and Moskowitz (2005). The independent variable of primary interest is the ranking score of a stock's monthly margin trade ratios, which is measured in three different ways: MG bal./TRD, MG/TRD, and MG bal./TA. Stocks that are ranked at the bottom (top) third based on their margin ratios in a given month take a value of 1 (3) and the other stocks take a value of 2. Other control variables include Log(Price) (stock price at the end of month), Log(TA) (total assets at the end of month t), E/P (earnings per share/price), HHI-Top10 (Herfindahl index of top 10 shareholders), Turnover (monthly stock turnover ratio), Return (monthly stock return adjusted for dividend distribution), Rm (monthly market return), and β (stock beta estimated using monthly return regression in the prior 12-months, from t−12 to t−1). MG × Post is an interaction variable between the corresponding margin ratio and Post, where Post is a dummy variable and takes a value of 1 in the post-crash period and 0 otherwise. ***, **, and * indicate significance levels of 0.01, 0.05, and 0.1, respectively.
In the second model (the two middle columns), the MG Rank is the ranking score of MG/TRD ratio, and the coefficient on MG/TRD is 0.030 and significant at the 0.01 level. The coefficient on the interaction variable MG × Post is −0.054 and significant at the 0.01 level. The coefficients on all control variables are identical to those in the first regression. When the MG Rank is measured by MG bal./TA ratio (the last two columns), the coefficient on MG bal./TA is 0.036, and the coefficient on MG × Post is −0.072; both of these are significant at the 0.01 level. The coefficients on all control variables are identical to those in the other two regressions.
The results so far support our hypotheses 1 and 2, namely price delay is larger in the pre-crash period than in the post-crash period and that the decline in price delay after the market crash is more pronounced for high-margin trade stocks than that for low-margin trade stocks. Combined with the large increase in market sentiment before the Chinese market crash (Figure 2c), these findings imply that investors in general are more susceptible to overconfidence and attribution bias before the market crash, and this bias slows down price discovery. It also implies that margin trades before market crash are largely driven by sentiment investors, which is evidenced by the large decline in price delay. We offer additional discussions in later sections.
We are aware that some of the control variables are likely to be correlated with each other. For example, the stock price is related to the stock return and market returns. Thus, we use different methods to check for possible multicollinearity. First, we check the variance inflation factor (VIF) in each regression. The maximum VIF in these regressions is 3.03, which is smaller than 10, suggesting that multicollinearity is not severe.8 Second, we run similar regressions by including one of the possibly correlated variables at a time. The coefficients on the margin ratios remain largely the same. Third, another concern is reverse causality, namely, margin traders may target stocks with greater price inefficiency. To alleviate this endogeneity concern, we use orthogonal regressions by regressing the margin ratios on firm control variables in the first step. Then, we use the residuals from the first step regression to replace the margin ratio in the basic model. The unreported results are consistent with those reported in the current table.9 We also report Durbin–Watson statistics in Table 3, which range from 1.47 to 1.62, indicating weak autocorrelation in the error term.
4.3 Price delay on market up- and down-days in different markets
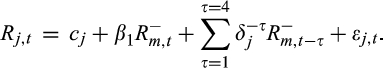 (5)
(5)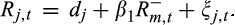 (6)
(6)where Rj,t and 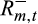 are the stock and market returns on down-day t, respectively. We classify trading days as down-days if the market return on a given day is negative. We obtain R2 from Equations 5) and 6) for each stock and compute the price delay on down-days in the pre- and post-crash periods separately. In the same vein, we also compute price delay on market up-days.
are the stock and market returns on down-day t, respectively. We classify trading days as down-days if the market return on a given day is negative. We obtain R2 from Equations 5) and 6) for each stock and compute the price delay on down-days in the pre- and post-crash periods separately. In the same vein, we also compute price delay on market up-days.
Panel A of Table 4 reports the comparison of price delays on up- and down-days in the pre-crash period. For the Low MG bal./TRD ratio group, the average price delay is 0.36 on up-days and 0.43 on down-days. The difference (Diff 1 = Down – Up) is 0.07 and significant at the 0.05 level, which indicates that price delay on down-days is about 19.4 percent (0.43/0.36 – 1) larger than that on up-days. For the Medium MG bal./TRD ratio group, the average price delays on up- and down-days are 0.38 and 0.44, respectively, and the difference is 0.06 and significant at the 0.01 level. For the High MG bal./TRD ratio group, the price delays on up- and down-days are 0.36 and 0.47, respectively. The difference is 0.11 and significant at the 0.01 level, which indicates that the price delay on down-days is about 30.6 percent (0.47/0.36 – 1) larger than that on up-days. The difference in the changes of price delay between the High and Low-margin ratio groups (Diff 3 – Diff 1) is 0.04 (= 0.11 – 0.07), which is not statistically significant at the 0.1 level. The results based on MG/TRD and MG bal./TA classifications are similar. The price delay is about 26.3 percent (0.48/0.38 – 1) larger on down-days than on up-days for the High MG/TRD group and about 19.6 percent (0.55/0.46 – 1) larger on down-days than on up-days for the High MG bal./TA group.
| Margin class | Up- versus down-days | MG bal./TRD | MG/TRD | MG bal./TA | |||
|---|---|---|---|---|---|---|---|
| Mean | T-stat | Mean | T-stat | Mean | T-stat | ||
| Panel A: Price delay for stocks in different margin classes in the pre-crash period | |||||||
| Low (n = 157) | Up-days | 0.36 | 16.24*** | 0.37 | 16.53*** | 0.26 | 16.14*** |
| Down-days | 0.43 | 18.59*** | 0.43 | 19.00*** | 0.31 | 18.00*** | |
| Diff 1 = Down − Up | 0.07 | 2.33** | 0.06 | 1.96** | 0.06 | 2.37** | |
| (Paired T-test) | |||||||
| Medium (n = 313) | Up-days | 0.38 | 26.24*** | 0.36 | 24.88*** | 0.38 | 25.77*** |
| Down-days | 0.44 | 28.79*** | 0.43 | 28.34*** | 0.46 | 30.63*** | |
| Diff 2 = Down − Up | 0.06 | 2.79*** | 0.07 | 3.52*** | 0.08 | 3.88*** | |
| (Paired T-test) | |||||||
| High (n = 157) | Up-days | 0.36 | 17.93*** | 0.38 | 19.58*** | 0.46 | 21.41*** |
| Down-days | 0.47 | 21.16*** | 0.48 | 21.30*** | 0.55 | 22.80*** | |
| Diff 3 = Down − Up | 0.11 | 3.84*** | 0.09 | 3.16*** | 0.09 | 2.70*** | |
| (Paired T-test) | |||||||
| High – Low | Diff 3 − Diff 1 | 0.04 | 1.15 | 0.03 | 0.92 | 0.03 | 0.91 |
| (Grand Diff) | (Pooled T-test) | ||||||
| Panel B: Price delay for stocks in different margin classes in the post-crash period | |||||||
| Low (n = 157) | Up-days | 0.18 | 17.41*** | 0.18 | 18.32*** | 0.17 | 18.44*** |
| Down-days | 0.18 | 12.34*** | 0.19 | 15.27*** | 0.16 | 14.02*** | |
| Diff 1 = Down − Up | 0.00 | 0.11 | 0.01 | 0.78 | −0.01 | −0.47 | |
| (Paired T-test) | |||||||
| Medium (n = 313) | Up-days | 0.16 | 25.23*** | 0.17 | 23.94*** | 0.16 | 24.39*** |
| Down-days | 0.18 | 19.60*** | 0.19 | 17.85*** | 0.17 | 19.73*** | |
| Diff 2 = Down − Up | 0.01 | 1.09 | 0.01 | 0.97 | 0.01 | −1.07 | |
| (Paired T-test) | |||||||
| High (n = 157) | Up-days | 0.19 | 16.73*** | 0.16 | 17.40*** | 0.20 | 17.20*** |
| Down-days | 0.21 | 15.14*** | 0.18 | 15.34*** | 0.24 | 14.16*** | |
| Diff 3 = Down − Up | 0.03 | 1.49 | 0.02 | 1.02 | 0.04 | 1.85* | |
| (Paired T-test) | |||||||
| High – Low | Diff 3 − Diff 1 | 0.02 | 1.29 | 0.00 | 0.20 | 0.04 | 2.33** |
| (Grand Diff) | (Pooled T-test) | ||||||
- Panels A and B report the price delay of stocks in different margin trade groups during up- and down-days in the pre- and post-crash periods, respectively. We classify a trading day as an up- (down-) day when the daily market return is greater (less) than zero. Following Boehmer and Wu (2013), we use the method of Hou and Moskowitz (2005) and estimate price delay separately for market up-days (Rm,t > 0) and down-day (Rm,t < 0) in the pre- and post-crash periods. Stocks ranked at the bottom (top) third based on the monthly margin ratios of MG bal./TRD, MG/TRD, and MG bal./TA in the pre-crash period are included in the Low (High) group, and the other stocks are included in the Medium group. The pre-crash period is from 1 December 2014 to 31 May 2015, and the post-crash period is from 1 July to 31 December 2015. We conduct paired T-tests for the differences in price delay between the up- and down-days for each margin trade group. The differences in the changes of test variables between the High and Low groups (Diff 3 – Diff 1) are based on pooled T-tests ***, **, and * indicate significance levels of 0.01, 0.05, and 0.1, respectively.
Panel B of Table 4 reports the price delay on up- and down-days in the post-crash period. As reported in Table 2, the price delays are much smaller after the market crash. A sharp contrast to the results in the pre-crash period is that the differences in the price delays between up- and down-days are insignificant regardless of how margin trade is measured. In addition, no apparent significant difference in price delay exists between the Low and High margin groups. Although the literature suggests that bad news travels slowly (Hong et al., 2000), our evidence indicates that this is the case only when market sentiment is high, i.e., in the pre-crash period. These results suggest that overconfident investors overestimate their own information and ability and ignore market information in the pre-crash period (Peng and Xiong, 2006). This is also consistent with the findings of Coulton et al. (2016) that bad news is incorporated into price more quickly for firms that are more sensitive to market movement.
4.4 Investor attention and changes in price synchronicity and sensitivity to market information
To provide further evidence that market crashes make investors more vigilant and that investor attention affects market efficiency, we investigate the changes in price synchronicity and the sensitivity to market movements during the pre- and post-crash periods. We use 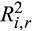 and β0 estimated from the restricted market model (2) as a measure of price synchronicity and sensitivity to market movement, respectively. Although
and β0 estimated from the restricted market model (2) as a measure of price synchronicity and sensitivity to market movement, respectively. Although 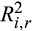 and the price delay are related to one another, they capture two different aspects of market efficiency. The price delay measures the speed that the current market information is incorporated into the stock price, whereas
and the price delay are related to one another, they capture two different aspects of market efficiency. The price delay measures the speed that the current market information is incorporated into the stock price, whereas 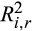 captures how much firm-specific information or idiosyncratic risk is capitalised into the stock price. As indicated by Roll (1988), DeLong et al. (1990), and Morck et al. (2000), a large R2 indicates that stock price variations are synchronous, and more (less) market-wide (firm-specific) information is incorporated in the stock price. Thus, these two measures provide additional insight regarding investor attention and its effect on information capitalisation and sensitivity to market movement in the context of Morck et al. (2000) and Roll (1988).
captures how much firm-specific information or idiosyncratic risk is capitalised into the stock price. As indicated by Roll (1988), DeLong et al. (1990), and Morck et al. (2000), a large R2 indicates that stock price variations are synchronous, and more (less) market-wide (firm-specific) information is incorporated in the stock price. Thus, these two measures provide additional insight regarding investor attention and its effect on information capitalisation and sensitivity to market movement in the context of Morck et al. (2000) and Roll (1988).
Panel A of Table 5 reports the results of price synchronicity. The average values of 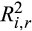 for the Low MG bal./TRD group are 0.33 and 0.61 in the pre- and post-crash periods, respectively, which is equivalent to an increase of 85 percent. The average increases of
for the Low MG bal./TRD group are 0.33 and 0.61 in the pre- and post-crash periods, respectively, which is equivalent to an increase of 85 percent. The average increases of 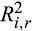 for both the Medium and High groups are 0.31, which represents a 97 percent increase for the Medium group and a 100 percent increase for the High group. The difference in the increase of
for both the Medium and High groups are 0.31, which represents a 97 percent increase for the Medium group and a 100 percent increase for the High group. The difference in the increase of 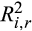 between the Low and High groups (Diff 3 – Diff 1) is 0.03 and significant at the 0.10 level. The results based on the MG/TRD and MG bal./TRD ratios are similar. For example, the increase in
between the Low and High groups (Diff 3 – Diff 1) is 0.03 and significant at the 0.10 level. The results based on the MG/TRD and MG bal./TRD ratios are similar. For example, the increase in 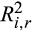 for the Low MG bal./TA group is about 49 percent (0.61/0.41 −1), and the increase in
for the Low MG bal./TA group is about 49 percent (0.61/0.41 −1), and the increase in 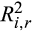 for the High MG bal./TA group is about 122 percent (0.60/0.27 – 1). The difference in the increases between the Low and High groups (Diff 3 – Diff 1) is 0.13, which is significant at the 0.01 level.
for the High MG bal./TA group is about 122 percent (0.60/0.27 – 1). The difference in the increases between the Low and High groups (Diff 3 – Diff 1) is 0.13, which is significant at the 0.01 level.
| Margin class | Period | MG bal./TRD | MG/TRD | MG bal./TA | |||
|---|---|---|---|---|---|---|---|
| Mean | T-stat | Mean | T-stat | Mean | T-stat | ||
| Panel A: Price synchronicity (R2) of stocks in different margin trade groups | |||||||
| Low (n = 157) | Pre-crash | 0.33 | 31.85*** | 0.33 | 29.16*** | 0.41 | 42.63*** |
| Post-crash | 0.61 | 57.70*** | 0.61 | 53.87*** | 0.61 | 59.64*** | |
| Diff 1 = Post − Pre | 0.28 | 18.69*** | 0.27 | 16.98*** | 0.20 | 14.13*** | |
| (Paired T-test) | |||||||
| Medium (n = 313) | Pre-crash | 0.32 | 43.66*** | 0.33 | 45.45*** | 0.30 | 46.79*** |
| Post-crash | 0.63 | 81.21*** | 0.62 | 80.55*** | 0.64 | 89.91*** | |
| Diff 1 = Post − Pre | 0.31 | 28.71*** | 0.29 | 27.87*** | 0.33 | 34.94*** | |
| (Paired T-test) | |||||||
| High (n = 157) | Pre-crash | 0.31 | 29.59*** | 0.30 | 30.54*** | 0.27 | 26.82*** |
| Post-crash | 0.62 | 58.75*** | 0.64 | 65.35*** | 0.60 | 48.77*** | |
| Diff 1 = Post − Pre | 0.31 | 20.99*** | 0.34 | 24.79*** | 0.33 | 21.03*** | |
| (Paired T-test) | |||||||
| High – Low | Diff 3 − Diff 1 | 0.03 | 1.64* | 0.07 | 3.60*** | 0.13 | 6.93*** |
| (Grand Diff) | (Pooled T-test) | ||||||
| Panel B: Sensitivity to market information (β) of stocks in different margin trade groups | |||||||
| Low (n = 157) | Pre-crash | 0.98 | 42.59*** | 0.84 | 37.63*** | 1.02 | 56.51*** |
| Post-crash | 1.36 | 59.11*** | 1.37 | 56.95*** | 1.30 | 53.05*** | |
| Diff 1 = Post − Pre | 0.38 | 11.55*** | 0.53 | 16.25*** | 0.28 | 9.25*** | |
| (Paired T-test) | |||||||
| Medium (n = 313) | Pre-crash | 0.84 | 59.86*** | 0.87 | 60.34*** | 0.79 | 56.01*** |
| Post-crash | 1.40 | 82.95*** | 1.40 | 83.72*** | 1.43 | 94.77*** | |
| Diff 1 = Post − Pre | 0.56 | 25.68*** | 0.54 | 24.28*** | 0.64 | 30.76*** | |
| (Paired T-test) | |||||||
| High (n = 157) | Pre-crash | 0.73 | 39.68*** | 0.82 | 35.30*** | 0.78 | 35.70*** |
| Post-crash | 1.47 | 70.61*** | 1.46 | 71.25*** | 1.48 | 64.25*** | |
| Diff 1 = Post − Pre | 0.74 | 26.83*** | 0.64 | 20.84*** | 0.70 | 21.90*** | |
| (Paired T-test) | |||||||
| High – Low | Diff 3 − Diff 1 | 0.37 | 8.48*** | 0.11 | 2.38** | 0.41 | 9.30*** |
| (Grand Diff) | (Pooled T-test) | ||||||
-
Panels A and B report price synchronicity and the sensitivity to market movement measured by
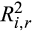 and β0, respectively. Both measures are estimated from the restricted market model Equation 2). Stocks ranked at the bottom (top) third based on the monthly margin ratios of MG bal./TRD, MG/TRD, and MG bal./TA in the pre-crash period are included in the Low (High) group, and the other stocks are included in the Medium group. We conduct paired T-tests for the differences in the test variables between the pre- and post-crash periods (Post – Pre) for each margin trade group. The pre-crash period is from 1 December 2014 to 31 May 2015, and the post-crash period is from 1 July to 31 December 2015. The differences in the changes of the test variables between the Low and High groups (Diff 3 – Diff 1) are based on pooled T-tests. ***, **, and * indicate significance levels of 0.01, 0.05, and 0.1, respectively.
and β0, respectively. Both measures are estimated from the restricted market model Equation 2). Stocks ranked at the bottom (top) third based on the monthly margin ratios of MG bal./TRD, MG/TRD, and MG bal./TA in the pre-crash period are included in the Low (High) group, and the other stocks are included in the Medium group. We conduct paired T-tests for the differences in the test variables between the pre- and post-crash periods (Post – Pre) for each margin trade group. The pre-crash period is from 1 December 2014 to 31 May 2015, and the post-crash period is from 1 July to 31 December 2015. The differences in the changes of the test variables between the Low and High groups (Diff 3 – Diff 1) are based on pooled T-tests. ***, **, and * indicate significance levels of 0.01, 0.05, and 0.1, respectively.
The results on the sensitivity to market information are reported in Panel B of Table 5. It is obvious that the sensitivity to market movement increases substantially after the market crash, and the increases are significantly larger for the high-margin trade stocks. For example, the average betas for the Low MG bal./TRD ratio group are 0.98 and 1.36 in the pre- and post-crash periods, respectively, indicating a 39 percent increase. The average increases in betas for the Medium and High groups are 0.56 and 0.74, which represent increases of 67 and 101 percent, respectively. The difference in the increase of beta between the Low and High groups (Diff 3 – Diff 1) is 0.37, which is significant both economically and statistically at the 0.01 level. The results based on MG/TRD and MG bal./TRD are similar.
These results uncover several important factors regarding investor attention and trade behaviour. First, the large R2 in the post-crash period indicate strong market co-movements and prevalent herding among investors. This is consistent with Peng and Xiong's (2006) argument that attention-constrained investors tend to allocate more attention to market-wide information than to firm-specific information. Second, the substantial increase in R2 combined with the significant decrease in price delay reveals a dramatic shift in investor behaviour. Third, the large beta in the post-crash period indicates that investors are more sensitive to market movement in down markets than in up markets. Fourth, the positive relationships between margin trade ratios and the increases in R2 and betas further indicate that investor overconfidence causes overreliance on their own judgement and less responsiveness to market information, resulting in long price delays before the market crash. This is consistent with the attribution bias literature (Hastorf et al., 1970; Thaler and Johnson, 1990; Gervais and Odean, 2001; Abreu and Brunnermeier, 2002). In contrast, after the market crash, investors pay much greater attention to market information, causing strong co-movement.
5 Robustness tests
5.1 Do margin trades reflect informed traders’ information or investor overconfidence?
One of our assumptions is that margin trades reflect investor overconfidence, which leads to the price delay in the pre-crash period. However, it is possible that margin trades reflect informed traders’ information. If the larger price delays before the market crash are driven by high sentiment and investor overconfidence, we expect that declines in abnormal returns (ARs) are larger for stocks of high-margin trades. In contrast, if margin trades reflect informed traders’ private information, the price decline of high-margin trade stocks is expected to be small. We compute the AR by running a time series regression of the market model for each stock using the monthly returns from month t−11 to t in each month t (i.e., a 12-month rolling window regression) and use the regression intercept as the AR0 for the stock in month t. The CAR0,1 is the stock's cumulative abnormal returns from month t to t+1, and the CAR0,2 is the summation of ARs from month t to t+2. Then, we compare the AR0 and CARs of stocks in different margin trade groups based on their margin ratios in the pre-crash period.
Panel A of Table 6 reports the results for AR0. For the Low MG bal./TRD group, the average values of AR0 are 2.79 and 1.94 percent in the pre- and post-crash periods, respectively, and the change is −0.85 percent and significant at the 0.1 level. For the Medium and High MG bal./TRD groups, the declines in AR0 are −1.94 and −2.69 percent, respectively, and both are significant at the 0.01 level. In addition, the difference in the declines between the Low and High MG bal./TRD groups (Diff 3 – Diff 1) is −1.84 percent, which is significant at the 0.01 level. For the Low and High MG/TRD groups, the declines in AR0 are −2.15 and −2.18 percent, respectively, and both are significant at the 0.01 level, but the difference between the Low and High groups is not significant. For the Low MG bal./TA group, the decline in AR0 is −0.03 percent and insignificant. However, the declines in AR0 for the Medium and High MG bal./TA groups are −2.0 and −3.40 percent, respectively, and both are significant at the 0.01 level. In addition, the difference in the declines of AR0 between the Low and High groups (Diff 3 – Diff 1) is −3.37 percent and significant at the 0.01 level.10
| Margin class | Period | MG bal./TRD | MG/TRD | MG bal./TA | |||
|---|---|---|---|---|---|---|---|
| Mean | T-stat | Mean | T-stat | Mean | T-stat | ||
| Panel A: Monthly abnormal returns (AR0) for stocks in different margin groups | |||||||
| Low (n = 157) | Pre-crash | 2.79 | 7.73*** | 2.63 | 8.21*** | 0.84 | 3.58*** |
| Post-crash | 1.94 | 6.06*** | 0.48 | 2.17*** | 0.82 | 3.67*** | |
| Diff 1 = Post − Pre | −0.85 | −1.76* | −2.15 | −5.53*** | −0.03 | 0.08 | |
| (Paired T-test) | |||||||
| Medium (n = 313) | Pre-crash | 2.78 | 13.89*** | 2.70 | 12.63*** | 2.81 | 15.06*** |
| Post-crash | 0.84 | 4.85*** | 1.15 | 5.95*** | 0.81 | 4.33*** | |
| Diff 1 = Post − Pre | −1.94 | −7.33*** | −1.55 | −5.37*** | −2.00 | −7.55*** | |
| (Paired T-test) | |||||||
| High (n = 157) | Pre-crash | 3.23 | 14.18*** | 3.55 | 15.17*** | 5.11 | 17.02*** |
| Post-crash | 0.53 | 2.35*** | 1.38 | 4.85*** | 1.71 | 5.79*** | |
| Diff 1 = Post − Pre | −2.69 | −8.36*** | −2.18 | −5.91*** | −3.40 | −8.08*** | |
| (Paired T-test) | |||||||
| High – Low | Diff 3 − Diff 1 | −1.84 | −4.16*** | −0.02 | −0.05 | −3.37 | −8.53*** |
| (Grand Diff) | (Pooled T-test) | ||||||
| Panel B: Cumulative abnormal returns (CAR0,1) for stocks in different margin groups | |||||||
| Low (n = 157) | Pre-crash | 5.95 | 8.23*** | 5.69 | 8.96*** | 2.04 | 4.15*** |
| Post-crash | 3.80 | 5.94*** | 0.78 | 1.80* | 1.48 | 3.42*** | |
| Diff 1 = Post − Pre | −2.15 | −2.23** | −4.91 | −6.3*** | −0.55 | 0.84 | |
| (Paired T-test) | |||||||
| Medium (n = 313) | Pre-crash | 5.92 | 14.60*** | 5.77 | 13.33*** | 6.03 | 16.06*** |
| Post-crash | 1.51 | 4.45*** | 2.21 | 5.82*** | 1.47 | 4.03*** | |
| Diff 1 = Post − Pre | −4.41 | −8.35*** | −3.57 | −6.20*** | −4.56 | −8.70*** | |
| (Paired T-test) | |||||||
| High (n = 157) | Pre-crash | 6.98 | 15.17*** | 7.53 | 15.79*** | 10.66 | 18.01*** |
| Post-crash | 1.05 | 2.36*** | 2.67 | 4.74*** | 3.43 | 5.78*** | |
| Diff 1 = Post − Pre | −5.93 | −9.29*** | −4.85 | −6.57*** | −7.23 | −8.62*** | |
| (Paired T-test) | |||||||
| High – Low | Diff 3 − Diff 1 | −3.78 | −4.43*** | 0.05 | 0.06 | −6.68 | −8.34*** |
| (Grand Diff) | (Pooled T-test) | ||||||
| Panel C: Cumulative abnormal returns (CAR0,2) for stocks in different margin groups | |||||||
| Low (n = 157) | Pre-crash | 9.35 | 8.38*** | 8.59 | 9.18*** | 3.31 | 4.47*** |
| Post-crash | 5.54 | 5.78*** | 1.20 | 1.83* | 1.94 | 3.08*** | |
| Diff 1 = Post − Pre | −3.81 | −2.59*** | −7.39 | −6.47*** | −1.37 | −1.41 | |
| (Paired T-test) | |||||||
| Medium (n = 313) | Pre-crash | 9.04 | 14.81*** | 8.95 | 13.53*** | 9.23 | 16.19*** |
| Post-crash | 2.22 | 4.50*** | 3.28 | 5.91*** | 2.26 | 4.20*** | |
| Diff 1 = Post − Pre | −6.82 | −8.69*** | −5.67 | −6.58*** | −6.97 | −8.90*** | |
| (Paired T-test) | |||||||
| High (n = 157) | Pre-crash | 10.57 | 15.28*** | 11.51 | 15.32*** | 16.25 | 17.74*** |
| Post-crash | 1.89 | 2.88*** | 4.13 | 4.95*** | 5.43 | 6.14*** | |
| Diff 1 = Post − Pre | −8.68 | −9.11*** | −7.39 | −6.58*** | −10.82 | −8.50*** | |
| (Paired T-test) | |||||||
| High – Low | Diff 3 − Diff 1 | −4.87 | −4.03*** | 0.00 | 0.00 | −9.45 | −8.14*** |
| (Grand Diff) | (Pooled T-test) | ||||||
-
Panel A reports the average monthly abnormal returns (AR0) of stocks in different margin trade groups in the pre- and post-crash periods. Panels B and C report the cumulative abnormal returns CAR0,1 and CAR0,2, respectively. In each month t, we run a time series regression of the market model for each stock using the monthly returns from month t−11 to t (i.e., a 12-month rolling window regression), and use the regression intercept as the AR0 for the stock in month t. The CAR0,1 is the stock's cumulative abnormal returns from month t to t+1
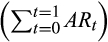 , and the CAR0,2 is computed as
, and the CAR0,2 is computed as 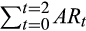 . Stocks ranked at the bottom (top) third based on the monthly margin ratios of MG bal./TRD, MG/TRD, and MG bal./TA in the pre-crash period are included in the Low (High) group, and the other stocks are included in the Medium group. The pre-crash period is from 1 December 2014 to 31 May 2015, and the post-crash period is from 1 July to 31 December 2015. We conduct paired T-tests for the difference in the test variables between the pre- and post-crash periods for each margin trade group. The differences in the changes of test variables between the High and Low groups (Diff 3 – Diff 1) are based on pooled T-tests. ***, **, and * indicate significance levels of 0.01, 0.05, and 0.1, respectively.
. Stocks ranked at the bottom (top) third based on the monthly margin ratios of MG bal./TRD, MG/TRD, and MG bal./TA in the pre-crash period are included in the Low (High) group, and the other stocks are included in the Medium group. The pre-crash period is from 1 December 2014 to 31 May 2015, and the post-crash period is from 1 July to 31 December 2015. We conduct paired T-tests for the difference in the test variables between the pre- and post-crash periods for each margin trade group. The differences in the changes of test variables between the High and Low groups (Diff 3 – Diff 1) are based on pooled T-tests. ***, **, and * indicate significance levels of 0.01, 0.05, and 0.1, respectively.
Panels B and C of Table 6 report the changes in CAR0,1 and CAR0,2, respectively. The CARs are significantly smaller in the post-crash periods than in the pre-crash periods, and the declines are larger for the high-margin groups, especially when margin trade is measured by MG bal./TRD and MG bal./TA ratios. For example, the declines in CAR0,1 for the Low and High MG bal./TRD are −2.15 and −5.93 percent, respectively, and the difference in the declines between the Low and High groups is −3.78 percent, which is significant both economically and statistically. The declines in CAR0,1 are −0.55, −4.56, and −7.23 percent, for the Low, Medium, and High MG bal./TA groups, respectively, and the difference in the declines between the Low and High groups is −6.68 percent and significant at the 0.01 level. The pattern of changes in CAR0,2 is similar to that of CAR0,1, and the difference in the changes of CAR0,2 between the Low and High MG bal./TA groups is −9.45 percent.
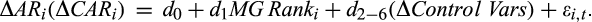 (7)
(7)where the dependent variables are the changes in AR0 (CAR0,1 and CAR0,2). The independent variables include the rank of margin trade ratio (MG Rank), which takes a value of 1, 2, or 3 if the stock is ranked at the bottom, medium, or top third based on its margin ratios (MG bal./TRD, MG/TRD, MG bal./TA) in the pre-crash period. Other independent variables are control variables of firm characteristics, which include the changes in earnings per share (∆EPS), debt ratio (∆D/TA), Herfindahl index of top 10 shareholders (∆HHI_Top10), turnover ratio (∆Turnover), and the changes in stock beta (∆β).
Panel A of Table 7 reports the regression results of the changes on AR0. The coefficient on MG bal./TRD (the first two columns) is −0.574 and significant at the 0.05 level, indicating that high-margin stocks experience significantly large declines in abnormal returns, confirming the results reported in Table 6. The coefficient on MG/TRD (the two middle columns) is insignificant. The coefficient on MG bal./TA is −1.382 and significant at the 0.01 level. Panel B of Table 7 reports the results of regressions on the changes to CAR0,1. The coefficients on MG bal./TRD and MG bal./TA ratios are −1.098 and −2.602, and these numbers are significant at the 0.05 and 0.01 levels, respectively; whereas the coefficient on MG/TRD is insignificant. In the CAR0,2 regressions reported in Panel C, the coefficients on MG bal./TRD and MG bal./TA ratios are −1.239 and −3.635 and significant at the 0.05 and 0.01 levels, respectively. Among the control variables, only the coefficients on ∆β remain consistently negative and significant at the 0.01 level in all regressions. To save space, the coefficients on control variables are not reported.
| Variable | Coefficient | T-stat | Coefficient | T-stat | Coefficient | T-stat |
|---|---|---|---|---|---|---|
| Panel A: Dependent var. = changes in AR0 from the pre-crash to the post-crash periods | ||||||
| Intercept | 0.698 | (1.47) | −0.464 | (−0.97) | 2.087 | (4.51)*** |
| MG bal./TRD | −0.574 | (−2.53)** | ||||
| MG/TRD | 0.085 | (0.41) | ||||
| MG bal./TA | −1.382 | (−6.20)*** | ||||
| (To save space, the coefficients on the control variables ∆EPS, ∆D/TA, ∆HHI_Top10, ∆Turnover, and ∆β are not reported) | ||||||
| Adjusted R2 | 0.102 | 0.093 | 0.146 | |||
| Obs. | 627 | 627 | 627 | |||
| Max VIF | 1.23 | 1.25 | 1.23 | |||
| Panel B: Dependent var. = changes in CAR0,1 from the pre-crash to the post-crash periods | ||||||
| Intercept | 1.041 | (1.13) | −1.337 | (−1.45) | 3.629 | (4.04)*** |
| MG bal./TRD | −1.098 | (−2.50)** | ||||
| MG/TRD | 0.246 | (0.60) | ||||
| MG bal./TA | −2.602 | (−6.01)*** | ||||
| (the coefficients on all other control variables are not reported in the table) | ||||||
| Adjusted R2 | 0.1202 | 0.1119 | 0.1602 | |||
| Max VIF | 1.23 | 1.23 | 1.15 | |||
| Panel C: Dependent var. = changes in CAR0,2 from the pre-crash to the post-crash periods | ||||||
| Intercept | 0.458 | (0.35) | −2.289 | (−1.75)* | 4.587 | (3.60)*** |
| MG bal./TRD | −1.239 | (−1.99)** | ||||
| MG/TRD | 0.311 | (0.54) | ||||
| MG bal./TA | −3.635 | (−5.92)*** | ||||
| (the coefficients on all other control variables are not reported in the table) | ||||||
| Adjusted R2 | 0.120 | 0.115 | 0.162 | |||
| Max VIF | 1.23 | 1.15 | 1.23 | |||
- In Panel A, the dependent variable is the change in a stock's average monthly abnormal returns (AR0) from the pre-crash to the post-crash periods. In Panels B and C, the dependent variables are the changes in a stock's cumulative abnormal returns CAR0,1 and CAR0,2, respectively. The main independent variable, a stock's margin trade ratio, takes a value of 1, 2, or 3 if the stock is ranked at the bottom, medium, or top third based on its ratios of monthly margin ratios MG bal./TRD, MG/TRD, and MG bal./TA in the pre-crash period. Control variables include the changes in earnings per share (∆EPS), changes in debt ratio (∆D/TA), the changes in Herfindahl index of top 10 shareholders (∆HHI_Top10), the turnover ratio (∆Turnover), and the changes in the stocks’ beta (Δβ). The pre-crash period is from 1 December 2014 to 31 May 2015, and the post-crash period is from 1 July to 31 December 2015. ***, **, and * indicate significance levels of 0.01, 0.05, and 0.1, respectively.
In summary, both the univariate and the regression analyses show that stocks of high-margin trades in the pre-crash period experience larger declines in abnormal returns after the crash, and the declines are unlikely to be due to the contemporaneous changes in firm fundamentals. This additional evidence also suggests that the margin trades are less likely driven by informed traders.
5.2 Do margin trades predict or destabilise price?
If margin trades reflect investor sentiment rather than informed traders’ information, more margin trades are expected on extreme market up-days, and fewer or negative net margin trades are expected on extreme market down-days. In contrast, if margin traders trade based on their private information, they buy (sell) undervalued (overpriced) stocks. Thus, more margin trades are expected on extreme down-days, and fewer margin trades are expected on extreme up-days, especially when extreme days are transitory. We classify a trading day as an extreme up-day if the daily return of an individual stock on that day (Rt) is equal to or greater than 7 percent (Rt ≥ 7 percent) or equal to or greater than 2 times the standard deviation (Rt ≥ 2δ) of its daily returns in a 12-month benchmark period from December 2013 to November 2014 prior to the pre-crash period. Similarly, a trading day is classified as an extreme down-day if the daily return of an individual stock is equal to or smaller than −7 percent (Rt ≤ −7 percent) or Rt ≤ −2δ. To reduce any possible contamination effect of multiple extreme days, we include only the extreme days that are not preceded by another extreme day during the prior nine days from t−9 to t−1.11
Panel A of Table 8 reports the margin trades on extreme day t unconditional on the following day t+1. Obviously, margin trade is very high on extreme up-days, especially in the pre-crash period. The mean (median) value of the net margin trade to the daily total trading amount (excluding margin trades) ratio is 2.40 (1.67) on up-days in the pre-crash period, and 2.11 (1.25) on up-days in the post-crash period. In sharp contrast, the mean (median) value of the margin trade ratio is −0.29 (−0.23) on extreme down-days before the crash and −1.64 (−1.25) on extreme down-days after the market crash. The negative value of net margin trade ratios indicates that margin traders liquidate their margin positions on down-days.12 In addition, the differences in the margin trade ratios on up-days are not significant between the pre- and post-crash periods, but the differences on down-days are significant between the pre- and post-crash periods, suggesting that margin traders are more sensitive to negative information after the crash. As additional evidence, Figure 3 shows the median values of daily net margin trade to total trade ratios surrounding extreme days from 10 days before (t−10, t−1) to 10 days after (t+1, t+10).
| Panel A: MG/TRD on extreme day t unconditional on day t+1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Extreme day (t) | Pre-crash period | Post-crash period | ||||||
| N | Mean | Median | T-stat | N | Mean | Median | T-stat | |
| Down-days | 1086 | −0.29 | −0.23 | −3.35*** | 1979 | −1.64 | −1.25 | −25.22*** |
| Up-days | 2750 | 2.40 | 1.67 | 29.81*** | 1631 | 2.11 | 1.25 | 20.21*** |
| Pooled t-test: Down versus Up | −2.69 | −19.33*** | −3.76 | −31.57*** | ||||
| Panel B: MG/TRD on extreme day t conditional on day t+1 in pre-crash period | ||||||||
|---|---|---|---|---|---|---|---|---|
| Conditional on day t+1 | Extreme down-day t | Extreme up-day t | ||||||
| N | Mean | Median | T-stat | N | Mean | Median | T-stat | |
| Small reversal | 236 | −0.36 | −0.24 | −1.89* | 418 | 3.00 | 2.08 | 13.26*** |
| Large reversal | 413 | −0.26 | −0.26 | −1.95** | 616 | 2.72 | 1.98 | 16.46*** |
| Overshot | 19 | 0.63 | 0.99 | 1.11 | 66 | 2.55 | 1.57 | 5.48*** |
| Continue | 418 | −0.32 | −0.12 | −2.22** | 1650 | 2.12 | 1.47 | 20.75*** |
| Pooled t-test: Overshot versus Continue | 0.95 | 1.39 | 0.42 | 0.84 | ||||
| Panel C: MG/TRD on extreme day t conditional on day t+1 in the post-crash period | ||||||||
|---|---|---|---|---|---|---|---|---|
| Conditional on day t+1 | Extreme down-day t | Extreme up-day t | ||||||
| N | Mean | Median | T-stat | N | Mean | Median | T-stat | |
| Small reversal | 327 | −1.54 | −1.13 | −11.15*** | 241 | 2.45 | 1.45 | 7.88*** |
| Large reversal | 664 | −1.22 | −0.80 | −9.88*** | 449 | 2.06 | 1.15 | 11.38*** |
| Overshot | 41 | −1.27 | −1.49 | −2.68*** | 68 | 1.00 | 1.12 | 1.95* |
| Continue | 947 | −1.99 | −1.58 | −22.13*** | 873 | 2.13 | 1.27 | 14.92*** |
| Pooled t-test: Overshot versus Continue | 0.73 | 1.64* | −1.14 | −2.14** | ||||
- Panel A reports the daily net margin trade to total trading amount (excluding margin trade) ratio (MG/TRD) on extreme day t unconditional on day t+1. A trading day t is classified as an extreme up-day if the daily return of a stock (Rt) is equal to or greater than 7 percent (Rt ≥ 7 percent) or Rt ≥ 2δ, where δ is the standard deviation of the stock's daily returns from December 2013 to November 2014. Similarly, an extreme down-day is when the daily return of a stock is equal to or smaller than −7 percent (Rt ≤ −7 percent) or Rt ≤ −2δ. Panel B reports the MG/TRD ratio on extreme day t conditional on day t+1. We classify day t+1 after an extreme down-day t into four categories: a continuation, a small reversal, a large reversal, or an overshot, depending on what occurs on day t+1. A continuation is that the stock return on day t+1 is non-positive after the extreme down-day t. A small reversal is that the closing price on day t+1 is greater than the closing price of day t but the reversal is smaller than 20 percent of the stock's return on down-day t, or Pt < Pt+1 ≤ Pt + 0.2 × (Pt−1 − Pt). A large reversal is when the stock return on day t+1 reaches more than 20 percent of its return on down-day t but the closing price on day t+1 still remains either at or below the closing price of day t−1, or Pt + 0.2 × (Pt−1 − Pt) < Pt+1 ≤ Pt−1 An overshot is that the closing price on day t+1 exceeds the closing price on day t−1 (Pt+1 > Pt−1). Similarly, after an extreme up-day t, a continuation is that the stock return on day t+1 is non-negative. A small reversal is a reversal of smaller than 20 percent of the stock's return on up-day t, or Pt − 0.2 × (Pt − Pt−1) ≤ Pt+1 ≤ Pt. A large reversal is a reversal of more than 20 percent of the stocks’ return on up-day t but remains above the closing price on day t−1, or Pt−1 ≤ Pt+1 < Pt − 0.2 × (Pt − Pt−1) An overshot after an extreme up-day t is that the stock's price on day t+1 is below the closing price on t−1, or Pt+1 < Pt−1. ***, **, and * indicate significance levels of 0.01, 0.05, and 0.1, respectively.
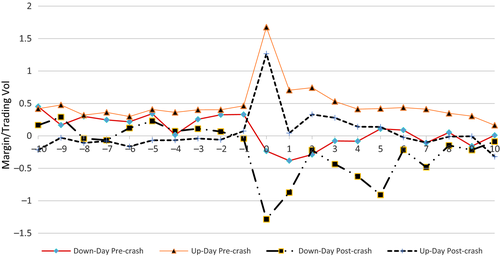
Following Boehmer and Wu (2013), we further classify an extreme down-day t into four categories: a continuation, a small reversal, a large reversal, or an overshot, depending on what occurs on the following day, t+1. Specifically, a continuation is that the stock return on day t+1 is non-positive after the extreme down-day t. A small reversal is that the closing price on day t+1 is greater than the closing price on day t but the reversal is smaller than 20 percent of the stock's return on the down-day t, i.e., Pt < Pt+1 ≤ Pt + 0.2 × (Pt−1 − Pt). A large reversal is if the stock return on day t+1 reaches more than 20 percent of its down-day t's return but the closing price on day t+1 still remains either at or below the closing price of day t−1, i.e., Pt + 0.2 × (Pt−1 − Pt) < Pt+1 ≤ Pt−1. An overshot is that the closing price on day t+1 exceeds the closing price on day t−1, i.e., Pt+1 > Pt−1. Similarly, after an extreme up-day t, a continuation is that the stock return on day t+1 is non-negative. A small reversal is a reversal of smaller than 20 percent of the stock's return on the up-day t, i.e., Pt − 0.2 × (Pt − Pt−1) ≤ Pt+1 ≤ Pt. A large reversal is a reversal of more than 20 percent of the up-day t's return but still remains above the closing price on day t−1, i.e., Pt−1 ≤ Pt+1 < Pt − 0.2 × (Pt − Pt−1). An overshot after an extreme up-day t is that the stock's price on day t+1 is below the closing price on t−1, Pt+1 < Pt−1.
Panel B of Table 8 shows the daily net margin trade to total trade ratio in the pre-crash period. The average values of margin trade ratios on extreme down-days are −0.36, −0.26, and −0.32 when the following day is a small reversal, a large reversal, and a continuation, respectively, and these numbers are statistically significant at either the 0.05 or 0.1 levels. The net margin trade to total trade ratio is 0.64 and insignificant when the following day is an overshot. In sharp contrast, on extreme up-days, the net margin trade to total trade ratios are not only positive but also large regardless of the condition on the following day, and the mean values of the ratios range from 2.12, when the following day is a continuation, to 3.0, when the following day is a small reversal. Panel C reports the net margin trade to total trade ratios after the market crash. On extreme down-days, all of the ratios are negative and significant at the 0.01 level regardless of the following day condition. Compared with the results on the down-days in the pre-crash period, the net margin trade to total trade ratios are not only consistently negative but also have a larger magnitude, ranging from −1.22 when the following day is a large reversal to −1.99 when the following day is a continuation. On extreme up-days, all the ratios are positive and significant at the 0.1 level or higher, and the magnitude is similar to that on extreme up-days in the pre-crash period.
These results show that margin traders play a pyramiding and de-pyramiding role in the markets. They increase margin trades substantially on extreme up-days and reduce their margin position on extreme down-days. More importantly, margin traders are more sensitive to bad news in the down market, which is evidenced by the significantly large magnitude of the negative net margin trade to total trade ratios on extreme down-days in the bear market. This additional evidence rejects the argument that margin trades reflect informed traders’ private information.
6 Conclusions and discussions
We use a unique sample and a special event to investigate the effects of investor attention and overconfidence on market efficiency. We find that the price delay in the pre-crash period is about twice the price delay in the post-crash period. The magnitude of the decrease in price delay after a crash is significantly larger for high-margin trade stocks. This result indicates that investor overconfidence impedes price discovery in market rallies because of attribution and confirmation biases. After the market crash, investors become more vigilant and react more strongly to negative surprises. Price delays are significantly larger on down-days than on up-days before the crash, and no apparent difference exists in price delays between the up- and down-days after the crash. This indicates that bad news travels slowly only when market sentiment is high. Margin trades increase substantially on extreme up-days and decrease on down-days, which suggests that margin traders trade on market momentum and add additional force to it.
Given these novel findings, there are several important issues worthy of further investigation. Chinese markets are known for pervasive investor herding and are driven by rumours and investor sentiment (Kang et al., 2002), and it would be interesting to see whether a similar pyramiding and de-pyramiding pattern exists in other markets. Baker et al. (2012) indicate that sentiment spreads across markets and forms global sentiment; it would be interesting to investigate whether sentiment spreads from emerging markets or from more established markets. Similarly, Benhabit et al. (2016) show that investor perceptions of synchronisation across countries can lead to actual synchronisation; it would be informative to see any lead-lag effect of such cross-country synchronisation.
Notes
Appendix A A: Correlation tests between market indices and investor sentiment index (ISI)
Panel A (B) reports Pearson, Spearman, Kentall's Tau, and Hoeffding Dependence correlation tests between the SHSE (SZSE) index and ISI in the pre-crash period, post-crash period, the whole sample period, and an extended period from January 2013 to December 2015. Note that June 2015 is excluded from both the whole sample period and the extended period.
| Pearson | Spearman | Kentall's Tau | Hoeffding Dependence | |
|---|---|---|---|---|
| Panel A: Correlations between the SHSE index and ISI | ||||
| 2014.12–2015.5 | 0.835 | 0.829 | 0.733 | 0.500 |
| (pre-crash) | (0.04) | (0.03) | (0.04) | (<0.01) |
| 2015.7–2015.12 | 0.939 | 0.874 | 0.739 | 0.579 |
| (post-crash) | (<0.01) | (<0.01) | (<0.01) | (<0.01) |
| 2014.12–2015.12 | 0.849 | 0.902 | 0.754 | 0.539 |
| (whole period) | (<0.01) | (<0.01) | (<0.01) | (<0.01) |
| 2013.1–2015.12 | 0.874 | 0.838 | 0.667 | 0.393 |
| (extended period) | (<0.01) | (<0.01) | (<0.01) | (<0.01) |
| Panel B: Correlations between the SZSE index and ISI | ||||
| 2014.12–2015.5 | 0.737 | 0.771 | 0.600 | 0.500 |
| (pre-crash) | (0.09) | (0.07) | (0.09) | (<0.01) |
| 2015.7–2015.12 | 0.931 | 0.856 | 0.699 | 0.482 |
| (post-crash) | (<0.01) | (<0.01) | (<0.01) | (<0.01) |
| 2014.12–2015.12 | 0.850 | 0.896 | 0.732 | 0.495 |
| (whole period) | (<0.01) | (<0.01) | (<0.01) | (<0.01) |
| 2013.1–2015.12 | 0.849 | 0.705 | 0.529 | 0.238 |
| (Extended period) | (<0.01) | (<0.01) | (<0.01) | (<0.01) |
Appendix B B: Price delay based on Standardized Excess Margin Trade (SXMGT) Index
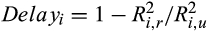 based on Hou and Moskowitz's (2005) method. We develop a standardized excess margin trade index (SXMGT) as a measure of excess margin trade for each stock and compute it as follows:
based on Hou and Moskowitz's (2005) method. We develop a standardized excess margin trade index (SXMGT) as a measure of excess margin trade for each stock and compute it as follows:
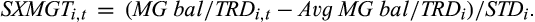
where MG bal./TRDi,t is the monthly margin trade balance to trading amount for stock i in month t during the pre-cash period. Avg MG bal./TRDi is stock i's average MG bal./TRD ratio from December 2013 to November 2014, a 12-month benchmark period prior to the pre-crash period. STDi is the standard deviation of MG bal./TRD for stock i during the benchmarked period. Stocks ranked at the bottom (top) third based on the average value of SXMGT in the pre-crash period are included in the Low (High) group, and the other stocks are included in the Medium group. We conduct paired T-tests for the differences in the price delay between the pre- and post-crash periods for each margin trade group. The differences in the changes of price delay between the Low and High groups (Diff 3 – Diff 1) are based on pooled T-tests. ***, **, and * indicate significance levels of 0.01, 0.05, and 0.1, respectively.




