The market premium for the option to close: evidence from Australian gold mining firms
Abstract
This study shows the market value of gold mining firms contains a premium for the option to close. The sample uses 41 gold mining producers listed on the Australian Stock Exchange from 1987 to 2013. The premium of the market price over the present value of cash flows is isolated and a pooled cross-sectional regression tests the degree of association between that premium and theoretical option premiums. The results show market prices incorporate a premium reflecting the option to temporarily close operations. The magnitude of the option premium to close depends on whether firms are out or in the money options.
1 Introduction
The nature and importance of mining projects to global economies requires suitable and accurate valuation models.1 Mining activities differ from conventional investment in that they are characterised by a sequence of distinct stages, typically: exploration, development and extraction. Each stage provides the firm with the option to proceed, defer or abandon a project. When a mine reaches the production stage, it has several operating options in the form of the option to temporarily close operations, abandon or otherwise alter the operating scale of the mine (Paddock et al., 1988; Twite, 2002). Real options theory argues this managerial flexibility has a recognisable and identifiable value.2
In examining whether market prices for Australian gold mining firms reflect any value inherent in operating flexibility, three questions are addressed. First, is the option to close valued by the market? Second, does the extent to which the option is in the money (moneyness) affect the value of the option to close the mine? Third, does the Brennan and Schwartz valuation model (Brennan and Schwartz, 1985a) have empirical validity with respect to gold mining operations. Addressing these questions jointly tests the Hotelling Valuation Principle (Miller and Upton, 1985b) and the Brennan and Schwartz model (Brennan and Schwartz, 1985a).
This research finds that market prices incorporate an option premium to close operations. Approximately 74 percent of the market value of mining operations is captured by the Hotelling Valuation Principle (HVP). The HVP is used to measure the discounted cash flow of expected future cash flows from mining operations. The option to close accounts for a further 63 percent of the difference between calculated HVP values and observed market values of mining operations. The existence and magnitude of this option premium depends on the moneyness of the firm's operations.
The remainder of this study is as follows: Section 2 presents the valuation methodologies relevant to mining firms. Section 3 outlines the research design, while section 4 presents the results and discussion of findings. Section 5 concludes the study.
2 Valuation methodologies
The gold mining industry offers a unique research platform to test the existence and magnitude of real option premiums. Gold-commodity markets provide observable values and volatility of the underlying asset (gold) required as an input into real options models. Two theoretical-valuation approaches, the Brennan and Schwartz (1985a) real-option valuation method and the HVP when applied together, isolate the estimated value of the option to close and the value of all options reflected in market prices.
2.1 Brennan and Schwartz real-options valuation
The B&S model is a seminal model in the real-options literature. For open and operating mining projects, the initial investment or development decisions have been made, and the producer manages flexibility options of optimising production or closing the mine. Brennan and Schwartz (1985a) derived a valuation process for an operating natural resource project based on Black and Scholes (1973) option pricing methodology.
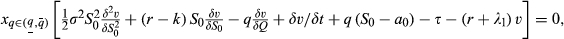 (1)
(1)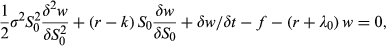 (2)
(2)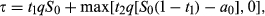 (3)
(3)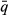 and q); r = real annual interest rate = ρ – π; ρ = nominal annual interest rate; π = the annual inflation rate; k = the commodity convenience yield3; f = periodic maintenance cost for a closed mine; λ1 = proportional rate of property tax on the value of the open mine; λ0 = proportional rate of property tax on the closed mine value; a0 = average cost of production per unit of commodity; τ1 = royalty rate; τ2 = income tax rate.
and q); r = real annual interest rate = ρ – π; ρ = nominal annual interest rate; π = the annual inflation rate; k = the commodity convenience yield3; f = periodic maintenance cost for a closed mine; λ1 = proportional rate of property tax on the value of the open mine; λ0 = proportional rate of property tax on the closed mine value; a0 = average cost of production per unit of commodity; τ1 = royalty rate; τ2 = income tax rate.The real-options approach has two advantages. First, it uses risk-free rather than risk-adjusted discount rates. Second, the need for estimates of the expected rate of change of the underlying cash flow and the output price is not required. Unlike DCF analysis, the model is not dependent on predictions of future prices and quantities sold. Uncertainty is modelled directly by selecting an appropriate stochastic process. The model easily incorporates the flexibility that arises from managerial control over the output (Kester, 1984; Trigeorgis and Mason, 1987; Dixit and Pyndyck, 1994; Trigeorgis, 1995; Sohn, 2012; Konstandatos, 2015).
The model's limitations flow from its assumptions. The B&S model presupposes the existence of a futures market in the commodity being extracted to calculate the convenience yield (k). B&S values the future revenue inflows and cost outflows assuming a known relationship between present and future values captured by the HVP and a specified stochastic behaviour for mining revenues. The value obtained using the B&S model calculates both the DCF value of expected future cash flows and the value of the option to close.
Existing empirical literature supports the advantages of real options over DCF methods. Mardones (1993) showed the option to optimise cut-off grades and stockpile mined material at an operating Chilean copper mine adds 2.4 percent to a DCF value. Cavender (1992) estimates that the flexibility to shutdown and restart a small US gold mine adds $3.8 million to the DCF value of the mine. The results of Brennan and Schwartz (1985a) Mardones (1993), Cavender (1992) and Palm et al. (1986) indicate that for the average profitable-producing-mineral asset, operating flexibility adds an average of 8 percent to DCF values. On a dollar basis, operating flexibility adds a relatively insignificant premium to DCF values (Davis 1996).
Paddock et al. (1988) valuation of the joint timing development and production flexibility options for deep in the money petroleum leases, found the option premium was irrelevant over and above a DCF valuation. They found a low correlation between their option-based values and industry tenders that generally correspond to market prices.
However, more recent empirical research applying real options to natural resources concludes that the value of real options in mining projects is significant. The price and volatility of the underlying commodity and the cost of extraction lead to mining projects to open, defer or shut down under different circumstances (Slade 2001; Moel and Tufano, 2002; Colwell et al., 2003; Twite, 2002; Hall and Nicholls, 2007; Grullon et al., 2012). These options to shut down or temporary close a mine have been demonstrated to increased value when a real-options model is applied in comparison with DCF (Blais, Poulin and Samis, 2005; Samis et al. 2006; Dessureault et al. 2007; Guj and Garzon, 2007; Konstandatos and Kyng, 2012; Konstandatos, 2015).
The contradictions in the research can be explained with reference to whether the current spot price is near the marginal or break-even price of the mine (moneyness). When the operating option to extract ore is deep in the money, the option to close has little value (out of the money), particularly if there is low probability of commodity price change. Likewise, when the option to extract is out of the money (commodity price less than the extraction cost) or near the money (commodity price close to the extraction cost) then the option to close is significant as it reflects the value of the saved extraction costs. The option value to close a currently open mine can be a substantial fraction of the total value of the mine, particularly when the commodity price is close to the extraction cost (Brennan and Schwartz, 1985a).
The volatility of the underlying commodity also contributes significantly to the value of the option, particularly as the commodity price decreases. As the firm has the option to temporarily close operations, it is able to avoid losses in the event of low commodity prices, but gets the full benefit of high commodity prices. The combination of high volatility and marginal operating mines (near the money options) should result in higher option value than low volatility and very low cost profitable (deep in the money) operating mines.
2.2 Hotelling valuation principal
The B&S model calculates the combined value of both DCF and the real options. Despite the increased use of real-option valuation techniques for strategic decision making and as an aid in capital budgeting decisions, Adamson (1999) states DCF techniques are the most widely applied technique for valuation of mining assets. However, to isolate the real options component the DCF value as capture by the HVP model, needs to be subtracted from observed market values. The HVP is an adaptation of the traditional DCF method.
The HVP model values a mineral in the ground by multiplying the current net price by quantity of mine reserves. The principle relies on Hotelling's (1931) theory of the price path of commodities known as the ‘R’ percentage rule. This rule determines that the expected trend of future net revenues and the appropriate discount rate are linked. Hotelling (1931) proposed that the unit price of an exhaustible natural resource, net of extraction costs, should grow at a rate equal to the discount rate. Optimal production requires the extraction rate of a mine to be such that the discounted-marginal-net profit of extracting ore today should be constant in all periods (Watkins, 2006). This implies the irrelevancy of the discount rate and future commodity prices. The advantage is that the model does not require forecasting future production-cash-flows as the present value of the expected return on holding the reserves cancels out the effect of discounting the future net cash flows regardless of when the resource is extracted. The model assumes the commodity is traded in an efficient market. The HVP provides the present value of total reserves in a discrete-time certainty framework and only values the firm's mining related activities.
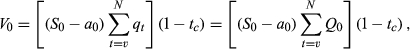 (4)
(4)Miller and Upton (1985a) extended Hotelling's ‘R’ percentage principle from determining the resource price to valuing the resource firm. It has been widely adopted by industry analysts, US National Income accountants, and the Bureau of Economic Analysis, in their effort to value national oil reserve stocks (Solow, 1974; Davis and Moore, 1998; Livernois, 2008) as well as natural gas export policy assessments in Canada (Watkins, 1992). Nabar (1997) and Eisenhauer (2005) also use the HVP model for gold mining valuation, while Harris and Ohlson (1987) use the HVP model for valuing oil and gas properties.
The HVP method is simple and avoids the difficulty of forming expected future cash flows and the cost of capital. Assuming Hotelling's (1931) ‘R’ percentage rule is correct then the HVP incorporates the present value of expected future cash flows from a firm's mining operations. The model does not account for the resolution of uncertainty over time and the potential option value in the ability of an operating mining firm to temporarily close operations. Empirical evidence suggests that the undervaluation relative to average observed market values might be as great as 18 percent (Paddock et al., 1988). The deficiencies in the DCF models including the HVP are well documented in the literature (Myers, 1984; Cheung, 1993; Moyen et al., 1996; Busby and Pitts, 1997; Twite, 2002).
3 Research design
3.1 Sample and data
The sample consists of 41 Australian gold mining firms for the period 1987–2013. Subsequent to 2004 the gold price experienced a substantial rise resulting in the sample of gold mining firms’ operations being all deep out of the money options making any option premium irrelevant over and above a DCF valuation. From 2005 the gold price rose substantially above the cost of extraction making the option to close unattractive. Figure 1 illustrates this point showing the spot price of gold exceeding the maximum cost of extraction for sample firms once the gold price exceeded $617.

The sample firms are relatively homogeneous with respect to their operating activities, debt levels, and exposure to macroeconomic factors such as interest rates. The homogeneity of these firms reduces the number of potentially confounding factors and measurement errors in the valuations. The disadvantage of using a single industry sample is that it reduces the ability to generalise the results. The sample firms on average have low levels of debt in contrast to the greater cross-sectional variation in the broader population. The mean and median amount of debt as a percentage of firm capitalisation is 22 and 5 percent respectively. Table 1 summarises the sample selection procedures. This final sample consisted of 41 gold producing firms yielding 234 firm-year observations.
| Total number of firms listed in the 1987 Jobson's Mining Year book | 445 | |
| Less: Non-gold mining firms or explorers over the sample period | 385 | |
| Firms forming initial sample | 60 | |
| Less: | ||
| Firms involved in diversified mineral extraction in addition to gold mining | 13 | |
| Firms inadequate disclosures of the proven and probable reserves or extraction cost | 3 | |
| Firms involved in substantial activities outside of gold mining | 3 | |
| 19 | ||
| Total firms in the sample | 41 |
3.2 Independent and dependent variables
The dependent variable in this research is the market option premium (MOP) while the independent variable is the theoretical option to close premium (TOP). Neither of these variables is observable and must be calculated from other variables. MOP measures the difference between the market value of mining operations (MVMO) and the present value of operating cash flows of a mine as captured by the HVP model. The TOP captures the value of the option to close an operating mine and is calculated as the difference between the B&S value minus the HVP value.
The market value of a mine is assumed to comprise three components: the estimated present value of expected future cash flows; the option to close (TOP); and, the value of all other operating options. If market prices incorporate these factors then valuation methods that explicitly capture these characteristics are likely to be more highly correlated with market prices (Chan and Faff, 1998; Twite, 2002). Figure 2 is a diagrammatic representation of the separation of market values into present values and real options components. Figure 2 shows the MOP may include the value of the option to close but it may also contain other options valued by the market such as growth options.
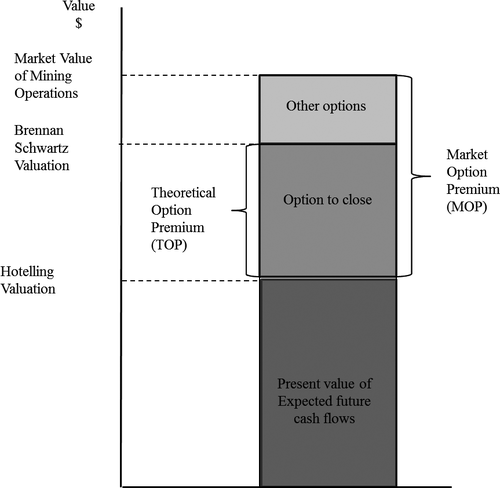
The HVP model (Miller and Upton, 1985b) estimates the present value of expected future cash flows from mining.4 The difference between the total MVMO and the HVP gives the value of all the option premiums the firm holds. Subtracting the HVP model (1985a) from the firm's B&S valuation gives the value of the option to close TOP.
Table 2 defines the variables needed to calculate the B&S Model and HVP model. The parameters for the B&S model are obtained directly from observable market and firm data with the exception of the convenience yield and price volatilities that are calculated from published data. Part A of Table 2 presents the variables that are common to both the B&S and the HVP model. Part B contains variables unique to the B&S model (1985a).
| Brennan & Schwartz (1985) | Hotelling Valuation Principle |
|---|---|
| Part A | |
| S0 = current commodity price at time 0 | S0 = current commodity price at time 0 |
| Q = quantity of mine reserves | Q0 = quantity of mine reserves |
| r = real annual interest rate = ρ−π | r, the real rate of interest cancels out as (S0 – a0) grows over time at a rate equal to the real rate of interest and subsequently discounted back at the same rate. |
| ρ = nominal annual interest rate | ρ = nominal annual interest rate |
| π = annual inflation rate | π = annual inflation rate |
| a0 = constant unit extraction cost | a0 = constant unit extraction cost |
| t1 = royalty rate: variable not shown separately as average production costs includes the costs of royalties. | t1 = royalty rate: variable not shown separately as average production costs includes the costs of royalties. |
| t2 = corporate income tax rate | tc = corporate income tax rate |
| Part B | |
| σ2 = commodity price variance | Not included in model |
| q = annual production or current rate of extraction | q = current rate of extraction in time period t, 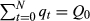 |
| k = the commodity convenience yield | Not included in model |
| f = periodic maintenance cost for a closed mine | Not included in model |
| λ1 = proportional rate of property tax on the value of the open mine | Not included in model but assumed to be zero |
| λ2 = the proportional rate of property tax on the closed mine value | Not included in model but assumed to be zero |
The MVMO requires estimation from the market values of equity and debt adjusted for gold inventory already extracted and the present value of other investments. Because none of the sample issued traded debt, the book value of financial debt was used as surrogate for the market value of debt.
3.3 Pooled cross-sectional GLS regression
After controlling for the present value of expected cash flows, the market value of mining operations (MVMO) should be positively related to the value associated with the option to close (TOP). An ordinary least squares regression and a pooled cross-sectional GLS fixed-effects model tests the association between the option to close (TOP) and the total market option premium (MOP) observed in market values that are in excess of the present value of cash flows from mining operations.
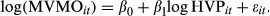 (5)
(5)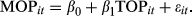 (6)
(6)The present value of operating options (MPO) encompasses the value of all other operating options that may affect firm value. These other options together with the present value of other cash flows are not valued in either the B&S or HVP valuation models. Using a fixed-effect pooled regression model, these omitted variables are captured explicitly in a time-constant term of the regression that is allowed to be different for each pool member. The unobserved effect is often interpreted as capturing unobserved characteristics of a firm, such as mine location, management quality or structure. In this study other operating options other than the option to close can be viewed as being (roughly) constant over the period in question (Woolridge 2002).
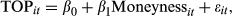 (7)
(7)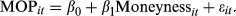 (8)
(8)The strength of the association between MOP and TOP should be inversely related to the degree of moneyness. As moneyness decreases (i.e. gold price – extraction cost nearing zero) there should be a stronger relationship between the observed market option premium and the option to close. By partitioning the sample into quartiles based on moneyness, a test is performed to determine if the slope coefficients between quartiles differ.
4 Results and discussion
The degree of moneyness affects the value of real options. Firm-year observations are classified based on moneyness of sample firms operating options. Moneyness is calculated as the underlying commodity price less the extraction cost on a per ounce basis. Table 3 shows that 10 of 234 firm-year observations (4.27 percent) are out of the money.
| Moneyness | Firm years | Percent of firm years |
|---|---|---|
| Out of the money | 10 | 4.27 |
| $0–$50 in the money | 20 | 8.55 |
| $51–$100 in the money | 30 | 11.97 |
| More than $100 in the money | 174 | 75.21 |
| Total | 234 | 100 |
4.1 Descriptive statistics
Estimates of HVP and B&S valuations that underlie the option premium constructs depend on key attributes of the sample firms. Table 4 presents the descriptive statistics for these attributes for the sample firms at fiscal year-end. All monetary values are measured in Australian dollars. The average firm has a mean (median) annual extraction level of 149,100 (83,411) ounces of gold at a mean (median) extraction cost of $330 ($328.50). The mean (median) level of proven and probable reserves is 1,259,189 (428,830) ounces of equivalent gold.
| Variable | Mean | Median | Max. | Min. | SD | Skewness |
|---|---|---|---|---|---|---|
| Gold price ($) | 500 | 492 | 649 | 412 | 60 | 1.5 |
| Extraction cost ($) | 330 | 328.5 | 617 | 111 | 87 | 0.3 |
| Market value of mining Operations ($M) | 260 | 106 | 2,302 | 0.663 | 391 | 3 |
| Reserves (ounces) | ||||||
| Proven & probable | 1,259,189 | 428,320 | 11,068,000 | 5,263 | 1,833,012 | 2.3 |
| Current extraction | 149,100 | 83,411 | 1,046,315 | 2,287 | 179,605 | 2.3 |
| Taylor's extraction rate (q) | 86,964 | 45,189 | 517,919 | 1,668 | 96,551 | 1.8 |
| Mine life (years) | ||||||
| Actual Est. mine life | 11.6 | 5.9 | 513 | 0.3 | 36 | 12.5 |
| Taylor's mine life | 10.5 | 9.5 | 21 | 3.2 | 4 | 0.6 |
| Intrinsic valuations | ||||||
| B&S ($M) | 435 | 137 | 6,130 | 0.74 | 756 | 3 |
| HVP ($M) | 241 | 74 | 2,970 | −42.31 | 433 | 3 |
The mean (median) gold price of $500 ($492) shows that on average the gold price is greater than the extraction cost for sample observations, with the majority of the sample (224 of a total of 234) exhibiting extraction options that are in the money. The remaining ten observations exhibit out of the money extraction options but remain open and operating.
The time to maturity of an option is also important in the valuation of a traditional financial option. The equivalent in the B&S model is mine life. Mine life is implied by the relationship between the quantity of reserves (Q) and the annual extraction rate (q). The longer the time to maturity of the option the higher its value, likewise, the option value will be greater the longer a mine's extraction horizon.
Table 4 reports the descriptive statistics for two different estimates of mine life. Mine life is calculated for each firm on a yearly basis as the total reported proven and probable reserves divided by the corresponding annual current extraction. The resulting mine lives based on this calculation are sometimes distorted by a lower than normal extraction rate in any one particular year. This may occur when there is a lower rate of extraction due to production difficulties or industrial relation issues where the mine is only operating for a portion of the year.
Taylor's estimates assume that the average mine life is approximately 6.5 years and adjustments are made to take into account individual firms proven and probable reserves. This adjustment increases mine life for firms who report small quantities of reserves and decreases mine lives where reported current extraction is low relative to the quantity of reserves.
Taylor's method winzorises the data by setting a maximum mine life of approximately 20 years, consistent with there being little value attached to very distant options in mines with very large reserves. There is only a difference between Taylor's mine life estimates and actual mine lives for extreme observations.
Table 4 provides descriptive statistics on valuations calculated from the B&S and HVP models. The mean (median) 435 (137) B&S5 valuations are considerably higher than the mean (median) 241 (74) HVP. This is consistent with B&S valuations incorporating the HVP values as well as the value of the option to close. Negative HVP values occur when the option to extract ore is out of the money (extraction cost exceeds spot price). Both HVP and B&S distributions are non-normal, where outliers due to differences in firm size are prevalent. Problems associated with firm size and non-normal distributions are overcome in the analysis using relative measures, MOP and TOP, capturing the percentage difference between the market value of mining assets and HVP, and the percentage difference between B&S values and HVP values.
4.2 HVP as an explanation of MVMO
Table 5 supports a significant positive association between HVP values and market values of mining operations (MVMO). HVP explains approximately 74 percent of the variation in market prices. Tests by quartiles based on moneyness indicate that the HVP model explains a larger portion of market values when moneyness of the option to extract increases. This suggests that the market attributes little value to operating options for firms’ options operating well in the money as they are less likely to change current operating status.
| Regression | Intercept | Coefficient β1 | t-Statistic | Adjusted R2 | Standard error of regression |
|---|---|---|---|---|---|
| OLS | 5.422 | 0.72 | 18.329a | 0.605 | 1.042 |
| GLS fixed effect – No weights | 10.753 | 0.42 | 6.045a | 0.738 | 0.069 |
| GLS fixed effect – Cross-sectional weights | 11.19 | 0.394 | 13.830a | 0.738 | 0.029 |
- Model: log (MVMOit) = β0 + βit log HVPit + εit.
- MVMO = Market value of mining operations (value of equity + value of debt less value of inventory and non-mine assets).
- HVP = Theoretical value of mining operations using the Hotelling Valuation Principal.
- a p < 0.0001.
The robustness of the results from Table 5 for the overall sample is tested by examining the relationship between HVP and MVMO across quartiles ranked on the moneyness of the option to extract. Table 6 presents the results of testing the relationship between HVP values and the MVMO by quartile. As predicted, the relationship is stronger when firms’ options are operating well in the money (quartile 4) as evidenced by a larger slope coefficient and higher adjusted R2.
| Quartile | Intercept | Coefficient | t-Statistic | Adj R2 | SE |
|---|---|---|---|---|---|
| 1 | 10.214 | 0.462 | 4.355a | 0.32 | 1.216 |
| 2 | 1.482 | 0.933 | 11.999a | 0.737 | 0.886 |
| 3 | 2.403 | 0.874 | 7.322a | 0.531 | 1.115 |
| 4 | 0.963 | 0.942 | 12.839a | 0.747 | 0.865 |
- Model: log (MVMOit) = β0 + βit log HVPit + ε.
- Quartiles ranked by moneyness.
- MVMO = market value of mining operations (Value of equity + value of debt – value of inventory and non-mine assets).
- HVP = theoretical value of mining operations using the Hotelling Valuation Principal.
- a p < 0.0001.
Quartile 1 in Table 6 containing both the out of the money option firms and the near the money option firms exhibits the weakest relationship between HVP values and MVMO. Quartiles 2, 3 and 4 contain extraction options that are all well in the money and their market values should reflect little option to close value, providing a stronger association between HVP values and market values.
The Ramsey RESET test for model misspecification indicates that the market is valuing something in addition to the HVP valuation. It is suggested this additional value is associated with the value of operating flexibility. This proposition is tested by examining the relationship between the two constructs, the market option premium and the theoretical option premium. The MOP measures the excess of the market value of mining operations over the present value of expected cash flows estimated by HVP. The TOP measures the excess of B&S values over HVP values, which yields the estimated value of the option to close. Both the theoretical and market options’ premiums are scaled by HVP values to overcome size differences between firms.
An unbalanced fixed-effects pooled cross-sectional model establishes a statistically significant relationship between the theoretical and market option premiums. The results support market values reflecting an option premium associated with the option to close with approximately 62 percent of the difference between HVP and the market value of mining operations being explained by the option to close.
Table 7 presents comparative results of a standard OLS regression using the Newey–West correction for autocorrelation. The Durbin–Watson statistic indicates there is no serial correlation, and this is supported by an insignificant Breusch–Godfrey serial correlation LM test for the model (χ2 = 3.469) at the 0.05 probability level.
| Variable | OLS | GLS fixed effect |
|---|---|---|
| Intercept | 0.627 | .612 |
| t-statistic | 1.283 | n/a |
| TOP | 0.745 | 0.832 |
| t-statistic | 5.240a | 12.172a |
| Adjusted R2 | 0.507 | 0.628 |
| SE of regression | 6.703 | 5.826 |
| Sum squared resid | 10,423.45 | 7,806.6 |
| Durbin–Watson stat | 2.0332 | 1.817 |
| Akaike info criterion | 6.6515 | 6.3795 |
| Schwarz criterion | 6.681 | 6.4385 |
- Model: MOPit = β0 + βit TOP + εit.
- MOP = market option premium measured as the market value of the firm less the HVP value.
- TOP = theoretical option premium calculate as B&S Value – HVP value.
- The fixed-effects model generates a separate intercept for each of the 41 cross-sectional units of which we report the average.
- The model treats this as a nuisance term and no significance level is given.
- a p < 0.01.
The estimated TOP values account for a substantial portion of the variation in MOP values of the sample firms. As predicted the coefficient on TOP is positive and statistically significant at the 0.01 level for both the GLS fixed-effects model at 0.8321 and for the OLS model at 0.7453. The adjusted R2 of 63 percent for the GLS fixed-effect design (50.68 percent for OLS) indicates substantial explanatory power for the theoretical option premium.
Because firms with real options operating out of the money and near the money find the option to close most valuable, then this should be reflected in larger option premiums. Thus, we expect that the TOP and MOP are inversely related to the degree of moneyness. Table 8 presents the results for tests of the pooled GLS fixed-effect models showing a statistically significant and negative association between both option premiums and moneyness.
| Variable | TOP | MOP |
|---|---|---|
| Intercept | 1.1879 | 2.4881 |
| Moneyness coefficient | −0.002 | −0.007 |
| t-statistic | 190.644a | 75.137a |
| Adjusted R2 | 0.554 | 0.521 |
| SE of regression | 8.172 | 9.375 |
| Sum squared resid | 12,822.15 | 16,873.81 |
- Models: TOPit = β0 + β1 Moneynessit + εit; MOPit = β0 + β1Moneynessit + εit.
- TOP represents the excess of B&S values over HVP values, scaled by HVP.
- MOP represents the excess of MVMO over HVP values, scaled by HVP.
- Moneyness is the spot price of gold less the average extraction cost.
- a p < significant at 0.0001.
For both regressions, the coefficient on moneyness is negative and highly statistically significant. Consistent with expectations, the results suggest that there is both an inverse relationship between moneyness and the value of the option to close and moneyness and MOP. As a firm's option to extract becomes deep in the money, the value of the option to close becomes smaller. Because TOP explains a significant portion of MOP (R2 62.74 percent reported in Table 7), then it is consistent that MOP will also decrease as the firm's extraction option moves deeper in the money.
The explanatory power of moneyness is similar for TOP (55.4 percent) and for MOP (52.10 percent) as shown in Table 8. The slightly lower explanatory power of moneyness for MOP may be attributable to the existence of these other operating options that are not related to moneyness.
The effect of moneyness was examined by dividing the sample into quartiles ranked on moneyness with quartile one consisting of firms with real options operating out of the money and near the money and the remaining quartiles consisting of firms with real options deeper in the money. As hypothesised, the mean and median values of TOP and MOP for each subsample are not equal, with quartile one being statistically and significantly different from the remainder of the sample. This test is based on a single-factor between-subjects analysis of variance (ANOVA).
Tests of the equality of the median TOP for quartiles are highly statistically significant for all quartile pairwise combinations. These results provide further support for the view that TOP is inversely related to the degree of moneyness. The market values of mining operations for firms’ that operate out of the money or near the money reflect a larger option to close value.
A GLS pooled time-series regression tested whether the strength of association between MOP and TOP is inversely related to the degree of moneyness. To test this, an interaction term is added to the MOP, TOP regression. Table 9 presents the results of this analysis. White's heteroskedasticity Consistent Covariance estimator is used to correct for heteroskedasticity. The results in Table 9 show the coefficient on β1 for TOP is positive sign and statistically significant as predicted and the interaction between TOP and moneyness, β2, is negative and statistically significant.
| Variable | Coefficient | SE | t-Statistic | p |
|---|---|---|---|---|
| TOP | 0.89 | 0.083 | 10.76 | 0.0001 |
| Moneyness * TOP | −0.004 | 0.0003 | −13.99 | 0.0001 |
| Adjusted R2 | 0.623 | Durbin–Watson stat | 1.96 | |
| SE of regression | 6.72 | F-statistic | 10.42 | |
| Sum squared resid | 8,615 | Prob (F-statistic) | 0.0001 |
- MOPit = β0 + β1TOPit − β2 (Moneyness * TOP) + ε.
- TOP represents the excess of B&S values over HVP values, scaled by HVP.
- MOP represents the excess of MVMO over HVP values, scaled by HVP.
- Moneyness is the spot price of gold less the average extraction cost.
These results support the proposition that MOP and TOP relationship is a function of moneyness. TOP is a statistically significant component of MOP for firms whose option to extract is out of the money and near the money but not for firms whose options are well in the money. This indicates that the attribute of moneyness of a firm's real option is an essential determinate to the existence and magnitude of the value of the option to close and the excess of market value over HVP values.
Consistent with the work of Miller and Upton (1985a,b), a significant relationship between HVP values and the market value of mining operations was found. This relationship is stronger for firms’ whose option to extract is deep in the money and weaker for firms’ whose option to extract is near the money and out of the money.
However, HVP values do not explain all of the variance of the market value of mining operations. Overall, our tests find the option to close has explanatory power for the market value of mining operations over and above the present value of expected future cash flows as measured by the Hotelling Valuation Principle. Support was also found for the hypothesis that the degree of moneyness affects the size of both the option to close and MOP values. The relationship between the option to close value and the excess of the market value of mining operations over HVP varies with the degree of moneyness with the option to close values being larger for real options that are out of the money or near the money. There is also evidence of interaction between the theoretical option premium and moneyness to explain the market valuation of mining operations.
5 Conclusion
This research examines whether the market values of mining operations for Australian gold mining firms reflect a premium for the option to close, as proposed by real-options theory. It also examines whether the magnitude of any option premium associated with the option to close varies with the moneyness of the option to close.
This research is motivated by the desire to understand the drivers of market prices. The gold industry was chosen as the research site because of the existence of world spot and futures markets that allow the calculation of real-option values for mining operations. While an extensive body of the literature suggests that real-options methodology is often an appropriate capital budgeting tool, there is only limited research to suggest that equity prices capture the value of these real options (Paddock et al., 1988; Quigg 1993; Kelly, 1998).
Estimating the present value of mining operations via the HVP model enables the calculation of a theoretical option premium. The Brennan and Schwartz (B&S) valuation method provides the value of an open operating mine including the present value of expected future cash flows plus the value of the option to close. The difference between the estimated value of a mine measured by the B&S valuation and the HVP value gives the theoretical value of the option to close (TOP).
This research documents the existence of an option premium reflected in the market value of mining operations. Support was found for the existence of an option premium associated with the option to close for firms that operate out of the money or near the money. However, the market does not appear to value as highly the option to close for firms whose operating option is deep in the money. This is consistent with the argument that firms operating deep in the money are unlikely to exercise their option to close down production. Firms that are marginal operators, experiencing higher extraction costs relative to the price of gold will find the option to close more valuable. The results suggest that market prices reflect this value and differentiate these firms from those that are deep in the money.
The results of this research contribute to our understanding of firm valuation and real-options analysis in a number of ways. First, evidence is reported that capital markets recognise the value inherent in operating flexibility in the mining industry. Further, a significant portion of the difference between the market value of mining operations and the value inherent in discounted future expected cash flows is attributed to the real-option valuation. This contributes to both asset pricing and valuation literature by validating the use of real-options techniques to capture the dimensions of investment projects that are value relevant to the market. In the gold mine industry, project appraisal techniques that do not use a real-options technique may lead to the rejection of projects that improve the utility of shareholders and maximise shareholder wealth.
Second, the existence and magnitude of the operating option, and specifically the value of the option to close, depends upon the moneyness of the operating options of the firm. Where larger differentials between spot commodity prices and the cost of production exist lower real-option values result.
Third, the research empirically tests the construct validity of the Brennan and Schwartz valuation model as descriptive of the value reflected in gold mining operations. It also provides evidence of the validity of the Hotelling Valuation Principle as descriptive of market prices for Australian gold mining firms that operate deep in the money.
Finally, the study provides a unique methodology to assess whether market prices reflect the value of real options. Because the B&S model incorporates the HVP valuation framework with real options, comparing the difference in value between the two models calculates the value of the option to close (TOP). A comparison of market values against the DCF isolates the operating option premium reflected in market prices (MOP). This methodology allows confirmation of whether the value of real options is reflected in market prices and validates the importance of real-option valuation as a suitable framework that is superior to HVP/DCF valuation alone.




