Rare disaster risk and the expected equity risk premium
Abstract
Consistent with the predictions of rare disaster models, we find that a proxy for the time-varying probability of rare disasters helps to explain fluctuations in expectations of the equity risk premium. Our proxy for disaster risk is a recently developed measure of global political instability, and the expected market risk premium is from Value Line analysts' expected stock returns. Consistent with long-run risk models, uncertainty about expected GDP growth and expected consumption growth is also significantly positively related to the expected market risk premium. We obtain similar results when we use the earnings–price ratio and the dividend–price ratio as proxies for the expected market risk premium.
1 Introduction
The expected equity market risk premium is one of the key factors in asset pricing models and plays a central role in portfolio management and valuation. As Mehra and Prescott (1985) challenged the finance profession with the ‘equity premium puzzle’, an extensive literature seeking explanations has emerged. The main focus of this study is on one of the potential explanations put forward – rare disaster risk.
Rietz (1988) shows that a low probability of a disastrously large drop in consumption can generate an average equity premium that is substantially higher than predicted by the standard economic model in Mehra and Prescott (1985). When disaster strikes, the stock market will plummet, whereas risk-free bonds provide investors with certainty when it is most needed: during disasters. Rietz argues that because of the very high marginal utility of consumption during disasters, investors are willing to pay a premium for this disaster insurance; that is, they are willing to accept a much lower return on bonds than on stocks compared to what would be expected based on the traditional concept of risk.
Barro (2006) derives a rare disaster asset pricing model and presents calibrations that use parameters based on three major contractions in gross domestic product (GDP): World War I, the Great Depression and World War II. His results confirm the suggestion in Rietz (1988) that the high observed equity premium can be explained by rare disasters. Further theoretical development in Gabaix (2012) also shows a how time-varying probability of rare disasters has the potential to explain several long-standing puzzles in economics and finance.
While promising in theory, empirical verification of disaster-based models is far from straightforward. An obvious problem is that rare disasters are infrequent, making robust empirical analysis difficult. Berkman et al. (2011) develop a time-varying global political instability measure to overcome this problem. They relate their rare disaster risk measure to realised stock market returns and find that an increase in rare disaster risk lowers contemporary world stock market returns and raises volatility. They also show that the crisis risk is priced: industries that are more crisis sensitive yield higher returns. They, however, fail to find support for one of the key predictions of rare disaster models: a positive relation between expected market returns and disaster probability.
Bansal and Yaron (2004) propose another potential resolution of the equity premium puzzle. They show that a model with consumption and dividend growth rates containing a small long-run predictable component and fluctuating volatility can justify the observed magnitude of equity premium. In a related strand of the literature, researchers also show that aggregate stock market returns can be predicted with observable variables such as the conditional volatility of returns (French et al., 1987) and interest rates (Campbell, 1987).
The theoretical models of the expected market risk premium discussed so far yield predictions about investors' expected returns. Empirical tests of the models typically proxy expected returns with realised returns. However, the use of realised returns is subject to criticism. For example, Brav et al. (2005) argue that realised returns are likely to be a noisy proxy in the presence of information surprises that do not cancel out over the period and complex learning effects. Following Brav et al. (2005), we re-examine the predictions of several models of the expected market risk premium with a more direct measure of expected returns based on the predictions of Value Line analysts. The use of this analyst-based measure immediately raises the question whether this is a valid proxy for the true market expectation. For example, it is documented that analysts exhibit optimism bias (Rajan and Servaes, 1997) and conflict of interest bias (Michaely and Womack, 1999). In addition, Greenwood and Shleifer (2014) conclude that return expectations from six different data sources are not consistent with a rational expectations representative investor model. While we cannot completely address the concern that Value Line analysts' expected stock returns are subject to similar problems, there are some features that could lessen the concern. First, we observe that our expected market risk premium measure is positively correlated with the dividend–price ratio (correlation = 0.78). In contrast, Greenwood and Shleifer (2014) find significantly negative correlations between the six expected return measures they consider and the dividend–price ratio and present this result as one of the reasons to conclude that their expected market return measures do not accord with rational expectations models. Second, the Value Line price estimates are from professional analysts who work for an independent research institution and thus are less likely to be affected by systematic bias. Finally, Value Line charges its subscribers for the service. This suggests that the subscribers value the service and are likely to incorporate the forecasts when they make investment decisions.
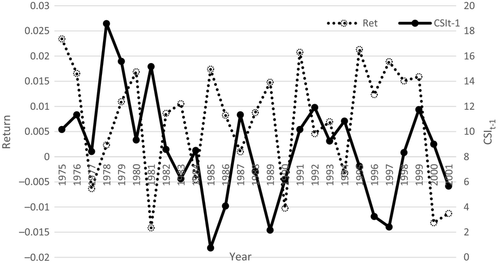
We find strong evidence that suggests that Value Line analysts expect higher returns in the face of heightened global political uncertainty. Figure 1 illustrates the main finding of our study. It plots the expected market risk premium based on Value Line analysts' forecasts against previous month's global political instability measure over the period 1975 through 2001.

This figure plots the value-weighted analysts' expected returns of individual firms in excess of 1-year constant-maturity T-bill rates and the previous month's Crisis Severity Index (CSI). The expected return of an individual firm is defined as the rate of return that equates the current market price of a stock to the present value of the target price expected to prevail in 4 years' time and future dividends. CSI is the sum of six political indicator values. Each point in the figure represents an annual average of the monthly figures within the same calendar year.
The correlation between the two annual series in Figure 1 is 0.50 (p-value is 0.006), and at a monthly frequency, the correlation is 0.33 (p-value of 0.001). This highly significant correlation confirms the main prediction in time-varying disaster risk models: investors' expected return on stocks relative to bonds is high when the probability of disasters is high (see, e.g. Gourio, 2008; Wachter, 2009; Gabaix, 2012). We also find that a one-standard-deviation increase in disaster risk raises the expected equity premium by one percent after accounting for the effects of all the other variables in the model.
In addition to the significant relation with disaster risk, we find that the expected market risk premium is significantly positively related to fluctuations in uncertainty about expected GDP growth and expected consumption growth, consistent with long-run risk models (Bansal and Yaron, 2004; Bansal and Shaliastovich, 2010). Our regression estimates suggest that a one-standard-deviation increase in uncertainty about economic growth increases the expected equity premium by 1.7 percent. Our results also indicate that our proxy for expected market risk premium is positively related to the term spread and the default spread. The model that includes all the explanatory variables explains about 44 percent of the time variation in the expected market premium.
In additional tests, we use popular valuation ratios such as earnings–price ratio (E/P) and dividend–price ratio (D/P) as proxies for expected returns (see, e.g. Fama and French, 2002). Consistent with the results based on the analyst-based expected market risk premium, we document that political risk is an important determinant of E/P and D/P over a long sample period from 1918 to 2007. Our evidence that valuation ratios vary with the perceived political instability extends the literature on determinants of the valuation ratios (see, e.g. Fairfield, 2000; Jain and Rosett, 2006; Zorn et al., 2009) and should be considered when these ratios (or their reciprocals) are used as a measure of stock valuation or mispricing (see, e.g. Weinstein, 1988; White, 2000).
Our contribution to the literature is as follows. First, consistent with the predictions of rare disaster models, we show that our analyst-based measure of expected return is positively related to political disaster risk. Second, using the same analyst-based measure for expected returns, we also find support for long-run risk models. Finally, we show that our main conclusions still hold if we use E/P and D/P as proxies for expected returns.
The rest of the study is organised as follows. Section 2 describes the variables and methodology. Section 2.1 presents the empirical findings. We conclude in Section 2.2.
2 Crisis severity index and expected returns
2.1 Crisis severity index1
Our source for international political crisis events is the International Crisis Behavior (ICB) database that contains detailed information on 455 international military-security crises since the end of World War I.2 The database provides a comprehensive set of information about each crisis including the trigger, characteristics of the ensuing conflict, superpower involvement and the outcome. Its attention to the triggers of crises is an attractive feature as it enables us to date the events that would have changed the perceived probabilities of crises. For example, a crisis was triggered by Iraq's deployment of troops near its border with Kuwait on 7 October 1994, which the United States perceived as a grave threat. On 10 October, President Clinton spoke with the leaders of the United Kingdom, France, Russia, Egypt and Turkey, seeking support for military action against Iraq, if necessary, which led Iraq to withdraw its forces from the Kuwaiti border. This crisis ended on 10 November when Iraq's National Assembly formally declared Iraq's recognition of the sovereignty of the state of Kuwait.
The main test in our study relates our proxy for the expected market risk premium to global political instability. To that end, we proxy the disaster probability with the number of starting and ongoing crises in each period. Some crises are more damaging than others. We expect that more severe crises are associated with higher disaster probabilities and will have a stronger impact on investors' expectations. To reflect the gravity, we use indicators for six severity dimensions – whether or not a crisis started with violence, violence used during the crisis, full-scale wars, gravity of value threat, whether the crisis is part of a protracted conflict, and great power or superpower involvement.3 We then assign each crisis a score of 1–7, by aggregating the six indicator values and adding 1 for being a crisis. For example, a crisis that started with violence and has great power involvement has a score of 3 – 1 for being a crisis, 1 for starting with violence and 1 for having great power involvement. We construct a monthly crisis severity index (CSI) by adding the scores of all crises starting and ongoing in each month.4
A brief discussion of recent history shows how our measure of global political instability in Figure 1 reflects the actual global political climate during the sample period of our main tests, from 1975 to 2001. The world is relatively stable at the start of our sample period in 1975, although there are several conflicts between the superpowers in the Middle East, Ethiopia and Angola. Crises flare up again at the end of the 1970s when the Soviet invaded Afghanistan. Mikhail Gorbachev's ascension to power in the Soviet Union in 1985 marked the end of the Cold War. The dissolution of the Soviet Union in December 1991 stirred up a few crises – for example crises involving North Korea, crises in and around the Balkans and crises in the Caucasus. However, with the United States as the only remaining superpower, the number of international crises declined noticeably. Nevertheless, several major crises did erupt in the post-Soviet Union era such as the Taiwan Strait conflicts, the Gulf War, conflicts between Israel and neighbouring countries, and crises stemming from terrorist attacks by the Al Qaeda network.
Table 1 presents descriptive statistics of the crisis variables in our sample period. An average month sees roughly 2.2 crises. The maximum number of international crises that begin in a particular month is four. The maximum number of crises that ended in a given month is also four. The CSI ranges from 0 to 28 and reaches its maximum in February 1979. The worst crises to start in our sample period had a crisis severity level of 6. These crises include 9/11, the Gulf War of 1990, several crises during the Iran/Iraq war (1980–1988), and the Mayaguez crisis that began on 12 May 1975, when a US-registered cargo ship, the Mayaguez, was seized off Cambodian coastal waters by the Khmer Rouge.
| Mean | Std. dev. | Min. | Max. | Sum | |
|---|---|---|---|---|---|
| Crises | 2.24 | 1.50 | 0 | 8 | 996 |
| Start | 0.48 | 0.72 | 0 | 4 | 215 |
| End | 0.48 | 0.72 | 0 | 4 | 213 |
| CSI | 7.75 | 5.44 | 0 | 28 | 3448 |
| Start CSI | 1.59 | 2.57 | 0 | 13 | 707 |
| End CSI | 1.59 | 2.58 | 0 | 19 | 707 |
| Violent start | 0.24 | 0.52 | 0 | 3 | 106 |
| GP involvement | 0.05 | 0.23 | 0 | 2 | 22 |
| Protracted | 0.28 | 0.54 | 0 | 3 | 126 |
| Grave | 0.24 | 0.49 | 0 | 3 | 106 |
| War | 0.08 | 0.28 | 0 | 2 | 36 |
| Violent | 0.22 | 0.48 | 0 | 3 | 96 |
- This table reports the mean, standard deviation, minimum, maximum and sum for all crisis variables used in our analysis for the sample period 1975–2001. Crises denotes the number of crises that take place in any month consisting of starting (Start), ongoing and ending (End) crises. Violent Start gives the number of crises that start with a violent act. GP involvement is the count of crises that involve great powers. Protracted is the number of crises that are part of a protracted conflict. Grave denotes the number of crises that involve a threat to existence, a threat of great damage or a territorial threat. Violent crises are the crises with either serious clashes or full-scale wars, and crises in the subgroup War include all full-scale wars. The Crisis Severity Index is constructed by adding 1 (for being a crisis) to the sum of one each for the six aspects (Violent Start, GP Involvement, Protracted, Grave, War and Violent).
The column in Table 1 with the heading ‘Sum’ shows that of a total of 215 crises that started in our sample period, 106 began with a violent break, 96 involved serious violence, and 36 were full-scale wars. There are 106 crises that involved threats to the most basic values during some portion of the crisis. In 22 of the crises, at least one major power was involved in the conflict, and 126 crises were part of a protracted conflict. The correlation between crisis variables is high and always significant at the one percent level (not reported). For example, crises that begin with a violent act (Violent start) tend to result in crises exhibiting either serious clashes or full-scale wars (Violent and War).
2.2 Expected return measure
A popular proxy for expected stock returns is the 1-month period ahead realised returns. However, a growing body of the literature emphasises that realised returns are a noisy proxy for expected returns and calls for alternative proxies (see, e.g. Elton, 1999; Fama and French, 2002).
As an illustration, Figure 2 plots the (annualised) realised market risk premium (CRSP value-weighted stock market return in excess of the 30-day T-bill rate) against the expected level of global political instability. In contrast to the positive correlation between global political instability and the expected market risk premium in Figure 1, the correlation between the realised market risk premium and global political instability in Figure 2 is negative and insignificant at −0.25 (p-value = 0.20). Thus, global political instability has no predictive power for 1-month period ahead realised returns.
This figure plots the annualised CRSP value-weighted stock market returns in excess of 30-day T-bill rates and the previous month's Crisis Severity Index (CSI). CSI is the sum of six political indicator values. Each point in the figure represents an annual average of the monthly figures within the same calendar year.
Paying heed to the call for alternative proxies for expected returns, we use expected return data compiled in Brav et al. (2005).5 The database provides annualised expected returns for individual stocks and is available on a monthly basis for the period January 1975–December 2001. The expected returns are based on target prices and dividend forecasts from Value Line, an independent research provider with no affiliation to investment banking. Value Line covers approximately 3800 stocks, comprising 92 percent of the NYSE, AMEX and NASDAQ in terms of market value.
To obtain expected returns, Brav et al. (2005) use the price Value Line expects to prevail in 4 years' time (the target price). To this price, they add expected dividends based on Value Line analysts' forecasts for both dividend growth rates and next year's dividends. With these inputs, expected return is defined as the rate of return that equates the current market price of a stock to the present value of the target price and future dividends. Value Line analyses each company on a quarterly cycle, but different stocks have different cycles such that expected return estimates are available for every month of the 27-year sample period.
To obtain expected annual excess returns, we subtract 1-year constant-maturity T-bill rates (from the public website of the Federal Reserve Bank of St. Louis, FRED) from analysts' expected stock returns. Descriptive statistics for the Value Line expected return data are shown in Table 2, along with the yearly averages of monthly expected excess returns used in Figure 1.
| Year | N | Mean raw | Std. dev. | Q1 | Median | Q3 | Mean VW excess |
|---|---|---|---|---|---|---|---|
| 1975 | 5571 | 0.3400 | 0.1260 | 0.2477 | 0.3262 | 0.4205 | 0.1858 |
| 1976 | 5050 | 0.2986 | 0.1027 | 0.2243 | 0.2875 | 0.3627 | 0.1839 |
| 1977 | 5851 | 0.2857 | 0.0930 | 0.2212 | 0.2806 | 0.3457 | 0.1983 |
| 1978 | 5860 | 0.2828 | 0.0879 | 0.2210 | 0.2783 | 0.3379 | 0.2001 |
| 1979 | 5958 | 0.3105 | 0.0993 | 0.2419 | 0.3100 | 0.3767 | 0.1967 |
| 1980 | 5799 | 0.3132 | 0.1211 | 0.2287 | 0.3159 | 0.3971 | 0.1828 |
| 1981 | 5974 | 0.2895 | 0.0927 | 0.2252 | 0.2881 | 0.3494 | 0.1420 |
| 1982 | 6010 | 0.3121 | 0.0984 | 0.2442 | 0.3073 | 0.3762 | 0.1846 |
| 1983 | 5056 | 0.1964 | 0.0731 | 0.1527 | 0.2019 | 0.2437 | 0.1063 |
| 1984 | 5610 | 0.2332 | 0.0728 | 0.1863 | 0.2292 | 0.2769 | 0.1197 |
| 1985 | 4989 | 0.1972 | 0.0783 | 0.1497 | 0.1908 | 0.2385 | 0.1033 |
| 1986 | 5191 | 0.1530 | 0.0710 | 0.1077 | 0.1478 | 0.1919 | 0.0769 |
| 1987 | 5292 | 0.1472 | 0.0785 | 0.0988 | 0.1380 | 0.1890 | 0.0588 |
| 1988 | 5395 | 0.1875 | 0.0730 | 0.1407 | 0.1801 | 0.2267 | 0.1016 |
| 1989 | 5245 | 0.1684 | 0.0701 | 0.1245 | 0.1628 | 0.2055 | 0.0716 |
| 1990 | 5196 | 0.2105 | 0.0918 | 0.1437 | 0.1968 | 0.2623 | 0.0951 |
| 1991 | 5202 | 0.1909 | 0.0848 | 0.1300 | 0.1786 | 0.2390 | 0.1000 |
| 1992 | 5184 | 0.1749 | 0.0803 | 0.1172 | 0.1670 | 0.2210 | 0.1098 |
| 1993 | 5292 | 0.1482 | 0.0722 | 0.0966 | 0.1443 | 0.1916 | 0.0975 |
| 1994 | 5184 | 0.1569 | 0.0657 | 0.1114 | 0.1539 | 0.1958 | 0.0904 |
| 1995 | 5174 | 0.1491 | 0.0611 | 0.1066 | 0.1444 | 0.1845 | 0.0747 |
| 1996 | 5067 | 0.1358 | 0.0653 | 0.0907 | 0.1289 | 0.1726 | 0.0582 |
| 1997 | 5101 | 0.1207 | 0.0622 | 0.0787 | 0.1137 | 0.1559 | 0.0423 |
| 1998 | 5100 | 0.1277 | 0.0813 | 0.0704 | 0.1153 | 0.1722 | 0.0321 |
| 1999 | 5328 | 0.1556 | 0.0868 | 0.0954 | 0.1486 | 0.2086 | 0.0439 |
| 2000 | 5645 | 0.1869 | 0.1033 | 0.1155 | 0.1830 | 0.2508 | 0.0584 |
| 2001 | 5771 | 0.1742 | 0.0926 | 0.1104 | 0.1601 | 0.2221 | 0.1085 |
- This table provides summary statistics on the distribution of Value Line's expected annual return by year constructed from Value Line target prices. The data, also used in Brav et al. (2005), are obtained from Reuven Lehavy's web page. The last column reports the value-weighted average expected returns in excess of 1-year constant-maturity treasury rates, where the weights are determined by the market capitalisations at the end of the preceding month.
There is a significant variation in the annual value-weighted averages of expected equity premium, ranging from 3.21 percent to 20.01 percent. Brav et al. (2005) report a positive cross-sectional correlation between the expected return and leverage (not reported) suggesting that the expected returns exhibit ‘reasonable’ model-free properties.
2.3 Other variables
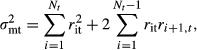
The second set of variables is motivated by Bansal and Shaliastovich (2010), who propose a long-run risk model where expected stock returns depend on investor estimates of expected growth and confidence about these estimates. Adopting the methodology of Bansal and Shaliastovich (2010), we directly estimate investors' expected growth and confidence from the cross section of forecasts from the Survey of Professional Forecasters (SPF), available from the Federal Reserve Bank of Philadelphia. Specifically, for each quarter, we proxy the expected growth rate in GDP with the average of next year's (four quarters ahead) forecast growth rates. Uncertainty in the average forecast is estimated by dividing the cross-sectional variance of the forecast annual growth rates at each point in time by the number of forecasts.7
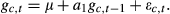
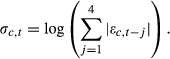
We also consider a set of predictor variables used in Ang and Bekaert (2007) and Campbell (1987), among others. We obtain monthly data for the stochastically detrended risk-free rate (the 3-month secondary market T-bill rate minus its backward 12-month moving average), the default spread between Moody's BAA and AAA corporate bond yields, and the term spread, defined as the difference between the 6-month T-bill rate and the 3-month T-bill rate (from the website of the Federal Reserve Bank of St. Louis).
For analyses using monthly estimates of the market risk premium, we match the most recently released observation with the monthly expected return. For example, the SPF data are released in the second month of each quarter and are matched with the three monthly return observations starting from the third month of the quarter. Other quarterly data are assumed to be available at the end of the quarter and are merged with the monthly observations in the following quarter. Summary statistics for the variables over the sample period of 1975–2001 are presented in Table 3.
| Panel A: Summary statistics | Mean | STD dev | Q1 | Median | Q3 | PP p-value |
|---|---|---|---|---|---|---|
| E t [MRP] | 0.1120 | 0.0564 | 0.0691 | 0.1027 | 0.1588 | 0.01 |
| Et−1 [lnσm] | 0.0401 | 0.0122 | 0.0306 | 0.0376 | 0.0475 | 0.01 |
| CSI t−1 | 8.63 | 5.74 | 4.00 | 9.00 | 12.00 | 0.01 |
| UNC t−1 | 0.0646 | 0.0871 | 0.0144 | 0.0359 | 0.0748 | 0.01 |
| RGDP t−1 | 0.0251 | 0.0135 | 0.0215 | 0.0252 | 0.0311 | 0.03 |
| RREL t−1 | −0.0004 | 0.0080 | −0.0052 | −0.0010 | 0.0045 | 0.01 |
| TERM t−1 | 0.0013 | 0.0024 | 0.0001 | 0.0012 | 0.0024 | 0.01 |
| Et−1 [lnσc] | −4.27 | 0.50 | −4.64 | −4.21 | −3.92 | 0.01 |
| DEF t−1 | 0.0111 | 0.0047 | 0.0076 | 0.0096 | 0.0139 | 0.01 |
| Panel B: Correlations | E t [MRP] | Et−1 [lnσm] | CSI t−1 | UNC t−1 | RGDP t−1 | RREL t−1 | TERM t−1 | DEF t−1 | Et−1 [lnσc] |
|---|---|---|---|---|---|---|---|---|---|
| E t [MRP] | 1 | ||||||||
| Et−1 [lnσm] | 0.04 | 1 | |||||||
| CSI t−1 | 0.33 | 0.09 | 1 | ||||||
| UNC t−1 | 0.46 | 0.07 | 0.08 | 1 | |||||
| RGDP t−1 | −0.06 | −0.15 | −0.03 | −0.24 | 1 | ||||
| RREL t−1 | 0.26 | 0.21 | 0.33 | 0.21 | −0.45 | 1 | |||
| TERM t−1 | 0.23 | 0.00 | 0.02 | 0.06 | 0.27 | −0.08 | 1 | ||
| DEF t−1 | 0.47 | 0.28 | 0.09 | 0.31 | −0.11 | 0.09 | 0.06 | 1 | |
| Et−1 [lnσc] | 0.42 | −0.14 | 0.25 | 0.29 | −0.05 | 0.10 | −0.16 | 0.29 | 1 |
- Panel A of this table reports summary statistics for the variables used in this study, and Panel B presents the correlation matrix. The sample period is 1975–2001 with a total of 324 months. Et[MRP] is the value-weighted expected return in excess of 1-year constant-maturity treasury yield. Et−1 [lnσm] is the expected stock market volatility for month t from an ARIMA (0,1,3) model calculated with information available at the end of month t−1. CSI t−1 is previous month's Crisis Severity Index (CSI). UNCt−1 and RGDPt−1 denote the cross-sectional mean and standard deviation of the most recent GDP growth rate forecasts, respectively. Et−1 [lnσc] is the log of the sum of the absolute value of the four preceding quarters' consumption growth AR (1) residuals. RRELt−1 is defined as the 3-month T-bill rate minus its trailing 12-month average. TERMt−1 denotes the difference between the 6-month and 3-month T-bill rates. DEFt−1 is defined as the difference between Moody's BAA and AAA bond yields. PP p-value denotes p-value from Phillips–Perron unit root test. Quarterly observations are converted to monthly observations by taking the most recently available quarterly observations. Correlation coefficients in bold denote significance at the five percent level.
The last column of Panel A in Table 3 reports the p-values from Phillips–Perron unit root tests. The null hypothesis of a unit root is strongly rejected for all the variables. In Panel B, the correlation between the analyst-based expected market risk premium and the CSI at monthly frequency is 0.33. Consistent with long-run risk models, expected GDP uncertainty and consumption risk are both positively related to our expected return measure. The CSI is significantly positively correlated with the stochastically detrended risk-free rate and consumption volatility.
3 Empirical results
3.1 Main results
To examine the relation between global political instability and expected market risk premium, we follow the return prediction literature and use linear regressions of expected returns on different sets of lagged explanatory variables. We assume that investors form expectations about global political instability based on the observed level of the CSI in the previous month.8 As analysts can update their expectations in response to new information, expected returns (which relate to the next 4 years) do not necessarily mechanically overlap, even if forecasting periods do. However, to the extent that the information set does not change completely, successive monthly expected returns are unlikely to be independent.9 Following previous studies, we use Newey–West standard errors (Newey and West, 1987) to address the serial correlation (see, e.g. Campbell, 1987; Bansal et al., 2005).10
Table 4 reports regression results for the monthly value-weighted Value Line expected returns in excess of 1-year constant-maturity T-bill rates. In addition to t-statistics based on Newey–West standard errors, we report one-sided bootstrap p-values – the fraction of the bootstrapped estimates that are smaller (greater) than or equal to zero when the relevant coefficient estimate from the regression is positive (negative) – in brackets.11
| Model | Intercept | Et−1 [lnσm] | CSI t−1 | UNC t−1 | RGDP t−1 | RREL t−1 | TERM t−1 | DEF t−1 | Et−1 [lnσc] | Adj. R2 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.1048 | 0.1797 | −0.0016 | |||||||
| [3.10] | [0.24] | |||||||||
| (0.0000) | (0.386) | |||||||||
| 2 | 0.0823 | 0.0419 | 0.0032 | 0.1041 | ||||||
| [2.89] | [0.06] | [2.87] | ||||||||
| (0.0001) | (0.4713) | (0.0003) | ||||||||
| 3 | 0.0638 | −0.0489 | 0.0029 | 0.2931 | 0.2358 | 0.2951 | ||||
| [2.45] | [−0.10] | [3.03] | [3.18] | [0.33] | ||||||
| (0.0030) | (0.4531) | (0.0001) | (0.0000) | (0.2973) | ||||||
| 4 | 0.0612 | −0.6957 | 0.0024 | 1.2135 | 3.6524 | 4.7284 | 0.2825 | |||
| [2.11] | [−1.20] | [2.15] | [1.91] | [2.91] | [3.76] | |||||
| (0.0035) | (0.0661) | (0.0021) | (0.0275) | (0.0068) | (0.0000) | |||||
| 5 | 0.2574 | 0.3168 | 0.0023 | 0.0416 | 0.2293 | |||||
| [3.10] | [0.67] | [2.16] | [2.38] | |||||||
| (0.0000) | (0.2533) | (0.0053) | ||||||||
| 6 | 0.1728 | −0.3380 | 0.0018 | 0.1922 | 0.3941 | 1.1228 | 3.8694 | 2.8912 | 0.0283 | 0.4425 |
| [2.67] | [−0.82] | [1.97] | [3.17] | [0.61] | [2.40] | [3.26] | [2.42] | [2.18] | ||
| (0.0002) | (0.1920) | (0.0060) | (0.0000) | (0.1567) | (0.0020) | (0.0007) | (0.0041) | (0.0028) |
- This table reports estimates from OLS regressions of Value Line analysts' expected returns in excess of 1-year constant-maturity treasury rates on lagged variables named at the head of the columns. The returns are value-weighted using the preceding month's market capitalisation. Newey–West corrected t-statistics with the optimal bandwidth proposed by Andrews (1991) in square brackets below the coefficient estimate. The sample period is 1975–2001. In brackets are one-sided bootstrap p-values from 10 000 iterations. All variable definitions are identical to Table 3.
The results in the first row show that expected market volatility has little impact on Value Line analysts' forecast annual expected excess returns. The t-statistic is only 0.24, and the adjusted R2 is negative. These results do not support the Merton's (1973) ICAPM consistent with previous empirical studies using realised returns that also document that the ICAPM risk and return trade-off is difficult to detect in the data (see, e.g. Baillie and DeGennaro, 1990; Campbell and Hentschel, 1992; Harvey, 2001). Adding the global political instability measure (row 2) greatly improves the fit of the model. The adjusted R2 is now 0.10, and the coefficient on CSIt−1 is significantly positive (t-stat. = 2.87). These results are consistent with the main prediction of time-varying rare disaster models and suggest that investors demand a higher risk premium when disaster probability is high. The point estimate of the regression coefficient is 0.0032, which indicates that a one-standard-deviation increase in CSI (5.74) results in a 1.8 percent increase in the expected market risk premium.
In rows 3–5 of Table 4, we report the estimates from regressions that include other predictor variables suggested in the literature. The inclusion of GDP forecast uncertainty and GDP growth is motivated by Bansal and Shaliastovich (2010). The significantly positive coefficient on GDP uncertainty accords well with their long-run growth model. Row 4 shows that the relative T-bill rate, the term spread and the default spread are all positively related to analyst-based expected stock market returns in excess of the 1-year T-bill rate. These results are broadly consistent with the predictive regressions in Bollerslev et al. (2009). Finally, as in Bansal et al. (2005), consumption volatility is positively related to the Value Line expected return measure. Note that in all model specifications, the coefficient on CSI is positive and significant at the conventional five percent level. When we include all the explanatory variables in row 6, CSI is marginally significant with a t-statistic of 1.97. The estimated coefficient suggests that with all the other variables in place, other things being equal, a one-standard-deviation increase in CSI (5.74) raises the expected return by one percent.
Overall, there is supporting evidence for the notion that heightened global political instability increases the expected market risk premium. The results also suggest that analysts predict a higher expected equity premium in the presence of long-run risk. A one-standard-deviation increase in UNCt−1 (0.0871) leads to a 1.7 percent increase in expected return. As in the case of realised returns, expected returns are positively related to both the term spread (TERMt−1) and the default spread (DEFt−1). Combined, the explanatory variables explain about 44 percent of the variation in analysts' expected returns.
3.2 Valuation ratios
This section considers the results of tests with earnings–price and dividend–price ratios as alternative proxies for expected stock market returns. We obtain the data from Robert Shiller's web page.12 E/P is defined as the trailing 10-year average of real earnings divided by the inflation-adjusted S&P composite price (reciprocal of P/E10 or CAPE in the data). D/P is computed as real dividends over the previous year divided by the real price.
We are not the first to employ the earnings–price ratio and the dividend–price ratio as proxies for expected returns. For example, Fama and French (2002) argue that because dividend and earnings growth are largely unpredictable, these ratios are effective proxies for expected stock returns. The results with the E/P and D/P as the dependent variable are reported in Table 5.13
| No. | Intercept | Et−1 [lnσm] | CSI t−1 | UNC t−1 | RGDP t−1 | RREL t−1 | TERM t−1 | DEF t−1 | Et−1 [lnσc] | Adj. R2 | Begin | End |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: E/P | ||||||||||||
| 1 | 0.0549 | 0.2976 | 0.0525 | 1926.02 | 2008.12 | |||||||
| [6.49] | [2.80] | |||||||||||
| 2 | 0.0454 | 0.2950 | 0.0013 | 0.1258 | 1928.02 | 2008.12 | ||||||
| [6.18] | [2.22] | [2.93] | ||||||||||
| 3 | 0.0472 | −0.0274 | 0.0012 | 0.1918 | −0.0234 | 0.3091 | 1968.12 | 2008.12 | ||||
| [3.17] | [−0.09] | [2.21] | [2.96] | [−0.09] | ||||||||
| 4 | 0.0245 | −0.3248 | 0.0013 | 0.3751 | 0.4209 | 3.7434 | 0.3632 | 1959.01 | 2008.12 | |||
| [2.72] | [−1.01] | [2.20] | [0.83] | [0.85] | [4.88] | |||||||
| 5 | 0.1288 | 0.2695 | 0.0012 | 0.0200 | 0.2393 | 1948.07 | 2008.12 | |||||
| [5.18] | [0.83] | [2.38] | [4.22] | |||||||||
| 6 | 0.0985 | −0.2977 | 0.0009 | 0.1266 | −0.0215 | 0.2038 | 0.9675 | 3.1956 | 0.0167 | 0.5459 | 1968.12 | 2008.12 |
| [2.42] | [−1.32] | [1.75] | [2.83] | [−0.13] | [0.83] | [2.28] | [3.59] | [2.21] | ||||
| Panel B: D/P | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.0261 | 0.3269 | 0.0261 | 0.1388 | 1926.02 | 2008.12 | |||||||
| [4.38] | [2.69] | [4.38] | |||||||||||
| 2 | 0.0225 | 0.3259 | 0.0005 | 0.0225 | 0.1612 | 1928.02 | 2008.12 | ||||||
| [3.92] | [2.53] | [1.92] | [3.92] | ||||||||||
| 3 | 0.0281 | −0.0907 | 0.0006 | 0.0790 | −0.0830 | 0.0281 | 0.3470 | 1968.12 | 2008.12 | ||||
| [4.64] | [−0.67] | [2.79] | [3.00] | [−0.92] | [4.64] | ||||||||
| 4 | 0.0215 | −0.2322 | 0.0006 | 0.2934 | 0.3743 | 1.2859 | 0.0215 | 0.3106 | 1959.01 | 2008.12 | |||
| [4.85] | [−1.54] | [2.43] | [1.71] | [1.93] | [3.98] | [4.85] | |||||||
| 5 | 0.0897 | −0.0503 | 0.0005 | 0.0137 | 0.0897 | 0.3431 | 1948.07 | 2008.12 | |||||
| [5.47] | [−0.37] | [2.25] | [4.14] | [5.47] | |||||||||
| 6 | 0.0502 | −0.1930 | 0.0005 | 0.0541 | −0.0762 | 0.1300 | 0.5610 | 1.1044 | 0.0067 | 0.0502 | 0.5296 | 1968.12 | 2008.12 |
| [3.14] | [−1.85] | [2.31] | [2.82] | [−1.12] | [1.27] | [3.59] | [3.29] | [2.21] | [3.14] | ||||
- This table reports estimates from OLS regressions of E/P and D/P on lagged variables named at the head of a column. E/P is the 10-year trailing average of real earnings divided by real price. D/P is real dividends in the preceding year divided by real price. Newey–West corrected t-statistics with 12 lags appear in square brackets below the coefficient estimate. The sample periods vary with data availability and are shown in the last two columns. All variable definitions are identical to Table 3.
For our analysis of the valuation ratios, we utilise all the observations available for each regression specification. We report the start date and the end date of the relevant sample period in the last two columns of Table 5, and note that these sample periods are considerably longer than the 1975–2001 period used in our previous tests with the Value Line expected returns. Despite this difference in sample periods, the results for the two valuation ratios in Table 5 are remarkably similar to those in Table 4. Most importantly, the regression coefficients on the CSI are positive and significant at the five percent level (with the exception of specification (6), with the E/P and specification (2) and with the D/P as the dependent variable, where the CSI is marginally significant at the 10 percent level).
The coefficient for expected market volatility is significantly positive for the longest sample period (Model 1), but becomes insignificant and even negative for sample periods that start after 1959 (Model 4). Consistent with the results in Table 4, GDP growth uncertainty, consumption volatility and the three financial predictors are positively related to both E/P and D/P. These results are in line with Jain and Rosett (2006) and show that macroeconomic variables can explain the E/P. More importantly, these tests show that (i) the results in the previous section are not specific to the use of Value Line analysts' expectations as proxy for market-wide expectations,14 and (ii) the results in the previous section are not limited to the period 1975–2001, but extend to the period 1928–2008. The results also suggest that the criticism of Greenwood and Shleifer (2014) does not apply to our measure of expected returns as we obtain similar results with the valuation ratios.
3.3 Robustness tests
3.3.1 Quarterly data
In the Value Line database, firms receive coverage only once per quarter and are therefore included in our value-weighted portfolio only once per quarter. One possible concern with our use of monthly data is that the firms that are covered in a particular month of each quarter are systematically different. We therefore repeat the analysis in Table 4 using quarterly value-weighted returns as dependent variable and all values for the explanatory variables measured at the beginning of each quarter. Table 6 presents the quarterly regression results.
| No. | Intercept | Et−1 [lnσm] | E t−1 [CSI] | UNC t−1 | RGDP t−1 | RREL t−1 | TERM t−1 | DEF t−1 | Et−1 [lnσc] | Adj. R2 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.0993 | 0.3044 | −0.0050 | |||||||
| [3.30] | [0.47] | |||||||||
| 2 | 0.0799 | 0.2169 | 0.0026 | 0.0739 | ||||||
| [4.33] | [0.50] | [3.17] | ||||||||
| 3 | 0.0588 | 0.0390 | 0.0027 | 0.3174 | 0.2877 | 0.3074 | ||||
| [3.05] | [0.10] | [3.70] | [6.09] | [0.85] | ||||||
| 4 | 0.0631 | −0.5477 | 0.0018 | 1.5960 | 2.2224 | 4.4254 | 0.2282 | |||
| [3.23] | [−1.29] | [2.27] | [2.77] | [1.44] | [3.83] | |||||
| 5 | 0.2635 | 0.4551 | 0.0018 | 0.0435 | 0.2207 | |||||
| [6.03] | [1.14] | [2.35] | [4.56] | |||||||
| 6 | 0.1740 | −0.2170 | 0.0015 | 0.2290 | 0.5088 | 1.3260 | 2.9054 | 2.4076 | 0.0292 | 0.4448 |
| [3.97] | [−0.59] | [2.15] | [4.61] | [1.54] | [2.45] | [2.15] | [2.33] | [3.28] |
- This table reports estimates from OLS regressions of Value Line analysts' expected returns in excess of 1-year constant-maturity T-bill rates on lagged variables named at the head of a column. The returns are measured quarterly and are value-weighted using the preceding quarter's market capitalisation. Newey–West-corrected t-statistics with four lags appear in square brackets below the coefficient estimate. The sample period is 1975–2001. All variable definitions are identical to those in Table 3. Monthly series are converted to quarterly series by taking the most recent observation.
These results are very similar to those in Table 4 and stronger, if anything. As before, the CSI, the measures of macroeconomic uncertainty and the interest rate spreads are significantly positively related to the quarterly Value Line expected returns.
3.3.2 Dynamics between CSI and economic variables
Although the results so far indicate that there is a positive relation between the expected equity premium and political risk, a possible concern is that the CSI merely proxies for economic risk. For example, political leaders have been known to start external conflicts in order to divert attention from domestic economic woes.15 If this is the case, then the current CSI could be affected by the past realisations of economic variables. To examine this issue, we estimate bivariate vector autoregressive models with the CSI and the macroeconomic variables and run Granger causality tests.16 Table 7 presents the results.
| Lag length | CSI caused | CSI causing | |||
|---|---|---|---|---|---|
| F-stat | p-value | F-stat | p-value | ||
| Et−1 [lnσm] | 3 | 0.0389 | 0.9898 | 1.9098 | 0.1259 |
| UNC t−1 | 1 | 2.1177 | 0.1466 | 7.7119 | 0.0058 |
| RGDP t−1 | 1 | 0.0072 | 0.9324 | 2.5953 | 0.1082 |
| RREL t−1 | 1 | 2.6715 | 0.1023 | 1.6399 | 0.2005 |
| TERM t−1 | 3 | 0.3292 | 0.8043 | 1.5330 | 0.2042 |
| DEF t−1 | 2 | 0.9006 | 0.4065 | 0.3917 | 0.6760 |
| Et−1 [lnσc] | 2 | 0.1427 | 0.8671 | 1.3350 | 0.2647 |
- This table reports the results of Granger causality tests from bivariate vector autoregressive regressions with the CSI and the economic variables listed. We select the lag lengths that optimise the four goodness-of-fit measures – Akaike Information Criterion, Hannan–Quinn information criterion, final prediction error and Schwarz criterion. When there is an equal division among the measures, we pick the shorter length.
Overall, there is little evidence that the lagged economic variables cause the current CSI. All the F-statistics in column 3 of Table 7 are insignificant at the 10 percent level. If anything, there is evidence that the lagged CSI causes economic uncertainty. For all the other macroeconomic variables, the F-statistics are insignificant in column 5 of Table 7 suggesting that the CSI does not Granger-cause them, either.
4 Conclusion
One of the fundamental predictions of rare disaster models is a positive intertemporal relation between disaster probability and the expected market risk premium. We empirically test this link using a measure of global political instability and Value Line analysts' expected rates of return. Consistent with the predictions of rare disaster models, global political instability is positively correlated with expected excess stock market return based on analysts' forecasts and with valuation ratios (E/P and D/P). We also find support for long-run risk models; uncertainty about expected GDP growth and expected consumption growth is significantly positively related to the expected market risk premium and valuation ratios. Interest rate spreads, which have been shown to be predictors of realised returns in the literature, affect analysts' expected returns in a similar fashion.




