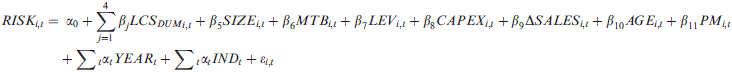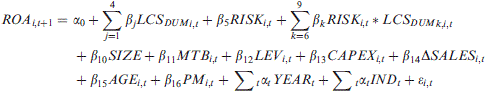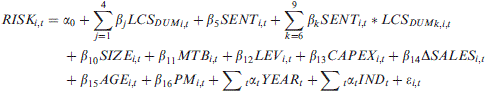Firm life cycle, corporate risk-taking and investor sentiment
Abstract
This study investigates the corporate risk-taking and the performance consequences at different stages of the firm life cycle. We find that risk-taking is higher in the introduction and decline stages of the life cycle, but lower in the growth and mature stages. We also find that risk-taking during introduction and decline stage (growth and maturity stage) affects future performance adversely (positively). We also document that managerial risk-taking propensities increase during periods of high investor sentiment and firms in different life cycle stages respond to sentiment differently. Collectively, these results suggest that the firm life cycle has explanatory power for corporate risk-taking behaviour.
1 Introduction
This study investigates empirically the corporate risk-taking propensities at different stages of the firm life cycle and the performance consequences of such risk-taking behaviour. We also examine whether marketwide investor sentiment affects risk-taking at different life cycle stages (LCS) differentially. Corporate risk-taking is the amount of uncertainty associated with expected outcomes and cash flows, because of new investments (Wright et al., 1996). Corporate risk-taking has important implications for firm growth, performance and survival (Bromiley, 1991), but has also been established in the literature as a serious agency problem (Low, 2009).
Owing to their high concentration of human capital, managers can reduce their risk at the firm level only, which exposes them to relatively high firm-specific risk. Therefore, they are likely to exhibit risk-aversion with consequent significant investment distortions (May, 1995; Parrino et al., 2005). Conservative risk choices could serve to satisfy a managerial goal of career protection, among others (John et al., 2008). Conversely, shareholders prefer that firms undertake any positive net present value (NPV) project, regardless of its associated risks (Faccio et al., 2011), because of their ability to diversify wealth. Thus, from an agency perspective, corporate risk-taking can indicate the extent to which management decisions are aligned with shareholder interests.
An extensive body of literature has investigated the determinants of corporate risk-taking decisions. Most of this research has concentrated on explaining risk-taking behaviour from an executive compensation perspective. Rajgopal and Shevlin (2002) find that employee stock option schemes provide managers with incentives to invest in risky projects. A positive association between executive compensation incentives and managerial risk-taking has also been reported by other studies (e.g. Coles et al., 2006; Armstrong and Vashishtha, 2012; Shen and Zhang, 2013) although such incentives affect future performance adversely (Shen and Zhang, 2013).
The existing research on the determinants of corporate risk-taking does not address adequately the effect of corporate life cycle on risky decision choices of firms. Corporate life cycle theory proposes that firms pass through a series of predictable patterns of development and that the resources, capabilities, strategies, structures and functioning of the firm vary significantly with the corresponding stages of development (Miller and Friesen, 1980, 1984; Quinn and Cameron, 1983). Hence, we argue that corporate risk-taking should also respond to changes in a firm's LCS. For example, a firm's resource bases are more fluid and require more risky investment for expansion during the early phase of the firm's life cycle, and increased risk-taking during the decline stage is motivated by the firm's desire to return to profitability. Our research responds to Baird and Thomas (1985, p. 231), who suggest that ‘risk is embedded in most long-range decisions… [and] thus studying the risk-taking propensities of the decision-makers as they interact with particular decision situations [LCS in this case] will help us better understand firms' strategies'. Because managerial risk-taking responds to executive compensation arrangements, we further argue and test whether variation in executive compensation during different LCS affects risk-taking differentially.
We then examine whether risk-taking at different LCS has varying performance implications. Miller and Bromiley (1990) find a significant negative relationship between income stream and risk-taking (fluctuation of financial ratios such as ROE or ROI). Using stock return risk, Aaker and Jacobson (1987) find that both systematic and unsystematic risks have a positive impact on ROI. Bromiley (1991), on the other hand, documented a negative association between risk-taking and future performance. A negative association is also reported by Cohen et al. (2013).
We argue, and test empirically, the proposition that risk-taking during different LCS may explain the inconclusive findings. For example, it is suggested that investments during the early stage of firm life cycle may not generate positive returns because of low product differentiation, lack of efficiency in the production process and shortage of financial resources (Lynall et al., 2003; Liao, 2006). With an increasing level of product differentiation during the growth phase, firm profitability starts to increase and peaks during the mature phase (Dickinson, 2011). However, firm profitability during the decline stage is again likely to deteriorate, because of negative NPV investments for firm survival (Benmelech et al., 2010).
Prior research on managerial risk-taking behaviour also confirmed that managerial risk-taking propensities vary depending on the state of the economy (Arif and Lee, 2014; McLean and Zhao, 2014). For example, periods with high growth expectations and easy access to capital are more likely to be accompanied by excessive risk-taking whilst periods of economic contractions might result in suboptimal risk-taking (McLean and Zhao, 2014). If markets are subject to mispricing, and if market signals drive corporate investment (Dow and Gorton, 1997), then there exists the potential for financial markets to systematically divert scarce resources to unproductive uses. Firms at different LCS have different capital requirements, with firms in the early stage requiring more capital to build up capacity and deter new entry into the market (Spence, 1977, 1979, 1981; Jovanovic, 1982). If external financing is less costly during periods of high investor sentiment, then managers of early stage firms rationally ‘cater’ to such sentiment by assuming more risk during such periods. As decline stage firms overinvest in an attempt to return to profitability, firms during this phase, too, will be catering to marketwide sentiment.
We use a parsimonious life cycle measure proposed by Dickinson (2011) as our primary independent variable. We use three different measures of risk widely used in the corporate risk-taking literature, and find that corporate risk-taking is higher during the introduction and decline stages of the firm life cycle, whilst lower during the growth and maturity phases of the firm life cycle, compared to the shake-out stage. We document that future operating performance is negative for risk-taking during the early and the decline stages of their life cycles, whilst it is positive for the growth and mature phases. With respect to the association between risk-taking and investor sentiment, we find that risk-taking is higher during periods of high investor sentiment. Importantly, the interaction between life cycle and investor sentiment with respect to risk-taking reveals that firms in both the early phase and decline phase engage in more risk-taking during periods of high market sentiment.
We contribute to the corporate risk-taking and organisation life cycle literature by demonstrating the importance of assessing real managerial decisions in the context of life cycle dynamism. Understanding this relationship provides investors with valuable insights into investment decision-making. Finally, our findings provide insights into the investor sentiment literature by revealing that corporate risk-taking by firms at different LCS varies appreciably during periods of high sentiment.
The remainder of the study is organised as follows: in Section 2, we review the relevant literature and develop testable hypotheses. Section 3 describes the sample, data sources and measurement of variables. Section 3.1 reports the results, and conclusions are given in Section 3.2.
2 Literature review and hypothesis development
An understanding of corporate decisions, including decisions regarding corporate risk-taking, is vital for assessing organisational dynamism. Corporate risk preferences and risk-taking are fundamental to decision-making and have important implications for firm growth, performance and survival (Bromiley, 1991; Shapira, 1995). The agency theory view of managerial risk-taking incorporates the idea that managers are rationally risk-averse because a significant nondiversifiable component of their wealth is tied to a particular organisation (Parrino et al., 2005). Therefore, unlike diversified shareholders who prefer managers to assume more risk, managers are natural risk-averters (Faccio et al., 2011).
Prior research on corporate risk-taking has ignored the potential impact of a firm's progression through its LCS. The dynamic resource-based view articulates the notion that general patterns and paths in the evolution of organisational capabilities change over time (Penrose, 1959; Rumelt, 1984; Wernerfelt, 1984). This theory proposes that the growth of a firm depends on the efficient and effective interaction between its resources and its management. Thus, the evolution of a firm's competitiveness, in terms of its resource base and capabilities, is the foundation of the firm's life cycle. The essence of firm life cycle theory suggests that the investment and financing decisions and the operating performance of a firm are greatly influenced by the change in its organisational capabilities.1
Following this line of argument, we posit that managerial risk-taking propensity should also vary with a change in the firm's LCS. We expect firms in the ‘introduction’ stage to make more risky investments to expand the resource base required to implement strategic objectives. Managerial optimism encourages firms to make early investments that deter competitors' entries into the market (Spence, 1977, 1979, 1981; Porter, 1980; Jovanovic, 1982). Similarly, a firm can position itself strategically by creating capital capacity early in its life cycle. Spence (1977) shows that firms can deter the entry of competitors by creating capacity and incurring significant capital expenditure early in the life cycle, making the product market unattractive to potential entrants. Spence (1981) further argues that the learning curve creates entry barriers and protection from competition by creating cost advantages for those who achieve large market shares early in the life cycle. Wernerfelt (1985) shows that in the presence of learning curves, declining price sensitivity and declining growth rates, growth maximisation early in the life cycle can be a means of profit maximisation. Therefore, the acquisition of market share, and capital capacity, is highly valued in the early LCS.
There are competing arguments regarding risk-taking during the growth phase of a firm's life cycle. Economic theory postulates that growth firms make early investments to deter competitors' entries into the market. Firms at this stage become larger through product innovation and diversification (Kazanjian and Drazin, 1989; Liao, 2006). Designing, selling and launching products require firms to build productive capacity, acquire fixed assets and to manufacture large quantities of inventory. Gaining market acceptance, growth firms achieve a higher level of performance (Dickinson, 2011).
Miller and Friesen (1984), on the other hand, suggest that complex product strategies during the growth phase require more managerial involvement in decision-making and, hence, there is less risk-taking. A team approach to management means that managerial risk-taking strategies will be carefully scrutinised by a team of people so that even the most promising proposals can be questioned by conservative managers. Also, the emphasis upon incremental rather than dramatic product innovation makes extremely dramatic moves less necessary.
- H1
Compared to the shake-out stage of a firm's life cycle, corporate risk-taking is higher during the introduction and decline stages of its life cycle but lower during the maturity stage.2
Agency theory proposes that shareholders prefer that firms undertake any positive NPV project, regardless of its associated risks, because shareholders are able to diversify risks (Faccio et al., 2011). As long as managerial interests are aligned with those with shareholders, corporate risk-taking would yield positive future benefits. On the other hand, misalignment of interests due to managerial self-serving behaviour and improperly designed incentives could affect future performance adversely.
However, the risk-taking and future performance relationship is not uniform across firms, as different firms pass through different life cycle phases with observable differences in risk-taking. For example, it is suggested that investments during the early stage of a firm's life cycle might yield negative returns because of low product differentiation, lack of efficiency in the production process and shortage of financial resources (Lynall et al., 2003; Liao, 2006). Another potential explanation for negative firm performance during the early stage of the life cycle is derived from agency theory. Agency theory arguments propose that during the early phase of the firm life cycle, managers may invest in diversifying strategies inefficiently, enter into hedging and insurance relationships, or seek opportunities to increase the longevity of the company, to the detriment of short-run optimisation (Donaldson and Lorsch, 1983; Doukas and Kan, 2004). This is exacerbated by a high degree of information asymmetry between managers and investors.
- H2
Compared to the shake-out stage of a firm life cycle, future firm performance will be negatively associated with risk-taking during the early and decline stages of the life cycle, but positively related to risk-taking during the growth and maturity stages.
As risk-taking in the form of capital investments requires access to external capital markets, it is important that the prevalent state of the economy is given adequate consideration. Stein (1996) argues that if the required return on a share is reflective of investor sentiment rather than the share's underlying risk, then the investment decision will depend on investor sentiment. Baker and Wurgler (2007, p. 129) define investor sentiment ‘as a belief about future cash flows and investment risks that is not justified by the facts at hand’.3 During periods of high investor sentiment, market mispricing (overvaluation) of equity encourages managers to issue more equity (Baker and Wurgler, 2000, 2002; Baker et al., 2003). They argue that overvaluation affects investment decisions through an equity channel (raising additional equity during periods of high investor sentiment translates into more investments). The agency hypothesis predicts that high accruals firms will use (overvalued) equity excessively to pay for mergers and acquisitions and overinvest in property, plant, and equipment (i.e. capital expenditures) and R&D (Jensen, 2005). Overvaluation of equity during a high investor sentiment period motivates managers of overpriced firms to take on negative NPV investment projects (Baker et al., 2003). Similarly, underpriced firms forego investment projects with positive NPV, that is market overvaluation (undervaluation) will coincide with higher (lower) levels of aggregate investment, even though the subsequent returns to these investments may be lower (higher) than expected (Arif and Lee, 2014). Either way, investor sentiment and managerial risk-taking should be positively correlated.
- H3
Risk-taking by firms in the introduction, growth and decline stage of their LC will be high during periods of high investor sentiment compared to periods of low investor sentiment.
3 Research design and sample description
3.1 Sample and data
Our sample includes all nonfinancial (excluding SIC 6000–6900) firms on the Compustat fundamentals annual file that has the required financial information from 1987 to 2013. Stock price information is acquired from the Centre for Research in Security Prices (CRSP) database. Our sample period begins in 1987 because, prior to that year, cash-flow data required for estimating the life cycle are unavailable.4 To avoid the undesirable influence of outliers, we winsorise the continuous variables at the 1st and 99th percentiles. We exclude observations with missing values from the measurement of the key dependent variable (risk-taking proxies), independent variable (life cycle proxy) and control variables. Table 1 presents the selection (panel A) and industry distribution (panel B) of the sample. Variable definitions are presented in the Appendix.
| Description | Total number of observations |
|---|---|
| Panel A: data and sample | |
| Data available in Compustat fundamentals annual file from 1987 to 2013 | 299 184 |
| Less: | |
| Financial firms | (75 908) |
| 223 276 | |
| Duplicates in terms of gvkey fyear | (92) |
| 223 184 | |
| Missing values for cash-flow variables (life cycle proxy) | (27 072) |
| 196 112 | |
| Firms with missing values for the control variables in regression model | (69 547) |
| 126 565 | |
| Missing values for dependent variable (STD_ROA) | (5562) |
| Final Sample (firm-years) | 121 003 |
| Industry | Total number of observations | % of observations |
|---|---|---|
| Panel B: industry distribution | ||
| Business equipment | 27 205 | 22.48 |
| Other | 19 663 | 16.25 |
| Manufacturing | 15 327 | 12.67 |
| Health care, medical equipment, and drugs | 14 498 | 11.98 |
| Wholesale, retail and some services | 14 004 | 11.57 |
| Consumer nondurables | 7864 | 6.50 |
| Oil, gas and coal extraction and products | 6531 | 5.40 |
| Telephone and television transmission | 4709 | 3.89 |
| Utilities | 4190 | 3.46 |
| Chemicals and allied products | 3540 | 2.93 |
| Consumer durables | 3472 | 2.87 |
| Total | 121 003 | 100 |
- This table shows sample selection for regression model 1 (STD_ROA). For regression model 2 (STD_RET) and model 3 (R&D/TA), final sample is 108 153 and 70 104, respectively.
We begin with an initial sample of 299 184 firm-year observations. Exclusion of financial firms (75 908 firm-years), duplicate observations and firms with missing values for the variables used in regression model (102 273 firm-years) yields a final sample size of 121 003 firm-year observations. The number of observations in any given regression varies from 121 003 to 70 104 firm-years depending on the model's specific data requirements. Panel B reports the composition of the sample by the twelve industry groups. The sample is distributed across industries unevenly, with the largest number being in the business equipment (22.48 percent) and other industries (16.25 percent).
3.2 Empirical model
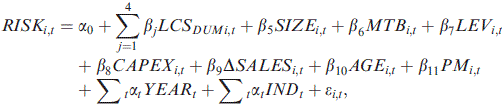 (1)
(1)Our main variable of interest is LCSi,t in the empirical model. We predict βj to be positive for the introduction and decline stages but negative for the growth and mature stage of the life cycle, compared to the shake-out stage.
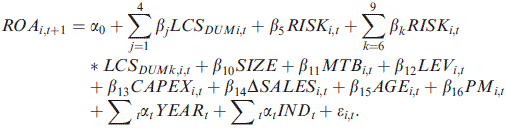 (2)
(2)Our dependent variable is 1-year-ahead ROA, a proxy for firm profitability. Our variable of primary interest is the interaction variables RISK*LCSDUM. We expect the coefficient to be negative for firms in the introduction and decline stage of their life cycle, whilst positive and significant for the growth and mature stages.
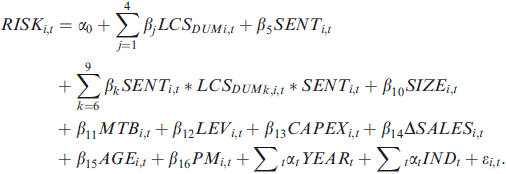 (3)
(3)We interact an investor sentiment proxy with firm LCS to evaluate the incremental effect of investor sentiment on the life cycle and risk-taking relationship. We expect the coefficient β5 to be significantly positive, supporting the notion that corporate risk-taking increases during periods of high investor sentiment. Investor sentiment is based on the common variation in six underlying proxies for sentiment: the closed-end fund discount, NYSE share turnover, the number and average of first-day returns on IPOs, the equity share in new issues, and the dividend premium (Baker and Wurgler, 2006). As each sentiment proxy is likely to include a sentiment component as well as idiosyncratic components, the authors use principal components analysis to isolate the common component. Investor sentiment, SENT, is an indicator variable coded 1 for a high sentiment period (SENT index greater than zero) and zero otherwise. This procedure yields 1987–88, 1996–97, 1999–01, 2004 and 2006–07 as high sentiment periods. We expect the coefficients on the interactive variable SENT*LCS to be positive for the introduction, growth and decline stages of a firm's life cycle compared to the shake-out stage.
3.3 Explanatory variables: estimation of firm life cycle proxies
Assessing the LCS at the firm level is difficult because the individual firm is composed of many overlapping, but distinct, product LCS. Moreover, firms can compete in multiple industries, and their product offerings are fairly diverse (Dickinson, 2011). To overcome this estimation problem, we follow the methodologies of Dickinson (2011) in order to develop proxies for the firms' stage in the life cycle.5 Dickinson (2011) relies on the economics literature in addressing the individual attributes of life cycle theory, such as production behaviour (Spence, 1977, 1979, 1981; Wernerfelt, 1985; Jovanovic and MacDonald, 1994), learning/experience (Spence, 1981), investment (Spence, 1977, 1979; Jovanovic, 1982; Wernerfelt, 1985), entry/exit patterns (Caves, 1998) and market share (Wernerfelt, 1985). Using these attributes, she develops a parsimonious firm-level life cycle proxy based on the predicted behaviour of operating, investing and financing cash flows across different LCS, which are the result of firm performance and the allocation of resources. She argues that cash flows capture differences in a firm's profitability, growth and risk and, hence, that one may use the cash flow from operating (OCF), investing (INVCF) and financing (FINCF) to group firms in LCS, such as ‘introduction’, ‘growth’, ‘mature’, ‘shake-out’ and ‘decline’.
The methodology is based on the following cash-flow pattern classification:
- Introduction: if OCF < 0, INVCF < 0 and FINCF ˃ 0;
- Growth: if OCF ˃ 0, INVCF < 0 and FINCF ˃ 0;
- Mature: if OCF ˃ 0, INVCF < 0 and FINCF < 0;
- Decline: if OCF < 0, INVCF ˃ 0 and FINCF ≤ or ≥ 0; and
- Shake-out: the remaining firm-years will be classified under the shake-out stage.
3.4 Dependent variable: estimation of firm risk-taking
Motivated by prior literature, we employ three measures of corporate risk-taking in our empirical analysis. Our first measure of corporate risk-taking, the standard deviation of return on assets (STD_ROA), captures the overall risk taken by the firm (Li et al., 2013). We measure standard deviation of the income before tax and extraordinary items, scaled by total assets, over the prior 3 years. Prior research (e.g. John et al., 2008; Zhang, 2009) shows that riskier corporate operations lead to more volatile earnings and, hence, STD_ROA is extensively used as a firm risk-taking proxy in the risk-taking literature. Our second measure of corporate risk-taking, the standard deviation of returns (STD_RET), captures a firm's equity risk and the consequences of changing investment strategies (Bargeron et al., 2010). We measure STD_RET as the annual standard deviation of monthly stock returns, computed from return data from the CRSP. High values of STD_RET denote more dispersion and, thus, high levels of risk (Markowitz, 1952; Bargeron et al., 2010). Finally, we use R&D expenditure scaled by assets (R&D/TA) as a proxy for firm risk-taking. Following prior research, we set R&D equal to zero when it is missing from Compustat. Prior studies suggest that R&D expenditures are a high-risk investment (Bhagat and Welch, 1995) as they have a low likelihood of success and their future pay-off is distant and uncertain (Li et al., 2013). Thus, this measure captures firm risk-taking in long-term corporate investment effectively.
3.5 Control variables
Prior studies suggest that managerial investment behaviour is impacted by internal factors (e.g. firms' financial resources, performance and growth) and the external environment (e.g. industry competitiveness and economic factors). Hence, the above regressions control for a number of variables that prior studies have found to be associated with corporate risk-taking (e.g. John et al., 2008; Faccio et al., 2011). Firm size (SIZE) is related to risk-taking negatively, as smaller firms are more aggressive and involved in more risky investment compared to larger firms (Perez-Quiros and Timmermann, 2000; Bargeron et al., 2010). Firms with high growth opportunities (GROWTH measured as the ratio of market value of equity to book-value of equity) are likely to take more risky investments and, hence, should be related to risk-taking positively. Li et al. (2013) show that firm-level leverage is negatively associated with corporate risk-taking, because leverage may constrain investment and corporate risk. Therefore, we control for firm-level leverage (LEV), measured as total debt scaled by total assets. Sales growth reflects firms' operating performance relative to the previous year. Studies (e.g. Anthony and Ramesh, 1992) show that investment is less rewarding when sales growth is slow. Thus, to capture the influence of firm-specific sales growth on corporate risk-taking, we control for firm sales growth. As higher levels of risk generally relate to larger returns, we control for the firm's current profitability by including profit margin (PM), measured as the income before tax and extraordinary items, scaled by sales. Prior studies suggest that a firm's capital expenditures are associated with corporate risk-taking (Coles et al., 2006). We measure capital expenditures (CAPEX), as capital expenditures scaled by market value of equity. Younger firms have more incentive to engage in risky investments, whilst older and more diversified firms exhibit less variability in performance (Adams et al., 2005). We control for this effect by including age (AGE), measured as the log of the number of years since the firm's first appearance in the CRSP database. Finally, to control for unobservable industry and year characteristics associated with firm risk-taking and LCS, we include year and industry dummy variables in all our regression specifications.
To take into account the time series and cross-sectional dependence in the error terms of our regressions, we calculate t-statistics using standard errors that are clustered by both firm and year (Petersen, 2009; Gow et al., 2010).
4 Empirical results
4.1 Descriptive statistics
Table 2 presents descriptive statistics for the variables included in the regression estimates. Panel A reports pooled descriptive statistics for the dependent, independent and control variables, and Panel B presents the Pearson's correlations. Panel A reveals that the mean (median) STD_ROA, STD_RET and R&D_TA are 0.153 (0.052), 0.041 (0.034) and 0.102 (0.040), respectively. These statistics are largely within the range of prior studies (e.g. Bargeron et al., 2010; Table 1). The mean values of SIZE (5.04), MTB (2.66), ΔSALE (0.22) and AGE (15.82) in Panel A also suggest the presence of growth and mature firms in the sample.
| Panel A: pooled descriptive statistics | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Variable | n | Mean | SD | 0.25 | 0.50 | 0.75 | INTRO | GROWTH | MATURE | SHAKE-OUT | DECLINE |
| STD_ROA | 121 003 | 0.153 | 0.391 | 0.023 | 0.052 | 0.128 | 0.359 | 0.087 | 0.079 | 0.150 | 0.302 |
| STD_RET | 108 153 | 0.041 | 0.027 | 0.022 | 0.034 | 0.051 | 0.058 | 0.035 | 0.033 | 0.047 | 0.062 |
| R&D/TA | 70 104 | 0.102 | 0.180 | 0.006 | 0.040 | 0.120 | 0.190 | 0.060 | 0.046 | 0.094 | 0.242 |
| SIZE | 121 003 | 5.043 | 2.491 | 3.258 | 5.009 | 6.802 | 3.682 | 5.710 | 5.671 | 4.369 | 3.449 |
| MTB | 121 003 | 2.655 | 5.443 | 0.978 | 1.763 | 3.194 | 3.347 | 2.777 | 2.422 | 2.060 | 2.605 |
| LEV | 121 003 | 0.185 | 0.215 | 0.003 | 0.122 | 0.294 | 0.182 | 0.214 | 0.181 | 0.160 | 0.143 |
| CAPEX | 121 003 | 0.064 | 0.090 | 0.014 | 0.035 | 0.077 | 0.056 | 0.086 | 0.060 | 0.051 | 0.042 |
| ΔSALE | 121 003 | 0.218 | 0.831 | −0.041 | 0.078 | 0.240 | 0.480 | 0.286 | 0.094 | 0.080 | 0.193 |
| AGE | 121 003 | 15.82 | 15.26 | 5.20 | 11.01 | 21.13 | 10.225 | 14.990 | 19.733 | 16.338 | 11.451 |
| PM | 121 003 | −0.764 | 4.582 | −0.086 | 0.034 | 0.103 | −2.862 | 0.016 | 0.047 | −0.418 | −3.297 |
| SENT__D | 113 620 | 0.465 | 0.499 | 0.000 | 0.000 | 1.000 | – | – | – | – | – |
| Panel B: correlation analysis | |||||
|---|---|---|---|---|---|
| Variable | INTRO | GROWTH | MATURE | SHAKE-OUT | DECLINE |
| STD_ROA | 0.235 | −0.105 | −0.147 | −0.003 | 0.114 |
| STD_RET | 0.264 | −0.140 | −0.232 | 0.066 | 0.228 |
| R&D/TA | 0.239 | −0.137 | −0.228 | −0.016 | 0.261 |
| SIZE | −0.244 | 0.167 | 0.196 | −0.089 | −0.191 |
| MTB | 0.057 | 0.014 | −0.033 | −0.036 | −0.003 |
| LEV | −0.007 | 0.082 | −0.014 | −0.039 | −0.058 |
| CAPEX | −0.041 | 0.151 | −0.037 | −0.050 | −0.073 |
| ΔSALE | 0.141 | 0.051 | −0.117 | −0.051 | −0.010 |
| AGE | −0.164 | −0.034 | 0.199 | 0.011 | −0.086 |
| PM | −0.204 | 0.106 | 0.137 | 0.025 | −0.165 |
- All variables, except those in italics, are significant at p < 0.001.
The life cycle-wise descriptive statistics reveal that the mean STD_ROA, STD_RET and R&D_TA are higher in the introduction (0.36, 0.06 and 0.19), shake-out (0.15, 0.05 and 0.09) and decline (0.30, 0.06 and 0.24) stages compared to the growth (0.09, 0.04 and 0.06) and mature (0.08, 0.03 and 0.05) stages of the firm life cycle. Consistent with the firm life cycle theory, our statistics also reveal that SIZE, AGE and PM progressively increase as firms move from the introduction to the mature stages and that these estimates then drop as firms move from the mature to the decline stage; the opposite pattern is observed for the MTB and ΔSALE variables.
In Table 2, panel B reveals that firm risk-taking proxies and most of the control variables are correlated significantly with life cycle proxies. As expected, all the three risk-taking proxies are associated positively (p < 0.001) with the introduction and decline stages of the firm life cycle, whilst being associated negatively (p < 0.001) with the growth and mature stages of the firm life cycle. Overall, the correlations among risk-taking proxies, life cycle proxies and the control variables are all in the expected directions and, thus, provide support for our measures and constructs.
4.2 Regression results
In Table 3, panel A presents the regression results for Equation 1 where risk-taking proxies are regressed on firm LCS and a set of control variables known to determine risk-taking decisions. The regression results provide strong evidence that risk-taking is high during the introduction and decline stages of the firm cycle whilst it is low during the growth and mature stages of the life cycle across all risk proxies, supporting H1. For example, the coefficients on STD_RET, a risk-taking proxy, range from −0.005 during the growth and mature stages to 0.007 during the decline stage of the firm life cycle.
| Variables | Predicted sign | Model (1) | Model (2) | Model (3) | With ‘STRATEGY’ included | ||
|---|---|---|---|---|---|---|---|
| Model (4) | Model (5) | Model (6) | |||||
| STD_ROA | STD_RET | R&D/TA | STD_ROA | STD_RET | R&D/TA | ||
| Panel A: firm life cycle and corporate risk-taking | |||||||
| Constant | ? | 0.17*** | 0.07*** | 0.08*** | 0.06*** | 0.06*** | −0.03 |
| [8.14] | [30.64] | [4.86] | [5.60] | [23.00] | [−1.57] | ||
| INTRO | + | 0.12*** | 0.004*** | 0.048*** | 0.04*** | 0.004*** | 0.03*** |
| [17.07] | [11.50] | [13.90] | [9.98] | [9.65] | [9.39] | ||
| GROWTH | +/− | −0.01*** | −0.005*** | −0.009*** | −0.01*** | −0.003*** | −0.006*** |
| [−3.44] | [−16.45] | [−4.54] | [−6.12] | [−9.39] | [−3.89] | ||
| MATURE | – | −0.01*** | −0.005*** | −0.01*** | −0.01*** | −0.003*** | −0.007*** |
| [−3.98] | [−16.98] | [−7.36] | [−7.93] | [−9.89] | [−5.20] | ||
| DECLINE | + | 0.05*** | 0.007*** | 0.09*** | 0.04*** | 0.006*** | 0.05*** |
| [7.65] | [17.89] | [20.62] | [9.44] | [11.67] | [11.72] | ||
| SIZE | – | −0.03*** | −0.006*** | −0.009*** | −0.01*** | −0.005*** | −0.004*** |
| [−25.93] | [−85.07] | [−13.99] | [−24.76] | [−63.73] | [−9.42] | ||
| MTB | + | 0.0006* | 0.000*** | 0.0006*** | 0.002*** | 0.0002*** | 0.001*** |
| [1.66] | [13.30] | [2.74] | [6.46] | [10.67] | [3.81] | ||
| LEV | − | 0.05*** | 0.001*** | 0.004 | −0.00 | 0.005*** | −0.03*** |
| [3.66] | [2.66] | [0.50] | [−0.15] | [6.09] | [−5.85] | ||
| CAPEX | + | 0.008 | 0.011*** | 0.16*** | 0.00* | 0.01*** | 0.16 |
| [0.35] | [8.09] | [7.78] | [1.88] | [5.88] | [10.57] | ||
| ∆SALES | + | 0.05*** | 0.001*** | 0.002** | 0.02*** | −0.00 | −0.008*** |
| [16.26] | [6.33] | [2.40] | [5.50] | [−0.15] | [−4.27] | ||
| AGE | − | −0.002* | –0.002*** | 0.000 | –0.009*** | –0.003*** | –0.006*** |
| [−1.72] | [−15.16] | [0.29] | [−5.23] | [−13.41] | [−4.65] | ||
| PM | + (?) | −0.02*** | −0.000*** | −0.007*** | −0.01*** | −0.0005*** | −0.007*** |
| [−15.16] | [−12.07] | [−18.48] | [−5.15] | [−7.36] | [−7.12] | ||
| STRATEGY | + | 0.004*** | 0.0005*** | 0.006*** | |||
| [15.72] | [16.49] | [25.60] | |||||
| Year | Yes | Yes | Yes | Yes | Yes | Yes | |
| Industry | Yes | Yes | Yes | Yes | Yes | Yes | |
| Observations | 121 003 | 108 153 | 70 104 | 68 038 | 67 609 | 41 912 | |
| Adj. R2 | 0.19 | 0.50 | 0.33 | 0.15 | 0.48 | 0.34 | |
| Panel B: firm life cycle, executive compensation and risk-taking | |||||||
| INTRO | + | 0.03*** | 0.006*** | 0.03*** | 0.03*** | 0.004*** | 0.02*** |
| [5.21] | [12.45] | [6.02] | [3.61] | [3.34] | [4.45] | ||
| GROWTH | +/− | −0.02*** | −0.002*** | −0.011*** | −0.02*** | −0.003*** | −0.009*** |
| [−6.75] | [−5.96] | [−5.79] | [−5.48] | [−3.99] | [−3.39] | ||
| MATURE | − | −0.019*** | −0.003*** | −0.017*** | −0.02*** | −0.003*** | −0.014*** |
| [−7.79] | [−12.74] | [−9.26] | [−6.71] | [−5.21] | [−6.01] | ||
| DECLINE | + | 0.08*** | 0.009*** | 0.07*** | 0.09*** | 0.009*** | 0.07*** |
| [7.78] | [13.57] | [10.43] | [6.45] | [5.28] | [7.73] | ||
| COMP | + | 0.0008*** | 0.003*** | 0.001** | −0.00 | 0.0001* | 0.002*** |
| [3.60] | [4.86] | [5.56] | [−0.43] | [1.89] | [3.23] | ||
| COMP*INTRO | + | – | – | – | 0.002** | 0.004** | 0.002** |
| [2.16] | [2.59] | [2.60] | |||||
| COMP*GROWTH | + | – | – | – | 0.019** | 0.0002** | 0.024 |
| [2.12] | [2.04] | [1.09] | |||||
| COMP*MATURE | ? | – | – | – | 0.001** | 0.00 002 | −0.00 |
| [2.42] | [0.21] | [−0.55] | |||||
| COMP*DECLINE | ? | – | – | – | 0.04 | 0.00 001 | 0.001 |
| [0.96] | [0.04] | [1.32] | |||||
| Other controls | Yes | Yes | Yes | Yes | Yes | Yes | |
| Year | Yes | Yes | Yes | Yes | Yes | Yes | |
| Industry | Yes | Yes | Yes | Yes | Yes | Yes | |
| Observations | 32 425 | 32 091 | 19 122 | 32 425 | 32 091 | 19 122 | |
| Adj. R2 | 0.14 | 0.53 | 0.39 | 0.14 | 0.54 | 0.39 | |
- In the regression models in Panel A, the indicator for the shake-out stage is omitted, and thus, the intercept term captures the effect of the shake-out stage. Other life cycle stage coefficients are compared relative to the shake-out stage. In panel B, compensation (COMP) is measured as the natural logarithm of Black–Scholes option value ($) retrieved from EXECUCOMP for the period 1992 to 2013. Robust t-statistics in brackets: ***p < 0.01, **p < 0.05, *p < 0.10.
As hypothesised in Section 2, a firm is more likely to undertake relatively larger, growth-oriented investments in the initial stage, whilst, in the mature stage, its investments are more likely to be geared towards maintenance of assets in place. Once a firm moves into the decline phase, managers are likely to assume more risk in an attempt to return to profitability, as declining sales during this phase generate negative returns. The negative coefficient during the growth phase may be explained by an observation of Miller and Friesen (1984), who suggest that complex product strategies during the growth phase require more managerial involvement in decision-making and, hence, there is less risk-taking.
We also include a proxy for firm strategy (STRATEGY) to incorporate the notion that variation in firms' strategies (for example, prospector versus defender-type business strategies) (Miles and Snow, 1978, Miles and Snow 2003) during different life cycle phases might differentially affect risk-taking behaviour. Our composite strategy score is derived from Bentley et al. (2013). Bentley et al. (2013) constructed their index using a wide variety of firm characteristics intended to capture the differences in the magnitude and direction of change regarding its products and markets (Hambrick, 1983). We find the coefficient on STRATEGY to be positive and statistically significant across all three risk proxies. Importantly, the coefficients on the LCS remain qualitatively unchanged. We also run the baseline regression model including CEO age (a proxy for CEO career concern) as a determinant of corporate risk-taking. Serfling (2014) documents that risk-taking by CEOs decreases with an increase in their age primarily because of less risky investment policies. We also find similar evidence as the coefficient on natural log of CEO age is −0.005 with a t-statistic of −9.23. Importantly, however, the sign and significance on the coefficient of LCS remains consistent with the baseline result. Control variables are generally consistent in terms of their significance and predicted direction. For example, large firms assume less risk, but firms with high growth opportunities take on more risk. The adjusted R2 of the risk proxies varies from a high of 0.50 for the STD_RET proxy to a low of 0.19 for the R&D/TA proxy.
Table 3, panel B examines whether variation in managerial incentives as proxied by incentive-based compensation during different LCS, differentially affects risk-taking. Agency theory proposes that a properly designed executive compensation scheme can motivate managers to mitigate investment distortions (Jensen and Meckling, 1976). However, a similar arrangement could encourage managers to engage in more risk-taking to maximise personal benefits. Although prior research has examined the association between compensation and risk-taking, these studies did not investigate the role of organisational evolution in the compensation–risk-taking relationship. The organisation will use different compensation systems at each LCS to motivate and reward its CEO to make effective decisions. This is very important as resolving these challenges and problems successfully allows the organisation to transition from one stage to another (Scott and Bruce, 1987; Phelps et al., 2007). Despite this theoretical underpinning, empirical evidence on the association between the mix and structure of executive compensation during different LCS is almost nonexistent (Kanagaretnam et al., 2009; is an exception). On the other hand, a growing literature confirms that incentive-based compensation encourages managers to take more risks (e.g. Coles et al., 2006; Armstrong and Vashishtha, 2012; Shen and Zhang, 2013). However, these two strands of literature remain disconnected.
We measure compensation using the natural log of incentive-based compensation retrieved from Execucomp. The sample period spans from 1992 to 2013. Models (1) to (3) show that the coefficient on compensation (COMP) is reliably positive and significant, implying that more incentive-based compensation encourages managers to assume more risk. Our main interest is the sign and significance of the interactive variables (COMP*LCS). Models (4) to (6) present the results. We find that the coefficient on the interactive variable COMP*INTRO is positive and significant across all three risk specifications. Because start-up firms are characterised as having a low level of product diversification and of production innovation, they may offer CEOs a large amount of stock-based pay to align the interests of shareholders in terms of motivating CEOs to expand product diversification and innovation (Wang and Sing, 2014). We also expect firms in the growth phase to award executives with long-term incentive pay to mitigate potential agency conflicts associated with the increased difficulties in monitoring CEO's investment behaviour (Mehran and Tracy, 2001). Our reported results show that the coefficient on COMP*GROWTH is positive and significant for two of the three risk proxies (STD_ROA and STD_RET). Firms in the maturity phase of their life cycle strive to avoid risk to maintain the stability of their business operations (Lester et al., 2008), which does not require them to award stock-based pay to CEOs for making risky decisions. The insignificant coefficient on COMP*MATURE supports this proposition. We do not develop a directional hypothesis for COMP*DECLINE, as there is a lack of theory as to the structure of incentive-based compensation for firms in the decline stage, although Kanagaretnam et al. (2009) find that growing firms grant more stock options to their CEOs than do stagnant firms. Taken together, our analysis of the effect of variation in executive compensation across firm LCS affect managerial risk-taking propensities differently.
We now discuss the results of Equation 2, which examines the effect of risk-taking during different LCS on future operating performance. We regress 1-year-ahead ROA on current-period risk proxies and the interaction between risk proxies and LCS. Results reported in Table 4 show that corporate risk-taking is negatively related to future performance across all three risk specifications. We are primarily interested in the interaction between LCS and risk-taking to discern the performance implications. We reveal that future performance worsens for risk-taking during the early phase (introduction) and decline phase of the firm LCS compared to the shake-out stage (coefficients on RISK*INTRO and RISK*DECLINE are −0.18 and −0.12, both significant at p < 0.05 for the STD_ROA risk proxy). This is consistent with the argument that low product differentiation and shortage of financial resources yield negative profit in the early stage, whilst in the decline stage, negative profit is explained by managerial incentives to invest in negative NPV projects.
| Variables | Predicted sign | Model (1) | Model (2) | Model (3) |
|---|---|---|---|---|
| STD_ROA | STD_RET | R&D_TA | ||
| ROA t+1 | ROA t+1 | ROA t+1 | ||
| Constant | 0.05*** | −0.06*** | −0.06* | |
| [3.15] | [−2.90] | [−1.68] | ||
| INTRO | − | −0.17*** | −0.15*** | −0.14*** |
| [−21.63] | [−20.44] | [−14.15] | ||
| GROWTH | + | 0.02*** | 0.03*** | 0.04*** |
| [4.57] | [8.02] | [6.13] | ||
| MATURE | + | 0.04*** | 0.05*** | 0.04*** |
| [8.37] | [11.36] | [6.09] | ||
| DECLINE | − | −0.17*** | −0.19*** | −0.16*** |
| [−17.09] | [−17.28] | [−12.49] | ||
| RISK | − | −0.25*** | −0.21*** | −0.64*** |
| [−6.88] | [−4.64] | [−9.17] | ||
| RISK*INTRO | − | −0.18*** | −0.06* | −0.33*** |
| [−4.39] | [−1.69] | [−3.98] | ||
| RISK*GROWTH | + | 0.12*** | 0.13*** | 0.31*** |
| [2.88] | [3.64] | [3.79] | ||
| RISK*MATURE | + | 0.13*** | 0.16*** | 0.48*** |
| [2.74] | [4.22] | [6.25] | ||
| RISK*DECLINE | − | −0.12** | −0.06*** | −0.09** |
| [−2.56] | [−3.55] | [−2.08] | ||
| SIZE | + | 0.03*** | 0.02*** | 0.03*** |
| [43.80] | [32.10] | [26.03] | ||
| MTB | +/− | 0.001*** | −0.00* | −0.00 |
| [2.80] | [−1.74] | [−0.21] | ||
| LEV | − | −0.12*** | −0.07*** | −0.11*** |
| [−11.38] | [−6.77] | [−7.58] | ||
| CAPEX | − | −0.08*** | −0.20*** | −0.24*** |
| [−3.88] | [−8.44] | [−6.46] | ||
| ∆SALES | ? | −0.009*** | −0.016*** | −0.03*** |
| [−2.85] | [−5.34] | [−9.15] | ||
| AGE | + | 0.007*** | 0.01*** | 0.01*** |
| [7.61] | [6.79] | [5.39] | ||
| PM | + | 0.02*** | 0.02*** | 0.02*** |
| [26.30] | [19.50] | [17.26] | ||
| Year | Yes | Yes | Yes | |
| Industry | Yes | Yes | Yes | |
| Observations | 104 501 | 95 391 | 60 956 | |
| Adjusted R2 | 0.34 | 0.30 | 0.36 | |
- In the regression models, the indicator for the shake-out stage is omitted and, thus, the intercept term captures the effect of the shake-out stage. Other life cycle stage coefficients are compared relative to the shake-out stage. Robust t-statistics in brackets: ***p < 0.01, **p < 0.05, *p < 0.10.
We find that the coefficient for the interaction RISK*GROWTH is positive and significant across all three specifications, as is the coefficient on RISK*MATURE (the respective coefficients are 0.12 and 0.18 significant at p < 0.01 for the STD_ROA risk proxy). This is consistent with economic theory, which postulates that profit margins are maximised by increases in investment and efficiency (Spence, 1977, 1979, 1981; Wernerfelt, 1985). As product differentiation generates higher profit margins, and growth firms expand by establishing brand identity and market share, growth firms generate a positive return (Dickinson, 2011).
Among the control variables, firm profitability is higher for larger firms (which are also older) because of scale economies or the ability to access capital at lower costs than smaller firms. Financial risk proxied by leverage is negatively related to future profitability because of the potential distress costs. Growth opportunities should affect firm performance positively, although the reported evidence is not consistent across the risk specifications. Capital expenditure (CAPEX) increases the denominator of ROA; hence, a negative relationship with future ROA is reported.
We now discuss the results for H3, which attempts to examine the moderating effect, if any, on the relationship between corporate risk-taking and life cycle. We investigate the interactive association between firm LCS and investor sentiment on managerial propensity to take risks. We measure investor sentiment using the Baker and Wurgler (2006) investor sentiment index. Results reported in Table 5 show that the coefficient on investor sentiment (SENT) is positive and statistically significant for the STD_ROA and STD_RET risk proxies. As SENT is measured as a dummy variable coded 1 for a high investor sentiment period and zero otherwise, the reported coefficient on SENT for the STD_ROA risk proxy implies a 3 percent increase in the STD_ROA in periods of high, compared to low, investor sentiment. The increase in the STD_RET, however, is much less pronounced. With respect to the interactions, Table 5 reveals that the coefficients for SENT*INTRO and SENT*DECLINE are positive and significant across all three risk specifications, supporting H3. We also find that the coefficient SENT*GROWTH is positive and significant, but only for the STD_RET-based risk proxy (coefficient 0.001, t-statistic 2.63, significant p < 0.05). The coefficient on the interactive variable SENT*MATURE is insignificant across all risk specifications, consistent with the proposition that mature companies do not have future growth opportunities and, hence, find little benefit in raising capital from the market. Overall, we provide evidence that managerial risk-taking during different LCS does vary with changes in economy-wide investor sentiment. It is interesting to note that, although risk-taking during high sentiment period goes up, there does not appear to be any evidence of less risk-taking during periods of low investor sentiment.
| Variables | Predicted sign | Model (1) | Model (2) | Model (3) |
|---|---|---|---|---|
| STD_ROA | STD_RET | R&D_TA | ||
| Intercept | ? | 0.27*** | 0.07*** | 0.12*** |
| [16.44] | [58.12] | [15.18] | ||
| INTRO | + | 0.05*** | 0.003*** | 0.02*** |
| [8.27] | [7.27] | [11.02] | ||
| GROWTH | +/− | −0.04*** | −0.006*** | −0.002** |
| [−12.15] | [−19.92] | [−2.09] | ||
| MATURE | − | −0.03*** | −0.006*** | −0.01*** |
| [−11.24] | [−18.60] | [−8.03] | ||
| DECLINE | + | 0.06*** | 0.0084*** | 0.06*** |
| [8.19] | [18.51] | [17.22] | ||
| SENT | + | 0.03*** | 0.006*** | 0.001 |
| [2.92] | [13.61] | [0.48] | ||
| SENT*INTRO | + | 0.02*** | 0.006*** | 0.012*** |
| [3.14] | [10.93] | [4.45] | ||
| SENT*GROWTH | + | 0.004 | 0.001*** | −0.003* |
| [0.82] | [2.63] | [−1.70] | ||
| SENT*MATURE | ? | 0.005 | −0.003 | −0.003 |
| [1.27] | [−0.59] | [−1.58] | ||
| SENT*DECLINE | + | 0.02** | 0.003*** | 0.018*** |
| [2.25] | [4.00] | [4.19] | ||
| Other controls | Yes | Yes | Yes | |
| Year | Yes | Yes | Yes | |
| Industry | Yes | Yes | Yes | |
| Observations | 108 378 | 98 795 | 69 807 | |
| Adjusted R2 | 0.38 | 0.42 | 0.25 | |
- Investor sentiment, SENT, is an indicator variable coded 1 for high sentiment period (SENT index greater than zero) and zero otherwise. This procedure yields 1987–88, 1996–97, 1999–01, 2004 and 2006–07 as high sentiment periods. In the regression models, the indicator for the shake-out stage is omitted, and thus, the intercept term captures the effect of the shake-out stage. Other life cycle stage coefficients are compared relative to the shake-out stage. Robust t-statistics in brackets: ***p < 0.01, **p < 0.05, *p < 0.10.
4.3 Two-stage least squares regression
Even though regression estimates suggest significant negative (positive) association between growth and maturity (introduction and decline) stages and corporate risk-taking, the sign, magnitude or statistical significance of these estimates may be biased due to endogeneity. To address this concern, we adopt a two-stage instrumental variable approach to re-examine the regression findings reported in Table 3. Hence, we use industry LCS and firm-level variables as instruments for firm life cycle proxies (i.e. dividend payment – a dummy variable that takes a value of 1 if the firm pays dividend in a given year, 0 otherwise, and organisation capital – measured following Eisfeldt and Papanikolaou, 2013). Use of industry LCS as instruments can be justified on the premise that industry level life cycle has a profound effect on the firm-level LCS (Lumpkin and Dess, 2001).
DeAngelo et al. (2006) demonstrate that corporate life cycle has a significant influence on the probability of dividend payment. They document that mature and profitable firms are more likely to pay dividends, whilst young firms with higher growth options are less likely to do so. In a recent study, Hasan and Cheung (2014) show that introduction and decline stages are likely to be associated with higher organisational capital. However, firms with a lower level of organisational capital are more likely to be in the growth and mature stages. These studies, thus, provide justification for the use of dividend and organisational capital as instruments.
Table 6, panel A reports that coefficients on the instrumental variables are significant at the conventional level, suggesting that industry life cycle and included firm-level variable have a significant effect on firm LCS. Results in Table 6, panel B, suggest that the relationship between life cycle proxies and corporate risk-taking remains robust after accounting for the endogenous relationship between the life cycle proxies and the risk-taking. The estimated coefficients (and p-values) of introduction (0.069, p < 0.05), growth (−0.083, p < 0.01), mature (−0.036, p < 0.10), decline (0.488, p < 0.01) in the two-stage least squares (2SLS) regression suggest that endogeneity cannot explain away the expected relationship between the life cycle and the corporate risk-taking.
| Explanatory variable | Introduction | Growth | Maturity | Decline |
|---|---|---|---|---|
| Panel A: first-stage regressions of life cycle proxies and validity of instruments | ||||
| Instruments | ||||
| ILC – introduction |
0.654*** (17.80) |
−0.040 (−0.79) |
0.234*** (4.23) |
0.068** (2.53) |
| ILC – growth |
−0.034 (−1.01) |
0.854*** (17.59) |
0.073 (1.36) |
0.032 (1.31) |
| ILC – maturity |
−0.049 (−1.45) |
−0.004 (−0.10) |
1.052*** (19.37) |
−0.016 (−0.64) |
| ILC – decline |
−0.059 (−1.14) |
0.103 (1.47) |
0.121 (1.57) |
0.694*** (16.81) |
| Dividend |
−0.046*** (−20.18) |
−0.113** (−29.60) |
0.190*** (44.70) |
−0.0229*** (13.98) |
| Organisation capital |
−0.000 (−0.32) |
−0.000*** (−3.09) |
−0.000 (0.21) |
0.000 (1.27) |
| Unreported control variables included in regression | ||||
| All variables in main test | Yes | Yes | Yes | Yes |
| Year FE | Yes | Yes | Yes | Yes |
| Industry FE | Yes | Yes | Yes | Yes |
| Observations | 87 703 | 87 703 | 87 703 | 87 703 |
| Adjusted R2 | 0.133 | 0.111 | 0.145 | 0.060 |
| Underidentification test | ||||
| Kleibergen–Paap rk LM statistic | 360.06 | |||
| p-Value | 0.000 | |||
| Weak identification test | ||||
| Corrected Cragg–Donald Wald F-statistic | 185.05 | |||
| Stock and Yogo (2005) 10% maximal IV size (critical value) | 29.18 | |||
| Test of overidentifying restrictions | ||||
| Hansen's J-statistic | 3.69 | |||
| p-Value | 0.16 | |||
| Panel B: second-stage regressions of corporate risk-taking on life cycle proxy | ||||
| Explanatory variable | ||||
| Potentially endogenous instrumented variable | ||||
| Life cycle proxy | 0.068** | −0.083*** | −0.036* | 0.488*** |
| (2.24) | (−3.46) | (−1.65) | (9.36) | |
| All variables in main test | Yes | Yes | Yes | Yes |
| Year dummies | Yes | Yes | Yes | Yes |
| Industry dummies | Yes | Yes | Yes | Yes |
| Hausman test for the effect of life cycle (coefficient 2SLS = coefficient OLS) | ||||
| Cluster-robust F-statistic | 519.62 | |||
| p-value | 0.000 | |||
- Results for two-stage analysis as described in Section 4.4. ILC stands for industry life cycle. Robust t-statistics in brackets: ***p < 0.01, **p < 0.05, *p < 0.10.
In support of the instruments, we also conduct underidentification, weak identification, Hansen's overidentifying restrictions and Hausman's endogeneity tests. In Table 6, underidentification test results (LM statistic) reveal that the excluded instruments are ‘relevant’. The weak instrument test results show that the excluded instruments are correlated with the endogenous regressors because the (corrected) Cragg–Donald Wald F-statistic (185.05) is greater than Stock and Yogo (2005) critical value (i.e. 29.18) at 10 percent. It is worth noting that Stock and Yogo (2005) provide critical values only for a range of possible circumstances up to three endogenous regressors. However, there are four endogenous regressors (proxies for four LCS) in Dickinson (2011) life cycle measures, and thus, Stock and Yogo (2005) cannot provide critical value in this circumstance. To address this problem, we follow the approach proposed by Angrist and Pischke (2008) and recently modified by Sanderson and Windmeijer (2013) and estimate a corrected version of the first-stage F-statistic that is suitable for our setting of more than three endogenous variables. Our corrected Cragg–Donald Wald F-statistic shows that a weak instrument is not a concern with our estimates. Results from Hansen's overidentifying restrictions test do not reject the null hypothesis (p > 0.10), suggesting that instruments are uncorrelated with the error term and are correctly excluded from the second-stage regression, which reflects the validity of the instruments used for the 2SLS regression. Finally, Hausman (1978) test significantly rejects (p < 0.001) the exogeneity of the firm life cycle proxies, justifying the use of the 2SLS regression estimates. Using industry life cycle variables and firm-level variables (organisational capital and a loss dummy variable that takes a value of 1 if there is operating loss in a given year), we also perform 2SLS for STD_RET and R&D/TA and inference remains the same.
4.4 Robustness tests
4.4.1 Alternative life cycle proxy and corporate risk-taking
As a robustness check, we test the association between firm life cycle and corporate risk-taking using the alternative life cycle measure of DeAngelo et al. (2006). They argue that firms with a high retained earnings to total assets ratio (RE/TA) are typically more mature, or old with declining investment, whilst firms with a low RE/TA tend to be young and growing. Therefore, they argue that RE/TA is an appropriate firm life cycle proxy.6 The coefficients on RE/TA are −0.013, −0.001 and −0.033 (all at p < 0.001) for the risk-taking proxies of R&D/TA, STD_RET and STD_ROA, respectively. Thus, regression results imply that, compared to young and growing firms, corporate risk-taking is negative and significant for mature stage firms.
4.4.2 Alternative sentiment index
We use the Michigan Consumer Sentiment Index (MCSI) developed by the University of Michigan and obtained from the Federal Reserve Economic Data as an alternative sentiment index. Every month the MCRC administers opinion surveys of households around the country. The survey uses a Likert scale to gauge perceptions on personal financial welfare, on countrywide financial welfare, and on consumer spending. Responses to the monthly survey questions are combined to form an overall measure of sentiment, the MCSI. The higher the value is the more confidence consumers have about the overall economy. Our untabulated results are generally consistent with the findings using the Baker and Wurgler (2006) sentiment index. The coefficient on SENT is 0.000 045 with a t-statistic of 5.65. The interactive coefficients of SENT with four life cycle proxies yield results similar to the Baker and Wurgler (2006) measure. Coefficients on INTRO*SENT and GROWTH*SENT are positive and significant at better than the 5 percent level. Coefficients on MATURE*SENT (DECLINE*SENT) are negative (positive) and are significant at better than the 1 percent level.
4.4.3 Macroeconomic determinants of corporate risk-taking
One plausible explanation for the relationship between firm life cycle and corporate risk-taking could be that risk-taking responds to macroeconomic factors, and omission of these variables could give rise to correlated omitted-variable problem. Furthermore, extant studies show that macroeconomic variables influence innovation, survival and stock return volatility of the firm (Errunza and Hogan, 1998; Everett and Watson, 1998). To rule out the possibility that macroeconomic factors could drive the result, we included three macroeconomic variables, namely inflation, industrial production growth and growth in real GDP in regression Equations 1 and 2. Untabulated regression coefficients show that inflation and industrial production growth are significantly positively associated with risk-taking, whilst real GDP growth is significantly negatively associated. However, the coefficient and statistical significance on LCS measures remain virtually unchanged.
4.4.4 Accruals quality and corporate risk-taking
In another robustness test, we included accruals quality as a misvaluation proxy that might affect risk-taking and, hence, provide a plausible alternative explanation (Polk and Sapienza, 2009). We regressed different proxies for risk-taking on accruals quality (modified Jones model of Dechow et al., 1995), LCS and other control variables. The coefficient on accruals quality is negative and significant at the 1 percent level. Importantly, the coefficients and statistical significance of all the life cycle variables remain qualitatively unchanged.
5 Conclusions
This study examines firm LCS as potential determinants of corporate risk-taking and investigates the possibility that prevalent investor sentiment might moderate any association between the two. Managerial risk-taking has important implications for firm growth, performance and survival (Bromiley, 1991), yet has the potential to cause serious agency problems by accepting value-destroying negative NPV projects and/or foregoing positive NPV projects. Managers have incentives to remain conservative in their investments because of the concentration of their human capital in one particular organisation. Prior research on the determinants of corporate risk-taking has primarily focused on the executive compensation structure. Although this stream of research is insightful in understanding whether properly designed executive compensation attenuates investment distortions by managers, it does not consider the dynamic nature of the organisational life cycle and its impact on corporate risk-taking. We fill this void in the literature.
We use the Dickinson (2011) parsimonious life cycle measure as our primary independent variable. We use three different measures of risk and find that managerial risk-taking is higher during the introduction and decline stages of the firm life cycle compared to the shake-out stage benchmark. Risk-taking is lower during the growth and maturity phases of the firm life cycle. With regard to the effect of risk-taking on future performance, we find that future performance worsens for risk-taking during the early phase (introduction) and decline phase of the firm LCS but improves for risk-taking during growth and mature stages. We also examine whether the association between risk-taking and firm LCS is moderated by investor sentiment. We argue that in a period of high investor sentiment, market mispricing could encourage managers to take on excessive risks in order to cater to high investor expectation. We find that early-stage firms as well as firms in the decline stage assume more risk during periods of high investor sentiment.
Notes
Appendix A
Variable definitions and measurement
| Variables | Definition and measurement |
|---|---|
| Dependent variable | |
| STD_ROA | Standard deviation of return on assets, measured as the standard deviation of the income before tax and extraordinary items (PI – XI) scaled by total assets (AT), over the prior 3 years |
| STD_RET | Annual standard deviation of monthly stock returns, computed from return data (RET) from the CRSP |
| R&D/TA | Research and Development expense (XRD) scaled by total asset (AT) |
| Firm life cycle proxies | |
| CLC | A vector of dummy variables that capture firms' different stages in the life cycle |
| RE/TA | Retained earnings (RE) as a proportion of total assets |
| Investor sentiment | |
| SENT | An indicator variable coded 1 for high sentiment period and zero otherwise. High sentiment periods are 1987–88, 1996–97, 1999–01, 2004 and 2006–07. Investor sentiment is based on the common variation in six underlying proxies for sentiment: the closed-end fund discount, NYSE share turnover, the number and average of first-day returns on IPOs, the equity share in new issues and the dividend premium (Baker and Wurgler, 2006). As each sentiment proxy is likely to include a sentiment component as well as idiosyncratic components, the authors use principal components analysis to isolate the common component. |
| Control variables | |
| SIZE | Natural logarithm of market value of equity (PRCC_F*CSHO) |
| MTB | Market-to-book ratio, measured as market value of equity (PRCC_F*CSHO) scaled by book-value of equity (CEQ) |
| LEV | Leverage, measured as total long-term debt (DLTT) scaled by total asset (AT) |
| CAPEX | Capital expenditure (CAPX) scaled by market value of asset (PRCC_F*CSHO + DLTT) |
| ΔSALE | Changes in sales (SALE) scaled by lagged sales (SALE) |
| AGE | Age is measured as the number of years since the firm was first covered by the Center for Research in Securities Prices (CRSP) (DATADATE – BEGDAT). For regression analysis, we measure AGE as natural log of (1+ age of the firm) |
| PM | Profit margin, measured as income before tax and extraordinary items (PI – XI) scaled by sales (SALE) |
| Year | Dummy variables to control for fiscal year |
| IND | Dummy variables to control for industry effect |