How to Design Auditor Liability When Judges Suffer from Hindsight Bias
The authors gratefully acknowledge the helpful comments provided by the editor, two anonymous reviewers, and seminar participants at the Universities of Hamburg, Magdeburg and Free University of Amsterdam.
Abstract
There is evidence that judges evaluate auditor effort with hindsight bias, overestimating the likelihood that the auditor has not met the standard of due care. In an analytical analysis, this paper shows that auditors will rationally anticipate judges’ hindsight bias and will thus likely exert excessive effort in the first place. Furthermore, the paper shows that, counterintuitively, (a) capping liability and (b) lowering the standard of due care to gross negligence are generally not helpful remedies to efficiently counteract hindsight bias. Indeed, a debiasing strategy intended to mitigate judges’ hindsight bias, such as by providing appropriate training, may actually cause excessive auditor effort. However, if the legislator tightens the standard of due care sufficiently, this will provide efficient incentives. At the same time, tightening the standard of due care is not a suitable remedy for a different form of hindsight bias, which induces a judge to find the auditor's behaviour reckless and to award punitive damages. Consequently, the proper design of remedies to mitigate the effects of judges’ hindsight bias depends on whether or not punitive damages are allowed.
On 25 June 2020, Wirecard—a major publicly listed fintech company based in Germany—had to file for bankruptcy after allegations of accounting fraud amounting to €3.2 billion (Jones and O'Donnell, 2020). There had been early warnings of misconduct. In April 2015, Financial Times reporters raised questions about inconsistencies in Wirecard's financial statements (McCrum, 2015). In February 2017, manager magazin released an article on a large, but non-transparent accounts receivables position in Wirecard's financial statements (Dohms, 2017). Βetween February and October 2019, the Financial Times published several articles containing allegations of non-existent clients as well as fraudulently inflated sales and net profits (McCrum and Palma, 2019; McCrum, 2019). But it was not until 5 June 2020 that Germany's Federal Financial Supervisory Authority accused Wirecard of market manipulation (Bartz, 2020). On 18 June 2020, Wirecard admitted that its auditor Ernst & Young had refused to sign off on the 2019 accounts—for the first time in 10 years. The European Securities and Markets Authority (ESMA) launched a Fast Track Peer Review of the role played by Germany's Federal Financial Supervisory Authority and Germany's Financial Reporting Enforcement Panel (FREP) in July 2020, questioning why the enforcement bodies had failed to respond more rapidly to the early warnings, and identifying a number of deficiencies (ESMA, 2020). FREP responded, stating that ESMA's findings had been ‘distorted by hindsight bias’ (Jones and O'Donnell, 2020).
Hindsight bias refers to the tendency to overestimate one's prior knowledge of an outcome or an event after learning the actual fact (Hawkins and Hastie, 1990). Decision-makers may assume in hindsight that a particular outcome was potentially foreseeable. Hindsight bias is a well-documented decision trap that has been investigated in several disciplines, including managerial choice (e.g., Bukszar and Connolly, 1988), accounting and auditing decisions (e.g., Anderson et al., 1993, Peecher and Piercey, 2008), and public policy (e.g., Schuett and Wagner, 2011).
Hindsight bias within the legal system has profound implications, especially regarding negligence and liability. Judges and jurors must ensure that defendants are treated fairly by judging based on the information available to the defendant before the damage event, despite being aware of the (negative) outcome (Harley, 2007). Prior studies investigating negligence found that participants with outcome knowledge evaluated a (negative) outcome as more foreseeable and the defendant as more negligent compared to participants with no outcome knowledge (e.g., Hastie and Viscusi, 1998; Kamin and Rachlinski, 1995; Strohmaier et al., 2021). The size of hindsight bias increases with the severity of adverse outcomes (e.g., Bornstein, 1998; Greene et al., 1999). There is evidence that judges are less prone to hindsight bias than, for instance, lay jurors; however, they are also not immune to this bias (Wittlin, 2014)1 as several studies have shown (e.g., Guthrie et al., 2000). If judges are subject to hindsight bias, they may overestimate the probability that the auditor had not exerted due care in light of a severe accounting scandal (Anderson et al., 1997, Kadous, 2000).
If judges are affected by hindsight bias, auditors will rationally adjust their behaviour in the first place; that is, they are likely to exert more and potentially excessive effort to prevent a scenario with incorrect financial statements. However, excessive auditor effort increases audit fees, and is not desirable from either an investor or a welfare perspective.
Our model analysis shows that only with a sufficiently mild hindsight bias auditors will exert excessive effort. If the judge's hindsight bias is sufficiently strong, however, auditors will perceive the costs to meet the level of due care desired by the judge to be too high, and will instead choose a lower but efficient level that minimizes the sum of effort costs and expected damage payments, similar to a strict liability setting. Hence, we establish a non-monotonic association between the size of the judge's hindsight bias and the auditor's effort level. This finding implies that remedies that have usually been suggested to mitigate excessive care do not necessarily work when judges’ hindsight bias is present.
What can a legislator do if she becomes aware of judges’ hindsight bias? The legislator can reduce auditors’ liability exposure. There are two ways to do that: she may either (a) cap auditor liability to a maximum amount of damage compensation or (b) lower the standard of due care (gross negligence).
We analyse the effects of liability caps and gross negligence in a simple auditor liability model following Schwartz (1997) and Shavell (2007). In the basic model, we assume a precise (rules-based) negligence rule (Ye, 2023), but relax this assumption later (see Appendix 4). We assume that a judge who suffers from hindsight bias will overestimate the ex-ante probability of damage after the occurrence of damage. Since this probability of damage depends on the auditor's effort level, the overestimation of the ex-ante damage probability implies an underestimation of the auditor's (documented) effort. We therefore model the judge's hindsight bias as an underestimation of the documented effort level x by the factor Thus, even when the auditor provides documents claiming to have exerted x, the judge will assess an effort level of with Consequently, the judge will ex-post overestimate the probability of auditor negligence.
Introducing a liability cap does not help to counteract the judge's hindsight bias; if the cap is too high, the auditor will still exert excessive effort; if the cap is too low, there will be suboptimal effort. With a liability cap, the auditor will not exert efficient effort. Reducing the liability standard to gross negligence will provide efficient incentives, if it exactly offsets hindsight bias. If the charge of gross negligence is too lenient, the auditor will simply exert due care in the eyes of the judge, which is suboptimal. If gross negligence is too strict, due care will induce excessive auditor effort.
Alternatively, debiasing strategies might mitigate the judge's hindsight bias, such as by the provision of training to increase awareness, or by a applying a ‘consider-the-opposite’ strategy. Counterintuitively, a debiasing strategy may indeed mitigate judges’ hindsight bias, but may also rather cause excessive auditor effort. This paper shows that the auditor will only exert excessive care when the judge's hindsight bias is sufficiently mild, but will exert efficient care when the bias is sufficiently pronounced.
Surprisingly, only sufficiently tight standards of due care will provide efficient incentives. The intuition behind this result is that with a tight standard of due care and hindsight bias on top, it is too costly for the auditor to meet the judge's requirement of due care. Instead, the auditor will choose a lower but efficient effort level; this level implies negligence, but efficiently balances the marginal costs of effort and its marginal expected benefits, namely the reduction in expected liability payments. Since the audit fee equals the sum of effort costs and expected liability payments in a competitive audit market, investors likewise prefer the efficient level.
In Appendix 4, we show that qualitative results still hold when we assume that the standard of due care is not precisely defined, for example, when accounting and auditing standards leave discretion. Again, the judge's hindsight bias tends to aggravate the problem of excessive auditor effort, and tightening the standard of due care sufficiently is the legislator's best response to counteract judges’ hindsight bias.
The literature mentions a second form of hindsight bias that is relevant for auditor liability. Awareness of an accounting scandal may affect the judge's perception of not only the auditor's negligent behaviour but their intentions (Harley, 2007). Thus, judges subject to hindsight bias might be more likely to assume that the auditor's behaviour is consciously dangerous or reckless. As a consequence, judges might be more willing to award punitive damages (Harley, 2007) if the legal system allows. Obviously, and similar to the other form of hindsight bias (overestimating the extent of negligent behaviour), the possibility of assessing reckless behaviour and punitive damages tends to induce excessive auditor effort in the first place. However, unlike in the case of the overestimation of negligence, punitive damages alone still induce efficient incentives if the standard of due care is precisely and efficiently defined. This is because the auditor avoids damage compensation when they exert due care. With this type of hindsight bias, debiasing strategies have no adverse effects.
If the judge suffers from both forms of hindsight bias (overestimating the extent of negligent behaviour and assessing reckless behaviour and punitive damages), the auditor will exert excessive care with or without tightening the standard of due care. Even though excessive care results in higher audit quality, shareholders would deem this level of audit quality too expensive. Overall, given that the judge overestimates the incidence of reckless behaviour, tightening the standard of due care will not contribute to providing efficient incentives.
In sum, when judges are subject to hindsight bias, our analysis suggests that the legislator should think about tightening the standard of due care in legal systems where punitive damages are not allowed, such as in continental Europe. However, provision of appropriate training to judges might not be desirable. Where punitive damages are permitted, such as in the US legal system, tighter standards are not desirable.
This paper contributes to the auditor liability literature by studying a widespread phenomenon of—supposedly—bounded rationality, namely hindsight bias. The auditor liability literature generally assumes rationality in terms of expected utility theory and focuses on other issues such as the effect of different negligence and damage apportionment rules on auditor effort (e.g., Schwartz, 1997; Hillegeist, 1999; Pae and Yoo, 2001; Willekens and Simunic, 2007; Schrank, 2021), the relationship between an auditor's liability exposure and the probability of client rejection (Laux and Newman, 2010), the interrelation between auditor liability, managerial reporting choices, and financial reporting quality (Patterson et al., 2019), and the role of reputation effects in auditor liability (Bigus, 2015b; Rothenberg, 2020).
Liu and Wang's (2006) paper is the one most closely related to our model, but differs in regard to the assumptions, results, and settings under investigation. Liu and Wang analyse the effects of legal errors in auditor liability on firm investments, assuming that the mean error of judges in assessing auditor effort is zero. With a mean error of zero, both overestimations and underestimations of auditor effort are equally possible. In fact, a symmetric deviation from the actual auditor effort may not necessarily imply a cognitive bias. With hindsight bias, however, it seems more plausible to assume that judges systematically underestimate auditor effort. The specification of the court error implies that Liu and Wang (2006, p. 1061) assume a vaguely defined negligence rule, where liability is possible even with very high levels of auditor effort. We follow Shavell (2007), however, and focus on a negligence rule that does not hold the auditor accountable if effort levels are sufficiently high. Consequently, our results differ significantly from those reported by Liu and Wang (2006). Liu and Wang (2006, p. 1061f.) find that the auditor's effort level increases monotonically in the variance of the legal error, and that the effort level chosen might be lower or higher than the socially optimal level (i.e., suboptimal and excessive effort). We show that the presence of the judge's hindsight bias may result in excessive auditor effort, but never in suboptimal effort. In addition, we find that the auditor will exert excessive effort when the judge's hindsight bias is sufficiently mild, but efficient effort when it is sufficiently strong. Somewhat in contrast to Liu and Wang (2006), this finding implies a non-monotonic association between the level of hindsight bias and auditor effort. Finally, given their different research focus, Liu and Wang (2006) also do not address remedies to counteract the error, for example, punitive damages, liability caps, or gross negligence.
For behavioural scientists, hindsight bias is considered to be at odds with rational decision-making, according to expected utility theory (Anderson et al., 1997).2 However, while the management accounting literature deals with deviations from expected utility theory quite frequently (e.g., Hartmann, 2005), there are only a few papers in the auditor liability literature. Fischbacher and Stefani (2007) suggest a game-theoretical concept that deviates from the Nash equilibrium and is based on experimental evidence. Bigus (2012) addresses auditors’ aversion to ambiguity concerning vaguely defined negligence rules, and Bigus (2015a) investigates auditor liability assuming auditor preferences according to Prospect Theory. While those papers address auditors’ bounded rationality, we consider the judge's bias to overestimate auditor negligence and even reckless behaviour.
In a broader context, the paper also deals with an important determinant of audit quality, namely the court's bounded rationality, and contributes to the extensive literature on audit quality (see, e.g. Hossain et al., 2023).
JUDGES’ HINDSIGHT BIAS: OVERESTIMATING THE PROBABILITY OF AUDITOR NEGLIGENCE
Model Setup
We use Schwartz's (1997) model, expanding it by judges’ hindsight bias. In this model, a firm seeking to expand operations attempts to raise capital from outside investors. The initial investment required is The prospects of expanding depend on the state of nature, which cannot be observed when capital is raised, but will be revealed in the future. At t = 0, the ex-ante probability of a favourable state is ; for an unfavourable state, it is . The cash return on the investment is ( in the favourable state. In the unfavourable state, the return is zero. The interest rate is zero.
We follow the literature (e.g., Ewert et al., 2000; Dittmann et al., 2010) and assume that well-diversified investors behave risk-neutrally (at the margin). Let us assume that, in the absence of an audit, the project has a negative net present value,
Outside investors may hire an auditor to reduce uncertainty about future cash flows. The auditor is risk-neutral and exerts an effort level ( at cost Let us assume that x is measured in monetary units. The effort level taken cannot be observed. Following Schwartz (1997), we assume that the auditor is the sole producer of the report. Investors decide whether or not to invest after reading the report.
We thus assume that the probability of damage decreases, albeit at diminishing rates, with higher audit quality as measured by the auditor's effort level.3 With a favourable state of nature, the auditor correctly reports the favourable state, Audit quality increases with a greater effort level, and is reflected by the term
Investors pay a non-contingent audit fee, K. We assume that the auditor's reservation utility is zero, and that there is a competitive audit market such that the audit fee only comprises the auditor's effort costs and their future expected liability payments, both of which are dependent on the effort level chosen.
A liability system allows investors who suffer damages due to inaccurate audit reports to recover damages from the auditor. In the basic model, we assume that investors do not bear litigation costs. Thus, investors bring a lawsuit if there is zero return and the auditor reported .4 Following Schwartz (1997), the difference between the initial investment and zero return represents a loss resulting from an inaccurate audit report; under negligence, damage compensation equals the initial investment, . Figure 1 depicts the game tree.
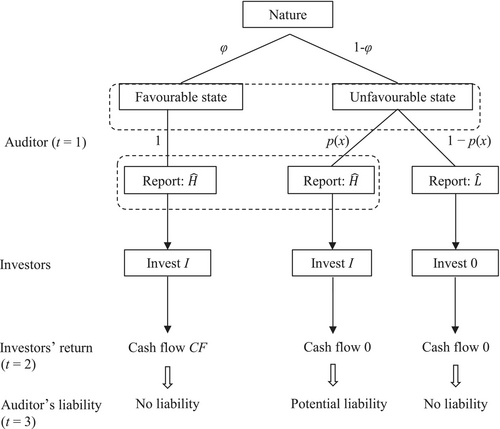
See Schwartz (1997). The probability of the favourable (unfavourable) state occurring is φ (1 − φ), respectively. denotes a favourable audit report, suggesting the realization of the favourable state of nature; denotes an unfavourable audit report. Given that the unfavourable state occurs, p(x) is the probability that the auditor will still report a favourable state. The higher the auditor's effort level x, the less likely it is that the auditor will report when in fact the state is unfavourable. If the auditor reports even though there is an unfavourable state of nature, the auditor will only be held liable if the judge finds that she has not met the standard of due care.
The auditor will be held liable if investors suffer damage and if the auditor fails to meet the standard of due care. The auditor has sufficient wealth to be able to pay damages. We assume a precise negligence rule under which, ex ante, the auditor knows precisely when she will violate the standard of due care, for example, similar to the case of exceeding a speed limit.5 We follow Shavell (2007) and assume that the legislator has defined the standard of due care as the efficient effort level x*.
In this section, we model a judge's hindsight bias as the tendency to overestimate her prior knowledge of an outcome or an event after learning the actual fact (Hawkins and Hastie, 1990).6 Lowe and Reckers (1994) and Kadous (2000) report evidence that outcome knowledge biases jurors’ evaluations of an auditor's negligence. After an accounting scandal has been revealed, the judge may question the auditor's general willingness or ability to see the ‘big picture’, even though they might be able to observe the documentation of audit efforts. Hindsight bias implies that after the occurrence of damage, the judge overestimates the ex-ante probability of damage . Since this probability of damage depends on the auditor's effort level, the overestimation of the ex-ante probability implies an underestimation of the auditor's effort,
We therefore model the judge's hindsight bias as an underestimation of the documented effort level x by the factor Thus, even when the auditor provides documents claiming to have exerted x, the judge will assess an effort level of with Consequently, the judge will ex-post overestimate the probability of auditor negligence. For simplicity, let us assume that the auditor knows the extent of the judge's hindsight bias.7
First-best Solution and Optimal Auditor Effort in the Absence of the Judge's Hindsight Bias
With report , the updated probability of an unfavourable state equals one, such that investors do not invest. If the auditor inaccurately reports with an unfavourable state of nature, they must pay damage compensation D = I if found negligent. If there is no negligence, D = 0.
There is only one local optimum: as defined in equation (6). Thus, in the absence of the judge's hindsight bias, the auditor will exert efficient effort.
The Effect of Hindsight Bias on the Auditor's Effort Level
The auditor knows that the judge will underestimate her actual effort level. Even if the auditor performs the efficient standard of due care , the judge will assess an effort level of . If the auditor does not meet the standard of due care augmented by the judge's hindsight bias (), the judge may find her negligent.
Proposition 1
Given that holds, social welfare decreases: . If investors will not undertake the investment (underinvestment).
Proof: See equations (5) and (8), and Appendix 1.
Interestingly, the auditor will exert excessive effort only in the case of sufficiently mild hindsight bias on the part of the judge, , but they exert efficient care if the judge's hindsight bias is sufficiently pronounced. Surprisingly, we find a non-monotonic association between the degree of the hindsight bias and the auditor's effort level, while Liu and Wang (2006) derive a positive association between the court's legal error and the auditor's effort level. This insight is also shown in Figure 2 and will have somewhat surprising effects on the remedies that previous literature has suggested to mitigate hindsight bias (see below).
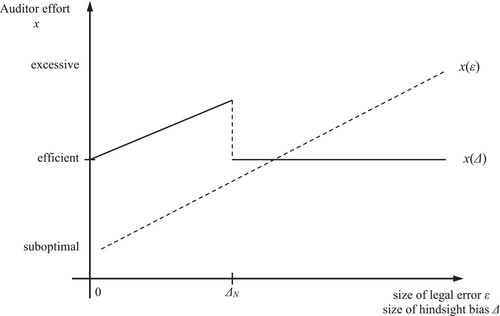
This graph shows how the size of legal error ε is associated with auditor effort x, x(ε), in Liu and Wang (2006, p. 1061, Lemma 1), and how the court's hindsight bias Δ is associated with auditor effort, x(Δ), in this paper. For convenience, x(ε) is depicted as a linear function, but according to Liu and Wang (2006) it might also be monotonically increasing in a non-linear fashion.
Excessive effort implies that the total audit costs—the sum of the effort costs and the expected damage payments—are greater than in the case of the efficient effort level. Higher total audit costs translate to a higher audit fee K. Thus, additional audit costs decrease the NPV of the investors’ project; the NPV may even become negative.
One might think that the problem of excessive care is exacerbated with stronger hindsight bias. However, this is not the case for hindsight biases equal to or exceeding the level This is because the effort costs for meeting the standard of due care as defined by the judge and for escaping liability are too high. It then pays to fall short of this standard and to take the risk of incurring damage payments. The auditor will then weigh the marginal benefits of additional effort against its marginal costs, and exert an efficient effort level.
Thus, if judges’ hindsight bias is sufficiently significant, the legislator will not need to interfere from an economics perspective. The question is how to mitigate the consequences of mild hindsight bias with , which induces excessive auditor effort and inflated audit fees. The legislator may consider (a) implementing debiasing strategies, (b) introducing a liability cap, or (c) introducing gross negligence. The following sections analyse the impact of these remedies.
Debiasing Strategies
The literature has suggested several debiasing strategies to mitigate hindsight bias (Wittlin, 2014). The ‘consider-the-opposite’ strategy requires subjects (here: judges) to think of alternative outcomes that could have occurred, for example, no audit failure. The advantage of this strategy is to see not only one possible story. Furthermore, hindsight bias can be mitigated by emphasizing the serious consequences of a verdict, for example, severe fines and expulsion from the Institute of Chartered Accountants (Clarkson et al., 2002). In addition, the separation of determining negligent behaviour from the evaluation of the auditor's actual conduct, possibly by different judges, may also insulate judges from hindsight bias (bifurcation strategy). However, in the audit context, judges probably read about audit failures in the media before litigation even starts. Hence, separation might often be impossible. Finally, judges may mitigate hindsight bias by gaining awareness of it, for example, by the provision of appropriate training (Australian Law Reform Commission, 2021).
Even though all these techniques have proven to be effective in reducing hindsight bias (e.g., Lowe and Reckers, 1994), there is no strategy available yet to completely eliminate hindsight bias (Wittlin, 2014). In the context of our model, this is bad news. If auditors know that the above debiasing strategies are applied, judges’ hindsight bias may fall below the threshold level as denoted in equation (9) or in Figure 2. If so, a debiasing strategy would cause excessive auditor effort, while without it the auditor may exert efficient care. Only a complete elimination of hindsight bias would prevent excessive care.
Mitigating the Effect of Judges’ Hindsight Bias by Capping Auditor Liability
While statutory auditor liability is not limited in some countries (e.g., generally in the US and in China; see He et al., 2017), other countries cap auditor liability to a maximum amount of damage compensation (e.g., Australia and Germany; see Azizkhani et al., 2010; Baker et al., 2001). Some countries (e.g., the UK) allow contractual liability caps. In what follows, we use CP to denote the auditor liability cap, with 0 < CP < I.
With hindsight biases in the range of , the auditor still exerts excessive effort, . For larger hindsight biases in the range of , they choose the suboptimal effort level, . Recall that an auditor will exert excessive effort in this range if there is no liability cap. Thus, while a liability cap mitigates the problem of excessive effort, it does not help to provide efficient incentives.
Proposition 2
Under a precise negligence rule, an auditor liability cap CP (I/4 < CP < I) induces excessive auditor effort with sufficiently mild hindsight bias (, see equation (11)) and suboptimal effort with (see equation (10)), but no efficient incentives. With a lower auditor liability cap CP (0 < CP < I/4), the auditor chooses suboptimal effort
Mitigating the Effect of Judges’ Hindsight Bias by Lowering the Standard of Due Care (Gross Negligence)
An intuitive alternative for counteracting judges’ hindsight bias would be to lower the standard of due care to gross negligence, , with . Ideally, gross negligence should be defined so as to cancel out judges’ hindsight bias, such that the following holds: . In that case, the auditor would exert efficient effort anticipating that the judge will effectively assess
If is not correctly calibrated, the auditor may not provide efficient effort. In the case gross negligence is defined as being too lenient, and the auditor will exert to make sure that the judge will still not hold them negligent. Nonetheless, this level implies suboptimal effort.
If equation (12) does not hold, the auditor will exert excessive effort at level albeit at a lower level than in the case of simple negligence ().
Hindsight Bias and Tightening the Standard of Due Care
With a sufficiently tight standard of due care, the auditor falls short of this standard. Instead, they will balance the marginal audit costs of additional effort with the marginal benefits (the reduction in expected damage payments), and find the optimally efficient level of effort. Figure 3 shows this effect.
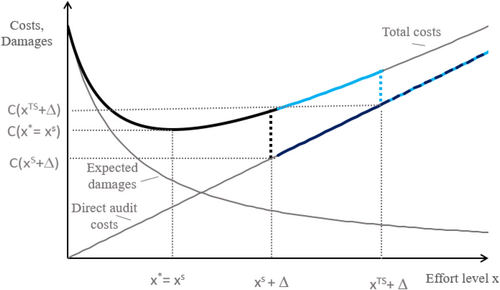
This figure shows how the auditor's level of effort x determines the expected damages, the direct audit costs, and total costs C(x); see also Shavell (2007). Note that the total cost functions have a discontinuity at some effort level at which the judge considers auditor effort to be non-negligent. Thus, for this and higher effort levels, the auditor will not bear any damage payments.
A judge's hindsight bias is denoted by and the efficient standard of due care by = x*. With a standard of due care , the auditor will exert + because C( + ) is then the global cost minimum, considering the judge's hindsight bias. There is another local cost minimum with the efficient level x*. However, total costs with the efficient level will be higher than with + since a judge suffering from hindsight bias will deem the efficient level to be negligent and will award damage payments (C(x*) > C( + )).
With a tighter standard of due care , there is a local cost minimum with the tighter standard + . However, the global cost minimum is at the efficient level x*, since C(x*) < C( + ). Thus, with a sufficiently tight standard of due care, the auditor will find it too costly to meet due care, and will choose the efficient effort level.
Proposition 3
Under a precise negligence rule, introducing gross negligence will induce an efficient level of effort if either holds or if it is not defined too leniently () and equation (12) holds. Otherwise, there will be either suboptimal or excessive effort. Tightening the standard of due care sufficiently in the sense of equation (13), however, will provide efficient incentives to the auditor.
Appendix 3 includes a game-theoretical analysis showing that Propositions 1, 2, and 3 continue to hold when investors bear positive transaction costs of bringing a lawsuit. In such a scenario, the investors will not necessarily sue the auditor for damage compensation.
Appendix 4 includes a model analysis which assumes that the standard of due care is not precisely, but vaguely defined. With a vague standard of due care, there is no sharp line between negligence and non-negligence ex ante, in contrast to adhering to or exceeding a speed limit, for instance. The standard of due care is defined rather vaguely, especially when accounting and auditing standards leave room for discretion. The analysis in the appendix shows that the qualitative results are similar to those derived under a precise negligence rule. In particular, with a vague negligence rule the judge's hindsight bias aggravates the problem of excessive auditor effort. A liability cap will generally not provide efficient incentives to the auditor. However, if the standard of due care is adequately tightened, the auditor will have efficient incentives.
Following the literature (e.g., Liu and Wang, 2006), we modelled the judge's bias indirectly in terms of how the judge perceives the level of auditor effort, but not as a distance between the posterior and prior distribution on auditor effort.10 This distance may stem from two different sources of bias: the first from overweighting the likelihood, and the second from underweighting the prior probability (Matsumori et al., 2018). Hindsight bias is usually, and often implicitly, attributed to overweighting the likelihood, while the latter effect is generally ignored.11 Matsumori et al. (2018) show that other cognitive biases, such as the base rate fallacy or representativeness bias, are structurally similar to hindsight bias. Hence, with an indirect modelling approach, those biases may also imply an underestimation of auditor effort.
Judges’ Hindsight Bias: Assessing the Auditor's Behavior as Reckless and Awarding Punitive Damages
Harley (2007) reports evidence that a judge's knowledge of an accounting scandal may sometimes also determine their beliefs about the auditor's intentions. Judges subject to hindsight bias seem more likely to find the auditor's behaviour consciously dangerous or reckless and, therefore, will require the auditor to pay punitive damages (Harley, 2007). Punitive damages are allowed in the US, but are prohibited in continental European countries, which have a civil law tradition (Corradi, 2018). The question is whether findings are qualitatively similar with this second notion of hindsight compared to the case in the previous section where the judge's hindsight bias results in an overestimation of negligence.
Case 1: Judge's hindsight bias results in awarding punitive damages
There is only one local optimum: . Thus, if the judge's hindsight bias only results in awarding punitive damages, the auditor will still have efficient incentives to exert the standard of due care, in contrast to the basic model in the previous section.
When we plausibly assume that punitive damages will increase with lower effort levels, with and the auditor will still exert due care. Thus, under a precisely and efficiently defined negligence rule, no remedy is necessary because the judge's hindsight bias will not affect the auditor's choice of effort level.
Under vague negligence, punitive damages exacerbate the problem of excessive effort, even in the absence of the judge's hindsight bias. Similar to the case of a precise negligence rule, introducing gross negligence or a tighter standard of due care will generally not provide efficient incentives (see analysis in Appendix 5).
However, in contrast to the other form of hindsight bias, debiasing strategies might be helpful for diminishing the propensity to award punitive damages.
Case 2: Judge's hindsight bias results in both awarding punitive damages and overestimating auditor's negligence
There are two local optima, both of which imply excessive care: and . Again, tightening the standard of due care to with > would result in excessive effort; the auditor chooses either or , depending on what minimizes the auditor's total costs. Only lowering the standard of due care to would then provide efficient incentives.
Proposition 4
Given that judge's hindsight bias results in an assessment of reckless behaviour and the awarding of punitive damages, the auditor will still have efficient incentives under a precisely and efficiently defined negligence rule. Given that the judge is subject to both forms of hindsight bias (assessment of punitive damages and overestimation of the auditor's negligence), the auditor exerts excessive care.
If the judge's hindsight bias implies an assessment of punitive damages, tightening the standard of due care will induce excessive effort; this differs from the case where the judge's hindsight bias implies an overestimation of the auditor's negligence only.
Proof: See equations (15) and (16).
Proposition 4 shows that the question of which legal remedies are beneficial in mitigating the effects of judges’ hindsight bias depends on the type of hindsight bias, and whether or not the legal regime allows punitive damages. In fact, the absence of punitive damages in European legislations allows the legislator to overcome the distortions caused by overly assessing reckless behaviour.
Table 1 summarizes the findings concerning judges’ hindsight bias specifications.
| Judges’ hindsight bias implies an overestimation of auditor negligence | ||||
|---|---|---|---|---|
| Without remedy | Efficient auditor incentives with liability cap? | Efficient auditor incentives with gross negligence? | Efficient auditor incentives with a tighter standard of due care? | Debiasing strategies to mitigate hindsight bias? |
| Excessive effort with sufficiently mild hindsight bias , see equation (9) | No efficient incentives | If due care is not defined too leniently and equation (12) holds | If the standard of due care is sufficiently tightened, see equation (13) | If is reduced such that equation (9) holds, debiasing will cause excessive effort |
| Judges’ hindsight bias implies an overassessment of auditor's reckless behaviour and punitive damages | ||||
|---|---|---|---|---|
| Without remedy | Efficient auditor incentives with liability cap? | Efficient auditor incentives with gross negligence? | Efficient auditor incentives with a tighter standard of due care? | Debiasing strategies to mitigate hindsight bias? |
| Efficient effort, see equation (14) | Not applicable | No efficient incentives | No efficient incentives, see equation (15) | Debiasing decreases extent of excessive effort |
| Judges’ hindsight bias implies an overestimation of auditor negligence and punitive damages | ||||
|---|---|---|---|---|
| Without remedy | Efficient auditor incentives with liability cap? | Efficient auditor incentives with gross negligence? | Efficient auditor incentives with a tighter standard of due care? | Debiasing strategies to mitigate hindsight bias? |
| Excessive effort, see equation (16) | Not applicable | Efficient incentives only with | Excessive effort | Debiasing may cause excessive effort |
- This table shows how different forms of judges’ hindsight bias affect auditor effort in the absence of any remedy, in the presence of a liability cap, in the presence of gross negligence, in the presence of a tight standard of due care, and in the presence of debiasing strategies.
CONCLUSION
This paper has three main findings. First, if hindsight bias on the part of judges refers to overestimations of the likelihood that the auditor will not meet the standard of due care, the auditor will tend to exert more than efficient (excessive) effort. Second, a liability cap limiting the auditor's damage compensation will counteract hindsight bias, but will not provide efficient incentives. Somewhat surprisingly, tightening the standard of due care sufficiently will induce efficient auditor effort. The intuition is that with sufficiently tight standards of due care, it is too costly for the auditor to meet the standard, and she will therefore efficiently balance the marginal (audit) costs and marginal benefits (reduced expected damage payments) resulting from increasing the effort level. These results generally also hold for the case of a vaguely defined standard of due care.
Third, another form of judges’ hindsight bias implies assessing the auditor's behaviour to be reckless, such that the judge awards punitive damages. With this type of hindsight bias, tightening the standard of due care will induce excessive effort; this differs from the case where judges’ hindsight bias implies that the judge will overrate the auditor's negligence only.
In sum, when judges are subject to hindsight bias, our analysis suggests tightening the standard of due care sufficiently in legal systems where punitive damages are not permitted, such as in European countries with a civil law tradition. If punitive damages are allowed, such as in the US legal system, tighter standards are not desirable.
We also find that debiasing strategies, such as the provision of appropriate training for judges, are warranted if the judges’ hindsight bias increases the propensity to award punitive damages. However, if judges overestimate the auditor's negligence, a debiasing strategy is not desirable, because reducing hindsight bias may cause auditors to exert excessive care. Future research could investigate whether auditor effort and audit fees indeed increase after judges have participated in training programs to increase their awareness of hindsight bias.
Our analysis abstracts from additional negative consequences of non-compliance, such as reputation losses (Rothenberg, 2020). In the presence of reputation losses, an auditor will be more willing to comply with the standard of due care defined by the judge who is subject to hindsight bias (overestimating negligence). We may therefore expect the auditor to be even more prone to exert excessive effort. Furthermore, we did not model hindsight bias directly, as Pohl et al. (2003) did in developing a cognitive process model.
Future research may extend our model by assuming that the auditor and investors are subject to biased individual decision-making. Furthermore, future work could model hindsight bias as a cognitive process (Pohl et al., 2003), possibly incorporating related anchoring and adjustment heuristics (Tversky and Kahneman, 1974).
More importantly, there is a need for more and novel empirical research on the types, probability, and extent of judges’ hindsight bias in financial misreporting cases, and how the characteristics of hindsight bias affect auditors’ incentives. This paper suggests several hypotheses that could be tested in experiments. First, given that judges’ hindsight bias implies an overestimation of negligence, we predict that auditors will exert efficient effort under a precisely and efficiently defined negligence rule if judges suffer from either no or strong hindsight bias, while auditors choose excessive effort with milder levels of hindsight bias. Second, we predict that in the presence of mild hindsight bias (overestimation of negligence), tightening the standard of due care will reduce the auditor's effort to an efficient level. However, the latter result will probably no longer hold when judges’ hindsight bias is related to an assessment of reckless auditor behaviour and of punitive damages.
Acknowledgement
Open Access funding enabled and organized by Projekt DEAL.
APPENDIX A: List of symbols
| Judge's hindsight bias in terms of an underestimation of auditor effort | |
| Level of judge's hindsight bias below which auditor exerts excessive care | |
| Level of judge's hindsight bias below which auditor exerts excessive care, given that there is a liability cap | |
| Probability of favourable state of nature (i.e., of a positive cash flow CF) | |
| Equilibrium probability of investors bringing a lawsuit when investors face positive transaction costs to do so | |
| Equilibrium probability of auditor exerting high effort when investors face positive transaction costs of bringing a lawsuit | |
| Cash flow of investment project in favourable state of nature | |
| Auditor liability cap, | |
| D | Damage compensation in case of an inaccurate report, equals investors’ initial investment I |
| Cumulative density function of auditor being held liable ex post by judge in the case of vaguely defined due care, depending on auditor effort and judge's hindsight bias ) | |
| Reflects the reduction in due care (gross negligence) with a vaguely defined standard | |
| I | Investors’ initial investment |
| Probability that auditor will provide an inaccurate audit and of damage, depending on auditor effort level | |
| Conditional probability that auditor will correctly report the favourable state of nature, it holds | |
| Conditional probability that auditor will wrongly report the unfavourable state of nature as being favourable, it holds | |
| Conditional probability that auditor will correctly report the unfavourable state of nature, it holds | |
| Punitive damage if judge's hindsight bias results in an overestimation of auditor's reckless behaviour and punitive damages are allowed, | |
| Social welfare of auditing depending on auditor's effort level It holds: | |
| T | Investors’ positive transaction costs when bringing a lawsuit |
| TS | Reflects the tightening of due care with a vaguely defined standard |
| Auditor's expected utility depending on the auditor's effort level | |
| Investors’ expected utility depending on the auditor's effort level | |
| Auditor's effort level | |
| Efficient auditor's effort level maximizing social welfare | |
| Precise standard of due care, efficiently defined: | |
| Standard of due care with gross negligence, it holds | |
| Standard of due care with tighter standard, it holds | |
| Auditor's individually optimal level of effort in the absence of punitive damages | |
| Auditor's individually optimal level of effort in the presence of punitive damages | |
| Auditor's individually optimal level of effort under vague negligence when tightening the standard of due care |
APPENDIX 1: PROOF OF EQUATION (9)
APPENDIX 2: DERIVATION OF EQUATION (11)
Note that requires a sufficiently high auditor liability cap, that is, In the case , equation (19) does not hold and the auditor exerts the suboptimal effort level , regardless of the extent of hindsight bias.
APPENDIX 3: JUDGES’ HINDSIGHT BIAS (OVERESTIMATION OF AUDITOR NEGLIGENCE) WITH A PRECISE STANDARD OF DUE CARE: GAME-THEORETICAL ANALYSIS
The basic model assumes that investors will inevitably bring a lawsuit once their return is zero. Thus, we assume zero transaction costs to bring a lawsuit. We now investigate whether the qualitative findings in Proposition 1 remain when we assume that investors bear the positive transaction costs T (T > 0) of bringing a lawsuit. With T > 0, investors may not always sue the auditor. They may instead decide to bring a lawsuit, depending on the auditor's expected actions and the judge's hindsight bias. The auditor, in turn, will decide on the effort level, depending on the investors’ decision to bring a lawsuit. This setting calls for game-theoretical analysis.
- Scenario 1: Investors’ transaction costs are high (.
- Scenario 2a: Transaction costs are low () and hindsight bias on the part of the judge is significant at (, see equation (9)) such that the auditor chooses efficient effort , but does not meet the standard of due care requested by the judge, .
- Scenario 2b: Transaction costs are low () and hindsight bias on the part of the judge is mild with () such that the auditor meets the excessive standard of due care requested by the judge, .
Scenario 1
With , transaction costs exceed or equal the amount of damage compensation, such that investors will not bring a lawsuit and the auditor will exert zero effort, inducing a damages probability of . The judge's hindsight bias therefore does not matter.
Scenario 2a
Given that transaction costs are low () and hindsight bias is significant, the auditor chooses efficient effort , but fails to meet the standard of due care because the judge is subject to hindsight bias. Consequently, investors will always bring a lawsuit once damage occurs. The analysis in section 2 shows that the auditor's effort level is then . There is an equilibrium in pure strategies.
Scenario 2b
Let us now discuss the effect of remedies in a game-theoretical setting. Introducing a liability cap with will increase the likelihood of Scenario 1 occurring, that is, that transaction costs will be too high to bring a lawsuit () and the auditor will then exert zero effort. With , an auditor will exert the suboptimal level if hindsight bias is significant (, see equation (11)) and an excessive standard of due care if bias is mild. Note again that the auditor never chooses efficient effort with a liability cap, which is consistent with the findings in the basic model.
When the standard of due care is lowered to gross negligence so that it cancels out the judge's hindsight bias, this will induce the auditor to exert efficient effort anticipating that the judge will effectively assess Given that transaction costs are sufficiently low (),14 we obtain an equilibrium in mixed strategies where investors sue with probability , and the auditor performs efficient effort with probability , and zero effort with probability 1 – μ*
If the legislator defines gross negligence too leniently such that , investors will sue with probability and the auditor will perform suboptimal effort with probability , and zero effort with probability 1 – μ*
In the other case, the auditor will only exert efficient effort with probability if equation (12) holds. If equation (12) does not hold, the auditor will choose excessive due care with probability , and zero effort with probability 1 – μ*
Tightening the standard of due care sufficiently, such that equation (13) holds, will result in an equilibrium with pure strategies, where the auditor performs efficient effort but does not meet due care from the judge's perspective, and consequently, investors will inevitably bring a lawsuit if damage occurs.
In sum, these findings are in line with those summarized in Propositions 2 and 3.
Derivation of equations (20) and (21), precise negligence, equilibrium in mixed strategies
The auditor's equilibrium probability of exerting due care (in the eyes of the judge) is reflected by while represents the investors’ equilibrium probability of bringing a lawsuit.
APPENDIX 4: JUDGES’ HINDSIGHT BIAS (OVERESTIMATING AUDITOR NEGLIGENCE) WITH A VAGUE STANDARD OF DUE CARE
The judge is less likely to find negligence ex post in the case of higher effort levels. Let us assume that efficient effort is in the ‘middle’ range, hence . This assumption seems plausible if judges generally try to find an efficient level of due care. Due to a lack of information, however, they might assign a lower or higher effort level ex post (Shavell, 2007). Note that the first-best solution is still defined by equation (6).
Again, there are potentially two local optima: and given that it is in the range of .15 Note that exceeds the efficient level because of and Thus, the auditor exerts excessive effort under vague negligence even in the absence of hindsight bias (see Shavell, 2007, pp. 224–27; Bigus, 2012).16 There is excessive effort with a vague standard of due care because the marginal benefit of additional effort is twofold: it reduces the probability of damage , but in the range of , it additionally reduces the prior beliefs that the judge will find the effort level to be negligent ex post. This second effect induces excessive effort.
If hindsight bias is relatively mild such that holds, there is only the corner optimum Consistent with findings under precise negligence, we obtain the result that with mild hindsight bias, an auditor will try to avoid negligence and will thus exert excessive effort.
Mitigating the Effect of Judges’ Hindsight Bias: Liability Caps
Recall that If the cap is lower than , the auditor will exert suboptimal effort, and excessive effort if it is higher. Thus, the problem of excessive effort is generally mitigated, but we only obtain an efficient solution with one specific liability cap. Since the parameters , and may vary with the specific accounting scandal, and since the judge's level of hindsight bias is likely to be individual as well, the liability cap would have to be case- and judge-specific. However, equation (30) suggests that the liability cap should increase in line with the size of damages I.
Mitigating the Effect of Judges’ Hindsight Bias: Changes in the Standard of Due Care
Tightening the standard of due care
Since does not increase with , but and do, there must be a single threshold level of which ensures that both equations (34) and (35) hold. For instance, if is sufficiently high such that holds, the auditor's effort costs associated with due care exceed the total expected auditor costs for the efficient level.
Proposition 5
Under a vague negligence rule, a liability cap will only provide efficient incentives if holds. A specific level of gross negligence will induce efficient effort if equation (32) holds. If the liability cap or gross negligence is not correctly specified, there will be suboptimal or excessive effort. If the standard of due care is adequately tightened according to equations (33-35)–(33-35), the auditor will have efficient incentives.
Proof: See equations (30-35)–(30-35).
To reduce redundancy, we have omitted a game-theoretical analysis, but the qualitative results remain when we assume positive transaction costs for bringing a lawsuit.17
APPENDIX 5: JUDGES’ HINDSIGHT BIAS: ASSESSING RECKLESS BEHAVIOUR AND PUNITIVE DAMAGES—THE CASE OF VAGUE NEGLIGENCE
Under a vaguely defined standard of due care, punitive damages will cause excessive effort. Potentially, there are two local optima: and Both local optima exceed the efficient level; does so because of and Note, however, that but not increases with , such that sufficiently large punitive damages induce the auditor to choose the corner optimum .
In the case , is the only local optimum.
Tightening the standard of due care will not provide efficient incentives, in contrast to the findings where hindsight bias was related to the overestimation of negligence. The reason is that with punitive damages, the marginal individual benefits of additional effort will exceed the marginal social benefits, since holds. Thus, the auditor will exert excessive effort, regardless of how much tighter the legislator sets the standard of due care.
Biography
Jochen Bigus ([email protected]) is at Freie Universität Berlin. Nadine Georgiou is at University of Innsbruck.
REFERENCES
- 1 Rachlinski et al. (2011) report experimental evidence that hindsight bias was typically found in the fact-finding process, but less so in the ruling and sentencing process.
- 2 However, some authors consider the evidence on hindsight bias not to be at odds with rational Bayesian updating. Kelman et al. (1998) find experimental evidence that individuals who could calculate the ex-ante probability of an outcome did not reassess priors when being told what outcome actually occurred. Wilson et al. (2021) show that hindsight bias tended to decrease when the actual outcome was too distant from the original estimate, emphasizing a rational aspect of this bias. Posner (1999) argues that seemingly observed hindsight bias of juries may simply be explained by a different assessment of standards (of due care). However, this leaves the question open of why juries should generally require relatively strict standards.
- 3 Note that the probability of damage is not a probability of audit failure because damage is possible, even with very high auditor effort levels. As such, damages may occur even if the auditor meets the standard of due care.
- 4 Appendix 3 includes a game-theoretical analysis assuming investors’ litigation costs to be positive.
- 5 Appendix 4 provides an analysis for the case of a vaguely defined standard of due care.
- 6 Hawkins and Hastie (1990) provide a second notion of judges’ hindsight bias: judges might be more willing to recognize the auditor's behaviour as reckless and therefore award punitive damages. See the next section.
- 7 The qualitative results remain the same when we model ∆ as a risky variable, or when the auditor cannot directly observe the judge's hindsight bias, but has information on the distribution of hindsight bias among all judges.
- 8 The second-order condition holds because p(x) is convex. There is a second solution for x* with a negative sign. We exclude negative effort levels due to the assumption that
- 9 If the standard of due care is not efficiently defined, the auditor will likely exert the inefficient standard. Hindsight bias then tends to add an additional distortion to auditor effort.
- 10 Pohl et al. (2003) propose a non-microeconomic, cognitive process model to simulate hindsight bias directly. To keep the model tractable, we chose an indirect modelling approach and abstracted from decision heuristics related to hindsight bias, especially anchoring and adjustment heuristics, see Tversky and Kahneman (1974). We are grateful to a reviewer for pointing out this limitation of our study.
- 11 We are grateful to a reviewer who brought this point to our attention.
- 12 In what follows, we do not refer to a liability cap because this would contradict the idea of punitive damages.
- 13 This assumption is not crucial to the results. We assume that the British Rule would only complicate the analysis. Investors would then have stronger incentives to bring a lawsuit.
- 14 In what follows, we do not discuss the case with high transaction costs ( since it is clear that investors will not sue in that case, and the auditor will exert zero care.
- 15 Since , cannot be a local optimum.
- 16 Note that this result holds when F(x) is linear—as in the model—or convex. If F(x) is—partly—concave, this result tends to hold, but does not generally hold; see Craswell and Calfee (1986).
- 17 The analysis is available on request.




