Advances in Equity Valuation: Research on Accounting Valuation

This special issue of Abacus was prompted and made possible through the annual conference of our research group MEAFA 1 at the University of Sydney, and especially by the contributions of visitors to MEAFA and their collaborations with members of the group. The six papers and added commentaries in this special issue of Abacus contain surveys and original contributions on the theory and empirical testing of a class of valuation models that is unique to accounting.

Beginning with works such as Edwards et al. (1987) and Feltham and Ohlson (1995), a mathematical reconciliation is now widely known between the present value of cash flows and the present value of accounting residual incomes. 2 The only rule of accounting practice (asset valuation) required by this analogy is the clean surplus rule, whereby the period change in book value of equity, after allowing for dividends, shows up exactly in each period's accounting income or profit. This requirement says nothing about how assets need to be valued (e.g., how depreciation is calculated). It is only when a finite time series of residual income numbers is used to value the firm, or, in other words, to predict the firm's future, that policy-based accounting rules (e.g., depreciated historical cost versus fair market value) start to matter.

Seeing that accounting valuation methods coincide mathematically with discounted cash flow models, researchers in accounting have returned to questions like why and how accruals accounting might produce ‘accounting numbers’ that anticipate or hint at the future prospects and current value of the firm. That way of thinking sets up the discipline of accounting as a science, with both theory and empirical results, each withstanding criticism and gaining respectability via the other. Whether that theory or testing is now sufficiently advanced to bring practical benefits is not the question. Any science in its development has to pass that stage.

The papers in this issue of Abacus all celebrate what an ‘accounting science’ of firm valuation and prediction has to offer, both at present and in terms of ideas for further development. The six papers and commentaries are written by highly-respected contributors to accounting valuation theory and testing, and together mark a body of work that has potential to change financial practice and add a new chapter to finance theory textbooks.

How is it that accounting numbers, that are only an accountant's distortion of actual cash flows, can be taken as the raw inputs for firm valuation? Surely cash flows are the valuation primitives. A possible answer is: (1) cash flows might be ideal inputs if they were more predictable by investors; and (2) accounting numbers carry hidden predictive meaning, because, first, the accountant or auditor is inside the firm and knows much about it and its future, and, second, the accounting valuation rules and practices (such as conservatism) are inherently predictive or informative in a way that is not easily emulated by starting with a blank sheet and trying to write a cash flow prediction into each time period.

A simple instance, much like that discussed in Penman's paper, is that by not recognizing a sale as a revenue until sufficiently confident of its realization, the conservative accountant implies something about the future payoff and its uncertainty that we would not see if we were to ask the firm or an analyst how much was sold this year. Another aspect of what can make accounting predictive is its rule that assets stay on the books only whilst, in the accountant's assessment, they have an economic future that warrants their current book value. That subjective assessment of an asset's prospects can be more accurate when made from inside the corporation by an independent observer than from an analyst's desk. Whether by the accountant's expertise and objectivity, or through a built-in property of the accounting framework, accounting numbers can in principle facilitate more accurate firm valuations and predictions than less constrained or formalized cash flow or dividend guesses, especially if those guesses are subject to the biases that come from alternative information sources such as a market analyst's over-optimism or the voice of vested interests.

The argument above is mainly about why the ‘numerator’ in accounting valuation models might be informative. That leaves the denominator or discount rate, regarding which there is less agreement. A fundamental theoretical problem, raised one way or another in all of the papers in this issue, is the question of whether risk and the cost of capital should be treated econometrically or economically (fundamentally). The econometric approach says that anything conditionally correlated with actual returns, as represented by its significance in a regression, is a ‘risk factor’, whether it looks like one or not. That is how variables that were initially regarded as anomalies under CAPM became newfound risk factors in an ‘n-factor’ CAPM.

In contrast, the economic ‘fundamentals’ approach says that risk is about the firm itself and what affects its cash flows causally, such as its unreliable suppliers or uncommitted customers. From that more intuitive perspective, risk under an asset pricing model like CAPM is anything that makes the firm's future cash flows less divorced from outside influences (e.g., interest rates or wage rates) and hence more correlated with other firms in the whole market.

Confusion arises, however, when discussion wavers back and forward across the two ways of talking. Under the econometric approach, the numerator and denominator are seen nearly always as independent inputs, hence the common distinction between cash flow (numerator) news and discount rate (denominator) news. On this approach, an earnings shock might change the numerator but not the denominator. Under the business fundamentals approach, an earnings shock is always both numerator and denominator news.

There is a deeper problem still. Let's suppose that the firm has a positive earnings shock, and through the ‘information dynamics’ of the assumed time series prediction model, that shock increases future earnings predictions. What should happen to the denominator? One answer is ‘nothing’, since the predicted covariances of those future earnings, or whatever variable captures ‘risk’, might not change. 3

No such convenient conclusion can stand up to economic logic. If a business is predicted to produce a series of earnings or cash with a higher mean but the same variability—as if the payoff distribution shifts to the right but with all the same correlation coefficients that it had previously—the discount rate cannot sensibly stay the same. It must generally decrease, because the asset becomes effectively more and more risk-free when its mean-to-variability ratio becomes larger.

Accounting valuation models that do not allow for this bond between numerator and denominator, under which ‘numerator news’ is logically also ‘denominator news’, have a flaw that might not be an issue practically (in the sense that there are lots of other issues in valuations that hinge on time series predictions of earnings, dividends, and so on), yet will always be a flaw theoretically, and thus in terms of good science.

Note importantly that models that allow in the numerator for risk do not have this issue. To see this, say that the asset price is P = (x − c)/R_f, where x is the usual ‘numerator’ in dollars, c is the absolute-dollar penalty for risk and R_f = (1 + r_f) is the risk-free discount factor. The implied discount factor, re-expressing the pricing calculation such that risk is in the denominator, is x/P, which equals

and hence decreases automatically with higher x (given fixed risk penalty c). Pricing models that do not make this natural adjustment of the denominator, when there is a change in the numerator, cannot give the same results. Usually the numerator x is an expected cash flow, but the same requirement must arise when x is an ‘accounting flow’, like expected earnings, rather than a cash flow.

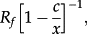
The papers and commentaries in this issue sit well alongside the history and ethos of Abacus. Accounting methods are treated as an information mechanism for financial decisions, including, of course, the big decisions in business requiring firm valuation. With decisions in mind, Abacus has a history of supporting normative or ‘theoretical’ design and critique of accounting rules, where critique is understood to include empirical testing.

The valuation methods presented and developed in this issue are founded implicitly on the latent information that accounting numbers (accruals) can carry relative to the cash flows on which they are based. The elegance and intellectual importance of these papers is that they help us understand how this embedded content exists, and how to extract it.