Accounting Valuation and Cost of Equity Capital Dynamics
The author is grateful to Demetris Christodoulou for suggesting this topic. He also wishes to thank his discussant, Paul Dunmore, and other participants of the MEAFA workshop held in January 2015 at the University of Sydney for comments on an earlier draft.
Abstract
This paper provides a selective survey of Ohlson and Vuolteenaho-type accounting valuation models. The focus is on the valuation, return, and cost of capital dynamics of these models. Emphasis is placed primarily on variations of these models that incorporate risk aversion, parameter uncertainty, and/or time-varying costs of equity. Empirical papers that address the dynamics of these models are also surveyed.
Current theories of accounting valuation are based primarily on Ohlson (1995) or Vuolteenaho (2002). 1Accounting is incorporated in these models via the clean surplus relation. 2Whereas the Ohlson (1995) model is generated from standard non-arbitrage conditions, the Vuolteenaho (2002) model is derived from assumptions about the time series properties (such as stationarity) of the book-to-market (B/M) ratio. As has been shown recently by Lyle et al. (2013), these two models are conceptually related to each other despite their disparate technical underpinnings.
Both models have been extended in different ways. Feltham and Ohlson (1995, 1996) generalize the basic Ohlson (1995) model to include (unconditional) accounting conservatism by decomposing the clean surplus relation into operating and financial asset components. Feltham and Ohlson (1999) incorporate dynamic risk aversion into accounting valuation. Gode and Ohlson (2004) allow for dynamic risk-free rates of interest. Lyle et al. (2013) extend Feltham-Ohlson (1999) to incorporate aggregate risk and to generate time-varying dynamic costs of capital (discount rates). Callen and Segal (2004) extend the Vuolteenaho model utilizing the Feltham-Ohlson clean surplus decomposition.
The purpose of this paper is to selectively review accounting valuation and interrelated cost of capital models focusing on the dynamics that underlie these models and on the dynamics that are consequences of these models.
Theory Of Ohlson-Type Models
Risk Neutrality
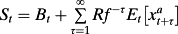 (1)
(1)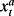 abnormal earnings.
3
abnormal earnings.
3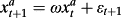 (2)
(2)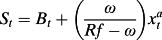 (3)
(3)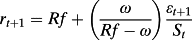 (4)
(4)The latter relation implies that equity returns are comprised of the risk-free rate plus a multiple of the shock to the (abnormal) earnings-to-price (E/P) ratio. Equation 4 also indicates, not surprisingly, that the more persistent are abnormal earnings, the greater the impact of any earnings shock on returns.
Taking expectations, equation 4 further implies that the firm's cost of equity (the expected return) is the constant risk-free rate of interest. The latter result is hardly surprising considering that investors are risk-neutral and the risk-free rate is an exogenous constant by assumption. It is well worth noting that many empirical applications of the Ohlson (1995) model replace the risk-free rate by some cost of capital measure usually based on the CAPM or the Fama-French three- or four-factor models. In addition to the fact that the CAPM (or Fama-French) and the Ohlson (1995) model are not generally consistent with each other (Morel, 2003), the risk neutrality assumption implies that it is conceptually incorrect to measure the cost of capital in an Ohlson (1995) framework other than by the risk-free rate, as follows directly from equation 4. 4
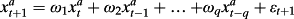 (5)
(5)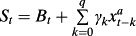 (6)
(6)Risk Aversion
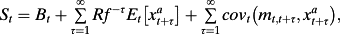 (7)
(7)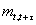 is the time t stochastic discount factor for cash flows expected at time (t+ τ).
6Equation 7 is the RIV extended to include dynamic stochastic discount factors as reflected in the dynamic conditional covariance terms.
is the time t stochastic discount factor for cash flows expected at time (t+ τ).
6Equation 7 is the RIV extended to include dynamic stochastic discount factors as reflected in the dynamic conditional covariance terms.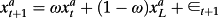 (8)
(8)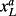 . This is essentially the same dynamic as in Ohlson (1995).
8However, the original Ohlson model is set in a risk-neutral world so that the firm's cost of capital is equal to the risk-free rate. If return on equity eventually converges to the firm's cost of capital because of competition, long-run abnormal earnings will converge to zero. By contrast, in a risk-averse world, the cost of capital is the risk-free rate plus a risk premium so that, if return on equity eventually converges to the firm's cost of capital, then abnormal earnings will converge to some long-run equilibrium value above zero. Hence, the long-run abnormal earnings variable is included in the dynamic.
. This is essentially the same dynamic as in Ohlson (1995).
8However, the original Ohlson model is set in a risk-neutral world so that the firm's cost of capital is equal to the risk-free rate. If return on equity eventually converges to the firm's cost of capital because of competition, long-run abnormal earnings will converge to zero. By contrast, in a risk-averse world, the cost of capital is the risk-free rate plus a risk premium so that, if return on equity eventually converges to the firm's cost of capital, then abnormal earnings will converge to some long-run equilibrium value above zero. Hence, the long-run abnormal earnings variable is included in the dynamic.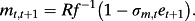 (9)
(9)The error term et+1 is assumed to have a mean of zero and a unit variance and to be (positively) correlated with ∈ t+1. 10The term σm,t is key in their analysis and represents the level of aggregate (systematic) risk in the economy. This formulation also assumes that risk-free rates are constant. Note that this dynamic is assumed to satisfy the general requirements of a stochastic discount factor, namely, that a stochastic discount factor must equal the inverse of the gross risk-free rate in expectation and take on non-negative values only (Cochrane, 2011). 11Although the form of this stochastic discount factor is fairly simple, the assumed volatility structure is a close discrete-time analog of the popular SABR stochastic volatility model commonly used in option pricing (Hagan et al., 2002). 12
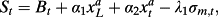 (10)
(10)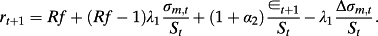 (11)
(11)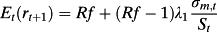 (12)
(12)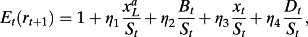 (13)
(13)Ohlson-type Model with Imperfect Parameter Information
Typically, the accounting valuation literature presupposes that parameters are perfectly observable to investors. Suppose, however, that investors have only imperfect information about the firm's long-run earnings (
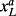 ) and they learn about long-run earnings over time. Accounting valuation models that involve learning were analyzed by Pastor and Veronesi (2003) in a continuous time framework and more recently by Lyle (2013) in a discrete time framework. The discussion that follows is based on an Ohlsonian version of the Lyle (2013) model.
15
) and they learn about long-run earnings over time. Accounting valuation models that involve learning were analyzed by Pastor and Veronesi (2003) in a continuous time framework and more recently by Lyle (2013) in a discrete time framework. The discussion that follows is based on an Ohlsonian version of the Lyle (2013) model.
15
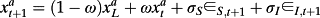 (14)
(14)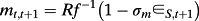 (15)
(15)Here the abnormal earnings dynamic is a function of long-run abnormal earnings
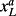 as well as an explicit function of both systematic risk ∈ S,t+1 and idiosyncratic risk ∈ I,t+1. The latter random variables are assumed to be normally and independently distributed with mean zero and variance of 1. In contrast to Lyle et al. (2013), the volatility parameter (σm) in the stochastic discount factor is assumed to be time-independent for simplicity.
as well as an explicit function of both systematic risk ∈ S,t+1 and idiosyncratic risk ∈ I,t+1. The latter random variables are assumed to be normally and independently distributed with mean zero and variance of 1. In contrast to Lyle et al. (2013), the volatility parameter (σm) in the stochastic discount factor is assumed to be time-independent for simplicity.
Now assume that investors cannot perfectly observe long-run abnormal earnings. Let
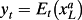 denote investors’ conditional belief at time t about long-run abnormal earnings. Investors are assumed to learn about long-run earnings over time by observing the time series of past abnormal earnings (which imperfectly incorporate long-term earnings) and the stochastic discount factor.
16In particular, investors optimally update past information about long-run abnormal earnings
denote investors’ conditional belief at time t about long-run abnormal earnings. Investors are assumed to learn about long-run earnings over time by observing the time series of past abnormal earnings (which imperfectly incorporate long-term earnings) and the stochastic discount factor.
16In particular, investors optimally update past information about long-run abnormal earnings
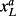 using a Bayesian updating mechanism as encapsulated in a Kalman filter (see Liptser and Shiryaev, 1977).
using a Bayesian updating mechanism as encapsulated in a Kalman filter (see Liptser and Shiryaev, 1977).
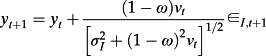 (16)
(16)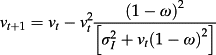 (17)
(17)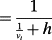 (18)
(18)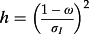 . Solving equation 18 forward yields:
. Solving equation 18 forward yields:
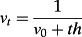 (19)
(19)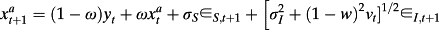 (20)
(20)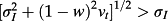 . Solving for firm value with imperfect information—see the Appendix—yields:
. Solving for firm value with imperfect information—see the Appendix—yields:
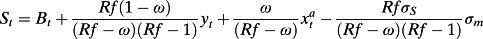 (21)
(21)The valuation equation with imperfect information about long-run abnormal earnings is almost identical to the valuation with perfect information except that now firm value is a function of investors’ conditional expectations of long-term earnings (yt).
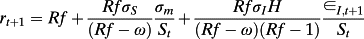 (22)
(22)In contrast to the perfect information case, returns are now an explicit function of idiosyncratic risk where the coefficient on idiosyncratic risk is a nonlinear but decreasing function of the firm's age t and increasing function of abnormal earnings persistence.
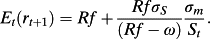 (23)
(23)This result appears counter-intuitive in light of the theoretical literature on parameter uncertainty and estimation risk, which maintains that a reduction in parameter uncertainty reduces the firm's cost of capital (Bawa et al., 1979; Barry and Brown, 1984). However, the result follows from the fact that the cost of capital in this model is solely a function of systematic risk and investors learn all that they can about systematic risk by observing the stochastic discount factor. Thus, the assumption that costs of capital necessarily fall with a reduction in investor uncertainty about valuation parameters is not correct in general.
The Term Structure of Costs of Equity Capital
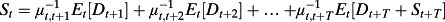 (24)
(24)Here each period's expected dividend is discounted at a potentially different discount rate (μt,t+T), yielding a term structure of discount rates.
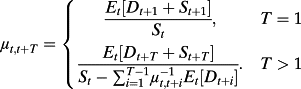 (25)
(25)To solve for any μt,t+T, T > 1, one must first solve for μt,t+1, which can then be used to solve for μt,t+2 and so on up to μt,t+T. This method of successive substitution is conceptually similar to deriving a term structure of bond yields recursively using the price of a one-period pure discount bond to solve for a one-period yield and then using that yield together with the price of a two-period pure discount bond to solve for the second-period yield and so on.
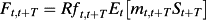 (26)
(26)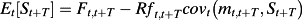 (27)
(27)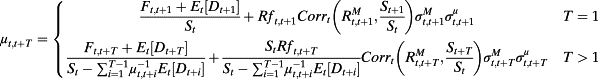
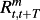 denotes the return on the market portfolio from period t to t+T,
denotes the return on the market portfolio from period t to t+T,
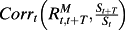 is the conditional correlation between the return on the market portfolio and the return on firm equity over the period t to t+T,
is the conditional correlation between the return on the market portfolio and the return on firm equity over the period t to t+T,
 is the conditional volatility of the return on the market portfolio from time t to t+T, and
is the conditional volatility of the return on the market portfolio from time t to t+T, and
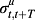 is the conditional volatility of the return on the firm's equity from time t to t+T. Hence, estimating a term structure of implied costs of equity from equation (28) requires estimates of equity futures prices, future risk-free rates, expected future dividends, future volatilities of the return of the market portfolio and of firm-level equity returns, and future correlations between the return on the market portfolio and equity returns.
is the conditional volatility of the return on the firm's equity from time t to t+T. Hence, estimating a term structure of implied costs of equity from equation (28) requires estimates of equity futures prices, future risk-free rates, expected future dividends, future volatilities of the return of the market portfolio and of firm-level equity returns, and future correlations between the return on the market portfolio and equity returns.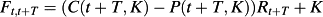 (29)
(29)Implied volatilities, strike prices, (future) risk-free rates, and times to expiry are obtained from the OptionMetrics implied volatility surface data set (Yan, 2011) and their coupon bond file. Implied volatilities estimated from option contracts traded on the S&P 500 Index proxy for expected market volatilities. Correlations between the firm-equity returns and the return on the market portfolio (the S&P 500 Index) are estimated using rolling 36 months of observations. 19
Dynamics and the Empirical Ohlson Literature
Many empirical papers make reference to and/or apply Ohlson-type valuation models. Generally speaking, these papers assume the same information dynamics as in Ohlson (1995) or Feltham and Ohlson (1995, 1996). However, empirical evidence suggests that the simple Ohslon (1995) and Feltham-Ohlson (1995) dynamics are not supported by the data. Bar-Yosef et al. (1987) find that their data are better described by a multiple lagged information dynamic than a single lag information dynamic. Morel (1999) finds that the (optimal) lag structures of the Ohlson (1995) information dynamic and the pricing relation do not yield consistent results.
Often, empirical papers that reference Ohlson-type models incorporate ‘other value-relevant’ variables in their valuation equation. The choice of these latter variables is necessarily ad hoc given that the model itself fails to specify which other variables are in fact value-relevant. However, Liu and Ohlson (2000) show how to finesse the ‘other value-relevant’ variables but at the cost of adding more expectational variables to the valuation equation. Callen and Segal (2005) use their technique to evaluate the Ohlson (1995) and Feltham-Ohlson (1995) valuation models empirically. They find that the latter models neither load properly nor predict particularly well out of sample. In fact, they seem to predict no better than a simple (forward) earnings per share model.
Three papers to date have addressed empirically the issue of accounting valuation when investors are risk-averse. Two of the latter have further addressed the issue of time-varying discount rates. Nekrasov and Shroff (2009) estimate the Feltham and Ohlson (1999) RIV valuation equation (7 above) using an historically-based covariance risk measure. Comparing value estimates based on the Feltham-Ohlson RIV with the CAPM and the Fama-French three-factor model, they find that their RIV yields smaller out-of-sample pricing errors.
Lyle et al. (2013) test both their valuation model and their related cost of capital dynamics. Comparing their valuation model with Ohslon (1995), the CAPM, and the Fama-French three-factor models, they find that their model yields significantly smaller prediction errors compared to the latter three benchmark models. They also find that the prediction errors of their model are significantly smaller than the prediction errors reported by Nekrasov and Shroff (2009) when comparing their Feltham-Ohlson RIV with the CAPM and Fama-French factor models.
Lyle et al. (2013) also evaluate the dynamic cost of equity capital estimates derived from their valuation model. They find that their costs of equity estimates load on firm fundamentals in the direction predicted by their theory. They further test their dynamic cost of equity estimates by comparison to future realized returns in accordance with standard asset pricing tests. In a cross-sectional analysis, they find that their one-month ahead costs of capital are highly significantly related to future realized monthly returns in contrast to monthly expected return estimates derived from standard factor models. They also employ time series portfolio tests and show that both portfolio average returns and risk-adjusted returns increase monotonically with their cost of equity estimates. Further, in contrast to standard factor models, portfolio return alphas are highly significant for their cost of equity estimates.
Callen and Lyle (2013) estimate firm-level term structures of implied costs of equity for the years 1996–2012 from equation (28) above using synthetic forward prices estimated from traded options data. They validate their method for calculating synthetic forward prices by estimating synthetic prices of traded S&P 500 futures index on the CME. They compare their synthetic index prices with actual prices and find that the synthetic prices approximate the actual prices to a very close degree.
Based on firm-level data, Callen and Lyle (2013) are able to reject the ubiquitous assumption that term structures of implied costs of equity are flat. Rather, they find that for most years and almost all Fama-French industries, term structures of equity capital and term structures of risk premia are significantly upward-sloping and concave. Their empirical results indicate that the upward slope in the implied cost of equity is an economically meaningful 70 basis points per year on average. They also find that during the crisis period of 2008–09 term structures flattened, consistent with sharp increases in interest rates and limited lending during this period. In addition to estimating firm-level term structures for maturities up to two years using options data, Callen and Lyle (2013) also estimate a long-run firm-level implied cost of equity based on extrapolating the shape of the options-based term structure using spline functions.
Callen and Lyle (2013) further compare the ability of their term structure model to predict realized returns with reference to standard factor models using monthly data and with reference to standard static implied cost of equity models, including Claus and Thomas (2001), Easton's (2004) PEG and the forward E/P ratio, using annual data. 20Both cross-sectional and time-series asset pricing tests indicate that their time-varying implied costs of equity capital, including the long-run estimate, are positively and significantly associated with future realized returns. In contrast, they find that traditional static implied costs of equity and factor model costs of equity are largely unassociated with future realized returns.
Finally, recent literature has shown that impending earnings announcements are perceived to be risky by the market in that equity returns tend to be predictably higher during earnings announcement months (e.g., Barber et al., 2015). Callen and Lyle (2013) find that their forward-looking implied term structure estimates capture this phenomenon ex ante. Specifically, they find that their term structure estimates predict higher future returns (conditional on information in the month before the announcement) in the month of the earnings announcement. In contrast, standard (backward-looking) finance factor models do not forecast future equity returns or anticipate predictable earnings announcement-month return premia.
The Accounting Variance Decomposition Model
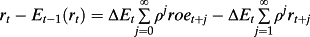 (30)
(30)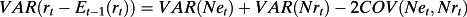 (31)
(31)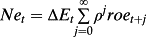 (32)
(32)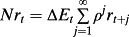 (33)
(33)The accounting variance decomposition analysis indicates the extent to which the volatility in returns is driven either by the volatility of earnings news or by the volatility of discount rate news or both. Thus, the accounting variance decomposition indicates the extent to which earnings and/or discount rates are value-relevant. However, the variance decomposition concept of value relevance differs from standard value relevance obtained by regressing the revision in returns on shocks to earnings in the earnings response coefficient (ERC) literature. ERC measures the value relevance of earnings from an ex post conditional perspective; that is, conditional on a shock to earnings of, say, 1%, what is the percentage expected revision to returns? In this ERC perspective, the larger the revision to returns the more value-relevant are earnings. But, because the ERC is an ex post metric, it fails to inform about the ex ante expected frequency of return shocks generated by earnings shocks. In contrast, the variance metric of information content measures the ex ante likelihood that earnings shocks will occur and generate return shocks. The greater the volatility of earnings shocks and the more persistent are earnings, the greater the ex ante likelihood that shocks to returns will occur.
The value relevance of accounting information cannot be measured solely by reference to an ERC-type analysis. A variance decomposition is also de rigeur. To illustrate the complementary nature of ERC and variance decomposition, Callen (2009) provides an example for which earnings are highly persistent, β = 0.90, but the variance of earnings is small, only 0.1% and there is no shock to ‘other information’. In this case, it can be shown that the ERC is 10 but the volatility of unexpected returns generated by the earnings shock is only 1.9%. This means that although shocks to earnings, when they occur, have a dramatic impact on returns, nevertheless, shocks to earnings, and hence shocks to returns, are expected to be relatively infrequent ex ante. Callen (2009) subsequently considers the diametrically opposite case where earnings are not very persistent, β = 0.1, and the variance of earnings is relatively large, say, 5%. Here, the ERC is only 1.11 but the volatility of unexpected returns generated by the earnings shock is 6.1%. In contrast to the first case, shocks to earnings are expected to occur relatively frequently ex ante but each shock that occurs ex post will have a relatively small impact on equity returns. Based on a typical ERC analysis, the researcher would have concluded that earnings in the first case (ERC = 10) are far more ‘value-relevant’ than in the second case (ERC = 1.11). However, as this example illustrates, the information contained in an ERC analysis together with the variance decomposition paint a very different picture about the true value relevance of earnings than that obtained from the ERC analysis alone.
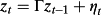 (34)
(34)One of the weaknesses of the VAR approach is that realistically one cannot estimate VAR parameters at the firm level given the paucity of sufficient time series data. Moreover, the more variables included in zt the more unstable are the coefficient estimates (Chen and Zhao, 2009). Instead, the VAR parameters are typically estimated at the industry level (or even at the economy-wide level) and the parameter estimates are then assumed to be constant across firms in the industry. Methods for estimating the VAR and the subsequent variance decomposition, including computer programs, are provided by Callen and Segal (2010).
In an influential attack on the variance decomposition methodology, Chen and Zhao (2009) claim that the relative variance contributions of different variables to unexpected returns in a variance decomposition analysis depend critically upon the method of estimation. They find empirically that whether discount rate news or earnings news drives the volatility of unexpected (bond) returns depends crucially upon which of these (discount rate news or earnings news) is estimated residually and which is estimated directly. In turns out, however, that their critique is flawed on a number of grounds as shown by Campbell et al. (2010) and especially Engsted et al. (2012). Importantly, Engsted et al. (2012) show inter alia that the VAR model is not meaningful unless it incorporates the fundamental valuation variable that gave rise to the variance decomposition in the first place (in their case the dividend–price ratio and in Vuolteenaho's case the M/B ratio), something which Chen and Zhao (2009) fail to do. Incorporating this variable in the VAR, Engsted et al. (2012) obtain results that are consistent with the extant literature and contrary to Chen and Zhao (2009).
The Empirical Accounting Variance Decomposition Literature
Vuolteenaho (2002) was the first to develop and estimate an accounting variance decomposition. He finds that earnings news rather than discount rate news is the main driver of unexpected stock return volatility at the firm level. In contrast, earnings news is largely diversified away in aggregate portfolios so that discount rate news is the main driver of unexpected returns at the aggregate level.
Callen and Segal (2004) incorporate the Feltham-Ohlson (1995, 1996) breakdown of the clean surplus relation into the Vuolteenaho model. They find that cash flow news, accrual news, and discount rate are all value-relevant and significant drivers of return volatility at the firm level. They further find that accrual and cash flow news have fairly similar impacts in driving returns and both dominate discount rate news.
Callen et al. (2005) analyze the relative value relevance of foreign and domestic earnings in driving returns using a variance decomposition analysis. Consistent with the literature, they find that both foreign and domestic earnings are value-relevant from an ERC perspective. They also find that foreign earnings are more persistent than domestic earnings, suggesting that foreign earnings are more value-relevant than domestic earnings from an ERC point of view. 23However, on the basis of a variance decomposition analysis, Callen et al. (2005) find that domestic earnings, rather than foreign earnings, are the primary driver of unexpected equity returns. Intuitively, the variance metric involves a trade-off between the persistencies of the earnings components and the variances of the earnings components. Although foreign earnings are more persistent than domestic earnings, domestic earnings are far more volatile than foreign earnings so that the variance of unexpected equity returns—the value relevance metric in a variance decomposition framework—is higher for domestic earnings than foreign earnings.
As noted above, Callen (2009) argues that value relevance requires both ERC and variance decomposition analyses. In the case of foreign versus domestic earnings, Callen et al. (2005) find that while a 1% shock to foreign earnings has a larger impact on equity returns than a 1% shock to domestic earnings, the likelihood of shocks occurring to domestic earnings is far larger than the likelihood of shocks occurring to foreign earnings. As this case illustrates, both ERC and variance decomposition metrics are required (at a minimum) in order to make adequate value-relevance statements.
Callen et al. (2006) evaluate the value relevance of discount rate news, cash flow news, and accruals around Securities and Exchange Commission (SEC) filing dates. The variance decomposition framework is a natural framework for determining the value relevance of these informational news components around SEC filings because, unlike preliminary earnings announcements which can reasonably be estimated and classified as good or bad news, SEC filings provide information that (potentially) revise the information conveyed by preliminary earnings announcements. Hence, the researcher is usually unable to determine ex ante whether the information conveyed by SEC filings is good or bad news. As a consequence, the value relevance metric for SEC filings has to be non-directional (unsigned). The variance decomposition methodology provides such an unsigned metric, namely, the variance of unexpected returns. Although other non-directional metrics have been employed by the literature, these fail to control for changes in costs of capital (discount rate news) that may be generated by the news event. By contrast, the variance decomposition methodology provides an empirically estimable relation between the non-directional value relevance metric and the variances of the informational news components and discount rate news. A variance decomposition explicitly estimates the impact of changes in costs of capital on security returns during the news event. Callen et al. (2006) show in their study that discount rate news increases significantly on SEC filing dates.
Conclusion
This paper provides a selective review of accounting valuation models and inter-related cost of capital models focusing on the dynamics that underlie these models and on the dynamics that are consequences of these models. Surprisingly, despite the relative simplicity of Ohlsonian and variance decomposition models, both can be generalized in various ways to address issues of concern both to theorists and empiricists. Of these, the most important in the author's view are issues involving the dynamics of valuation and the dynamics of returns such as estimating time-varying discount rates, estimating term structures of costs of equity capital, and addressing the effect of parameter uncertainty on firm valuation and costs of capital.
Appendix: Imperfect Information Dynamics
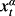 in the matrix form:
in the matrix form:
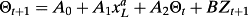 (A1)
(A1)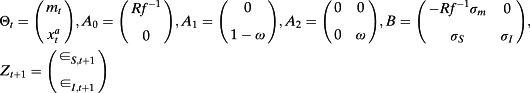
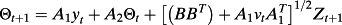 (A2)
(A2)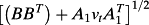 yields equation 20 in the text. Similarly, one can use their equation 13.149:
yields equation 20 in the text. Similarly, one can use their equation 13.149:
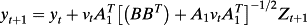 (A3)
(A3) (A4)
(A4)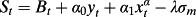 (A5)
(A5)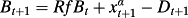 (A6)
(A6)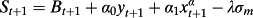 (A7)
(A7)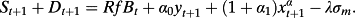 (A8)
(A8)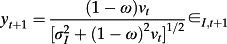 (A9)
(A9)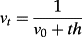 (A10)
(A10)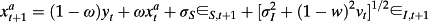 (A11)
(A11)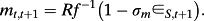 (A12)
(A12)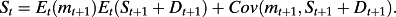 (A13)
(A13)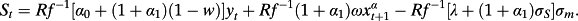 (A14)
(A14)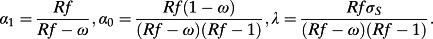
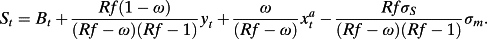 (A15)
(A15)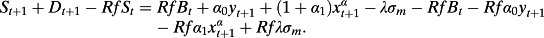 (A16)
(A16)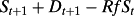
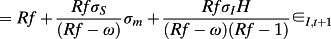 (A17)
(A17)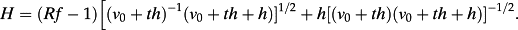 (A18)
(A18)Dividing both sides of A17 by St yields the return equation 22 in the text.
References
- 1 The model by Pastor and Veronesi (2003) offers an alternative accounting valuation approach. I will refer to their model below when discussing parameter uncertainty and learning. Otherwise, this paper focuses on the Ohlson and Vuolteenaho-type models.
- 2 A pre-cursor linear ‘accounting’ valuation model by Garman and Ohlson (1980) allows for a richer set of information dynamics than Ohlson (1995). Nevertheless, absent clean surplus, there is no conceptually meaningful accounting in the Garman-Ohlson model. Tippet and Warnock (1997) incorporate a stochastic clean surplus relation into the Garman-Ohlson model but find that it is rejected by their data.
- 3 If xt denotes earnings then
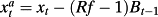 .
. - 4 There is a lot of confusion about this issue in the literature.
- 5 See also Myers (1999) and Morel (2003) on this issue.
- 6 Formally, the stochastic discount factor mt,t+ τ is defined as the marginal rate of substitution between time period t and time period t+ τ aggregate consumptions (Feltham and Ohlson, 1999; Ang and Liu, 2001; Cochrane, 2005). That is,
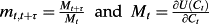 where U(⋅) is a representative agent's utility function and Ct is aggregate consumption.
where U(⋅) is a representative agent's utility function and Ct is aggregate consumption. - 7 See Callen and Lyle (2013) and the literature cited there.
- 8 Following Ohlson (1995), Lyle et al. (2013) also include another valuation-relevant variable, which we disregard for simplicity.
- 9 To keep their analysis tractable, Lyle et al. (2013) also assume that the level of risk in the economy follows a random walk: σm,t + 1 = σm,t + ξt+1,where ξt+1 is a mean zero random variable independent of et+1.
- 10 On average it is unlikely to be otherwise as long as growth in the economy and growth in firm-level abnormal earnings are positively correlated. The discount factor represents the marginal rate of consumption in the economy or growth in the economy. Therefore shocks to the discount rate factor are driven by shocks to aggregate consumption or shocks to aggregate growth, represented by et+1 which, in turn, should be positively related to shocks to (abnormal) earnings ∈ t+1.
- 11 The latter property would be satisfied in a continuous time analog of their model. It is assumed to hold in their discrete model.
- 12 Additionally, if one assumes that shocks to the discount factor are driven by shocks to the market portfolio, this discount factor can be shown to produce standard CAPM-type models for expected returns.
- 13 λ1 can be shown to be a function of both idiosyncratic and systematic risk.
- 14
Alternatively, substituting out dividends, the firm's cost of capital can be expressed solely as a linear function of firm accounting characteristics:
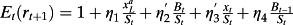 , .
, . - 15 Lyle's model is based on Vuolteenaho (2002).
- 16 One can also incorporate other information in the model such as a (costless) disclosure signal about long-run abnormal earnings. The results are similar. See Lyle (2013).
- 17 With strong abuse of notation, we retain the notation ∈ S,t+1 and ∈ I,t+1 without denoting the change in the filteration.
- 18 H in equation 22 takes the value:H = (Rf − 1)[(ν0 + th)− 1(ν0 + th + h)]1/2 + h[(ν0 + th)(ν0 + th + h)]− 1/2.
- 19 More recently, Callen and Lyle (2013) estimate correlations based solely on forward-looking data.
- 20 Easton and Monahan (2005) and Ogneva (2012) show that the Claus-Thomas model tends to dominate other static implied cost of equity models. In contrast, Botosan et al. (2011) show that the PEG model dominates.
- 21 Vuolteenaho (2002) is based in turn on the variance decomposition framework of Campbell and Shiller (1988).
- 22 Formally, roet = log(1 + Xt/Bt−1) where Xt is earnings in period t and Bt is book value of equity at period t.
- 23 See Bodnar and Weintrop (1997) and Christophe (2002) on this issue.




