Review of Recent Research on Improving Earnings Forecasts and Evaluating Accounting-based Estimates of the Expected Rate of Return on Equity Capital. Discussion of Easton and Monahan
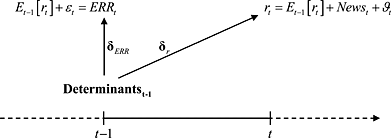
Easton and Monahan (henceforth, EM) (2005) examine the construct validity of accounting-based proxies for the expected rate of return (henceforth, ERRt) by associating them with future realized returns, controlling for the discount rate news component and the cash flow news component in those returns. As the derivation of these ERRt relies on current information only, the association test results allow inferences about their usefulness for investing and capital budgeting purposes. Contrary to expectations, their main results on the full cross section (Table 4) reveal a significantly negative (insignificant) coefficient for four (three) of the seven ERRt they evaluate, raising doubts about their construct validity.
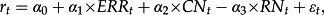 (1)
(1)Evaluating Determinants
BPW (2011) and Botosan and Plumlee (2005) evaluate ERRt not only based on their association with realized returns, but also based on associations with a set of determinants, which, like the ERRt, are estimable from information at time t–1. EM (2016) question the informativeness of such tests because the empirical finance and accounting literature has, so far, largely failed to agree on a set of risk factors. 2 Furthermore, they argue that, if a universally accepted set of risk factors existed, we would not need ERRt in the first place, as a predicted value from asset pricing regressions might serve as expected returns proxy.
In the figure above, δr is the vector of k loadings from a cross-sectional regression of future realized returns on k determinants. 3 Similarly, δERR is from a cross-sectional regression of a specific ERRt metric on the same k determinants.
Assuming the determinants are equal to a known set of risk factors at time t–1,
 needs to be estimated from historical data at the time of the investment decision (i.e., using returns up to year t–1 and determinants up to year t–2). Deriving an expected return for year t, however, requires an additional assumption about (or estimation of) the persistence parameters of each element of
needs to be estimated from historical data at the time of the investment decision (i.e., using returns up to year t–1 and determinants up to year t–2). Deriving an expected return for year t, however, requires an additional assumption about (or estimation of) the persistence parameters of each element of
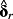 , which might even differ across loadings. If the asset pricing model contains factor-mimicking portfolio returns, the additional difficulty of forecasting the factor premia arises.
4 Lastly, the set of risk factors in t–1 need not match the risk factors in t. Because of the uncertainties in historical loadings, expected factor premia and the set of relevant risk factors, ERRt might forecast out-of-sample realized returns with less bias or higher accuracy than a predicted value from the asset pricing model, even if the set of risk factors at t–1 is known.
5
, which might even differ across loadings. If the asset pricing model contains factor-mimicking portfolio returns, the additional difficulty of forecasting the factor premia arises.
4 Lastly, the set of risk factors in t–1 need not match the risk factors in t. Because of the uncertainties in historical loadings, expected factor premia and the set of relevant risk factors, ERRt might forecast out-of-sample realized returns with less bias or higher accuracy than a predicted value from the asset pricing model, even if the set of risk factors at t–1 is known.
5
As EM (2016) discuss, the challenge is even bigger in reality, where the set of risk factors is not known. Inferences about the construct validity of ERRt from
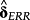 rely, in the best case, on theoretical predictions about the sign of the relation between
rely, in the best case, on theoretical predictions about the sign of the relation between
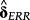 and the (true) expected return. More commonly, however, benchmark associations are based on significant results from realized-return regressions (
and the (true) expected return. More commonly, however, benchmark associations are based on significant results from realized-return regressions (
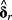 ) in prior work.
) in prior work.
Using some
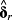 as benchmarks for
as benchmarks for
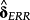 , however, is difficult for a number of reasons. Prior work might have used different test assets (firms versus various kinds of portfolios), different samples,
6 and a different empirical operationalization of the same fundamental construct of interest. The sign and significance of the loading on one determinant
, however, is difficult for a number of reasons. Prior work might have used different test assets (firms versus various kinds of portfolios), different samples,
6 and a different empirical operationalization of the same fundamental construct of interest. The sign and significance of the loading on one determinant
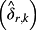 might also depend on the inclusion or exclusion of other determinants in the model, but prior work may not have tested the exact specification of interest. In addition, one study's risk factor may be another study's anomaly.
7 Put another way, a determinant of the (total) realized return may be associated with the expected return component, and therefore considered a risk factor, but it might also be associated with the news or measurement error in returns (Newst and ϑt in the figures).
might also depend on the inclusion or exclusion of other determinants in the model, but prior work may not have tested the exact specification of interest. In addition, one study's risk factor may be another study's anomaly.
7 Put another way, a determinant of the (total) realized return may be associated with the expected return component, and therefore considered a risk factor, but it might also be associated with the news or measurement error in returns (Newst and ϑt in the figures).
In short, an isolated analysis of
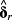 cannot rule out that determinants are determinants of the news or of the measurement error in returns, and not of the expected returns themselves. Similarly, regarding
cannot rule out that determinants are determinants of the news or of the measurement error in returns, and not of the expected returns themselves. Similarly, regarding
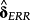 in isolation cannot rule out that the determinants are correlated with the measurement error in the ERRt (εt). Therefore, I agree with EM (2016) insofar as the interpretation of
in isolation cannot rule out that the determinants are correlated with the measurement error in the ERRt (εt). Therefore, I agree with EM (2016) insofar as the interpretation of
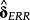 alone can teach us little about the construct validity of the ERRt as proxies for the expected return.
alone can teach us little about the construct validity of the ERRt as proxies for the expected return.
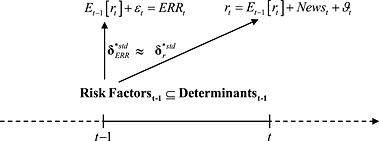
Taking this agreement as a starting point, I suggest that the design and purpose of a determinants test can be altered to yield more informative inferences. Instead of evaluating the ERRt, the determinants are considered ‘candidate risk factors’ and are themselves evaluated using a form of variable selection model with two equations. Specifically, both regressions could jointly filter the initial set of k determinants by requiring significant and statistically indistinguishable (‘similar’) standardized slope coefficients,
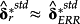 . By construction, such a test would hold the empirical definitions of the determinants, the test assets, and the sample constant, eliminating the need to ‘import’ benchmark values for
. By construction, such a test would hold the empirical definitions of the determinants, the test assets, and the sample constant, eliminating the need to ‘import’ benchmark values for
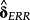 from prior research.
from prior research.
If common determinants exist,
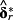 and
and
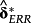 define a common component in realized returns and ERRt, respectively. I hypothesize that a joint determinants test, relying on the similarity of
define a common component in realized returns and ERRt, respectively. I hypothesize that a joint determinants test, relying on the similarity of
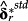 and
and
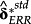 , makes it less likely that significant loadings are driven by measurement error in either dependent variable (εt and ϑt), or by (future) news in returns.
8
, makes it less likely that significant loadings are driven by measurement error in either dependent variable (εt and ϑt), or by (future) news in returns.
8
As it is assessable at time t–1, the predicted value from the ERRt regression on the selected risk factors is an (ex-ante) measure of expected return. The difference to a predicted value from asset pricing regressions on future returns alone is that
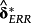 describes a contemporaneous relation of risk factors with ERRt, while the selection of those risk factors is conditional on their historical association with future returns. In that sense, the aforementioned concerns about the over-time persistence of
describes a contemporaneous relation of risk factors with ERRt, while the selection of those risk factors is conditional on their historical association with future returns. In that sense, the aforementioned concerns about the over-time persistence of
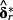 cannot play a role, but the uncertainty about whether the set of risk factors is constant over time remains.
cannot play a role, but the uncertainty about whether the set of risk factors is constant over time remains.
In short, using jointly selected risk factors out of an initial set of ‘candidate determinants’ adds a step to the process, but indirectly addresses the same basic research question. It also tests for an association of ERRt with returns, while trying to control for possible correlations in the ‘imperfections’ of both proxies for the expected return. In this framework, the existence of a set of risk factors (with
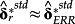 ) is congruent with the construct validity of the ERRt.
) is congruent with the construct validity of the ERRt.
An important practical benefit from the identification of the
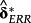 loadings is that they can be estimated and applied in real time to define a firm-specific expected return.
9 Using the loadings allows the computation of a (predicted value for an) ERRt for the large set of firms that have sufficient data on the risk factors, but without either price data and/or the well-behaved forecast data to compute ERRt directly, for example, all private firms.
10
loadings is that they can be estimated and applied in real time to define a firm-specific expected return.
9 Using the loadings allows the computation of a (predicted value for an) ERRt for the large set of firms that have sufficient data on the risk factors, but without either price data and/or the well-behaved forecast data to compute ERRt directly, for example, all private firms.
10
If application to firms outside the ERRt sample is the goal, the initial set of candidate determinants should depend on what data are available for those target firms (or samples). If price and returns data are available for the target firm, the initial set of candidate factors can include market-wide factor returns and price-based ratios (such as B/M); if not, the initial set of candidate factors needs to be limited to firm-specific fundamental (e.g., accounting-based) characteristics.
Correlations, Slopes, and Paths
It is my general sense, and consistent with EM (2016), that the results of EM (2005) have contributed to a widespread view about the construct validity of accounting-based ERRt being low, an inference based on the negative or weak α1 coefficients in Regression (1). On the positive side, this has surely spurred much interesting work in this area. In this section, however, I present the first of two arguments for why the interpretation of the results might have been too pessimistic.
In my view, both EM and BPW do not present one, but two distinct sets of cross-sectional results to their research question. With this section, I attempt to re-allocate some of the emphasis more equally than the allocation of text and table space in those papers suggests.
Rather than treating the early tables as mere descriptive statistics, I argue that the positive (univariate) correlations between realized returns and ERRt already provide one answer to the research question. EM (2005) provide significance tests for those correlations, showing that rGLS and rCT are significantly (in one-sided tests) correlated with returns, in the hypothesized positive direction. BPW's average correlations are all positive, but they do not provide significance tests. Neither paper provides univariate regression coefficients and the average descriptive statistics are insufficient for their computation by the reader. Assuming that the standard deviation of returns is much larger than the standard deviation of ERRt in each cross section, the regression coefficient is likely to be a multiple of the correlation coefficient with equal sign.
I draw attention to the correlation results because the univariate associations (correlations or regression coefficients) allow inferences about the construct validity of ERRt under the assumption that explicit controls for news components in returns are not necessary in cross-sectional tests. The multivariate (main) results, on the other hand, allow inferences under the two assumptions that (i) news components vary systematically across firms in the cross section, and, hence, controls in empirical tests are necessary, and (ii) the returns decomposition is correctly specified and no mechanical relations between the regression variables exist.
Controlling for news might not be necessary because news are not large, not systematic, or because they affect all firms of the cross section similarly (i.e., the news are a cross-sectional constant) and therefore cancel out in cross-sectional tests. 11
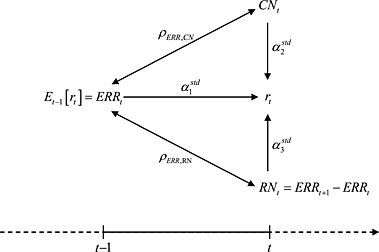
Put differently, and referring to the path diagram above (error terms are omitted), the argument implies that investors may consider it less important through which of the three ‘paths’ the univariate correlation of ERRt and returns in each cross section operates: either through a direct effect (
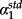 , the standardized multivariate slope coefficient from Regression (1)), a mediated effect through cash flows news (
, the standardized multivariate slope coefficient from Regression (1)), a mediated effect through cash flows news (
 ), or a mediated effect via discount rate news (
), or a mediated effect via discount rate news (
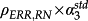 ). Any form of returns decomposition simply allocates the (constant) univariate correlation differently to the three paths; that is, through variation in the α1,2,3 coefficients. For example, if measurement error in both news proxies increases,
). Any form of returns decomposition simply allocates the (constant) univariate correlation differently to the three paths; that is, through variation in the α1,2,3 coefficients. For example, if measurement error in both news proxies increases,
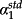 (α1) approaches the univariate correlation (slope coefficient).
(α1) approaches the univariate correlation (slope coefficient).
To summarize, EM and BPW contain two sets of answers to their common research question, derived under opposing assumptions about whether requiring controls for news in cross-sectional analyses is necessary or not. As inferences about the construct validity of ERRt may depend on the validity of these assumptions, further exploration in this field would be very valuable.
Sampling Under Data Constraints
This section discusses the implicit sampling due to data constraints as a second reason for why the results in EM (2005) may have been interpreted too pessimistically. The argument is as follows. For the entire cross section of their sample, the results under the returns decomposition approach are either statistically weak or even contradictory to theory and their hypothesis. However, Section 6 of EM (2005) documents results for cross-sectional tercile partitions of their sample. Across Panels B and C, Table 9 shows five of the 42 coefficients of interest (seven ERRt metrics × three terciles × two grouping variables) are significantly positive, and 16 coefficients are significantly negative.
The important insight from these results, in my view, is not necessarily that significance of the coefficients in the hypothesized positive direction can be established for fractions of the sample, nor that it remains scarce. The important insight is that there is substantial variation around the aggregate result from the full cross section, despite the crudeness of a tercile sample split. Interpreted narrowly, the results speak to the ‘contribution’ of those tercile subsamples to the overall sample results. Interpreted more broadly, the results point to the existence of subsamples in EM's overall sample for which the hypothesized association appears to hold.
The immediate question then arises as to the importance of these tercile subsamples for the entire population of firms, rather than for the specific sample used by EM. In other words, each tercile subsample, by construction, contains a third of EM's sample, but the open and important question is how many firms, or how much weight, each of these subsamples represents in the population of firms to which we would like to generalize the results of EM's tests.
To make this question more general, the ‘subsamples’ should not really be thought of as just the specific tercile splits in EM's design, but rather as any form of (sub-)sampling that spans cross-sectional variation in the results. Specifically, the cross-sectional variation in the coefficients opens up the possibility that any form of subsamples with the hypothesized relation between ERRt and returns simply comprise only a small portion of the actual EM test sample, but a large portion of the overall population. In short, the EM test sample might not be representative of the population of firms from which it was drawn.
The reason for non-representativeness, or non-randomness, of a test sample is data requirements. Aggregated across the seven ERRt examined by EM, the firm-year-level observations must have analyst following (specifically, IBES coverage), positive earnings per share (EPS) forecasts over the next two years, and positive earnings growth from year t+1 to year t+2 (through either an explicit forecast of EPSt+2, or a positive long-term growth forecast that can be used to calculate EPSt+2 from EPSt+1). 12 In short, a systematic form of sample attrition could arise implicitly, through the stringent data requirements of the expected return proxies.
These are the motivating observations for Ecker et al. (2015), where we explore the issue of implicit sampling biases in general, and in the specific context of the associations between ERRt and returns. We recognize the stringency of the data constraints in the ERRt derivation, which may lead to a departure (non-randomness) of actual research samples vis-a-vis the (larger) population of firms to which test results are intended to generalize. Any firm in the population has, on a conceptual level, an expected return; empirical proxies for that expected return are just not attainable from machine-readable data sources such as IBES, and we suspect the implicit sampling is far from random. Initial, circumstantial evidence for why this might be the case is traceable to the nature of the data requirements. Sell-side analysts tend to follow firms that are on average larger; requiring positive earnings and positive earnings growth will filter out (expected-) loss-making firms by definition. The final test sample is thus likely to exclude relatively smaller firms with lower profitability and less stable growth prospects.
I conjecture that, at a minimum, such a sample will have smaller variation in their true expected returns (as well as in their ERRt proxies) compared to the overall cross section of firms. At a minimum, a reduction in the variance of the independent variable leads to a reduction in test power, relative to a hypothetical test on the population. On the other hand, it is knowable, for example, from the descriptive statistics in Ecker et al. (2015), that the ERRt sample exhibits a much reduced variation in realized returns, that is, the dependent variable.
Ecker et al. (2015) posit that the results of EM's (2005) test should be generalizable, in the best of all worlds, to all firms. Some form of limitation, however, is unavoidable in practice. As the association of interest is with realized returns, some degree of reliability and standardization of the measurement of these returns is necessary. Private firms will have measureable realized returns only at discrete and widely spaced points in time, for example, at sale transactions or at equity financing transactions. Therefore, we define the population as limited to listed firms, and to listed firms on US stock exchanges, which have dollar-denominated prices. 13
In our data-constrained ERRt sample, we find significantly negative correlations with returns for four of the five ERRt we consider, and one correlation is insignificantly negative. We also find the differences in the marginal distribution of returns in each monthly cross section between sample and population to be large, and statistically significant in 401 of the 402 months in our sample period. In other words, while the joint distribution in the population is and remains unknown, the marginal distribution of returns is changed significantly by requiring the availability of ERRt.
We resample the observations from the data-restricted sample such that the returns distribution in the resampled set of firms is indistinguishable from the returns distribution in the population. That is, we aim to offset the measurable non-randomness in the test sample induced by data constraints with a non-random sampling scheme. Effectively, the final (resampled) test sample aims to mimic a sample that is randomly drawn from the population with regard to the marginal distribution of returns, despite consisting of data-restricted observations (i.e., with ERRt data) only. The associations of interest, between returns and ERRt, in those resampled ‘distribution-matched’ samples, are quite different from the benchmark results from unmodified samples: in one specification, all correlations are significantly positive, and four of the five are statistically indistinguishable from 1.
The approach is logically linked to the previous discussion of results in EM's tercile subsamples. If the results do not vary across subsamples of the data, we should not expect any change in the overall result when we reweight the subsamples to match the corresponding weight of that subsample in the population of firms.
Taking an alternative perspective on the sample bias issue, I note that both EM and BPW could have chosen a completely different empirical design by identifying an intentionally biased sample for which the posited results are most likely to hold. Specifically, a researcher could have further limited the test sample, even after the implicit sampling through data constraints, to firms that are more mature, and closer to steady state. 14 Steady-state proxies are, of course, hard to come by. Firm size (and, hence, firm-level diversification) might be one such proxy. 15 The tercile-split variables in EM might also be steady-state proxies; that is, steady-state firms might have a low long-term growth rate, for example, close to the inflation rate, or have a rich information environment, and, hence, low absolute forecast errors. In short, maybe steady-state firms are the firms that drive the hypothesis-consistent results in EM's tercile splits. There might be other and more direct empirical steady-state indicators, of course.
My point is that for certain non-random test samples, the hypothesized association between ERRt and returns might hold quite well, simply because such firms are closer to a pricing equilibrium. On one hand, the equilibrium assumption is inherent in the derivation of the ERRt, and conditioning on steady state might therefore help reduce measurement error in both ERRt and returns. On the other hand, conditioning on steady state might also render it less important (both conceptually and empirically) to introduce direct controls for the cash flow news and discount rate news components of realized returns in the regression itself, as the sampling scheme can be expected to decrease the magnitude of the news. 16
A ‘biased sample’ research design differs markedly from the first ‘generalization’ approach, which considers the ERRt and the returns as valid proxies for all firms, regardless of data availability. The ‘biased sample’ research design, however, introduces a conceptual divide into two subsamples of the population, one for which the hypothesis should not hold yet, due to immaturity, or steady state violations, of the member firms, and another subsample for which the hypothesis should hold. As such, results from the second subsample are not supposed to be generalizable to the first; rather, firms in the immature subsample are expected to migrate to the mature subsample over their lifetime, that is, as they converge to steady state. 17
Conclusion
Establishing the validity of accounting-based proxies for expected returns is an important prerequisite for their use. This discussion proposes a joint determinants test of ERRt and returns that is consistent with the evaluation framework of Easton and Monahan (2005, 2016) and Botosan et al. (2011). I also discuss two arguments for why the results in Easton and Monahan (2005) might have been interpreted too negatively. The first argument is that the univariate results in Easton and Monahan (2005) and Botosan et al. (2011) may be more consistent with the hypothesized positive association between ERRt and returns. The second argument is the implicit non-random sampling through data constraints, which leads to sample-specific results that are not generalizable to a population of firms to which the results should, in theory, apply. Combined, the discussion points out arguments for why the construct validity of accounting-based proxies for expected returns may be higher than previously thought.
References
- 1 Quite possibly motivated by a negative interpretation of EM's aforementioned results, one stream of literature develops alternative ERRt metrics, or tries to improve on the accuracy of input data by removing analyst forecast biases (Guay et al., 2011; Larocque, 2013; Mohanram and Gode, 2013), by replacing analyst forecasts with mechanical models (Hou et al., 2012; Gerakos and Gramacy, 2013; Li and Mohanram, 2014), or by jointly estimating ERRt and implied growth rates (Nekrasov and Ogneva, 2011, discussed by Monahan, 2011).
- 2 For the purposes of this discussion, risk factors can be either risk factor betas or characteristics.
- 3 An intercept might be included in the regressions, but this question is less important for the purpose of this section.
- 4 In their examination of CAPM-based and three-factor-based expected returns on the industry level, Fama and French (1997) first document substantial time-series volatility in realized loadings. More importantly, they attribute most of the imprecision of these expected returns to the time-series volatility in realized risk-factor premia. Fama and French conjecture that factor-model-based expected returns are even worse on the firm level or project level, as the loadings for individual firms or even projects are likely estimated with less precision and hence show higher time-series volatility.
- 5 Corroborating this conjecture, BPW (2011, Table 6) report that a predicted value from the Fama-French (1993) three-factor model, augmented by a momentum factor, is one of only two expected return proxies (out of 12 in total) that do not yield a significantly positive coefficient in regressions of realized returns.
- 6 I return to the sampling issue later in the paper.
- 7 Most prominently, the size and book-to-market (B/M) effects were considered CAPM anomalies before Fama and French (1992, 1993) considered them risk factors and incorporated them in an asset pricing model. Carhart's (1997) momentum factor has been considered mispricing, yet is being used in asset pricing regressions (as in BPW, for example).
- 8 It is also possible to augment the determinants regression on realized returns with explicit news proxies. It is an empirical question if those controls improve the identification of risk factors, or if the comparison of
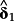 to
to
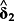 is sufficient.
is sufficient. - 9 In that sense, the determinants approach is superior to a principal component analysis of ERRt and returns to filter out the ‘expected return’.
- 10 Even if earnings can be forecasted using proprietary pro-forma (or mechanical) models, the set of firms for which ERRt can be derived is still limited to listed firms with price data. To my knowledge, it is an open question how a predicted value from a determinants model would perform relative to an ERRt derived from proprietary earnings forecasts. Such a test effectively compares the estimation error from an incorrect identification of risk factors, combined with the estimation error in their loadings, with the estimation error in the proprietary (or mechanical) earnings forecast.
- 11 Vuolteenaho (2002) provides some exploratory results on the extent to which cash flow news in particular, but also discount rate news are ‘diversified away’ through cross-sectional aggregation. I am reluctant to draw strong conclusions from the documented decrease in the magnitudes of both news items, because his sample and his empirical implementation of the returns decomposition are both very different from the designs in EM and BPW.
- 12 There are other data constraints, for example, positive book value of equity on Compustat, that either do not specifically pertain to the ERRt, or are presumably not incrementally binding, over and above the ERR-imposed data constraints. EM (2005) also restrict their sample to firms with a December fiscal year-end, but it is hard to hypothesize any systematic impact of that restriction on the results.
- 13 As we also perform tests on factor betas, we require 12 consecutive months of returns. Statistical tests indicate that this requirement does not meaningfully affect the marginal distribution of the monthly returns.
- 14 Alternatively, a researcher could choose sample periods (not firms) that were less affected by news, and therefore closer to steady state.
- 15 Fama (1998) favours value-weighting as a way to explain return anomalies. Analogously, the construct validity of ERRt could be implemented in the form of weighted least squares.
- 16 Within his pooled design, Vuolteenaho (2002, Table 4) provides direct evidence that the magnitudes of both types of news are decreasing with firm size.
- 17 It is, to my knowledge, an untested avenue of research to what extent the research of adjusting earnings forecasts by analysts, or even replacing the analyst with a mechanical model, is consistent with deriving steady-state earnings forecasts. Mechanical forecasts, for example, simply impose past linear associations with a select set of current determinants to derive future earnings forecasts. The exact definition of this set is not very important according to Hou et al. (2012), Gerakos and Gramacy (2013), and Li and Mohanram (2014). The open questions are then (a) if such linear extrapolations from currently known determinants ‘force’ steady state in the earnings forecasts, and (b) if it is this steady-state advantage that outweighs the inherent imperfection of any necessarily limited set of forecast determinants.