The Effect of Operating Leverage on Managers' Capital Investment Decisions*
Accepted by Leslie Berger. This paper is based on my second-year summer paper at Michigan State University. I am grateful to Kyonghee Kim (advisor) for the invaluable guidance and support. I also thank Leslie Berger (editor), two anonymous reviewers, Matt Anderson, John (Xuefeng) Jiang, Ranjani Krishnan, Adam Presslee, and the faculty members and other doctoral students in the Department of Accounting and Information Systems at Michigan State University and School of Accounting and Finance at the University of Waterloo for helpful comments. I thank Eli Broad College of Business for generously funding this study.
ABSTRACT
enHolding all else constant, a larger proportion of fixed costs in the cost structure (i.e., higher operating leverage) implies a greater profit volatility for a given level of demand fluctuation. In a setting where operating leverage is irrelevant to the choice of investment projects, I experimentally examine whether managers under high operating leverage (as opposed to low operating leverage) choose a less profitable project for lower variability in anticipated earnings. Inconsistent with the hypothesis, I find that the level of operating leverage has an insignificant impact on managers' investment choices, providing preliminary evidence that managers may correctly identify the level of operating leverage as irrelevant. Notably, providing the cost structure information to managers, regardless of whether it pertains to high or low operating leverage, increases the likelihood of selecting the more profitable investment. Additional analyses suggest that the excerpt on operating leverage might prime managers to deliberate more on the investment decisions. Managers who receive the cost structure information dedicate more time to assessing the investment projects, which in turn aids in identifying the more profitable project.
RÉSUMÉ
frL'EFFET DU LEVIER D'EXPLOITATION SUR LES DÉCISIONS DES GESTIONNAIRES EN MATIÈRE D'INVESTISSEMENT
Toutes autres variables constantes, une proportion plus importante des coûts fixes dans la structure des coûts (c.-à-d., un levier d'exploitation élevé) se traduit par une plus grande volatilité des bénéfices à un niveau donné de fluctuation de la demande. Dans une situation où le levier d'exploitation n'est pas pertinent pour le choix des projets d'investissement, nous vérifions à l'aide d'une expérience si les gestionnaires qui disposent d'un levier d'exploitation élevé (par rapport à un levier d'exploitation faible) choisissent un projet moins rentable au profit d'une variabilité plus faible des résultats prévus. Contrairement à l'hypothèse posée, nous établissons que le niveau de levier d'exploitation a un impact non significatif sur les choix d'investissement des gestionnaires, fournissant ainsi des données préliminaires indiquant que les gestionnaires peuvent déterminer correctement que le niveau du levier d'exploitation n'est pas pertinent. Fait à noter, les gestionnaires qui obtiennent de l'information sur la structure de coûts, qu'elle fasse état d'un levier d'exploitation élevé ou faible, sont plus susceptibles d'opter pour les investissements les plus rentables. D'autres analyses portent à croire que l'information propre au levier d'exploitation peut inciter les gestionnaires à soupeser davantage leurs décisions d'investissement. Les gestionnaires qui reçoivent de l'information sur la structure des coûts consacrent davantage de temps à l'évaluation des projets d'investissement, ce qui les aide à identifier les projets les plus rentables.
1 INTRODUCTION
Capital investments play a crucial role in managerial decision-making (Graham et al., 2015; Graham & Harvey, 2001; Haka, 2006). This paper examines the effects of operating leverage in a firm's historical cost structure on the manager's capital investment decision. Importantly, I focus on a setting in which the cost structure does not influence investment outcomes and, therefore, should be irrelevant to the decision-making. Drawing on dual-process theories of information (Finucane, 2012; Slovic et al., 2005), I hypothesize that a manager's experiential perception of operating risk (e.g., anxiety associated with a high level of risk), tied to operating leverage in the firm's cost structure, leads managers to choose a less profitable project in favor of lower variability in anticipated earnings.
A practical example of the decision-irrelevance of historical cost structures is a manager's reshoring decision. Media articles and professional reports have advocated for the reshoring of Canadian firms' offshore production facilities over the years (Carmichael, 2012; Yakabuski, 2020). Although firms may have strategically chosen to produce overseas, changes in the operating environment can lead to reshoring opportunities that are independent of the historical cost structure. Additionally, firms can face significant adjustment costs during unanticipated operational disruptions. The supply chain challenges posed by the COVID-19 pandemic and the Pacific Northwest floods of 2021 intensified calls for reshoring (KPMG, 2022; Lampert & Gordon, 2021; Thomson, 2022). As this example demonstrates, managers often encounter a cost structure as a given, unrelated to investment outcomes. In such scenarios, managers should consider the historical cost structure irrelevant to the investment decision.
Operating leverage measures the proportion of fixed costs in a firm's total operating costs. Ceteris paribus, a higher (lower) proportion of fixed costs subjects a firm to a greater (lower) level of earnings volatility for a given level of fluctuation in revenue (Datar & Rajan, 2021; Lev, 1974). Prior studies in accounting have amassed considerable evidence that managers adjust operating leverage as a long-term response to changes in the firm's operating environments and regulations (Aboody et al., 2018; J. V. Chen et al., 2024; Holzhacker et al., 2015; Kallapur & Eldenburg, 2005). Relatively understudied, however, is managers' use of cost structure information in other operating decision-making. Specifically, the literature is silent on whether and how managers incorporate the information in corporate investments. This paper attempts to fill this gap by substantiating whether managers attend to cost structure information in capital investment decisions.
A firm's cost structure is generally a component of its strategies and is adjustable in the long term, in response to changes in operating environment and production technologies (J. V. Chen et al., 2024; Kallapur & Eldenburg, 2005). In the long run, a firm's cost structure and capital investment decisions likely affect each other in a dynamic relationship through such channels as the firm's systematic risk (Lev, 1974) and capital structure (Z. Chen et al., 2019; Mandelker & Rhee, 1984). However, in the short run, high adjustment costs make a firm's cost structure difficult to shift (Balakrishnan et al., 2014; Banker & Byzalov, 2014; Golden et al., 2020).
I rely on the relative stationarity of cost structure in the short term to study a setting where a firm's historical cost structure does not influence outcomes of investment projects. In the setting of this study, a manager is responsible for choosing between two mutually exclusive capital investment projects that differ only in the variance of unit contribution margin (“CM uncertainty”) and are otherwise identical.1 The information germane to the investment choice is the expected profits from either investment project. The level of operating leverage in the firm's historical cost structure is irrelevant to the expected profits and thus to the investment decision.
Despite the decision-irrelevance of the cost structure information explained above, psychology theories suggest that managers may nevertheless allocate nonzero weights to the information. Dual-process theories of information contend that individuals intuitively perceive risk in two fundamentally different ways: the fast, intuitive “experiential system” and the slow, deliberative “analytic system” (Finucane, 2012; Slovic et al., 2005). The experiential system can misguide evaluation of risk and benefits, even in the presence of analytic information processing (Alhakami & Slovic, 1994; Finucane, 2012; Finucane et al., 2000; Slovic et al., 2005). Because the experiential perception of risk is automatic and rapid, these theories would predict that managers rely on experiential (or affective) responses to the cost structure information in making capital investment decisions. As negative affect associated with the high level of operating risk spills over to the decisions, I hypothesize that managers in a higher (as opposed to lower) operating leverage position are more likely to prefer the less profitable investment project that has a lower CM uncertainty.
To test this hypothesis, I conduct a controlled lab experiment that operationalizes key features of the setting of interest. I design a 31 between-subjects experiment in which 100 undergraduate students assume the role of a manager at a fictional manufacturing company. I manipulate operating leverage in the firm's historical cost structure, randomly assigning one third of participants each to high and low operating leverage conditions. I assign the remaining third to a control group that does not receive any information about the historical cost structure. I ask participants to read the background information and choose between two mutually exclusive investment projects that represent the setting discussed above.
The findings show that 30% of the participants chose the project with higher CM uncertainty (which has higher expected profits), while 70% chose the project with lower CM uncertainty. Inconsistent with the hypothesis, however, the level of operating leverage in their cost structure does not appear to influence their investment choices. Participants in the high operating leverage condition are not significantly more likely to choose the project with lower CM uncertainty than those in the low operating leverage condition (p = 0.71).2
Next, I report noteworthy findings from the post hoc analyses. I find that the presence of cost structure information significantly influences managers' investment decisions. Compared to participants who did not receive the cost structure information, participants who received the information (either high or low operating leverage) were more likely to choose the more profitable investment project with higher CM uncertainty.
This finding may be attributed to priming effects (Bargh et al., 1996; Bargh & Ferguson, 2000) whereby participants provided with a vivid excerpt on an accounting concept (i.e., operating leverage) deliberated more on the investment decision task at hand. Consistent with this rationale, I find in a path analysis that participants with the cost structure information deliberated more on the investment decisions, compared to participants with no cost structure information, when they had some prior accounting knowledge (p = 0.02); in turn, the greater deliberation is significantly associated with more profitable investment decisions (p < 0.01). In addition, I find some evidence that participants provided with the cost structure information were cognizant of economic decision-making criteria. Relative to those in the control group, participants in this group were more likely to mention costs (p = 0.05) and product demand (p = 0.10) as a rationale behind their investment decisions.
This study contributes to the literature in two ways. First, this study is among early studies in accounting that examine how managers use information about the firm's cost structure in their operating decisions (Chang et al., 2024; Matsumura et al., 2023). In this paper, I show that managers presented with information on the firm's cost structure in a salient way chose to invest in a more profitable investment choice. This finding adds to prior studies that investigate how additional information (Swain & Haka, 2000) or the use of decision aids (Iyer et al., 2012; Sawers, 2005) guides the manager's decision-making process in capital investments.
Second, I add to studies that examine the influence of affect on the manager's capital investment decisions (Farrell et al., 2014; Fehrenbacher et al., 2020; Kida et al., 2001; Moreno et al., 2002; Sawers, 2005) by considering the influence of a firm's operating leverage in its cost structure as a source of non-interpersonal, negative affect arising from an abstract construct. Most papers in this stream focus on strong interpersonal affect, and to the best of my knowledge, this paper is the first to show that the presence of a firm's fundamental accounting information (i.e., cost structure) can influence the manager's investment decisions.
2 SETTING OF INTEREST AND HYPOTHESIS DEVELOPMENT
Setting of Interest
I examine a setting in which a manager has to choose a capital investment project under stochastic demand, revenue, and costs. Three cardinal features characterize the decision-making in this setting. First, the manager faces two investment choices that differ only in the variance in unit contribution margin of the output (“CM uncertainty”) and are otherwise identical (J. V. Chen et al., 2024; Detemple & Kitapbayev, 2020; Kallapur & Eldenburg, 2005).3 As the demand and unit contribution margin are independent in this setting, CM uncertainty directly translates to volatility in total profits. The significance of CM uncertainty as a key aspect of managers' investment decisions is well documented in the literature. Kallapur and Eldenburg (2005) examine changes in Washington hospitals' cost elasticity in response to the introduction of Medicaid, an exogenous increase in the CM uncertainty. Detemple and Kitapbayev (2020) model a manager's investment choice and timing under varying levels of CM uncertainty parameterized as the correlation between the revenue and costs.
Second, production incurs variable costs, and managers can costlessly idle the production (McDonald & Siegel, 1985). This feature implies that managers can opt to record zero revenue and zero costs (and hence zero profit) when the market is forecast to be adverse. Both investment choices are consequently insulated from loss. Importantly, investment choice with the higher CM uncertainty offers significantly greater expected profits with the option to idle the production. That is, while the distribution of profit is more dispersed under the higher CM uncertainty, the variability comes mostly from the greater upside potential after the loss is truncated.
Third, the product market environments are exogenous, and managers' investment choices do not alter the demands or the price of the product. This setting also abstracts away from factors that may influence both the cost structure and capital investment decisions of a firm (e.g., long-term strategies, capital structure).
Decision (Ir)relevance of Cost Structure Information
Ceteris paribus, a higher operating leverage (i.e., higher proportion of fixed costs in a firm's total operating costs) corresponds to a greater volatility of profits for a given level of demand fluctuation (Datar & Rajan, 2021). Consistent with this intuition, theoretical research notes operating leverage as a source of a firm's systematic risk (Lev, 1974). Prior empirical studies document empirical evidence that managers utilize operating leverage as a long-term adjustment to their firms' risk profiles (Aboody et al., 2018; Holzhacker et al., 2015; Kallapur & Eldenburg, 2005).
Despite the well-established understanding of operating leverage as an aspect of a firm's operating risk, consequences of a cost structure remain understudied in the literature. An emerging strand of studies in accounting show how a manager reflects information on the firm's cost structure in other operating decisions. Mastilak (2011) provides early empirical evidence that the classification of costs into cost pools affects what information managers receive and how the managers use the information therein. Matsumura et al. (2023) provide evidence from a lab experiment that managers with more complex cost systems (who have more confidence in the cost system) are less likely to attribute declining profitability to the cost system. Chang et al. (2024) document a dynamic interdependence between the firm's cost structure and the manager's inventory choices. Their findings suggest that managers use these two components as substitutes when responding to demand uncertainty.
This paper studies whether managers can identify decision (ir)relevance of the cost structure information. I consider two cost structures with differing levels of operating leverage: low operating leverage (low fixed costs, high variable costs) and high operating leverage (high fixed costs, low variable costs). Importantly, the only relevant information when evaluating the two investment projects in this study is the expected profits—in the setting of interest, the firm's historical cost structure does not influence the expected profit from the investment under consideration and is therefore irrelevant to the investment decision.
Influence of Experiential Risk Perception on Investment Decisions
The dual-process theories of information contend that humans employ an analytic system (“slow, deliberative analysis we apply to assessing risk and making decisions about how to manage hazards”) and an experiential system (“fast, intuitive, affective reactions to danger”) in perceiving risk (Epstein, 1994; Finucane, 2012; Slovic et al., 2005, p. 58). Slovic et al. (2005) refer to the two fundamentally different approaches to risk perception: “Risk as feelings refers to individuals' fast, instinctive, and intuitive reactions to danger. Risk as analysis brings logic, reason, and scientific deliberation to bear on risk management” (p. S35). The “experiential” perception of risk as feelings suggests that rapid, affective responses in perception of risk can drive the subsequent decision-making, even when the analytic system is active. For example, affective responses can misguide individuals' evaluation of risk and benefits, leading individuals to make economically suboptimal decisions (Alhakami & Slovic, 1994; Finucane, 2012; Finucane et al., 2000; Slovic et al., 2005).
A related stream of studies in accounting documents rich experimental evidence of managers attending to affect in the context of capital investment decisions. Kida et al. (2001) find that relative to those in the control group, managers exposed to negative affect are more likely to reject economically profitable investments. Moreno et al. (2002) similarly show that managers with induced affect accept (reject) investment choices that elicit positive (negative) affect. These papers suggest that managers avoid investment alternatives associated with negative affect, likely because they derive disutility from the negative affect. Sawers (2005) finds that negative affect triggered by choice difficulty leads managers to avoid making capital investment choices. Fehrenbacher et al. (2020) document that while managers with induced positive (negative) interpersonal affect are more (less) likely to accept an economically profitable capital investment, accountability of the decision-making mitigates such associations under positive affect. In summary, this literature suggests that managers factor in the influence of affect in capital investment decisions, incremental to profits from the investment.
While most of these studies focus on strong interpersonal affect (e.g., interactions with a person who induces strong fear, frustration, or anger), the use of affect heuristics in decision-making is not confined to extreme emotions. Images (e.g., words, numbers, symbols) are fundamental to affect heuristics (Finucane, 2012), and seemingly neutral, simple stimuli can influence investment decisions. For instance, MacGregor et al. (2000) show that willingness to invest in stocks is positively correlated with images associated with industry groups.
In my setting, managers exposed to higher operating leverage in the historical cost structure are subject to a higher operating risk. The risk-as-feelings theory would predict that as managers instinctively rely on affective response to the (decision-irrelevant) cost structure information in making a capital investment decision, negative affect associated with operating risk can spill over to the decision.4 I posit that because of the negative affect, they value the investment choice with a greater profitability and more upside potential more negatively and opt for the less profitable project with smaller upside volatility in profits. I predict that managers with higher (as opposed to lower) operating leverage in their cost structure are more likely to prefer investment projects with lower CM uncertainty. Thus, I formally state my hypothesis as follows:
Hypothesis.Managers are more likely to choose an investment project that has lower uncertainty in unit contribution margin when in a high operating leverage position than a low operating leverage position.
3 METHOD5
Participants
I test my hypothesis using a laboratory experiment. I recruit a total of 106 undergraduate students from 2 large public universities in Canada and the United States.6 Prior studies (e.g., Libby et al., 2002; Matsumura et al., 2023) argue that students are appropriate participants for tasks not requiring specific experience. While capital investment decisions are typically complex, the task in this study requires only an understanding of the material, not necessarily experience in capital investments. However, to ensure that participants understand the accounting-specific context of the experiment content, I recruit most participants from accounting courses.7 I conducted the experiment in-person in proctored computer labs where each participant used a computer to access a Qualtrics-based instrument. The recruited participants are 53.8% male with mean age of 21.0, and 32.7% had some full-time work experience. I observe no systematic differences between the conditions in terms of biological sex, age, and accounting courses taken (p = 0.11 to 0.93).
Procedures
I design the experiment using a vignette to operationalize features of the setting described in Section 2. Participants assume the role of managers working for a fictional manufacturing company tasked with making a single capital investment decision. The sequence of this experiment is that participants (1) read the instructions and background information, (2) read about the investment choices, (3) receive information about the forecasted market conditions, (4) make an investment decision, (5) decide the number of units to produce, and (6) respond to a post-experiment questionnaire (PEQ) including demographic questions. I collect the PEQ to understand participants' rationales for their investment decisions and considerations of the historical cost structure. I require participants to pass a block of comprehension checks questions at the end of stages (1) and (2) to ensure an understanding of the material.8 The investment and production decisions are irreversible, and participants cannot return to previous pages once they pass comprehension checks. The investment and production decisions are linked to the company's profits, based on which I compensated participants. I detail the compensation scheme in the following subsection. Table 1 summarizes the experiment sequence.
| 1 | Participants read the instructions and background information |
| 2 | Participants read about the investment choices |
| 3 | Participants receive information about the forecasted market conditions |
| 4 | Participants make investment decisions |
| 5 | Participants decide the number of units of the output to produce |
| 6 | Participants complete the PEQ:
|
A key feature of this experimental design is that participants commit to an investment choice or production volume only after they receive information about market conditions. Participants, therefore, acknowledge that their investment and production decisions can reflect the information about market conditions and that uncertainty arises only from the realization of forecasted market conditions. Such a design reflects the setting of interest and obviates potential concerns about capital adjustment, inventory costs, or other factors that can confound investment decisions.
Independent Variable
I manipulate between subjects the historical cost structure of the company. Specifically, I randomly assign participants to a historical cost structure with a high operating leverage (High OL), a low operating leverage (Low OL), or the control group that receives no information about the cost structure (No OL).
All participants begin by reading about the background of the company: they work for a manufacturer of seaplane engines planning to implement quality control technology that incurs production costs for each unit of the engine. Next, participants in the High OL or the Low OL conditions proceed to paragraphs that explain operating leverage in general, the use of operating leverage as a measure of cost structure, and how different levels of sales revenue result in different profits.9 Participants in the High (Low) OL condition then learn that their company has a high (low) operating leverage in its cost structure, whereby the company's historical cost structure is 85% (15%) fixed and 15% (85%) variable. I reiterate the historical cost structures in relative terms, mentioning that such a level of operating leverage is significantly higher (lower) than those of industry peers.
Dependent Variables
After reading the background, participants make an investment decision. As explained in Section 2, the investment choice set includes two technologies that are identical in all other aspects and differ only in CM uncertainty (i.e., low CM uncertainty or “Eta” and high CM uncertainty or “Lambda”). I operationalize the low (high) CM uncertainty by setting the correlation between the unit sales price of the engine and unit variable cost as 0.95 (0.05). Under the high correlation parameter, the fluctuation of the unit variable cost for the technology is similar to that of the product's unit sales price, hence low CM uncertainty. Conversely, the fluctuation of the unit variable cost is dissimilar to that of the unit sales price under the low correlation parameter, hence high CM uncertainty.10
Eta (Lambda) represents the investment choice with a lower (greater) expected profit and lower (greater) upside potential. With the option to idle the production, Eta will yield profits in the range of 0–4,180 liras with a mean of 1,678 and a standard deviation of 1,462. In comparison, Lambda will yield profits in the range of 0–8,087 liras with a mean of 2,709 and a standard deviation of 2,867. Panel A of Table 2 presents 12 equally likely scenarios of demand and unit contribution margin for each technology presented to participants.
| Panel A: Forecasted market conditions displayed prior to investment decisions | |||
|---|---|---|---|
| Potential outcome (Scenario #) | Profit/loss per unit of seaplane engine (in liras) | Demand of seaplane engine (units) | |
| Eta (Technology 1) | Lambda (Technology 2) | ||
| 1 | 280 | −4,173 | 84 |
| 2 | 4,180 | 8,087 | 101 |
| 3 | 1,390 | −4,633 | 97 |
| 4 | 10 | 2,387 | 95 |
| 5 | 2,890 | 2,827 | 112 |
| 6 | 3,610 | 5,377 | 103 |
| 7 | 2,910 | 827 | 111 |
| 8 | 1,590 | 6,517 | 62 |
| 9 | −130 | −323 | 84 |
| 10 | 340 | −3,373 | 97 |
| 11 | 210 | 547 | 98 |
| 12 | 2,720 | 5,937 | 91 |
| Panel B: Forecasted market conditions displayed to participants who chose to invest in Eta | ||
|---|---|---|
| Scenario | Unit profit/loss (in liras) | Demand of seaplane engine (units) |
| 1 | 280 | 84 |
| 2 | 4,180 | 101 |
| 3 | 1,390 | 97 |
| 4 | 10 | 95 |
| 5 | 2,890 | 112 |
| 6 | 3,610 | 103 |
| 7 | 2,910 | 111 |
| 8 | 1,590 | 62 |
| 9 | −130 | 84 |
| 10 | 340 | 97 |
| 11 | 210 | 98 |
| 12 | 2,720 | 91 |
| Panel C: Forecasted market conditions displayed to participants who chose to invest in Lambda | ||
|---|---|---|
| Scenario | Unit profit/loss (in liras) | Demand of seaplane engine (units) |
| 1 | −4,173 | 84 |
| 2 | 8,087 | 101 |
| 3 | −4,633 | 97 |
| 4 | 2,387 | 95 |
| 5 | 2,827 | 112 |
| 6 | 5,377 | 103 |
| 7 | 827 | 111 |
| 8 | 6,517 | 62 |
| 9 | −323 | 84 |
| 10 | −3,373 | 97 |
| 11 | 547 | 98 |
| 12 | 5,937 | 91 |
- Notes: This table presents the forecasted market information presented to participants during the experiment. Panel A lists unit profit/loss for investment choices Eta and Lambda and demand of seaplane engine under the 12 potential outcomes (“Scenarios”). Panel B (Panel C) shows the above information in alternative presentations, as presented to participants who chose to invest in Eta (Lambda) on the previous screen after they commit to the investment choice but before they make production decisions. I program the instrument to randomly realize one of these scenarios toward the end of the experiment to validate participants' understanding of the setting and determine their compensations.
Participants make investment decisions based on the information presented so far. I first ask participants to assess how appealing each technology looks (“How appealing does each technology look to you?”) on a scale of 1 (not appealing at all) to 7 (extremely appealing). Next, participants choose to invest exclusively in one of the two technologies. As mentioned above, participants are aware that the investment decision is irreversible. The primary dependent variable is Chose_Lambda, a binary indicator coded as one if the participant chose to invest in Lambda, and zero otherwise.11
I then prompt participants to make production decisions, conditional on the investment decision made in the previous stage. I present a part of Panel A of Table 2 to participants again, but this time the contribution margin information is displayed only for the technology that the participants chose to invest in. I ask participants to enter the number of units they would produce under each scenario presented. Panel B (Panel C) of Table 2 shows the production decision questions as displayed to participants who chose to invest in Eta (Lambda) in the previous screen. The production decision mainly serves to validate participants' understanding of the overall experiment design and to determine participants' compensation.12
Compensation
I compensate (penalize) participants with $1 for every 100,000 liras of profit (loss) realized. I incorporate the penalty to induce symmetry in the mapping between participants' performance and resulting compensation. Among the participants that completed the experiment, the mean (median) compensation is $11.58 ($11.35), and overall the compensation ranges from $5.51 to $18.09. I made all compensations on site in cash before participants exited the computer lab. Mean compensations display no significant difference across the experiment conditions.
4 RESULTS
The sample for this study begins with 104 responses from participants who completed the experiment. I require participants to pass all comprehension and manipulation check questions before proceeding to investment decisions. For the final sample, I retain 100 (96%) participants who passed each block of the comprehension checks within two attempts. Participants therefore have similar levels of understanding of the experiment.
Descriptive Statistics
Panel A of Table 3 shows descriptive statistics for participants' investment decisions, perceived appeals of the investment options, and control variables used throughout this paper. On average, participants find Eta more appealing (mean = 5.25) than they do Lambda (mean = 3.94) (p < 0.01). Consistent with the perceived appeals of the investment choices, 70% of the participants chose to invest in Eta and 30% of the participants chose to invest in Lambda. These findings suggest that on average, participants chose the less profitable investment project. The Pearson correlation matrix in Panel B of Table 3 corroborates this pattern. Chose_Lambda is strongly positively (negatively) correlated with Appeal_Lambda (Appeal_Eta) (p < 0.01 for both). Participants' prior exposure to accounting subjects (Acc_Exp) is marginally correlated with Chose_Lambda (p = 0.10). Therefore, I control for Acc_Exp in subsequent tests.
| Panel A: Summary statistics | ||||
|---|---|---|---|---|
| No OL (n = 32) | Low OL (n = 33) | High OL (n = 35) | Overall (n = 100) | |
| Appeal_Eta | 5.31 | 5.18 | 5.26 | 5.25 |
| (0.97) | (1.01) | (1.07) | (1.01) | |
| Appeal_Lambda | 3.63 | 4.12 | 4.06 | 3.94 |
| (1.01) | (1.52) | (1.53) | (1.38) | |
| Appeal_diff | −1.69 | −1.06 | −1.20 | −1.31 |
| (1.65) | (2.19) | (2.29) | (2.07) | |
| Chose_Lambda | 0.16 | 0.36 | 0.37 | 0.30 |
| (0.37) | (0.49) | (0.49) | (0.46) | |
| Acc_Expa | 5.84 | 5.70 | 6.37 | 5.98 |
| (4.07) | (5.75) | (4.64) | (4.84) | |
| Deliberation | 92.76 | 98.61 | 101.12 | 97.61 |
| (51.63) | (53.18) | (65.2) | (56.76) | |
| Panel B: Pearson correlation matrix | |||||||
|---|---|---|---|---|---|---|---|
| Variables | (1) | (2) | (3) | (4) | (5) | (6) | (7) |
| (1) Any_OL | |||||||
| (2) University | 0.02 | ||||||
| (3) Appeal_Eta | −0.04 | −0.18 | |||||
| (4) Appeal_Lambda | 0.16 | −0.05 | −0.48* | ||||
| (5) Appeal_diff | 0.13 | 0.05 | −0.81* | 0.90* | |||
| (6) Chose_Lambda | 0.22* | −0.03 | −0.55* | 0.58* | 0.66* | ||
| (7) Acc_Exp | 0.02 | −0.07 | 0.03 | −0.05 | −0.05 | 0.17 | |
| (8) Deliberation | 0.06 | −0.27* | −0.11 | 0.13 | 0.14 | 0.26* | 0.11 |
- Notes: This table reports descriptive statistics for the key variables (n = 100). Panel A shows the mean and, in parentheses, standard deviation of each variable in each condition and for the full sample. Panel B shows a Pearson correlation matrix for the key variables. * denotes two-tailed significance level of 5%. aThe number of observations is 99 due to missing response(s). See Appendix 1 for variable definitions.
Test of Hypothesis
My hypothesis predicts that compared to those in the Low OL condition, participants in the High OL condition are more likely to invest in a project that has lower CM uncertainty. Panel A of Table 4 displays marginal means of Chose_Lambda across the experiment groups (Group) after removing influences of the covariate Acc_Exp, its interaction with experiment groups, and University. Panel B of Table 4 reports the results of an ANCOVA model with Group and the covariates as independent variables and Chose_Lambda as the dependent variable.14 After controlling for the covariates, the mean values of Chose_Lambda differ across the experiment groups, with the differences approaching marginal statistical significance (p = 0.12).
| Panel A: Marginal means of investment choices across experiment groups | |||
|---|---|---|---|
| Variable | No OL | Low OL | High OL |
| Chose_Lambda | 0.17 (0.08) |
0.37 (0.08) |
0.37 (0.08) |
| Panel B: Effects of operating leverage on investment choice: ANCOVA | |||||
|---|---|---|---|---|---|
| Source | Partial sum of squares | df | Mean square | F | p |
| Group | 0.91 | 2 | 0.46 | 2.19 | 0.12 |
| Acc_Exp | 0.64 | 1 | 0.64 | 3.07 | 0.08 |
| Group×Acc_Exp | 0.27 | 2 | 0.13 | 0.65 | 0.53 |
| University | 0.03 | 1 | 0.03 | 0.12 | 0.73 |
| Error | 19.16 | 92 | |||
| Panel C: Planned contrasts in investment choices | |||
|---|---|---|---|
| Variable: Chose_Lambda | Contrast | Unadjusted p | Bonferroni-adjusted p |
| Low OL versus High OL | 0.06 | 0.71 | |
| No OL versus High OL | 0.39 | 0.05 | 0.16 |
| No OL versus Low OL | 0.32 | 0.09 | 0.26 |
| No OL versus Any OL | 0.35 | 0.04 | |
- Notes: This table reports effects of operating leverage on investment choices. Panel A displays marginal means of Chose_Lambda in each experiment group. The marginal means are drawn from appropriate correction from the ANCOVA results in Panel B. Delta-method standard errors are reported in parentheses. Panel B shows results of an ANCOVA where Chose_Lambda is the dependent variable. Panel C reports planned contrasts that compare Chose_Lambda between the High OL and the Low OL conditions, the High OL and the No OL conditions, the Low OL and the No OL conditions, and any OL (mean of the High OL and the Low OL conditions) and the No OL conditions. See Appendix 1 for variable definitions.
The ANCOVA results imply that while Chose_Lambda does not significantly differ across all conditions, significant differences may exist within specific subsets of the experiment conditions, particularly given that the p-value is reasonably close to marginal significance (Montgomery, 2017). I therefore proceed with planned contrasts to directly compare the High OL and the Low OL conditions. Panel C of Table 4 reports contrasts in Chose_Lambda across all pairs of experiment groups. While my hypothesis predicts a negative and significant contrast for the High OL condition compared to the Low OL condition (i.e., participants in the High OL condition are more likely to choose Eta), the observed contrast is positive and insignificant (p = 0.71). The results do not support the hypothesis.
4.1 Effects of Cost Structure Information on Investment Decisions
Interestingly, pairwise comparisons involving participants in the No OL condition reveal significant differences. I find that participants in both the High OL and the Low OL conditions were significantly more likely to choose Lambda than those in the No OL condition (unadjusted p = 0.05 for No OL vs. High OL; unadjusted p = 0.09 for No OL vs. Low OL).15 I collapse the High OL and the Low OL conditions and compare their mean (“any OL”) and the No OL condition. The comparison confirms that participants in any OL condition (as opposed to the No OL condition) were significantly more likely to choose Lambda (p = 0.04).
Importantly, Lambda has the higher expected profits and offers greater upside potential. The planned contrast results suggest that different levels of operating leverage do not lead to different investment decisions, but the presence of information on the firm's historical cost structure led participants to prefer the more profitable investment choice. I discuss interpretations and implications of these results next in “Additional Analyses.”
Additional Analyses
4.1 Priming Based on the Accounting Excerpt
In Section 2, I argue that different levels of operating leverage in the firm's historical cost structure are irrelevant to investment decisions in the setting of interest. While the results of the experiment show that investment decisions under the High OL and the Low OL conditions do not differ significantly, I find that participants saliently presented with any cost structure information chose Lambda, the investment choice that is on average more profitable, after controlling for prior exposure to accounting and the university. A reasonable follow-up question is why and how participants chose the more profitable alternative when presented with the historical cost structure information. In this subsection, I exploit the metadata from the experiment and participants' responses to the PEQ to advance an interpretation that may explain the above finding.16
It could be that the exposure to the excerpt on operating leverage resulted in priming effects for the participants in the High OL and the Low OL conditions. Priming is “the incidental activation of knowledge structures, such as trait concepts and stereotypes, by the current situational context” (Bargh et al., 1996, p. 230). Studies on priming effects would suggest that being presented with an excerpt on operating leverage incidentally activates participants' existing knowledge of accounting and encourages them to apply the knowledge to the investment decision (Bargh & Ferguson, 2000; Weingarten et al., 2016).
I conduct post hoc analyses to examine whether participants demonstrated behavior consistent with the priming effect. In the presence of priming, participants in the High OL and the Low OL conditions would undertake the investment decision more carefully. The additional efforts rendered in the task in turn may have helped these participants make more profitable investment decisions. In addition, given that priming effect primarily concerns activation of knowledge (Bargh et al., 1996) and retrieval of memory (Neely, 1977; Schacter & Buckner, 1998), I expect the priming effect to vary across different levels of prior accounting education. I examine this inference using the timestamp that displays how much time the participants spent on each page of the experiment. I define Deliberation as the number of seconds a participant spent on the investment decision page. For the additional analyses here, I define Any_OL as a binary indicator coded as one if the participant received cost structure information (high or low operating leverage), and zero otherwise.
I find results consistent with this rationale. Panel A of Table 5 shows the mean and standard deviation of Deliberation by Any_OL, separately for participants whose Acc_Exp is below and above the sample median. While Deliberation does not differ significantly across the No OL condition and any OL conditions on average (p = 0.56 from the untabulated test of mean difference) and when their Acc_Exp is below median (p = 0.50), participants with above-median Acc_Exp deliberated more when they were presented with the historical cost structure information (p = 0.06). This pattern accords well with results of subsample regressions in Panel B of Table 5. The subsample regression results in Column 1 (Column 2) exhibit an insignificant (significant) difference in Deliberation between the No OL and any OL conditions in the subsample where Acc_Exp is at or below (above) the sample median (p = 0.43 [p = 0.03]). This result supplements the argument that cost structure information nudged more knowledgeable participants to attend to the decision-making more deliberatively.
| Panel A: Descriptive statistics of Deliberation by Any_OL and Acc_Exp | ||||||
|---|---|---|---|---|---|---|
| No OL | Any OL | All | ||||
| n | Mean (SD) | n | Mean (SD) | n | Mean (SD) | |
| Low Acc_Exp | 16 | 115.73 | 33 | 102.62 | 49 | 106.09 |
| (57.8) | (65.33) | (62.67) | ||||
| High Acc_Exp | 16 | 69.79 | 35 | 97.34 | 51 | 88.69 |
| (32.31) | (53.72) | (49.42) | ||||
| All | 32 | 92.76 | 68 | 99.9 | ||
| (51.63) | (59.25) | |||||
| Panel B: Effects of cost structure information and accounting experience on deliberation: OLS | ||
|---|---|---|
| (1) Low Acc_Exp | (2) High Acc_Exp | |
| Dependent variable | Deliberation | Deliberation |
| Any_OL | −15.13 | 31.30** |
| (0.43) | (0.03) | |
| University | −28.19 | −33.85** |
| (0.15) | (0.01) | |
| Constant | 126.30*** | 82.48*** |
| (0.00) | (0.00) | |
| Observations | 49 | 51 |
| R2 | 0.06 | 0.19 |
| Panel C: Effects of cost structure information on investment decisions through deliberation: Path analysis | |||
|---|---|---|---|
| Dependent variable | (1) Deliberation | (2) Chose_Lambda | (3) Chose_Lambda |
| Any_OL | −29.42 | 0.41*** | |
| (0.13) | (0.01) | ||
| Acc_Exp | −3.72 | 0.04** | |
| (0.12) | (0.03) | ||
| Any_OL×Acc_Exp | 6.15** | −0.04* | |
| (0.02) | (0.08) | ||
| University | −28.36*** | 0.03 | |
| (0.01) | (0.74) | ||
| Deliberation | 0.002*** | 0.002*** | |
| (0.01) | (0.00) | ||
| Constant | 125.86*** | 0.10 | −0.32* |
| (0.00) | (0.28) | (0.06) | |
| Observations | 99 | 99 | 99 |
9.28 (0.05) |
0 (N/A) |
||
| 2.32 | N/A | ||
| RMSEA | 0.12 | 0 | |
| SRMR | 0.06 | 0 | |
- Notes: This table shows channels through which cost structure information affects investment decisions. Panel A reports the number of observations, mean, and standard deviation of Deliberation by Any_OL and the median split of Acc_Exp. Panel B shows results of OLS analyses that regress Deliberation on Any_OL and University in subsamples with the low and high Acc_Exp. Panel C reports the results of a path analysis that runs from Any_OL, Acc_Exp, their interaction term, and University to Deliberation and then to Chose_Lambda. The dependent variable in Column 1 is Deliberation and in Columns 2 and 3 is Chose_Lambda. Coefficients of interest are highlighted in gray. Two-tailed p-values are presented in parentheses. See Appendix 1 for variable definitions. *, **, and *** represent significance levels of 10%, 5%, and 1%, respectively.
I conduct a path analysis to explain the above findings in a more nuanced manner. Panel C of Table 5 reports results of the path analysis displaying effects of providing cost structure information on participants' deliberations (Column 1) and effects of deliberation on the investment decisions (Column 2 and Column 3). In Column 1, the estimated coefficient on the interaction term is positive and significant (p = 0.02), meaning that presented with the cost structure information, more knowledgeable participants spent more time deliberating the investment decision. In Column 2 and Column 3, the path from Deliberation to Chose_Lambda is positive and strongly significant (p < 0.01), implying that the quality of investment decisions improves in the time spent on decision-making.17,18 Goodness-of-fit statistics indicate that these specifications have a good fit overall.19 Figure 1 visualizes the structure and results of the path analysis in Column 1 and Column 2.
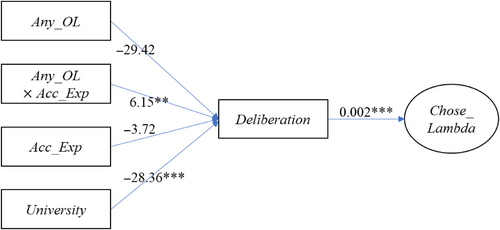
Notes: This figure visualizes a path analysis model that tests the effect of cost structure information on investment decisions through deliberation (n = 99). I report the estimated path coefficient next to each path. See Appendix 1 for variable definitions. *, **, and *** represent significance levels of 10%, 5%, and 1%, respectively.
The next tests supplement the analysis of participants' deliberation by probing the rationales behind their investment decisions. I collect up to 250 words of written responses to the PEQ questions that ask participants to explain why they chose one of the two investment options (“Why did you choose to invest in {selected investment choice} over {unselected investment choice}?”). I identify the most frequently appearing words in the responses and categorize them into five clusters of keywords related to profits from the investment, risks associated with the investment, or production.20 I then analyze whether the likelihood of mentioning these keywords in the rationale differs between participants in any OL and the No OL conditions. Table 6 presents the results of these OLS regressions. Coefficient estimates on Any_OL are positive and significant for keywords related to costs (p = 0.05) and the market (p = 0.10) and are insignificant for other keyword categories (p = 0.24 to 0.63). This finding provides some evidence that participants who were provided with the historical cost structure information were mindful of economic-based criteria in investment decisions.
| (1) | (2) | (3) | (4) | (5) | |
|---|---|---|---|---|---|
| Dependent variable | Mentioned_profitability | Mentioned_costs | Mentioned_market | Mentioned_risk | Mentioned_production |
| Any_OL | 0.04 | 0.18** | 0.13* | −0.07 | 0.11 |
| (0.63) | (0.05) | (0.10) | (0.50) | (0.24) | |
| University | 0.02 | −0.04 | 0.00 | 0.00 | 0.08 |
| (0.79) | (0.69) | (0.96) | (0.98) | (0.34) | |
| Constant | 0.74*** | 0.14* | 0.06 | 0.69*** | 0.13 |
| (0.00) | (0.10) | (0.38) | (0.00) | (0.13) | |
| Observations | 100 | 100 | 100 | 100 | 100 |
| R2 | 0.00 | 0.04 | 0.03 | 0.00 | 0.02 |
- Notes: This table shows the results of OLS regressions that analyze effects of cost structure information on investment rationale. The dependent variable in each column represents a binary indicator set to one if the participant mentioned words related to profitability, costs, market, risk, or production in the investment rationale, and zero otherwise. Coefficients of interest are highlighted in gray. Two-tailed p-values are presented in parentheses. See Appendix 1 for variable definitions. *, **, and *** represent significance levels of 10%, 5%, and 1%, respectively.
4.2 Robustness Checks
A feasible alternative explanation about the above results is that participants did not comprehend the experiment material and/or that the materials themselves are poorly designed, potentially compromising the inferences of this study. I address the concern by conducting two sets of robustness checks. First, I repeat the above analyses using subsamples of participants with better comprehension of the experiment. Specifically, I examine participants who (1) passed each block of the comprehension checks in one attempt (n = 82), (2) had taken at least one accounting course (n = 87), (3) chose the investment consistent with their stated appeals (n = 94), or (4) opted to idle the production in all scenarios predicting losses (n = 67).21,22
Panel A of Table 7 reports contrasts in Chose_Lambda between the No OL and any OL conditions for these subsamples. The magnitude and statistical significance of the contrast remain qualitatively similar for subsamples (1), (2), and (3).23 The difference in investment choices between the No OL and any OL conditions is insignificant in subsample (4). Panel B of Table 7 shows the path analysis results of the effects of cost structure information on investment decisions through Deliberation using these subsamples. The regression coefficients on and Deliberation are largely similar to those reported in Table 5, in terms of statistical significance and magnitude. In untabulated results, I also find that the effects of cost structure information on investment rationales remain nearly identical in all subsamples (p = 0.05 to 0.09 [p = 0.10]) for the cost-related [market-related] keywords.
| Panel A: Contrasts in investment choices between No OL versus any OL conditions | |||
|---|---|---|---|
| Variable: Chose_Lambda | N | Contrast | p |
| (1) Passed comprehension checks in one attempt | 81 | 0.34 | 0.08 |
| (2) Previously taken accounting courses | 86 | 0.31 | 0.13 |
| (3) Consistent between appeal and investment choice | 93 | 0.34 | 0.04 |
| (4) Applied the option to idle in loss scenarios | 67 | 0.20 | 0.39 |
| Panel B: Effects of cost structure information on investment decisions through deliberation: Path analysis | ||||||||
|---|---|---|---|---|---|---|---|---|
| Passed comprehension checks in one attempt | Previously taken accounting courses | Consistent between appeals and investment choice | Opted to idle in loss scenarios | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| Dependent variable | Deliberation | Chose_Lambda | Deliberation | Chose_Lambda | Deliberation | Chose_Lambda | Deliberation | Chose_Lambda |
| Any_OL | −45.30** | 0.45** | −29.18 | 0.389** | −32.52* | 0.41*** | −64.17** | 0.40** |
| (0.04) | (0.01) | (0.22) | (0.04) | (0.08) | (0.01) | (0.04) | (0.05) | |
| Acc_Exp | −4.73* | 0.05** | −4.56* | 0.05** | −3.76 | 0.03* | −8.59** | 0.04 |
| (0.07) | (0.03) | (0.09) | (0.03) | (0.10) | (0.07) | (0.05) | (0.15) | |
| 8.34*** | −0.04 | 6.25** | −0.04 | 6.02** | −0.03 | 11.55** | −0.03 | |
| (0.01) | (0.13) | (0.04) | (0.14) | (0.02) | (0.13) | (0.01) | (0.38) | |
| University | −33.62*** | 0.05 | −32.55*** | 0.06 | −24.09** | 0.01 | 0.07 | |
| (0.01) | (0.61) | (0.01) | (0.57) | (0.03) | (0.91) | (0.46) | ||
| Deliberation | 0.002*** | 0.003*** | 0.002** | 0.003*** | ||||
| (0.01) | (0.00) | (0.02) | (0.00) | |||||
| Constant | 139.52*** | −0.35* | 134.80*** | −0.39* | 124.52*** | −0.29* | 154.24*** | −0.52** |
| (0.00) | (0.07) | (0.00) | (0.05) | (0.00) | (0.09) | (0.00) | (0.02) | |
| Observations | 81 | 81 | 86 | 86 | 93 | 93 | 67 | 67 |
- Notes: This table reports effects of cost structure information on investment decisions in subsamples. Panel A reports contrasts in Chose_Lambda between any OL (High OL or Low OL conditions) and No OL conditions from ANCOVA results (untabulated) for the participants who (1) demonstrated the highest level of comprehension, (2) had prior exposure to accounting courses, (3) consistently reported investment appeals and the investment choice, or (4) opted to idle the production for all scenarios in which loss was expected. Panel B reports the results of a path analysis that runs from Any_OL, Acc_Exp, their interaction term, and University to Deliberation and then to Chose_Lambda in the above subsamples. The dependent variable in Columns 1, 3, 5, and 7 (Columns 2, 4, 6, and 8) is Deliberation (Chose_Lambda). For all subsamples, , RMSEA = 0, SRMR = 0. Coefficients of interest are highlighted in gray. Two-tailed p-values are presented in parentheses. See Appendix 1 for variable definitions. *, **, and *** represent significance levels of 10%, 5%, and 1%, respectively.
Second, I examine the inferences using alternative variables and model specifications. I employ the difference between reported appeal of Lambda and that of Eta (Appeal_diff) as an alternative for Chose_Lambda. Additionally, because individuals' demographic (age and biological sex) and experience-related (years of post-secondary education and work experience) attributes may confound the relationships between the cost structure information and investment decisions, I control for these variables. In untabulated tests, all inferences remain qualitatively unchanged. In summary, the findings of this study are robust to removing participants with poorer comprehension, using an alternative outcome variable, and employing additional control variables. The empirical evidence collectively alleviates the concern that poor design choices or participants' comprehension contaminate the results of this study.
5 CONCLUSION
I study whether the level of operating leverage in a firm's cost structure influences managers' capital investment decisions in a setting where the cost structure should be decision-irrelevant. Using risk-as-feelings hypothesis as the theoretical lens, I posit that managers with higher (as opposed to lower) operating leverage in their cost structures are more likely to prefer investment projects with lower variance in the unit contribution margin of the output (“CM uncertainty”). Experiment results show that participants in the high operating leverage condition are not more likely to prefer an investment project with lower CM uncertainty. Additional analyses reveal that participants presented with the historical cost structure information, irrespective of the level of operating leverage, are significantly more likely to make more profitable investment decisions than are participants who did not receive any cost structure information. Supplementary analyses show that the participants with the historical cost structure information deliberated more on the decision when they had more prior exposure to accounting, and the likelihood of choosing the more profitable investment choice increased in deliberation. This finding suggests that the excerpt on a fundamental accounting concept (i.e., operating leverage) may have primed the participants to approach the task more deliberatively.
This study adds to the accounting literature that examines how managers impound information about firms' cost structures in making other operating decisions (Chang et al., 2024; Matsumura et al., 2023). I extend this stream of studies by showing that managers presented with the cost structure in a salient way made more profitable investment decisions. This finding adds to the extant work that studies how additional information (Swain & Haka, 2000) or the use of decision aids (Iyer et al., 2012; Sawers, 2005) guide managers' decision-making processes in capital investments.
This paper is also related to the strand of literature that examines the influence of affect on managers' capital investment decisions (Farrell et al., 2014; Fehrenbacher et al., 2020; Kida et al., 2001; Moreno et al., 2002; Sawers, 2005). While most of these studies focus on strong interpersonal affect (e.g., fear), this study considers the influence of a firm's operating leverage in its cost structure as a source of non-interpersonal, negative affect arising from an abstract construct.
Acknowledgement of some limitations is due. First, while the findings suggest that the presence of historical cost structure information aids managers' investment decisions, the exact nature of the information that triggers such decisions remains an open question. The specific cue that helps managers' decision-making may arise from information about the firm's fundamentals or the cost structure; the decision-making benefits may be generated by an excerpt on general accounting knowledge or, more broadly, the information acquisition activity itself. Second, inferences based on investment appeals and choices are unable to expound other aspects of managers' investment decisions, including inter-project resource allocations and the timing of investment. Finally, I test my hypothesis in an abstract setting where managers have full information about the distribution of market conditions and their production decisions are immediately implemented with no transaction costs. Future research may exploit more complex links between cost structure information and managerial decision-making by exploring these links.
APPENDIX 1: VARIABLE DEFINITIONS
| Name | Definition | Range |
|---|---|---|
| Group | Categorical variable that represents each experiment group | {High OL, Low OL, No OL} |
| Any_OL | Binary variable equal to one if the participant is assigned to the High OL or the Low OL condition, and zero otherwise | {0, 1} |
Appeal_Eta (Appeal_Lambda) |
Participant's response to the question: “How appealing do you find Eta (Lambda)?” | {1, 2, …, 7} |
| Appeal_diff | Difference between the stated appeals of each investment choice (i.e., Appeal_Lambda − Appeal_Eta) | {−7, −6, …, 6, 7} |
| Chose_Lambda | Binary variable equal to one if the participant chose to invest in Lambda, and zero otherwise | {0, 1} |
| Acc_Exp | Participant's response to the question “Approximately how many accounting courses have you completed (enter a number between 0 and 20)?” | {0, 1, …, 20} |
| University | Binary variable equal to one if the data are collected from University B, and zero otherwise | {0, 1} |
| Deliberation | Number of seconds the participant spent on the investment decision page | [0, ] |
Mentioned_topic (topic {profitability, costs, market, risk, production}) |
Binary variable equal to one if the participant mentioned words related to a specific topic in the investment rationale, and zero otherwise | {0, 1} |
APPENDIX 2: CONSTRUCTION OF INVESTMENT CHOICES
I create two technologies in the experiment to emulate investment choices that have different levels of CM uncertainty but are identical in all other aspects. I elaborate on their technical details in this appendix.
Population distributions
I first employ three parameters that follow trivariate normal distributions that denote the unit price and cost variables. The parameters are as follows:
I then incorporate demand for seaplane engines, a parameter that follows a separate normal distribution with mean of 100 and SD of 10. Given these parameters, the unit contribution margin of Eta (Lambda) before the truncation of loss follows the normal distribution with mean 2,000 (2,000) and SD 1,803 (4,610).24 With the option to idle the production applied, the distribution for Eta (Lambda) becomes a left-truncated normal distribution with mean 2,121 (3,010) and SD 1,600 (3,340).
To illustrate the distributions, I simulate 1 million random draws from each distribution after the truncation. Figure 2 depicts simulated histograms of unit contribution margin of a seaplane engine with each technology. The figure displays that while the distribution of contribution margin with Lambda is more dispersed, most of the variance comes from the upside as the left tail is truncated at zero. The simulation results reveal that Lambda is more profitable than Eta in approximately 60% of direct comparisons of unit contribution margins.
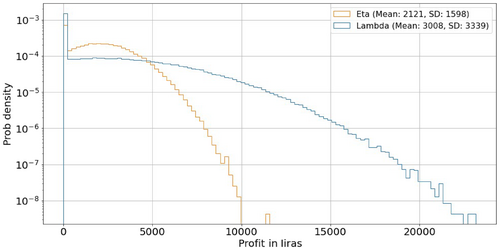
Notes: This figure depicts histograms of unit contribution margin with Eta and Lambda simulated with 1 million random draws from their respective population distributions. The horizontal axis presents profit in liras, and the vertical axis presents probability density. The legend shows the mean and SD of the unit contribution margin with each technology. See the text for the parameters used to generate these simulation results.
Outcome Scenarios
I make 12 random draws from each distribution to construct the 12 equally likely scenarios presented to participants. I then adjust unit variable cost of Lambda under each scenario equally to hold the expected profits from each technology constant before a participant applies the option to temporarily idle the production.25
In the experiment, I present to participants the unit variable costs of seaplane engine with each technology and the demand of seaplane engine under the 12 scenarios constructed above. Unit contribution margin with Eta (Lambda) under Scenario is defined as less . The exact presentation of this information to participants is described in Panel A of Table 2.
I present the above information to participants again, after they commit to an investment choice but before they make production decisions. However, because participants have committed to an investment choice, participants only receive the variable cost information for the technology they chose to invest in. Panel B (Panel C) of Table 2 depicts the exact presentation of this information to participants who chose to invest in Eta (Lambda).
REFERENCES
- 1 CM uncertainty directly translates to volatility in total profits in this setting. Section 2 discusses how the accounting literature views CM uncertainty as a key aspect of investment decisions.
- 2 All p-values reported throughout this study are two-tailed.
- 3 The illustrative example of a firm's reshoring decision mentioned in Section 1 is also useful in explaining this feature. An offshore facility potentially entails risks associated with exchange rates, local regulations, and supply chain that will likely be reflected in the product price, whereas such risks have less effects on the product price at a domestic facility. In this case, an overseas (domestic) facility represents the case of a high (low) CM uncertainty, which implies that the firm's profit from the product market also has a high (low) variability.
- 4 I expect the spillover of risk to hold in this setting, even though managers can opt to idle the production. While the option protects managers from downside risk, the investment decision is not without risk in the sense that the outcomes are stochastic with upside potentials.
- 5 The experiment was approved by the Office of Research Ethics or Institutional Review Board at the universities where the experiment was conducted.
- 6 I collected data for all conditions at University A in Canada (62 participants recruited) and 3 weeks later at University B in the United States (44 recruited; 42 completed the experiment). Assignments into experiment conditions did not differ significantly across these two universities (p = 0.85). Participants at University B were on average older by 0.84 years (p = 0.02). I observe no systematic differences in their self-reported biological sex, work experiences, and accounting experiences across these two universities (p = 0.13 to 0.43). To ensure that fundamental differences between these universities do not confound my inferences, I control for the university in all analyses. I also conduct the analyses with additional control variables in Section 4.
- 7 A small number of participants signed up through finance or other business courses. Most participants (85.6%) completed at least one accounting course at the university level (Mean accounting courses taken = 5.99).
- 8 The first (second) block of comprehension checks consists of four (three) questions based on the information presented in the previous screen. Participants who incorrectly answered any question in a given block had to attempt the entire question set again without knowledge of which question(s) they answered incorrectly. In “Additional Analyses” in Section 4, I discuss the results of the experiment using the subset of participants who demonstrated the highest level of comprehension.
- 9 While I expect the participants to be knowledgeable in the basic cost-volume-profit analysis, participants with no prior exposure to accounting concepts may have difficulties understanding the concept of operating leverage. I repeat my analyses after removing participants who have not taken any accounting courses in “Additional Analyses” in Section 4.
- 10 I elaborate on details regarding construction of the investment choices in Appendix 2.
- 11 In “Additional Analyses” in Section 4, I also employ Appeal_diff, the difference between participant's responses to the above question of perceived appeals of Lambda and Eta, as an alternative dependent variable.
- 12 Absent inventory costs, the rational production decision under a given scenario is to produce at least as many units as demanded in the market (to idle the production) if the expected contribution margin is positive (negative). I discuss participants' use of this option in “Additional Analyses” in Section 4.
- 13 All compensations were in Canadian (US) dollars at the Canadian (US) university at which I conducted the experiment. Costs of living around the universities suggest that despite differences in nominal values, the levels of compensation are comparable across the two universities. I use the dollar sign ($) interchangeably to denote either Canadian or US dollars.
- 14 The use of ANOVA with a dichotomous dependent variable is a valid design choice (Luepsen, 2021; Lunney, 1970). The sample size and distribution of Chose_Lambda satisfy the conditions that produce appropriate Type I error rate and statistical power (Lunney, 1970).
- 15 Because the contrasts involve more than two experiment groups, I also obtain Bonferroni-adjusted p-values for contrasts between the No OL and the High OL conditions and the No OL versus the Low OL conditions. I report both unadjusted and Bonferroni-adjusted p-values in Panel C of Table 4.
- 16 I acknowledge that the findings can be attributed to other alternative interpretations, including dilution effects (Nisbett et al., 1981), temporary shifts in risk preferences (Mengel et al., 2016), accounting education as a trigger for greed (Wang et al., 2011), and effects of additional information guiding decision-making.
- 17 I include the path UniversityDeliberation in this analysis to address unobservable differences between participants from the two universities. In an untabulated test in which University directly affects Chose_Lambda without mediation by Deliberation, the significance and magnitude of the path Any_OL×Acc_ExpDeliberation remain similar.
- 18 Alternatively, I conduct a multi-group path analysis testing these paths separately for the high- and the low-Acc_Exp groups, instead of including Any_OL×Acc_Exp. Untabulated results reveal significantly different coefficients on the path Any_OLDeliberation across the groups (p = 0.04).
- 19 I follow prior studies in structural equation modeling and accounting to select an appropriate combination of statistics (Gimbar & Mercer, 2021; Hooper et al., 2008; Hu & Bentler, 1999; Kline, 2023). These studies recommend that in addition to the model , researchers report root mean square error of approximation (RMSEA) and standardized root mean square residual (SRMR).
- 20 Three topics concerning the investment profits emerge: profitability (“profit,” “loss,” “money,” and “P/L”), costs (“operating leverage” and “cost”), and market (“demand,” “meet,” and “sales price”). Other frequently mentioned words pertain to risk (“risk,” “fluctuate,” “safe,” and “vary”) or production (“produce” and “idle”). I also include derived words (e.g., “varying,” “variance,” “varied”) in the analyses.
- 21 The size of each subsample suggests that while not every participant demonstrated perfect understanding of the material, it is unlikely that poor comprehension undermines the inferences of this study in general.
- 22 I also examine whether the responses suggest participants made investment decisions based on wild guesses (“random,” “guess,” “whatever,” and “whichever”). I do not find any participant who submitted such responses.
- 23 The statistical significances drop, likely due to the smaller sample sizes in the subsamples.
- 24 SD of unit contribution margin under Eta: . SD of unit contribution margin under Lambda: .
- 25 In their distributions, variable costs of Eta and Lambda have the equal mean of 28,000.




