A Conceptual Framework for Learning Management Accounting†
Abstract
enThis paper demonstrates how Schoenfeld's (1985) conceptual framework for mathematics can provide an alternate framework for learning and thereby teaching management accounting. The four-part framework—heuristics, resources, beliefs, and controls—is a refinement to problem-based learning with three attributes in regard to management accounting. First, all aspects for teaching management accounting are integrated into a single framework or theory. Consistency among all parts of management accounting clarifies student and instructor roles in the learning process. Second, the framework's problem-solving focus with linkages to explanatory materials or resources allows students to be rigorously informed about the functionality of management accounting heuristics. Third, transition or extension of relatively simple, standard problems to more complex nonstandard problems or cases is facilitated by introducing appropriate beliefs and controls. In effect, this approach enables management accounting, and particularly case analysis, to be taught with more structure.
Un cadre conceptuel pour l'apprentissage de la comptabilité de gestionRésumé
frLes auteurs montrent comment le cadre conceptuel de Schoenfeld (1985) propre aux mathématiques peut également s'appliquer à l'apprentissage, et donc à l'enseignement, de la comptabilité de gestion. Ce cadre conceptuel à quatre volets — heuristique, ressources, croyances et contrôles — est une version raffinée du modèle d'apprentissage fondé sur la résolution de problèmes comportant trois attributs relatifs à la comptabilité de gestion. Premièrement, tous les aspects de l'enseignement de la comptabilité de gestion se trouvent intégrés dans un même cadre ou dans une même théorie. La cohésion de tous les éléments de la comptabilité de gestion permet de clarifier les rôles de l'étudiant et de l'enseignant dans le processus d'apprentissage. Deuxièmement, le fait que le cadre conceptuel soit axé sur la résolution de problèmes et renvoie à des ressources ou des documents explicatifs permet de renseigner rigoureusement les étudiants sur la fonctionnalité de l'heuristique de la comptabilité de gestion. Troisièmement, la transition ou l'extension qu'exige le passage de problèmes courants relativement simples à des problèmes ou cas plus complexes et inusités est facilitée par l'introduction de croyances et de contrôles appropriés. Dans les faits, cette méthode permet un enseignement mieux structuré de la comptabilité de gestion et de l'analyse de cas en particulier.
The discipline of accounting has been redefined in recent decades from a traditional record keeping and compliance-based reporting role to providing information that firms need to formulate, communicate, and accomplish strategic initiatives (Barksy et al., 2002; Bates and Whittington, 2009; Blocher, 2009). Consequently, in academic institutions efforts have been made to redesign curricula actively to develop a range of capabilities including critical thinking and communication skills. These developments have been preceded by pronouncements from various academic and professional accounting bodies calling for substantive curriculum changes in accounting education and more specifically management accounting education (e.g., Institute of Management Accountants, 2008; Accounting Education Change Commission, 1990). This paper adds to the body of knowledge of how problem-based learning (PBL) can be refined to re-engineer management accounting course curricula to meet the changing expectations for accounting professionals entering the workforce. This contribution is important in light of the recognition that the curriculum needs to develop critical thinking skills and the ability to provide quality advice for decision making, an aim supported by the American Institute of Certified Public Accountants (Blocher, 2009: 4).
PBL has received much attention in the education literature in recent times (e.g., Kirschner et al., 2006) and more specifically in the accounting education literature (e.g., Tho et al., 2003; Milne and McConnell, 2001; Hansen, 2006). It is viewed as a progressive educational approach that uses complex, real-world problems as the motivation or starting point and focuses on the learning process. There is considerable research that supports the benefits to be derived from using a PBL approach (e.g., Schmidt, 1983; Kaufman and Mann, 1996).
PBL has been used in medical education to cope with the explosion in knowledge that showed traditional rote learning to be seriously deficient (Evensen and Hmelo, 2000). Given that accounting professionals are facing a similar knowledge explosion, PBL can also be successfully applied in educating accounting professionals. Moreover, it is considered to be a waste of scarce time and instructor capacity to expect accounting students to learn material that, in many instances, proves obsolete before they graduate. What is needed in educating accounting professionals is to help them acquire the skills that will enable them to “learn quickly, effectively and independently when they need it” (Boud and Feletti, 1997: 4). This view is supported by critiques of management accounting education (e.g., Boer, 2000; Maher, 2000). As Maher (2000) indicates, focusing on problem-solving skills, rather than the “facts” of management accounting can educate students to be creative problem solvers who add substantial value to their organizations.
A description of an actual situation, commonly involving a decision, a challenge, an opportunity, a problem, or an issue faced by a person (or persons) in an organization. The case allows you to step figuratively into the position of a particular decision maker.
it appears that there may only be very marginal benefits from using business cases to develop students into more balanced learners. Furthermore, this effect only occurs when students take charge and become actively involved in the case presentation. For those students who do not assume an active role in the case presentation, learner balance decreases.
Similarly, Healy and McCutcheon (2010) have highlighted that case studies per se do not necessarily foster deep learning and personal skill development. They call for a more extensive consideration of the manner in which accounting educators engage with the case study method. A purpose of this paper is to address this call by adding more structure to the teaching of management accounting.
The incorporation of a conceptual framework for learning management accounting is intended to refine PBL in management accounting education. Despite the strong support for PBL, management accounting textbooks often seem to be unsystematic in terms of providing any consistent approach to teaching problem solving. More specifically there seems to be limited prior literature on the development of conceptual frameworks for learning management accounting. Bonner (1999) presents a “framework” for choosing teaching methods for different types of accounting learning objectives. Blocher (2009) explains how he uses a strategic emphasis to teach cost management. Wessels and Roos (2009) provide a “conceptual framework” for developing management accounting course syllabi, with the intention of assisting instructors with design, delivery, and assessment. However, there is little evidence to suggest that problems and cases presented in textbooks (the major learning resource) systematically develop contents that test students' learning using a PBL approach.
Given that business mathematics comprises an important aspect of management accounting, we conjecture that a conceptual framework for learning mathematics—Schoenfeld's (1985)—may be suitable for learning management accounting. The crucial unknown is whether Schoenfeld's conceptual framework for learning mathematics can be transferred to management accounting. The major purpose of this paper is to adapt a convincing management accounting framework from Schoenfeld's mathematical framework. This adapted framework may not necessarily be pedagogically better for students' understanding, nor easier to teach. It is presented as an alternative framework for teaching and learning management accounting that may over time be found to be pedagogically superior. Schoenfeld's framework is used by mathematics teachers (e.g., Burton, 2004); and cited frequently by nonmathematics teachers (e.g., Marshall, 1995; Halpern, 1996), but it is not usually cited by accounting educators. With the focus on student learning, Bloom et al.'s (1956) taxonomy of educational objectives will serve as the underlying criteria.
The evidence gathered for this study suggests that Schoenfeld's (1985) conceptual framework for mathematics can provide an alternate framework for teaching and learning management accounting. The four-part framework—heuristics, resources, beliefs, and controls—is a refinement to PBL with three attributes in regard to management accounting. First, all aspects for teaching management accounting are integrated into a single framework or theory. Consistency among all parts of management accounting clarifies student and instructor roles in the learning process. Second, the framework's problem-solving focus with linkages to explanatory materials or resources allows students to be more rigorously informed about the functionality of management accounting heuristics. Third, transition or extension of relatively simple, standard problems to more complex nonstandard problems or cases is facilitated by introducing appropriate beliefs and controls. In effect, management accounting, especially case analysis, is taught with more direction, rather than expecting it to be learned through unspecified “practice.”
The remainder of the paper will explain how these conclusions are reached. The next section describes Schoenfeld's conceptual framework for learning mathematics. The third section applies Schoenfeld's framework to management accounting. The fourth section concludes the paper and includes suggestions for testing the suggested framework.
Framework for mathematical problem solving
Schoenfeld's (1985) framework is considered a successful means for improving general mathematical thinking and problem-solving skills (Halpern, 1996: 9). With a mission to assist with developing problem-solving skills, and in particular reasoning strategies, Schoenfeld's framework is part of PBL (Hmelo-Silver, 2004: 240). Its development was guided by two questions: “What does it mean to think mathematically?” and, “How can we help students to do so?” The resulting framework is a set of behaviors for navigating around “facts and procedures” to acquire the skills to think mathematically and to solve nonstandard problems.
The framework has four components—resources, heuristics, controls and belief systems—which overlap and intersect one another. Although the framework is still widely accepted in mathematics literature (e.g., Mathematical Sciences Education Board, 1990; Carlson et al., 2008), its major contribution, along with Polya (1957), is the establishment of a rational approach to mathematical problem solving, referred to as “self-regulated learning” (Stockton, 2010: 3–8, 56). Two aspects of Schoenfeld's (1985) framework have been studied: beliefs (Hofer and Pintrich, 1997; Muis, 2008; Schoenfeld, 1992; Stockton, 2010) and control (Winnie and Hadwin, 1998; Zimmerman, 2000). Stockton (2010: 9) claims the only test of self-regulated learning was done by Muis (2008: 199–200), who confirmed Schoenfeld's assertion that rational problem solvers are more successful than empirical solvers In this context, empirical solvers are described as having no idea of how to progress and thus they try every conceivable plausible solution as with a “wild goose chase.” Muis's (2008) study included 268 Canadian university undergraduate mathematics and statistics students.
Resources
This is the inventory of pertinent mathematical facts and procedures accessible to the problem solver. Resources can be brought to bear on particular problems. Schoenfeld's mathematical resources include intuitions and informal knowledge regarding the domain, facts, algorithmic procedures, “routine” nonalgorithmic procedures, and an understanding (propositional knowledge) of the agreed-upon rules for working in the domain. An example of informal knowledge in mathematics would be understanding what is meant by the expression, perpendicular line.
Heuristics
exploiting analogies, introducing auxiliary elements in a problem or working auxiliary problems, arguing by contradiction, working forward from the data, decomposing and recombining, exploiting related problems, drawing figures, generalizing and the using “inventor's paradox,” specializing, using reductio ad absurdum and indirect proof, varying the problem, and working backward.
Schoenfeld's (1985) use of heuristics is comparable to Marshall's (1995: 123–27) schema. Marshall (1995) starts her book, Schemas in Problem Solving, with a quote from philosopher Immanuel Kant's Critique of Pure Reason, “There can be no doubt that all our knowledge begins with experience.” She concurs with Schoenfeld that learning consists of the accumulation of experiences and that similar experiences get grouped under “the broad umbrella called a schema.” Marshall (1995: vii) defines schema as a way repetitive experiences are put together for “storage, synthesis, generalization, and retrieval.” Schema is, according to Marshall, an integral part of “learning and remembering,” and as one item of information is recalled from memory, other items of information associated with the same schema are subsequently “activated and available for mental processing.”
Control
This third category recognizes that it is not merely the availability of known resources and heuristics, but also competent decision-making that is necessary for success. Control refers to how problem solvers select and deploy available resources and heuristics or “rules of thumb.” Important decisions are included in the control category, including what to do when solving a problem. Moreover, control decisions determine the level of efficiency with which resources and heuristics are used. Behaviors of significance include planning, monitoring and assessing, decision making, and conscious meta-cognitive acts.
Schoenfeld (1985) considers these to be executive decisions with “global consequences for the evolution of a solution.” More specifically, Schoenfeld (1985: 27) states these are “decisions about what paths to take” and consequently about the paths and directions abandoned. The decisions involve the choice and use of significant parts of the limited resources, including the limited time of the problem solver.
Belief Systems
Underlying mathematical problem-solving are the “mathematical world views.” These views determine the student's orientation to problems, resources, heuristics, and control. Schoenfeld (1985) indicates, that upon detailed investigation into problem-solving activities, many students had significant misunderstandings about mathematics. Appropriate mathematical beliefs allow students to make the best use of the other three parts of the framework. In other words, belief systems shape the cognition that occurs with the pursuit of problem solving. Some examples include beliefs about self, about the environment, about the topic, and about mathematics (Schoenfeld, 1985).
Although Schoenfeld may appear to be teaching strategy rather than subject matter, he was, more fundamentally, building … a mathematical belief system … [and as he was] … working in the culture of mathematics, not in the culture of schooling, he did not have the students stop at what, in culture of school practice, would mark the end: an answer.
Schoenfeld (1985) provides this four-part behavioral process or toolbox for solving complex mathematical problems. At this stage, it appears that it might be suitable for management accounting. The critical issue is this: can Schoenfeld's mathematical framework be transferred to management accounting?
Framework for management accounting problem solving
In this section, Schoenfeld's framework is applied to management accounting. It will be recalled that mathematics is a basic component of management accounting. Management accounting uses mathematical calculations, which may be financial or nonfinancial. Financial information comes from a firm's financial accounting system, which is based on double-entry bookkeeping. Although double-entry bookkeeping is not mathematical per se, it is numerical. This numeracy enables calculations to be undertaken with financial information. An example of this information is the calculation of the contribution margin, which is defined, generally, as revenue less variable costs.
Nonfinancial management accounting information comes from any part of the firm or its value chain. That information tends to be expressed in numerical terms, allowing for mathematical assessment. An example of nonfinancial information is a plant capacity utilization rate. As with financial information, nonfinancial information acquires meaning because of numeracy.
An assessment of how Schoenfeld's (1985) framework can be transferred to management accounting via its four key parts is presented below.
Resources
This is the inventory of management accounting facts and procedures accessible to problem solvers. Management accounting resources are mainly the materials presented in management accounting textbooks (e.g., Tonge and Willett, 2009). Typically management accounting textbooks are organized by topic-based chapters, which can be divided into two parts: text materials and end-of-chapter testing materials. The text materials provide thorough backgrounds or resources. Although “there is too much detail” for standard problems, the nuanced descriptions and explanations in the text materials equip students to do nonstandard problems or cases. An example of resources would be the discussion of variance analysis in Chapter 7 of Horngren's Cost Accounting: A Managerial Emphasis (Horngren et al., 2009). The text material defines a variance as the difference between actual results and expected performance1 and then demonstrates how numerous variances are calculated with flexible budgeting. It also describes how the flexible budget is based on standard costs and demonstrates the respective journal entries of a standard costing system, and the management use of variance analysis.
Resources may also include other course materials such as the instructor's lecture notes and the respective slides, supplementary cases and readings, discussions with fellow students, work experiences, and course prerequisites.
Heuristics
In management accounting, the schemas or heuristics are more commonly called management accounting techniques. Management accounting numerically-based heuristics or “problem-solving techniques” are “carefully delineated and carefully taught.” An example would be the “contribution margin” which, as noted, is revenues less variable costs. Another example is capital budgeting, which discounts cash flows for long-term investment decisions.
To demonstrate this point, a break-even analysis can be used as an example. The break-even point refers to the sales level at which sales minus variable costs equals fixed costs. This heuristic tends to be discussed in textbook chapters covering cost–volume–profit analysis—e.g., Chapter 3 of Horngren et al. (2009)—and it is reinforced with exercises and problems at the end of the chapter. In other words, the break-even analysis is a resource as it is discussed in the text material in the chapter, but it becomes a heuristic in the exercises and problems provided for practice in the end-of-chapter materials.
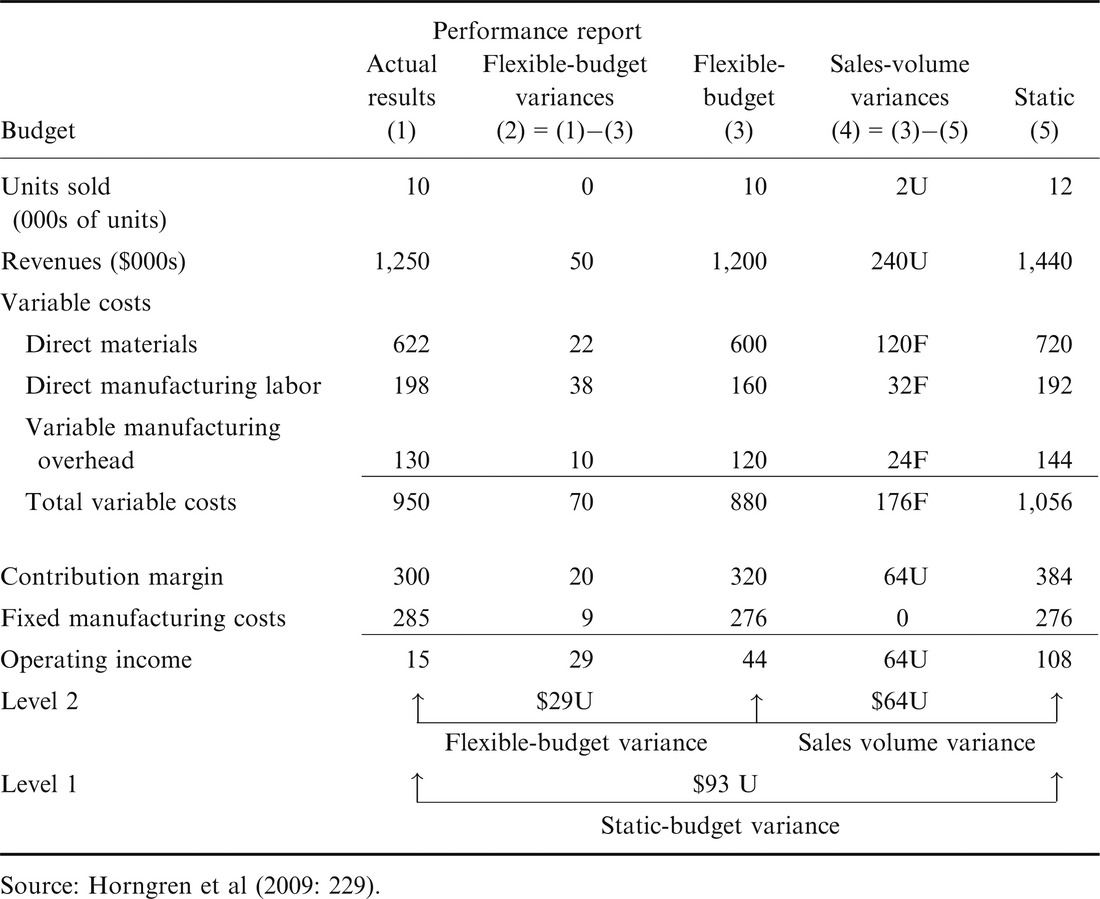
Another example of a management accounting heuristic is variance analysis in Chapter 7 of Horngren et al. (2009). The variance analysis technique is called a performance report, as shown Table 1.
The performance report explicitly calculates the variances for flexible budgets, sales volume, and static budget. It also enables numerous other variances to be calculated (e.g., price variances, efficiency variances). The exercises and problems at the end of chapters test students in how to apply the performance report for different sets of data and users. For example, exercise 7-19 in Horngren (2009: Ch. 7) provides the basic performance report but with only the data for static budget and actual results columns; students are asked to calculate the missing fields in the remaining four columns. Problem 7-35 is more challenging. It provides numbers for some fields, but students are asked to calculate some of the missing fields. In essence, the performance report embeds a heuristic—that is, expected to be understood and probably memorized—to be applied to different datasets.
In Schoenfeld's terms (1985: 2), the mathematical exercises and problems at the end of chapters with single answers would be considered standard problems whereas cases with multiple possible answers would be considered nonstandard problems. A problem is nonstandard when “the students will not be able to solve them by simply recalling and applying familiar solution patterns.” Problem solving requires the use of management accounting “techniques” which, as noted, are comparable to Schoenfeld's heuristics and Marshall's (1995) schemas.
- Absorption costing. This is a heuristic where the fixed manufacturing costs, as well as certain variable costs, are charged to the cost of goods sold to indicate cost.
- Cost–volume–profit analysis. With the contribution margin as the denominator, this heuristic specifies the sales volume needed to cover the predetermined fixed costs, and perhaps income taxes and profits.
Management accounting heuristics are explicit with exercises or problems. For example, the standard problem requires students to learn and apply the heuristic with different sets of data. As such, the heuristic operates at Bloom et al.'s (1956) third level of educational objectives, application. Bamber and Bamber (2006: 278) state that most end-of-chapter exercises and problems do not challenge students beyond application.
Students perceived that an awareness of multiple solutions and insights into the complexity of “real world” business decisions were the most important benefits arising from the use of case studies.
These findings came from research conducted on a final undergraduate year compulsory course entitled “advanced management accounting.” The case study method was adopted as a significant component of the course. The research instrument required the students to respond to a series of questions categorized by three headings, of which one was labelled “cognitive benefits.”
Ballantine and McCourt Larres (2004: 173–74) also develop a pedagogical case continuum for how management educators use case studies. This allows our assumption of a case or nonstandard problem to be clarified. They fix one end with the Harvard Business School cases, which are used as the “primary learning mechanism” providing an “integrated, inductively-driven teaching process.” The other end of the continuum is fixed with “short case studies on an irregular basis to illustrate real-world practice.” Our management accounting framework presupposes something in the middle, similar to Ballantine and McCourt Larres medium length, ambiguous (i.e., nonstandard problems) problem-based cases that require student preparation and discussion with little instructor guidance.
Control
Schoenfeld (1985) recognizes that it is not only the available or known resources and heuristics but also “competent decision-making [that] is necessary for success.” Control refers to how management accounting practitioners or students select and deploy available resources and heuristics. Control is concerned with matching heuristics with the problems for solving.
Briefly, control would require a number of steps such as careful assessment or reading of the management accounting problem to be solved; reviewing pertinent resources; considering the possible heuristics that match or, in other words, could be used to solve the problem; implementing the heuristic most appropriate to solve the problem; and reviewing the results against the original problem to ascertain if it was solved. If the problem remained unsolved, students were expected to start the problem-solving algorithm all over again.
Control, as noted, refers to how problem solvers select and deploy available resources and heuristics. With standard problems, the challenge is not great. The management accounting problems are generally in forms that are similar to those used when learning the heuristics. It requires simple matching, and the control comes into play when the student has learned to apply the heuristics.
Control is less straightforward with nonstandard management accounting problems or cases; and that is why the “case approach” is used, with a format such as problems–analyses–recommendations. There are other formats. Nevertheless, the case approach by providing “reflection and learning” can be thought of as a metaphor for PBL (Greenhalgh, 2007: 185). Students often read the case question once or twice to understand its essence. These questions often emphasize issues that have gone wrong in the context presented. While reading, students are asked to identify the apparent problems by circling or highlighting certain parts or by making brief notes. Then, students review these identified apparent problems, adding to them any problems revealed by related analysis of financial statements and other supplementary information.
First, students can make a list of the apparent problems and then arrange and assemble these problems into groups.
Second, students can explain the relationship within and among groups or categories that emerge at this stage. This may involve Bloom's analysis or the breaking of the apparent problems into parts in order to understand the relationships among parts. The grouping process should be governed by two criteria: (1) similar or related apparent problems should be grouped together; and (2) associations among apparent problems within a group should be specified.
Third, the relationships among categories must be explained. Bloom's synthesis may be used in putting together parts to form a new whole. The explanation should reveal the real problem or problems. Once disclosed, the real problem or problems should be explained with a heuristic or with heuristics in the “analyses” section of the case format.
As mentioned previously, in a case-type problem, the real problems to be solved are often the issues that are wrong in the specific organizational context. These issues make the organization suboptimal in some ways, and the suboptimality exists to the extent that some management accounting heuristics are not being practiced or implemented. For example, after examining numerous apparent problems, a real problem may be determined to be inaccurate determination of overhead. Therefore, the solution may involve recommending implementation of activity-based costing for a more accurate allocation of overhead. The real problem and the recommendation are two sides of the same coin. In other words, the problem cannot be seen independent of the heuristic.
Belief Systems
The management accounting world views determine the effectiveness of the problem-solving. These views enable the bringing together of resources, heuristics, and control. Appropriate beliefs allow students to excel with problem solving. Examples of management accounting beliefs include:
- A neo-classical economic foundation; more revenues and more profits are desirable; as are less costs and less expenses;
- A financial accounting foundation provided by double-entry bookkeeping systems; all financial accounting information can be reconciled with debits and credits;
- Managers make decisions with management accounting information; and
- Nonfinancial information is an insightful alternative to the more abstract financial accounting information (Schwartz et al., 2007; Blocher, 2009).
To make heuristics, resources, and controls work effectively, it is necessary for students and practitioners to believe in the validity of management accounting information for assisting managers to plan, make decisions, evaluate performance, and control an organization. In addition to believing in management accounting, it is necessary to trust the managers to be effective in using that information. The most important belief is that information as provided by management accounting is useful for the purposes intended.
Application of the Framework
By focusing on matching problems with heuristics, beliefs are important for solving standard and, especially, nonstandard problems. Consider the nonstandard problem or case captured with Table 2. There are three parts to the table: (1) an operating statement with actual annual results, a budget, and variances between actual and budget; (2) the summary results from the costs of quality reports for the years 2005 to 2010; and (3) the summary results of customer satisfaction reports for the years 2005 to 2010. The operating statement in the first part of Table 2 resembles the performance report heuristic in Table 1, explained in Chapter 7 of Horngren et al. (2009). The cost of quality report in the second part of the table is from the heuristic by the same name in Chapter 19 of Horngren et al. (2009). This report accumulates all costs associated with product quality, the costs incurred in generating quality or the costs arising from the lack of quality. The third part of Table 2 contains another heuristic from Chapter 19 of Horngren et al. (2009): customer satisfaction reporting with various attributes of the company's products.
| Operating statement | |||
|---|---|---|---|
| (For the year ending December 31, 2010, $millions) | |||
| Budget | Actual | Variance | |
| Revenues | 432.0 | 436.6 | 4.6 |
| Cost of goods sold | |||
| Variable costs: | |||
| Materials | 125.4 | 129.6 | (4.2) |
| Manufacturing labor | 21.2 | 22.8 | (1.6) |
| Manufacturing overhead | 47.4 | 50.2 | (2.8) |
| Sales support | 17.2 | 17.4 | (0.2) |
| Total costs | 211.2 | 220.0 | (8.8) |
| Contribution margin | 220.8 | 216.6 | (4.2) |
| Fixed expenses: | |||
| Manufacturing overhead | 98.8 | 132.2 | (33.4) |
| Sales overhead | 21.4 | 21.2 | 0.2 |
| Administration overhead | 37.2 | 37.4 | (0.2) |
| Total expenses | 157.4 | 190.8 | (33.4) |
| Operating income | 63.4 | 25.8 | (37.6) |
| Cost of quality report | ||||||
|---|---|---|---|---|---|---|
| ($millions) | ||||||
| 2010 | 2009 | 2008 | 2007 | 2006 | 2005 | |
| Prevention | 2.2 | 6.2 | 6.4 | 6.0 | 5.6 | 5.2 |
| Inspections | 0.2 | 2.6 | 2.8 | 2.4 | 2.0 | 2.0 |
| Internal failure | 4.2 | 2.2 | 2.0 | 1.4 | 1.6 | 1.6 |
| External failure | 13.6 | 1.2 | 0.4 | 1.2 | 0.6 | 0.8 |
| Total | 20.2 | 12.2 | 11.6 | 11.0 | 9.8 | 9.6 |
| Customer satisfaction | ||||||
|---|---|---|---|---|---|---|
| (Highly unsatisfied, 0% to highly satisfied, 100%) | ||||||
| 2010 | 2009 | 2008 | 2007 | 2006 | 2005 | |
| Quality | 61.5 | 85.5 | 84.7 | 85.9 | 86.1 | 85.3 |
| Durability | 58.3 | 93.3 | 92.7 | 92.2 | 92.7 | 93.6 |
| Value for Money | 48.6 | 75.1 | 77.5 | 76.6 | 78.1 | 76.4 |
| Finishes | 88.6 | 53.8 | 56.3 | 55.8 | 54.7 | 53.1 |
The company tied to Table 2 is a manufacturer of quality household furniture. In the past years, two changes were introduced. The company contracted out more production to reduce costs and it added more product finishes to meet customer demand. With the contracting out of the production, the company made quality control the responsibility of the contractors. Warranty work is charged to manufacturing overhead. Operating income has declined by nearly 60 percent from what was expected. You are required to determine the reasons for the decline in operating income and recommend actions to improve operating income.
A nonstandard problem (case) requires students to match the problems underlying Table 2 and the above quotation with sensible heuristics. The student's matching of problems with heuristics is based on the belief that management information (financial or nonfinancial) can solve such problems. The starting point with cases is the control, the case approach consisting of problems, analyses, and recommendations. Students must have knowledge and understanding of the relevant heuristics, as well as the resources and beliefs to enable the matching of heuristics with problems. With the narrative, the operating statement in Table 2 could be analyzed by students with the performance report heuristic in Table 1. Although there are no units, students observing that budget and actual sales are essentially the same would assume that the actual mix and unit prices are the same as budget and thus the performance report could be used. The variance analysis in Table 2 equates to the performance report without a volume variance. The decline in operating income is largely attributed to variable and fixed overhead; the other variances are minor and often offsetting. The cost of quality report shows that in the recent year, there were reduced expenditures for prevention and inspections (because quality control was delegated to suppliers), and increased outlays for internal and external failures probably because product quality decreased. This is verified by the customer satisfaction decreases for quality, durability, and value for money.
An explanation of the operating income decrease is that customers are less satisfied with their purchases of household furniture. The reduction in outlays for prevention and inspection can explain the increases in internal and external failure, which are reflected in more charges to manufacturing overhead. They also explain the reduction in customer satisfaction. These are the apparent problems, and their resolutions or recommendations are needed to improve product quality, durability, and value for money. The real problem is that products are now of poor quality. The recommendations could include improving product quality—perhaps by increasing inspections to 100 percent, and by training and monitoring contractors to improve quality. Replacement of contractors that are not meeting quality standards may also be justified.
In summary, through matching of nonstandard problems with heuristics, students identify the real problems, which constitute the first part of the control, the case format. The heuristics enable the issues to be analyzed, synthesized or explained in cause-and-effect terms; this is the second part of the case approach. By analyzing the issues with heuristics, solutions or recommendations are generated. Christensen and Carlile (2009: 244) explain this as the relationship between the “descriptive theory” of analyses and “prescriptive theory” of the recommendations.
[Cases] enable you to learn by doing and by teaching others. What you learn becomes deeply ingrained and stays with you. The repetitive opportunity to identify, analyze, and solve a number of issues in a variety of settings prepares you to become truly professional in your field of work. … Cases provide an opportunity to become deeply involved in decisions actually faced by real people in real organizations, to take ownership, to feel the pressure, to recognize the risks, and to expose your ideas to others.
The framework can lead to more passive learning if standard problems are emphasized. Only with nonstandard problems can the framework lead to more active learning. From an examination of the literature, Wynn-Williams et al. (2008: 117) found that to encourage active learning, “students must frame the problems themselves, and must decide what information to gather and what management tools [or heuristics] to use.” This framing is integral to case analysis.
This section has endeavoured to place management accounting problem solving into Schoenfeld's (1985) framework. Schoenfeld's framework refines PBL. In putting the focus on problems solving, PBL does not differentiate between rational and empirical approaches to problem solving (Muis, 2008). Schoenfeld, in contrast, puts forth an approach that is rational rather than empirical (Muis, 2008). Heuristics are learned and then appropriately applied. Schoenfeld emphasizes the selection among previously learned heuristics to solve problems. It is the use of carefully learned heuristics through resources, controls, and beliefs that enables students to solve rationally and effectively unstructured management accounting problems.
Concluding comments
Schoenfeld's (1985) conceptual framework for mathematics is intended to guide instructors in facilitating students' learning of mathematics. In adapting that framework to management accounting, the intent is to facilitate student learning of management accounting by focusing on “problem-solving strategies.” Paraphrasing Schoenfeld, it is putting emphasis on the facts that (1) understanding management accounting involves more than mastering the subject matter and (2) the process of problem-solving is absolutely central to the performance of management accountants.
Heuristics of a mathematical nature produce management accounting information that may be financial or nonfinancial. Most of these heuristics exist in management accounting textbooks as well as in other teaching materials. The source of these heuristics is either the practice of management accounting or the problems that face management accountants. For the latter, academic management accountants develop new heuristics for practice; for example, activity-based costing and the balanced scorecard (Cooper and Kaplan, 1991; Kaplan and Norton, 1992).
To facilitate the learning of management accounting heuristics, instructors need to explain clearly, provide examples, and test the application abilities of students. Instructors also need to get students to apply the heuristics with different datasets. To do this well, students need to have resources that can be gained through textbooks and other teaching materials. Student knowledge and comprehension of resources need to be tested by having them explain the intricacies of the materials rather than merely repeat memorized definitions and explanations. It is also important to instruct students on the beliefs that underlie management accounting; of course they need to be tested on beliefs in order to facilitate learning.
From the perspective of educational outcomes (Bloom et al., 1956), student knowledge and comprehension of management accounting plus the ability to apply management accounting heuristics are prerequisites for case analysis. In addition, it is necessary to engage in a case based approach to teaching—another “control” in Schoenfeld's terms—to assist students as they grapple with analysis and synthesis (Bloom et al., 1956) in determining the appropriate heuristics for ascertaining the real problems in case analysis.
The distinguishing feature of the framework is making explicit the communication to students as to how the teaching will proceed and accordingly what is important to learn to earn marks given the motivating forces of assessment. The heuristics and their functionality need to be the focus. Learning outcomes and assessment techniques need to be consistent with the proposed framework.
A fair question is how this framework differs from the normal textbook approach to teaching management accounting. Consider a normal textbook, the 8th Canadian edition of the popular Managerial Accounting by Garrison et al. (2009). Each chapter has a narrative text section clearly laid out with learning objectives followed by the end-of-chapter assignment and testing materials consisting of questions, exercises, problems, cases, and research. Garrison's narrative text section is clearly part of Schoenfeld's resources for explaining the heuristics. Garrison's “questions” test students on their understanding of the text material at Bloom's first, or knowledge, level; the framework would require the questions on quizzes and examination to be at a higher cognitive level, say at Bloom's comprehensive level, to facilitate greater understanding of the heuristics. Garrison's “exercises” and “problems” clearly address the framework's structured problem solving. Unfortunately, Garrison's “cases” with prescribed answers do not test unstructured problems; they are essentially multipart structured problems. The instructor wanting to use the proposed framework would need to supplement the Garrison textbook with cases that contain unstructured problems. Garrison's “Research” exercises that require students to examine company Web pages for management accounting topics tends to be part of what the proposed framework considers to be “resources.” As to “beliefs” and “controls,” Garrison is largely silent, but an instructor using the framework could readily incorporate both into the delivery of a course.
The framework proposed in this paper does differ from regular teaching from existing textbooks but could be used with most textbooks with only modest augmentation. Nonstandard problems (i.e., cases) would need to be added. Probably the largest demand on the instructor would be to explain how the course will be taught using the adapted Schoenfeld's framework.
This paper simply presents Schoenfeld's framework as an alternate for teaching and learning management accounting. It is silent on the comparative costs and benefits of the different frameworks. Only future research can show that the framework has an advantage in teaching and learning management accounting. It is also important to understand the additional costs that will be incurred for added benefits when teaching with the Schoenfeld framework. First, the structure and processes as outlined in this paper would need to be studied carefully when instructors develop revised learning objectives and assessment techniques. Second, assessments will need to be added by the instructor for testing students on text materials and on unstructured problems/cases. Third, the instructor will need to add explicit course content on Schoenfeld's controls and beliefs. As for students, the Schoenfeld framework will require them to become more active and deep learners.
Two steps are suggested for testing this proposed conceptual framework. First, test the efficacy of the management accounting framework for facilitating students' learning. A suggested approach with multiple-section courses would be to compare learning with and without the framework. The content and final examinations (with structured and unstructured problems) would be the same. Each would be taught with the same unstructured problems/cases—the textbooks may need to be supplemented. Hopefully, the same instructors would teach with and without the framework. The framework sections would be taught as discussed in this paper. The sections being taught without the framework would be taught according to suggestions made by the textbook publishers, including the publisher's slides and multiple-choice test banks. In effect, this would culminate in a test of rational learning against empirical learning (Muis, 2008).
Second, seek practicing management accountants' input on the validity of management accounting heuristics taught in textbooks. It is not clear from the literature whether the existing management accounting heuristics in textbooks are currently valid for the practice of management accounting. This can be tested by surveying practitioners on the contemporary validity of those heuristics and asking them to supply additional heuristics that they currently use. This survey could be supplemented by observing how practicing management accountants actually solve problems and noting the management accounting heuristics being used.
As the learning outcomes are explicit through the focus on heuristics and nuanced by resources, beliefs, and controls, the framework will assist instructors in selecting or developing appropriate management accounting problems and cases. Compared to assigning a chapter, the framework focuses explicity on what needs to be taught and learned. The adoption of this framework of student learning may allow instructors to teach management accounting more systematically.
Finally, teaching and learning might be more successful if, as suggested in the paper, we pay closer attention to how the learning processes take place.2 The proposed conceptual framework of resources, heuristics, control, and beliefs is intended to assist us in achieving such success.