Benchmarking the Mantel test and derived methods for testing association between distance matrices
Mathias Currat, Juan I. Montoya-Burgos contributed equally to this work.
Abstract
Testing the association between objects is central in ecology, evolution, and quantitative sciences in general. Two types of variables can describe the relationships between objects: point variables (measured on individual objects), and distance variables (measured between pairs of objects). The Mantel test and derived methods have been extensively used for distance variables. Yet, these methods have been criticized due to low statistical power and inflated type I error when spatial autocorrelation is present. Here, we assessed the statistical power between different types of tested variables and the type I error rate over a wider range of autocorrelation intensities than previously assessed, both on univariate and multivariate data. We also illustrated the performance of distance matrix statistics through computational simulations of genetic diversity. We show that the Mantel test and derived methods are not affected by inflated type I error when spatial autocorrelation affects only one variable when investigating correlations, or when either the response or the explanatory variable(s) is affected by spatial autocorrelation while investigating causal relationships. As previously noted, with autocorrelation affecting more variables, inflated type I error could be reduced by modifying the significance threshold. Additionally, the Mantel test has no problem of statistical power when the hypothesis is formulated in terms of distance variables. We highlight that transformation of variable types should be avoided because of the potential information loss and modification of the tested hypothesis. We propose a set of guidelines to help choose the appropriate method according to the type of variables and defined hypothesis.
1 INTRODUCTION
In quantitative sciences, a common task is to analyse the relationships between two or more variables measured over the same set of objects (i.e., individuals, populations, and habitats). Two types of variables can describe the relationships between these objects. The first type describes an attribute of the object and can be measured directly on each object individually, such as the weight, size, or colour. This type of variable is referred thereafter to point variable and is represented as a descriptor of nodes (objects) in Figure 1a. Several efficient methods to examine the relationship among such variables are available (see Legendre et al., 2015; Legendre & Fortin, 2010). The second type of variable describes the distance or resemblance between two objects and is measured between pairs of objects. The simplest example is the least-cost path separating two objects (e.g., two populations) across a geographic area. This measure cannot be obtained on a single object without information pertaining to the second object of the pair (the geographic position of the second population) and the environmental resistance separating these objects (see Figure 1b). Similarly, in population genetics, the fixation index (FST) is widely used to estimate genetic differentiation between pairs of populations (e.g. de Queiroz et al., 2017). If represented in our three-dimensional network in Figure 1a, the objects would be populations, and the edges would be pairwise FST values or least-cost path. We term this type of variable distance variable, which includes pairwise similarity (S) and dissimilarity (D) variables. Although the two types of matrices (S and D) are distinguished by the association between identical objects, which take a value of one or zero, respectively, we prefer to use thereafter the most commonly used term distance rather than the most generic term resemblance (see Legendre & Legendre, 2012).
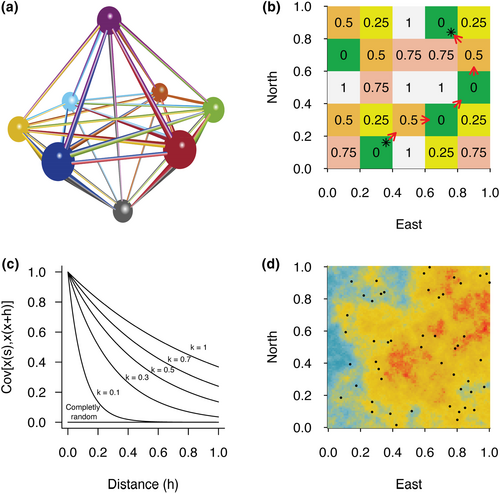
If the variables of interest are two distance variables, a distance hypothesis could be formulated, and the linear or monotonic relationship between these variables can be assessed using the classical Mantel test (Mantel, 1967; Mantel & Valand, 1970). The Mantel test was originally developed to study the spatiotemporal dispersion of diseases (Mantel, 1967), and since then, it has been applied in different fields of the life sciences (e.g., Mateo-Sánchez et al., 2015; Poloni et al., 1997; Sokal, 1979). The Mantel test was later extended into the partial Mantel test (PMT), which assesses the correlation between two pairwise distance matrices while controlling for the effect of a third variable, also expressed as a pairwise distance matrix (Smouse et al., 1986). A generalization was developed to test the correlation among multiple independent distance variables: the multiple regressions on distance matrices (MRM) (Hubert & Golledge, 1981; Manly, 1986, 1997). These distance matrix-based methods gained popularity because of their ease of use and their ability to summarize many variables in a single index (Guillot & Rousset, 2013). When analysing variables of different types (i.e., point variables and distance variables), it is common practice to compute pairwise distance matrices from the point data (e.g. computing genetic distances from allele frequencies or Euclidean distances from geographic coordinates) to analyse the full dataset using distance matrix-based methods from the Mantel test family (e.g. Araya-Ajoy & Dingemanse, 2014; Ossi & Kamilar, 2006).
Through numerical simulations, Legendre and Fortin (2010) identified a lower statistical power of the Mantel test and its derived forms compared to linear correlation, regression, and canonical analysis methods, such as Pearson linear correlation and redundancy analysis (RDA). Nevertheless, they stated that the Mantel test is still appropriate if the hypothesis can solely be formulated in terms of distances. However, to perform the analyses, they simulated correlated point variables with the desired correlation intensity, from which they computed pairwise Euclidean distance matrices and tested the correlation between matrices using the Mantel test. The hypothesis was thus based on point variables, but tested with distance variable methods. Here, we extended their analysis by imposing a level of correlation directly on the distance variables, i.e., on distance matrices hypotheses in non-Euclidean space.
In population and landscape genetics, testing for spatial autocorrelation (i.e., isolation by distance) is one of the most common applications of the Mantel test (Diniz-Filho et al., 2013). Spatial autocorrelation may appear, among other factors, because landscape variability modulates gene flow, leading to patterns of isolation by distance, or due to the effect of natural selection and genetic drift on the genetic structure of populations (Legendre & Fortin, 2010). When the tested variables are spatial autocorrelated, Guillot and Rousset (2013) pointed out the inflated type I error associated with the Mantel test and PMT. They assessed type I error by simulating variables with fixed values of spatial autocorrelation. Here, we extend their analysis by assessing the type I error rate of the Mantel test, PMT, and MRM on variables displaying a range of spatial autocorrelation intensities instead of the same intensity for all variables. Specifically, we perform a detailed analysis of the performance of the Mantel test and its derived methods, namely, the PMT and MRM, with special attention given to deciphering the conditions under which these methods are accurate and well suited. Finally, we discuss guidelines for selecting appropriate approaches according to the type of variables and hypotheses tested.
2 MATERIALS AND METHODS
2.1 Analyses using distance matrices
We assessed the performance of three methods designed to test the relationship between distance matrices: (1) the Mantel test, which compares the relationship between two variables measured on a set of n objects organized into n x n pairwise distance matrices, estimating a correlation coefficient through a permutation method (e.g., Monte Carlo randomization); (2) the partial Mantel test (PMT), which is an extension of the Mantel test that allows controlling for the effect of a third distance variable that may be correlated with the two first variables; and (3) multiple regressions on distance matrices (MRM), which extends the classical Mantel test and PMT methods by testing the association of a response distance matrix with any number of explanatory distance matrices. The MRM method has attracted growing attention because (i) it considers the effect of multiple explanatory variables; (ii) nonparametric relationships can be analysed; (iii) many data types can be analysed (e.g., count, presence/absence, continuous, and categorical variables); and (iv) it may be used to test and quantify spatial autocorrelation on different spatial scales (Lichstein, 2007).
2.2 Simulating autocorrelated data
To evaluate the type I error rate, we simulated datasets composed of two unrelated variables (x and y) in the case of the Mantel test and the PMT, while in the case of MRM, we simulated one or more explanatory variables (xi) unrelated to a response variable (y), each variable being spatially autocorrelated. We generated pseudo-observations (si) by using a Gaussian random field, which is a widely used model for generating spatially autocorrelated data (e.g. Ober et al., 2011). In all spatially explicit variables, the covariance between data points x taken at some spatial location s is assumed to decrease exponentially with the distance (h) according to Cov[x(s), x(s + h)] = exp(−|h|/k), where k is a scale parameter expressing how correlated generated data are, giving meaningful results relative to the data sampling window length (see Guillot & Rousset, 2013). The larger the value of k, the more autocorrelated the dataset; however, autocorrelation decreases with distance (Figure 1c).
Our aim was to generate results comparable to the previous study by Guillot and Rousset (2013). Consequently, we followed their procedure, consisting of simulating a spatially autocorrelated landscape where a distance variable is computed as the pairwise distance between data samples using the Euclidean distance (). Distance matrices obtained were used to measure type I error rate, as presented by Guillot and Rousset (2013). Figure 1d represents an example of a spatially autocorrelated variable over a square space and the distribution of random samples.
We ran 200 independent simulations per spatial autocorrelation condition (k = [0,1]) with two sample sizes: 50 samples (n = 50) and 200 samples (n = 200). We calculated type I error rate for (i) the Mantel test (MT), (ii) the partial Mantel test (PMT), using geographic distance as the third matrix, and (iii) the multiple regressions on distance matrices (MRM) using up to five distance matrices. Because we did not include any correlation between the variables xi and y in our simulations, the null hypothesis of no relationship between them is expected to be true in all cases. We estimated a 95% confidence interval for the type I error rate associated with each method. The confidence interval was estimated using an asymptotic Gaussian approximation: , where is the proportion of type I error, n is the sample size, and z is the standard normal deviation associated with a two-tailed probability α.
All analyses were performed by using R (R Development Core Team, 2019). We used the RandomFields package (Schlather et al., 2015) for generating autocorrelated variables, the vegan package (Oksanen et al., 2007) for computing the Mantel test and PMT, and the ecodist package (Goslee & Urban, 2007) for performing the MRM (see Appendix S1). Note that all p-values are estimated using the upper tail of the null distribution, this procedure being the output in the vegan library. It is also a common practice when testing the Mantel test with spatially autocorrelated data (Legendre et al., 2015).
2.3 Statistical power of the mantel test
We used Monte Carlo simulations to assess the statistical power of the Mantel test for detecting correlations between two point variables (case 1) and two distance variables (case 2) with predetermined correlation values (ρ(x,y)). We fixed a negative, null or positive correlation between the variables using ρ(x,y) = [−0.5, 0, 0.5]. The null hypothesis is true for ρ(x,y) = 0 and false for ρ(x,y) = 0.5 or ρ(x,y) = −0.5. We generated the values of two correlated variables with the method of Iman and Conover (1982), which outputs pairs of positive random values with the desired correlation (or absence of correlation). We tested different sample sizes n = [5, 10, 25, 50, 100], in which n represents the number of objects compared (Figure 1a). This simulation framework results in a dataset with two variables exhibiting the specified amount of correlation, a dataset we subsequently used to assess the power of the Mantel test. To evaluate the consequences of using the Mantel test to evaluate the correlation between point variables (case 1), we followed the procedure performed by Legendre and Fortin (2010). This procedure imposes the correlation on point variables and then uses these correlated point variables to compute distance variables in the form of pairwise Euclidean distances to run the Mantel test. Because point variables and distance variables do not express the same information, we also evaluated the power of the Mantel test when a correlation is imposed directly on distance variables (case 2). This second case evaluates situations in which the tested hypothesis is based on pairwise distances between objects (Figure 1a). This could also represent any computation of distance based in a non-Euclidean space that preserves the negative or positive direction of the pairwise differences (e.g., absolute distance based on species richness or habitat variables; see Somers & Jackson, 2022). We note that the number of pairs of correlated values in case 1 is n, as opposed to n(n-1)/2 in case 2. The statistical power was estimated as the probability of not having false negatives: 1- P(reject H0 | H0 is true).
We used the package mc2d (Pouillot & Delignette-Muller, 2010) to generate variables with imposed correlations, and the ecodist package (Goslee & Urban, 2007) to perform the Mantel test. The latter package allows computation of two-tailed p-values, which we preferred in this section as our imposed correlations between tested variables have intensities smaller and larger than zero (see Appendix S1).
2.4 Simulation of genetic divergence
We explored the performance of the Mantel test when considering a hypothesis formulated as distance variables affected by spatial autocorrelation, and thus potentially influenced by an inflated type I error. We used forward-in-time, individual-based genetic simulations, representing two species, each made up of a series of populations diverging from a common ancestral population. Two scenarios were explored, each simulating 100 generations of divergence for 12 populations per species linearly arranged in a stepping stone manner: (i) scenario 1: independent evolution without gene flow among populations, and (ii) scenario 2: bi-directional gene flow where migration of individuals occurs between neighbour populations. While no spatial autocorrelation is expected in scenario 1, some is to be expected in scenario 2. Tested distance variables were estimated as the pairwise genetic differentiation between populations, measured as the FST within both species (see Figure S1).
We ran 200 independent simulations of evolutionary differentiation for these two unrelated species (each species represented by a grid of populations). We used the Mantel test to evaluate the level of autocorrelation among FST values, computed after 100 generations (t = 100). We also used this test to assess the correlation level of FST values between species 1 and 2 evolving under: (a) scenario 1 for the first species versus scenario 1 for the second species, (b) scenario 2 versus scenario 2, and (c) scenario 1 versus scenario 2. Phenotypic attributes, including flying or swimming capacity, among others, could explain different migration regimes in two species inhabiting the same geographic area. The correlation level between species FST matrices depends on processes driving independent evolutionary trajectories. We also used the partial Mantel test to analyse the correlation of FST values of both species, as well as a Pearson correlation for the level of heterozygosity of both species. Note that in the last condition, the hypothesis is based on point variables (heterozygosity) rather than on distance variables (FST). The Mantel and partial Mantel test were computed on the ecodist package with two-tailed p-values.
Simulations were performed with the R package ‘glads’ (Quilodrán et al., 2020). The purpose of this individual-based approach is to generate insight into how genetic and demographic processes can generate patterns of divergence between populations. The simulations have three levels of scale: (i) ‘genotypes’ that may influence (ii) ‘phenotypes’, which in turn may affect (iii) ‘population demography’. Because this implementation focused on neutral evolution, individuals were simply characterized by their genetic diversity (genotype) and sex (phenotype), and grouped in populations (demography) (see below). The individuals belong to two theoretical species, with parameter values inspired by silvereyes (Zosterops lateralis), following Sendell-Price et al. (2020).
Each species started (t = 0) with 120 individuals characterized by 10 randomly drawn biallelic SNPs distributed along a chromosome of 100 Mb. Individuals were assigned a sex by considering a 50% sex ratio. At the beginning of simulations, all populations within a species started with equal allelic frequencies, representing the common ancestry of the 12 populations. This initial genetic diversity was randomly assigned to each of the 200 independent simulations. Each population was iterated over time measured as generation step. At each generation, mating pairs were formed in a number limited by the number of females, with males randomly selected. The offspring number was assigned from a Poisson distribution with a mean (λ = 3) that varied with population density (N): . We included a density-dependent effect (σdem = 0.01) to limit population growth, keeping every population between 100 and 150 individuals.
The offspring genotype was defined by crossover points along the parental genomes, obtained through a Poisson process. This considered the physical position of each SNP along the chromosome, with the probability of a crossover occurring between two SNPs defined by the expected per base recombination rate (ρ = 1.5 cM/Mb). The mutation rate per site per generation was μ = 1.1 x 10−8. No migration between populations was set for scenario 1 (m = 0), but gene flow between populations was set for scenario 2 using a random distribution m = [0.001,0.018]. More information about this framework is available in Quilodrán et al. (2020) and Appendix S1.
3 RESULTS
3.1 Type I error rate
When only one variable x or y is affected by spatial autocorrelation, type I error rate is lower than the threshold of 5% for the Mantel test (Figure 2a). Results are similar for PMT, showing that both methods are valid when one of the two variables (x or y) is not affected by spatial autocorrelation (Figure 2b). However, if both variables show a level of autocorrelation higher than k ≈ 0.2, these methods exhibit type I error rates significantly higher than the threshold of 5%. When controlling for geographic distance, sensitivity to type I error is less pronounced with the PMT than with the Mantel test when spatial autocorrelation is small (Figure 2a vs. Figure 2b). However, the PMT is unable to maintain a type I error rate smaller than 5% when k > 0.2. These results are obtained for a sample size of n = 50, but a similar trend is found with a sample size of n = 200 (see Figure S2).
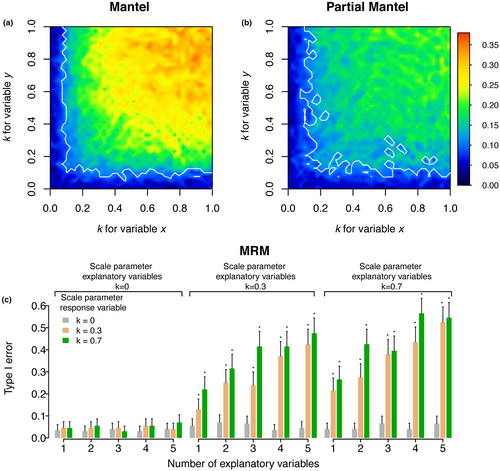
When examining type I error rate associated with MRM, our results show that if no autocorrelation is present within the dataset, there is no inflated type I error (k = 0; Figure 2c). This finding is also true when either the response (y) or all the explanatory variables (xi) are not autocorrelated. However, an inflated type I error rate appears when autocorrelation is present in both the response (y) and explanatory variables (either one or more xi). In this case, type I error rate increases as the number of explanatory variables affected by autocorrelation increases, and as the level of autocorrelation within the dataset increases (in our example: k = 0.3 and k = 0.7; Figure 2c).
3.2 Statistical power of the mantel test
We ran a power analysis on the Mantel test by setting predefined negative, positive, or no correlations between two positive random variables (ρ(x,y) = [−0.5, 0, 0.5]). To be comparable with previous studies, these variables were first considered point variables and were subsequently used to compute distance variables. Second, we considered these variables to be two distance variables linked with the predefined correlation intensity and organized them into pairwise distance matrices. Our results (Table 1) indicate that the Mantel test exhibits low power when the correlation is applied to point variables later transformed into distance variables. In this case, the Mantel coefficient r is always much smaller than the applied correlation intensity. Furthermore, when the correlation set between the original point variables is negative (ρ(x,y) = −0.5), the Mantel test does not detect the negative nature of the association. However, the Mantel test has no power issue when the correlation is directly set on distance variables. In such a case, the value of Mantel's r is very close to the predetermined correlation value, and the test is able to find the correct nature of the association between the two distance variables, including a negative correlation. Lastly, our results also indicate that statistical power increases with the sample size n (number of objects compared) as the measured and initially imposed correlation values become similar (Table 1, Figure S3).
| n | Correlation imposed ρ(x,y) | 1. Point variables transformed into distance variables | 2. Distance variables | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean of Mantel r | Power lower tail | Power upper tail | Power two-tailed | Mean of Mantel r | Power lower tail | Power upper tail | Power two-tailed | ||
| 5 | 0 | −4.3E-03 | 0.03 | 0.04 | 0.03 | 6.9E-04 | 0.04 | 0.04 | 0.04 |
| 10 | 0 | 1.9E-03 | 0.05 | 0.05 | 0.05 | −1.2E-03 | 0.05 | 0.05 | 0.05 |
| 25 | 0 | −5.8E-04 | 0.05 | 0.05 | 0.05 | 8.0E-04 | 0.05 | 0.05 | 0.05 |
| 50 | 0 | −8.4E-04 | 0.04 | 0.05 | 0.05 | −9.9E-05 | 0.05 | 0.05 | 0.05 |
| 100 | 0 | 5.4E-04 | 0.05 | 0.05 | 0.05 | −3.4E-05 | 0.05 | 0.05 | 0.05 |
| 5 | 0.5 | 0.02 | 0.05 | 0.04 | 0.05 | 0.40 | 0.24 | 0.00 | 0.14 |
| 10 | 0.5 | 0.08 | 0.15 | 0.03 | 0.15 | 0.46 | 0.96 | 0.00 | 0.92 |
| 25 | 0.5 | 0.14 | 0.49 | 0.01 | 0.47 | 0.47 | 1.00 | 0.00 | 1.00 |
| 50 | 0.5 | 0.16 | 0.83 | 0.00 | 0.81 | 0.48 | 1.00 | 0.00 | 1.00 |
| 100 | 0.5 | 0.17 | 0.98 | 0.00 | 0.98 | 0.48 | 1.00 | 0.00 | 1.00 |
| 5 | −0.5 | 0.03 | 0.05 | 0.04 | 0.05 | −0.40 | 0.00 | 0.24 | 0.15 |
| 10 | −0.5 | 0.09 | 0.16 | 0.03 | 0.16 | −0.46 | 0.00 | 0.96 | 0.92 |
| 25 | −0.5 | 0.14 | 0.49 | 0.01 | 0.48 | −0.47 | 0.00 | 1.00 | 1.00 |
| 50 | −0.5 | 0.15 | 0.83 | 0.00 | 0.81 | −0.48 | 0.00 | 1.00 | 1.00 |
| 100 | −0.5 | 0.17 | 0.99 | 0.00 | 0.98 | −0.48 | 0.00 | 1.00 | 1.00 |
- Note: Power is the proportion of rejection of the null hypothesis (H0) when an alternative hypothesis (H1) is true, at the 5% significance level. n is the sample size; ρ(x,y) is the correlation imposed between the two variables. Power of lower tail, upper tail and two-tailed refer to H0 ≤ 0, H0 ≥ 0, H0 = 0, respectively. The data presented correspond to 10′000 simulations.
3.3 Simulation of genetic divergence
We performed forward-in-time evolutionary simulations of the genetic diversity of two unrelated species, each distributed in 12 populations, diverging over the course of 100 generations (Figure 3 and Figure S1). When species evolved in the absence of among-population gene flow (scenario 1 vs. scenario 1), we notice no inflated type I error rate associated with the Mantel test when comparing the FST values of both species. Similarly, no inflated type I error is observed when populations of a single species are evolving in the presence of bi-directional gene flow in a stepping stone manner (scenario 1 vs. scenario 2). Yet, inflated type I error is noted when both unrelated species evolve under the same condition of bi-directional gene flow (scenario 2 vs. scenario 2) (Figure 3). In this last situation, the partial Mantel test performs better but still has a level of non-corrected inflated type I error rate (Figure S4). When analysing a hypothesis based on point variables, a Pearson correlation between the heterozygosity of both species is less affected by inflated type I error rate (Figure S5).
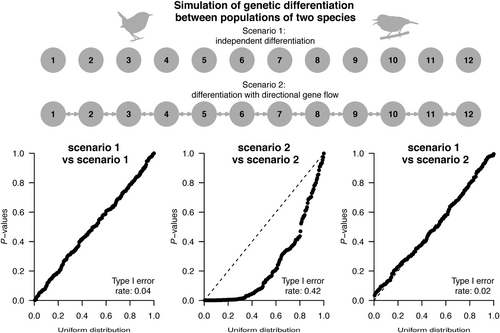
Because populations are evolving independently in scenario 1 (i.e., without gene flow), no spatial autocorrelation emerges, i.e., the null hypothesis of no isolation by distance is randomly rejected by the Mantel test (Figure S6a). However, there is spatial autocorrelation in scenario 2 (i.e., bi-directional gene flow) since FST values are influenced by the distance separating pairs of populations, with the Mantel test often being statistically significant when testing isolation by distance (Figure S6b). These results confirm our theoretical expectation (Figure 2), stating that the null hypothesis (H0) would be randomly rejected without excess of type I error when tested variables are not autocorrelated (scenario 1 vs. scenario 1), or when a single variable is autocorrelated (scenario 1 vs. scenario 2).
4 DISCUSSION
The Mantel test and its derived methods (i.e., the PMT and MRM) are distance matrix-based approaches to test linear relationships among distance variables (Wagner & Fortin, 2013). They have been largely used to test hypotheses in quantitative sciences and more specifically in ecology and evolution, but the accuracy of results has been criticized due to an inflated type I error rate when variables are spatially autocorrelated or due to a low statistical power (Debastiani & da Silva Duarte, 2017; Guillot & Rousset, 2013; Harmon & Glor, 2010; Legendre et al., 2015; Legendre & Fortin, 2010; Zeller et al., 2016). Here, we (1) reassess the conditions under which these methods are valid for testing associations among variables, and (2) improve upon previous evaluation by testing their performance in a wider range of distance hypothesis scenarios.
4.1 Autocorrelated variables: type I error
Two variables may produce significant linear relationships simply because they are both autocorrelated, even though they are otherwise linearly unrelated to each another (Bivand, 1980; Dutilleul et al., 1993; Legendre et al., 2002). Our results indicate that the Mantel test and PMT are not affected by an inflated type I error rate when there is no spatial autocorrelation within the data or when spatial autocorrelation affects a single variable (x or y). A similar result was observed by Legendre et al. (2005) in a simulation study with a fixed value of autocorrelation per variable on the Mantel test. We extended this analysis for a range of autocorrelation values in order to quantify the inflated type I error, as well as for the MRM, which is also not affected by inflated type I error when no spatial autocorrelation is present, or when spatial autocorrelation is present only in the response variable or in one or more explanatory variables. When spatial autocorrelation is present in both the response and at least one explanatory variable, we show that the type I error rate increases with the intensity of spatial autocorrelation and the number of autocorrelated explanatory variables, as similarly identified by previous studies of the Mantel test and PMT (Crabot et al., 2019; Guillot & Rousset, 2013; Oden & Sokal, 1992; Raufaste & Rousset, 2001; Rousset, 2002). Although the PMT aims to correct the spatial correlation and performs slightly better than the Mantel test, it is not sufficient to correct the spatial correlation affecting both variables tested (see Raufaste & Rousset, 2001; Rousset, 2002).
4.2 Testing for spatial autocorrelation and isolation by distance (IBD)
In eco-evolutionary studies, the Mantel test is the most commonly used tool for testing isolation by distance (IBD) (Perez et al., 2018), i.e., for testing the effect of geographic distance (spatial autocorrelation) on population genetic structure (Figure S6). However, it has been argued that Mantel's r does not provide an accurate decomposition of spatial genetic variation (Legendre & Fortin, 2010) and that it cannot answer the question of how migration limitation affects the spatial distribution of genetic variation within a species (Meirmans, 2015). The problem can be explained as follows. For a given spatial scale, when the migration rate is extremely low, a very limited fraction of the total genetic variation will be spatially autocorrelated because populations will be genetically different irrespective of the geographic distance separating them. This very limited spatial autocorrelation will result in a small value of Mantel's r. With an increasing migration rate, an increasing fraction of the total genetic variation will be spatially autocorrelated, leading to increasing values of Mantel's r. Nonetheless, this trend is gradually attenuated when the increase in migration starts to reduce genetic differences among populations to the point where the relationship with geographic distance starts to decrease. From that point on, the fraction of the total genetic variation that is spatially autocorrelated decreases gradually, leading to the expectation of a matching reduction in Mantel's r. However, this expectation is not met as Mantel's r continues to grow as the migration rate increases (Meirmans, 2015), thus gradually losing its relationship with spatial autocorrelation of the total genetic variation. This description reflects the gradual loss of collinearity between spatial autocorrelation and increasing population structure, a situation that violates the linearity assumption of the Mantel test. Consequently, the classical interpretation of Mantel's r remains valid when the migration rate or gene flow (a combination of migration rate and population size) does not disrupt the linear relationship between variables. In other cases, alternative methods should be used to test for isolation by distance (see Meirmans, 2015). Note that evaluating the spatial correlation on distances classes through Mantel correlograms could help identify non-linear relationships (Diniz-Filho et al., 2013).
4.3 Statistical power of the mantel test
It has been claimed that the Mantel test should be avoided and restricted to hypotheses that can only be formulated in terms of distance variables due to the persistent low statistical power of this method (Harmon & Glor, 2010; Legendre et al., 2015; Legendre & Fortin, 2010). For point variables simulated with a determined correlation value, it has been shown that the correlation retrieved by the Mantel test is usually smaller than the one originally imposed (Dutilleul et al., 2000) and that the Mantel test cannot detect the sign in case of negative relationships between variables (Legendre & Fortin, 2010). Our analyses show that a relationship initially negative becomes positive after point variables are transformed into distance variables, therefore modifying the initial correlation between these points. Current criticisms are thus valid when Euclidean distance matrices are computed from correlated point variables without reformulating the null hypothesis. By using the simple difference between data points instead of Euclidean distance, Somers and Jackson (2022) identified negative relationships that are lost when using Euclidean methods. We extended this analysis by showing no problem of power if the Mantel test is applied to correlated distance variables computed directly from the pairwise relationships between objects, i.e., the tested hypothesis is based on distance variables in non-Euclidean space. These novel findings suggests the low power of the Mantel test and related methods based on Euclidean distances should not be generalized to other distance measures that could either be computed directly between pairs of objects (Figure 1a), or computed from data points in non-Euclidean space (Somers & Jackson, 2022).
When point variables are transformed into distance variables, they do not express the same information. This is the reason why it is recommended not to use distance matrix-based methods on distance variables computed from point variables when testing hypotheses on original point variables. It is thus important to formulate the tested hypothesis in terms of distance variables when using the Mantel test or any other related methods. Our results clearly show that if we simulate correlated distance variables, the Mantel test does not suffer from a lack of power. Overall, we stress here that there is no reason to avoid using methods testing for association among distance matrices as long as the hypothesis is formulated in terms of distance.
There are a number of situations where the relationships between objects (Figure 1a) can only be described (or is best described) as pairwise distance variables, with the associated hypotheses thus formulated as distances. In landscape genetics, the least cost path taking into account the resistance of the environment, for instance, can be analysed with pairwise distance variables describing how much gene flow can occur between populations (reviewed in Spear et al., 2010). When considering species as objects, some ecological or genetic interactions are better described by such pairwise distance variables, including the reciprocal competition intensity, the interbreeding rate, or the size of interaction zones between species.
4.4 Choosing the method according to the variables
We suggest some general guidelines for choosing suitable procedures to test for the relationship between two or more variables and to avoid the pitfalls that we and others have identified (Figure 4). First, the basic assumptions justifying the use of methods testing for linear relationships should not be violated (e.g. Rencher & Schaalje, 2008). Second, because hypotheses formulated using distance variables do not convey the same information as when formulated using point variables, any kind of data transformation should be avoided. Third, if data transformation cannot be avoided, the tested hypothesis has to be formulated in the context of the set of variables being analysed (point variables or distance variables, Figure 1a). In this last case, for example, one may be interested whether there is an association between a trait frequency within populations (i.e., the response variable expressed as a point variable) and the environmental resistance separating pairs of populations (i.e., the explanatory variable is expressed as a pairwise distance variable). Alternatively, one may ask whether the number of migrants between pairs of populations (i.e., response variable expressed as a distance variable) is related to each population's census size (i.e., the explanatory variable expressed as a point variable).
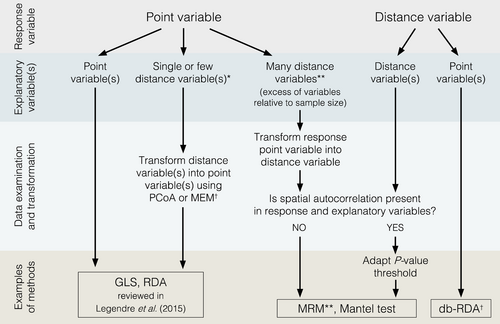
We refer to explanatory and response variables in our decision scheme (Figure 4), however, note that there is no discrimination between these variables when testing for correlations (e.g., Mantel test and PMT) instead of causal relationships (e.g., MRM). Perhaps, the more straightforward case is when the response variable is in the form of a distance variable and there are one or more explanatory variables in the form of point variables. In this case, distance-based redundancy analysis (db-RDA), which was originally described by Legendre and Anderson (1999) could be the adequate method. The distance matrix of the response data is transformed into principal coordinates (PcoA), and these are used as input into a redundancy analysis (RDA). PcoA consists of using the N-dimensional coordinates directly as point variables in linear models. However, because this transformation method is developed from a Euclidean framework (Borcard & Legendre, 2002), it cannot be extended to distance variables represented in a non-Euclidean space. This could be the case when distance variables are obtained without previous transformation from point variables, in which case distance-matrix based methods should be preferred (see threshold correction below).
The situation becomes slightly more complex when the response variable is in the form of a point variable and explanatory variables are in the form of distance variables. When there are one or a few explanatory variables, we advise transforming the distance variable(s) into point variables and then using dedicated methods that consider the spatial autocorrelation of point variables, such as generalized least squares (GLS), geostatistical mixed-effect models (GMM), or RDA. A distance variable can be transformed into point variables by deriving its N-dimensional coordinates through PcoA, as well as by considering derived methods, such as principal coordinates of neighbour matrices (PCNM) or Moran's eigenvector maps (MEM) (Borcard et al., 2004; Borcard & Legendre, 2002; Dray et al., 2006). Because a loss of information may occur during the transformation process, the number of coordinate dimensions that captures enough explained variance might be kept and used in methods that allow multiple explanatory variables, such as RDA, GLS, or mixed-effect models. However, when transforming distance variables into point variables, an important issue is the multiplication of explanatory variables, which implies a careful interpretation of the results because of the difficulty in interpreting the many axes of a previously single distance variable. When the number of explanatory variables is large relative to the sample size (i.e., the number of objects compared), then testing methods may perform poorly (e.g. Harrell Jr et al., 1996). Moreover, these transformation methods are not well suited for non-Euclidean distance variables, which may still be preferentially analysed with distance matrix-based methods. In both last cases, it is therefore preferable to transform the response point variable into a distance variable and then analyse the matrices with the Mantel test or MRM approach, as long as the hypothesis is formulated in terms of distance. Note that selection of explanatory variables using MRM has to be avoided, as Franckowiak et al. (2017) showed that indices usually used for model selection (i.e., AIC, AICc, and BIC) perform poorly due to maximum likelihoods being based on mis-specified models.
When using the Mantel test and derived methods, substantial spatial autocorrelation in both the response and explanatory variables may lead to an inflated type I error rate. Recent approaches tried to overcome this problem by replacing the permutation method of classical Mantel statistics, which assume samples are exchangeable, an assumption that is violated under the influence of autocorrelation and pseudo-replication (Clappe et al., 2018; Wagner & Dray, 2015). Crabot et al. (2019) proposed a promising alternative, but it is limited by the definition of a spatially weighted matrix that strongly influences the performance of the approach when it is misestimated. We advise estimating the amount of spatial autocorrelation within variables using the parameter k presented in Diggle et al. (2007) or using Mantel's r, Moran's I (Moran, 1950) or Geary's c (Geary, 1954) (Borcard & Legendre, 2012; Wagner, 2004). Note that simultaneously testing autocorrelation with different methods could prevent false-negative results. Yet, this does not guarantee that Type I errors can be avoided, and other statistics may be preferred if the dataset could be expressed as point variables (e.g., mixed-effect models). If the dataset could only be expressed as a distance variable and spatial autocorrelation is found on both sides of a regression equation, or within both variables tested for correlation, the expected excess type I error can be corrected by adapting the significance threshold (Diniz-Filho et al., 2013). A conservative procedure consists in dividing the significance level of 5% by the number of times this threshold level is found in the type I error rate associated with the k value estimated from a model of spatial autocorrelation (e.g. Diggle et al., 2007). In the context of our simulations, considering the most critically inflated type I error rate of ~55% obtained with the MRM approach and a k = 0.7 for all variables (Figure 3), the standard threshold of 0.05 should be divided by 11, resulting in a corrected significance level of 0.0045. The same could be extended to the Mantel test and PMT that have a maximum error (k = 1) of ~40% and ~30%. Hence, dividing the threshold by eight or six, respectively, could result in a conservative use of these statistics.
5 CONCLUSION
Our detailed analysis shows under which conditions the Mantel test and its related methods remain valid approaches. We conclude that no reasons exist to avoid them as long as the hypothesis is formulated in terms of distance variables and spatial autocorrelation is absent, either in the response or explanatory variables when testing causal relationships (e.g., MRM), or in a single variable when testing correlations (e.g., Mantel test). We show that the previously identified loss of statistical power is due to the practice of transforming point variables into Euclidean distance variables without reformulation of the null hypothesis. Indeed, data transformation from a point variable to a distance variable, and vice versa, leads to a critical loss of information (Figure S7) and should thus be avoided. When the research involves both variable types, one type of variable has to be transformed into the other type and the null hypothesis has to be reformulated in the context of the chosen variable type (Figure 4). Finally, our proposed set of guidelines may help further applications choose the most accurate method according to the hypothesis tested.
AUTHOR CONTRIBUTIONS
CSQ, MC, and JIMB conceived the original idea. CSQ performed the statistical analysis and wrote the first draft of the paper. JIMB proposed additional analyses and reworked the draft of the paper. All authors interpreted the results, and contributed critically in the writing of the final version of the manuscript.
ACKNOWLEDGEMENTS
This study was supported by grants from the Swiss National Science Foundation n° P5R5PB_203169 to CSQ, 31003A_182577 to MC, and 310030_185327 to JIMB. We thank Lionel Di Santo for his careful reading of a previous version of this manuscript. All computations were performed using the High-Performance Computing (HPC) cluster at baobab.unige.ch.
Open Research
OPEN RESEARCH BADGES
This article has earned an Open Data badge for making publicly available the digitally-shareable data necessary to reproduce the reported results. The data is available at [[insert provided URL from Open Research Disclosure Form]].
The authors declare no conflict of interest.
DATA AVAILABILITY STATEMENT
The R script used in the analysis is included as supporting information of the manuscript (Appendix S1).




