Designing Optimal Crop Revenue Insurance
Research on this article was initiated while O. Mahul was visiting the Department of Agricultural and Resource Economics, University of California at Berkeley. We acknowledge with the usual caveat the very helpful comments of the reviewer and editor.
Abstract
When the indemnity schedule is contingent on the farmer's price and individual yield, an optimal crop revenue insurance contract depends only on the farmer's gross revenue. However, this design is not efficient if, as is the case with available contracts, the coverage function is based on imperfect estimators of individual yield and/or price. The producer's degree of prudence and the extent of basis risks have important influences on the optimal indemnity schedule. In this broader context, optimal protection is not provided by available U.S. crop insurance contracts and may include combinations of revenue insurance, yield insurance, futures, and options contracts.
Farmers generally face joint price and output (yield) risk. Alternatives for managing these sources of risk have recently expanded with innovations in revenue insurance, which aims to provide protection against price declines and/or low yield. In 1991, the Canadian Department of Agriculture introduced the Gross Revenue Income Program which paid indemnities based on a fifteen-year moving average of crop-specific revenue. The U.S. Federal Agricultural Improvement and Reform Act of 1996 also changed the risk environment for U.S. producers of major crops by allowing some growers to elect revenue insurance policies. The Risk Management Agency launched a revenue insurance program known as Income Protection (IP). Two private sector programs were also approved: Crop Revenue Coverage (CRC) and Revenue Assurance (RA). Revenue insurance choices continued to expand with the introduction of a new product called Group Risk Income Protection launched in 1999 (Harwood et al. 2000). In Europe, the first revenue insurance contract was proposed to U.K. farmers in 1999 and other policies should be offered to European producers in the near future.
This article investigates the design of an optimal crop revenue insurance contract, given the risks typically faced by farmers and the information typically useable by insurers, using recent theoretical developments on optimal insurance in incomplete markets. As a preliminary case, we show that the optimal crop revenue insurance policy when the indemnity schedule is contingent on the individual farmer's crop yields and prices depends only on the farmer's gross revenue, defined as the sum of the products of acreage, individual yield, and the price which the producer receives for each crop output. This result confirms and generalizes the comparison of specific contracts in Hennessy, Babcock, and Hayes.
However, real-world markets often are not complete because the indemnity function is based on imperfect estimators of the individual yields and/or prices. Indeed, in several insurance products introduced in the last decade, indemnity payments are based on aggregate measures of price and yield. In such informational environments, optimal indemnity payments are shown to be contingent not only on the product of the aggregate estimates of yield and price, but also on the aggregate estimates of price and yield taken separately. A heuristic example of optimal insurance coverage, assuming a quadratic utility function, identifies and highlights the role of bias and basis risks in the aggregate measures in determining the optimal indemnity schedule.
The second purpose of this article is to investigate how the optimal revenue insurance policy can be used to derive important features of the efficient hedging strategy with crop yield and revenue insurance policies and with futures and options contracts offered on financial markets. The complementarity/substitutability between revenue insurance contracts and other hedging tools is analyzed. Under yield and/or price basis risks, the optimal revenue insurance contract is shown to be replicated with yield insurance, revenue insurance, and futures contracts if the producer's preferences are quadratic, insurance contracts are sold at an actuarially fair price, and futures markets are perceived as unbiased. Finally, the results are used to cast further light on informative numerical simulations of the risk-reducing performance of insurance and hedging contracts recently presented in the agricultural economics literature (Wang et al.; Heifner and Coble; Coble, Heifner, and Zuniga; Mahul, 2002).
The Model
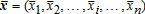 with a joint cumulative distribution function defined over the support
with a joint cumulative distribution function defined over the support , where
, where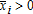 for i = 1,…, n. Hence, the producer's gross revenue is R(x) when x = (x1,…, xn) ∈ X is realized. The function R is assumed to be nondecreasing with respect to each argument:
for i = 1,…, n. Hence, the producer's gross revenue is R(x) when x = (x1,…, xn) ∈ X is realized. The function R is assumed to be nondecreasing with respect to each argument:
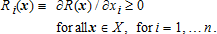 (1)
(1) , with a joint cumulative distribution function defined over the support
, with a joint cumulative distribution function defined over the support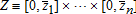 , where
, where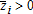 for i = 1,…, n, and is correlated with
for i = 1,…, n, and is correlated with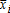 . The insurance policy is described by a couple [I(·), Q] where I(z) is the indemnity payment transferred from the insurance company, which is assumed to be risk-neutral, to the risk-averse insured producer when the vector z is realized and Q is the insurance premium. We assume that a feasible indemnity function must be nonnegative:
. The insurance policy is described by a couple [I(·), Q] where I(z) is the indemnity payment transferred from the insurance company, which is assumed to be risk-neutral, to the risk-averse insured producer when the vector z is realized and Q is the insurance premium. We assume that a feasible indemnity function must be nonnegative:
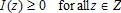 (2)
(2)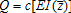 (3)
(3)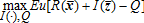 (4)
(4)Optimal Insurance Using Individual Yield and Price
We assume in this section that the indemnity schedule of the insurance contract is based on the farmer's yields and prices and the insurance company can perfectly observe these individual parameters, zi = xi for all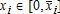 and i = 1,…, n. It can be easily shown (see the appendix) that the optimal insurance contract, the solution to program (4) subject to constraints (2) and (3), provides full coverage below a trigger gross revenue
and i = 1,…, n. It can be easily shown (see the appendix) that the optimal insurance contract, the solution to program (4) subject to constraints (2) and (3), provides full coverage below a trigger gross revenue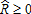 such that
such that . When the producer faces multiple uncertainties affecting his gross revenue, it is optimal to purchase a unique insurance contract covering all sources of risks at the same time, with full insurance below a gross revenue trigger. In other words, the payoff function I*(·) is the least expensive risk-sharing tool to reach a predetermined insurance coverage. This provides a slight and intuitive generalization of Raviv's work, which examined this problem with additive losses (see also Gollier and Schlesinger).
. When the producer faces multiple uncertainties affecting his gross revenue, it is optimal to purchase a unique insurance contract covering all sources of risks at the same time, with full insurance below a gross revenue trigger. In other words, the payoff function I*(·) is the least expensive risk-sharing tool to reach a predetermined insurance coverage. This provides a slight and intuitive generalization of Raviv's work, which examined this problem with additive losses (see also Gollier and Schlesinger).
The optimality of full insurance against aggregate revenue loss above a deductible implies that it dominates insurance using separate contracts for different components of income, or for price and yield. For example, insurance displaying full coverage on the farmer's gross revenue below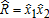 is less costly than price insurance providing full coverage below price
is less costly than price insurance providing full coverage below price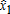 and crop insurance providing full coverage below yield
and crop insurance providing full coverage below yield , consistent with the comparison of these contracts in Hennessy, Babcock, and Hayes (see result 1). Other contract comparisons covered by our general result include that a whole-farm revenue insurance contract provides, for a given premium, a better coverage than the sum of crop-specific revenue insurance contracts. Equivalently, for a predetermined coverage level, whole-farm revenue insurance is less costly than crop-specific revenue insurance, as found by Hennessy, Babcock, and Hayes (see result 2).
, consistent with the comparison of these contracts in Hennessy, Babcock, and Hayes (see result 1). Other contract comparisons covered by our general result include that a whole-farm revenue insurance contract provides, for a given premium, a better coverage than the sum of crop-specific revenue insurance contracts. Equivalently, for a predetermined coverage level, whole-farm revenue insurance is less costly than crop-specific revenue insurance, as found by Hennessy, Babcock, and Hayes (see result 2).
Despite the interpretation of the above-mentioned model that producers would like to cover multiple risks by purchasing an “umbrella” contract displaying full coverage above a deductible on the gross revenue, real-world insurance markets are often based on indices of individual yield and price as an imperfect signal of the producer's gross revenue. In the following section, we examine the design of an optimal insurance policy against joint yield and price risk in this context of incomplete markets.
Optimum Insurance Using Aggregate Yield and Price
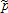 , with
, with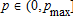 , and individual yield
, and individual yield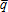 , with
, with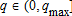 , are written as linear functions of the price index
, are written as linear functions of the price index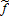 and the yield index
and the yield index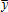 , respectively:
, respectively:
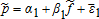 (5)
(5)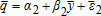 (6)
(6)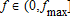 ,
,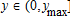 ,
,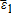 and
and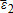 are zero-mean random variables. Such a relationship is obtained when the stochastic individual price (yield) is projected orthogonally onto the stochastic price (yield) index.1 Assume that basis risks are (unconditionally) independent of indices, that is,
are zero-mean random variables. Such a relationship is obtained when the stochastic individual price (yield) is projected orthogonally onto the stochastic price (yield) index.1 Assume that basis risks are (unconditionally) independent of indices, that is,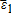 and
and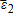 are independent of
are independent of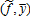 and each other.2 Note, however, that no specific assumptions are made about the stochastic dependence between the price index and the yield index. Price and yield indices are assumed to be perfectly observable and therefore yield and price basis risks are caused only by heterogeneity among farmers. Given the available information, an optimal insurance policy [I(·,·), Q] is the solution to the program (4) subject to constraints (2), (3), (5), and (6) where
and each other.2 Note, however, that no specific assumptions are made about the stochastic dependence between the price index and the yield index. Price and yield indices are assumed to be perfectly observable and therefore yield and price basis risks are caused only by heterogeneity among farmers. Given the available information, an optimal insurance policy [I(·,·), Q] is the solution to the program (4) subject to constraints (2), (3), (5), and (6) where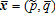 ,
,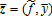 , and R(p,q) = pq. This leads to the following characterization of the optimal (single) crop revenue insurance contract.
, and R(p,q) = pq. This leads to the following characterization of the optimal (single) crop revenue insurance contract.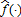 decreases (increases) with y. For all (f,y): I* (f, y) > 0, the marginal indemnity functions satisfy
decreases (increases) with y. For all (f,y): I* (f, y) > 0, the marginal indemnity functions satisfy
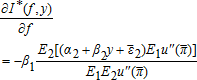 (7)
(7)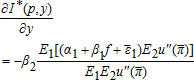 (8)
(8)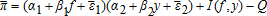 and Ej is the expectation operator conditional on
and Ej is the expectation operator conditional on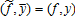 with respect to
with respect to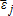 , for j = 1, 2.
, for j = 1, 2.
-
If β1 > 0, a trigger function
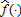 exists such that
exists such that
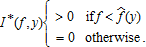
-
If β1 < 0, a trigger function
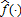 exists such that
exists such that
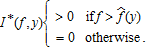
The proof of Proposition 1 is found in the appendix. The form of the optimal single-crop revenue insurance policy depends on the sign of the regression coefficients β1 and β2. If β1 is positive (negative), indemnity payments are made whenever the realized price index is below (above) the trigger level. This trigger price is a function of the realized yield index, and it decreases (increases) as the yield index increases if β1β2 is positive (negative). The indemnity function decreases (increases) with the realized price index p if β1 is positive (negative) and it decreases (increases) with the realized yield index y if β2 is positive (negative). Because price and yield expressed in equations (5) and (6) enter symmetrically in our model, the trigger yield defined as a function of the realized price index would also lead to the optimal revenue insurance contract design presented in Proposition 1.
This proposition is related to, but distinct from, Proposition 1 of Mahul (2000), which addresses optimal insurance contract design in the presence of non-additive (uninsurable) background risk. First, the trigger price is a function of the realized yield index in our model with two insurable risks, while it is a constant when a single risk is insurable, as in Mahul (2000). Second, the non-additivity of basis risks in our model does not come from the relationship between individual and aggregate parameters (yield and price), as in Mahul (2000), but from the multiplicative relationship between yield and price in the gross revenue function. The price (yield) basis risk interacts with the yield (price) index; there are thus cross-interactions between basis risks and insurable risks.
The impact of actuarially fair insurance, that is, c′(e) = 1 for all e ≥ 0, and costly insurance, that is, c′(e) > 1 for some e > 0, on the trigger function is presented in the following proposition.
Proposition 2. Under actuarially fair insurance, the optimal trigger function satisfies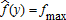 for all y, if β1 > 0, and
for all y, if β1 > 0, and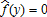 for all y if β1 < 0. Under costly insurance, it satisfies
for all y if β1 < 0. Under costly insurance, it satisfies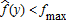 for some y, if β1 > 0, and
for some y, if β1 > 0, and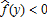 for some y, if β1 < 0.
for some y, if β1 < 0.
The proof of Proposition 2 is found in the appendix. This proposition shows that full coverage, that is, the trigger price equals the highest realization of the commodity price index, is optimal when insurance is offered at a fair price, whereas partial insurance is optimal when insurance is costly, that is, the insurance premium is higher than the actuarial value of the insurance policy.
The remaining part of this section focuses on the most realistic case where the individual price and the price index are positively correlated, that is, β1 > 0, and where the individual yield is positively correlated with the yield index, that is, β2 > 0. Observe first that if the insurance indemnity is based on individual price and individual yield, that is,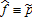 and
and , then partial derivatives (7) and (8) are equal to −q and −p for all (p, q): I*(p, q) > 0, respectively. The optimal insurance contract is thus
, then partial derivatives (7) and (8) are equal to −q and −p for all (p, q): I*(p, q) > 0, respectively. The optimal insurance contract is thus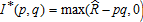 with
with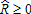 , as shown in the preceding section.
, as shown in the preceding section.
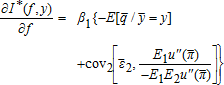 (9)
(9)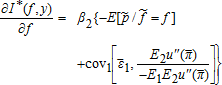 (10)
(10)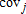 is the covariance operator with respect to the
is the covariance operator with respect to the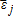 basis risk, for j = 1, 2, conditional on
basis risk, for j = 1, 2, conditional on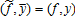 . The optimal marginal indemnity function with respect to the price index, expressed in equation (9), is affected by the regression coefficient between the individual price and the price index, by the bias between the individual yield and the yield index through the expectation of the individual yield conditional on the yield index, and by the
. The optimal marginal indemnity function with respect to the price index, expressed in equation (9), is affected by the regression coefficient between the individual price and the price index, by the bias between the individual yield and the yield index through the expectation of the individual yield conditional on the yield index, and by the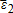 yield basis risk through the covariance term. Thus, this case contrasts with previous results where preferences do not affect the optimal contract when price is non-random and the relationship between individual yield and area yield is linear (Mahul 1999). Here the slope is higher or lower than
yield basis risk through the covariance term. Thus, this case contrasts with previous results where preferences do not affect the optimal contract when price is non-random and the relationship between individual yield and area yield is linear (Mahul 1999). Here the slope is higher or lower than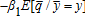 depending on whether the covariance term is positive or negative. Because the profit function π increases with ɛ2, this covariance term is positive, null or negative depending on whether the marginal utility function u′ is convex, linear or concave in wealth. The role of u‴ has been established in hedging decisions by Losq. The condition u‴ > 0 is called “prudence” by Kimball in reference to precautionary saving. The marginal indemnity function with respect to the aggregate price is thus higher than
depending on whether the covariance term is positive or negative. Because the profit function π increases with ɛ2, this covariance term is positive, null or negative depending on whether the marginal utility function u′ is convex, linear or concave in wealth. The role of u‴ has been established in hedging decisions by Losq. The condition u‴ > 0 is called “prudence” by Kimball in reference to precautionary saving. The marginal indemnity function with respect to the aggregate price is thus higher than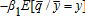 if the producer is prudent. From a similar analysis, the marginal indemnity function with respect to the aggregate yield in (10) is higher than
if the producer is prudent. From a similar analysis, the marginal indemnity function with respect to the aggregate yield in (10) is higher than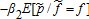 if the producer exhibits prudence.
if the producer exhibits prudence.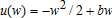 with b > 0 and w < b. The limitations of this function as a representation of attitudes towards risk are well known (e.g., the index of absolute risk aversion increases with wealth), but this case shows the role of bias in the indices independent of prudence. This function can also represent the preferences of a risk-neutral producer facing a quadratic and convex profit tax schedule who thus adopts apparent risk-averse behavior.3 In this case, the covariance terms in equations (9) and (10) are zero because u‴ = 0 and the partial derivatives become
with b > 0 and w < b. The limitations of this function as a representation of attitudes towards risk are well known (e.g., the index of absolute risk aversion increases with wealth), but this case shows the role of bias in the indices independent of prudence. This function can also represent the preferences of a risk-neutral producer facing a quadratic and convex profit tax schedule who thus adopts apparent risk-averse behavior.3 In this case, the covariance terms in equations (9) and (10) are zero because u‴ = 0 and the partial derivatives become
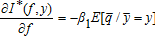 (11)
(11)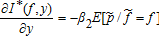 (12)
(12)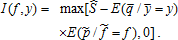 (13)
(13)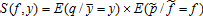 . Payoffs are made whenever S(f, y) is lower than the trigger level
. Payoffs are made whenever S(f, y) is lower than the trigger level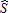 . From equations (5) and (6), this can be rewritten as
. From equations (5) and (6), this can be rewritten as
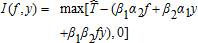 (14)
(14)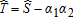 . The indemnity schedule depends not only on the gross revenue index fy but also on the price index f and on the yield index y taken separately. In this quadratic case, the trigger function defined in Proposition 1 satisfies
. The indemnity schedule depends not only on the gross revenue index fy but also on the price index f and on the yield index y taken separately. In this quadratic case, the trigger function defined in Proposition 1 satisfies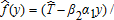
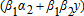 . It is a decreasing and convex function of the realized yield index whereas, under an insurance contract against price only, the optimal trigger price function is a constant independent of the yield index.4
. It is a decreasing and convex function of the realized yield index whereas, under an insurance contract against price only, the optimal trigger price function is a constant independent of the yield index.4The optimal insurance policy in (14) can also be viewed as an optimal insurance contract against gross revenue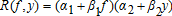 where the individual price (yield) is a deterministic linear function on the price (yield) index, that is, there are no yield and price basis risks. The optimal indemnity schedule for a producer with a quadratic utility function facing yield and/or price basis risk thus has the same form as that of a risk-averse producer with a general utility function facing no basis risk; indemnities are paid whenever S(f, y) = R(f, y) is below a trigger level. If the indemnity is based on the price index and on the individual yield then, from equation (14) with α2 = 0 and β2 = 1, the indemnity function is contingent on the insurable gross revenue fq and on the individual yield q; gross revenue insurance is still insufficient to replicate the optimal insurance policy.
where the individual price (yield) is a deterministic linear function on the price (yield) index, that is, there are no yield and price basis risks. The optimal indemnity schedule for a producer with a quadratic utility function facing yield and/or price basis risk thus has the same form as that of a risk-averse producer with a general utility function facing no basis risk; indemnities are paid whenever S(f, y) = R(f, y) is below a trigger level. If the indemnity is based on the price index and on the individual yield then, from equation (14) with α2 = 0 and β2 = 1, the indemnity function is contingent on the insurable gross revenue fq and on the individual yield q; gross revenue insurance is still insufficient to replicate the optimal insurance policy.
The design of an optimal single crop revenue insurance policy is now used to investigate the optimal hedging strategy with insurance policies and hedging tools available in real-world markets.
Insurance and Hedging Decisions
The U.S. Risk Management Agency (RMA) has developed a variety of agricultural insurance contracts in collaboration with private-sector insurance companies. The producer can buy insurance based on individual yields using multiple peril crop insurance (MPCI) or on aggregate yields using the Group Risk Plan (GRP). He can also purchase individual revenue insurance through IP, RA, or CRC policies based on individual yields and futures prices or aggregate revenue insurance using the Group Risk Income Protection (GRIP) program (see Barnett for a detailed description of these insurance policies). While the MPCI still represents the largest RMA business, the new revenue insurance products have attracted considerable interest. In the 2002 crop year, 41.98% of total U.S. crop insurance premiums were spent on the MPCI program, 29.36% on the CRC contract, 18.57% on the RA contract, 1.10% on the GRP contract, 0.48% on the GRIP contract, and 0.31% on the IP contract. In terms of insured acreage, crop yield insurance (MPCI and GRP) covered 55.55% of total U.S. insured acres, while crop revenue insurance (CRC, RA, IP, and GRIP) covered 43.88% of total U.S. insured acres (RMA).
Farmers have also the opportunity to hedge against yield and price variations on financial markets. Beside price futures contracts and options on futures to manage price risk, they can use Crop Yield Insurance (CYI) futures and options launched by the CBOT in 1995 to hedge against crop yield risk. The underlying instruments are the official state-based yield estimates released during the growing and harvesting season by the U.S. Department of Agriculture (Vukina, Li, and Holthausen).5
The purpose of this section is to examine how revenue insurance contracts can be combined with crop insurance policies and financial hedging instruments in order to replicate the optimal insurance contract against joint yield and price risk characterized in the preceding section.
We know from our preliminary results that, when there are no basis risks, the optimal insurance policy depends only on individual gross revenue and this policy displays full insurance under a critical level. Consequently, crop insurance and hedging tools turn out to be redundant.
Unfortunately, to the best of our knowledge, real-world insurance markets do not provide such revenue insurance. When insurance is sold at an actuarially fair price and the indemnity payment is based on price and yield indices, the partial derivatives of the optimal coverage expressed in equations (9) and (10) show that the optimal insurance design is (piecewise) linear in yield and price indices under a quadratic utility function, but not in general. Hence, the optimal insurance policy cannot in general be replicated with existing insurance and financial contracts because the latter are piecewise linear. This creates a second source of incompleteness, in addition to uninsurable/unhedgeable basis risks. In this general framework, there are roles for other financial instruments. The optimal hedging strategy will be based on a combination of revenue insurance contracts, crop insurance contracts and price futures and options. The use of options occurs because of the nonlinearity of optimal coverage with respect to price and yield indices, even if hedging contracts are sold at a fair price. This analysis extends Moschini and Lapan who provide a rationale for the use of options under multiple sources of uncertainty when price risk can only by hedged and under specific assumptions (the utility function is of CARA type and random variables are joint normally distributed).
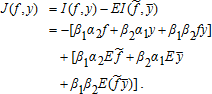 (15)
(15)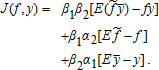 (16)
(16)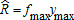 . It thus provides full insurance against
. It thus provides full insurance against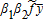 . In addition, the producer selects on financial markets a short (long) price futures position with a futures price at planting equal to the expected price and an optimal hedge ratio equal to |β1α2| if α2 is positive (negative), and a short (long) CYI futures position against the
. In addition, the producer selects on financial markets a short (long) price futures position with a futures price at planting equal to the expected price and an optimal hedge ratio equal to |β1α2| if α2 is positive (negative), and a short (long) CYI futures position against the yield risk with a futures yield at planting equal to the expected aggregate yield and an optimal hedge ratio equal to |β2α1| if α1 is positive (negative).7 Crop revenue insurance, CYI futures, and price futures contracts are thus complementary. The GRIP policy sold at a fair price with no restriction on the revenue guarantee does not allow the producer to have the most efficient coverage; additional futures contracts are needed but options contracts are redundant. The final wealth of the insured producer is
yield risk with a futures yield at planting equal to the expected aggregate yield and an optimal hedge ratio equal to |β2α1| if α1 is positive (negative).7 Crop revenue insurance, CYI futures, and price futures contracts are thus complementary. The GRIP policy sold at a fair price with no restriction on the revenue guarantee does not allow the producer to have the most efficient coverage; additional futures contracts are needed but options contracts are redundant. The final wealth of the insured producer is
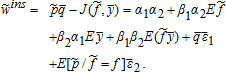 (17)
(17)Following the same method, it can be easily shown that when a revenue insurance policy has an indemnity schedule based on individual yield and futures price, the optimal indemnity function in equation (16) where α2 = 0 and β2 = 1 can be replicated by purchasing the IP policy at a coverage level; = β1 with a maximum revenue guarantee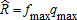 . It thus provides full coverage against the random variable
. It thus provides full coverage against the random variable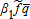 . The farmer also purchases the MPCI contract with price election ps = α1, if positive, and yield guarantee
. The farmer also purchases the MPCI contract with price election ps = α1, if positive, and yield guarantee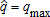 . It provides full coverage against individual yield variability. Revenue insurance and individual crop insurance turn out to be complementary, whereas futures contracts and options on futures are redundant. The insured producer's final wealth is
. It provides full coverage against individual yield variability. Revenue insurance and individual crop insurance turn out to be complementary, whereas futures contracts and options on futures are redundant. The insured producer's final wealth is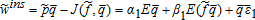 . The only source of uncertainty borne by the insured producer stems from the zero-mean random variable
. The only source of uncertainty borne by the insured producer stems from the zero-mean random variable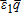 .
.
Although the above-mentioned results must be viewed as exploratory because they depend strongly on three restrictive assumptions, they allow us to highlight the complementarity of existing contracts in replicating the optimal (single) crop revenue insurance design. This theoretical approach offers a first theoretical basis for interpreting recent numerical simulations (Wang et al.; Coble, Heifner, and Zuniga; Mahul 2002).
When the revenue insurance program is based on individual yield and futures price, we have shown that, under our three restrictive assumptions, the optimal insurance coverage can be replicated with the IP contract rather than the CRC policy. However, the latter insurance product turns out to have the highest enrollment among U.S. farmers. This observation is a priori in contradiction with the above theoretical results. This may be a consequence of existing constraints on the yield guarantee and coverage level in the actual IP and CRC programs, and of the subsidization levels implicit in these policies. Because these insurance policies are sold at a price that is less than the actuarial premium, thanks to the premium subsidies, producers should be induced to select the policy that displays the highest coverage. By construction, the CRC product generates a higher coverage than IP and RA products. However, for identical insurance premiums, the IP product should be preferred to the CRC product. This seems to be confirmed by recent numerical simulations (Heifner and Coble, Mahul 2002).
Conclusions
This work is a first attempt to provide a theoretical analysis on the design of an optimal (single) crop revenue insurance contract when the producer faces joint yield and price risk. As a preliminary result, we have shown that if the indemnity schedule is contingent on individual yield and individual price, then the optimal insurance contract depends only on the individual gross revenue and it displays full insurance under a trigger revenue. In this context of complete markets, crop yield insurance contracts and hedging instruments, including futures and options, turn out to be redundant.
The main contribution of this article is to investigate insurance and hedging when the indemnity schedule is contingent on a yield and/or price index that are not identical to individual producer yield and/or price. In this context of incomplete markets, the indemnity schedule of an optimal single crop revenue insurance policy depends not only on the gross revenue index but also on the price index and on the yield index. It thus provides a rationale for combining existing revenue insurance contracts, crop insurance policies and price and yield hedging instruments, as indicated by numerical simulations (Heifner and Coble, Wang et al., Mahul 2002). In addition, we have shown how the optimal revenue insurance contract can be perfectly replicated under restrictive assumptions; the producer's utility function is quadratic and unconstrained yield and revenue insurance policies and hedging instruments are sold at fair prices. The IP program is complementary with the MPCI program, and price futures and yield options contracts are redundant. The GRIP plan is complementary with the yield and price futures contracts; options contracts are redundant.
These theoretical results, which are complementary to recent works based on numerical simulations, may offer useful information to designers of revenue insurance programs. In addition, they bring the general efficiency of the CRC contract into question, and point to a continuing role for futures contracts on yield and price as complements to other currently available crop and revenue insurance contracts.
Some obvious extensions of our model could be undertaken. For example, the assumption of independence of yield and price basis risks could be dropped, and a nonlinear relationship between individual parameters and their associated indices could be considered. Extension to multicommodity farms would complicate the analysis, but preserve the general message that multiple contracts are optimal when contracts cannot be contingent on individual prices and yields. Recognition of real-world constraints on the yield guarantee and on the coverage level would introduce new sources of incompleteness that require further investigation.
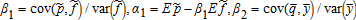 and
and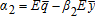 .
.Appendix
Optimum Insurance Contract Design Using Individual Yield and Price
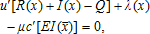 (A1)
(A1)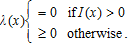 (A2)
(A2)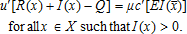 (A3)
(A3)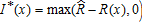 with
with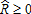 .
.Proof of Proposition 1
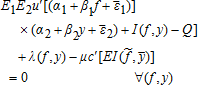 (A4)
(A4)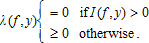 (A5)
(A5)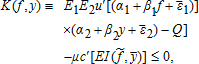 (A6)
(A6)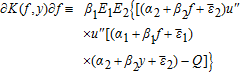 (A7)
(A7)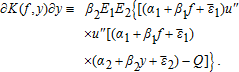 (A8)
(A8)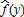 such that
such that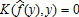 . Obviously, this trigger relationship could be defined on yield rather than price because price and yield are perfectly symmetric in our model. This implies that under realized price index f and realized yield index y indemnity payments are made whenever f is lower (higher) than
. Obviously, this trigger relationship could be defined on yield rather than price because price and yield are perfectly symmetric in our model. This implies that under realized price index f and realized yield index y indemnity payments are made whenever f is lower (higher) than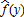 if β1 is positive (negative). From the theorem of implicit functions, we have
if β1 is positive (negative). From the theorem of implicit functions, we have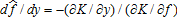 evaluated at
evaluated at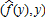 . The trigger function
. The trigger function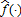 thus decreases (increases) with y if the product β1β2 is positive (negative). For couples (f, y) such that I(f, y) > 0, (A4) becomes
thus decreases (increases) with y if the product β1β2 is positive (negative). For couples (f, y) such that I(f, y) > 0, (A4) becomes
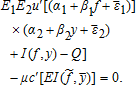 (A9)
(A9)Differentiating (A9) with respect to f and y and rearranging the terms leads to the optimal marginal coverage characterized by equations (7) and (8).
Proof of Proposition 2
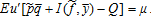 (A10)
(A10)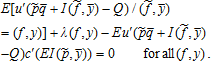 (A11)
(A11)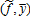 gives
gives
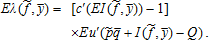 (A12)
(A12)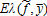 equals zero and, by definition of λ (·,·), I*(f, y) must be positive almost surely. Given Proposition 1, this is satisfied if
equals zero and, by definition of λ (·,·), I*(f, y) must be positive almost surely. Given Proposition 1, this is satisfied if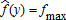 for all y. This proves the first part of the proposition.
for all y. This proves the first part of the proposition.If insurance is costly, i.e., c′(e) > 1 for some e > 0,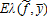 must be positive. This implies that the non-negativity constraint (2) must be binding for some couples (f, y) with a positive probability. This implies that
must be positive. This implies that the non-negativity constraint (2) must be binding for some couples (f, y) with a positive probability. This implies that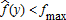 for some y if β1 > 0, and
for some y if β1 > 0, and for some y if β1 < 0. This proves the second part of the proposition.
for some y if β1 < 0. This proves the second part of the proposition.




