Is Diet Quality Improving? Distributional Changes in the United States, 1989–2008
The authors thank two anonymous reviewers and the editor, Brian Roe, for comments and suggestions that greatly strengthened the paper. Research for this study was supported by USDA-ERS Cooperative Agreement No. 58-4000-1-0025. The views expressed here are those of the authors and cannot be attributed to the Economic Research Service or the U.S. Department of Agriculture. All remaining errors are our own.
Abstract
This article measures changes in the distribution of dietary quality among adults in the United States over the period 1989–2008. Diet quality is a direct input to health, is often used as a proxy for well-being, and is an outcome variable for a wide variety of economic interventions. For the population as a whole, we find significant improvements across all levels of diet quality. Further, we find improvements for both low-income and higher-income individuals alike. Counterfactual distributions of dietary quality are constructed to investigate the extent to which observed improvements can be attributed to changes in the nutritional content of foods and to changes in population characteristics. We find that 63% of the improvement for all adults can be attributed to changes in food formulation and demographics. Changes in food formulation account for a substantially larger percentage of the dietary improvement within the lower-income population (19.6%) vs. the higher-income population (6.4%).
Poor nutrition is a contributing factor to four of ten major causes of death in the United States: coronary heart disease, cancer, stroke, and type 2 diabetes (Jemal et al. 2008). Poor diet quality is associated with increased risks of coronary heart disease, stroke, and diabetes (Chiuve et al. 2012), cardiovascular disease (Nicklas, O'Neil, and Fulgoni 2012), breast cancer (Shahril), colorectal cancer (Reedy et al. 2008), and prostate cancer (Bosire et al. 2013). Moreover, diet quality is often used as a measure of well-being in developing countries (Ravaillon 1996) and developed countries (Strauss and Thomas 1998). In this article, we study how the distribution of adult diet quality in the United States has evolved over the last two decades.
Improving dietary quality has long been a focus of government policy because of its direct impact on human health, particularly among the poor. Specific interventions have included increasing the resources available to households to buy food (e.g., Supplemental Nutrition Assistance Program [SNAP])1 and providing healthy foods directly to individuals (e.g., the School Breakfast Program, School Lunch Program, Special Supplemental Nutrition Program for Women, Infants, and Children [WIC], and Fresh Fruit and Vegetable Program). Policies have also aimed at increasing the information available to individuals about what constitutes a healthy diet: the Food Guide Pyramid was released in 1992 and subsequently updated in 2005 as MyPyramid and in 2011 as MyPlate; federally approved SNAP education programs grew from seven active states in 1992 to 50 in 2004; mandatory nutrition labeling was enacted in 1994; and mandatory calorie postings in restaurants was introduced in 2011. Current policy proposals seek to improve diet quality by restricting the range of foods eligible for purchase under SNAP and changing the relative prices of foods via taxes or subsidies.
In this article, we use stochastic dominance to compare the distribution of dietary quality over time and between income groups. Stochastic dominance is frequently used in the economics literature to analyze the distribution of income or wealth. This empirical approach allows us to completely characterize the nature of the changes in dietary quality over time, paying close attention to low-income individuals, whose diets are of particular concern to policymakers. Stochastic dominance is particularly well suited to studying diet quality, where exact thresholds between “good” diets and “poor” diets is fuzzy.
Further, we construct counterfactual distributions of dietary quality to investigate the extent to which observed improvements can be attributed to changes in the nutritional content of foods and to changes in demographics. In short, we ask how would the distribution of dietary quality change if food in 1989 were formulated as it was in 2008? Further, what would have the distribution of dietary quality looked like in 1989 had the demographic landscape of 2008 prevailed?
When comparing the observed distributions of dietary quality, we find a statistically significant and economically meaningful improvement across the entire population over the period 1989–2008. Improvements occur for individuals in households above and below our chosen poverty threshold. Counterfactual estimates indicate that 53.3% of the dietary improvement in the U.S. population can be attributed to changes in demographics (i.e., an aging, more educated, and ethnically diverse population) and an additional 10.1% of the improvement is attributed to changes in food composition (e.g., decreases in saturated fats, sugars, and sodium). The residual 36.6% is unexplained by either changes in demographics or food composition.
The article proceeds as follows. We begin by describing a widely used measure of dietary quality—the Healthy Eating Index 2005 (HEI-2005)—that forms the basis of our analysis. We then turn to a description of our primary data sources, the National Health and Nutrition Examination Survey (NHANES) and the earlier Continuing Survey of Food Intakes by Individuals (CSFII); we extend the HEI-2005 to the earlier study period of 1989–91. We then motivate our empirical approach by providing a brief overview of stochastic dominance. After the presentation of results, we discuss the economic and policy implications in the final section.
Diet Quality
The healthfulness of an individual's diet depends on two factors: energy balance and dietary quality. Energy balance is the relationship between calories consumed and energy expended, which results in body weight management (Hall et al. 2012). Dietary quality can be expressed as a per calorie metric that measures the degree to which a diet complies with a set of criteria (here, the Dietary Guidelines for Americans via the HEI). In this article, we focus on dietary quality, and we note that there is evidence that higher quality diets are associated with decreased obesity rates (i.e. improved energy balance) (Epstein et al. 2001, 2008).
We use the HEI—developed in 1995 to measure compliance with the U.S. government's recommendations for healthful eating—as our measure of diet quality. The HEI has been widely used and evaluated as a valid measure of diet quality (Guenther et al. 2008). In the medical literature, the HEI has been found to be a significant predictor of medical outcomes, notably of all-cause mortality, mortality due to malignant neoplasms (Ford et al. 2011), and overweight and obesity (Guo et al. 2004). Further, the HEI has been extensively used by economists to measure the outcome of policy interventions—for example, welfare reform (Kramer-LeBlanc, Basiotis, and Kennedy 1997), School Breakfast Program (Bhattacharya, Currie, and Haider 2006), food stamps and WIC (Wilde, McNamara, and Ranney 1999), nutrition labeling (Kim, Nayga, and Capps 2001), and unusually cold weather (Bhattacharya et al. 2004). Finally, it is has also been found to be associated with food insecurity (Bhattacharya, Currie, and Haider 2004) and has been proposed as a possible indicator of food deserts (Bitler and Haider 2011).
Every five years, the Dietary Guidelines for Americans are revised by the USDA and Health and Human Services based on the advice of an expert advisory panel. These guidelines are the U.S. government's official recommendations for healthful eating and form the basis for information provided to consumers. Many of the USDA's food-assistance programs must be in compliance with the Dietary Guidelines for Americans. The HEI was updated in 2005 to reflect the 2005 Dietary Guidelines for Americans (frequently called the HEI-2005; see Guenther, Reedy, and Krebs-Smith 2008).2 Because the HEI-2005 was constructed with the 2005 Dietary Guidelines for Americans as its basis, one can think of using this index as a consistent measure of dietary quality, with 2005 defined as the base period.
The HEI (henceforth, HEI refers to the HEI-2005) is the sum of twelve components based on consumption of various foods or nutrients. Each component assigns a score ranging from 0 to 5 (total fruit, whole fruit, total vegetables, dark green/orange vegetables and legumes, total grains, whole grains), 0 to 10 (milk, meats and beans, oils, saturated fat, sodium), or 0 to 20 for the percentage of calories from solid fats, alcoholic beverages, and added sugars, creating a maximum score of 100. Table 1 provides exact details of the scoring.
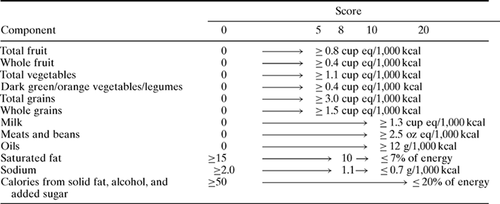
Healthy Eating Index 2005 Standards for Scoring Source: Recreated from Guenther et al. (2007).
There is debate among nutritionists about how a given HEI score maps into the notion of “healthy” versus “unhealthy” diet quality. One generally accepted rule of thumb is that total scores of more than 80 are considered “good,” scores of 51–80 are considered “needs improvement,” and scores of less than 51 are considered “poor.” Characterizing a diet based on a single cutoff is difficult (analogous to characterizing what it means to be poor based on a poverty line). A key advantage of the stochastic dominance methods used in this research is that they allow general statements about improvements in dietary quality over time or between subpopulations without having to define a specific threshold.
It is worth repeating that the components of the HEI are density based (the ratio of an individual's component intake to their total calorie intake) rather than quantity based. By design, the HEI measures the relative quality of foods consumed, independent of total calories (and of energy expenditure). We use the total HEI score as the underlying metric of interest in this study for two reasons. First, the HEI score has been extensively validated and tested as a measure of diet quality (Guenther et al. 2008). Second, joint tests of dominance are limited in practice to two or three dimensions, rather than the dozen component scores that make up the HEI.3
Data
Our sample uses nationally representative, repeated cross-sectional, individual food intake data from two surveys: the CSFII (1989–91 and 1994–96), and the continuous waves of the NHANES (2001–08). In both surveys, respondents report 24-hour dietary intakes and demographic information, including income and household size.4 Each survey wave is an independently drawn sample, which is representative of the United States, with the USDA overseeing the food intake component in both surveys. Finally, for consistency across samples, we focus on adults aged 20 years and older.
The HEI is calculated by linking the USDA's MyPyramid Equivalents Database (MPED) to food intake surveys. The MPED decomposes individual foods into MyPyramid guideline equivalents so that each HEI component can be computed as shown in table 1. As noted, because there is no officially released MPED for the 1989–91 CSFII, the HEI has not been previously computed for surveys before 1994. Of the 3,953 unique foods reported by adults aged 20 and older on day 1 in the 1989–91 CSFII, 3,907 (98.8%) of these foods are also reported in the 1994–96 CSFII. We therefore use the 1994–96 MPED to calculate the HEI for individuals in 1989–91.5
We classify individuals as low-income if household income falls below 185% of the Federal Poverty Guidelines. This is a policy-relevant threshold that serves as an upper bound on the cutoff for many federal nutrition assistance programs. During our sample period, the cutoff for SNAP was 130%, and the cutoff for WIC was 185%. The Federal Poverty Guidelines are also used as an eligibility criterion for the National School Lunch Program, School Breakfast Program, Child and Adult Care Food Program, and the Expanded Food and Nutrition Education Program.6 Table 2 reports the mean HEI scores for the population as a whole and for individuals above and below 185% of the poverty line for each of the periods in our sample.7
| Population | 1989–91 | 1994–96 | 2001–04 | 2005–08 |
|---|---|---|---|---|
| U.S. population | 50.16 (13.97)a | 51.10 (13.88)a | 51.50 (11.91) | 52.46 (12.49) |
| [10.09, 96.42] | [10.69, 97.47] | [13.52, 99.46] | [8.78, 95.38] | |
| No. | 9,498 | 9,867 | 8,640 | 9,258 |
| Low-income | 48.96 (19.83)a | 49.36 (15.45)a | 49.65 (13.29)a | 51.37 (14.99) |
| [10.09, 90.25] | [10.69, 93.81] | [15.08, 99.46] | [8.78, 94.60] | |
| No. | 4,965 | 3,433 | 3,551 | 3,857 |
| Higher-income | 50.56 (11.19)a,b | 51.73 (13.16)a,b | 52.36 (11.09)b | 52.92 (11.29)b |
| [11.51, 96.42] | [13.63, 97.47] | [13.52, 93.97] | [10.00, 95.38] | |
| No. | 4,533 | 6,434 | 5,089 | 5,401 |
- a Note: Standard deviations are given in parentheses. Maxima and minima are given in brackets.
- a Within-population mean is significantly lower than that in 2005–08 at the 5% level.
- b Within-year higher-income mean is significantly different from low-income mean at the 5% level.
Table 2 shows a consistent pattern of increasing dietary quality across groups over time. Comparing the most recent period of 2005–08 to the earlier periods, we see a significant increase (at the 5% level) for the population at large over the periods 1989–91 and 1994–96. Low-income individuals appear to have a stagnant HEI score over the period 1989–2004, and then a significant increase in the period 2005–08. We also compare low- and higher-income individuals within year and find that higher-income individuals have significantly higher mean HEI scores for all years in the data, although in the final year of the data, the mean HEI gap between groups is smallest.
Stochastic Dominance
We have seen that mean HEI scores have increased for all groups over the interval 1989–2008. But does the mean HEI obscure variation in dietary quality across individuals? For example, is the increase in diet quality due to general improvements across the population at a steady rate or due to larger improvements among those with the lowest (or highest) diet quality? To address these possibilities, we study the entire distribution of dietary quality for groups of interest using an approach common in the study of income and well-being: stochastic dominance.8
Definitions
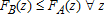
First- and second-order stochastic dominance
Distributional studies of well-being often look to higher orders of stochastic dominance, notably second-order stochastic dominance (SOSD). Whereas first-order stochastically dominance (FOSD) counts the number of individuals falling below a given healthy diet threshold (which would, in turn, determine the headcount ratio), SOSD captures the depth or severity of inadequate diets. SOSD is sensitive to the extent to which diets fall in the lower tails of the distribution.
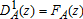 , and likewise for B, so that FOSD of B over A can be written as
, and likewise for B, so that FOSD of B over A can be written as 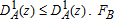 . FB will second-order stochastically dominates FA if
. FB will second-order stochastically dominates FA if
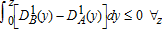
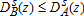 where,
where,
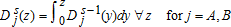
Stochastic dominance maps into social welfare under fairly standard assumptions about the utility derived from a healthy diet (Deaton 1997). For example, if B first-order stochastically dominates A, then for any social welfare function W defined on the distribution of diet quality F(z) such that 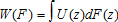 where U is any monotonically nondecreasing utility function of z (U′≥0), it must be true that social welfare derived from distribution B will be at least as high as the welfare derived from A. We can extend the mapping of social welfare to SOSD by requiring U to be nondecreasing and concave in z (U′≥0,U′′≤0). Note that because dominance of order s implies dominance of order s+1, it follows that the latter is a less stringent condition. Thus, welfare implications are the strongest in the first-order case. Finally, we also make the standard assumption of anonymity so that each individual is weighted equally in the social welfare function.
where U is any monotonically nondecreasing utility function of z (U′≥0), it must be true that social welfare derived from distribution B will be at least as high as the welfare derived from A. We can extend the mapping of social welfare to SOSD by requiring U to be nondecreasing and concave in z (U′≥0,U′′≤0). Note that because dominance of order s implies dominance of order s+1, it follows that the latter is a less stringent condition. Thus, welfare implications are the strongest in the first-order case. Finally, we also make the standard assumption of anonymity so that each individual is weighted equally in the social welfare function.
Estimation
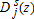 in empirical analyses is (Davidson and Duclos 2000):
in empirical analyses is (Davidson and Duclos 2000):
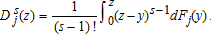 (1)
(1)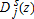
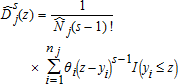 (2)
(2)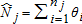 is the population size in distribution j (with corresponding sample size nj), and I(⋅) is the indicator function. The first-order case leads to the empirical CDF
is the population size in distribution j (with corresponding sample size nj), and I(⋅) is the indicator function. The first-order case leads to the empirical CDF
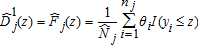 (3)
(3)Inference
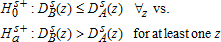
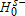 ), the signs would be reversed. One could also posit a null of equality, but notice that rejection of both
), the signs would be reversed. One could also posit a null of equality, but notice that rejection of both 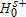 and
and 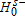 implies rejecting equality.
implies rejecting equality. Bishop, Formby, and Thistle (1989) propose a multiple testing procedure by hypothesizing dominance in both directions—that is, testing the null of 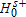 and
and  versus their respective alternatives and drawing inferences from the combined acceptance/rejection. A variety of approaches to drawing inferences based on the Bishop, Formby, and Thistle (1989) procedure have been proposed, such as multiple comparison tests (Anderson 1996; Davidson and Duclos 2000) or Kolmogorov–Smirnov-type tests (Barrett and Donald 2003; Bennett 2010; Linton, Massoumi, and Whang 2005; McFadden 1989). Multiple comparison approaches are based on arbitrarily chosen ordinates, which can lead to test inconsistency (Barrett and Donald 2003; Davidson and Duclos 2000). Therefore, in this study we use a Kolmogorov–Smirnov-type statistic that compares all objects within the support of the two distributions.
versus their respective alternatives and drawing inferences from the combined acceptance/rejection. A variety of approaches to drawing inferences based on the Bishop, Formby, and Thistle (1989) procedure have been proposed, such as multiple comparison tests (Anderson 1996; Davidson and Duclos 2000) or Kolmogorov–Smirnov-type tests (Barrett and Donald 2003; Bennett 2010; Linton, Massoumi, and Whang 2005; McFadden 1989). Multiple comparison approaches are based on arbitrarily chosen ordinates, which can lead to test inconsistency (Barrett and Donald 2003; Davidson and Duclos 2000). Therefore, in this study we use a Kolmogorov–Smirnov-type statistic that compares all objects within the support of the two distributions.
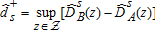 (4)
(4)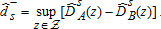 (5)
(5)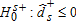 , and similarly for decreased diet quality (FA dominating FB) using
, and similarly for decreased diet quality (FA dominating FB) using 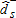 . When the distributions are mutually independent, Kolmogorov–Smirnov-type tests based on
. When the distributions are mutually independent, Kolmogorov–Smirnov-type tests based on 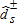 are consistent (McFadden 1989).9 Test statistics are calculated using
are consistent (McFadden 1989).9 Test statistics are calculated using
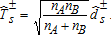 (6)
(6)Because there are infinitely many FA(z) satisfying the null such that FB(z)≤FA(z), the limiting null distribution is not uniquely defined and depends on the underlying unknown distributions of FA and FB. We follow Barrett and Donald (2003) and use the least favorable configuration to construct the null distribution. The least favorable configuration is the point in the null distribution that is least favorable to the alternative hypothesis (i.e., FA=FB). As a result, the test is conservative; rejection of the null under the least favorable configuration implies rejection at any point in the null distribution. We construct a bootstrap distribution of 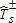 to simulate the p values.
to simulate the p values.
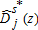 be defined as above from (2) but computed on a random bootstrap sample drawn with replacement from distribution j.10 The statistic is recentered by the observed values so that we have
be defined as above from (2) but computed on a random bootstrap sample drawn with replacement from distribution j.10 The statistic is recentered by the observed values so that we have 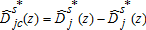 . We can then define recentered bootstrap functionals
. We can then define recentered bootstrap functionals 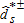 by replacing
by replacing 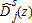 > with
> with 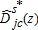 in (4) and (5). The recentered bootstrap t statistics are
in (4) and (5). The recentered bootstrap t statistics are
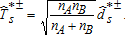 (7)
(7)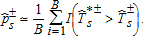 (8)
(8)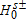 if
if 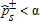 ” where α represents the conventional levels of statistical significance. Thus under the Bishop, Formby, and Thistle (1989) procedure, rejection of the null
” where α represents the conventional levels of statistical significance. Thus under the Bishop, Formby, and Thistle (1989) procedure, rejection of the null 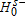 in favor of
in favor of 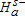 coupled with a failure to reject
coupled with a failure to reject 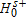 is viewed as statistical evidence in favor of FB dominated FA at order s.
is viewed as statistical evidence in favor of FB dominated FA at order s.Robustness Check for FOSD
To determine the stochastic rankings of two distributions, we must distinguish between four possible true states of nature: the distributions are equal, A lies above B, A lies below B, or the curves cross. The Bishop, Formby, and Thistle (1989) procedure described above distinguishes between these four states by conducting two one-sided tests. The result is lower power in detecting a crossing of the CDFs, which could lead to overclassification of dominance (Dardanoni and Forcian 1999; Gastwirth and Nayak 1999). This is at least partially due to the fact that rejection of 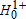 or
or 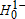 by itself is consistent with both FOSD and a crossing—hence, the use of two one-sided tests to rule out the crossing under the Bishop, Formby, and Thistle (1989) procedure.
by itself is consistent with both FOSD and a crossing—hence, the use of two one-sided tests to rule out the crossing under the Bishop, Formby, and Thistle (1989) procedure.
A second drawback to the Bishop, Formby, and Thistle (1989) procedure is how the total error probability α is apportioned to each one-sided test (Dardanoni and Forcian 1999). As is typical with standard hypothesis testing, the one-sided critical value c(α) is based on ensuring that the probability of committing a type I error (i.e., rejecting 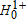 ,
, 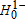 , or both when they are true) is less than the nominal level α. But as noted by Dardanoni and Forcian (1999), the Bishop, Formby, and Thistle (1989) procedure does not allow one to control how the total error probability α is allocated to each classification (equality, dominance in one direction, dominance in the opposite direction, or a crossing).
, or both when they are true) is less than the nominal level α. But as noted by Dardanoni and Forcian (1999), the Bishop, Formby, and Thistle (1989) procedure does not allow one to control how the total error probability α is allocated to each classification (equality, dominance in one direction, dominance in the opposite direction, or a crossing).
Bennett (2013) improves on the Bishop, Formby, and Thistle (1989) procedure by writing it as a two-stage test that allows one to test for a crossing while giving the researcher flexibility in allocating the total error rate to each stage. Let α and β denote a pair of prespecified significance levels for the first and second stage, respectively. The first stage is to posit a null of equality (FA=FB) and determine rejection or acceptance based on the critical value a(α). If we accept the null, then we infer that the distributions are indistinguishable. Upon rejection, however, the second stage determines the state of nature among the three alternatives (A dominates B, B dominates A, or they cross) using the critical value b(α,β). This allows β to be the portion of the total error probability α allocated to a crossing (i.e., αβ) and the remaining α(1−β) is split evenly between dominance in either direction.
Bennett (2013) tabulates asymptotic critical values of a(α) and b(α,β) for frequently used significant levels. In the applications below, we wish to calculate the asymptotic p values. To do so, we need to preset the total error rate α, the level at which we are controlling for falsely rejecting equality. We use two levels of significance (10% and 1%) so that the second stage is robust to our choice of α. The associated a(α) critical values are a(0.1)=1.2239 and a(0.01)=1.6277 (see table 1 in Bennett 2013).
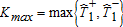 and
and 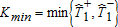 , respectively. We are interested in the distribution of Kmin conditional on rejecting equality. In other words, if Kmin is large enough (i.e., larger than the second stage critical value b(α,β)) conditional on Kmax>a(α), then we reject the null in favor of a crossing. Asymptotically, as shown in proposition 2.6 in Bennett (2013), if FA=FB and b<a then
, respectively. We are interested in the distribution of Kmin conditional on rejecting equality. In other words, if Kmin is large enough (i.e., larger than the second stage critical value b(α,β)) conditional on Kmax>a(α), then we reject the null in favor of a crossing. Asymptotically, as shown in proposition 2.6 in Bennett (2013), if FA=FB and b<a then
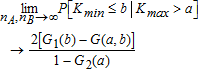 (9)
(9)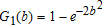 (10)
(10)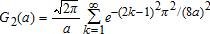 (11)
(11)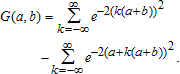 (12)
(12)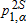 ) are calculated from (9) where we use two levels of α. Thus, a
) are calculated from (9) where we use two levels of α. Thus, a 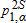 value below conventional levels of significance is evidence that the distributions cross. Put differently, larger p values are consistent with the null hypothesis that the distributions do not cross.
value below conventional levels of significance is evidence that the distributions cross. Put differently, larger p values are consistent with the null hypothesis that the distributions do not cross.Results
Our main results are summarized in tables 3 and 4 and depicted in figures 2–4. Tables report the bootstrapped p values for tests of increases and decreases in diet quality (Barrett and Donald 2003), as well as the asymptotic two-stage p values (Bennett 2013). The final column summarizes the inferred ranking of distributions based on these tests. In short, we find that there has been a statistically significant and economically important improvement in the HEI scores over the period under study. For any level of dietary quality, more Americans have higher HEI scores in 2005–08 than they did in the period 1989–91. However, there are differences between income groups with regards to when and where the improvements occurred (table 5).
| Distribution | Bootstrap Tests | Two-Stage | ||||||
|---|---|---|---|---|---|---|---|---|
| A | B | 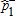 |
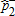 |
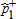 |
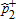 |
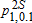 |
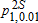 |
Inferred Ranking |
| 1989–91 | 1994–96 | 0.007 | 0.010 | 0.900 | 0.660 | 0.507 | 0.362 | A≺1B*** |
| 2001–04 | 0.028 | 0.002 | 1.000 | 0.937 | 0.999 | 0.999 | A≺1B** | |
| 2005–08 | 0.002 | 0.000 | 1.000 | 0.877 | 0.981 | 0.966 | A≺1B*** | |
| 1994–96 | 2001–04 | 0.129 | 0.149 | 0.383 | 0.925 | 0.003 | 0.001 | ND |
| 2005–08 | 0.010 | 0.003 | 0.999 | 0.863 | 0.981 | 0.965 | A≺1B*** | |
| 2001–04 | 2005–08 | 0.133 | 0.051 | 0.991 | 0.790 | 0.972 | 0.950 | A≺2B* |
- a
Notes: The
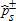 values refer to one-sided tests of the null hypothesis
values refer to one-sided tests of the null hypothesis 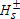 using equation (8). The asymptotic
using equation (8). The asymptotic 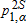 values are calculated from (9), where α=0.1, 0.01. The notation A≺sB reads, “Distribution B dominates distribution A at order s,” while ND indicates no dominance at order 1 or 2. Inferred ranking is based on statistical significance levels of 1% (indicated by a triple asterisk), 5% (indicated by a double asterisk), and 10% (indicated by a single asterisk).
values are calculated from (9), where α=0.1, 0.01. The notation A≺sB reads, “Distribution B dominates distribution A at order s,” while ND indicates no dominance at order 1 or 2. Inferred ranking is based on statistical significance levels of 1% (indicated by a triple asterisk), 5% (indicated by a double asterisk), and 10% (indicated by a single asterisk).
| Distribution | Bootstrap Tests | Two-stage | ||||||
|---|---|---|---|---|---|---|---|---|
| A | B | 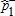 |
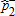 |
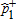 |
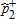 |
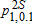 |
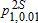 |
Inferred Ranking |
| Low income | ||||||||
| 1989–91 | 1994–96 | 0.218 | 0.257 | 0.570 | 0.654 | 0.027 | 0.009 | ND |
| 2001–04 | 0.290 | 0.140 | 0.977 | 0.952 | 0.927 | 0.878 | ND | |
| 2005–08 | 0.008 | 0.000 | 1.000 | 0.882 | 0.998 | 0.996 | A≺1B*** | |
| 1994–96 | 2001–04 | 0.332 | 0.300 | 0.575 | 0.889 | 0.034 | 0.012 | ND |
| 2005–08 | 0.006 | 0.003 | 0.991 | 0.855 | 0.984 | 0.971 | A≺1B*** | |
| 2001–04 | 2005–08 | 0.031 | 0.033 | 0.997 | 0.818 | 0.998 | 0.996 | A≺1B** |
| Higher income | ||||||||
| 1989–91 | 1994–96 | 0.007 | 0.006 | 0.880 | 0.684 | 0.429 | 0.289 | A≺1B*** |
| 2001–04 | 0.004 | 0.000 | 0.999 | 0.897 | 0.999 | 0.999 | A≺1B*** | |
| 2005–08 | 0.002 | 0.000 | 1.000 | 0.906 | 0.985 | 0.973 | A≺1B*** | |
| 1994–96 | 2001–04 | 0.083 | 0.106 | 0.553 | 0.932 | 0.032 | 0.011 | ND |
| 2005–08 | 0.007 | 0.010 | 0.991 | 0.886 | 0.957 | 0.926 | A≺1B*** | |
| 2001–04 | 2005–08 | 0.135 | 0.137 | 0.913 | 0.697 | 0.555 | 0.410 | ND |
- a
Notes: The
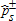 values refer to one-sided tests of the null hypothesis
values refer to one-sided tests of the null hypothesis 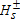 using equation (8). The asymptotic
using equation (8). The asymptotic 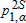 values are calculated from (9), where α=0.1,0.01. The notation A≺sB reads, “Distribution B dominates distribution A at order s,” while ND indicates no dominance at order 1 or 2. Inferred ranking is based on statistical significance levels of 1% (indicated by a triple asterisk), 5% (indicated by a double asterisk), and 10% (indicated by a single asterisk).
values are calculated from (9), where α=0.1,0.01. The notation A≺sB reads, “Distribution B dominates distribution A at order s,” while ND indicates no dominance at order 1 or 2. Inferred ranking is based on statistical significance levels of 1% (indicated by a triple asterisk), 5% (indicated by a double asterisk), and 10% (indicated by a single asterisk).
| Between Period | Total | |||
|---|---|---|---|---|
| HEI range | 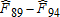 |
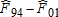 |
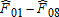 |
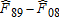 |
| All adults | ||||
| 0–40 | 2.80 | 12.61 | 6.21 | 21.64 |
| 40–50 | 5.65 | 6.83 | 9.54 | 22.01 |
| 50–60 | 12.41 | 1.86 | 10.25 | 24.52 |
| 60–100 | 20.38 | −3.64 | 15.10 | 31.83 |
| 0–100 | 41.23 | 17.66 | 41.09 | 100.00 |
| Low income | ||||
| 0–40 | 2.70 | 8.49 | 8.33 | 19.41 |
| 40–50 | −1.91 | 6.99 | 14.73 | 19.85 |
| 50–60 | 4.40 | 0.81 | 20.57 | 25.80 |
| 60–100 | 11.35 | −4.18 | 27.84 | 34.94 |
| 0–100 | 16.54 | 12.11 | 71.47 | 100.00 |
| Higher income | ||||
| 0–40 | 2.98 | 15.14 | 4.49 | 22.70 |
| 40–50 | 8.58 | 8.46 | 6.04 | 23.07 |
| 50–60 | 15.24 | 4.36 | 4.40 | 24.00 |
| 60–100 | 23.27 | −0.99 | 7.92 | 30.23 |
| 0–100 | 50.07 | 26.97 | 22.85 | 100.00 |
- a
Note: Numbers represent the percentage of the twenty-year improvement coming from the area bounded by the HEI range and the two distributions.
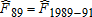 ;
; 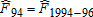 ;
; 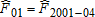 ; and
; and 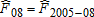 .
.
Between Periods
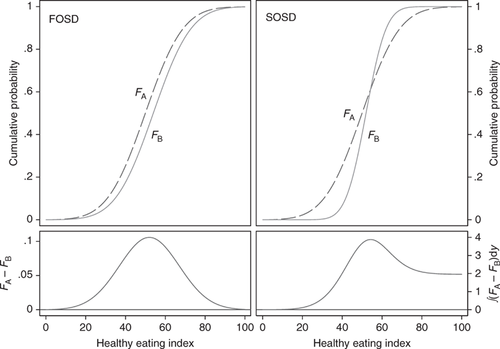
Figure 2 shows the empirical CDFs for the U.S. adult population in each period. Distributions shift systematically to the right over time, in other words toward a more nutritious diet. Because the shifts are relatively small, in this and subsequent figures, we present the estimated difference between the earliest period (1989–91) and the latest period (2005–08) in a subpanel. The area under the difference curve in the subpanel is equal to the area between the distributions. We can see the twenty-year improvement was positive and pointwise statistically significant for the empirically relevant range of HEI scores.
Distribution of adult HEI-2005 scores in the U.S. population Notes: Confidence intervals are calculated pointwise by bootstrapping. See online supplementary appendix for this figure in color.
From the first three rows of table 3, we see that in comparing the period 1989–91 to all subsequent periods, the null of decreasing dietary quality is strongly rejected and in no case do we reject the null of an increase in diet quality. In comparing the periods 1994–96 and 2001–04, we are unable to order the distributions in either the first- or second-order case. We do find strong evidence that the period 2005–08 first-order stochastically dominates the period 1994–96, but the results are fairly weak with regards to an ordering of the periods 2005–08 and 2001–04.
Some care is required in interpreting the last two columns of table 3 because they report results from Bennet's two-stage test. As noted, these p values are for the null hypothesis that the CDFs do not cross, as determined by both Kmax and Kmax being statistically large. Loosely speaking, these can be interpreted as the (conditional) probability of rejecting the hypothesis of no crossing. Thus, a 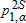 value below conventional levels of significance can be interpreted as evidence that the distributions cross. Bennet's two-stage test supports the main findings in that there is no statistical evidence that the 1989–91 distribution crosses any of the later years.
value below conventional levels of significance can be interpreted as evidence that the distributions cross. Bennet's two-stage test supports the main findings in that there is no statistical evidence that the 1989–91 distribution crosses any of the later years.
Between Income Groups
We now turn our attention to direct comparisons of individuals above and below 185% of the poverty guideline. As noted, we choose 185% of the poverty line as our cutoff because it is an upper limit on the threshold for many federal nutrition assistance programs.12 Panel (a) of figure 3 presents the empirical CDFs and the difference between the periods 1989–91 and 2005–08 for low-income individuals; panel (b) likewise for higher-income individuals. Table 4 presents results from statistical tests of dominance by income group. For both groups, we find strong evidence that the distribution of dietary quality in the period 2005–08 first-order stochastically dominates the distribution in the earliest period, with no evidence of a crossing.13
Distribution of adult HEI-2005 scores by income group Notes: Confidence intervals are calculated pointwise by bootstrapping. See online supplementary appendix for this figure in color.
Results support the observation in table 2 that a significant portion of dietary improvement among low-income individuals occurred over the period 2001–08. For example, in comparing the period 1989–91 to the period 1994–96, we find no evidence of a partial ordering according to the bootstrap results, and the two-stage test confirms this by finding significant evidence of a crossing. In comparing the period 1989–91 to the period 2001–04, again the bootstrap results are silent on the ordering, as is the asymptotic test, indicating no dominance at orders 1 or 2. However, in comparing the most recent time period 2005–08 to any of the earlier distributions, all tests show a statistically significant, first-order improvement in dietary quality, with no evidence of a crossing.
Comparing distributions among higher-income individuals, we can see that the period 1989–91 is first-order dominated by each subsequent period, with no evidence of a crossing. Comparing the period 1994–96 to the period 2001–04, the bootstrap results indicate a weak rejection of 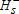 , which could lead one to infer a partial ordering. However, when consulting the asymptotic two-stage test, we find significant evidence of a crossing, thereby ruling out first-order dominance. We do see that the period 2005–08 first-order stochastically dominates the period 1994–96, but we cannot rank the two most recent time periods.
, which could lead one to infer a partial ordering. However, when consulting the asymptotic two-stage test, we find significant evidence of a crossing, thereby ruling out first-order dominance. We do see that the period 2005–08 first-order stochastically dominates the period 1994–96, but we cannot rank the two most recent time periods.
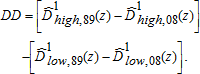 (13)
(13)As shown in figure 4, considering lower levels of dietary quality below a HEI of 45, we find higher-income individuals experienced a greater improvement over the period 1989–2008 than low-income individuals. Whereas at higher levels of the HEI distribution, low-income individuals experienced greater increases in dietary quality. In other words, we find some evidence that within the poor dietary quality population, low-income individuals experienced less improvement over the 20-year period than higher-income individuals.
Differences in dietary improvements among low- and higher-income populations Notes: Confidence intervals are calculated pointwise by bootstrapping. See online supplementary appendix for this figure in color.
Rate and Location of Change
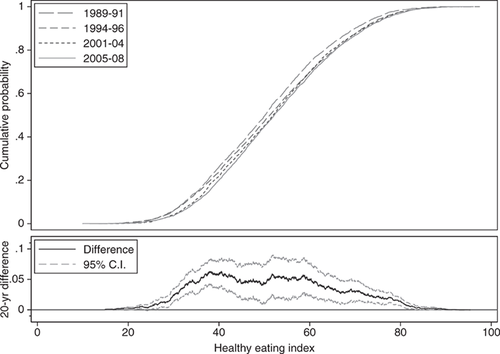
Given the differential gains in dietary quality noted above, we now investigate when in time and where in the distribution of dietary quality these improvements took place. For consistency and cross-sample/population comparisons, we focus on fixed portions of the distribution of dietary quality. An obvious choice is to use quartiles, which are all roughly segmented by HEI scores of 40, 50, and 60.14 Table 5 measures the amount of dietary improvement occurring in a particular quartile between two time periods as the percentage of total improvement 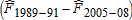 . That is, we measure the area bounded by the two empirical CDFs within each quartile range of the HEI scores. For example, the percentage of improvement in the United States over the 20-year period that occurred in the bottom quartile (<40) between 1989–91 and 1994–96 was 2.8%. The last column of table 5 measures the overall improvements over the period 1989–2008 within each quartile of the distribution of dietary quality.
. That is, we measure the area bounded by the two empirical CDFs within each quartile range of the HEI scores. For example, the percentage of improvement in the United States over the 20-year period that occurred in the bottom quartile (<40) between 1989–91 and 1994–96 was 2.8%. The last column of table 5 measures the overall improvements over the period 1989–2008 within each quartile of the distribution of dietary quality.
For the U.S. adult population, improvements below the median (HEI <50) occurred steadily over the period 1989–2008. In the upper range of dietary quality (HEI above 50), however, virtually all of the gains occurred over the periods 1989–96 and 2001–08. Overall, there were slightly higher gains in the upper quartiles compared to the lower quartiles for the U.S. population.
Comparing the between-period improvements by income group, we see that 71.5% of the total improvement in the diets of the low-income population occurred more recently over the period 2001–08. This is in contrast to the higher-income population, which saw the majority of their improvements occurring over the period 1989–2001 (77.1%). Improvements in the lower quartiles for the higher-income population have been relatively steady over the 20-year period, whereas most of the improvement in low-income diets within the lower quartiles occurred more recently over the period 1994–2008. In other words, at the lower end of the distribution of dietary quality, low-income individuals have seen comparatively limited or lagging improvements.
Table 5 emphasizes the reasons for targeting the most vulnerable group at risk of poor diets—the low-income, low–dietary quality population. This is best seen by examining the last column of table 5, which measures the total gains over the 20-year period within each quartile. The higher-income population has had almost proportional gains across all levels of HEI, whereas the low-income population has seen less improvement in the lower quartiles of diet quality.
Counterfactual Analysis
We now explore whether factors that evolve gradually over time within the population can help explain observed improvements in the distribution of HEI scores between 1989 and 2008. We focus on two factors in particular: changes in food formulation and changes in the demographic landscape.15 In the figures below, we focus on the differences between the observed 2005–08 distribution and the 1989–91 counterfactual distributions.
Food Reformulation
The composition of the food supply has changed considerably over the last twenty years in response to changes in policy, regulation, technology, and consumer tastes. For example, Vesper et al. 2012 found that levels of transfats in the population declined after new labeling requirements were put in place in 2003. We now investigate how much of the improvement in dietary quality can be attributed to changes in food composition.
To identify foods and food mixtures that have undergone food reformulation (e.g., changes in the type of fat used in processed foods), we use the USDA Food and Nutrient Database for Dietary Studies (FNDDS). FNDDS consists of a series of databases updated every two years in conjunction with the continuous waves of NHANES to reflect the current state of food formulation and packaging. We combine the FNDDS to cover the period 1994–2008. We briefly explain the method here, with more details in the online supplementary appendix.
To construct the distribution of dietary quality in the period 1989–91 as if food were formulated in the period 2005–2008, we first identify all foods coded as reformulated in the 1994–2008 FNDDS. We then replace the nutrient values for these food items in the 1989–91 CSFII with the reformulated values found in the FDNNS. We also replace the MPED values of the 1989–91 reformulated foods with their 2005–08 values. We then construct a new HEI score based on updated nutrient and MPED values for each respondent in the 1989–91 sample. Figure 5 displays the results from the reformulation counterfactual, as well as results from the next section.
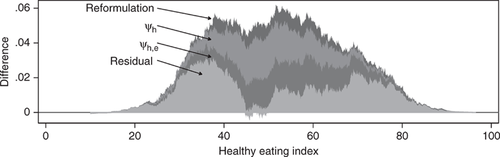
Differences between the 1989–91 counterfactual distributions and observed 2005–08 distribution Notes: “Reformulation” is defined in the subsection Food Reformulation. ψh is a reweighting function (see subsection Demographic Changes), which includes dummies for female sex and race/ethnicity fully interacted with age groups, and ψh,e additionally includes education dummies, all as defined in table 5.
The distribution of HEI that accounts for reformulation lies everywhere to the right of the original 1989–91 distribution over the relevant range of the HEI. The implication is that, holding food choices constant, changes in food composition could be a contributing factor to dietary improvement. In figure 5, the indicated shaded area represents the change in the empirical CDFs attributed to reformulation. The ratio of this area to the total area provides a scalar measure of change. Here, improvements attributed to reformulation represent about 10.1% of the total difference between the period 1989–91 and the period 2005–08.
An important caveat is that this exercise captures partial equilibrium effects, and some care must be taken interpreting these results. Our counterfactual analysis cannot account for the fact that individuals in the period 1989–91 might have chosen different foods had their foods been formulated as they were in the period 2005–08. Nevertheless, it shows how food reformulation, all else equal, can play an important role in changing dietary quality.
Demographic Changes
The United States of 2005–08 is an older, more diverse, and better educated country than the United States of 1989–91. To the extent that these factors are correlated with healthy eating, they may explain some of the improvements in dietary quality. Table 6 illustrates demographic changes using data from our sample and from the U.S. Census. There is a clear decrease in the population aged 30–44 years and a concomitant rise in the population aged 45–64 years. The decrease in the non-Hispanic white population has come from an increase in the Hispanic and other race/ethnicity groups. Finally, the overall educational attainment in the population has also increased.
| 1989–91 | 2005–08 | 1990 | 2005–07 | |
|---|---|---|---|---|
| Demographic | CSFII | NHANES | Censusa | Censusb |
| Aged 20–29 yearsc | 21.7 | 19.4 | 22.7 | 19.1 |
| Aged 30–44 years | 35.9 | 28.3 | 33.5 | 29.1 |
| Aged 45–64 years | 26.2 | 35.4 | 26.1 | 35.0 |
| Aged ≥65 years | 16.3 | 16.8 | 17.6 | 16.8 |
| Non-Hispanic white | 78.8 | 71.9 | 78.4 | 69.5 |
| Non-Hispanic black | 10.8 | 11.3 | 10.6 | 11.3 |
| Hispanic | 7.7 | 11.6 | 7.6 | 12.8 |
| Other race/ethnicity | 2.7 | 5.2 | 3.4 | 6.4 |
| Did not attend high school | 8.5 | 6.0 | 9.6 | 6.1 |
| High school, no college | 46.2 | 37.8 | 44.5 | 39.7 |
| Attended college | 45.2 | 56.2 | 45.9 | 54.2 |
| Total No. | 9,377 | 9,257 |
- a U.S. Census Bureau, General Population Characteristics (CP-1, 3-4).
- b U.S. Census Bureau, 2005–07 Annual Community Survey three-year sample.
- c All numbers are expressed as the percentage of the adult population aged 20 and older
To investigate the effect of evolving population characteristics, we construct counterfactual distributions of HEI scores following an approach proposed by DiNardo, Fortin, and Lemieux. We ask, “What would the distribution of HEI scores look like had the demographic landscape of 2005–08 prevailed in 1989–91?” We focus on age, race/ethnicity, and educational attainment, all of which have been found to be correlated with diet healthfulness (Popkin, Siega-Riz, and Haines 1996). The intuition is to adjust each individual's sampling weight in the base period 1989–91 conditional on a set of demographics such that it captures the relative probability that the individual would be represented in the more recent 2005–08 sample.
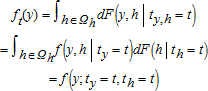 (14)
(14)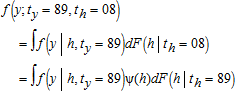 (15)
(15)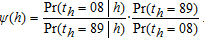 (16)
(16)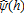 , notice the conditional probabilities Pr(th=t|h) can be estimated using a probit model by pooling the data and estimating the probability an individual is observed in time t conditional on a set of characteristics. Because we only compare two dates, the unconditional probabilities Pr(th=t) are simply the weighted sums of individuals in period th over the weighted sums of individuals in both periods. Because we are interested in applying the above methodology to tests of stochastic dominance, we replace an individual's sampling weight θi with
, notice the conditional probabilities Pr(th=t|h) can be estimated using a probit model by pooling the data and estimating the probability an individual is observed in time t conditional on a set of characteristics. Because we only compare two dates, the unconditional probabilities Pr(th=t) are simply the weighted sums of individuals in period th over the weighted sums of individuals in both periods. Because we are interested in applying the above methodology to tests of stochastic dominance, we replace an individual's sampling weight θi with 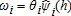 in equation (2).
in equation (2).Although long-run demographic changes such as sex, age, and race/ethnicity are plausibly exogenous, the claim that education is uncorrelated with omitted factors that affect diet quality is less plausible. However, we are interested in how changes in the distribution of education affects changes in diet quality, rather than how education affects diet quality. In other words, the conditional independence assumption E[ε|h]=0 is unnecessary for our decompositional analysis. Rather, we only need the weaker assumption of ignorability (also called unconfoundedness or selection on observables) to compute the aggregate compositional effects of all demographics. Ignorability asserts that the correlation between education (or any variable in h) and the error term is the same in both periods.16
Because of the aggregate decompositional nature of the DiNardo, Fortin, and Lemieux methodology (as opposed to a Oaxaca-style decomposition), the reweighting function ψ(h) does not distinguish between individual variables in the vector h. In the interests of transparency, we construct the counterfactual distributions in two stages. First, we construct a counterfactual distribution accounting for purely demographic changes (sex, age, and race/ethnicity) and denote this reweighting function by ψh. We then construct a counterfactual distribution accounting for changes in demographics and changes in education levels, denoted by ψh,e.17 We investigate the effects of the ordering herein.
Figure 5 decomposes the change in the distribution of HEI into four main parts: improvements attributed to reformulation (as shown in the previous section); additional improvements attributed to changes in demographics, with and without education; and, finally, the residual change. As noted above, 10.1% of total improvement can be attributed to changes in food composition. Here we find that roughly equal proportions of the total improvement in HEI scores can be attributed to changes in sex, age, and race/ethnicity (26.6%) and education (26.7%) over the twenty-year period.18 This leaves 36.6% of the improvement unexplained by reformulation and demographics (i.e., the residual improvement). The residual improvement encompasses many competing factors, such as changes in tastes, relative food prices, scientific discovery, and attitudes toward food in general.
As above, care must be taken in interpreting these results. One important limitation of the partial equilibrium nature of the counterfactual analysis is that food choices in the counterfactual population would not affect the set of foods made available by food manufacturers. Although this assumption is economically unappealing, the exercise provides insight into the effects of changing demographics on diet quality via clear and tractable analytical techniques.
Counterfactuals by Income Group
The counterfactual analyses above suggest that an important part of the improvement in dietary quality can be attributed to changes in food composition and demographics. Given that improvements occurred at different rates for different parts of the HEI distribution for lower-income versus higher-income individuals, we now ask whether changes in food composition and demographics account for differing amounts of improvement by income group. Results are presented in figure 6.
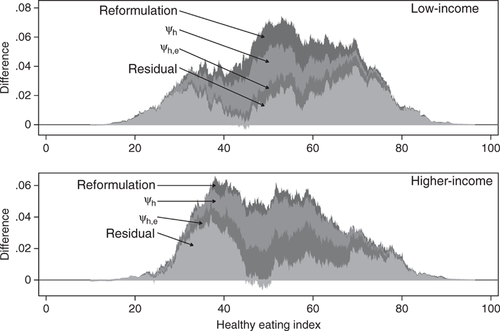
Differences between the 1989–91 counterfactual distributions and observed 2005–08 distribution by income group Notes: “Reformulation” is defined in the subsection Food Reformulation. ψh is a reweighting function (see subsection Demographic Changes), which includes dummies for female sex and race/ethnicity fully interacted with age groups, and ψh,e additionally includes education dummies, all as defined in table 5.
Changes in food composition account for a substantially larger percentage of the dietary improvement for lower-income individuals (19.6%) compared with their higher-income counterparts (6.4%). This is consistent with the observation that low-income individuals eat more processed foods (Drewnowski and Barratt-Fornell 2004), where much of the reformulation is occurring. Changes in sex, age, and race/ethnicity account for a similar share of the improvement for low-income (25.3%) versus higher-income individuals (26.8%). For low-income individuals, changes in educational attainment account for half that of higher-income individuals (13.5% versus 27.0%). The remaining residual share of the twenty-year improvement is larger within the low-income population (41.6%) than the higher-income population (39.8%). This suggests that further research into the determinants of diet quality of low-income individuals may be warranted.
Robustness
The order in which we construct counterfactual distributions using the DiNardo, Fortin, and Lemieux (1996) approach can influence the results. To investigate the robustness of our findings to ordering, we estimate the model using an alternative ordering for each of the three population groups of interest (total population, low-income, higher-income). Note that because reformulation is not estimated, but rather derived from data, it does not matter in which order it is considered. Furthermore, the total aggregate effect (ψh,e) remains the same as well. For example, in either case, all demographics account for 53.3% of the total improvement within the U.S. population.
Table 7 provides estimates for the original order as presented above, as well as an alternative ordering where we first consider educational attainment ψe and then use ψh,e as before. The result places bounds on the magnitude for each set of demographics. For example, the effect of education ranges between 15.6% and 26.7% for the total population, 5.0% and 13.5% for the low-income group, and 16.0% and 27.0% for the higher income group. Although point estimates change, relative comparisons remain substantively the same—changes in education appear to account for a larger share of the improvement for the higher-income group relative to the lower-income group. We note that the bounds are relatively large, and credibly point-identifying each effect remains a task for future work.
| U.S. | Low | Higher | |
|---|---|---|---|
| Order | Population | Income | Income |
| Original order | |||
| 1. Reformulation | 10.1 | 19.6 | 6.4 |
| 2. Sex, age, race/ethnicity | 26.6 | 25.3 | 26.8 |
| 3. Education | 26.7 | 13.5 | 27.0 |
| Total: reformulation & demographics | 63.4 | 58.4 | 60.2 |
| Alternative Order | |||
| 1. Reformulation | 10.1 | 19.6 | 6.4 |
| 2. Education | 15.6 | 5.0 | 16.0 |
| 3. Sex, Age, Race/Ethnicity | 37.7 | 33.7 | 37.7 |
| Total: reformulation & demographics | 63.4 | 58.4 | 60.2 |
- a Note: Numbers represent the percentage of total improvement and may not sum accordingly due to rounding.
Discussion and Conclusion
Conventional wisdom maintains that the quality of the American diet has been deteriorating for at least the past two decades.19 In contrast, we document a previously unknown pattern of improvement in U.S. dietary quality. We find statistically significant improvements for all adults over the period 1989–2008, at all levels of dietary quality.
An important caveat is that the HEI measures diet quality on a per calorie basis and does not account for excess calorie consumption. To our the best of our knowledge, few studies have examined the quantity–quality isoquant of food in health production, and those that have generally do so within the context of specific foods in an experimental framework. In a series of dietary intervention experiments, Epstein et al. (2001, 2008) found that increasing healthy food consumption reduced obesity to a greater degree than reducing unhealthy food consumption. Moreover, in Epstein et al. (2008) individuals in the increase-healthy-food group showed no relapse in weight gain in a two-year follow-up. The implication is that a shift toward a healthier diet could have additional positive impacts on health outcomes driven by quantity, such as obesity. The mechanism is generally thought to be a higher level of satiation, which in turn leads to a reduction in overall calories consumed.
Although we find that higher-income individuals consistently have higher dietary quality than low-income individuals, we also find some evidence that the gap is shrinking over the sample period. An important caution is that the diets of low-income individuals in the lowest portion of the diet quality distribution continue to lag.
We also show that most of the improvement in dietary quality can be attributed to changes in food formulation and changes in demographics. Moreover, we find that changes in food formulation help explain considerably more of the improvement in dietary quality for low-income individuals than for higher-income individuals. These findings suggest that the direct and indirect effects of policy on food composition may represent understudied policy levers.
How large are these results? In a prospective study that roughly covers our sample period, Chiuve et al. (2012) found significantly lower risks of major chronic diseases across the entire distribution of HEI scores for both women (over the period 1984–2008) and men (over the period 1986–2008) who were free of chronic disease at baseline. For example, those in the second quintile were 7% less likely to report a chronic disease than those in the lowest quintile, all else equal. One way to assess the magnitude of changes in HEI over time is to see how many individuals move from low to moderate levels of dietary quality over the period under study. In the period 1989–91, the twentieth percentile of the HEI distribution was 37.3. In 2005–08, a HEI value of 37.3 represented the 15.4th percentile of the HEI distribution. In other words, 4.6% of individuals moved out of this higher-risk category between 1989 and 2008 because of improvements in diet quality.
Findings of a small but statistically significant increase in dietary quality should not overshadow the fact that there is still considerable room for improvement. Moreover, an important residual share of the change in dietary quality over the period remains unexplained, especially in the tails of the distributions. Because of the sheer number of overlapping and time-varying policy initiatives—particularly those that target the poor—credibly identifying effects of specific policies remains a challenging task for future work.
Supplementary material
Supplementary material is available at http://oxfordjournals.org/our_journals/ajae/online.
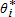 for each sample individual. These weights are used in equation (2) to create the bootstrap distribution of
for each sample individual. These weights are used in equation (2) to create the bootstrap distribution of 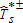 .
.



