Female Social Networks and Farmer Training: Can Randomized Information Exchange Improve Outcomes?
Kathryn Vasilaky is the VP of Research and Strategy at a Washington Tech startup, Troopswap [email protected]: Agricultural and Resource Economics, 220B Symons Hall, University of Maryland 20742.
This article was presented in an invited paper session at the 2012 ASSA annual meeting in Chicago, IL.The articles in these sessions are not subjected to the journal's standard refereeing process.
In the last few decades, the focus of economic growth in developing countries has shifted from country-wide prescriptions to testable micro-development programs at the local level. Agricultural growth, in particular, is seen as the building block for alleviating hunger and poverty, as agriculture is the primary source of livelihood in the rural developing world. Programs aimed at increasing agricultural productivity are regarded as the most powerful means to reducing poverty as compared to nonagricultural programs (Asfaw et al. 2011). An essential stage in any program intended to increase agricultural productivity is the dissemination of new techniques and technologies by agricultural extension agents and trainers. This stage is frequently one of the weakest links in the process. One of the reasons for the lack of clear success in this effort is that trainers’ success in reaching and affecting the marginal farmer1 relies on the effectiveness of social networks, which are often unknown to an outsider and difficult to identify. Furthermore, while extension agents may bring new technologies, what works best in practice in a remote village can differ widely from what is taught or what outside trainers perceive as being important for local production. It is through individuals’ personal ties that external information is disseminated within a remote area, tested and localized, ultimately creating usable and believable knowledge. Thus, many outside trainers are not exploiting local socials networks in the transfer of technology.
This research examines the effects of a training program, which emphasized the use of social networks and social capital to encourage learning and adoption of a relatively new cash crop, cotton, to female heads of households. The impact of the social network based program is then compared to the impact of a concurrently run standard extension training program. Because both programs were randomized at the village level, I am able to identify and compare their impacts without the potential for confounding or within village spillover effects. The social network based program (SNP) implemented here had two stages in treatment villages: 1) it trained each participating female in one aspect of growing cotton (e.g. thinning, spacing, harvesting2), and 2) it exogenously increased the size of the average woman's social network by randomly pairing cotton growing women in mentoring relationships. The standard training program (TR) consisted of weekly visits and training sessions by agricultural extension agents during the stages of land preparation, weeding, planting, thinning, and harvesting. I show that the SNP increases productivity up to 50% for farmers producing at the average yield of production (200 kilograms of cotton per acre), and that the social network based training program had more significant effects on yields for the poorest performing farmers than the standard training program.
Gandhi et al. (2007) uses a similar experimental design for identifying the effects of agricultural training for the marginal farmer, but relies on the existing networks of individuals to disseminate information, and uses digital video for teaching new agricultural techniques rather than the peer mentoring used in this study. Similarly, Duflo, Kremer, and Robinson (2006) estimates the diffusion of information across already-existing networks, but not the impact of social networks themselves in diffusing information. However, using existing networks to study information flow and learning is plagued by the endogeneity of individuals’ networks. Field, Feigenberg, and Pande (2011) is one recent study that uses a randomized encouragement design to perturb existing networks amongst micro-finance communities in Bangladeshi villages by varying the meeting frequency of these groups to understand the impact of network effects on loan repayment. Other research, such as Leonard (2007) and Marmaros and Sacerdote (2002) use natural exogenous variation to identify network effects. Leonard (2007) uses the sudden and exogenous replacement of clinicians in local health facilities to identify health care quality's effect on patient's learning about health care via their social network. Marmaros and Sacerdote (2002) uses the exogenous placement of college freshman to identify the effects of social networks on future labor outcomes.
Randomization of the SNP at the village level allows me to test the effects of social capital on females’ productive outcomes for a new technology without statistical bias. By comparing outcomes of farmers assigned to the SNP to farmers in a control group, over time, I can estimate the impact of expanding a female's network. The estimated network effects will not be diluted by potential spillovers of the SNP, because individuals in the treated and control groups are situated in separate villages. Furthermore, the SNP was implemented in the presence of a randomly assigned cotton-training program, denoted as TR. Thus I can compare the two programs’ effects on productive outcomes, as well as test for whether any additive effects exist when individuals receive both training programs.
I avoid the type of network endogeneity that occurs when measures of social capital are defined using descriptive statistics of an individual's network: the size of the network, the average age and work experience in the network, and the education level in the network; or using descriptive statistics of the individual's network's choices: number of individuals who adopt a technology, number of individuals who share information about a new technology, or the network's average level of investment into the technology. Such characteristics of an individual's network reflect her ability to connect with such individuals, which would likely be correlated with her productive outcomes. This endogeneity issue is known as the reflection problem, and refers to the idea that an individual's outcome can reflect her network's average outcomes because she and her network are influenced by the same unobservable shocks, and not because the individual is in fact mimicking her network's actions (Manski 1993). More complex graph-based measures of networks-including cohesion3 or reach of the network4 -can lead to a better understanding of information pathways across social networks, but do not deal with the empirical issues of endogeneity.
The next section motivates the sample population selected for this study. This is followed by a description of the data, background setting and randomization process. An empirical model and estimation results follow. A discussion of the findings concludes.
Data
The full sample population is comprised of male- and female-headed households that grew cotton in 2008 in rural Uganda. The SNP was directed at female-headed households5, while cotton training was administered to both groups. In the first stage, we6 randomly selected cotton growing villages from a complete list of all cotton growing villages in one Eastern district (Bukedea District) and one Northern district (Oyam District) of Uganda. We then stratified the sample by female- and male-headed household status. The SNP consisted of an in-depth survey of the grower's social networks, household demographics and production, being taught one aspect about growing cotton, and being paired with a “buddy” in their village area with whom they were encouraged to develop an agricultural link.
The pairing occurred by first stratifying the cotton growing participants into 2 to 3 geographic areas of the village7, and then randomly pairing individuals. I used a random number generator to pair participants by drawing numbers from a uniform distribution, U[0,x], without replacement, where x represents the total number of individuals in the group. For example, if the group was comprised of 14 women, then x=14. A random re-pairing occurred if the individuals were already neighbors, or if both were to receive training8 so as to maximize the effects of the training program.
Randomization
In order to capture the effect of a social network intervention, randomization occurred at the village level as we would expect externalities from both programs, SNP and TR, between the treated and untreated within a village. By randomizing the SNP and TR programs across villages, I am able to measure the effect of the SNP treatment, the TR treatment, and the complimentary effect of both treatments. I will compare my three treatment groups: SNP (N=60), TR (N=120) and SNP+TR (N=96) to the control groups (N=50) who received no treatments. The majority of individuals in the SNP treatment group participated in the games and pairing, but a small group only participated in the pairings.
The first round of a large-scale household survey was administered to 36 villages in 4 regions of Uganda: North (13 villages), Northeast (13 villages), West (5 villages) and West-Nile (5 villages)9 from February through May 2009. Note that while only some villages were selected to receive one of two agricultural technology programs, every village in the sample was visited by our team. Therefore, the effects from my results cannot be attributed purely to a behavioral response to our visits.
To facilitate farmers learning proper cotton growing techniques, and to estimate the impact of a low-budget agricultural training program, villages were randomly selected for participation in the TR. A total of 13 villages received SNP, and 18 villages received TR. In each village, approximately 14 heads of households were randomly selected to be visited by a local agronomist three times a week to undergo five training stages in 2009 : pre-planting in March through April; planting in May; pesticides use in July through August; harvesting in October through November; and marketing in December and January. Half of the participant sample are female heads of households. Among the 18 villages randomly selected for agricultural training, another subset of villages was chosen to participate in the SNP. Among the 8 villages not selected for agricultural training, 4 received the SNP and 4 did not.
In the SNP group, each pair received a Polaroid photo of themselves and their team member, identified cultivation issues and were encouraged to choose production goals, as well as potential times when they would meet to exchange their learned information. In this way participants were strongly encouraged to build a relationship around what they would learn in the coming year about growing cotton via their new link.
Choice to Grow Cotton
I first look at the impact of the SNP on farmers’ decisions to grow cotton in the presence of the training intervention, clustering all standard errors at the village level to account for within-village correlations between households’ error terms on outcomes. Table 1, Columns 1 and 2, estimates the effect of the SNP and TR on remaining a cotton grower between 2009 and 2010, particularly as both the North and East experienced some level of drought during the growing season. I use a Probit model to predict the probability that a grower continues to grow cotton. Column 1 indicates that the presence of the SNP in a village positively and significantly impacted a farmer's decision to continue to grow cotton, where the outcome variable is zero if the individual ceased to grow cotton in 2010, and equals one if they planted cotton. The marginal effect of expanding a farmer's network by one link increases the probability of remaining a cotton grower by 18%. On the other hand, introducing training to a farmer increases the probability of remaining a cotton grower by only 11% and is insignificant. Table 1, Column 2, estimates an Ordered Probit model, where the decision to not plant is 0, the decision to plant but then realize no yields is assigned a 1, and the decision to plant and realize positive yields is assigned a 2. These estimates reveal the significance of both SNP and TR in effecting the decision to grow cotton and one's success at growing cotton.
| Yield | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | |
| VARIABLES | 0=Dropped 1=Attempted | 0=Dropped 1=Attempted&0 2=>0 | Yield | Information Learned | Network Size | TRIPLE D: Yield | DID: Yield | Yield<500 | Yield<400 |
| SNP | 0.565** | 0.699*** | 60.18* | 0.0483** | 0.273 | 64.98* | 47.69 | −3.759 | −1.875 |
| (0.249) | (0.225) | (35.19) | (0.0210) | (0.440) | (35.50) | (32.16) | (25.22) | (22.74) | |
| TRAINING | 0.334 | 0.428** | 102.8* | 0.0406* | 0.677 | 41.88 | 28.48 | 11.14 | 22.29 |
| (0.212) | (0.187) | (55.63) | (0.0239) | (0.448) | (38.36) | (28.64) | (26.35) | (20.50) | |
| TrxSNP | 0.0657 | 0.0159 | 1.976 | −0.0375 | −0.780 | −26.17 | 29.62 | 19.79 | |
| (0.318) | (0.286) | (75.30) | (0.0356) | (0.545) | (59.57) | (33.56) | (29.30) | ||
| Constant | 0.0966 | 42.33*** | 0.378*** | 3.708*** | 153.0*** | 162.0*** | 190.3*** | 173.6*** | |
| (0.174) | (14.83) | (0.0146) | (0.338) | (20.63) | (26.30) | (32.27) | (27.36) | ||
| t | −99.22*** | −105.3*** | −89.06*** | −78.29*** | |||||
| (23.64) | (21.42) | (25.61) | (21.49) | ||||||
| SNPxt | 3.162 | 14.52 | 68.11* | 76.24*** | |||||
| (29.85) | (27.50) | (37.18) | (26.73) | ||||||
| TRxt | 76.11* | 84.77*** | 100.7** | 83.33* | |||||
| (43.19) | (24.61) | (46.13) | (43.68) | ||||||
| TRxSNPxt | 17.17 | −37.62 | −48.06 | ||||||
| (49.50) | (60.53) | (53.09) | |||||||
| Sex | −45.84* | −44.87* | −46.30** | −46.25** | |||||
| (26.30) | (24.46) | (19.78) | (18.55) | ||||||
| Observations | 325 | 325 | 325 | 324 | 263 | 646 | 646 | 596 | 574 |
| R−squared | 0.057 | 0.021 | 0.012 | 0.057 | 0.057 | 0.062 | 0.064 | ||
- a Sex=1 if Female.
- b Robust standard errors in parentheses.
- c *** p<0.01, **p<0.05, *p<0.1.
Cotton Output
Table 1, Columns 6–9, estimates a triple difference in difference (η coefficient), and difference in difference across the TR and SNP variables (γ and δ coefficients respectively), on yields per acre. I am interested in the coefficients on SNP*t, γ, and SNP*TRxt, η, that is, the pure impact of the SNP intervention over time on outcomes, and the additive impact of the SNP relative to the TR treatment over time. At the same time, I also check that the estimated coefficients on SNP, and TR, not interacted with time, are insignificant. SNP, and TR are dummies for having been selected for the SNP and TR treatments. They capture whether selected households are significantly different in their yields from households who were not. Similarly, the t variable measures whether there is a significant time trend in yields, which I expect to be negative given the drop in yields between 2009 and 2010. Selection into the programs was random as indicated by the insignificant effect of TR and SNP, not interacted with time. The negative and significant coefficient with respect to t reveals the downward trend in yields that is exhibited in the summary statistics of Table 2. The estimated impacts of SNP*t,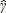 
, and of SNP*TR*t, 
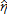are insignificant. The additive effect of SNP on TR program is insignificant everywhere.
| 2009 | 2010 | Total | |
|---|---|---|---|
| Social Network | 0.475 | 0.475 | 0.478 |
| Intervention (SNP) | (0.500) | (0.500) | (0.500) |
| Training | 0.658 | 0.658 | 0.660 |
| Intervention (TR) | (0.474) | (0.475) | (0.474) |
| Sex | 0.48 | 0.48 | 0.48 |
| (Female=1) | (0.50) | (0.50) | (0.50) |
| Kgs Cotton | 140.8 | 79.54 | 109.9 |
| (201.5) | (129.2) | (171.6) | |
| Acres | 0.983 | 0.586 | 0.783 |
| (0.701) | (0.593) | (0.678) | |
| Yield (Kgs/Acre) | 182.0 | 139.5 | 160.6 |
| (208.7) | (234.9) | (223.1) | |
| Kgs Seed | 4.976 | 3.232 | 4.097 |
| (3.799) | (3.000) | (3.527) | |
| Yield Per | 52.83 | 36.96 | 44.83 |
| Seed | (78.32) | (62.70) | (71.27) |
- a Robust standard errors in parentheses.
As Table 2 indicates, yields are overdispersed, where the variance in yields exceeds its mean. As Figure 1 shows, the average producer, before and after the treatments, is clustered below a 500 kilogram yield per year, so that the deviation from the mean yield is quite high for those few producers in the right tail of the distribution. Hence, the above result that the SNP treatment had an insignificant impact is not surprising if the upper portion of the yield distribution could gain little from the program. I would not expect a significant impact from social networks for the highest producers, who are already far above the mean yield, given that their knowledge base is likely saturated for this type of information. It is farmers with production yields in the low- to mid-quantiles that I would expect to benefit the most from new networks and basic growing information. I did not exclude top producing farmers from the study, however, because they may play a critical role in information dissemination.
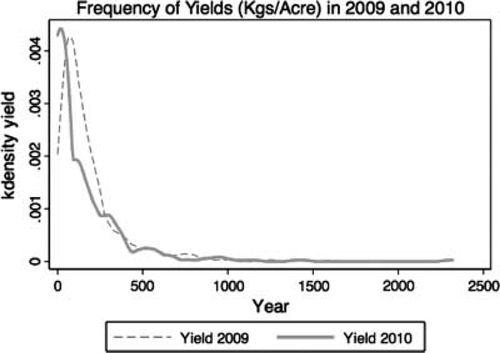
Non-Parametric Frequency of Yields
SNP and Training as Substitutes
I have found that the complementary impact of SNP on TR is insignificant, that is, the estimate of η is insignificant in all of my specifications. This may because the TR program induces its own social networking effect such that SNP does not bring any additional gain to individuals who received TR. Therefore, each intervention seems to affect individuals’ outcomes independently. I therefore, look at how the impact of the SNP (with and without TR) compares to the impact of TR (with and without SNP).
Table 1, Columns 9, indicates that the effect of the SNP is to increase yields by 74 kilograms per acre controlling for the TR program, while the TR program increases yields by 82 kilograms per acre controlling for the SNP program. I confirm this by estimating the double difference regressions for the SNP and TR programs within the following groups: those who did and did not receive TR, and those who did and did not receive the SNP, respectively. SNP had its greatest economic and statistical impact for individuals who did not receive TR, where SNP increased yields by 74 kilograms per acre for those without TR versus 26 kilograms per acre for those who did receive TR, which was insignificant. Similarly, the effects of the TR program are derived from those groups who did not receive the SNP. Therefore, the two programs appear to be feasible substitutes at increasing productivity in villages.
Whether social capital behaves as a substitute or complement to standard training programs may depend on the program type itself. Jonathan Isham and Ramawamy (2002) suggest that when programs are delivering private goods with large information spillovers, then the influence of social capital on information sharing is high. The highest returns to investments in social capital, however, are when “the economic good that a development project is designed to deliver is characterized by high levels of non-exclusiveness or non-rivalry.” Of course, most training programs aim to deliver new knowledge, where knowledge is the quintessential public good. In that sense, I believe that the marginal investment in a social assessment will be relatively small compared to the potential benefits of the investment, regardless of whether the agricultural training itself is meant to deliver a private good.
What is significant about this finding is that, whereas a training program requires the coordination of several agricultural extension agents12, repeated travel to remote villages along unpaved roads, as well as coordination with the recipients of the training, the SNP is a one-time pairing of individuals and dissemination of information. A training program such as TR would cost between 300–600 dollars per village per year. Uganda has over 95 districts, each with around 10 sub-counties, and 5–10 villages per sub-county. For a conservative estimate, for over five thousand villages, the cost of a training program could range from one to three million US dollars (USD), depending on the number of trainers and their expertise. The SNP would amount to a one-time travel cost and the time of one individual to organize the SNP.
New Links or Information?
I test whether the effects that I pick up from the SNP program are caused by learning or new networks. I look at the impact of SNP and TR on individuals’ true social networks over time, and on the amount of information that they learned through the training programs. If SNP affected networks and not learning, then I can deduce that it was through networks, primarily, that the SNP program had its greatest impact.
To do this, I will first check the impact of the SNP and TR programs on an individual's stated cotton network size between 2009 and 2010. Stated network size is gathered from the response to a survey question; “How many farmers did you speak to about cotton growing issues in the past growing season?” Secondly, I will test the impact of the SNP and TR programs on the information learned on yields. I can devise a measure of information correctly learned and stated using surveyees’ results from a quiz, which was included in the 2010 follow-up household survey, and was administered to all participants in the treatment and control groups. I calculate the percentage of correctly answered questions out of 12 questions13.
As a check to my cross sectional results, I compare them with my previous panel estimates in Columns 6–9. Namely, I repeat the first regression of yields on the SNP and TR programs using the 2009–2010 panel, and then compare this SNP effect to the SNP effect when using only the 2010 cross section. Given that the assignment of programs is random, the impact of SNP and TR should not be statistically different whether I use panel or cross-sectional data. The slope estimates on SNP are statistically significant in predicting yields at the 10% level and in predicting information learned at the 5% level.
Table 1, Columns 4, shows that the impact of SNP is statistically significant in explaining participants’ quiz outcomes on the twelve information points14 in year two of the study. The impact of SNP is not significant in explaining an individual's potential change in network size from 2009 to 2010 in Column 5. This may suggest that receiving the information via social networks versus increasing network size is the channel by which the SNP program affected outcomes most. Of course, we should keep in mind that the program only encouraged a change in network size by one link.
Thus, these results suggest that it was the information taught and shared rather than the size of a person's network that had the greatest impact on SNP participants’ yields. In particular, one information point about growing cotton would not have been enough to improve a farmer's productive outcomes. However, these results are not conclusive as I only have cross-sectional data from 2010 to estimate the impact of the SNP on learning and networks. Therefore, neither individual random effects in the error term nor individual fixed effect variables as regressors can be used to control for unobservable variation that may be correlated with Information.
Discussion
In this paper I have estimated the impact of a year-long social network based agricultural training program, whose learning and mentoring process emphasizes the importance of information dissemination to all farmers in a village network. In particular, socially and geographically distant farmers are the most in need of training, but are the least likely to receive it. My results indicate that the social network based training program had a significant impact on yields for the poorest subsistence farmers. For the average female Ugandan farmer, who produces between 100 and 200 kilograms per acre per year, the SNP increased yields by up to 74 kilograms per acre, and this effect declines for the highest yielding farmers.
The two programs evaluated provide different methods of training individuals, at widely dispersed costs, with distinctly different effects along the distribution of producers. In comparison to the training intervention, the SNP has its greatest impact for the lowest-yielding farmers making it a low cost tool for reducing poverty. This is a substantial finding, given that females comprise 80% of the agricultural labor force in Uganda, yet rarely receive personal agricultural training. Furthermore, the results found here with female-headed households may also serve as an example for low yielding male producers, as female heads of household, like males, manage and allocate their resources.
These results, however, are far from conclusive due to the length of time and size of the training experiment. A follow-up survey of the villages studied here is necessary to test the long term effects of the program on production and learning outcomes. In addition, continuous rewards and incentives for information exchange as well faster methods of information dissemination may improve the efficacy and scalability of the social network based program.
