Removal and Mark–Recapture Methods for Estimating Abundance: Empirical and Simulation Results for Mottled Sculpin in Streams
Abstract
Most studies that investigate biases in stream fish abundance estimators focus on salmonines, yet nongame species comprise a major portion of fish assemblages. We evaluated mark–recapture (the Lincoln–Petersen estimator with Chapman correction) and removal (constant capture probability and generalized removal estimators) methods for estimating abundance of Mottled Sculpin Cottus bairdii, and we tested whether assumptions of the abundance estimators (i.e., the population is closed during sampling; and marks are detected) were reasonable. Over 2-d periods, fish in eight streams were sampled by using backpack electrofishing in 90-m reaches (each divided into three 30-m subreaches) to assess movement. Removal abundance estimates were significantly lower than mark–recapture estimates. Moreover, removal estimates were 52% lower than the known number of marked individuals, likely because capture probability (q) was low and declined with subsequent sampling passes. Survival of fish held in cages was 100%; there were no undetected marks among fish held overnight. For all streams combined, 11% of recaptured fish that were marked in the core subreach were recaptured on day 2 in an adjoining subreach. In five of the eight study streams, movement of marked fish from the core subreach was not detected, suggesting that in most streams the population was closed to movement. Using computer simulations, we found that low numbers of recaptures (mean < 6) negatively biased the mark–recapture estimator; however, the estimator was positively biased when the study population was open to movement—meaning that marked and unmarked fish were lost from the study reach as new, unmarked fish entered. Our results indicate that the removal estimator was negatively biased. We recommend using the mark–recapture method to estimate abundance when q is low (e.g., 0.21 in our study), with the caveat that study reach length must be sufficient to minimize fish movement across reach boundaries when block nets cannot be maintained between sampling events.
Received January 14, 2014; accepted September 22, 2014
Unbiased estimates of abundance are a critical part of successful fisheries management. Two commonly used methods for estimating abundance are mark–recapture and removal techniques. Mark–recapture methods for two sampling periods rely on marks being applied to a subset of the target population during the first sampling event; the ratio of marked to unmarked fish captured during the second sampling event is used to estimate abundance (Seber 1982; Williams et al. 2002). In studies of stream fishes, the two sampling events often are conducted on consecutive days. Removal methods temporarily remove fish captured during consecutive passes within a single sampling event (i.e., often during a single day), and the statistical estimator then uses the depletion rate (i.e., reduction in fish captures over consecutive passes) to estimate abundance (White et al. 1982; Williams et al. 2002). An advantage of using the removal method in streams is that it often requires less sampling time than mark–recapture methods (i.e., one visit to a sampling site rather than two visits; Rodgers et al. 1992; Meyer and High 2011). Although both methods can produce valid estimates when the underlying model assumptions are met, some assumptions can be problematic when applied to stream fishes, and nearly all evaluations of these techniques have focused on salmonines rather than nongame fishes (e.g., Rosenberger and Dunham 2005; Korman et al. 2009).
Three common closed-population models for estimating stream fish abundance are the Lincoln–Petersen mark–recapture model with Chapman correction (Chapman 1951; Seber 1982), the constant capture probability removal model (Mb; Otis et al. 1978; White et al. 1982), and the generalized removal model with heterogeneous capture probability (Mbh; Otis et al. 1978; White et al. 1982). Capture probability (q) refers to the likelihood that a fish is captured during a sampling pass, and we consider the case where sampling is conducted via electrofishing in a stream. Each model requires that specific assumptions are met to ensure valid abundance estimates. The Lincoln–Petersen model with Chapman correction assumes (1) a closed population (i.e., no additions or deletions of individuals during sampling), (2) equal q for marked and unmarked fish, and (3) that marks are not lost or overlooked (Williams et al. 2002). The assumptions of model Mb are (1) a closed population (except for removals), (2) equal sampling effort for each removal pass, and (3) constant q for each sequential removal pass (Zippin 1958; Seber 1982; White et al. 1982). The assumptions of model Mbh are the same as those of model Mb, except that the q for the first removal pass may differ from that of subsequent removal passes (White et al. 1982). Thus, model Mbh permits fish possessing higher q to be captured first and fish exhibiting lower q to be captured in subsequent passes, thus theoretically negating the most likely source of bias in populations exhibiting heterogeneous q.
Failure to satisfy model assumptions can substantially bias the abundance estimators (Gatz and Loar 1988). A major deficiency of model Mb is its tendency to be negatively biased when q is low because the accuracy of the estimator requires a large proportion of the population to be captured (Zippin 1958; Riley and Fausch 1992; Peterson et al. 2004). Another common source of bias for model Mb is violation of the constant q assumption, which results in the overestimation of q and the underestimation of abundance (Zippin 1958; White et al. 1982; Bohlin et al. 1989; Peterson et al. 2004). This issue is often addressed by employing the more general removal model, Mbh, which allows q to differ between the first and subsequent sampling passes (i.e., involves estimation of more than one parameter for q) and relaxes model Mb's assumption of a constant q for each sequential removal pass (White et al. 1982). However, field studies employing removal methods to estimate abundance of stream-dwelling salmonines have shown that estimates often are negatively biased for both Mb and Mbh (Riley and Fausch 1992; Riley et al. 1993; Peterson et al. 2004; Sweka et al. 2006; Habera et al. 2010; Meyer and High 2011; but see Saunders et al. 2011), whereas mark–recapture methods often provide less-biased estimates of salmonine abundance than removal methods (Peterson and Cederholm 1984; Rodgers et al. 1992; Rosenberger and Dunham 2005; Korman et al. 2009).
Past evaluations of bias associated with abundance estimators have focused on salmonines, despite the often high proportions of small, nongame fishes in many streams. One such nongame species is the Mottled Sculpin Cottus bairdii, a widely distributed species that dominates many fish assemblages in small streams of North America (Becker 1983; Adams and Schmetterling 2007). Although abundance estimation techniques have been commonly applied in ecological studies of sculpins Cottus spp. (e.g., Petrosky and Waters 1975; Ruetz et al. 2002; Grossman et al. 2006), the question remains as to how well studies that have evaluated bias in salmonine abundance estimators can be applied to sculpins. For instance, Mottled Sculpin exhibit restricted movements over short temporal scales (Petty and Grossman 2004; Breen et al. 2009), which should make the closed-population assumption more reasonable. However, Mottled Sculpin are benthic, are often associated with rocky substrate, and lack gas bladders (Becker 1983); these characteristics can make capture via electrofishing difficult and may result in a lower value of q for sculpins relative to salmonines. Low values of q often are associated with decreased accuracy and precision of abundance estimators (e.g., Zippin 1958; Williams et al. 2002). Moreover, studies on salmonines have found that q can be associated with environmental conditions, which may explain differences in biases among streams or geographic regions (Peterson et al. 2004; Speas et al. 2004; Price and Peterson 2010).
We assessed bias in abundance estimators based on the Lincoln–Petersen model with Chapman correction (hereafter, mark–recapture method) and the removal models Mb and Mbh by using field studies of Mottled Sculpin populations in combination with computer simulations. We also were interested in determining whether gradients in environmental conditions among streams could explain (1) differences in the effectiveness of electrofishing for sampling Mottled Sculpin and (2) differences in Mottled Sculpin movement (i.e., which could affect the assumption of a closed population). Our specific objectives were to (1) assess the performance of abundance estimates using mark–recapture and removal methods in wadeable streams, (2) test whether the assumptions of the abundance estimators (i.e., the population is closed during sampling; and marks are detected) were reasonable in our study, and (3) evaluate whether differences in environmental conditions among streams were associated with Mottled Sculpin q and movement, which could affect the accuracy and precision of abundance estimates.
METHODS
Study area.
This study was conducted on eight streams during June–July 2011 (Table 1): six tributaries of the Kalamazoo River; Sand Creek, a tributary of the Grand River; and Curtis Creek, a tributary of the St. Joseph River (Homola et al. 2014). Although the study streams varied with respect to width, discharge, specific conductivity, turbidity, and substrate composition (Table 1), all streams were wadeable, and the Mottled Sculpin was one of the most abundant species in the fish assemblage of each stream (Homola et al. 2014). Sampling was conducted when each stream was at or near base flow.
| Stream | Latitude (°N) | Longitude (°W) | Depth (m) | WW (m) | Discharge (m3/s) | Temp (°C) | SPC (S/cm) | Turbidity (NTU) | Fine (%) | Cobble (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| Augusta Creek (AC) | 42.2348 | −85.2113 | 0.32 ± 0.02 | 7.04 ± 0.30 | 0.32 ± 0.03 | 19.0 ± 0.1 | 436 ± 10 | 10.5 ± 1.9 | 22 ± 5 | 7 ± 4 |
| Curtis Creek (CC) | 41.5257 | −85.4528 | 0.19 ± 0.02 | 5.10 ± 0.58 | 0.08 ± 0.00 | 13.1 ± 0.3 | 291 ± 3 | 3.9 ± 0.1 | 35 ± 14 | 20 ± 9 |
| Lee Creek (LC) | 42.1602 | −85.4907 | 0.17 ± 0.02 | 1.93 ± 0.20 | 0.02 ± 0.00 | 15.0 ± 0.2 | 443 ± 2 | 5.7 ± 1.0 | 5 ± 3 | 22 ± 14 |
| Portage Creek (PC) | 42.1175 | −85.3854 | 0.23 ± 0.04 | 3.58 ± 0.32 | 0.04 ± 0.01 | 16.3 ± 0.1 | 389 ± 14 | 4.3 ± 1.1 | 100 ± 0 | 0 ± 0 |
| Rice Creek (RC) | 42.1671 | −84.5721 | 0.46 ± 0.05 | 10.00 ± 0.83 | 0.73 ± 0.14 | 20.1 ± 0.3 | 522 ± 6 | 6.5 ± 0.0 | 33 ± 6 | 37 ± 13 |
| Spring Brook (SB) | 42.2194 | −85.3172 | 0.35 ± 0.03 | 4.53 ± 0.29 | 0.20 ± 0.02 | 12.6 ± 0.1 | 421 ± 10 | 3.8 ± 1.0 | 18 ± 5 | 15 ± 6 |
| Sand Creek (SC) | 42.5845 | −85.4996 | 0.24 ± 0.03 | 10.00 ± 0.45 | 0.22 ± 0.01 | 21.3 ± 0.1 | 615 ± 14 | 4.3 ± 1.0 | 63 ± 19 | 7 ± 4 |
| Wilder Creek (WC) | 42.1360 | −84.5452 | 0.43 ± 0.06 | 4.32 ± 0.31 | 0.12 ± 0.02 | 16.3 ± 0.3 | 423 ± 2 | 7.3 ± 0.8 | 34 ± 5 | 30 ± 12 |
Field protocol.
Data collection at each site was conducted over 3 d. On day 1, we measured and marked a 90-m stream reach and divided it into three 30-m subreaches to evaluate movement of marked individuals. Sampling reaches were chosen so that we could effectively sample fish from all areas of the reach (e.g., log jams and water depths > 1.5 m were avoided). All fish sampling was conducted with an AbP-3 pulsed-DC backpack electrofisher (220 V; duty cycle = 10%; pulse rate = 50 pulses/s; ETS Electrofishing, Verona, Wisconsin) and one additional netter. Beginning at the downstream end of the 90-m stream reach, we conducted one electrofishing pass through all three subreaches. Each Mottled Sculpin captured during the first pass was marked with a unique partial fin clip indicating the specific subreach of capture. On day 1, if fewer than 40 Mottled Sculpin were captured during the first sampling pass, then we performed an additional sampling pass on the same day (this only occurred in Augusta Creek, and all fish were released once the two sampling passes were completed). Mottled Sculpin were released throughout the central 20 m of the subreach from which they were captured.
On day 2, four removal passes were conducted via backpack electrofishing beginning at the downstream boundary of each 90-m stream reach. At the completion of fish sampling in each subreach, the numbers of marked and unmarked individuals were recorded. All captured individuals were held in stream enclosures (one for each subreach) until the completion of the fourth removal pass, after which the fish were released. Stream enclosures consisted of 151-L (diameter = 53 cm; height = 70 cm) plastic containers with eight holes (20 × 20 cm) covered by 4-mm-mesh netting to allow water exchange. We maintained at least 1 h between successive removal passes of the same 30-m subreach.
A subset of Mottled Sculpin captured on day 2 from each stream was held overnight in stream enclosures to assess mark detection (i.e., to evaluate whether we recognized a marked fish) and to record short-term mortality caused by stress from electrofishing and handling. After completion of sampling on day 2, 10 unmarked fish and 5–10 marked fish were retained from each subreach and were held overnight. The next day, survival and mark detection of Mottled Sculpin in the stream enclosures were assessed, and the fish were then released.
Environmental variables were measured in each study reach to characterize differences among streams. Depth and water velocity (at 60% of depth from the surface) were measured at three points along four to six transects in each 90-m study reach (thalweg and half the distance between the thalweg and streambank; n = 12 or 18 measurements/stream). Water velocity was measured with a Marsh-McBirney Flo-Mate meter. Stream width was measured for each transect (n = 4 or 6 measurements/stream). Specific conductivity and temperature were measured using a YSI Model 30 meter at 50% depth in the thalweg once each day (n = 3 measurements/stream). Percent composition of the substrate was assessed visually based on the maximum diameter of particles (fine: <2 mm; gravel: 2–32 mm; cobble: >32 mm) as determined by one observer at one point (thalweg) along each transect (n = 4 or 6 measurements/stream). Turbidity (NTU) was measured each day with an Oakton TN-100 portable turbidimeter (n = 3 measurements/stream).
Data analysis.
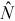) was calculated as (Chapman 1951; Seber 1982)
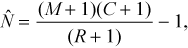(1)Model Mb was also used to estimate the number of marked Mottled Sculpin (i.e., a known quantity) in each 90-m stream reach. We used a paired t-test (observations paired by stream) to assess whether the removal estimate differed from M (the number of fish that were marked in the stream reach on day 1). For this test, we assumed that all fish marked on day 1 were available for capture on day 2—that is, marked fish did not leave the 90-m stream reach where they were marked, they did not die, and they did not lose their marks (below, we explore whether these assumptions were reasonable). We only investigated model Mb because we did not find a significant difference in estimated total abundance between models Mb and Mbh (see Results).
We assessed whether “estimated” q (based on the removal model Mb) was biased by comparing it with “measured” q. Estimated q for model Mb was calculated with CAPTURE for the marked subpopulation. Measured q was calculated as (number of marked fish captured during an electrofishing pass on day 2)/M. We used a paired t-test (observations paired by stream) to compare the measured q from the first electrofishing pass on day 2 with the estimated q from model Mb. Additionally, to evaluate the model Mb assumption that q was constant among electrofishing passes, we used Pearson's product-moment correlation coefficient (Pearson's r) to assess whether measured q decreased with successive electrofishing passes. Finally, Pearson's r between measured q and environmental variables (discharge, percentage of fine substrate, specific conductivity, and turbidity) was calculated to assess whether environmental conditions among streams affected our ability to capture Mottled Sculpin.
Individual movement was examined to evaluate the assumption that the population was closed. We quantified movement by determining whether Mottled Sculpin that were marked in the core 30-m subreach on day 1 were recaptured in an adjoining subreach during the first electrofishing pass on day 2. The percentage of movement was calculated as follows: (number of marked fish from the core 30-m subreach that were captured in a different subreach during pass 1 of day 2)/(total number of marked fish from the core subreach that were captured in the 90-m stream reach during pass 1 of day 2). Pearson's r for the relationship between percentage of movement and stream discharge or substrate type (percentage of fine substrate) was then calculated to evaluate whether environmental conditions among streams affected fish movement and thus the assumption of a closed population.
Simulation study.
Simulations of mark–recapture sampling were conducted in R (R Development Core Team 2010) to determine the likely direction and magnitude of bias in the mark–recapture abundance estimator caused by the observed levels of movement in the study streams. The main steps of the simulation program were (1) specify habitat and fish parameters; (2) specify number of iterations at 5,000; (3) assign spatial locations to all fish; (4) take the first random sample; (5) allow all fish to move; (6) take the second random sample; (7) find the actual number of fish in the study area; (8) calculate the mark–recapture abundance estimate; (9) find the number of fish that moved into and out of the core study reach between samples 1 and 2; (10) iterate 5,000 times; and (11) summarize and plot the results.
The stream in the simulation consisted of three zones: a study reach (i.e., where sampling was conducted) bracketed by two buffer reaches to allow fish to move in and out of the study reach between the first (day 1) and second (day 2) random samples. The only important habitat parameter was the length of each zone (90 m; zone width does not affect simulation results). Other parameters were the initial number of fish in each zone, values of q for day 1 (capture, mark, and release) and day 2 (recapture), and parameters specifying the range and shape of the probability distribution for fish movement distances.
Initial longitudinal (lengthwise) locations of fish in each zone were assigned by generating uniformly distributed pseudorandom variates. Only the longitudinal component of location affects simulation results because it alone determines the zone in which a fish resides. We used values of 75, 300, and 600 fish/zone in the simulations (e.g., 75 individuals in the upstream buffer zone, 75 individuals in the study reach, and 75 individuals in the downstream buffer zone). Determining which fish were captured during a given sampling pass was accomplished by generating Bernoulli pseudorandom variables with a probability of success equal to the specified q. We assessed values of q of 0.1, 0.2, 0.4, and 0.6. The q was the same for fish sampling conducted on days 1 and 2. Longitudinal distances moved by fish between sampling events on days 1 and 2 were determined by generating pseudorandom variables from a symmetric beta distribution, with both shape parameters set to 4, the location of the mode set to zero, and the movement range set to 0, 60, or 180 m (Figure 1). Fish abundance in the study reach was estimated for each iteration, and the number of iterations was set to 5,000. Parameter values in the simulation were chosen to represent the range of conditions encountered in field sampling.
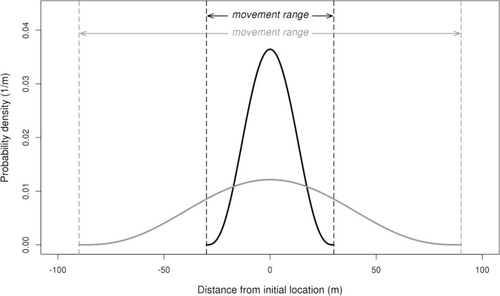
Probability density function describing the simulated movement of fish for movement ranges of 60 (black line) and 180 m (gray line) using a beta distribution with the mode set to zero and both shape parameters set to 4. Movement occurred between days 1 and 2 in the simulation. The maximum displacement of a fish in either direction (upstream or downstream) is one-half the movement range.
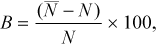(2)
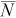is the mean estimated abundance in the study reach (based on 5,000 iterations) and N is the true abundance in the study reach (White et al. 1982). Thus, B is an inverse measure of accuracy, with lower B indicating increased accuracy.RESULTS
The number of Mottled Sculpin marked on day 1 (i.e., M) in the 90-m stream reaches of all eight streams totaled 668, ranging from 34 individuals in Augusta Creek to 161 individuals in Sand Creek. On day 2, the number of Mottled Sculpin (both marked and unmarked) captured during the recapture pass (C) in the 90-m stream reaches totaled 597, ranging from 34 individuals in Augusta Creek (with passes 1 and 2 used for calculations, as noted previously) to 150 individuals in Sand Creek. There was a strong positive association between M and C in a 90-m stream reach (Figure 2), suggesting that both the true number of Mottled Sculpin in the 90-m reach and q were similar for a given stream on days 1 and 2. The slope (0.917) of the regression line was significantly different from zero (t6 = 10.33, P < 0.001) and the relationship between M and C was nearly 1:1 (H0: slope = 1.0, t6 = −0.93, P = 0.387), whereas the intercept (−1.968) did not differ significantly from zero (t6 = −0.24, P = 0.817; Figure 2). The number of marked fish that were recaptured on day 2 (i.e., R) during the recapture pass totaled 148, ranging from 7 individuals in Curtis Creek to 46 individuals in Sand Creek. With the exception of Curtis Creek, all streams had an R of at least 11 individuals. Across the eight streams, we observed 100% survival and mark detection among the 405 Mottled Sculpin (165 marked and 240 unmarked) that were held overnight in enclosures, indicating that the closed-population assumption was reasonable with respect to mortality and that marks were detected.
Relationship between the number of Mottled Sculpin marked on day 1 (M) versus the number of Mottled Sculpin (both marked and unmarked) captured on day 2 during the recapture pass (C) for each 90-m stream reach; the least-squares regression line is shown (R2 = 0.947).
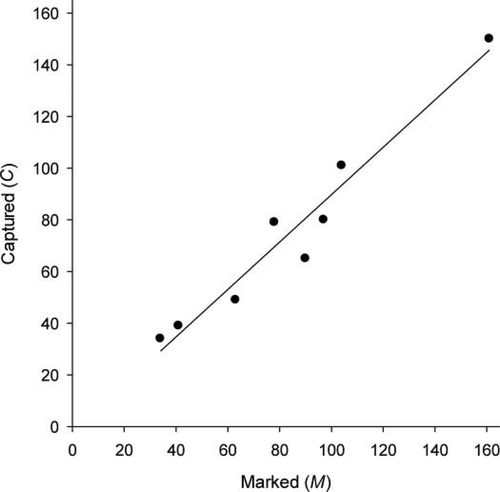
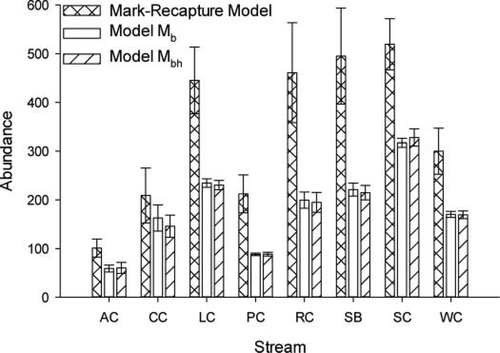
Estimates of Mottled Sculpin abundance differed significantly among the three models (F2, 14 = 26.29, P < 0.001; Figure 3). The mark–recapture estimate was significantly greater than the removal estimates (contrast: F1, 14 = 52.57, P < 0.001), but there was no significant difference between abundance estimates for models Mb and Mbh (contrast: F1, 14 = 0.01, P = 0.923). On average, abundance estimates from the removal models were 45% lower than estimates from the mark–recapture model. Moreover, estimates of marked fish abundance on day 2 using model Mb were significantly lower than M (paired t-test: t7 = 5.28, P = 0.001; Figure 4A). On average, abundance estimates from model Mb were 52% less than M.
Estimated abundance (±SE) of all Mottled Sculpin (i.e., marked and unmarked) in each 90-m stream reach as determined from the mark–recapture model (Lincoln–Petersen estimator with Chapman correction), model Mb (removal estimator with constant capture probability), and model Mbh (generalized removal estimator). Abbreviations for stream names are defined in Table 1.
(A) Estimated number (±SE) of marked Mottled Sculpin (i.e., number marked on day 1) based on removal model Mb compared with the number actually marked on day 1 (M); and (B) “estimated” capture probability for marked Mottled Sculpin (based on removal model Mb) and “measured” capture probability ([number of marked fish caught during pass 1 on day 2]/M). Abundance and capture probability were estimated for day 2; sampling was for the 90-m stream reach. Abbreviations for stream names are defined in Table 1.
Removal models overestimated the q of Mottled Sculpin, which biased abundance estimates downward. The measured q for the marked subpopulation was significantly lower on the first electrofishing pass than the estimated q of the marked subpopulation based on model Mb (paired t-test: t7 = 7.31, P < 0.001; Figure 4B). Moreover, the measured q for the marked subpopulation significantly declined with each electrofishing pass (Pearson's r = −0.72, P < 0.001, n = 32; Figure 5). We found no significant association between measured q of the marked subpopulation and stream discharge (Pearson's r = −0.47, P = 0.243; Figure 6A), percentage of fine substrate (Pearson's r = 0.30, P = 0.472; Figure 6B), specific conductivity (Pearson's r = 0.36, P = 0.387; Figure 6C), or turbidity (Pearson's r = 0.23, P = 0.589; Figure 6D). None of the environmental variables we examined was significantly correlated with the other environmental variables (P > 0.23).
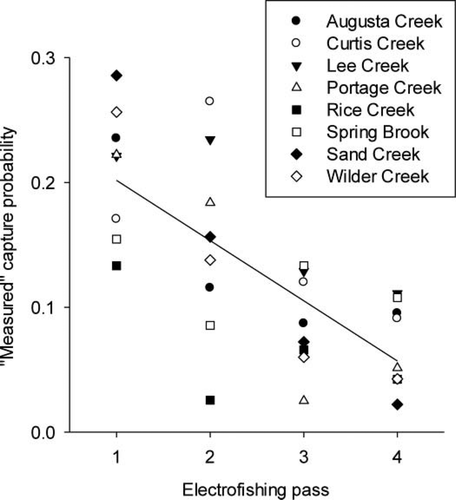
“Measured” capture probability for marked Mottled Sculpin (i.e., [number of marked fish caught during pass i on day 2]/[number of fish marked on day 1 and available for capture], where i = 1, 2, 3, or 4) during each electrofishing pass in the 90-m stream reach. The least-squares regression line is given to show the direction of the significant Pearson's product-moment correlation (P < 0.05).
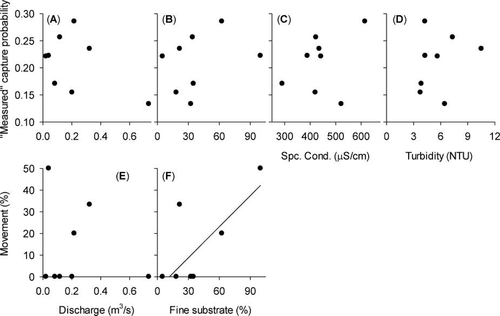
Relationship between environmental variables and (A)–(D) “measured” capture probability (i.e., [number of marked fish caught during pass 1 on day 2]/[number of fish marked on day 1]) or (E), (F) percentage of Mottled Sculpin captured, marked, and released in the core 30-m subreach on day 1 that were recaptured in a different subreach during the recapture pass on day 2. The least-squares regression line in panel F shows the direction of the significant Pearson's product-moment correlation (P < 0.05).
Most Mottled Sculpin were recaptured in the same subreach from which they were originally captured and marked. For five of the eight streams, none of the fish marked in the core 30-m subreach on day 1 was recaptured in a different subreach on day 2 during the recapture pass; the three streams in which fish moved to an adjacent subreach were Augusta Creek (1 of 3 individuals moved), Portage Creek (2 of 4 individuals moved), and Sand Creek (1 of 5 individuals moved). For all streams combined, 4 of 38 marked individuals (11%) were recaptured in an adjoining subreach. In the three streams where we observed movement, one fish moved upstream and three moved downstream. Finally, although the percentage of movement was not significantly associated with stream discharge (Pearson's r = −0.17, P = 0.691; Figure 6E), we found a significant positive association between the percentage of movement and the percentage of fine substrate (Pearson's r = 0.73, P = 0.040; Figure 6F), indicating that differences in habitat among streams could affect Mottled Sculpin movement.
Our simulation demonstrated how q, movement range, and true N affected the precision (i.e., inverse of the 90% range) and accuracy (i.e., inverse of B) of the mark–recapture abundance estimator. For the 12 cases with no movement (i.e., movement range = 0), precision generally increased with increasing q for each true N but increased most when true N was highest (Table 2). For instance, the 90% range of the estimator for a true N of 300 fish was 75% of true N at a q of 0.2 (100 × [433 − 208]/300) and was 13% of true N at a q of 0.6, whereas the 90% range of the estimator for a true N of 600 fish was 53% of true N at a q of 0.2 and was 9% of true N at a q of 0.6 (Table 2). When there were very few recaptures, on average (
< 6), and no movement, B of the mark–recapture estimator was negative (i.e., true N was underestimated, on average), ranging from −3% to −38% (Table 2). We were most likely to have few recaptures in cases where both q and true N were small (e.g., q = 0.1 and true N = 75). Cases where negative B was most pronounced had, on average, less than 1 recapture. When the average number of recaptures was roughly 6 fish or greater, B in the abundance estimator was negligible (Table 2).
) calculated using the mark–recapture estimator (equation 1), percent relative bias (B; equation 2), the central 90% range (NPR) of the abundance estimates (i.e., interval between the 5th and 95th percentiles of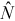 
), and mean number of recaptures (
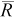). Bold italics indicate cases where the NPR does not include the true N.| Movement range = 0 m | Movement range = 60 m | Movement range = 180 m | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| True N | q |  |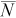
B (%) | NPR |  |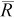
 |
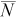B (%) | NPR |  |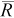
 |
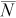B (%) | NPR |  |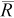
| 75 | 0.1 | 46 | −38 | 17–97 | <1 | 48 | −36 | 17–98 | <1 | 51 | −32 | 19–103 | <1 |
| 0.2 | 73 | −3 | 37–143 | 3 | 78 | 5 | 39–157 | 3 | 94 | 26 | 43–207 | 2 | |
| 0.4 | 75 | 0 | 57–101 | 12 | 82 | 10 | 61–112 | 11 | 103 | 37 | 70–155 | 9 | |
| 0.6 | 75 | 0 | 66–85 | 27 | 83 | 10 | 71–97 | 24 | 103 | 38 | 83–129 | 20 | |
| 300 | 0.1 | 287 | −4 | 139–593 | 3 | 317 | 6 | 147–689 | 3 | 374 | 25 | 165–860 | 2 |
| 0.2 | 300 | 0 | 208–433 | 12 | 328 | 9 | 223–495 | 11 | 414 | 38 | 259–660 | 9 | |
| 0.4 | 300 | 0 | 261–347 | 48 | 330 | 10 | 281–391 | 44 | 411 | 37 | 337–503 | 35 | |
| 0.6 | 300 | 0 | 282–320 | 108 | 331 | 10 | 306–357 | 98 | 413 | 38 | 369–463 | 78 | |
| 600 | 0.1 | 607 | 1 | 341–1,071 | 6 | 650 | 8 | 360–1,155 | 6 | 824 | 37 | 420–1,594 | 4 |
| 0.2 | 601 | 0 | 465–784 | 24 | 662 | 10 | 500–881 | 22 | 829 | 38 | 593–1,160 | 17 | |
| 0.4 | 600 | 0 | 544–666 | 96 | 660 | 10 | 589–740 | 87 | 826 | 38 | 719–950 | 70 | |
| 0.6 | 600 | 0 | 574–629 | 216 | 660 | 10 | 626–699 | 196 | 826 | 38 | 764–895 | 157 | |
Allowing fish to move caused B to shift toward the positive direction. Except in cases with the smallest values of both true N and q, the movement ranges of 60 and 180 m produced a positive B (i.e., true N was overestimated, on average) for all combinations of true N and q (Table 2). The magnitude of positive B was not strongly affected by q or true N except when there was a pronounced negative bias because the average number of recaptures was very small (e.g., q = 0.1 and true N = 75). With the exception of the cases with few recaptures (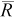
< 6; Table 2), there was a positive B of about 10% for a movement range of 60 m and 38% for a movement range of 180 m (Table 2). Movement ranges of 60 and 180 m resulted, on average, in 9% and 27% (respectively) of fish emigrating from the core study reach. Overall, our simulations showed that when fish movement occurs between days 1 and 2, thus violating the mark–recapture estimator's assumption of a closed population, a substantial positive bias can result.
For the cases we investigated, the 90% range of abundance estimates usually included the true N, even when there was movement bias. However, when precision of the abundance estimator was sufficiently high relative to the bias created by movement, the 90% range of the abundance estimator no longer included the true N (Table 2). These exceptional cases involved a combination of low accuracy (due to movement) and high precision (due to high q and/or high true N).
DISCUSSION
Our study showed that estimates of Mottled Sculpin abundance in streams can differ markedly depending on the estimation method. Both mark–recapture and removal methods can be biased when estimating Mottled Sculpin abundance. If q is low, then removal methods are likely to be negatively biased, especially if q declines with each successive sampling pass (Zippin 1958; Peterson et al. 2004). In our study, even fitting the more general removal model, Mbh, did not adequately account for this issue with four sampling passes. Mark–recapture methods are a better option in such cases. In the simulations, we found that potentially important causes of bias in the mark–recapture estimator include a situation of few recaptures (which can easily be evaluated and was not an issue in our field study) and the movement of fish across the boundaries of the study reach (discussed below). Our empirical results are the first to evaluate mark–recapture and removal methods for estimating the abundance of sculpins and are similar to results from studies of other stream fishes, including juvenile Coho Salmon Oncorhynchus kisutch (Peterson and Cederholm 1984; Rodgers et al. 1992), Rainbow Trout O. mykiss (Rosenberger and Dunham 2005; Korman et al. 2009), Brown Trout Salmo trutta (Nordwall 1999), three salmonine species (Meyer and High 2011), and five minnow species (Gatz and Loar 1988). In all cases, abundance estimates obtained by using removal methods were lower than those obtained from mark–recapture methods.
Removal models underestimated the number of marked Mottled Sculpin in our streams because the models overestimated q. Our results add to a growing body of literature demonstrating that negative bias is common in removal estimators for salmonines (Riley and Fausch 1992; Riley et al. 1993; Peterson et al. 2004; Sweka et al. 2006; Korman et al. 2009; Habera et al. 2010; Meyer and High 2011) unless q is high (Saunders et al. 2011), which seems unlikely for Mottled Sculpin. Thus, negative bias in the removal method appears to be likely for many nongame species that have not yet been evaluated, especially if q is low to moderate.
The magnitude of bias in the removal estimator is dependent on three factors: first-pass q (q1; higher q1 equates to less bias), reduction in q among successive passes (constant q among successive passes equates to less bias), and true N (higher true N equates to less bias; Zippin 1958; Peterson et al. 2004; Korman et al. 2009). The measured q1 for Mottled Sculpin (0.21) in our study was greater than values for most groups of fishes evaluated in Georgia warmwater streams and was about twice as high as the value reported for Banded Sculpin Cottus carolinae (Price and Peterson 2010), whereas it was about half the value reported for Mottled Sculpin in Appalachian streams (Hense et al. 2010). Interestingly, Hense et al. (2010) used a removal model to estimate q, which could overestimate it (Peterson et al. 2004). In our study, measured q of Mottled Sculpin declined with each electrofishing pass, consistent with studies of salmonines (Peterson et al. 2004; Young and Schmetterling 2012) and Smallmouth Bass Micropterus dolomieu (Dauwalter and Fisher 2007). This, in conjunction with our low to moderate values of q1, was the likely cause of negative bias in the removal estimator.
The bias we measured in the removal model for Mottled Sculpin agrees with expectations from modeling results. For instance, Peterson et al. (2004) reported results from a simulation of five-pass removal sampling for a population of 100 individuals with q of 0.1–0.6 and reductions in capture efficiency per pass (e.g., q1/q2, where qi is the capture probability for pass i) of 1–2, with 1 representing no change in qi between passes and 2 representing a 50% decline between passes. For our study, the measured q1 was 0.21 and capture efficiency between passes 1 and 2 was 1.4 (0.21/0.15; see Figure 5). The simulation results of Peterson et al. (2004) predicted a B of about −53% for our conditions. This finding fits well with our empirical results, which indicated that the removal abundance estimates were 45% lower than mark–recapture estimates and that the removal estimates of the number of marked fish were 52% lower than M. Similarly, Zippin (1958) showed that for three-pass removal sampling with a q1 of 0.2 and an absolute decrease in q of 0.05 between successive sampling passes (q1 − q2 ≈ 0.06 in our study), the expected B in abundance was about −51%.
We found no evidence that measured q was associated with environmental variables in our study, whereas other studies have shown that q was associated with environmental conditions (Peterson et al. 2004; Speas et al. 2004; Hense et al. 2010; Price and Peterson 2010). This could indicate either that the q of Mottled Sculpin is relatively constant across space or that we need to assess the relationship between q and environmental variables over a greater environmental gradient and with a larger sample size (the number of streams in our study was less than those in studies that have detected significant relationships).
Our simulations showed that the mark–recapture estimator has a positive bias (unless the number of recaptures is very low; see below) when a population is open to movement. The positive estimator bias occurs in mobile populations because both marked and unmarked fish leave the study reach between sampling events, while only new, unmarked fish enter the study reach, thus decreasing the proportion of marked fish (Seber 1982; Nordwall 1999; Williams et al. 2002). In our simulations, the magnitude of the positive bias was proportional to the amount of movement and was not affected by q as long as there were sufficient recaptures. The mark–recapture method should have provided unbiased estimates of Mottled Sculpin abundance in most of our streams, as movement from the core 30-m subreach was not observed in five of the eight streams. Nevertheless, fish movement between sampling events may vary among streams (because of differences in habitat) and among species. For instance, Price and Peterson (2010) found that about 35% of Banded Sculpin moved out of unblocked study reaches during mark–recapture sampling in Georgia streams; this value seems higher than expected given the amount of movement we observed for Mottled Sculpin. We found that Mottled Sculpin movement was associated with the amount of fine substrate in our streams; higher movement in study reaches with a greater percentage of fine substrates may have been due to a lack of cover for the fish to hide in during sampling, causing them to move more. Similarly, physically complex substrates reduced Rainbow Trout movements in response to electrofishing (Peterson et al. 2005).
Our finding that the mark–recapture estimator is positively biased when a population is open to movement assumes that the movement behavior and q of marked and unmarked fish are similar. If sampling causes fish to alter their behavior (e.g., flee the sampling site), then the effect of movement could differ from the results of our simulations depending on the particular behavioral responses of marked fish (i.e., in the study reach) and unmarked fish (i.e., inside and outside of the study reach). Although we did not evaluate whether q of marked and unmarked fish were similar, violating this assumption can produce bias in the mark–recapture abundance estimator depending on whether marked fish are less likely (positive bias in the estimator) or more likely (negative bias in the estimator) to be captured than unmarked fish in the study reach (Williams et al. 2002).
We recommend that when conducting mark–recapture studies to obtain abundance estimates, fish movement across sampling boundaries should be examined to determine the potential for bias. By evaluating movement in our study streams, we identified the streams in which the mark–recapture abundance estimates could be biased. Using block nets for mark–recapture estimates is problematic in many streams because the nets typically must be left out overnight and may subsequently accumulate excessive debris (e.g., Temple and Pearsons 2006). Researchers should take advantage of natural barriers (e.g., waterfalls or shallow riffles) when selecting a study reach. If fish movement could be a problem, then we recommend the use of a longer study reach so that the proportion of fish that can leave or enter the reach between the first and second sampling events is small relative to the number of fish that are present in the reach (Bohlin et al. 1989; Gwinn et al. 2011; Young and Schmetterling 2012). In our simulations, positive bias in the mark–recapture abundance estimator declined as the proportion of fish moving across reach boundaries decreased.
Our simulations also showed that in the absence of movement, the mark–recapture estimator is negatively biased when there are few recaptures (i.e.,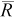 
< 6 without movement). This agrees with analytical findings that the mark–recapture estimator has negligible bias when the number of recaptures is seven or more (Robson and Regier 1964; Seber 1982). Our results also agree with the results of field experiments with Rainbow Trout, where mark–recapture abundance estimates of less than 10 individuals were negatively biased (Rosenberger and Dunham 2005) and undoubtedly were based on few recaptures. Finally, our simulations showed that the magnitude of bias in the mark–recapture estimator is more difficult to predict when there is movement across sampling boundaries and there are few recaptures.
One key assumption of our field study was that marked fish remained in the study reach during the 2-d study period. This was important for (1) accuracy of the mark–recapture estimator (discussed above), (2) determining the number of marked fish in the study reach on day 2 (estimated with the removal method), and (3) calculating the measured q. If some of the marked fish left the study reach, then the number of marked fish in the study reach may be lower than reported in Figure 4A. Movement of marked fish out of the study reach would result in underestimation of the measured q. The assumption that the population is closed to movement in the study reach was reasonable for the five study streams where there was no evidence of marked fish movement out of the core 30-m subreach. There was evidence of movement (which does not necessarily mean any fish left the 90-m study reach) in three streams (Augusta, Sand, and Portage creeks). However, we did not find a pattern wherein the removal model underestimated the number of marked fish to a lesser extent for these streams than for the five streams without evidence of movement (Figure 4A), as would be expected if marked fish were moving out of the study reach. Similarly, measured q1 for day 2 was similar among streams (Figure 4B). Overall, we discount the possibility that movement of marked fish strongly affected our conclusion of negative bias from the removal model. Future field studies can improve on our approach by assessing movement at the spatial scale of fish crossing the sampling (i.e., study reach) boundaries (e.g., Albanese et al. 2003).
We also found that model assumptions associated with mark detection and sampling-induced mortality of Mottled Sculpin in our study were reasonable. First, our marking technique for Mottled Sculpin was robust. We found no evidence that marks went undetected, thus satisfying an assumption of the mark–recapture model. Second, capture (via backpack electrofishing) and handling of Mottled Sculpin did not cause a detectable increase in mortality during our study, which is consistent with previous studies that have assessed the short-term survival of sculpins after electrofishing (Barrett and Grossman 1988; Ruetz et al. 2003, 2006). Nevertheless, electrofishing with pulsed DC can cause mortality and injuries among some fishes (Clément and Cunjak 2010; Panek and Densmore 2013) and can alter fish behavior and physiology (Mesa and Schreck 1989; Densmore and Panek 2013).
In conclusion, we found that the removal estimator was negatively biased when q1 was low and when q declined among sampling passes. In situations where q is low, we recommend the use of mark–recapture methods to estimate fish abundance. Capture probability should be measured by using a mark–recapture approach with environmental covariates rather than relying on a removal model that likely overestimates q (e.g., Peterson et al. 2004; Carrier et al. 2009; Korman et al. 2009). Moreover, estimates of q can be used to adjust CPUE as an alternative approach for estimating abundance (Dauwalter and Fisher 2007; Hense et al. 2010; Price and Peterson 2010; Bergman et al. 2011). Our measured q was relatively constant among streams, indicating that CPUE may be a good index of abundance (Pine et al. 2003) for Mottled Sculpin. Our study highlights the importance of evaluating the accuracy of abundance estimators to better understand the magnitude and direction of potential bias.
ACKNOWLEDGMENTS
We thank Stacy Provo for assistance with field work and Steve Kohler for suggestions on study sites. Dave Janetski, Steve Kohler, and Jennifer Waller provided helpful feedback on the manuscript. Funding was provided by Grand Valley State University's Office of Undergraduate Research and Scholarship, the Student Summer Scholars program, and the Bill and Diana Wipperfurth Student Research Scholarship (to B.S.H.). J.J.H. was supported by a graduate assistantship from the Annis Water Resources Institute.
