A Comparison of Size Structure, Age, and Growth of Red Snapper from Artificial and Natural Habitats in the Western Gulf of Mexico
Abstract
Red Snapper Lutjanus campechanus support economically important fisheries in the Gulf of Mexico (GOM) and have been classified as overfished since the first stock assessment was conducted in 1988. Although the stock is now showing signs of recovery, management could benefit from a better understanding of regional or even habitat-level differences in stock demographics, as these dynamics ultimately determine overall stock productivity. From 2012 to 2014, we used a fishery-independent vertical line survey to assess Red Snapper relative abundance, size and age structure, and growth parameters at standing oil and gas platforms, decommissioned platform artificial reefs, and natural banks in the western GOM. We captured 1,170 Red Snapper ranging from 275 to 855 mm TL. Vertical line CPUE data showed no differences among the three habitat types. Ages determined for 1,143 individuals ranged from 2 to 30 years; however, most (90%) were younger than age 8. Size and age frequencies revealed that natural banks supported a greater proportion of large and relatively old fish compared to standing platforms or artificial reefs, although this difference was heavily influenced by a single bank that had significantly larger and older Red Snapper than other sites. Mean age was not significantly different among habitat types. Among a suite of growth models fitted to size-at-age data, the logistic model provided the best fit and suggested that fish from artificial reefs reached larger sizes at age than fish from either standing platforms or natural banks. Our study provides the first estimates of habitat-specific growth parameters for Red Snapper in the western GOM, and this information can benefit future stock assessments. This study also highlights the potential benefits of artificial reefs to Red Snapper and indicates that all habitats could contribute similarly to stock productivity on a per-unit-area basis.
Received December 21, 2016; accepted March 14, 2017 Published online May 26, 2017
The Red Snapper Lutjanus campechanus is an early maturing, long-lived, demersal reef fish distributed over the western Atlantic continental shelf from North Carolina to the Yucatan Peninsula, including the Gulf of Mexico (GOM; Hoese and Moore 1998). Red Snapper are commonly associated with natural habitats, including shell ridges, reefs, and banks, and also a wide assortment of artificial structures, such as designated artificial reefs (e.g., reef pyramids, ships, and decommissioned oil and gas platforms) and existing oil and gas infrastructure (e.g., production platforms and pipelines; Moseley 1966; Wells and Cowan 2007; Gallaway et al. 2009; Topping and Szedlmayer 2011; Piraino and Szedlmayer 2014). In fact, Red Snapper may account for a significant proportion of the total fish abundance at both natural and artificial habitats (Stanley and Wilson 1997, 2000; Gledhill 2001). Consequently, directed recreational and commercial fisheries commonly target Red Snapper at these habitats (e.g., Garner and Patterson 2015).
In U.S. waters of the GOM, the Red Snapper stock has been exploited since the mid-19th century and has been classified as overfished since the first stock assessment was conducted in 1988 (Goodyear 1988; Hood et al. 2007; SEDAR 2013). Despite this status, Red Snapper continue to support economically valuable fisheries. For example, from 2010 to 2014, the recreational fishery averaged over 370,000 targeted trips generating at least US$45 million in economic impact, while commercial dockside revenues from Red Snapper landings during that period averaged $13.4 million (GMFMC 2015). Nevertheless, due to the continued overfished status of GOM Red Snapper and consequent rebuilding mandates, the fishery has been and remains subject to severe regulatory measures (Hood et al. 2007; Strelcheck and Hood 2007; SEDAR 2013).
Given that GOM Red Snapper occur across a variety of natural and artificial habitats, consideration of potential differences in stock demographics among habitats is critical for accurate assessments of stock status and subsequent management recommendations. In addition, the distribution of Red Snapper among these habitat types and potential changes in the availability of different habitats undoubtedly influence stock dynamics (Pulliam and Danielson 1991). Studies identifying demographic differences among habitats are especially timely as changes in the relative amount and types of artificial habitats in the northwestern GOM are occurring. For example, the number of oil and gas platforms (hereafter, “standing platforms”) has decreased over the past decade as removals through the decommissioning process have exceeded—and likely will continue to exceed—new installations (Pulsipher et al. 2001; BSEE 2016). Some of these structures will be converted to artificial reefs via state reefing programs, such as Rigs-to-Reefs (RTR), which involve partial removal or toppling of the platforms (Macreadie et al. 2011). Although all GOM states have active artificial reef programs, Louisiana and Texas are particularly active and have the largest RTR programs; as of July 2015, over 470 decommissioned platforms had been retained as artificial reefs in these programs (BSEE 2016). Nevertheless, the majority of platform structures will be returned to shore and scrapped, ceasing their role as fish habitat (BSEE 2016). Thus, an understanding of habitat-specific demographics is imperative to predict the effects these changes in habitat may have on GOM Red Snapper as well as to inform the industry and fisheries managers regarding the utility of these structures as artificial reefs.
Due to a heavy reliance on fishery-dependent data sources, the vast majority of information on Red Snapper life history has been amassed from artificial habitats (SEDAR 2013); however, data on the life history of Red Snapper at various habitat types are limited. Specifically, few studies have simultaneously compared Red Snapper demographics from artificial reefs and nearby natural habitats, leaving significant uncertainty in the role artificial reefs play in maintaining the GOM stock. Saari (2011) and Kulaw (2012) provided the first fishery-independent comparisons of Red Snapper demographics among standing platforms, artificial reefs, and shelf-edge natural banks in the northern GOM off the coast of Louisiana, and they demonstrated differences in age structure, size at age, and age at maturity among habitats. In addition, several recent studies have compared Red Snapper diets and trophic ecology between artificial and natural reefs in the northern GOM (Simonsen et al. 2015; Tarnecki and Patterson 2015; Schwartzkopf and Cowan 2017). Further studies of this nature from different regions have been recommended in recent stock assessments (SEDAR 2013; Calay et al. 2015) and are warranted, as such GOM-wide comparisons with fish from natural habitats are essential to understanding how artificial reefs function to support marine fish populations (Carr and Hixon 1997; Love et al. 2006).
The overall goal of this study was to provide new information necessary to evaluate the relative importance of artificial and natural habitats in supporting the GOM Red Snapper stock. To accomplish this goal, we conducted a fishery-independent assessment of Red Snapper sampled from standing platforms, RTR artificial reefs, and natural banks off the Texas coast in the western GOM. Red Snapper relative abundance was estimated using vertical line surveys at each habitat type. In addition, we compared the size structure, age, and growth of Red Snapper among the three habitat types to identify potentially important subregional differences in these demographic parameters.
METHODS
Study area
The continental shelf of the northwestern GOM is dominated by open expanses of mud, silt, and sand substrates, offering little to no vertical relief (i.e., <1 m; Parker et al. 1983; Rezak et al. 1985). Hard reef habitat is generally limited to natural banks located on the mid- to outer shelf, although there are exceptions (see Rooker et al. 2004; Versar 2009; Nash et al. 2013). The prevalence of these features increases as one moves northward along the Texas shelf and continues east along the outer Louisiana shelf edge (Rezak et al. 1985). In addition, artificial structures, including standing platforms and artificial reefs, also provide reef habitat for a variety of marine life in the region (Gallaway and Lewbel 1982; Ajemian et al. 2015a).
In this study, sampling occurred at three standing platforms (BA-A-133A, MU-A-85A, and MU-A-111A), three artificial reefs (BA-A-132, MI-A-7, and MU-A-85), and three natural banks (Baker Bank, South Baker Bank, and Aransas Bank) in the western GOM (Figure 1). The artificial reefs were developed as part of the Texas Parks and Wildlife Department's (TPWD) Artificial Reef Program and consisted of multiple decommissioned RTR structures at each reef site. The natural banks were part of a group of bathymetric features known as the South Texas Banks, which have a different geological origin and ecology than many of the other shelf-edge banks in the GOM (Rezak et al. 1985; Nash et al. 2013). Sites were interspersed within the 60–90-m isobaths and were located approximately 65–80 km offshore to limit spatial variability and maintain similar hydrographic conditions. A nepheloid layer with varying thickness persisted at all sites, likely affecting the ecology of these habitats (Shideler 1981; Rezak et al. 1985; Tunnell et al. 2009).
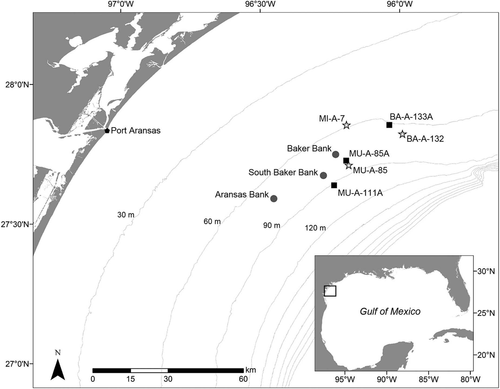
Map of the study area in the western Gulf of Mexico (GOM), depicting locations of artificial reefs (stars), natural banks (circles), and standing platforms (squares) that were sampled with fishery-independent vertical line surveys from 2012 to 2014. Gray contour lines represent relevant bathymetry within the study area (30-m isobaths), while the inset map shows the location of the study area relative to the GOM. Artificial habitats were established in the GOM during the 1970s and 1980s: BA-A-133A (standing platform installed in 1976), MU-A-85A (standing platform installed in 1977), BA-A-132 (original platform installed in 1980; reef creation in 1992), MI-A-7 (original platform installed in 1980; reef creation in 2002), MU-A-111A (standing platform installed in 1981), and MU-A-85 (original platform installed in 1986; reef creation in 2006). Artificial reefs were created via toppling or partial removal of the original standing platform.
Sampling procedure
Red Snapper were sampled at the three habitat types with standardized vertical line gear from October 2012 through October 2014. When sampling occurred, all sites were visited within a similar time frame (i.e., 2–3 weeks) to minimize potential effects of seasonality. Vertical line gear conformed to the specifications of the Southeast Area Monitoring and Assessment Program (SEAMAP) and consisted of commercial-grade bandit reels that were spooled with 136-kg-test (300-lb-test) monofilament mainline, which terminated in a 7.3-m backbone (i.e., leader) constructed with 181-kg-test (400-lb) monofilament. The backbone contained 10 equally spaced, 45-kg-test (100-lb-test) monofilament gangions, each terminating with identical circle hooks (Mustad 39960D, size 8/0, 11/0, or 15/0; all hooks fished on a given backbone were identical in size) that were baited with cut Atlantic Mackerel Scomber scombrus. A 4.5-kg sash weight was attached to the end of the backbone to allow the gear to fish vertically.
A vertical line “set” consisted of one deployment of each hook size (i.e., 30 hooks fished per set). Therefore, upon arrival at the sampling location, a randomly selected hook size was deployed over either the port or starboard bow of the vessel, and the backbone was allowed to soak for 5 min. The gear was then retrieved, and a second hook size (randomly chosen from the two remaining sizes) was immediately deployed off the opposite side of the vessel. After retrieval of this second backbone, the backbone containing the third (unused) hook size was fished. Hook sizes were then rotated such that each hook size was fished on the first, second, and third drop at a site on a given sampling day. We conducted three replicate sets (i.e., 1 drop of each hook size in each set; 9 drops total) at each site visited on a given sampling day. At standing platforms and RTR artificial reefs, each set was conducted around the artificial structure. Because natural banks were considerably larger than artificial structures (~1 km2 compared to ~0.006 km2, respectively), sampling at natural banks was constrained to an area that was approximately equivalent to the extent of artificial habitats. To do this, a grid with cells the size of the sampling area at artificial sites was overlain onto multibeam imagery of the natural bank in ArcMap version 10.3.1 (ESRI 2015). Grid cells were sequentially numbered, and a single cell was randomly selected for sampling before each sampling trip by using a random number generator. Locations for the three vertical line sets were then randomly allocated within the selected grid cell using the “Create Random Points” tool in ArcMap. Water quality data, including temperature (°C), dissolved oxygen (DO) concentration (mg/L), and salinity (‰), were measured at each site with a vertical cast from surface to depth using a Hydrolab DS5 DataSonde.
Fish processing
Upon retrieval of the gear, each Red Snapper was given a temporary tag labeled with that individual's unique call number and was retained on ice for later processing. In the laboratory, fish were measured (SL, FL, and TL; mm), weighed (total weight [TW]; kg), and sexed. Other tissues (stomach and gonad) and hard parts (sagittal otoliths) were also extracted and stored for future study.
Sagittal otoliths were weighed (g) and processed in accordance with the guidelines of VanderKooy (2009). The left otolith of each fish was embedded in epoxy and then was thin sectioned (0.5 mm) in the transverse plane by using an Isomet 1000 precision sectioning saw. If the left otolith was unavailable, the right otolith was used. Thin sections containing the core were mounted to slides by using thermoplastic cement and then were viewed under a dissecting microscope with reflected light. For each section, two independent readers made blind counts of opaque annuli along the dorsal edge of the sulcus acusticus, and the edge condition was coded following VanderKooy (2009). When counts of opaque annuli differed, the two readers examined the sections a second time. If counts still differed after the second read, the section was jointly examined, and if a consensus could not be reached, that section was discarded from further analyses. Precision between readers was assessed using the average coefficient of variation (ACV = SD/mean × 100; Chang 1982) and average percent error (APE; Beamish and Fournier 1981).
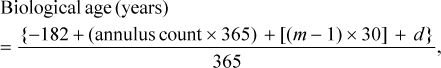 (1)
(1)where m is the ordinal month of capture; and d is the ordinal day of the month of capture.
Data analyses
Analysis of variance was used to test for potential differences in Red Snapper CPUE (fish/set), TL, TW, and age among the three habitats. To account for variation among sites, site was nested within habitat and treated as a random factor in the models. To determine the effect of hook size on the size of captured Red Snapper, we used ANOVA to test for differences in mean TL, and we used Kolmogorov–Smirnov two-sample tests (K–S tests) to compare length frequencies among hook sizes. We also used ANOVA to determine whether Red Snapper size or age composition differed between consecutive sets among habitats. Data were assessed for homogeneity of variance and normality of residuals and were log transformed if necessary. Tukey contrasts were used for post hoc comparisons when ANOVA detected differences among habitats. As an ancillary analysis, we also examined differences in mean TL, TW, and age among sites with ANOVA and visually assessed the distributions of these variables with box plots. Length, weight, and age frequency distributions among habitats were evaluated with pairwise G-tests (Sokal and Rohlf 1995). If differences in frequency distributions were detected, standardized residuals were evaluated to determine which categories (i.e., length, weight classes, or age-groups) had the greatest contribution to the observed difference (Agresti 2007). All testing was carried out in R version 3.3.1 (R Core Team 2016) by using α = 0.05.
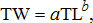 (2)
(2)where a is a constant and b is an exponent describing the curve of the relationship, with b = 3 indicating isometric growth (Beverton and Holt 1996). Nonparametric bootstrapping with replacement (n = 10,000) was used to estimate 95% confidence intervals (CIs) for parameters a and b for each habitat (Efron and Tibshirani 1993). If the CIs overlapped, model parameters were considered similar between habitats.
Following the multimodel inference approach of Katsanevakis and Maravelias (2008), we fitted four types of nonlinear growth models to Red Snapper length-at-age and weight-at-age data: the original three-parameter von Bertalanffy growth model (VBGM; von Bertalanffy 1938), a two-parameter VBGM that is commonly used when younger fish are lacking in the sample (e.g., Fischer et al. 2004), the Gompertz growth model (Ricker 1979), and the logistic growth model (Ricker 1979). Each of the four candidate growth models was fitted to length-at-age and weight-at-age data separately for each habitat, and 95% CIs were estimated for all model parameters with nonparametric bootstrapping as described above. To minimize potential bias due to few fish in the older age-groups, size-at-age data were constrained to individuals of ages 2–10 only. An information-theoretic approach (Burnham and Anderson 2002) was used to assess the likelihood of the candidate models among habitats. Akaike's information criterion (AIC; Akaike 1973) with the small-sample bias correction (AICc; Hurvich and Tsai 1989) was used to assess the goodness of fit for each model. The model with the lowest AICc is considered the best-fitting model, and models with an AICc difference (Δi) ≤ 2 are considered strongly supported (Burnham and Anderson 2002). Akaike weights (wi), which range from 0 to 1, were also calculated to assess the likelihood of each model given the data, with the greatest wi corresponding to the most plausible model of the candidate set (Burnham and Anderson 2002). We selected the best-fitting growth model to compare growth among habitats.
Overall differences in growth curves among habitats were evaluated using likelihood ratio tests (Kimura 1980). Pairwise comparisons were conducted to assess differences because three habitats were included in the data set. The first hypothesis tested was that growth could be modeled equally well for both data sets by using a single curve (i.e., coincident curves). If a significant difference was detected (α = 0.05), nested models were constructed, and null hypotheses assuming that one parameter was similar between habitats (e.g., equal asymptotic length L∞) or two parameters were similar between habitats (e.g., equal L∞ and growth coefficient k) were sequentially tested.
RESULTS
During the sampling period, fishery-independent vertical line surveys captured 1,170 Red Snapper. After discarding vertical line sets that were unsuitable for abundance estimation (e.g., snagged on structure; fished longer than 5 min), 42 sets at artificial reefs captured 410 Red Snapper, 42 sets at natural banks captured 387 Red Snapper, and 37 sets at standing platforms captured 356 Red Snapper (1,153 total individuals). Vertical line CPUE was similar among habitats (F2, 6 = 0.04, P = 0.960), averaging 9.76 fish/set (SE = 0.76) at artificial reefs, 9.62 fish/set (SE = 0.88) at standing platforms, and 9.21 fish/set (SE = 1.05) at natural banks. Male : female ratios did not deviate from the expected 1:1 ratio at artificial reefs (1:0.86; χ2 = 2.12, P = 0.146), natural banks (1:0.85; χ2 = 2.66, P = 0.103), or standing platforms (1:0.92; χ2 = 0.63, P = 0.429).
Red Snapper ranged from 275 to 855 mm TL and from 0.26 to 8.26 kg in TW. Among habitats, mean length was similar (F2, 6 = 0.64, P = 0.558), averaging 548.5 mm TL (SE = 10.91) at natural banks, 517.2 mm TL (SE = 12.09) at artificial reefs, and 510.3 mm TL (SE = 10.65) at standing platforms. Red Snapper TW averaged 2.38 kg (SE = 0.12) at natural banks, 2.17 kg (SE = 0.13) at artificial reefs, and 1.98 kg (SE = 0.11) at standing platforms and was not significantly different among habitats (F2,6 = 0.47, P = 0.645). Hook size had a significant effect on the size of captured Red Snapper (F2,279 = 36.87, P < 0.001); mean TL increased with hook size at all habitats (natural banks: 8/0, mean = 517.5 mm, SD = 95.86; 11/0, mean = 552.3 mm, SD = 69.58; 15/0, mean = 569.9 mm, SD = 67.66; artificial reefs: 8/0, mean = 451.3 mm, SD = 75.08; 11/0, mean = 501.8 mm, SD = 90.24; 15/0, mean = 595.2 mm, SD = 82.27; standing platforms: 8/0, mean = 478.1 mm, SD = 76.35; 11/0, mean = 504.9 mm, SD = 72.86; 15/0, mean = 550.2 mm, SD = 72.12). Correspondingly, TL distributions differed among the three hook sizes regardless of habitat type (K–S tests: P < 0.028). There was no difference in mean TL (F4, 104 = 1.20, P = 0.317) or age (F4, 105 = 0.23, P = 0.317) as sampling progressed (i.e., no difference between sets) at any of the three habitats sampled.
Length frequency distributions were different among all habitats (artificial reefs versus natural banks: G = 97.93, df = 12, P < 0.001; artificial reefs versus standing platforms: G = 64.48, df = 10, P < 0.001; natural banks versus standing platforms: G = 42.48, df = 12, P < 0.001). An evaluation of standardized residuals suggested that artificial reefs had over two times more fish under 400 mm TL than expected when compared with natural banks (25.1% versus 11.4%; Figure 2A). Similarly, standing platforms had more small fish than natural banks, especially those under 500 mm TL. Natural banks generally had greater proportions of larger fish than either standing platforms or artificial reefs. For example, 45.2% of Red Snapper from natural banks were 550–700 mm TL compared with 33.3% of fish at artificial reefs and 33.6% of fish at standing platforms. Standing platforms had a greater proportion of 400–600-mm TL Red Snapper than artificial reefs; however, nearly twice as many fish less than 400 mm TL were sampled at artificial reefs (25.1%) than at standing platforms (14.4%; Figure 2A). Weight frequency distributions also differed among the three habitats (artificial reefs versus natural banks: G = 81.16, df = 16, P < 0.001; artificial reefs versus standing platforms: G = 47.03, df = 12, P < 0.001; natural banks versus standing platforms: G = 42.52, df = 16, P < 0.001). A greater proportion of larger fish (TW > 2.5 kg) was sampled from the natural banks (41.7%) than from artificial reefs (29.9%) or standing platforms (27.5%; Figure 2B). Weight frequency distributions were more similar between artificial reefs and standing platforms, as both were dominated by smaller individuals. Standardized residuals suggested that the main differences stemmed from a greater proportion of fish less than 1 kg at artificial reefs and more 1.0–1.5-kg fish at standing platforms (Figure 2B). No differences were observed in TW–TL regressions among habitats, as 95% CIs overlapped for both the a and b parameters. Length–weight data were then pooled, and the overall TW–TL regression parameters estimated were a = 2.19 × 10−8 (95% CI = 1.80 × 10−8 to 2.64 × 10−8) and b = 2.92 (95% CI = 2.89–2.95).
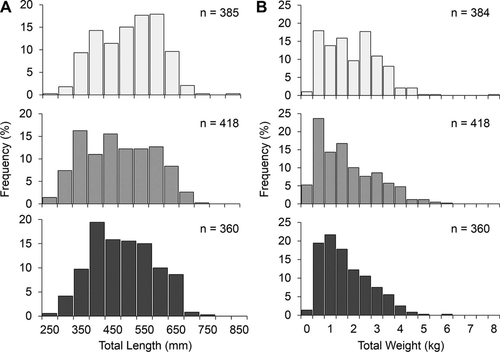
A) Length frequency (50-mm bins; e.g., 350 = 350–399 mm TL) and (B) weight frequency (0.5-kg bins) of Red Snapper captured at natural banks (light gray bars), artificial reefs (gray bars), and standing platforms (dark gray bars) in the western Gulf of Mexico.
Otolith-derived ages were estimated for 1,143 Red Snapper. After the first read, agreement between readers was 84.3%, with an ACV of 2.63% and an APE of 1.86%. The second read increased agreement to 93.0%, with an ACV of 1.12% and an APE of 0.8%. Consensus on the remaining 80 otolith sections was achieved in the third joint reading. Red Snapper ages ranged from 2 to 30 years; however, individuals of ages 3–7 comprised the vast majority of fish sampled (90.6%; Figure 3A). Only five individuals were older than 10 years. Mean age was not significantly different among habitats (F2, 6 = 1.31, P = 0.338), averaging 5.04 years (SE = 0.22) at artificial reefs, 5.22 years (SE = 0.15) at standing platforms, and 5.77 years (SE = 0.20) at natural banks. Age frequency distributions differed among all habitats (artificial reefs versus natural banks: G = 161.75, df = 9, P < 0.001; artificial reefs versus standing platforms: G = 43.55, df = 9, P < 0.001; natural banks versus standing platforms: G = 45.72, df = 9, P < 0.001). A general pattern included a greater proportion of young fish at artificial reefs and standing platforms than at natural banks. For example, 7.0% of individuals from natural banks were age-2 and age-3 fish, compared to 15.2% of individuals from standing platforms and 25.4% of individuals from artificial reefs (Figure 3A). In contrast, a greater proportion of age-6 and older fish was observed at natural banks (42.2%) compared to standing platforms (32.7%) or artificial reefs (27.1%). All age frequency distributions displayed relatively sharp declines from the age-7 bin to the age-8 bin. Artificial reefs and standing platforms also exhibited sharp declines after age 5, whereas the age frequency distribution for natural banks did not (Figure 3A). Cohort frequency distributions for all habitats displayed evidence of a strong 2009 year-class, which constituted 34–40% of the fish sampled from each habitat (Figure 3B). Despite overall similarities between cohort frequencies, some differences among habitats were evident, including strong representation of the 2007 year-class at natural banks and strong representation of the 2011 year-class at artificial reefs, which were not observed at the other habitats.
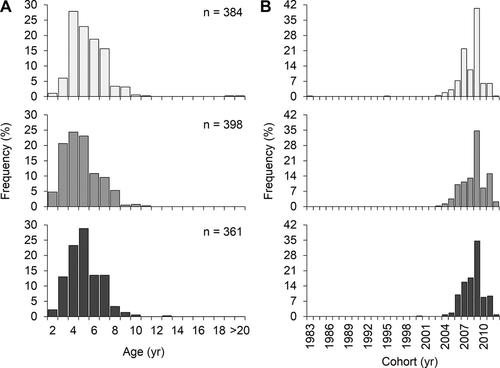
Histograms displaying the (A) age frequency (years; >20 = age-20 and older fish) and (B) cohort frequency (calendar year) of Red Snapper captured with vertical lines at natural banks (light gray bars), artificial reefs (gray bars), and standing platforms (dark gray bars) in the western Gulf of Mexico.
The evaluation of mean TL, TW, and age among sites suggested that the means for all three variables differed (P < 0.001). Tukey contrasts revealed that fish sampled at Baker Bank were significantly longer (mean = 600.5 mm; SE = 6.4), heavier (mean = 2.89 kg; SE = 0.08), and older (mean = 6.5 years; SE = 0.1) than fish from any of the other sites. In addition, 80% of the Red Snapper sampled at Baker Bank were age 6 or older, and most were derived from the 2007 year-class (34%).
Among the four models that were fitted to TL-at-age and TW-at-age data, the logistic growth model provided the best fit to the data for each habitat (Tables 1, 2). The Gompertz model was the second most supported model, although the logistic model consistently had at least twice as much support as the Gompertz model (based on wi). Generally, the two-parameter VBGM and three-parameter VBGM had considerably less support (Tables 1, 2). Based on AICc, the logistic model was selected to compare growth among habitats.
| Model | L∞ | g | k | t0 | AICc | Δi | wi |
|---|---|---|---|---|---|---|---|
| Artificial reefs | |||||||
| Logistic | 761.70 | 0.40 | – | 3.01 | 4,257.00 | 0.00 | 0.74 |
| (719.79, 822.74) | (0.34, 0.47) | – | (2.75, 3.41) | ||||
| Gompertz | 816.65 | 0.27 | 1.72 | – | 4,259.41 | 2.41 | 0.22 |
| (754.95, 914.76) | (0.21, 0.33) | (1.60, 1.91) | – | ||||
| 3-P VBGM | 950.99 | – | 0.14 | –0.62 | 4,263.25 | 6.25 | 0.03 |
| (830.44, 1,209.36) | – | (0.09, 0.20) | (–1.37, –0.08) | ||||
| 2-P VBGM | 832.00 | – | 0.20 | – | 4,266.87 | 9.87 | 0.01 |
| (790.09, 880.82) | – | (0.18, 0.22) | – | ||||
| Natural banks | |||||||
| Logistic | 702.69 | 0.46 | – | 2.74 | 4,181.74 | 0.00 | 0.54 |
| (666.88, 754.54) | (0.37, 0.57) | – | (2.53, 3.01) | ||||
| Gompertz | 727.77 | 0.35 | 1.91 | – | 4,183.37 | 1.64 | 0.24 |
| (682.10, 798.80) | (0.26, 0.44) | (1.58, 2.45) | – | ||||
| 2-P VBGM | 790.71 | – | 0.21 | – | 4,184.16 | 2.42 | 0.16 |
| (747.75, 841.04) | – | (0.19, 0.24) | – | ||||
| 3-P VBGM | 778.45 | – | 0.23 | 0.12 | 4,186.09 | 4.35 | 0.06 |
| (711.83, 904.06) | – | (0.15, 0.31) | (–0.76, 0.73) | ||||
| Standing platforms | |||||||
| Logistic | 715.93 | 0.39 | – | 2.70 | 3,868.16 | 0.00 | 0.76 |
| (670.04, 787.15) | (0.31, 0.48) | – | (2.41, 3.17) | ||||
| Gompertz | 754.60 | 0.28 | 1.59 | – | 3,870.97 | 2.81 | 0.19 |
| (692.54, 865.09) | (0.20, 0.36) | (1.43, 1.86) | – | ||||
| 3-P VBGM | 836.34 | – | 0.17 | –0.67 | 3,874.32 | 6.16 | 0.04 |
| (732.88, 1,079.12) | – | (0.09, 0.24) | (–1.76, 0.06) | ||||
| 2-P VBGM | 751.53 | – | 0.23 | – | 3,876.15 | 7.99 | 0.01 |
| (713.69, 795.53) | – | (0.21, 0.26) | – | ||||
| Model | W∞ | g | k | t0 | AICc | Δi | wi |
|---|---|---|---|---|---|---|---|
| Artificial reefs | |||||||
| Logistic | 4.99 | 0.64 | – | 5.61 | 707.74 | 0.00 | 0.46 |
| (4.55, 5.64) | (0.56, 0.74) | – | (5.26, 6.09) | ||||
| Gompertz | 6.41 | 0.31 | 5.47 | – | 709.10 | 1.36 | 0.23 |
| (5.44, 8.13) | (0.25, 0.38) | (4.72, 6.65) | – | ||||
| 2-P VBGM | 8.14 | – | 0.20 | – | 709.16 | 1.41 | 0.23 |
| (7.13, 9.45) | – | (0.18, 0.21) | – | ||||
| 3-P VBGM | 7.95 | – | 0.20 | 0.06 | 711.16 | 3.42 | 0.08 |
| (6.25, 11.73) | – | (0.14, 0.27) | (–0.73, 0.66) | ||||
| Natural banks | |||||||
| Logistic | 4.05 | 0.69 | – | 5.13 | 741.18 | 0.00 | 0.67 |
| (3.70, 4.55) | (0.57, 0.83) | – | (4.81, 5.57) | ||||
| Gompertz | 4.53 | 0.41 | 6.52 | – | 743.61 | 2.43 | 0.20 |
| (3.97, 5.44) | (0.31, 0.53) | (4.81, 9.66) | – | ||||
| 3-P VBGM | 4.88 | – | 0.31 | 0.80 | 745.16 | 3.98 | 0.09 |
| (4.16, 6.23) | – | (0.22, 0.42) | (–0.08, 1.43) | ||||
| 2-P VBGM | 5.87 | – | 0.23 | – | 746.52 | 5.34 | 0.05 |
| (5.16, 6.75) | – | (0.21, 0.26) | – | ||||
| Standing platforms | |||||||
| Logistic | 3.83 | 0.69 | – | 5.09 | 639.52 | 0.00 | 0.99 |
| (3.47, 4.36) | (0.57, 0.83) | – | (4.75, 5.58) | ||||
| Gompertz | 4.45 | 0.38 | 5.74 | – | 649.48 | 9.96 | 0.01 |
| (3.81, 5.58) | (0.28, 0.49) | (4.44, 8.07) | – | ||||
| 2-P VBGM | 5.45 | – | 0.24 | – | 652.64 | 13.12 | 0.00 |
| (4.76, 6.34) | – | (0.21, 0.26) | – | ||||
| 3-P VBGM | 4.97 | – | 0.27 | 0.37 | 653.87 | 14.35 | 0.00 |
| (4.06, 6.92) | – | (0.18, 0.37) | (–0.62, 1.06) | ||||
Visually, logistic models of TL at age among the three habitats were quite similar until around age 6, when growth curves for natural banks and standing platforms began to increase at a slower rate than the curve for artificial reefs (Figure 4). There was no evidence that models differed between natural banks and standing platforms (Table 3). However, likelihood ratio tests suggested that the TL-at-age model for artificial reefs was significantly different than the models for natural banks or standing platforms (P < 0.05; Table 3). Although no significant differences were found in subsequent likelihood ratio tests for equal parameters between artificial and natural banks, the smaller L∞ for natural banks (702.7 mm) may have been driving the overall model difference, as this estimate was not contained within the 95% CI of L∞ for artificial reefs (Table 1). Between artificial reefs and standing platforms, the hypothesis of equal L∞ and g (i.e., instantaneous growth) parameters was rejected (χ2 = 12.54, P = 0.002; Table 3), suggesting that separate L∞ and g parameters were warranted. Similar to natural banks, the estimate of L∞ for standing platforms (715.9 mm) was lower than the L∞ estimated for artificial reefs (761.7 mm) and was not contained in the 95% CI (719.8–822.7).
| TL at age | Total weight at age | ||||||
|---|---|---|---|---|---|---|---|
| Null hypothesis | χ2 | df | P | Null hypothesis | χ2 | df | P |
| Artificial reefs versus natural banks | |||||||
| Coincident curves | 8.86 | 3 | 0.031 | Coincident curves | 26.62 | 3 | <0.001 |
| Equal L∞ | 3.35 | 1 | 0.067 | Equal W∞ | 7.64 | 1 | 0.006 |
| Equal g | 1.22 | 1 | 0.269 | Equal g | 0.39 | 1 | 0.532 |
| Equal t0 | 2.01 | 1 | 0.156 | Equal t0 | 3.01 | 1 | 0.083 |
| Equal L∞ and g | 5.18 | 2 | 0.075 | Equal W∞and g | 18.09 | 2 | <0.001 |
| Equal L∞ and t0 | 3.35 | 2 | 0.187 | Equal W∞ and t0 | 20.49 | 2 | <0.001 |
| Equal g and t0 | 2.22 | 2 | 0.330 | Equal g and t0 | 5.39 | 2 | 0.068 |
| Artificial reefs versus standing platforms | |||||||
| Coincident curves | 22.18 | 3 | <0.001 | Coincident curves | 22.18 | 3 | <0.001 |
| Equal L∞ | 1.54 | 1 | 0.214 | Equal W∞ | 11.95 | 1 | <0.001 |
| Equal g | 0.03 | 1 | 0.872 | Equal g | 0.46 | 1 | 0.497 |
| Equal t0 | 1.75 | 1 | 0.186 | Equal t0 | 3.57 | 1 | 0.059 |
| Equal L∞ and g | 12.54 | 2 | 0.002 | Equal W∞ and g | 28.49 | 2 | <0.001 |
| Equal L∞ and t0 | 1.76 | 2 | 0.416 | Equal W∞ and t0 | 43.86 | 2 | <0.001 |
| Equal g and t0 | 4.21 | 2 | 0.122 | Equal g and t0 | 6.21 | 2 | 0.045 |
| Natural banks versus standing platforms | |||||||
| Coincident curves | 5.47 | 3 | 0.140 | Coincident curves | 5.37 | 3 | 0.146 |
| Equal L∞ | – | – | – | Equal W∞ | – | – | – |
| Equal g | – | – | – | Equal g | – | – | – |
| Equal t0 | – | – | – | Equal t0 | – | – | – |
| Equal L∞ and g | – | – | – | Equal W∞ and g | – | – | – |
| Equal L∞ and t0 | – | – | – | Equal W∞ and t0 | – | – | – |
| Equal g and t0 | – | – | – | Equal g and t0 | – | – | – |
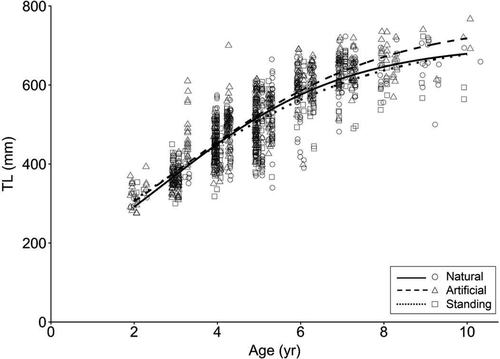
Logistic growth models of Red Snapper TL at age fitted separately by habitat type in the western Gulf of Mexico. Data are displayed for natural banks (circles and solid curve), artificial reefs (triangles and dashed curve), and standing platforms (squares and dotted curve).
Logistic models of TW at age were quite similar among all habitats from age 2 through age 5 or 6, at which point the artificial reef growth curve continued to increase but at a faster rate than the curves for natural banks or standing platforms (Figure 5). Like the TL-at-age models, no difference was observed between the TW-at-age models for natural banks and standing platforms, and all three model parameters for these two habitats were similar (Tables 2, 3). The TW-at-age model for artificial reefs was significantly different than the models for either natural banks or standing platforms (P < 0.001; Table 3). Likelihood ratio tests indicated that the W∞ estimate for artificial reefs (4.99 kg) was significantly greater than the W∞ estimates for natural banks (4.05 kg) or standing platforms (3.83 kg; Table 3). Confidence intervals confirmed this difference, as the 95% CI for W∞ at artificial reefs did not overlap with those for natural banks or standing platforms (Table 2). The estimate for the t0 parameter was not significantly different among habitats (i.e., artificial reefs versus natural banks: P = 0.083; artificial reefs versus standing platforms: P = 0.059); however, the estimate for artificial reefs (t0 = 5.61) was not contained within the 95% CIs for natural banks or standing platforms.
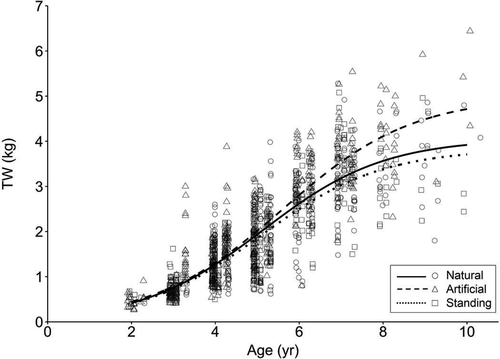
Logistic growth models of Red Snapper total weight (TW) at age fitted separately by habitat type in the western Gulf of Mexico. Data are displayed for natural banks (circles and solid curve), artificial reefs (triangles and dashed curve), and standing platforms (squares and dotted curve).
DISCUSSION
An accurate evaluation of stock status requires an understanding of stock dynamics at regional or even subregional levels, such as among habitats, as these finer-scale dynamics ultimately influence overall stock productivity (Pulliam 1988; Pulliam and Danielson 1991; Cadrin and Secor 2009; Kerr et al. 2010). Our study provides new information on Red Snapper demographics at the habitat level and suggests that differences in length, weight, and age frequencies and growth exist among Red Snapper at artificial reefs, standing platforms, and natural banks in the western GOM region. We documented that the proportion of relatively large, old Red Snapper was greater at natural banks than at standing platforms or artificial reefs. Saari (2011) also reported differences in length and weight frequencies from similar habitats off the coast of Louisiana; however, a higher percentage of large fish (e.g., ≥550 mm TL) was sampled from artificial reefs (toppled RTR structures; 60%) than from standing platforms (42%) or natural banks (27%), and no difference in age frequencies among habitats was observed. In contrast, nearly 50% of Red Snapper sampled from natural banks in this study were at least 550 mm TL compared with 36% of Red Snapper at artificial reefs and 35% of those at standing platforms. The differences between studies may be influenced by the habitat types surveyed in each study. For example, while artificial reefs in both studies consisted of RTR structures located in similar depths (60–80 m), the natural banks surveyed by Saari (2011; Alderdice, Bouma, Jakkula, and Rezak-Sidner banks) are classified as shelf-edge banks and are geologically distinct from the South Texas Banks we surveyed (e.g., result of salt diapirism versus relict coralgal reefs; Rezak et al. 1985). The shelf-edge banks also occur in much deeper water than the banks in our study (e.g., ambient depths = 90–150 m [Saari 2011] compared to 72–84 m [present study]) and are located in much closer proximity to the Mississippi River and its associated productivity (Grimes 2001), which may also contribute to the observed differences between the study by Saari (2011) and our study. Finally, both studies sampled relatively few sites covering a relatively small area of the shelf, simply due to sampling logistics related to offshore field studies. Therefore, inferences regarding the patterns described here should be interpreted with regard to the spatial extent of the respective studies. Regardless, the lack of similar trends among habitats in Louisiana (Saari 2011) and Texas (present study) highlights the potentially complex nature of subregional stock dynamics for Red Snapper in the GOM.
Our study employed a standardized, fishery-independent vertical line survey (e.g., Gregalis et al. 2012), which permitted estimates of Red Snapper relative abundance (i.e., CPUE) among the three habitats. A key assumption when using CPUE data to estimate relative abundance is that CPUE is proportional to true abundance (Quinn and Deriso 1999). Because Red Snapper can form dense aggregations (Stanley and Wilson 1997), gear saturation may have been a potential issue affecting estimates of relative abundance, as the SEAMAP vertical lines used in this study consisted of only 10 hooks per backbone. Although vertical lines were not close to being fully saturated (i.e., one fish per hook), relative abundance in our study was similar among artificial reefs, standing platforms, and natural banks surveyed—a finding that is inconsistent with previous studies demonstrating higher relative abundance of Red Snapper at artificial habitats than at natural habitats (Patterson et al. 2014; Karnauskas et al. 2017; Streich et al. 2017). For example, remotely operated vehicle transects conducted at artificial reefs and natural banks in the same region estimated that Red Snapper density was nearly eight times greater at artificial reefs (Streich et al. 2017). These previous studies relied on video-based surveys, which are generally less affected by gear saturation and may provide less-biased indices of abundance given adequate environmental conditions (e.g., visibility; Harvey et al. 2012; Ajemian et al. 2015b). Several studies have successfully paired traditional fishery sampling gear with visual- or video-based surveys to quantify gear bias and selectivity (Cappo et al. 2004; Harvey et al. 2012; Patterson et al. 2012; Bacheler et al. 2013; Robinson et al. 2015). Given the potential for gear saturation and other biases, a paired video-based survey that evaluates the efficacy of vertical line gear in estimating relative abundance among the habitats sampled here is warranted.
Although gear selectivity likely plays some role, the limited number of older fish (i.e., age > 10) in our study is likely attributable to ontogenetic changes in Red Snapper habitat selection (Allman et al. 2002; Mitchell et al. 2004; Allman and Fitzhugh 2007; Gallaway et al. 2009). Previous studies of Red Snapper growth have relied on other sampling means to obtain large fish, including tournaments that target larger individuals (Patterson et al. 2001; Fischer et al. 2004) or landings from the commercial fishery, where the longline sector selects for larger and older individuals (Schirripa and Legault 1999; Allman and Fitzhugh 2007). In addition, Red Snapper may rely less on structured “reef” habitat as they grow older, possibly spending more time over open, soft-bottom habitats as they reach a size refuge from predation (Gallaway et al. 2009). This hypothesized shift in habitat use is supported by an abundance of significantly older Red Snapper (median age = 12 years; range = 3–53 years) sampled during research longline surveys conducted away from structured habitats in the western GOM (Mitchell et al. 2004; Campbell et al. 2014) and may partially explain the decline in age frequencies for ages 7–9 observed in our study (Figure 3). Furthermore, in a hook size selectivity analysis by Campbell et al. (2014), 15/0 hooks on vertical lines fished at high-relief reef habitat captured significantly smaller Red Snapper than 15/0 hooks on bottom longlines fished over open mud bottom away from structured habitat. Thus, while the 15/0 hooks used in our study are certainly capable of capturing much larger Red Snapper, the lack of larger, older fish from vertical lines fished on high-relief reefs suggests that these larger fish are not prevalent on the habitats sampled in this study (Campbell et al. 2014). In addition, fishermen commonly target structured habitats like artificial reefs (Grossman et al. 1997; Garner and Patterson 2015; Schuett et al. 2016; Simard et al. 2016); therefore, another feasible explanation is that the structured habitats we sampled may not support as many older fish simply due to higher fishing mortality at structured habitats in comparison with open, soft-bottom habitats. It is also important to remember that GOM Red Snapper remain in an overfished state (SEDAR 2013; Calay et al. 2015) and only recently have habitat-specific (i.e., natural versus artificial habitats), fishery-independent comparisons of Red Snapper demographics been conducted (Saari 2011; Kulaw 2012; Glenn 2014; present study). As such, the “normal” age structure among these habitats is unknown. Our study represents the first attempt to describe the age structure among habitats in the western GOM, but continued monitoring will be required to assess how age structure changes among these habitats as the stock recovers.
Although habitat differences were the overarching focus of this study, our ancillary analysis of site-to-site differences in Red Snapper mean TL, TW, and age among sites revealed that Baker Bank supported conspicuously more larger and older fish than any of the other sites. Furthermore, most of those fish were age-6 or age-7 individuals from the 2007 year-class. Previous studies suggest that processes influencing Red Snapper year-class strength operate at large spatial scales, as strong year-classes are represented in fishery landings consistently among all regions of the GOM (Allman and Fitzhugh 2007; Saari et al. 2014). Our data displayed evidence of a strong 2009 year-class at all habitats, but the strong representation of the 2007 year-class was only observed at Baker Bank, which contributed significantly to the predominance of larger and older fish at natural banks compared to artificial reefs or standing platforms. Given the similarity in water quality data (thermocline presence and depth, DO, and salinity) and the proximity of all sites sampled in our study, this difference in year-class representation suggests that site-specific factors, such as fishing mortality and/or habitat area (i.e., footprint), are also important drivers of apparent year-class strength. For example, Baker Bank had the largest footprint of any site we sampled (1.33 km2 compared to 0.31–0.50 km2 at the other natural banks and <6.73 × 10–3 km2 at artificial reefs and standing platforms), which may effectively reduce fishing effort per unit area, thereby allowing greater survival to older ages. Furthermore, targeting of artificial reefs by fishermen (Garner and Patterson 2015; Simard et al. 2016) would also lead to decreased abundance of larger individuals at artificial habitats compared to the natural habitats sampled in this study. An alternative explanation could be that sites with a greater habitat area provide greater resources per capita (e.g., Frazer and Lindberg 1994), which would potentially support larger Red Snapper and could even be selected for by larger individuals (i.e., habitat selection). Clearly, additional studies similar to that of Strelcheck et al. (2005) are necessary to evaluate these hypotheses relating the effects of habitat size and habitat type on Red Snapper demographics.
We fitted four types of growth models to size-at-age data for Red Snapper from the three habitat types and found little support for either parameterization of the VBGM. Fitting multiple growth models to size-at-age data and selecting the best model via information-theoretic approaches have been recommended and are increasingly common in peer-reviewed literature, as the traditional VBGM may not always accurately represent size-at-age data (Katsanevakis 2006; Katsanevakis and Maravelias 2008; Gervelis and Natanson 2013; Ainsley et al. 2014; Natanson et al. 2014; Dippold et al. 2016). Our results suggest that the logistic model was the best in describing growth of Red Snapper among all habitats for both TL-at-age and TW-at-age data. Other studies of Red Snapper growth have used the VBGM, which may adequately fit size-at-age data, especially when older fish are present in the sample (Patterson et al. 2001; Wilson and Nieland 2001; Fischer et al. 2004). Few fish older than age 10 were sampled in this study (n = 5), and a different growth model may have been justified if a greater number of old Red Snapper had been sampled; however, given the data, use of the logistic model in our study was appropriate.
Logistic growth curves fitted to size-at-age data from each habitat suggested that growth at artificial reefs was different than growth at natural banks or standing platforms. Among TL-at-age and TW-at-age models, evidence suggested that larger estimates of asymptotic mean size (i.e., L∞ and W∞) at artificial reefs were driving the differences. Although Saari (2011) used the two-parameter VBGM to describe growth, some similar patterns in growth were observed among habitats. For example, estimates of L∞ and W∞ at natural banks were lowest, indicating that Red Snapper at natural banks reached smaller maximum sizes on average. In addition, lower estimates of t0 (i.e., the inflection point of the logistic curve) at natural banks and standing platforms in this study implied that the instantaneous growth rate was beginning to slow earlier at those two habitat types than at artificial reefs, potentially indicating earlier maturation at natural banks and standing platforms. Because few old fish were present in our samples, parameter estimates derived from our growth curves should be interpreted with some caution. In particular, asymptotic mean size may have been poorly estimated because fewer age-9 and age-10 individuals from each habitat were sampled. Estimates of L∞ and W∞ from all habitats were generally smaller than those estimated by Saari (2011); however, this pattern is consistent with previous findings that Red Snapper in the western GOM reach smaller mean asymptotic sizes than those from the northern GOM (Fischer et al. 2004; Saari et al. 2014). Nevertheless, confidence in the patterns we observed could be strengthened with additional samples that include a greater representation of old individuals.
Despite the putative differences in growth among habitats, predicted mean TL at age was similar throughout the range of ages compared (e.g., predicted mean TL at age 10 was only 40 mm greater at artificial reefs than at standing platforms or natural banks). Differences in predicted mean TW at age displayed a more significant divergence between artificial reefs and standing platforms or natural banks. As a demonstration, consider three average Red Snapper, each residing at one of the three habitats examined and weighing approximately 1.25 kg. The fish residing at an artificial reef would weigh approximately 3.54 kg by age 7, or about 0.5 kg heavier than its counterparts on a natural bank or standing platform. By age 10, the fish at the artificial reef would reach approximately 4.71 kg, nearly 1 kg heavier than the fish residing at the natural bank or standing platform. This example assumes that most fish display relatively long-term residency at a particular habitat type, an assumption that may have limited support based on the findings of previous studies (see review by Patterson 2007). For example, tag–recapture studies conducted off the Texas coast have found that 52% (Diamond et al. 2007) to 94% (Fable 1980) of tagged Red Snapper were recaptured at their original tagging location, although the mean time at liberty was only about 6 months. Diamond et al. (2007) reported that fish traveled an average distance of 9.8 km and up to 58.3 km, and Curtis (2014) reported that acoustically tagged individuals displayed movement distances of 2.7–13.1 km, which would potentially allow fish to move between sites in our study given the distances between sites (mean = 20.6 km, SD = 11.9; range = 2–52 km). Interestingly, Diamond et al. (2007) stated that fish moving from natural habitats tended to be recaptured at natural habitats, and likewise fish moving from artificial habitats tended to be recaptured at artificial habitats. Thus, while our example of habitat-specific growth is simplified and reliant on long-term residency at a particular habitat, it demonstrates the potential effects of habitat differences on Red Snapper growth.
Several factors, including gear selectivity, habitat size, and the fishery-independent nature of this study, undoubtedly influenced the growth curves that were derived for each habitat. Although we did not observe any differences in mean size or age as the sampling proceeded, hook size selectivity likely played a major role. For example, differences in mean TL and TL distributions of Red Snapper captured with the various hook sizes we used (8/0, 11/0, and 15/0) would almost certainly result in growth curves differing from curves derived based on data from commercial landings. This is especially true given that the commercial vertical line fleet primarily uses 8/0 and 9/0 hooks (63% of the fleet; Scott-Denton et al. 2011). Selectivity curves are broad for the hook sizes used here (Campbell et al. 2014), but commercial catch would almost certainly not represent the population of fish inhabiting these structures. Furthermore, both commercial and recreational fleets target artificial habitats (SEDAR 2013; Garner and Patterson 2015). As such, growth estimated from previous studies based on fishery landings may be biased due to habitat characteristics, such as the small size of artificial habitats and the associated high densities (and potential effects on growth) of Red Snapper at these habitats (Karnauskas et al. 2017). Current estimates of growth parameters used in the stock assessment are based on an average growth curve derived from fish captured at all habitats (but largely derived from artificial reefs due to the nature of the directed fisheries); however, Karnauskas et al. (2017) estimated that artificial reefs held less than 14% of the population across the northern GOM. Thus, the growth parameters currently used in the assessments may not be representative of a majority of the Red Snapper population. As such, the habitat-specific growth curves produced here can contribute to more reliable assessments of the GOM Red Snapper stock.
Collectively, our study indicates that Red Snapper size structure, age structure, and growth differ among habitats in the western GOM. These differences are perhaps not surprising given the disparate characteristics of each habitat type (e.g., footprint, relief, etc.) and documented differences in fish community structure between natural and artificial habitats across the GOM (Patterson et al. 2014; Streich et al. 2017). Nevertheless, these findings provide new insight into habitat-specific contributions to GOM Red Snapper stock productivity. For example, while growth appears to differ at artificial reefs (e.g., greater TW at age than was observed at standing platforms or natural banks), the effect of this difference is dependent upon associated reproductive potential. Reproductive potential is generally positively correlated with increasing size and age (Porch et al. 2007, 2015; Lowerre-Barbieri et al. 2015); therefore, if the observed increase in TW at age of Red Snapper at artificial reefs corresponds to increased reproductive potential compared to fish at natural banks or standing platforms, then artificial reefs may contribute more to stock-specific production on a per-unit-area basis. Similarly, the preponderance of larger, older individuals at natural habitats (especially Baker Bank) may indicate higher reproductive potential at natural habitats. Downey (2016) showed that gonadosomatic indices, spawning frequency, and batch fecundity were similar among the three habitats in our region; however, sample sizes were too low to statistically evaluate those variables by age. Nevertheless, Downey's (2016) findings hint that similar-aged fish have similar reproductive potential among the three habitats. These results would imply that RTR artificial reefs, standing platforms, and natural banks all contribute similarly to stock-specific production on a per-unit-area basis; however, the relative importance of each habitat to overall stock recovery and maintenance will depend on the distribution of fish at each habitat type (Pulliam 1988; Pulliam and Danielson 1991). Studies estimating Red Snapper abundance among habitats are limited, but some have demonstrated that absolute abundance is likely significantly greater on natural habitats simply due to their larger habitat area (Karnauskas et al. 2017; Streich et al. 2017). For example, Karnauskas et al. (2017) modeled the abundance and biomass of Red Snapper across the northern GOM based on fishery-independent vertical line and bottom longline surveys. Based upon sampling primarily conducted within the Alabama Artificial Reef Zone, they estimated that artificial reefs held less than 14% of the total Red Snapper abundance and contributed even less in terms of biomass and spawning potential due to a prevalence of younger individuals. Nevertheless, given the growth benefits we identified, our study suggests that artificial reefs can be valuable habitat for Red Snapper on a per-unit-area basis. Finally, although we provide the first comparison of habitat-specific growth of Red Snapper in the western GOM, our sampling universe was limited by several constraints commonly affecting field studies in fisheries, such as sampling time, distance of sites from port (74.1–111.1 km [40–60 nautical miles]), and other similar logistics. We recommend that future studies investigating habitat-specific differences in Red Snapper demographics pool resources to increase the spatial extent of the sampling area (i.e., more sites). This will lead to greater confidence in the resulting growth analyses and will help to refine our understanding of how different habitats contribute to the maintenance of the GOM Red Snapper stock.
ACKNOWLEDGMENTS
We thank the staff, students, and interns of the Center for Sportfish Science and Conservation for their help in sampling and processing Red Snapper. Staff at the Harte Research Institute for Gulf of Mexico Studies also contributed essential logistic support. We are grateful to the two anonymous reviewers, who provided constructive comments that significantly improved the manuscript. Funding for this research was provided by the TPWD Artificial Reef Program through interagency contract numbers 415254, 439195, and 474362. Further funding for this work was provided by the Marine Fisheries Initiative Program (Grant Number NA14NMF4330219).




