Proportionate spatial sampling and equal-time sampling of mobile animals: A dilemma for inferring areal dependence
Abstract
Abstract Patch or island area is one of the most frequently used variables for inference in conservation biology and biogeography, and is often used in ecological applications. Given that all of these disciplines deal with large spatial scales, exhaustive censusing is not often possible, especially when there are large numbers of patches (e.g. for replication and control purposes). Therefore, data for patches or islands are usually collected by sampling. We argue that if area is to be used as an inferential factor, then the objects under study (i.e. the patches) must be characterized on an areal basis. This necessarily means that fixed-area sampling is inadequate (e.g. a single standard quadrat or transect set within patches irrespective of the patch area) and that some form of area-proportionate sampling is needed (e.g. a fixed areal proportion of each patch is surveyed by random allocation of standard quadrats across each patch). However, use of area-proportionate sampling is not usually dissociated from the increased temporal intensity of sampling that arises from using this approach. The dilemma we see is deciding how much of the area-specificity of variables such as species richness, rare-species indices or probabilities of occurrence of individual species is related to the area-proportionate survey protocol and how much is due to the temporal intensity of surveys. We undertook a study in which we balanced temporal and spatial effects by increasing the time spent surveying smaller patches of vegetation to account for the area-ratio difference. The estimated species richness of birds of the box–ironbark system of central Victoria, Australia, was found to depend strongly upon area when area-proportionate sampling alone was performed. When time-balancing was imposed upon area-proportionate sampling, the differences between smaller (10-ha) and larger (40-ha) areas were much reduced or effectively disappeared. We show that species found in the additional surveys used to conduct the time-balancing were significantly less abundant than species recorded in area-proportionate sampling. This effect is probably most severe for mobile animals, but may emerge in other forms of sampling.
Introduction
In many problems in ecology, conservation biology and biogeography, workers wish to infer the effects of natural or anthropogenic processes within patches or ‘objects’ of different areas. When dealing with large-scale and long-time-frame situations, it is often not possible to census patches or islands fully. In lieu of censusing, by which we mean gathering ‘complete information’, sampling is necessary. If inferences are to be made about species richness or composition with respect to area (either as a single factor or as one of several factors), then how can sampling surveys be conducted to allow one to characterize the biota of patches or islands of possibly very different area?
A commonly used option is to have a standard sampling unit set within patches (read ‘patches and islands’ henceforth) irrespective of area (e.g. Major et al. 2001). This is a simple approach but one we do not favour. Our data from a series of studies in a variety of forest and woodland areas in Victoria, Australia (Mac Nally et al. 2000, 2001; Watson et al. 2000), show that a fixed-area, fixed-effort (i.e. same number of repeat surveys per sampling unit) approach will yield a similar species richness per sampling unit irrespective of areal context. That is, richness and species-accumulation functions in a standard sampling transect (in our case, 2 ha, for birds) are similar whether the transect is set within a 10-ha or an 80-ha fragment (see Fig. 1). These are empirical observations that are not necessarily theoretically predictable. Thus, we have little confidence that fixed-effort (especially through fixed-area) sampling will contain area-specific information.
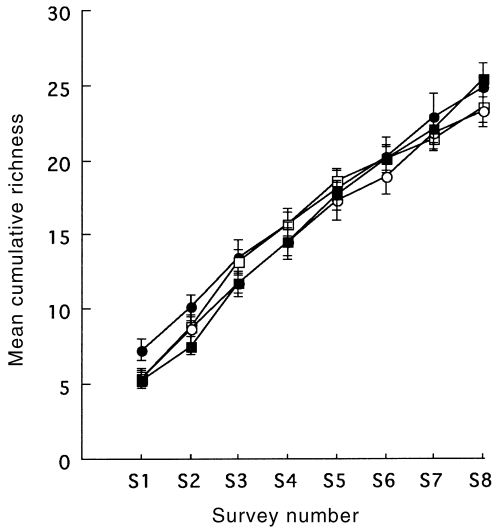
Mean species-accumulation curves as a function of sequential survey rounds for individual 2-ha transects set within forest fragments of different areas: (•), 10 ha (n = 15); (□), 20 ha (n = 20); (), 40 ha (n = 15); (□), 80 ha (n = 20). Error bars are standard errors. Source: Mac Nally et al. (2000).
Moreover, the characterization of the biota by using fixed effort will necessarily be poorer as the disparity between patches of different size increases. A single sampling unit (of fixed size) cannot characterize equally well the biotas of patches differing by an order or orders of magnitude. The more similar in area the sampling unit is to the area of the patch, the more complete will be the characterization. For example, a 2-ha patch should be well characterized by a 2-ha sampling transect, whereas a 10 000-ha patch would be very poorly characterized by a single 2-ha sampling transect.
In short, use of fixed effort in patches of different sizes produces information that is different from what one is normally interested in, namely, the overall richness and biotic composition of whole patches. The focus in fixed-area sampling is on the biota of locations of arbitrary sites (of a fixed area) within patches of different area rather than on the biota of the patches themselves in totality. It is difficult for us to conceive of many situations in which the former information is of much ecological or conservation use if area is a potential explanatory variable.
This raises the option of a scaled effort such that a fixed areal fraction of patches underlies the sampling regime. This is what we mean by ‘proportionate spatial sampling’. To characterize the biotas of different-sized patches, a number of randomly positioned sampling transects proportional to the relative areas would be used. However, relative areas of patches may differ by orders of magnitude. For example, Kitchener et al. (1982) studied birds in remnant patches of the Western Australian wheat-belt that ranged in size from 34 ha (North Yoting) to 7808 ha (Bendering). Given the practical impossibility of exhaustively censusing these areas (22 remnants totalling 26 940 ha), use of area-proportionate sampling suggests that 230 standard sampling units should have been used in Bendering for every one in North Yoting. Kitchener et al. (1982) were vague in describing their survey methods, asserting that they spent at least 5 days in each remnant and 10 days in ‘several of the larger remnants’. So, although there was an acknowledged implicit need for area-related sampling, its implementation was not systematic.
We believe in principle that area-proportionate sampling is needed to characterize the biotas of different-sized patches if area-specific inferences are to be drawn. In practice, there are two drawbacks. First, as just related, strict area-proportionate sampling may not be feasible in the context of systems of remnants or archipelagos of widely differing areas. More importantly from our perspective, given standardized methods (e.g. point-based, fixed-time counts, variable-width or constant-width transects, etc.; Burnham 1985; Recher 1989), area-proportionate sampling translates into a proportionately larger amount of time spent in larger patches than in smaller ones (e.g. 230 times as long in Bendering as in North Yoting). From experience, we believe that a longer time spent in any one location will elevate the likelihood of detecting rare (or secretive) species and hence generate an increased species richness. Therefore, a policy of using area-proportionate sampling, although needed to characterize systems of patches differing in area, may provide more chance of detecting rare species in a non-linear way. Preston (1962) highlighted this rare-species effect long ago.
The gist of the problem is that area-specific information requires area-specific surveying, yet this is not usually dissociated from a greater temporal investment in acquiring that area-specific information in larger areas; larger temporal investment will turn up more species irrespective of area surveyed. In other words, how much of the area-effect that we might find is a reflection of elevated survey times in larger patches? We emphasize again that this problem relates to situations in which area per se is part of the inference, and therefore that the ‘objects’ of interest are the whole fragments or islands under study. In this case, individual sampling quadrats or transects are of little interest in themselves and are merely vehicles for attempting to characterize the whole fragments or islands.
The present study is an exploration of how perceived species richness depends upon area-proportionate sampling and time-balancing. By time-balancing we mean adjusting a sampling programme underlain by area-proportionate sampling such that the total fraction of patches of different sizes surveyed is fixed but in such a way that equal amounts of time are spent surveying each patch. Therefore, if the larger and smaller patches differ by a factor A, then there are A times as many randomly positioned sampling units set within the larger patch than the smaller one. This represents area-proportionate sampling. To offset the time difference, each sampling unit in the smaller patch is surveyed A times as frequently as each sampling unit in the larger patch. Thus, spatial representativeness is considered and time imbalances are eliminated. Our analysis provides an indication of whether the problem we perceive is a severe one and, if it is, whether many existing results need to be re-evaluated for their susceptibility to unsupportable interpretations due to the space–time balancing effect. We also assess the likely generality of the effect and consider possible solutions to the problem.
Test arena
We probed the space–time dilemma by balancing amounts of time spent within different sized areas but by still conducting proportionate-area sampling in studies of avifaunas in central Victoria, Australia. Mac Nally et al. (2000) have reported on impacts of habitat fragmentation by using the reference area method of Bolger et al. (1991). Reference areas are notional virtual fragments (sensuWright et al. 1998) of comparable habitats to fragments but located within extensive habitat blocks. Reference areas are used in lieu of information on the prior biota of the actual fragments, for which data are rarely available. This is ‘space-for-time’ substitution.
Comparing different-sized fragments is confounded because of the expected species–area relationship. Therefore, to identify fragmentation-specific effects, comparisons are made not between different-sized fragments (10 ha, 20 ha etc.) but between same-sized fragments and reference areas, with an anticipation that these differences will become exaggerated in smaller units. In the current study, we contrast results obtained in 10-ha and 40-ha fragments and in 10-ha and 40-ha reference areas, where the latter are surveyed in the same way as fragments but are set within continuous forest blocks (>6000 ha; see Mac Nally et al. 2000). Fragments and reference areas are referred to generically as ‘units’.
Proportionate-areal sampling was achieved by using a fixed number of transects per unit area (i.e. one 2-ha transect per 10 ha), which were randomly positioned within units. Equal-time sampling was accomplished by repeatedly sampling the smaller units so that as many surveys were conducted in a unit as in any other unit irrespective of its area. The design is illustrated in Fig. 2. A 10-ha and a 40-ha unit are shown with the appropriate numbers of sampling transects in each. Indicated by arrows are numbers of surveys on each transect in any single sampling round, where at least several repeated rounds are conducted within a study. Notice the temporal interspersion of surveys within rounds (indicated by the order of the numerals) so that no temporally biased survey effects should occur. The adopted design mixes survey visits among all units (20 in all, see the Study areas section in the Methods) so there is little chance of bias.
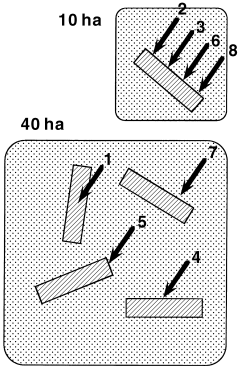
Schematic design of sampling design for 10- and 40-ha units. Each oblong represents a 2-ha transect. Each arrow indicates a survey, with the numbers indicating an instance of the visitation order for transects.
Our specific questions are:
- 1
To what extent are perceived species richness–area relationships of the avifaunas functions of temporal effects when proportionate-area sampling is used?
- 2
Are species detected in the second, third and fourth surveys in 10-ha units those expected to be more likely to be detected with greater sampling effort, that is, comparatively rare taxa?
Methods
Study areas
Forest and forest fragments set in the agricultural landscape of north-central Victoria, Australia, were used, which were within the former domain of the box–ironbark forest system. Box–ironbark forests occur on gentle slopes and hills (150–400 m a.s.l.) on the dry inland side of the Great Dividing Range of south-eastern Australia (ECC 1997). Mean annual rainfall ranges from 400 to 700 mm, with most falling during the cooler part of the year (May–September); summer months are generally hot and dry.
Fragments of approximately 10 ha (mean 10.6 ha ± 3.3 SD; n = 5), and approximately 40 ha (35.6 ± 8.2 SD; n = 5) were used (see Mac Nally et al. 2000 for details). All fragments were clearly spatially isolated in aerial photographic surveys from the mid-1960s, but obtaining photographs from earlier aerial surveys has proved problematic. However, consultation with land-holders indicated that the temporal isolation of fragments is of the order of 50–80 years. All fragments were <5 km from large (>6000-ha) tracts of native forest, and there was no significant difference in these distances between 10- and 40-ha fragments.
Reference areas were located within existing large tracts of box–ironbark forest in the vicinity of St Arnaud (143°20′E, 36°40′S), Dunolly (143°18′E, 36°51′S) and Rushworth (145°02′E, 36°38′S). In each block, a 1000-ha area of relatively uniform forest was found. A total of five 40-ha and five 10-ha reference areas were randomly positioned and orientated within the forest blocks. To reduce the potential impact of habitat variability, fragments and the large selection areas for reference sites, upon inspection, were thought to consist of ≥60% Grey Box, Eucalyptus microcarpa, by trunk basal area.
Fragments and reference areas were sampled by using standard, fixed-width transects. Each transect was 250 m × 80 m, or 2 ha in size. There was one such transect in a 10-ha area, and four in a 40-ha unit. To ensure representative coverage of each unit, the unit was divided into a number of equal areas corresponding to the number of transects to be positioned. Thus, there were four areas in a 40-ha unit and just one in a 10-ha unit. The centre-point and orientation with respect to north of the transect within each division were randomly assigned.
Bird surveys
All units were surveyed seven times between October 1996 and September 1998. The seven surveys were organized into ‘rounds’ in which all surveys in units were completed within a certain period. For all rounds, each of the four transects within the 40-ha units were surveyed once. To balance time spent in each unit size-class, all transects within 10-ha units were surveyed four times in each round. Thus, area-proportionate sampling (one 2-ha transect per 10 ha of area) and time-balancing (same total survey time per unit irrespective of area) were both accommodated in the design. There were 560 surveys and, given the design of the sampling, equal numbers of surveys in fragments and reference areas, and in 40- and 10-ha units.
All surveys were conducted by one observer only (G. Horrocks) to avoid possible interobserver variability (see Cunningham et al. 1999). The observer proceeded along the mid-line of the transect at near-constant pace (0.75 km h-1; hence 20 min per survey). Individual birds ahead of the observer on the transect were used for the analyses reported here. Surveys were not conducted if there were more than a light sprinkling of rain, in high wind or in high temperatures (>35°C).
To avoid possible systematic sampling biases due to observer fatigue or weather, a restricted random-visitation ordering for survey transects was used. The restricted approach was necessary because of the logistic demands of surveying a large region (approximately 9000 km2). Transects were partitioned into 12 geographical groupings consisting of approximately equal numbers of fragment and reference area transects. These groupings were visited in random order, as were transects within groupings and multiple visits to each 10-ha transect for the time-balanced sampling.
Relative abundances
We characterized the relative abundance of each species by finding the maximum recorded density (on any single occasion) on each of the 50 transects, summing these values, then scaling these sums according to the maximum value for any species. The latter was 458 (= 9.2 average maximum per transect) for the Musk Lorikeet, Glossopsitta concinna. The density index for this species was set to 100, and all other species' indices were divided by 4.58.
Analyses
- 1
For each 40-ha unit (i.e. fragment or reference area), total species richness over the course of the survey programme was determined. If a species occurred on any of the four transects in any of the seven rounds (28 surveys per 40-ha unit), it was classed as ‘present’. Species richness for the unit was the total number of presences.
- 2
For each 10-ha unit, only the first survey in each round was considered (only seven surveys per 10-ha unit). If a species occurred on the transect in any of the first surveys in any of the seven rounds, the species was classed as present. Again, species richness for the unit was the total number of presences.
- 3
For each 10-ha unit, all surveys in all rounds were considered. If a species occurred on the transect in any of these surveys (28 surveys per 10-ha unit), the species was classed as present. Species richness for the unit was the total number of presences.
Given that the data for the singly and multiply surveyed 10-ha units were not independent, we could not use any conventional parametric post-hoc means comparisons. Therefore, we used a randomization approach involving all 30 species-richness means (five each for the singly and multiply surveyed 10-ha and the 40-ha size-classes for real fragments and for reference areas). Two groups of five such means were randomly sampled (without replacement) from the 30 values and the absolute difference in means of the two groups was computed. This process was repeated 1000 times to produce a one-sided test for the difference among means of groups of five. The upper 5% confidence limit was treated as the critical difference for assessing statistical significance.
Asymptotic richness
We also used species-accumulation curves to make asymptotic estimates of species richness, R, using the nonlin modelling routine of systat (Wilkinson 1989). The following function was fitted:
R = R̂S/(S +R1/2)
where R is the observed richness for S survey rounds (S ∈ {1, 2,…, 7}), and R̂1/2 is the number of survey rounds needed to reach R̂/2 (see Mac Nally & Lake 1999). We used a number of plausible loss functions (e.g. least-squares, L1-norm, Poisson-based log-likelihood) and all gave similar results; data presented here are for the Poisson log-likelihoods and errors are mean absolute residuals.
Results
In the 560 surveys, 94 species of birds were recorded on the transects. Species noted most consistently (total numbers of occurrences in surveys rather than abundance per se) were: Red Wattlebird, Anthochaera curunculata (291 surveys = 52%); Yellow-tufted Honeyeater, Lichenostomus melanops (253); Fuscous Honeyeater, Lichenostomus fuscus (236); Striated Pardalote, Pardalotus striatus (234); Brown Treecreeper, Climacteris picumnus (233); Musk Lorikeet (225); and White-plumed Honeyeater, Lichenostomus penicillatus (208). Species encountered just once were: Crested Bellbird, Oreoica gutturalis; Horsfield's Bronze-cuckoo, Chrysococcyx basalis; Pallid Cuckoo, Cuculus pallidus; Sacred Kingfisher, Todiramphus sanctus; Western Gerygone, Gerygone fusca; White-eared Honeyeater, Lichenostomus leucotis; Australian Hobby, Falco longipennis; Pacific Black Duck, Anas superciliosa; Whistling Kite, Haliastur sphenurus; White-faced Heron, Egretta novaehollandiae; and White-fronted Chat, Epthianura albifrons. There was only a single record of an exotic species (Common Starling, Sturnus vulgaris), which was excluded from further consideration.
On a survey basis, 27 species were recorded significantly more frequently in transects located in fragments, whereas 16 species were more frequently found in reference areas (standard normal approximation, Z, to binomial test with p[probability of occurrence]=q[probability of absence]= 0.5). The most extreme ‘fragment specialists’ (ranked by Z-score) were: White-plumed Honeyeater (98% of recorded surveys in fragments; 208 survey records for this species); Noisy Miner, Manorina melanocephala (100%; 134); Red-rumped Parrot, Psephotus haematonotus (97%; 110); Australian Magpie, Gymnorhina tibicen (96%; 113); Willie Wagtail, Rhipidura leucophrys (95%; 92); Little Raven, Corvus mellori (93%; 42); Galah, Cacatua roseicapilla (74%; 134); Welcome Swallow, Hirundo neoxena (97%; 32); Laughing Kookaburra, Dacelo novaeguineae (96%; 24); Striated Pardalote (62%; 234); and Australian Magpie-lark, Grallina cyanoleuca (100%; 14). Species apparently preferring large forest blocks were: Fuscous Honeyeater (89% of records in reference areas; 236 survey records for this species); Yellow-tufted Honeyeater (77%; 253); Brown-headed Honeyeater, Melithreptus brevirostris (92%; 52); Spotted Pardalote, Pardalotus punctatus (81%; 68); Black-chinned Honeyeater, Melithreptus gularis (77%; 79); Grey Currawong, Strepera versicolor (100%; 18); White-throated Treecreeper, Cormobates leucophaeus (100%; 18); Little Lorikeet, Glossopsitta pusilla (77%; 40); Painted Button-quail, Turnix varia (100%; 11); Buff-rumped Thornbill, Acanthiza reguloides (83%; 23); White-naped Honeyeater, Melithreptus lunatus (68%; 59); Scarlet Robin, Petroica multicolor (100%; 7) and Weebill, Smicrornis brevirostris (66%; 67).
Mean species richness
The results of the randomization procedure yielded a mean absolute difference among groups of five values of 4.4 species. The upper 5% limit was 10.2. Therefore, any difference in means exceeding 10.2 was regarded as statistically significant.
There was no significant difference in mean species richness between the 10-ha fragments and the 10-ha reference areas when each was surveyed only once per round (Table 1, Fig. 3). The means differed by 2.2 species (Table 1). Similarly, the mean species richness for the 40-ha fragments was similar to that of the 40-ha reference areas, differing by just 4.4 species (Table 1, Fig. 3).
| Fragment | Reference area | ||||
|---|---|---|---|---|---|
| 10 ha (4) | 40 ha | 10 ha (1) | 10 ha (4) | 40 ha | |
| Fragments | |||||
| 10 ha (1) | 7.8 | 15.8* | 2.2 | 10.8* | 11.4* |
| 10 ha (4) | – | 8.0 | 10.0 | 3.0 | 3.6 |
| 40 ha | – | 18.0* | 5.0 | 4.4 | |
| Reference area | |||||
| 10 ha (1) | – | 13.0* | 13.6* | ||
| 10 ha (4) | – | 0.6 | |||
| 40 ha | – | ||||
- Entries are differences of means (see Fig. 3); *significant difference (viz. > 10.2, the upper 5% value derived from 1000 randomizations).
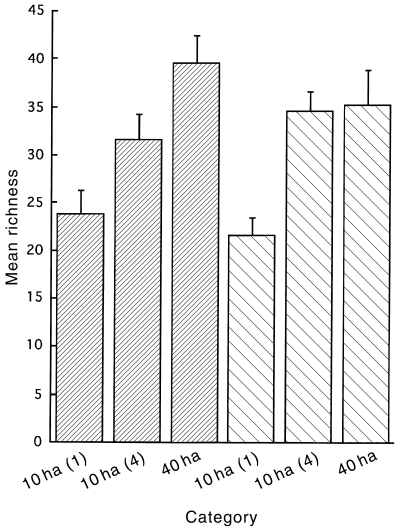
Mean (±SE, n = 5) observed species richness for () fragments and () reference areas. Columns in each set are: singly surveyed 10-ha units, multiply (four) surveyed 10-ha units and 40-ha units.
The mean richness for single-survey 10-ha fragments was significantly less than that for the 40-ha fragments (15.8 species; Table 1). A similar situation held for reference areas (13.6 species; Table 1).
In fragments, greater time spent in multiply surveying the 10-ha fragments led to elevation of mean species richness, although the increase was not significant (7.8 species; Fig. 3). Means also did not differ significantly between the 10-ha and 40-ha fragment classes (8.0 species). In reference areas (Fig. 3), the mean for multiply sampled 10-ha reference areas was essentially the same as for 40-ha reference areas (0.6 species) and was significantly elevated above the mean for the singly sampled 10-ha reference areas (13.0 species).
Species found only in multiple surveys
Fragments
In 10-ha fragments, 44 species were found in first surveys in any of the rounds across the five fragments, which would correspond to the species detected if a standard, area-specific survey effort were carried out. Twelve species were detected in the subsequent second, third or fourth surveys only (in any of the rounds), which would have been detected only if time-balancing were taken into account. Based on the abundance indices described (Relative abundances section in the Methods), the species found in first surveys were significantly more abundant than those found only in subsequent surveys (mean density indices: 18.4 ± 21.0 SDvs 3.3 ± 5.6 SD; standard-normal variate corresponding to Mann–Whitney U = 3.53, P < 0.001).
Reference areas
In the 10-ha reference areas, 44 species were also detected in first surveys in any of the rounds across the five reference areas. Eighteen species were found only in the subsequent second, third or fourth surveys only (in any of the rounds). The species found in first surveys were significantly more abundant than those found only in subsequent surveys (mean density indices: 17.7 ± 21.0 SDvs 5.4 ± 11.1 SD; standard-normal variate corresponding to Mann–Whitney U = 4.05, P < 0.0001).
Of the 27 species found in the subsequent surveys in either fragments or reference areas, the mean density index was 4.5 ± 9.7 SD. The only relatively common species in the list was the White-browed Woodswallow, Artamus superciliosus (index = 46.7). Twenty species (74%) had indices <3. The mean index of the other 67 species was 12.5 ± 18.8 SD, with 28 (42%) species having indices <3. Significantly fewer species recorded in first surveys had indices <3 compared with species recorded in subsequent surveys (χ2 = 8.3, 1 d.f., P < 0.01).
Asymptotic richness estimates
The accumulation curve for multiply surveyed 10-ha fragments falls almost midway between the curves for 40-ha fragments and for singly surveyed 10-ha fragments (Fig. 4a). The curves for multiply surveyed 10-ha and for 40-ha reference areas are virtually identical, with both positioned well above the curve for singly surveyed 10-ha reference areas (Fig. 4b). In all cases, species saturation does not seem to have been reached.

Mean (±SE, n = 5) species-richness accumulation curves for (a) fragments and (b) reference areas. (•), 40-ha units; (), multiply sampled 10-ha units; (□), singly sampled 10-ha units.
Values of asymptotic richness estimates, R̂, were: 31.9 ± 0.3 (singly surveyed 10-ha fragments, error is mean absolute deviation), 37.3 ± 0.5 (multiply surveyed 10-ha fragments), 50.5 ± 0.4 (40-ha fragments), 35.4 ± 0.2 (singly surveyed 10-ha reference areas), 45.6 ± 0.6 (multiply surveyed 10-ha reference areas) and 46.3 ± 0.5 (40-ha reference areas). Thus, even with identical sampling schemes, comparisons of avifaunas of different areas would not be consistent between fragments and reference areas. There appears to be a substantial real difference in mean richness between 10- and 40-ha fragments, but that difference is much exaggerated by adopting a proportionate-area survey scheme without time-balancing (i.e. mean deduced difference [area-proportionate] of (50.5 − 31.9) = 18.6 ± 0.7 species vs (50.5 − 37.3) = 13.2 ± 1.0 species [with time-balancing]). In reference areas, the dependence of species richness on area appears to be entirely due to the time differential (i.e. mean deduced difference [area-proportionate] of (46.3 − 35.4) = 10.9 ± 0.6 species vs (46.3 − 45.6) = 0.7 ± 1.1 species [with time-balancing]).
The value of R1/2 (the number of surveys at which R̂/2 is reached) was 4.7 for singly surveyed 10-ha reference areas, but just 2.5 for singly surveyed 10-ha fragments, which is the greatest of all other curves. This indicates that species accumulation in singly surveyed 10-ha reference areas is much slower as a function of numbers of surveys conducted than for any of the other curves.
Discussion
This paper is directed at the issue of sampling in ecological problems in which the area of patches (or islands) is to be used as a, or one of several, potential explanatory variables. Therefore, if full censusing is possible on objects of different areas (e.g. Peake & Quinn 1993; Douglas & Lake 1994), then this is not a difficulty in this context. If area per se is not to be included as a potential explanatory factor, then there is no problem here either. But if area is to be used as a predictor and patches cannot be censused, then the patches must be adequately characterized with respect to area. This is not a statistical issue per se but a data quality issue. Although great strides have been made in statistical design/analysis over the past 30 years in ecology and related disciplines (replication, controls, power, avoiding ‘pseudoreplication’ etc.), much less attention has been paid to the quality of data obtained. Patch area is intimately connected to the spatial scale of observation, which has emerged as an important consideration in recent decades (Kotliar & Wiens 1990; Holling 1992; Levin 1992, 2000). The impact of scale on data quality in experimentation and surveying is attracting increasing notice (Carpenter 1996; Mac Nally 1997, 2000, 2001).
The question is: how can this area-specific, ‘adequate characterization’ be carried out? We are confident that fixed-area/effort surveying in patches of different area will not encapsulate area-specific information, based on our empirical measurements of avian richness in forests and woodlands (Fig. 1); it would be illuminating to see whether other workers find similar results with mobile animals, especially birds. Intuitively, an area-proportionate sampling programme with random positioning of sampling units should provide such area-specific information, which is not dissimilar in rationale to the random stratified sampling used extensively in ecological research.
However, area-proportionate sampling also introduces a time imbalance, with more survey units in larger patches and, using standardized survey methods, longer times spent surveying those patches. The sampling dilemma that we perceive relates to the need on the one hand to conduct patch-area-proportionate sampling to produce patch-area-specific information on richness and species composition, and on the other hand balancing the amounts of time spent in conducting area-proportionate sampling. The latter is a problem because there is likely to be a non-linear relationship between the likelihood of detecting a given rare species and the amount of time spent in survey. Such a relationship has been documented for reptiles in the same box–ironbark system of central Victoria, Australia, as was used in the present study (Mac Nally & Brown 2001).
In the current study, differences in mean richness between 10- and 40-ha units, which were significant under proportionate-area sampling (one transect per 10 ha), dissipated when time-bias was eliminated by multiply surveying 10-ha units. The same effect was found in fragments set within agricultural landscapes and in ‘reference areas’ within continuous large forest blocks. Moreover, just the kinds of species that one might expect to contribute to such a time-based problem were more likely to be recorded with multiple surveying: relatively non-abundant taxa. Boulinier et al. (1998) have illustrated how differences in detectability among species influence species-richness estimates. Different abundances clearly contribute to differences in detectability, along with differences in behavioural overtness or secretiveness and mobility and range of movement.
Generality of the phenomenon?
The time aspect has a profound impact as illustrated in our study system. How general might this effect be? First, the taxa involved in this study, woodland birds, are among the most mobile organisms and outcomes may reflect effects relatively specific to birds. Unlike most organisms, many birds can traverse relatively large distances (104−106 body lengths) in short times (<1 week). Thus, some species may have not been ‘missed’ in the first surveys in 10-ha units as such but rather may have ‘arrived’ between the first and subsequent surveys. Such an effect would be unlikely in most reptiles or arboreal mammals (Deacon & Mac Nally 1998; Mac Nally & Brown 2001), in which mobility is much less than that in birds. It is potentially a problem for other mobile animals such as bats (Bennett et al. 1998), butterflies (Haddad 1999) and some fishes (Vadas & Orth 1993; Chapman & Kramer 2000).
Although this ‘arrival’ phenomenon may be a factor, we think that carefully conducted surveys on specified sampling units does involve considerable loss of information concerning the presence of species in particular units. Our data for on- and off-transect records show that, in some cases, as many species are recorded off-transect as on (Mac Nally & Watson 1997). It is often frustrating ‘knowing’ certain species are present yet being unable to count these in statistical comparisons because this will violate comparability and introduce bias. Many of the bird species recorded off-transect have relatively piercing or far-carrying calls; their inclusion would clearly introduce a bias against species with less strident voices.
Second, the range of areas involved in our example is small, up to just 40 ha. It is possible that this happens to be a critical range in which the space–time effect is most pronounced for woodland birds. Presumably, area-proportionate sampling in very large areas would produce a representative picture of the avifauna for those units, whereas time-balanced sampling in small areas would not produce a comparably large richness. In the Western Australian wheat-belt example, there is a 230-fold difference between the largest and smallest units. Even if time-balancing were used in conjunction with area-proportionate sampling among units, it is virtually impossible that the species richness of the 34-ha North Yoting and 7808-ha Bendering remnants would converge as in our example. However, this may be of little comfort to conservation ecologists because typical remnant areas in many fragmented landscapes are <100 ha (Bennett 1990, 1992a, 1992b; Bolger et al. 1991; Harris & Silva-Lopez 1992; Holl et al. 1993; Barrett et al. 1994; Daily & Ehrlich 1995; Forman 1995; Bender et al. 1998; Bennett et al. 1998; Trzcinski et al. 1999; Watson et al. 2000).
Asymptotic species-richness estimators
If species richness were the only variable of interest, then there may be a temptation to rely on asymptotic richness estimates to deal with the area specificity. There has been a steady stream of proposals for sampling-based, asymptotic species-richness estimators over the past 20 years (Bunge & Fitzpatrick 1993; Colwell & Coddington 1994; Dawson et al. 1995; Nichols & Conroy 1996; Gimaretcarpentier et al. 1998; Nichols et al. 1998). Many of the estimators depend upon numbers of rare species in ‘collections’, such as species recorded just once or twice. Many also do not require that surveys be conducted in such a way that patches are representatively sampled in a spatial sense. Thus, in principle, one could set up a station in the middle of a 20 000-ha patch and record just those individual animals that passed by that station (say, within 10 ha), which would hardly characterize the patch.
Our results for the asymptotic species-accumulation curve fitting relate to functional differences between fragments and reference areas. In the latter, there should be few impediments to most species passing through any given 10-ha sampling area. Given sufficient time, the number of species identified should converge to that found for larger areas, at least up to a point. In fragments, many species are unlikely to reach or persist in smaller plots, whereas larger areas probably support or attract more species.
In conservation applications, species richness may not be the only consideration. Workers often wish to model the occurrence of individual taxa as a function of area and other landscape and patch attributes, or attempt to distinguish compositional differences of biotas of different kinds (i.e. different vegetation communities or sites subject to different land-use pressures, for example Major et al. 2001). The problem of adequate characterization is much more profound in these applications because composition of biotas entails much higher level information than species richness per se.
Possible solutions to the dilemma
Our main purpose here is to alert ecologists to this sampling dilemma, and especially to generate thinking about how to address the problem. One solution may be to balance total survey time yet maintain the area-proportionate methodology. In the current study, this might be achieved by maintaining the ‘2 ha per 10 ha’ area-proportionate sampling rule (hence one transect for 10-ha units and four for 40-ha units) but alter the timing of surveys such that the single 2-ha transect in the 10-ha unit takes four times longer than each transect in the 40-ha unit. Each of the standard surveys took 20 min, which means that under the revised scheme the transects within the 10-ha units would take 80 min (at a snail's pace of 0.188 km h-1!). Similar protocols could be used if point-based methods were used: the number of points proportional to area and total time spent on any one point count adjusted to satisfy time balancing. We recognize that this is also a stop-gap solution because the range of patch, fragment or insular areas in many studies covers a great spread. In the Western Australian wheat-belt example, we noted that the area ratio of the largest and smallest remnants is 230. It seems difficult to see how a representative sampling scheme could be enacted in this situation that would also take time-balancing into account.
Two other approaches may be useful: (i) asymptotic modelling; and (ii) Monte Carlo simulation. We have outlined an example of asymptotic modelling in the previous section, where repeated sampling is used to develop asymptotic estimates of probable species richness at particular scales. These estimates can then be used to interpret effects of ecological processes or of human impacts. These are probably of little use for species-composition applications.
It may be more generally fruitful to develop iterative Monte Carlo procedures that would be tailored to specific situations. A possible route may be to use space-for-time substitution on replicates of like units. For example, Mac Nally et al. (2000) used 15 10-ha fragments. Data for a first round of surveys for these units (a ‘pilot’ survey-programme) could be used to estimate parameters for density distributions of species observed in these 15 surveys, which may often be of a Poisson form. These data could be used collectively to develop projected species complements of any one of the units, assuming the units are ‘replicates’ of the treatment in question (e.g. 10-ha fragments) and have similar expected sampling distributions. It would then be possible to randomly resample thousands of times from these observed and projected distributions with differing numbers of simulated survey rounds to estimate how many surveys would be needed for well-defined asymptotic estimates of species richness in any single unit and for having a given level of confidence in detecting a particular species if it were present. One obvious limitation is the seasonality of many avian species, which would make selection of the time of the initial sampling round critical. Such a scheme could be continually updated with each completed survey round so that better estimates of required numbers of surveys per site could be computed.
Acknowledgements
We gratefully acknowledge the support of the Australian Research Council (Large Grant No. A19531268 to R. Mac Nally and A. F. Bennett) and an Australian Research Council Small Grants Scheme grant to R. Mac Nally. The following people provided important input by commenting on earlier drafts of this manuscript or by suggesting improvements to certain aspects of the work, for which we are most grateful: Andrew Bennett, Nick Bond and Sam Lake; comments by anonymous referees provoked important clarifications in this manuscript.




