Analysis of cosmic microwave background data on an incomplete sky
Corresponding Author
Daniel J. Mortlock
1 Astrophysics Group, Cavendish Laboratory, Madingley Road, Cambridge CB3 0HE
2 Institute of Astronomy, Madingley Road, Cambridge CB3 0HA
Search for more papers by this authorCorresponding Author
Anthony D. Challinor
1 Astrophysics Group, Cavendish Laboratory, Madingley Road, Cambridge CB3 0HE
Search for more papers by this authorCorresponding Author
Michael P. Hobson
1 Astrophysics Group, Cavendish Laboratory, Madingley Road, Cambridge CB3 0HE
Search for more papers by this authorCorresponding Author
Daniel J. Mortlock
1 Astrophysics Group, Cavendish Laboratory, Madingley Road, Cambridge CB3 0HE
2 Institute of Astronomy, Madingley Road, Cambridge CB3 0HA
Search for more papers by this authorCorresponding Author
Anthony D. Challinor
1 Astrophysics Group, Cavendish Laboratory, Madingley Road, Cambridge CB3 0HE
Search for more papers by this authorCorresponding Author
Michael P. Hobson
1 Astrophysics Group, Cavendish Laboratory, Madingley Road, Cambridge CB3 0HE
Search for more papers by this author1 The condition number of a matrix is (the absolute value of) the ratio of its greatest and smallest eigenvalues; it is large for ill-conditioned matrices, and infinite for singular matrices.
2 Here I˜ is the i′max×i′max identity matrix, as distinct from the (potentially larger) imax×imax identity matrix, I.
3 If M is diagonal then the notation M±1/2 is used here to denote the matrix defined by , where δi,j is the Kronecker delta function. Thus M1/2 only exists if the diagonal elements of M are non-negative and M−1/2 only exists if the diagonal elements of M are strictly positive.
4 The definition of B given in Section 2.2 implies that [(AB)T]2=(AB)T and it is hence a projection operator if lmax→∞.
5 This definition, with the (−1)m term, correpsonds to that given by Abramowitz & Stegun (1971) and Gradshteyn & Ryzhik (2000) but differs from that used by Arfken (1985) and Brink & Satchler (1993).
6 A band-limited function can, by (somewhat circular) definition, be constructed from a finite sum over spherical harmonics.
Abstract
Measurement of the angular power spectrum of the cosmic microwave background is most often based on a spherical harmonic analysis of the observed temperature anisotropies. Even if all-sky maps are obtained, however, it is likely that the region around the Galactic plane will have to be removed as a result of its strong microwave emissions. The spherical harmonics are not orthogonal on the cut sky, but an orthonormal basis set can be constructed from a linear combination of the original functions. Previous implementations of this technique, based on Gram–Schmidt orthogonalization, were limited to maximum Legendre multipoles of lmax≲50, as they required all the modes have appreciable support on the cut-sky, whereas for large lmax the fraction of modes supported is equal to the fractional area of the region retained. This problem is solved by using a singular value decomposition to remove the poorly supported basis functions, although the treatment of the non-cosmological monopole and dipole modes necessarily becomes more complicated. A further difficulty is posed by computational limitations – orthogonalization for a general cut requires
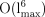 operations and
operations and
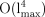 storage and so is impractical for
lmax≳200 at present. These problems are circumvented for the special case of constant (Galactic) latitude cuts, for which the storage requirements scale as
storage and so is impractical for
lmax≳200 at present. These problems are circumvented for the special case of constant (Galactic) latitude cuts, for which the storage requirements scale as
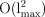 and the operations count scales as
and the operations count scales as
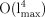 . Less clear, however, is the stage of the data analysis at which the cut is best applied. As convolution is ill-defined on the incomplete sphere, beam-deconvolution should not be performed after the cut and, if all-sky component separation is as successful as simulations indicate, the Galactic plane should probably be removed immediately prior to power spectrum estimation.
. Less clear, however, is the stage of the data analysis at which the cut is best applied. As convolution is ill-defined on the incomplete sphere, beam-deconvolution should not be performed after the cut and, if all-sky component separation is as successful as simulations indicate, the Galactic plane should probably be removed immediately prior to power spectrum estimation.
Acknowledgments
- 1 Abramowitz M., Stegun I. A., 1971, Handbook of Mathematical Functions. 9th ed Dover Publications, New York
- 2 Anderson E. et al., 1992, Lapack User's Guide. Soc. for Indust. and App. Math., Philadelphia
- 3 Arfken G., 1985, Mathematical Methods for Physicists. 3rd edn Academic Press, Boston
- 4
Baccigalupi C. et al., 2000, MNRAS, 318, 769
10.1046/j.1365-8711.2000.03751.x Google Scholar
- 5 Barreiro R. B., 2000, New Astron Rev., 44, 179
- 6 Bennett C. L. et al., 1992, ApJ, 396, L7
- 7 Bersanelli M. et al., 1996, COBRAS/SAMBA, The Phase A Study for an ESA M3 Mission. ESA Report D/SCI(96)3
- 8
Birkinshaw M., 1999, Phys. Rep., 310, 97
10.1016/S0370-1573(98)00080-5 Google Scholar
- 9 Bond J. R., Jaffe A. H., Knox L., 1998, Phys. Rev. D, 57, 2117
- 10 Borrill J., 1999, in L. Maiani, F. Mechiorri, N. Vittorio, eds, 3K Cosmology: EC-TMR Conference. Am. Inst. Phys., New York, p. 277
- 11 Brink D. M., Satchler G. R., 1993, Angular Momentum. 3rd edn Clarendon Press, Oxford
- 12 Bouchet F. R., Gispert R., 1999, New Astron., 4, 443
- 13 Challinor A. D., Mortlock D. J., Van Leeuwen F., Lasenby A. N., Hobson M. P., Ashdown M. A. J., Efstathiou G. P., 2002, MNRAS, submitted
- 14 Coble K. et al., 1999, ApJ, 519, L5
- 15 De Bernardis P. et al., 2000, Nat, 404, 955
- 16 Delabrouille J., 1998, A&AS, 127, 555
- 17 De Oliveira-Costa A., Kogut A., Devline M. J., Netterfield C. B., Page L. A., Wollack E. J., 1997, ApJ, 482, L17
- 18 Efstathiou G., Bridle S. L., Lasenby A. N., Hobson M. P., Ellis R. S., 1999, MNRAS, 303, L47DOI: 10.1046/j.1365-8711.1999.02433.x
- 19 Golub G. H., Van Loan C. F., 1996, Matrix Computations. 3rd edn The Johns Hopkins Univ. Press, Baltimore
- 20 Górski K. M., 1994, ApJ, 430, L85
- 21 Górski K. M. et al., 1994, ApJ, 430, L89
- 22 Gradshteyn I. S., Ryzhik I. M., 2000, Table of Integrals, Series and Products. 6th ed. Academic Press, New York
- 23 Halverson N. W. et al., 2002, ApJ, submitted
- 24 Haslam C. G. T., Klein U., Salter C. J., Stoffel H., Wilson W. E., Cleary M. N., Cooke D. J., Thomasson P., 1982, A&A, 100, 209
- 25 Hivon E., Górski K. M., Netterfield C. B., Crill B. P., Prunet S., Hansen F., 2002, ApJ, submitted
- 26 Hobson M. P., Magueijo J., 1996, MNRAS, 283, 1133
- 27 Hobson M. P., Jones A. W., Lasenby A. N., Bouchet F. R., 1998, MNRAS, 300, 1DOI: 10.1046/j.1365-8711.1998.01777.x
- Hu et al. HuW.SugiyamaN.SilkJ.Nat 386 37
- Jarosik et al. 1998 JarosikN.et al. T. Trân Tranh Vân Y. Giraud-Héraud F. Bouchet T. Damour Y. Mellier Fundamental Parameters in Cosmology1998 249Editions FrontieresParis
- 30 Jones A. W., Hobson M. P., Lasenby A. N., 1999, MNRAS, 305, 898DOI: 10.1046/j.1365-8711.1999.02467.x
- 31 Knox L., 1995, Phys. Rev. D, 52, 4307
- 32 Landau L. D., Lifshitz E. M., 1975, Quantum Mechanics. Pergamon Press, Oxford
- 33 Lee A. T. et al., 2001, ApJ, 561, L1
- 34 Lewis A. M., Challinor A. D., Turok N. G., 2001, Phys. Rev. D, submitted
- 35 Linde A., 1990, Particle Physics and Inflationary Cosmology. Harwood Academic Publishers, Dubbo
- 36 Lineweaver C. H., 1998, ApJ, 505, L69
- 37 Maino D. et al., 1999, A&AS, 140, 383
- 38 Natoli P., De Gasperis G., Gheller C., Vittorio N., 2001, A&A, 372, 346
- 39 Netterfield C. B., Devlin M. J., Jarosik N., Page L., Wollack E. J., 1997, ApJ, 474, 47
- 40 Netterfield C. B. et al., 2002, ApJ, submitted
- 41 Oh S. P., Spergel D. N., Hinshaw G., 1999, ApJ, 510, 551
- 42 Padin S. et al., 2001, ApJ, 549, L1
- 43 Press W. H., Teukolsky S. A., Vetterling W. T., Flannery B. P., 1992, Numerical Recipes: The Art of Scientific Computing. 2nd edn Cambridge Univ. Press, Cambridge
- 44 Prunet S., Teyssier R., Scully S. T., Bouchet F. R., Gispert R., 2001, A&A, 374, 358
- 45 Schlegel D., Finkbinder D., Davies M., 1998, ApJ, 500, 525
- 46
Scott P. F. et al., 1996, ApJ, 461, L1
10.1086/310000 Google Scholar
- 47 Smoot G. F. et al., 1992, ApJ, 396, L1
- 48 Stolyarov V., Hobson M. P., Ashdown M. A. J., Lasenby A. N., 2002, MNRAS, submitted
- 49 Sunyaev R. A., Zel'dovich Y. B., 1970, AP&SS, 7, 3
- 50 Szapudi I., Prunet S., Pogosyan D., Szalay A. S., Bond J. R., 2001, ApJ, 548, 115
- 51 Tanaka S. T. et al., 1996, ApJ, 468, L81
- 52 Tegmark M., 1997, Phys. Rev. D, 56, 4514DOI: 10.1103/physrevd.56.4514
- 53 Tegmark M., Efstathiou G. P., 1996, MNRAS, 281, 1297
- 54 Toffolatti L., Argüeso Gómez F., De Zotti G., Mazzei P., Francheschini A., Danese L., Burigana C., 1998, MNRAS, 297, 117DOI: 10.1046/j.1365-8711.1998.01458.x
- 55 Van Leeuwen F. et al., 2001, MNRAS, submitted
- 56 Varshalovich D. A., Moskalev A. N., Khersonskii V. K., 1988, Quantum Theory of Angular Momentum. World Scientific, Singapore
- 57 Wandelt B. D., Górski K. M., 2001, Phys. Rev. D, 63, 123002DOI: 10.1103/physrevd.63.123002
- 58 Wandelt B. D., Hivon E., Górski K. M., 2001, Phys. Rev. D, 64, 083003
- 59 Wang X., Tegmark M., Zaldarriaga M., 2002, Phys. Rev. D, submitted
- 60 Wilson G. W. et al., 2000, ApJ, 532, 57
- 61 Wright E. L., Hinshaw G., Bennett C. L., 1996, ApJ, 458, L53
This paper benefited from useful discussions with several members of the Planck collaboration, in particular Mark Ashdown, Franc¸ois Bouchet, Martin Bucher, Rob Crittenden, Jacques Delabrouille, George Efstathiou, Krzysztof Górski, Floor van Leeuwen and Ben Wandelt. DJM was funded by PPARC. ADC acknowledges a PPARC Postdoctoral Research Fellowship. MPH acknowledges a PPARC Advanced Fellowship.
Appendix A: Spherical harmonics
Appendix A: Spherical harmonics
The spherical harmonics form a complete set of orthonormal basis functions over the entire sphere. They are most commonly defined as complex functions (e.g. Landau & Lifshitz 1976; Brink & Satchler 1993), but it is more convenient to use real harmonics in this application. Adapting the notation of Górski (1994), the real spherical harmonics are given by
Yl,m(r^)=Yl,m(θ,φ)=λl,|m|[cos(θ)]sm(φ),
((A1))where l≥0 and |m|≤l and
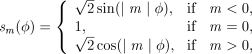 ((A2))
((A2))implying that  . For
0≤m≤l and
−1≤x≤1 the normalized associated Legendre functions are defined by
. For
0≤m≤l and
−1≤x≤1 the normalized associated Legendre functions are defined by
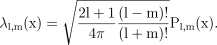 ((A3))
((A3))Hence 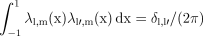 . Under the same conditions the (unnormalized) associated Legendre functions are given by5
. Under the same conditions the (unnormalized) associated Legendre functions are given by5
 ((A4))
((A4))with the Legendre polynomials given by
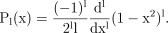 ((A5))
((A5))A real field on the sphere, a(r^), can be expanded in terms of spherical harmonic coefficients, given by
al,m=∫SYl,m(r^)a(r^) dΩ.
((A6))This can be inverted to give
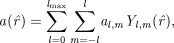 ((A7))
((A7))provided that lmax→∞, due to the orthonormality of the spherical harmonics on the full sphere:
∫SYl,m(r^)Yl′,m′(r^) dΩ=δl,l′δm,m′.
((A8))If a finite lmax is used this inversion is no longer possible for general a(r^), although it does still hold for band-limited functions.6
Whilst the two indices l and m have quite distinct interpretations, it is convenient to combine them into a single index, i, which allows the definition of vectors Y(r^)=Yi(l,m)(r^) and a=ai(l,m). Two obvious indexing schemes present themselves: grouping in l and m. The first, as introduced by Górski (1994), is natural for power spectrum estimation and very simple:
i(l,m)=l2+l+m+1.
((A9))The two ‘inverses’ of this relationship are
l=int[(i−1)1/2]
((A10))and
m=i−(l2+l+1).
((A11))The second choice of ordering is useful in cases of azimuthal symmetry in which the orthogonality expressed in equation (A2) is maintained, and grouping in m is achieved by defining
 ((A12))
((A12))The ‘inverses’ in this case are given by
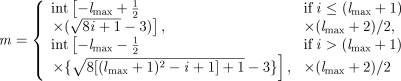 ((A13))
((A13))and
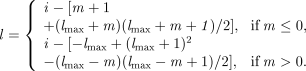 ((A14))
((A14))Other indexing schemes have been used in the more specific case of simulated Planck data-sets in which the sky coverage is periodic in azimuth (van Leeuwen, private communication), but are beyond the scope of this paper.
Appendix B: Integration of products of associated Legendre functions
In Section 2.3 integrals of the form
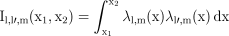 ((B1))
((B1))arose; here the λl,m(x) are the normalised associated Ledengre functions, defined in equation (A3), and m is assumed to be non-negative. These integrals can be evaluated quickly and accurately using a combination of closed formulæ and recursion relations.
The associated Legendre functions, Pl,m(x) (defined in equation A4), are solutions of the ordinary differential equation (e.g. Arfken 1985)
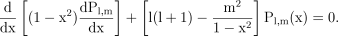 ((B2))
((B2))Multiplying this equation by Pl′,m(x) and integrating (from x1 to x2) by parts twice yields
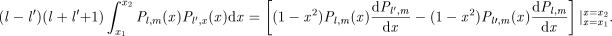 ((B3))
((B3))This is a reflection of the standard result that integrals of solutions of a self-adjoint differential equation (as equation B2 is) can be expressed as boundary terms (e.g. Arfken 1985). The derivatives in equation (B2) can be removed by using the standard recursion relationship (e.g. Gradshteyn & Ryzhik 2000)
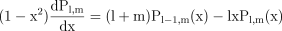 ((B4))
((B4))to yield, for l≠l′,
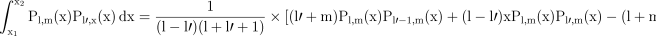 ((B5))
((B5))Note that the first term must be omitted if l′=m and that the third term must be omitted if l=m; these Legendre functions are implicitly zero from equation (A4). Finally, this can be normalized according to equation (A3), giving
 ((B6))
((B6))An alternative derivation of this result was presented by Wandelt et al. (2001); it is also in principle equivalent to equation (13) in section 5.9 of Varshalovich, Moskalev & Khersonskii (1988), but their application of equation (B4) is in error.
For the case l=l′, a recursion relation is required, starting with l=m. Combining equations (A3) and (A4),
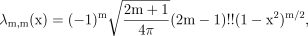 ((B7))
((B7))where n!!=1×3×⋯×(n−2)×n for odd n. Integrating by parts and using equation (B7) again gives
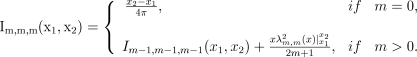 ((B8))
((B8))Moving to l=m+1, the standard relationship (e.g. Gradshteyn & Ryzhik 2000) that
λ m+1,m(x)=(2m+3)xλm,m(x)
((B9))combines with equation (B7) to give
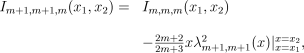 ((B10))
((B10))where the first term is given in equation (B8).
The last step is to derive a recursion relation relating Il,l,m(x1,x2) to Il−1,l−1,m(x1,x2) and Il−2,l−2,m(x1,x2). Equation (C22) of Wandelt et al. (2001) gives a four-term recursion to obtain Il,l′,m(x1,x2); it can be applied successively (once swapping l and l′) to obtain
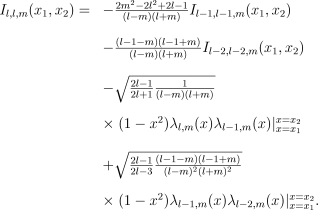 ((B11))
((B11))In summary, equation (B6) can be used to evaluate all Il,l′,m(x1,x2) for which l≠l′, and equations (B8), (B10) and (B11) combine to give all Il,l,m(x1,x2) recursively.
Appendix C: Treatment of non-cosmological modes
All the cosmological information encoded in the CMB is expected to be contained in the l≥2 modes; the l=0 mode in an isotropic universe can be normalised arbitrarily and the l=1 modes can be set to zero by adopting an appropriate reference frame. None the less, observations of the microwave sky will yield non-zero monopole and dipole values for a number of reasons (e.g. the observer's motion; Galactic emission; extragalactic point sources). Hence these low-order modes must be included in the analysis of CMB data, but should be kept separate from the cosmological modes, as is naturally the case if spherical harmonic coefficients are used to describe the data. It is also important to note that the properties of the basis functions themselves are unimportant – the essential requirement is that only four of the cut-sky harmonic coefficients contain information on the unwanted modes.
The method of orthogonalization summarized in equations (11), (12) and (14) does not explicitly impose any particular structure on the conversion matrix, A (which relates harmonic coefficients on the incomplete sphere to those on the full sphere by a′=ATa;equation 24). The non-cosmological modes are kept separate from the cosmological modes if the first four columns of AT have only zeros from the fifth row on, assuming the full-sky harmonic coefficients are indexed using l-ordering (Appendix A). This is achieved naturally if AT is constructed to be upper triangular, as in the case of the Cholesky decomposition described in Section 2.2.1. The other decomposition methods discussed in Section 2.2 do not share this property, and so the resultant conversion matrices must be adjusted explicitly.
One way of achieving this is to use a partial Householder transform (e.g. Press et al. 1992). The last i′max−i elements of the ith column of a general i′max×imax matrix can be set to zero by the transformation M′=PiM, with the orthogonal Householder matrix defined by
 ((C1))
((C1))where mi is given by
 ((C2))
((C2))and i≤min(i′max,imax) is assumed. Provided that the Householder matrix applied to B is that generated from AT, the transformations A′T=PiAT and B′=PiB leave equations (12) and (14) unaffected as Pi is orthogonal by construction. Applying P1, P2, P3 and then P4 to the successively updated AT ensures that the l=0 and l=1 modes influence only the first four cut-sky harmonic coefficients, as required. This procedure could be continued, moving AT successively closer to upper triangular form, although this cannot be achieved in full as AT has more columns than rows.
Special mention must be made of the constant latitude cut case, the symmetry of which can only be utilized if the spherical harmonics are indexed using m-ordering (Appendix A). In this case only the m=0 and m=±1 blocks have any contribution from the monopole or dipole, and each can be treated separately. Further, the ordering within these blocks is such that the non-cosmological modes are in the first rows, and so the above algorithm can be applied to each of three blocks as is. The only slight inconvenience is that it is no longer the first four cut-sky modes that contain the non-cosmological information, and the relevant modes must be flagged explicitly.
This paper has been typeset from a tex/latex file prepared by the author.




