Mating patterns, relatedness and the basis of natal philopatry in the brown long-eared bat, Plecotus auritus
Abstract
The brown long-eared bat, Plecotus auritus, is unusual among temperate zone bats in that summer maternity colonies are composed of adult males and females, with both sexes displaying natal philopatry and long-term association with a colony. Here, we describe the use of microsatellite analysis to investigate colony relatedness and mating patterns, with the aim of identifying the evolutionary determinants of social organization in P. auritus. Mean colony relatedness was found to be low (R = 0.033 ± 0.002), with pairwise estimates of R within colonies ranging from −0.4 to 0.9. The proportion of young fathered by males in their own colony was investigated using a Bayesian approach, incorporating parameters detailing the number of untyped individuals. This analysis revealed that most offspring were fathered by males originating from a different colony to their own. In addition, we determined that the number of paternal half-sibs among cohorts of young was low, inferring little or no skew in male reproductive success. The results of this study suggest that kin selection cannot account for colony stability and natal philopatry in P. auritus, which may instead be explained by advantages accrued through the use of familiar and successful roost sites, and through long-term associations with conspecifics. Moreover, because the underlying causes of male natal dispersal in mammals, such as risk of inbreeding or competition for mates, appear to be avoided via extra-colony copulation and low male reproductive skew, both P. auritus males and females are able to benefit from long-term association with the natal colony.
Introduction
To understand the evolutionary causes and consequences of social organization in a species requires knowledge of its mating system, an estimation of genetic relatedness among constituent individuals within a social group and an assessment of dispersal patterns and gene flow among groups. Such parameters are frequently difficult to identify in wild populations by direct observation alone as mating or parental behaviour may be difficult to observe, or incidents of multiple copulation or shared parental care may make such observations unreliable. As a result, the use of genetic techniques to determine kinship in wild populations accurately is increasingly common. One taxonomic group which particularly benefits from the use of such techniques is the Chiroptera (bats) (Rossiter et al. 2000). These mammals are often difficult to study directly, owing to their inaccessible roosting sites and nocturnal activity. Furthermore, the tracking of individuals between maternity colonies and mating sites is often difficult.
The brown long-eared bat (Plecotus auritus, Family: Vespertilionidae) is a temperate zone species, widespread across central and northern Europe. Its life cycle follows that of other temperate zone bat species (Racey 1982; Racey & Entwistle 2000) in that oestrus is extended throughout autumn and the winter hibernation (Strelkov 1962). Spermatozoa are stored in the female reproductive tract until fertilization in spring (Racey 1979), and a single young is born in mid-summer. During summer, bats form mixed sex maternity colonies, located in tree holes, bat boxes or the roof spaces of buildings (Swift 1991; Entwistle et al. 1997). It is only at this time that P. auritus is sufficiently accessible for study. This species is unusual among temperate zone bats in that adult males also occur in these summer colonies, although their genetic relationship with other colony members remains unclear (Entwistle et al. 2000). Towards the end of summer the colonies disperse, and during autumn and winter, when mating occurs, bats become less conspicuous, roosting singly or in small groups within the summer roost, or in transient roost sites or hibernacula (Stebbings 1966; Strelkov 1969).
Ringing studies of P. auritus at summer roosts in Great Britain have demonstrated that both sexes and all age classes show long-term association with their colonies and, while emigration of adults or young cannot be discounted, it is rarely observed (Boyd & Stebbings 1989; Park et al. 1998; Entwistle et al. 2000). Given this temporal and spatial stability in colony composition, colonies may be comprised of closely related individuals, a factor which could have important consequences for the evolution of mating systems, dispersal patterns and social behaviour. A previous study of genetic population structure in P. auritus (Burland et al. 1999) provided evidence for the occurrence of natal philopatry in both sexes, but also suggested that considerable gene flow among colonies occurs, probably via extra-colony mating rather than the permanent exchange of individuals.
Here, we describe the use of microsatellite analysis to estimate genetic relatedness and identify mating patterns within P. auritus colonies. We investigate whether levels of genetic relatedness within colonies reflect the marked philopatry to the natal colony previously identified in both sexes of this species and determine if adult males achieve reproductive success within their own colonies, or father offspring in other colonies, as suggested by Burland et al. (1999). We also investigate whether an extended oestrus, coupled with a mating system based on multimale female defence polygyny or promiscuity (Entwistle 1994; Park et al. 1998), prevents a high skew in male reproductive success in P. auritus.
Analysis of male mating patterns in P. auritus by inference of parentage using a maximum likelihood approach (i.e. Marshall et al. 1998) was not appropriate, as such procedures ignore a number of issues. First, adults from the same colony as the offspring are more likely to have been caught and typed than adults from other colonies, which include those colonies not visited during the study. This can bias parentage assignment in favour of parents from the same colony as the offspring. Second, although untyped individuals are each less likely to be the parent than an individual scored as having a compatible genotype, there may be a sufficiently large number of untyped bats with compatible genotypes to make an untyped parent more likely. Third, where the genotype of the offspring indicates that none of the typed adults could be its parent, it follows that the actual parent must be untyped. This adult will be either from the same colony as the young, or from elsewhere, and the probability of the parent being from the same colony as the offspring will depend on the relative number of bats in the offspring’s colony and in other colonies. Fourth, more than one adult may have a genotype compatible with parentage, and restricting attention to the single most likely parent discards information.
To overcome these problems we estimated the proportion of offspring having fathers from the same colony (hf) and the proportion of offspring having mothers from the same colony (hm) using a Bayesian approach, incorporating parameters describing the number of untyped individuals in the natal colony of the offspring and in the study population overall. We made use of prior information from ringing studies, which provided estimates of population size and the extent of female mobility. The combined results of our analyses allow predictions to be made regarding the evolutionary causes and consequences of social organization in P. auritus, in particular the high levels of natal philopatry and colony stability observed in this species.
Methods
This study was conducted on the same population as used in Burland et al. (1999), and was enhanced by the availability of extensive ringing data compiled for this population since 1984 (Burland 1998; Entwistle et al. 2000). The study area was situated within the Grampian and Highland regions of northeast Scotland, at approximately 57° N, where summer colonies are located within the attics of buildings (Entwistle et al. 1997). The three main study sites (number of colonies sampled in parentheses) were Deeside (n = 20), Speyside (n = 3) and Kirkmichael (n = 3), a more detailed account of which can be found in Burland et al. (1999). Colony visits were conducted during three consecutive summers (1994–1996). Bats were caught under licence by hand or static net and held in cloth bags. The sex and reproductive status of each bat were determined using the criteria outlined for females by Racey (1974) and males by Entwistle et al. (1998). For each individual, wing membrane biopsy punches were obtained under licence, and DNA was extracted from a single wing biopsy and genotyped at six highly polymorphic Plecotus auritus microsatellite loci (five autosomal, one X-linked) as previously described (Burland et al. 1998, 1999).
Calculation of relatedness
Estimation of Hamilton’s (1964) relatedness coefficient (R) was conducted using genotypes from the five autosomal P. auritus loci (Paur 01, 02, 04–06) using the programs relatedness 4.2 and kinship 1.1.2 (Queller & Goodnight 1989; Goodnight & Queller 1999). Standard errors were estimated by jackknifing over loci (Queller & Goodnight 1989). To ensure the loci gave values of R close to expected values for known relatedness, the mean R was calculated for 10 known mother–offspring pairs (expected value for outbred pairs: 0.5) and 20 unrelated dyads originating from two colonies situated 71 km apart (expected value: 0.0).
Estimates of pairwise and mean relatedness were determined between females, males, females and males, and among all individuals for 23 colonies (total n = 656, Table 1). In addition, to determine whether relatives clustered preferentially with one another within the roost, the pairwise and mean relatedness of bats found within the same cluster (i.e. a group of individuals roosting in physical contact with one another) on each visit was also estimated. To remove any bias introduced by mother–offspring pairings, only adult members of clusters were investigated.
| R ± standard error (no. of individuals compared) | ||||
|---|---|---|---|---|
| Colony | Females–females | Males–males | Males–females | All |
| AN | −0.14 ± 0.06 (9) | −0.07 ± 0.07 (13) | −0.11 ± 0.10 (22) | −0.09 ± 0.07 (22) |
| AL | 0.04 ± 0.05 (10) | 0.1 ± 0.05 (6) | 0.06 ± 0.05 (16) | 0.05 ± 0.05 (16) |
| BH | 0.2 ± 0.12 (6) | 0.12 ± 0.05 (7) | 0.11 ± 0.12 (13) | 0.14 ± 0.1 (13) |
| CR | −0.01 ± 0.06 (8) | 0.03 ± 0.03 (16) | 0.04 ± 0.03 (24) | 0.03 ± 0.04 (24) |
| DL | 0.01 ± 0.04 (12) | 0.04 ± 0.08 (5) | 0.10 ± 0.06 (17) | 0.04 ± 0.04 (17) |
| DC | 0.03 ± 0.03 (15) | 0.01 ± 0.01 (18) | 0.05 ± 0.02 (33) | 0.03 ± 0.02 (33) |
| DH | 0.08 ± 0.03 (18) | −0.02 ± 0.03 (20) | 0.04 ± 0.02 (38) | 0.03 ± 0.02 (38) |
| DM | 0.22 ± 0.06 (5) | 0.03 ± 0.2 (3) | 0.23 ± 0.1 (8) | 0.2 ± 0.09 (8) |
| DV | 0.03 ± 0.02 (17) | 0.11 ± 0.08 (29) | 0.1 ± 0.05 (46) | 0.07 ± 0.04 (46) |
| EL | 0.02 ± 0.1 (26) | −0.04 ± 0.06 (28) | −0.02 ± 0.05 (54) | −0.01 ± 0.06 (54) |
| HS | −0.14 ± 0.06 (3) | −0.04 ± 0.05 (9) | 0.01 ± 0.06 (12) | −0.02 ± 0.05 (12) |
| HC | 0.15 ± 0.12 (8) | −0.03 ± 0.04 (6) | 0.06 ± 0.04 (14) | 0.08 ± 0.07 (14) |
| KH | 0.06 ± 0.03 (12) | 0.00 ± 0.08 (5) | −0.05 ± 0.08 (17) | 0.01 ± 0.01 (17) |
| LF* | 0.03 ± 0.01 (18) | — | — | 0.03 ± 0.01 (18) |
| LW† | — | 0.04 ± 0.08 (9) | 0.08 ± 0.11 (10) | 0.06 ± 0.08 (10) |
| MC | −0.15 ± 0.09 (2) | 0.05 ± 0.07 (5) | 0.07 ± 0.12 (7) | 0.07 ± 0.07 (7) |
| PM | −0.02 ± 0.03 (52) | −0.02 ± 0.02 (62) | 0.00 ± 0.01 (114) | −0.02 ± 0.03 (114) |
| RC | −0.02 ± 0.05 (11) | 0.17 ± 0.14 (5) | 0.06 ± 0.06 (16) | −0.02 ± 0.02 (16) |
| SK | 0.05 ± 0.04 (18) | −0.05 ± 0.04 (12) | 0.00 ± 0.05 (30) | 0.02 ± 0.04 (30) |
| SH | 0.03 ± 0.05 (7) | 0.07 ± 0.09 (5) | 0.02 ± 0.09 (12) | 0.03 ± 0.03 (12) |
| TS | 0.05 ± 0.02 (50) | 0.04 ± 0.02 (34) | 0.04 ± 0.3 (84) | 0.04 ± 0.02 (84) |
| TB | 0.18 ± 0.07 (11) | 0.18 ± 0.08 (9) | 0.18 ± 0.06 (20) | 0.17 ± 0.06 (20) |
| WI | 0.18 ± 0.11 (19) | 0.08 ± 0.04 (12) | 0.1 ± 0.04 (31) | 0.14 ± 0.06 (31) |
| Mean | 0.042 ± 0.009 | 0.022 ± 0.007 | 0.039 ± 0.002 | 0.033 ± 0.002 |
| (337) | (318) | (638) | (656) | |
- * No males were sampled.
- † †Only one female was sampled.
Analysis of parentage
For the analysis of parentage we used individuals classified as ‘young of the year’ between 1993 and 1996 (n = 78) in four Deeside colonies for which extensive ringing data were available (colonies DC, DV, PM, TS). Those individuals born in 1993 were identified from the ringing records. The number of young sampled in each colony, with the number in each respective year (1993–1996) in parentheses, were as follows: DC = 10 (0, 1, 8, 1); DV = 9 (0, 0, 4, 5); PM = 36 (4, 11, 13, 8); TS = 23 (0, 5, 9, 9). Of these, seven young were found attached to the nipple of a female, and in each case genetic compatibility between the offspring and female indicated that she was the mother (Burland 1998). For all other young, neither the mother nor the father was known. Following the identification of isolation by distance within the study area (Burland et al. 1999) putative parents were restricted to only those caught in Deeside colonies. Male offspring were considered as candidate fathers of all young born 1 year or more after their birth. Females were considered as candidate mothers of young born 2 or more years after their birth, as the earliest females give birth is at the end of their second year (Stebbings 1966; Entwistle 1994).
Microsatellite genotypes determined using the five autosomal loci for 520 individuals (including the 78 offspring) from 20 Deeside colonies were used to assess parentage by calculating the probability of the offspring’s genotype given a particular pair of parents, which we write as
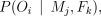
where the genotypes of the offspring, mother and father are given by Oi, Mj and Fk, respectively. This can be calculated where the genotype is unknown, and it takes into account mutation and scoring errors. Details of this calculation are given in the Appendix.
The likelihood is a function of several parameters. The number of adult bats is assumed to be the same for males and females, and is described by Nui for the number of untyped adults in each of the four colonies and Nt is half the total number of adult bats in the region. The probabilities of a mother or father being from the natal colony of the offspring are hm and hf, respectively. We use the symbol θ to represent this whole set of parameters.
We obtained the likelihood of the data by calculating the probability of the offspring genotypes having been produced by every possible pairwise combination of mother and father:
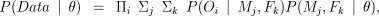
where Πi indicates the product over all offspring; Σj indicates the sum over all possible mothers including all those typed and untyped in all colonies; Σk indicates the equivalent sum for fathers; P(Oi ∣ Mj,Fk) is the probability of offspring i’s genotype given that its mother was female j and its father was male k. This calculation is set out in the Appendix; P(Mj,Fk ∣ θ) is the probability that the mother was female j and the father was male k before observing the genotypes, given θ. The calculation of this probability is also set out in the Appendix.
The values of θ, including hm and hf were estimated using the Metropolis algorithm (Metropolis et al. 1953) which is a Markov chain Monte Carlo (MCMC) method that draws a sample from the posterior distribution of the parameters specified by P(Data ∣ θ) P(θ) (see Appendix). This algorithm requires that P(θ), the prior distribution for hm, hf, Nui and Nt are specified.
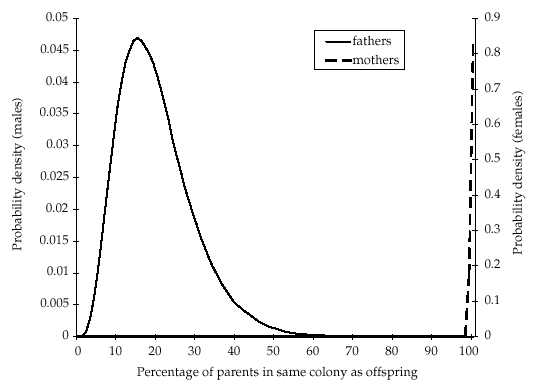
The size of the natal colony of each offspring has previously been estimated between three and five times for different years (between 1991 and 1995) using mark–release–recapture data (Entwistle et al. 2000; T. M. Burland, unpublished). Each estimate was represented by a normal probability density with the estimated mean and standard error. The combined estimates for each colony were obtained from the product of the independent densities, and we produced a prior distribution for the number of untyped individuals in each of the four colonies by subtracting the number that had been typed (Fig. 1).
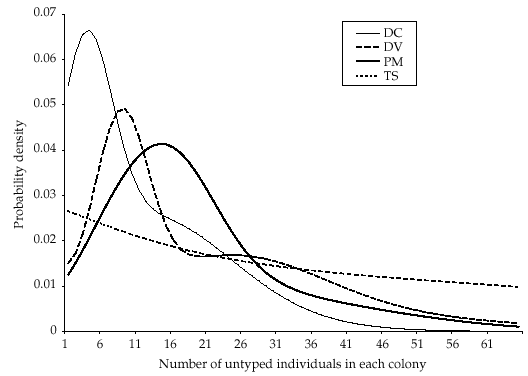
Prior distributions for the number of untyped individuals, determined from mark–release–recapture information, within each of the natal colonies of the offspring used in the parentage analysis. Modal estimates (95% confidence intervals) were as follows: DC = 4 (0–32); DV = 9 (0–49); PM = 14 (0–46); TS = 0 (0–60).
The priors for the other parameters were independent. While offspring are expected to be born into the same colony as that in which their mother is resident, ringing data showed that females are occasionally captured in different colonies on different occasions (two of 605 recaptures; Burland 1998). The prior for hm was the beta distribution that gives the relative likelihood for a binomial sample with two occurrences out of 605 observations. The prior distribution for hf was uniform between 0 and 1, reflecting our ignorance of the mating patterns and the locations of the fathers.
The priors for the number of untyped individuals of each sex in the overall population were set to be uniform between 200 and 2000, which we believe define the lower and upper boundaries, respectively, for the size of the untyped population. These values were estimated using mean minimum and maximum colony sizes derived from mark–recapture data (Entwistle et al. 2000), combined with a knowledge of roost numbers in the study area obtained from over 20 years of field work (Speakman et al. 1991; Entwistle et al. 1997; Racey 1998). Forty-nine P. auritus roosts are currently identified within Deeside (Entwistle et al. 1997). The lower value of 200 is less than that obtained by multiplying the number of known roosts by the minimum estimate of mean colony size (14.45 of each sex, assuming an equal sex ratio). The upper value of 2000 was estimated from the maximum estimate of mean colony size (23.1 of each sex), assuming that only half the colonies within the study region have been identified (n = 98). We believe that given the extensive field work conducted on P. auritus in Deeside, it is unlikely that less than half the roosts within the study area have been identified. Furthermore, this estimate of population size (2000 of each sex, total n = 4000) is greater than the maximum population size previously estimated for P. auritus in an area encompassing both Deeside and its adjoining river valley (total n = 2037; Entwistle 1994).
Mating patterns and male reproductive success
Various hypotheses regarding mating patterns in P. auritus, in particular individual male reproductive success, were tested using the program kinship 1.3 (Goodnight & Queller 1999). The program utilizes microsatellite genotypes to calculate both the likelihood that two individuals (a dyad) are related by a given pedigree and a likelihood ratio for any pair of hypothesized pedigrees (Goodnight & Queller 1999). The program uses simulations to allow statistical significance to be attached to its results. In addition, it calculates a type II (false-negative) error rate, the rate at which dyads in the sample set which are of the pedigree defined in the primary hypothesis are not identified by the program as being of that pedigree (Goodnight & Queller 1999).
The 78 young included previously in the parentage analysis were used for this analysis. Pairwise comparisons between young could be partitioned into four categories (total n = 3003): I, young born into the same colony in the same year (n = 293); II, young born into different colonies in the same year (n = 663); III, young born into the same colony in different years (n = 672); IV, young born into different colonies in different years (n = 1375).
The presence of a skew in male reproductive success was investigated by identifying the proportion of half-sibs present within each of the four categories. This was achieved by determining whether each dyad within each category was more likely to be a half-sib pair (the primary hypothesis, Rm = 0.5 Rp = 0 or Rm = 0 Rp = 0.5) than unrelated (the null hypothesis, Rm = 0 Rp = 0), where Rm and Rp are the probabilities that the individuals in the dyad share an allele identical by descent from the mother and father, respectively (Goodnight & Queller 1999). Using the allele frequencies obtained for Deeside individuals at all six microsatellite loci (n = 520), 100 000 simulations were performed to provide values of the likelihood ratio in which 95% of simulated unrelated dyads could be excluded. The mode of inheritance for haploids was specified as ‘maternal’ to allow for the inclusion of the X-linked locus.
Dyads which returned a ratio value above that determined by the simulations using either primary hypothesis (Rm = 0.5 Rp = 0 or Rm = 0 Rp = 0.5) were regarded as sibling pairs. Further classification into ‘maternal’ or ‘paternal’ half-sibs was not possible from the genetic data alone, as the parental origin of most alleles could not be determined in the genotype of young. However, given that females give birth to only one offspring per year (Swift 1991) and rarely move between colonies (see above), sibling pairs identified in categories I, II and IV were regarded as paternal half-sibs. In contrast, sibling pairs identified in category III could be maternal half-sibs, paternal half-sibs or full-sibs. In an attempt to distinguish between full- and half-sib dyads in category III, we compared the primary hypothesis that sibling pairs were more likely to be full-sibs (Rm = 0.5 Rp = 0.5) than half-sibs (null hypothesis: Rm = 0.5 Rp = 0 or Rm = 0 Rp = 0.5). In addition, to identify any presence of parent–offspring dyads in categories III and IV the primary hypothesis (Rm = 1.0 Rp = 0 or Rm = 0 Rp = 1.0) was tested against the null hypothesis (Rm = 0.0 Rp = 0.0).
The estimates obtained for the number of dyads related to a particular degree (half-sibs, full-sibs, parent–offspring) were adjusted for type I and type II error rates (α and β, respectively) using the following reasoning. By definition of the error rates, the expected number of comparisons classified as significant, S, is given by:
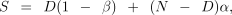
where N is the total number of dyads and D is the number of truly related dyads. Rearranging we obtain D̂ an estimate of D:
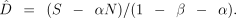
Results
Relatedness estimates
The mean R calculated for known unrelated individuals (expected value: 0.0) was −0.01 (±0.03, n = 20), whereas the mean R value for known mother–young pairs (expected value: 0.5) was 0.66 (±0.06, n = 10). Mean R values calculated among females, among males, between males and females, and among all individuals in each of the 23 colonies, and across all colonies, are given in Table 1. Across colonies, no category gave consistently greater R values than any other when assessed using Wilcoxon matched-pair sign-rank tests. Furthermore, no significant relationship was found between colony R value and colony size using the Spearman rank correlation coefficient. The distribution of pairwise R estimates within colonies (Fig. 2) demonstrated a wide range of R values (−0.4 to 0.9), with the majority of dyads unrelated or distantly related (less than a second-order relative, R < 0.25).
Proportion of pairwise R estimates in each relatedness class among females (4167 comparisons), males (4327 comparisons) and between males and females (7980 comparisons) within the same summer colony, summed across all colonies.
Pairwise and mean values of R among individuals within the same cluster were determined for 17 clusters found between May and September (1994–1996). Mean R values for individual clusters ranged from −0.44 (±0.031) to 0.123 (±0.086), while pairwise R values within clusters ranged from −0.4 to 0.6.
Location of parents
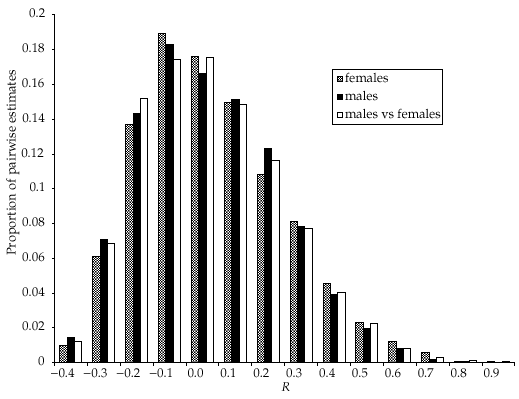
Posterior distributions for the proportion of mothers and fathers caught in the same colony as their offspring (hm and hf, respectively) are shown in Fig. 3. The modal estimate for hm was 100%[95% confidence interval (CI) 98–100%], whereas for hf the mode was 15% (95% CI 5–41%). The posterior distributions for the number of untyped individuals of each sex in each natal colony and in the overall population are shown in Fig. 4(a,b), respectively. Modal estimates in two of the colonies (DC and DV) suggest that more individuals remain untyped than estimated from mark–recapture data alone (Fig. 1). Conversely, less untyped individuals than previously estimated may be in colony PM, whereas the analysis is uninformative for colony TS. Results for the overall population show that while there is sufficient information to demonstrate that a large number of individuals (> 300) remain untyped (Fig. 4b), the absence of a peak in the distribution means that we have not obtained a precise estimate.
Posterior distributions determined from Markov chain Monte Carlo (MCMC) analysis for proportion of mothers and fathers found within the same colony as their offspring.
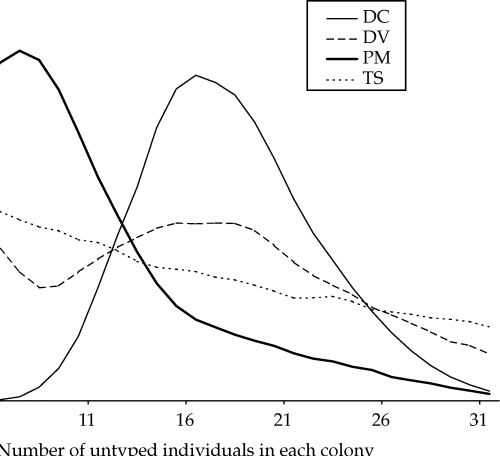
Posterior distributions determined from Markov chain Monte Carlo (MCMC) analysis for the number of untyped individuals within (a) the natal colonies of the offspring and (b) the entire study population. Modal estimates (95% confidence intervals) for the natal colonies were as follows: DC = 16 (9–26); DV = 15 (2–29); PM = 7 (0–22); TS = 0 (0–28).
Assessment of mating patterns
The numbers of offspring dyads observed as having a likelihood ratio exceeding that of 95% of simulated unrelated pairs (S) are given for each category in Table 2. The corresponding type II (false-negative) error rate for the identification of half-sibs was 0.48. When both type I error and type II error rates were taken into consideration (i.e. α = 0.05, β = 0.48), the estimated proportion of true half-sibs approximated to 1% of dyads in all but category III. Within this category, the estimated proportion of siblings was 10.3%. The number of parent–offspring pairs identified was extremely low (Table 2) and had a type II error rate close to zero. As such, estimates of the proportion of sibling pairs in categories III and IV are unlikely to be biased by the presence of parent–offspring pairs. Of the 66 pairs identified as siblings in category III, 22 were more likely to be full-sibs than half-sibs at the 95% level (type II error rate: 0.47). Following correction, this equates to 60% of all sibling pairs in category III being full-sibs.
| No. of dyads for which a significant likelihood ratio (P < 0.05) was obtained (S) | |||
|---|---|---|---|
| Category of dyad | Total number of dyads (n) | Siblings (Rm = 0.5 Rp = 0) or (Rm = 0 Rp = 0.5) | Parent–offspring (Rm = 1.0 Rp = 0) or (Rm = 0 Rp = 1.0) |
| I | 293 | 16 (1%) | N/A |
| II | 663 | 36 (1%) | N/A |
| III | 672 | 66 (10.3%) | 6 |
| IV | 1375 | 73 (1%) | 14 |
- N/A, not applicable (see text).
Discussion
Location of parents
This study supports the proposition that females rarely move between summer maternity colonies (Fig. 3). However, the high proportion of offspring in a colony fathered by males from a different colony (Fig. 3) suggests extensive mixing of individuals from different colonies during the mating season. Such mixing is in contrast to the spatial structuring identified in the summer population (Entwistle et al. 2000), but is consistent with the predictions of Burland et al. (1999) that extra-colony copulation is the primary mechanism of gene flow. The indication that a small proportion of fathers may originate from the same colony suggests either that some mating may occur within the summer roost site, or that bats from the same summer colony also associate at other mating sites.
The results also suggest that a high number of untyped bats in the population contribute towards the gene pool (Fig. 4). This can be accounted for by two nonexclusive explanations. First, many Plecotus auritus colonies may remain undetected. Given that genetic isolation by distance is apparent within the population over relatively short distances (40 km; Burland et al. 1999), such colonies are probably located close by. This is consistent with the finding that the identification of new colonies within the study area has shown no asymptote (Entwistle 1994). Second, a proportion of individuals from known colonies remain untyped. This is consistent with the posterior distributions of colony sizes, which demonstrate that in at least some colonies, a higher number of untyped bats may be present than indicated from mark–release–recapture data alone (Fig. 1). Furthermore, the colony studied most intensively since 1991 (PM; Entwistle 1994; Burland 1998) gave the lowest and most consistent prior and posterior estimates of the number of untyped individuals (1, 4).
Mating patterns and assessment of male reproductive skew in P. auritus
Goodnight & Queller (1999) have demonstrated that four loci, each with 20 uniformly distributed alleles, are generally sufficient to distinguish between unrelated and half-sib dyads in 50% of cases, while just two loci are sufficient to distinguish unrelated dyads and parent–offspring pairs. This study used six highly polymorphic loci (number of alleles = 7–24, mean = 14.2; Burland et al. 1998). As such, the assessment of male reproductive skew in P. auritus presented here may be regarded as relatively robust, especially as estimates of the exact proportion of offspring which share the same father take into account both type I and type II error rates. Whilst the genetic data alone were not able to distinguish between maternal and paternal half-sibs, behavioural data show that females only give birth to one offspring a year, and do not move between colonies. This strongly supports the assertion that any siblings identified in categories I, II and IV will be paternal half-sibs.
The small proportion of half-sibs present in categories I, II and IV (Table 2) suggests that fertilization success, either within single colonies or within the population as a whole, is not dominated by a few males, either within or between years. While the proportion of half-sib dyads born within the same colony between years (category III) was higher than in other categories (Table 2), this probably stems from the presence of maternal half-sibs in this category (although the presence of full-sibs in this category cannot be discounted, see below). The detection of little or no skew in male reproductive success in this species fits well with the prediction that the extent to which males can defend females is a crucial factor governing mating systems (Clutton-Brock 1989). In P. auritus, oestrus and mating extend throughout autumn, winter hibernation and into spring, when ovulation occurs, making female defence throughout oestrus unlikely. Interestingly, however, the results differ to those from a genetic study of the little brown bat (Myotis lucifugus), another temperate zone species for which mating may occur throughout winter (Thomas et al. 1979), which suggested that some skew in male reproductive success may occur (Watt & Fenton 1995).
The data of this study suggest either that P. auritus females mate singly and at random with respect to one another, or that multiple mating by females occurs, with possible sperm competition. This study is unable to predict the number of males each female mates with each year, although multiple mating by females is known to occur in other vespertilionid bats (Pearson et al. 1952; Thomas et al. 1979; Mayer 1995; McCracken & Wilkinson 2000). However, a recent study of the relative testes mass in bats suggests that the risk of sperm competition in P. auritus is small (Wilkinson & McCracken 2001), and hence multiple mating by females may be relatively infrequent.
The results also suggest that a high proportion of sibling pairs in category III may be full-sibs. However, it is likely that the number of markers employed in this study may be insufficient to distinguish fully between half- and full-sibs. While four loci can distinguish between unrelated and half-sib dyads, seven loci (each with 20 uniformly distributed alleles) are required to distinguish between half- and full-sibs, especially when the maternal genotype is unknown (Goodnight & Queller 1999). Despite this, correction for type I and type II errors suggests that a high proportion of the sibling pairs identified are full-sibs. This may be indicative of single mating by females, coupled with loyalty to mating sites of both males and females between years, as previously suggested for the greater horseshoe bat, Rhinolophusferrumequinum (Rossiter et al. 2000).
Colony relatedness
The five loci used to estimate relatedness in this study gave the expected estimate for unrelated individuals, although the mean R for mother–offspring pairs was higher than predicted. However, this R estimate, which was based on a small sample size (n = 10), may have been biased by the inclusion of one or more mother–offspring pair which was more closely related than outbred first-order relatives (true R > 0.5). Larger sample sizes, such as those employed in this study (Table 1, Fig. 2), would be less biased in this manner. Moreover, the low standard errors (obtained by jackknifing over loci) reported for the overall mean estimates of R (Table 1) suggest that these loci provide a reliable measure of relatedness.
This study identified generally low mean R within colonies (Table 1) and found that the majority of individuals within a colony were unrelated or distantly related (Fig. 2). This finding appears to contradict inferences arising from ringing studies (Entwistle et al. 2000). High mean colony relatedness, predicted from high colony stability and natal philopatry in both sexes, appears to be negated by both a low skew in male reproductive success and high incidence of extra-colony fertilizations, such that few paternal sibling pairs are born into a colony either within or between years. This effect may be further confounded by low female fecundity (0.7 young per female per year; Entwistle 1994) and high juvenile mortality (up to 68% in their first year; Burland 1998), both of which will reduce the proportion of maternal siblings within the colony. Similar factors have been proposed for the low levels of relatedness found within colonies of the vampire bat, Desmodus rotundus (Wilkinson 1985).
Despite this, some highly related individuals were identified within the colonies (Fig. 2). While this finding may be a result of the high standard errors expected with pairwise estimates of R (Queller & Goodnight 1989), the results from the parentage and mating patterns analysis do suggest that some first-order (parent–offspring, full-sib) and second-order relatives (half-sibs) will be present.
Causes of natal philopatry and colony stability in P. auritus
Temperate zone bat species are believed to form summer maternity colonies to provide the appropriate thermal and social conditions for the growth and survival of offspring (McNab 1982). P. auritus is highly selective in its choice of summer diurnal roost (Entwistle et al. 1997), which may, therefore, be a limiting resource. By returning to the same roost site each year, individuals can be assured of the thermal benefits of clustering with conspecifics at a site previously proven to provide suitable environmental conditions to support growth and maturation in young and survival in adults. However, such advantages of colony membership fail to explain the observation that movement between even well-established P. auritus colonies located close to one another amounts to less than 1% of all recaptures in both sexes and all ages (Burland 1998; Entwistle et al. 2000).
Further explanations are therefore necessary to account for the levels of colony stability and natal philopatry observed. The mean levels of relatedness determined in this study suggest that kin selection is not an adequate explanation for colony stability in this species. This is further supported by the finding that individuals do not appear to cluster preferentially with kin within the roost. Hence, the evolutionary basis for long-term stability and natal philopatry in P. auritus maternity colonies remains unclear. One explanation may stem from the additional benefits accrued through reciprocal behaviour. Wilkinson (1987, 1992a,b) has demonstrated that colony stability and familiarity with conspecifics, rather than high relatedness, are the primary factors promoting reciprocal or mutualistic behaviour in bats, such as food sharing, communal nursing and information transfer. Similarly, Kerth & König (1999) and Kerth et al. (2000) suggest that colony fidelity in female Bechstein’s bats stems from the social benefits of remaining with familiar individuals, both related and unrelated. This may also apply to P. auritus. However, communal nursing has not been observed (de Fanis & Jones 1995; McLean & Speakman 1996), and it is unlikely that information transfer regarding foraging sites is necessary, as bats travel only short distances to feeding sites (< 3 km; Entwistle et al. 1996) where they forage singly by gleaning (Swift 1991).
One further aspect of social organization in P. auritus which deserves consideration is the behaviour of adult males. Ringing studies in northeast Scotland suggest that males remain associated with their natal colony once mature, and that males are frequently found within their colonies over time periods exceeding those required for maturation of putative female offspring (Burland 1998; Entwistle et al. 2000). Both occurrences are rare within the social groups of mammalian species, especially where females are also philopatric. More commonly, inbreeding avoidance, competition for mates and/or competition for resources result in permanent male dispersal from the natal group and a limited tenure of adult males (Greenwood 1980; Dobson 1982; Moore & Ali 1984). However, the high incidence of extra-colony paternity inferred by this study suggests that P. auritus instead avoids inbreeding and competition for mates by mating with individuals from outside the natal colony, although inbreeding may also be avoided by mating with only distantly or unrelated bats from the same colony. Moreover, competition for mates may be less intense in P. auritus than in more polygynous species. Whilst competition for resources could arise among colony members, this may be reduced by the segregation of foraging areas between males and females (Entwistle et al. 1996, 2000). Hence, if inbreeding and competition for mates or resources are avoided without permanent dispersal from the natal colony, any benefits accrued by P. auritus females by remaining within their natal colony, may also be accrued by males.
Acknowledgements
Bats were caught and sampled under licences from Scottish Natural Heritage and the Home Office. We are extremely grateful to the householders for access to colonies at their properties. A. Overall, S. Le Comber, J. Worthington Wilmer, J. Dallas and two anonymous referees provided helpful comments on earlier drafts of the manuscript. T.M.B. was supported by a NERC studentship.
Appendix
The function giving the probability of an offspring’s genotype in terms of its parents’ genotypes, P(Oi ∣ Mj, Fk), was calculated assuming Mendelian segregation for parents of known genotype and that parents of unknown genotype produced gametes according to the population allele frequencies. Mutation and mis-scoring of alleles were described by a single process with rate µ per gamete per generation, which changed allele length by one unit up or down.
We will write T(A ∣ Pi) for the probability that a parent transmits an A allele to its offspring. We will also use the more specific terms T(A ∣ Mj) for the mother and T(A ∣ Fk) for the father. We can then calculate the probabilities of the genotypes AB and AA using the standard expressions:
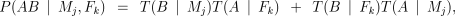
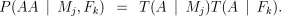
The probability of a parent transmitting an A allele is given by the expression
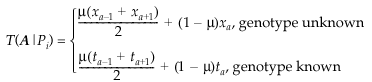
The first term in each case represents the possibility that the parent had an allele of adjacent length, but that it was converted to an A by mutation (or mis-scoring). The second term deals with the case where an A was transmitted without mutation (or mis-scoring).
In the case when the parent’s genotype is unknown, the terms xa, xa+1 and xa−1 are the population frequencies for, respectively, the A allele (xa), the next largest allele (xa+1) and the next smallest (xa−1). When the parent’s genotype is known, ta represents the probability of obtaining an A allele under Mendelian segregation (i.e. 0.5 if the genotype is AB, 1 if it is AA).
The calculation of the likelihood also requires the term P(Mj,Fk ∣ θ) which gives the probability of a particular pair of parents for offspring i before the genotypic data were observed, given the parameter values θ. We assume that θ describes the biology of the species sufficiently, so that knowing the identity of the mother j gives no further information about the father k. In that case, the term can be calculated as the product of the values for each parent:

These were calculated according to:
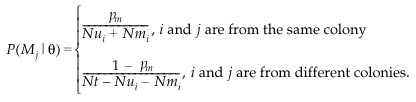
The parameter pm is the probability that i and j are from the same colony. Nui and Nmi are the number of unmarked and marked females in i’s colony and Nt is the total number of females. The upper expression gives an equal probability of being the mother to all females in the colony; the lower gives an equal probability to all outside females.
The value for fathers is calculated similarly:
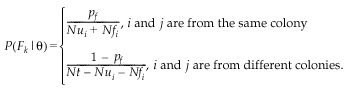
Recall that, as we assume an equal sex ratio, Nui and Nt are the same for adult males and females. The essential difference is that parameter pf replaces pmi and Nfi refers to marked males.
Implementation of the Metropolis algorithm
An arbitrary combination of parameters was chosen from the prior distribution to start the run. At each step in the algorithm a new value was chosen for each parameter from a uniform distribution 1/10th of the total range, centred on the current value. The value, Lnew, was calculated for the new parameter set θnew according to

If Lnew was greater than the value for the previous combination, Lold, then the algorithm stepped to the new values. If it was smaller, then the step to the new values was accepted with probability Lnew/Lold, otherwise the old values were retained.
After a burn-in period of 25 000 iterations the distribution of parameter values for the next 250 000 iterations was recorded. The relative densities of the hm values are shown in Fig. 3. The distributions from replicate runs from different starting points were essentially indistinguishable. The pascal version of the program is available on request from R. A. Nichols ([email protected]).
Assumptions
Population size was assumed to be equal across years and in a 1:1 sex ratio. Knowledge of the species biology and experience of collecting from these populations suggests that these are close approximations (Entwistle et al. 2000). The error/mutation rate was set at µ = 1/100 which is higher than that detected when samples were scored twice (1 out of 855), and is in excess of observed mutation rates for microsatellites. The expression for T(A ∣ P) assumes that allele frequencies are equal between roosts. This is supported by a small intercolony FST estimate within Deeside (0.015; T. M. Burland, unpublished). The prior distributions are supported by ringing evidence, apart from those for hf (the parameter of interest) and Nt. The sensitivity of hf to the latter was investigated by carrying out runs with Nt fixed to its minimum and to its maximum. This shifted the estimates of hf, but did not result in overlapping distributions for hf and hm.
References
Tamsin Burland is a postdoctoral research assistant at Queen Mary, University of London. This work formed part of her PhD, carried out at the Zoological Society of London and Aberdeen University. Elizabeth Barratt, formerly a research fellow at the Zoological Society of London, is currently working as a wildlife consultant, specializing in bats. Richard Nichols is Reader in Genetics at Queen Mary, University of London, and uses Markov chain Monte Carlo methods to estimate parameters of biological interest from molecular genetic data. Paul Racey is Regius Professor of Natural History at Aberdeen University, where he heads NERC’s Molecular Genetics in Ecology Initiative.




