Assignment of paternity groups without access to parental genotypes: multiple mating and developmental plasticity in squid
Abstract
We present a novel approach to investigating sibling relationships and reconstructing parental genotypes from a progeny array. The Bayesian method we have employed is flexible and may be applicable to a variety of situations in addition to the one presented here. While mutation rates and breeding population allele frequencies can be taken into account, the model requires relatively few loci and makes few assumptions. Paternity of 270 veined squid (Loligo forbesi) hatchlings from three egg strings collected from one location was assigned using five microsatellite loci. Paternal and maternal genotypes reconstructed for each of the three strings were identical, strongly indicating that a single female produced the strings that were fertilized by the same four males. The proportion of eggs fertilized was not equal between males in all three strings, with male 1 siring most offspring (up to 68% in string 1), through to male 4 siring the least (as low as 2.4% in string 1). Although temperature had a profound effect on incubation time, paternity did not affect this trait at 12 °C or 8 °C.
Introduction
Studies of mating systems, behaviour and selection have engendered considerable interest in investigating sibling relationships within a mixed parentage brood or half-sib ‘progeny array’ (for instance, Baker et al. 1999; Dewoody et al. 2000; Neff et al. 2000a,b; Valenzuela 2000). Recent investigation of the veined squid, Loligo forbesi, showed that females of this species produce egg strings of mixed paternity, although the precise number of parents and full-/half-sibling relationships within broods were not identified (Shaw & Boyle 1997). We have extended this approach considerably with a more detailed analysis of genetic relationships within egg strings, and investigated novel methods for assignment of paternity without access to parental genotypes. Our method has wider applications than the examples presented here.
Squid are notable for their short life span (approximately 1 year), rapid growth rate and large, terminal reproductive effort (Boyle & Boletzky 1996). Mating of L. forbesi, as in other cephalopods, involves the transfer of packets of sperm (spermatophores) from male to female. L. forbesi females lay eggs in batches of approximately 100 in encapsulated strings, clusters of which are found attached to rocks or other hard surfaces, such as the lines of fishing creels. Observation of mate-guarding by large males and opportunistic copulation by smaller, ‘sneaker’ males indicates that loliginid females may mate with several different males before depositing spawn (F. P. DiMarco & R. T. Hanlon, unpublished data in Hanlon & Messenger 1996; R. T. Hanlon M. J. Smale & W. H. H. Sauer, unpublished data in Hanlon & Messenger 1996; Hanlon 1996). Association of parents and offspring in the wild, would require the capture of squid and eggs at the point of spawning; clearly capture of all possible fathers would be impossible.
Investigation into genetic components of growth rates in squid has been promoted by two observations. First, embryos of loliginid squid show clear differences in embryonic developmental rate within egg strings (P. R. Boyle, unpublished observation). Second, catch survey data indicates that L. forbesi populations have a bi-modal distribution of size (mantle length) at maturity, most clear among males, which may be related to growth rate (Boyle & Pierce 1994; Collins et al. 1999). In view of these observations, and the fact that single egg strings may contain the progeny of several males, we have incubated wild-caught egg strings and collected emerging hatchlings in a controlled, laboratory environment in order to determine whether paternity influences embryonic development time. Investigation into the genetic component of quantitative traits in the absence of full pedigree is an emerging field (see Thomas & Hill 2000). This work presents a method for reconstructing sibships for such studies where no pedigree is available.
The problem of inferring sibling relationships from genetic data when we have unknown parental genotypes is, in essence, a clustering problem. Offspring cluster into groups defined by shared parentage but resolution of these groups is a difficult problem. A pair of individuals taken from the same group may not share any common alleles over all marker loci. Information about clustering comes through the patterns of shared alleles across all offspring and for each locus combined. Clustering based on estimated relatedness using the R coefficient of Queller & Goodnight (1989) has been used recently to infer paternity (Valenzuela 2000), however, this approach gives no estimate of uncertainty, and proves unreliable for the data presented here.
Approaches to paternity inference based on likelihood (e.g. Marshall et al. 1998) are inappropriate when parental genotypes are unavailable, as we have to sum over all possible parental genotypes (Dewoody et al. 2000). In all but the simplest of problems this is impossible: for three fathers with four marker loci and five alleles per locus, there are of the order 1014 different sets of paternal genotypes. Further combinatorial explosion occurs when we consider the possible sibling-relationships within the sample. Neff et al. (2000a,b) developed probability models for the estimation of the number of parents and relative proportion of offspring when partial parental genotypes and allele frequencies in the breeding population are available. However the method does not estimate the relatedness of offspring.
A parsimonious approach, paternity assignment ‘by eye’— picking the minimum number of males consistent with the offspring genotypes — is a useful way of assessing the minimum number of fathers (method 1: see below). As with phylogeny reconstruction, a parsimonious estimator may be accurate when there are sufficient highly polymorphic markers. However, this approach has severe limitations: the true number of fathers tends to be underestimated; there is no way of determining uncertainty of estimates, and misscoring and mutation cannot be dealt with easily. Furthermore, without a framework for assessing which paternity assignment is better, there may be more than one equally parsimonious solution.
Recently there has been an increase in the use of Bayesian methodology in genetics (Shoemaker et al. 1999; Pritchard et al. 2000 describe a recent application to genotype clustering). In Bayesian inference, probability models are fitted to data and results summarized as a posterior probability distribution of model parameters and unobserved random variables (Gelman et al. 1995). This approach has the advantages of asking directly relevant questions and giving a framework for the inclusion of other pertinent information, such as allele frequencies in the breeding population from which the sample was taken.
With complex problems it is generally not viable to calculate the posterior distribution directly. However, advances in computationally intensive statistical techniques, in particular Markov chain Monte-Carlo (MCMC), make it possible to sample from the distributions of interest for problems with complex dependencies. Inference can then be based on summary statistics from these samples.
Here we take a Bayesian approach, modelling the joint distribution of all the observed data (genotypes of the sample and the breeding population) and unobserved quantities of interest (relationships within the sample and the number of parents). A key advance is to use data augmentation (Gelman et al. 1995) to add further unobserved variables — the genotypes of the parents — making likelihood calculations feasible for large problems.
We present a computationally tractable method for drawing inferences about sibling relationships within a sample (method 2: see below). This method uses a combination of MCMC techniques to sample from the distribution of parents and sibling relationships that could have produced the observed sample, proportional to their probability under the model. This approach differs from conventional simulations (Dewoody et al. 2000) by simulating only those sibling relationships and parental genotypes that could lead to the observed offspring genotypes. Unlike the method of Neff et al. 2000a, the method requires no knowledge of any putative parental genotypes, although such information could be incorporated into the model. We use the method to draw inferences about sibling relationships within squid egg strings, and investigate the properties of inferences based on less complete data. As in previous studies, the number of loci and allelic diversity are important factors affecting the confidence with which assignments can be made, with number of loci being the more significant (Bernatchez & Duchesne 2000). We find that three loci may be sufficient to give good discrimination for polymorphic markers (greater than 10 alleles). However, less polymorphic loci demand many more markers.
Materials and methods
Egg-string collection and rearing
Egg-string masses were collected in the 1997–98 spawning season, courtesy of creel fisherman in the Dunstaffnage area of Argyll, Scotland. The egg-masses were held in seawater until removed into the laboratory. The frequency with which the creel pots were lifted and egg-strings collected ensured that no more than 24 h would elapse between collection and laboratory rearing.
Three egg strings were separated from a single egg mass (collected in January 1998) and held in seawater at fixed temperatures of 12 °C (string 1) or 8 °C (strings 2 and 3). Light was maintained at a constant 12 h/12 h-light/dark regime. As the Loligo forbesi embryos hatched, they were collected from each string daily and stored in ethanol.
DNA extraction and microsatellite analysis
DNA was extracted from each individual hatchling using a proteinase K, phenol–chloroform procedure (Jones et al. 1997). DNA was resuspended in TE buffer (10 mm Tris-HCl pH 7.5, 1 mm EDTA). Concentration of DNA was estimated by fluorimetry using a Hoeffer DyNA Quant 200 fluorimeter, and the DNA was diluted to a concentration 5 ng/µL. The DNA from each individual was used as template in polymerase chain reactions (PCR) using fluorescent-labelled oligonucleotide primers (PE-Biosystems) designed to amplify the L. forbesi microsatellite loci Lfor5, Lfor6, Lfor11, Lfor13 and Lfor15 (Table 1). PCR mixes (10 µL) contained 20 ng of template DNA, each deoxynucleotide triphosphate at 200 µm, each primer at 500 nm, 0.02 units of Taq polymerase (Bioline), 1× PCR buffer [16 mm (NH4)2SO4, 67 mm Tris-HCl, pH 8.8, 0.01% Tween 20] and MgCl2 at concentrations given in Table 1. Thermal cycling was as follows for all loci except Lfor11: 2 min at 92 °C, then 30 cycles of 92 °C for 1 min, 1 min at specific annealing temperature (Table 1) and 72 °C for 10 s. Themal cycling for Lfor11 was as follows: 2 min at 92 °C, 10 cycles of 92 °C for 30 s, 30 s at 55 °C reducing by 0.5 °C per cycle, then 25 cycles of 92 °C for 30 s, 30 s at 55 °C, and a final extension for 5 min at 72 °C. Alleles were scored from 4% polyacrylamide denaturing gels run by NCIMB Ltd, University of Aberdeen, UK, for 1 h at 750 V on an ABI Prism 377 DNA sequencer.
| Microsatellite locus | Number of alleles | MgCl2 concentration (mM) | Annealing temperature (°C) | Reference | GenBank accession no. |
|---|---|---|---|---|---|
| 1 Lfor5 | 12 | 2.5 | 57 | Shaw (1997) | U66151 |
| 2 Lfor6 | 8 | 2.5 | 57 | Shaw (1997) | U66152 |
| 3 Lfor11 | 18 | 2.0 | 55–50 | Emery et al. 2000 | AF167997 |
| 4 Lfor13 | 12 | 2.0 | 55 | Emery et al. 2000 | AF167999 |
| 5 Lfor15 | 21 | 2.0 | 55 | Emery et al. 2000 | AF168001 |
Estimates of background breeding population allele frequencies used were provided by previous population-level studies (Fig. 1) (Lfor5 and Lfor6 from Shaw et al. 1999; Lfor11, 13 and 15 from Emery et al. 2000). Fisher’s exact tests using the genepop 3.1c computer program (Raymond & Rousset 1995) indicated no evidence of linkage disequilibrium between any of the loci used (J. M. Murphy, personal communication).
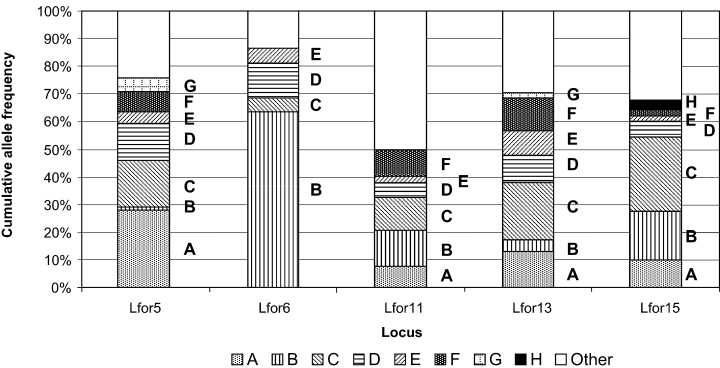
Breeding population allele frequency estimates for the loci used in this study. Alleles found in the egg strings at each locus are represented by the letters A–H in order of PCR product size. Alleles not found in the egg strings but present in the breeding population, are combined in the ‘other’ category. Allele frequencies were obtained from a survey of 48 individuals (Lfor5 and Lfor6; Shaw et al. 1999), 46 individuals (Lfor11 and Lfor13) or 45 individuals (Lfor15).
Parsimonious identification of paternity groups (method 1)
Assuming shared maternity of offspring and Mendelian inheritance of alleles within an egg string, it is possible to assign paternity based on a reconstruction of the minimum number of paternal genotypes. As all progeny inherit one maternal and one paternal allele, every member of the egg string should therefore inherit one of two maternal alleles and one of a pool of paternal alleles, depending on the number of fathers. Maternal alleles can be identified by their higher frequency and the universal presence of one of the two alleles in every member of the string. Paternal alleles from different loci, consistently found associated with each other among the progeny, can be assumed to have come from the same father. Sharing of alleles between the different parents can lead to ambiguities, although using sufficient numbers of highly polymorphic loci should allow any uncertainties to be resolved.
Bayesian method for identification of paternity groups (method 2)
Under the Bayesian (or direct probability) paradigm, inferences are made on the posterior probability distribution of variables of interest, conditional on observed data and prior models. This posterior density is proportional to the prior probability (before any data are observed, based on our knowledge about the problem) multiplied by the likelihood of observing the data under the model. Our data consist of the vectors Y and B, the genotypes of the hatchlings and our sample from the breeding population. Vector Y consists of elements, (yl(i,1),yl(i,2), the genotype of the ith individual at the lth locus where i = 1, … , Ny and l = 1, … L, where Ny is the number of offspring sampled and L the number of loci. Vector B is similarly defined, with i = 1, … Nb , the sample size from the breeding population.
Our primary interest is in the sibling relationships within the sample, described by the parental vectors of fathers, af and mothers, am. The nf fathers are labelled from 1 to nf, with element af(i) giving the father of individual i. Similarly, mothers are labelled from 1 to nm and the mother of j is am(j). If af(i) = af(j) and am(i)= am(j)then offspring i and j are full-siblings; if af(i)≠ af(j) and am(i)≠ am(j), i and j are unrelated; otherwise i and j are half-siblings. Note that these labels are arbitrary (for example, we can swap the labels of males 1 and 2 with no change to the sibling relationships) and thus there are nf! × nm! different labellings that give the same set of sibling relationships.
In order to make inferences about the parentage of the offspring we require probability models for the observed offspring and breeding population genotypes, the parental genotypes and sibling relationships. These involve modelling the mutation process, the distribution of parental genotypes and patterns of sibling relationships in the sample. We model our problem more generally than is needed for the application here, as we allow for the possibility of more than one maternal genotype.
Modelling paternity and maternity share
The most basic assumption is that each male is equally likely to be the father of an individual in the sample, so that the joint probability of paternity vector and number of fathers is:
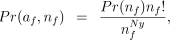 (1)
(1)where P(nf) is the prior probability of nf males and we have the factor nf!, as each labelling of males is equally likely. It has been seen in other species (e.g. Valenzuela 2000) that with shared paternity some males tend to be over-represented (note that we will discuss males, but the same models are used for females also). Hence, this model may be over-simplistic, and we model differential male success. Our model is based on the Ewens’ sampling formula (Ewens 1972), a distribution used to describe the distribution of alleles in population genetics for the infinite allele model, but with applications in other diverse areas such as species allocation in ecology (Lambshead 1986). It has density:
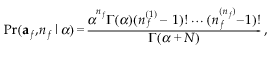 (2)
(2)where nf(i) is the total offspring of male i, and Γ is the gamma function (Abramowitz & Stegun 1965). This is a one-parameter model giving the joint distribution of the number of males contributing to the sample and paternity share. This distribution can be constructed by considering sampling offspring one at a time. The first offspring is allocated to father number one; the second can then share a father with the first, with probability 1/(1 + α), or it can have a different father, with probability α/(1 + α). After you have sampled j offspring, and have seen r different fathers, and with the number of offspring for father i given by ai (so that Σai = j), the probability that the father of the next offspring is father i is αi/(j + α) and the probability that it is a new father is α/(j + α). Thus α is a measure of how likely new types are, and hence large α gives support to many fathers. The distribution gives support to both even and uneven spreads of paternity and has the property of noninterference, that is, if a father is removed, the remaining offspring follow the same distribution. Eqn 2 is different to the standard Ewens’ formula: the ordering of the paternal vector af is important here. We model maternal share with the same distribution with parameter β, and assume independence between paternity and maternity.
Augmented parameter space
In order to simplify likelihood calculations the key idea is to augment the parameter space with parental genotypes, which we denote by the vectors of mothers, M, and fathers, F. These vectors are defined similarly to Y and B, so that M consists of elements, (ml(i,1),ml(i,2)), with i = 1, … , nm, the number of mothers. This simplifies the likelihood calculations considerably, but increases the dimension of the Markov chain. The increased cost of updating the parental genotypes in the Markov chain is far outweighed by the benefit of simplified likelihood calculations; the possible parental genotypes are so numerous that to enumerate them all would be too computationally expensive.
We use a Dirichlet distribution to model the prior density of allele frequencies in the breeding population at each locus (Balding & Nichols 1995; Pritchard et al. 2000),
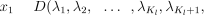 (3)
(3)where Kl is the number of alleles in the offspring at locus l. We assume that all loci are independent. We only consider those alleles in the offspring sample and pool alleles present in the breeding population but not the offspring as allele Kl+1. In all analyses here, we choose λi = 1 for all i giving a uniform distribution on allele frequencies. If in our breeding population, nlk genes with allelic type k are sampled from locus l, the posterior distribution of allele frequencies at this locus is
 (4)
(4)The Dirichlet distribution is conjugate with the multinomial and we do not include the breeding population relative allele frequencies p explicitly. For mother i, and locus l, the probability of sampling parental genotypes (ml(i,1),ml(i,2)) is multinomial-Dirichlet with parameters nl + λ (for details see Gelman et al. 1995). Assuming loci are physically unlinked and parental genotypes independent (and that they give no additional information about allele frequencies) the probability of M, and F is the product over all loci and all parents.
The likelihood of the data, Y, conditional on M, F, af, am and mutation rate, µ, is calculated assuming simple Mendelian inheritance; ignoring mutation, the probabilities can be 0, ¼, ½ or 1. Furthermore, we assume that conditional on parent genotypes, offspring are independent, so that this likelihood may be multiplied over marker loci and individuals. We include the possibility of mutation or misscoring of marker alleles (for our models these are not discriminated, and we use mutation for both). We assume that mutations occur independently and at a constant rate of µ per gamete across all loci and at an equal rate for maternal and paternal gametes. Further, for computational simplicity, we assume that a mutated allele is equally likely to be any of the Kl + 1 alleles with equal probability, including the original allele, i. Thus, the probability that a gamete mutates from allele i to allele j is µ/(Kl + 1) where Kl is the number of alleles in the offspring at locus l. More realistic models are possible, however, our focus of interest is not on the mutation process.
Statistical inference
We collectively denote M, F and other unobserved variables (such as the mutation rate µ) by θ. Our problem is to draw meaningful and correct inferences about af and am conditional on our observed data Y and B. From Bayes’ rule we have
Pr(af,am,θ ∣ Y,B) ∝ Pr(Y ∣ af,am,θ,B)Pr(af,am,θ ∣ B)(5)
The RHS of (5) can be expanded using the distributions described above to give
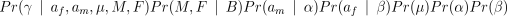
This gives a complete specification of the model, given prior distributions for the mutation rate µ, and the Ewens’ sampling formula parameters α and β.
We use a reversible jump MCMC approach to inference (further details given in the Appendix). A Markov chain with an equilibrium distribution proportional to the RHS of eqn 5 is constructed in the space of all the unobserved variables (M, F, af, am, µ, α, and β). After a suitable burn-in period of 160 000 iterations, samples are collected from the chain. These samples are of length 1000 (short runs) or 5000 (long runs), with 400 iterations between each sample. Initial tests were performed using different starting values and the posterior distributions were identical with these values, further, the correlation between posterior densities and number of fathers was close to zero. Features of the unknown distribution are investigated by examining properties of these samples. Our interests are in the number of mothers and fathers and in patterns of sibship. Details of the MCMC method, its implementation and checks on its correctness are given in the Appendix.
Data analysed
The method was tested against simulated data for which the posterior was known (described in the Appendix). The analyses presented here were performed on all hatchlings from egg string 1. In addition data sets were generated from subsets of the data, in order to investigate the precision of parentage assignment on real data, under different experimental designs. These subsets were constructed in two ways:
- 1
From subsets of the loci in the true sample. Thus, we have 5 data sets with a single locus, 10 with 2 loci, 10 with 3 loci and 5 with 4 loci. This enabled us to investigate how may loci were appropriate for paternity assignment.
- 2
By rebinning the original data. This was done by counting the alleles at each locus l in the background sample KlB and then dividing the range of alleles into KlB/2 evenly spaced intervals. The alleles were rebinned and labelled by the midpoints of these new intervals, and the same intervals were used to bin the offspring data. Rebinning the data like this was not designed to model the allocation of alleles, rather we wanted to investigate what levels of precision were obtained by using less variable data. Binning the data in this way allows us to keep the features of data from a practical survey, rather than simulated data, while enabling us to consider the effects of less variable marker loci.
Data sets were constructed using 1 and 2 (above) individually and by a combination of both. This gave a total of 63 data sets that were analysed.
Prior distributions
The prior for the mutation rate was chosen to be a gamma distribution with a shape parameter of 2, and mean 0.001. The 95% equal tail probability interval lies between 0.00014 and 0.0028, which is in line with observed mutation rates for microsatellite markers (Weber & Wong 1993), but allows values as low as 5 × 10−6 and as high as 5 × 10−3 with low probability. Prior values for the distribution of paternal and maternal vector parameters, α and β, were more difficult to quantify, but for α a gamma distribution with shape parameter 1 and mean 0.25, and for β a gamma with shape parameter 1 and mean 0.005 were used. The prior number of fathers and mothers produced from these can be seen in Table 2. A low probability of more than one mother for the egg string was allowed in case of laboratory error, and to improve the mixing properties of the Markov chain.
| 0 | 1 | 2 | 3 | 4 | 5 | ≥ 6 | ||
|---|---|---|---|---|---|---|---|---|
| Number of fathers | Posterior | — | 0 | 0 | 0.0004 | 0.8598 | 0.1394 | 0.0004 |
| Prior | — | 0.4562 | 0.2560 | 0.1452 | 0.0744 | 0.0354 | 0.0328 | |
| Number of mothers | Posterior | — | 0.9994 | 0.0006 | 0 | 0 | 0 | 0 |
| Prior | — | 0.9762 | 0.0234 | 0.0004 | 0 | 0 | 0 | |
| Total mutations | Posterior | 0.0004 | 0.7550 | 0.2312 | 0.0128 | 0.0006 | 0 | 0 |
| Prior | 0.5032 | 0.2888 | 0.1314 | 0.0498 | 0.0166 | 0.0068 | 0.0034 |
Source code, an extended manual and executables for the Parentage computer program used for the analysis with example data are available for download (http://www.maths.abdn.ac.uk/~ijw).
Data revision using internal checks
In identifying a hypothesis for parental allele distribution by method 1 or method 2, alleles among the offspring also become apparent that are not compatible with it, assuming Mendelian inheritance. Such alleles are an indication of mutations, misscored alleles, or that the hypothesis is incorrect. Additionally, individuals that are difficult to assign to a paternity group, or whose assignment is ambiguous or in doubt can be identified. In the case of the data presented here, method 1 was used as an initial screen of egg string 1. Repeat PCR reactions and gel electrophoresis of alleles not compatible with a possible 3-father model identified misscored alleles among the incompatible group and confirmed that a fourth father was possible. This was confirmed by repeating the process with egg strings 2 and 3. Method 2 has also independently been used to identify alleles requiring to be checked in a similar way. It has not proved necessary to increase the value of µ for these initial screens.
Results
Parsimonious identification of paternity groups (method 1)
There were up to eight alleles per locus indicating multiple paternity with a minimum of three fathers associated with each string. Comparison of the genotypes of every hatchling in the three egg strings allowed their assignment into paternity groups which are shown in Table 3. The same set of alleles was found at each locus in all three strings, with the exception of the rare allele E from locus 1 which was absent from egg string 1.
| Putative Maternal (M) and Paternal (P) alleles at loci 1–5 | Number of hatchlings | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 (Lfor5) | 2 (Lfor6) | 3 (Lfor11) | 4 (Lfor13) | 5 (Lfor15) | String 1 | String 2 | String 3 | |||||||||
| Paternity group | M | P | M | P | M | P | M | P | M | P | n | % | n | % | n | % |
| Group 1 | C F | F H | B B | D E | A C | D E | F C | B G | A F | D H | 57 | 67.9 | 61 | 63.5 | 48 | 53.3 |
| Group 2 | C F | B G | B B | B C | A C | B C | F C | D F | A F | C E | 17 | 20.2 | 24 | 25.0 | 22 | 24.4 |
| Group 3 | C F | A D | B B | A F | A C | C F | F C | A C | A F | B G | 8 | 9.5 | 8 | 8.3 | 16 | 17.8 |
| Group 4 | C F | A E | B B | B B | A C | C E | F C | C E | A F | B E | 2 | 2.4 | 3 | 3.1 | 4 | 4.4 |
| Exception 1 (eggstring 1) | C | F | B | D | C | D | C | G | E | H | Placed in group 1 | |||||
| Exception 2 (eggstring 3) | F | H | B | E | C | D | F | B | F | G | Placed in group 1 | |||||
Identification of putative maternal alleles was possible for all individuals at all loci except locus 4, where individuals homozygous for two alleles (i.e. CC and FF individuals) indicated that both maternal alleles were also present amongst the fathers. Because of this, it was not possible to distinguish maternal/paternal alleles for CF heterozygotes. Identical maternal alleles were found for all loci in all three strings, and as these came from a single location, it was assumed that they were all laid by the same female.
Groups of hatchlings that shared the same father were then constructed based on association of paternal alleles at different loci, assuming Mendelian inheritance. With no mutations or misscoring of alleles, each full sibling group should contain no more than two paternal alleles. The four paternity groups constructed for all three strings contained the same sets of alleles and were assumed to be the offspring of the same four males in each case. Ambiguous maternal/paternal alleles at locus 4 were then assigned based on the homozygous members of their particular paternity group (i.e. the presence of CC homozygotes in group 2 suggested that C was the paternal allele in CF heterozygotes).
Two individuals had alleles that did not conform to the expectations of Mendelian inheritance, both with an allele at locus 5 that was not consistent with its placement in a full-sibling group based alleles at all other loci (highlighted in Table 3). The first of these (in string 1) was placed in paternity group 1. At locus 5, this individual had the genotype EH. Allele H is consistent with the paternal alleles found in group 1 (all have either D or H). Allele E however, is not consistent with the maternal alleles found at locus 5 in any of the strings (alleles A or F). The second of these individuals (egg string 3) was also placed in paternity group 1. Its FG genotype was consistent with the maternal alleles in the strings, but paternal allele G was not found among the other members of group 1. All alleles of both individuals at other loci were consistent with their placement in group 1. Identification of mutations, as opposed to multiple paternity, has been discussed by Fitzsimmons (1998).
Bayesian identification of paternity groups (method 2)
The results presented here are for egg string 1. Analysis of egg strings 2 and 3 produced concordant results, identifying the same maternal genotype and paternity groups (Table 3). Analysis of all 3 strings together essentially eliminated uncertainty in the allocation of offspring to each of the four paternity groups (results not shown).
Table 2 gives the results of a long run of 5000 samples from the posterior distribution for the original data, with the priors (results before observing any data). Four fathers have by far the highest support (86% of the time) with a small (0.4%) posterior probability of three and six fathers. The posterior probability of five fathers was 14%, high compared with the prior. Despite this evidence of five or more fathers, large uncertainty in paternity was restricted to three offspring only (Fig. 2). For binned data the uncertainty in paternity assignment was more serious. Seventy-six per cent of the time, the data support a single mutation with a small chance of two or more mutations.
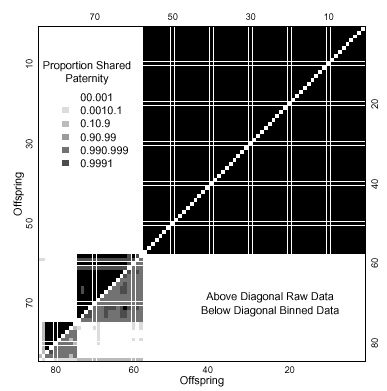
Shared paternity for string 1. The horizontal and vertical axes indicate individual offspring (1–84) sorted by paternity group and hatching date within each group. Squares above the diagonal indicate inferences based on the full dataset, and those below the diagonal are based on binned data (binning technique described in text). Black squares represent pairs of individuals who share a father with high probability (> 0.999) and white squares a low probability (< 0.0001), intermediate values indicated in legend. Therefore, individuals 1–57 share the same father with a probability of between 0.999 and 1 using unbinned or binned data. Values for both analyses based on 5000 values sampled from the posterior distribution with a burn-in of 160 000 iterations and a thinning interval of 400 iterations between samples. Prior distributions: µ ~ gamma(2,2000), α ~ gamma(1,4), and β ~ gamma(1,200).
Limited data
String 1 was also examined using limited numbers of loci with both unrestricted and binned allele data in a total of 63 analyses (Table 4). Each analysis consisted of a short run of 1000 samples from the posterior distribution. Unrestricted allele data resulted in estimates of four or five paternity groups (i.e. consistent with using the full data set) with higher frequencies than binned allele data using the same sets of loci, although there was little bias in any of the estimates. For three loci there was a large variation in the consistency of the analyses (Table 5). The proportion with four or five fathers was from 0.19 [loci 1, 4, 5] to 1.00 [loci 1, 2, 3 and loci 3, 4, 5]. From these data it appears that subsets with both loci 1 and 5 produce estimates that are least consistent with using full data. This is confirmed by considering the analysis of just loci 1 and 5 together (results not shown) where less than 10% had four or five fathers, and the median number was three. This is due to the low number of offspring that are associated with the fourth father, for which differences are not seen in loci 1 or 5.
| Number of data sets | Number of Loci | Unrestricted (U) or Binned (B) | Mean fathers | S.D. fathers | p4 | p4 + p5 |
|---|---|---|---|---|---|---|
| 5 | 1 | u | 5.9 | 1.5 | 0.23 | 0.45 |
| 10 | 2 | u | 4.4 | 1.0 | 0.31 | 0.52 |
| 10 | 3 | u | 3.9 | 0.43 | 0.57 | 0.68 |
| 5 | 4 | u | 4.0 | 0.32 | 0.75 | 0.86 |
| 1 | 5 | u | 4.2 | — | 0.83 | 1.00 |
| 5 | 1 | b | 5.3 | 1.6 | 0.18 | 0.35 |
| 10 | 2 | b | 5.9 | 1.5 | 0.16 | 0.35 |
| 10 | 3 | b | 4.9 | 1.2 | 0.29 | 0.49 |
| 5 | 4 | b | 4.3 | 0.46 | 0.51 | 0.73 |
| 1 | 5 | b | 3.9 | — | 0.63 | 0.75 |
| Loci included | Mean fathers | S.D. fathers | Minimum fathers | Median fathers | Maximum fathers | p4 | p4 + p5 |
|---|---|---|---|---|---|---|---|
| 1,2,3 | 4.1 | 0.25 | 3 | 4 | 6 | 0.94 | 1.00 |
| 1,2,4 | 4.0 | 0.71 | 1 | 4 | 8 | 0.63 | 0.76 |
| 1,2,5 | 3.4 | 0.56 | 3 | 3 | 6 | 0.29 | 0.32 |
| 1,3,4 | 3.7 | 0.56 | 1 | 4 | 6 | 0.63 | 0.68 |
| 1,3,5 | 3.3 | 0.47 | 1 | 3 | 5 | 0.28 | 0.28 |
| 1,4,5 | 3.2 | 0.43 | 3 | 3 | 5 | 0.18 | 0.19 |
| 2,3,4 | 4.3 | 0.51 | 4 | 4 | 7 | 0.70 | 0.98 |
| 2,3,5 | 4.2 | 0.53 | 3 | 4 | 6 | 0.73 | 0.94 |
| 2,4,5 | 4.3 | 0.94 | 1 | 4 | 7 | 0.34 | 0.70 |
| 3,4,5 | 4.0 | 0.14 | 4 | 4 | 6 | 0.99 | 1.00 |
| prior | 3.1 | 2.2 | 1 | 2 | 15 | 0.12 | 0.19 |
Egg incubation time and paternity
Time to first hatchling emergence of the strings reared at 8 °C (117 days) was approximately double that of the string reared at 12 °C (58 days). The association between incubation time and temperature was found to be significant (P = 0.0001, r = 0.293) using a Mantel test. There was no apparent relationship between hatching time and paternity (P = 0.3839, r = 0.147), with hatchlings from all four paternity groups emerging throughout the hatching period (Fig. 3).

Daily emergence of hatchlings associated with each of the four putative fathers (see Table 3) from (a) Eggstring 1 (b) Eggstring 2 (c) Eggstring 3.
Discussion
Both methods employed to estimate sibling relationships produce concordant results. However, the parsimonious approach (method 1) is severely limited by its subjectivity, making it difficult to choose between alternative hypotheses, and lacking estimates of confidence for any putative relationship in the egg string. Mutations, which are not individually predictable, also make a simple approach following Mendelian rules hard to implement. It is difficult to decide whether an anomalous allele has been inherited from a rare parent or is the result of mutation, especially when the mutation occurs in the putative paternal allele. In spite of these limitations, method 1 provides a useful procedure for identification of potential sibling relationships, albeit in a limited set of circumstances where all members of a progeny array share one parent.
Using the Bayesian approach (method 2), sibling relationships can be reconstructed with an estimate of confidence for every individual in the egg string, although the unpredictability of mutation is also a potential problem here. Mutation rates in microsatellites are highly variable depending on species, locus and even allele (Schlötterer et al. 1998). There are two individuals in the three strings (270 individuals, 1350 separate microsatellite amplifications) each of which has an allele that does not fit with the other members of the string or paternity group. Both of these anomalies occur at locus 5 (Lfor15). Although mutation cannot be modelled precisely due to the complexity of factors affecting mutation rates and mechanisms, the model permits an appropriate range based on published empirical data, and in practice the method allows identification of possible misscoring of alleles that would artificially increase the mutation rate. In contrast to the subjective estimates of method 1, assumptions used in the model are quantified and may be changed where appropriate. However, paternity may not be resolved from restricted data sets where some alleles are shared between fathers and/or the frequency of offspring from one father is low. Reconstructing paternity groups using method 2 with data from string 1 showed there was most doubt in the allocation of the two individuals assigned to father 4 (Fig. 2). Where such problems exist, it is necessary to re-examine allele scoring and perhaps repeat PCR reactions. This is particularly important where allocation of an individual in a group could rest on a single allele (as in some possible combinations of alleles in groups 3 and 4). Method 2 can be used in this way to produce hypotheses, indicating inconsistencies and difficult allocations which can then be checked (with more loci if necessary). The possibility of cryptic paternity, where some of the offspring from two different males cannot be distinguished due to mutually compatible genotypes in the offspring is accounted for in method 2. However, this assumes a large, outbreeding population where it is unlikely that the potential fathers would be closely related. Loligo forbesi conforms to these expectations in Scottish waters (Shaw et al. 1999).
As the reconstructed genotypes of the putative parents were identical for all the three egg strings, which were found closely associated in the same location, it can be assumed that they were laid by a single female fertilized by the same four males. The sibling group of a particular father constituted a similar proportion of each egg string (Table 3). This suggests mixing of sperm from the different males rather than sequential use of spermatophores by this female, the chance of successful fertilization remaining approximately constant for each male. The relative number of offspring attributed to each male could be governed by a number of factors, the most obvious including the number of spermatophores contributed by each male, and the time between transfer and utilization.
Behavioural mechanisms for sperm precedence have been observed in other cephalopods, such as the cuttlefish, Sepia officinalis, where males flush jets of water at the buccal membrane of the female prior to spermatophore transfer, in an attempt to remove spermatangia from previous matings (Hanlon et al. 1999). Mate guarding in Loligo suggests that there is some investment by males in assuring paternity, but the effort put into and success gained by this strategy will depend on population density and operational sex ratio (Birkhead & Møller 1992). Loligo vulgaris reynaudii forms dense spawning aggregations, with smaller males remaining on the periphery attempting opportunistic copulations (Sauer et al. 1997). In L. forbesi, the sex ratio changes as the breeding season progresses, with early bias towards males (Pierce et al. 1994). Clearly, the frequency and advantages of multiple mating for each sex require further investigation. Possibly in a species with a semelparous life history, where individual offspring have little chance of recruitment, the benefits could be increased fitness, genetic diversity of offspring, and fertility assurance (Smith 1984; Newcomer et al. 1999). Offspring of each of the fathers emerge throughout the hatching period, indicating that time to hatching is not related to paternity under these conditions. The period between spawning and hatching of eggs is strongly influenced by temperature, with the egg string reared at 12 °C taking 58 days until first hatching, while those reared at 8 °C took twice as long (118 days). Hence, the extended spawning period and seasonal spread in reaching maturation in L. forbesi (Boyle & Boletzky 1996; Collins et al. 1997) suggest a strong environmental influence, possibly extending to the within-string differentiation of embryonic maturity previously observed in loliginid squid (P. R. Boyle, unpublished observation). Measurable effects of paternity on developmental traits have still to be elucidated, requiring further work with larger samples of egg strings to determine the frequency of multiple paternity, the average number of fathers per string, and the proportions of eggs fertilized by each. The wide range in the proportion of offspring attributed to each male shows that comprehensive genotyping rather than subsampling of strings is necessary to ensure identification of all fathers.
To conclude, method 1 permits a minimum number of fathers to be assigned to egg strings without access to parental genotypes although assuming single maternity. However, method 2 is more generally applicable, requiring few prior assumptions to estimate both maternal and paternal inputs to progeny arrays. The latter approach should find widespread application in behavioural, ecological and conservation genetic arenas where it is necessary to determine parentage of large progeny arrays of indeterminate provenance in essentially outbred populations.
Appendix
Implementation of MCMC and testing
Here, the MCMC methodology used for the program Parentage will be described. The core of the Monte-Carlo technique is that the distribution of interest and samples from that distribution are interchangeable, and hence inferences about the distribution may be made by investigating properties of random samples from the distribution. Markov chain Monte Carlo (MCMC) methods generate (approximately) random samples from a distribution of interest π(θ) by constructing a Markov chain with equilibrium distribution equal to π(θ). After a suitably long burn-in samples are taken from the chain. To produce approximately independent samples the chain may be thinned by sampling every tth iteration, reducing the correlation between successive samples. Implementation issues about the length of burning and the thinning interval are reviewed in Brooks (1998). For the problem discussed here we have a Markov chain of variable dimension as the number of fathers and mothers, and hence the number of parental genotypes is itself a variable. Hence a variable dimension MCMC must be constructed. Here we used Reversible Jump Markov chain Monte Carlo (RJMCMC).
There are a number of standard methods for the construction of the Markov chain, such as the Metropolis–Hastings algorithm and Gibbs sampling (for further details see Brooks 1998). These give rules for the construction of updating steps to move about the chain. These give a chain with the correct properties provided that the updates produce a chain that is aperiodic and irreducible (it is possible to move between any two states given enough steps). We have a number of such updating schemes, one of which is chosen at random in every iteration of the chain (a random scan). These steps are either Gibbs sampling; Metropolis–Hastings updates and dimension changing Metropolis–Hastings moves (RJMCMC).
Gibbs updates
Gibbs updates work by sampling from the full conditional distribution of some of the components of the chain. While the full distribution may not be accessible, sampling from these full conditional distributions is possible here. The five updating steps that we use are sampling proportional to:
- 1
Pr(af ∣ M,F,am,µ,α,β,Y),
- 2
Pr(am ∣ M,F,af,µ,α,β,Y),
- 3
Pr(af,am ∣ M,F,µ,α,β,Y),
- 4
Pr(M ∣ F,am,af,µ,B), and
- 5
Pr(F ∣ M,am,af,µ,B).
Details of Metropolis–Hastings update steps
Consider changes to a location θ in parameter space. A new candidate location is θ chosen from a proposal distribution q(θ′ ∣ θ) . The new proposal is then accepted if the value of
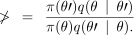 (6)
(6)
is greater than one. If ν is less than one then the new location θ is accepted with probability ν, if it is not accepted, the chain remains at its current location θ. Metropolis–Hastings updates are used to move around the space of values for the continuous random variables µ, α and β, with a proposal distribution centred around the current value and uniform on a logarithmic scale.
Dimension changing updates
Changes to the number of fathers, nf change the dimension of the space as the size of the vector F changes, as do changes to nm. Green (1995) extends the Metropolis–Hastings algorithm described above, giving a recipe that allows for the change in dimension of the space. We take this approach, proposing an increase or decrease in the number of fathers of 1 with equal probability (if nf = 1 then we always increase, but for simplicity we will not deal with this here). We then propose a new paternal vector a′f sample the new genotypes directly in the changed dimension. If the number of fathers is increased then one father, a father k (with nfk > 0 offspring) is chosen uniformly from those available and j[j~unif(1, nfk)], of his offspring are allocated at random to the new father. If the number of fathers is decreased two fathers are chosen at random and their offspring combined. This gives us the new paternal vector a′f. New paternal genotypes are then sampled proportional to
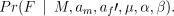
The forward and backward transition densities are thus well defined and we can calculate an acceptance probability, u, in a similar way to the Metropolis–Hastings updates.
Mixing
These steps give good mixing for relatively small problems, up to the size of string 1. Testing with multiple chains from dispersed starting values gave identical results after burn-in. However with larger problems, mixing can become slow. Parentage allows multiple chains to be run in parallel, each with a different stationary distribution, and additional steps where swaps between chains are attempted (Metropolis-coupled MCMC). These distributions are chosen so that the chains have a ‘temperature’ gradient with the hottest chains mixing most quickly, and so that mixing in the slowest chain, with the required stationary distribution is improved. Further details are given on the download page (http://www.maths.abdn.ac.uk/~ijw).
Testing of RJMCMC algorithms
Testing of the algorithm was done in two stages. The first test was to assume that all genotypes were unknown. With no data to learn from, the posterior distribution of offspring share and number of fathers should agree with the prior. This was the case for all models. Further tests were performed by comparing posterior distributions with naïve simulations for very small data sets. Naïve simulations were based on simulating the number of mothers and fathers from the prior distributions; drawing parental genotypes from the breeding population frequencies; simulating sibling relationships, and finally simulating offspring genotypes. If the offspring genotypes agreed with the observed data then the relationships and parental genotypes were retained, otherwise they were discarded. This was repeated until 10 000 sets of relationships had been retained. In all cases the posterior distributions from Parentage agreed with the naïve distributions.
Acknowledgements
This work was conducted under NERC DEMA programme grant GST/02/1723.
References
Aidan Emery uses molecular biological techniques to investigate the genetics and biology of invertebrate species, including disease vectors. He has recently moved to the Natural History Museum. Ian Wilson’s research interests are on the application of computer intensive statistical methods to population genetic problems. Stephen Craig has recently completed a PhD on developmental plasticity in squid. Prof. Peter Boyle has a special interest in determining how cephalopod development relates to aspects of their ecology, population structure, dynamics and recruitment. This output represents one of the primary goals of the NERC DEMA (Developmental Ecology of Marine Animals) Thematic Programme of which he was a steering committee member. Les Noble employs molecular approaches to elucidate the population genetic structure and evolution of a variety of animal systems, with special emphasis on host–parasite interactions.




