Genetic variability characterization of the moroccan houbara bustard (Chlamydotis undulata undulata) inferred from pedigree analysis
Abstract
A Moroccan Houbara Bustard pedigree was analyzed to evaluate the genetic variability in captive breeding population using genealogical approaches. The whole Houbara breeding flock (WP) for the period 1993–2004 was made up of 531 birds comprising 346 females and 185 males. The reference population (RP) comprised 198 individuals ready for reproduction from 2000 to 2004 cohorts. The corresponding percentage of known ancestors was estimated as 98.23% for the parent generation, 41.19% for the grandparent generation and 7.00% for the great grandparents generation. The average generation interval for Houbara was computed as 4.64 years. Genetic variability loss per generation was ascertained using the effective population size (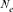 ), the founder genome equivalent (fge), the effective number of ancestors and founders (fa) and (fe), respectively, for the RP and across each cohort. The results showed no bottleneck events in the breed but some loss of genetic variability just after the initiation of the conservation program. However, the annual effective population size based on the realized increase in inbreeding (
), the founder genome equivalent (fge), the effective number of ancestors and founders (fa) and (fe), respectively, for the RP and across each cohort. The results showed no bottleneck events in the breed but some loss of genetic variability just after the initiation of the conservation program. However, the annual effective population size based on the realized increase in inbreeding (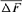 ) was estimated to be 207 for the RP and 1,000 for the WP. With regard to conservation breeding schemes, the genealogical evidence presented here is very useful as it revealed the positive effect of migration on Houbara breeding. The mating strategies will assist in the future control and management of the genetic variability of this population. Zoo Biol. 32:366-373, 2013. © 2012 Wiley Periodicals, Inc.
) was estimated to be 207 for the RP and 1,000 for the WP. With regard to conservation breeding schemes, the genealogical evidence presented here is very useful as it revealed the positive effect of migration on Houbara breeding. The mating strategies will assist in the future control and management of the genetic variability of this population. Zoo Biol. 32:366-373, 2013. © 2012 Wiley Periodicals, Inc.
INTRODUCTION
The Houbara Bustard (Chlamydotis undulata) is an avian species that belongs to the Otididae family. It is divided into three subspecies. Chlamydotis undulata undulata [Jacquin, 1784] is found in Northern Africa (north Mauritania, Morocco, Algeria to Egypt). Chlamydotis undulata macqueenii [Gray, 1832] is found in Asia (from the Middle East to Altai) and lives in Sinai, Arabia, Baluchistan, Jordan, north Caspian Sea, north-west India, Afghanistan, Pakistan, Kazakhstan, Iran, Iraq, and Mongolia. Chlamydotis undulata fuertaventurae [Rothschild et al., 1894] is the endemic subspecies to Canary Islands. The International Union for Conservation of Nature [IUCN, 2011] classifies the Houbara species as “vulnerable.” The Houbara is also prohibited from international trade [CITES, 2012]. In Morocco, since 1993, the subspecies has been bred under captivity in HRH Prince Sultan Bin Abdul Aziz Al Saud International Foundation for Conservation and Development of Wildlife (IFCDW) at Agadir city (30 28N, 9 55W) and in the Desert Ecological Research Station at Errachidia city (31 58N, 4 20W). A total of 107 clutches were collected from north-eastern Morocco between 1993 and 1995 out of which 19 males and 58 females were artificially hatched and used as “wild stock founders” to establish the breeding and conservation program at IFCDW. During the 1996 breeding season 15 wild birds, and in 1998 five additional wild birds, were collected from Errachidia-Erfoud-Boudnib zone and randomly recruited to be part of the foundation breeding population [IFCDW, ]. A total of 1,455 chicks were successfully hatched in captivity between 1995 and 2000, and 454 were released into the wild. At the onset of the Houbara breeding programe, selection of breeding pairs was not based on molecular profiling nor on paternity tests and the breeding operation was planned only according to breeders’ behavioral charts and cycles (artificial insemination [AI], display, semen collection, and egg laying). However, more attention was given to avoid the most critical mating combinations such as: father/daughter, mother/son, and sister/brother. Fortunately, the majority of the necessary records and database about those breeding charts were kept and electronically stored in Houbara studbook and software.
The continual maintenance of genetic diversity is essential and crucial when conserving local threatened breeds. Furthermore, the level of genetic diversity is linked to population adaptability and consequently to the breed's capacity to cope and respond to selection [Mäki-Tanila et al., 2010]. Since 1997, Houbara Bustard genetic diversity for both captive and wild birds has been studied and assessed using an array of molecular markers [Dawson et al., 1999; Idaghdour et al., 2004] but no genealogical study has ever been carried out from bustard populations.
The objective of this study was to analyze the genealogical information of the Moroccan captive Houbara Bustards, to ascertain their generation intervals, genetic diversity, inbreeding, and coancestry, and to compare four different approaches computing the 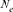 in order to advance genetic and breeding management initiatives and strategies.
in order to advance genetic and breeding management initiatives and strategies.
MATERIALS AND METHODS
Sampling and Paternity Tests
A total of 531 Houbara constitutes the whole population (WP) containing all founders, ancestors, and their offspring. A sample of 110 birds (base population) was made up of wild founders and individuals with unknown parents, and another of 198 individuals from the 2000 to 2004 breeding seasons constitutes the reference population (RP) defined as the population of interest that include living reproductive breeders approaching the last generation. The remaining 223 individuals constitute the population of dead animals from the 1993 to 1999 cohorts. The establishment of the Houbara pedigree and the assessment of paternities were made possible by the utilization of both breeding and molecular information. A set of 22 microsatellites [Chbel et al., 2002] was used to determine paternity of the progeny generated from artificial insemination. Females are usually inseminated by semen mixed from several males in order to enhance the fertilization process and increase the egg production and female reproductive performance.
Genealogical Parameters
Pedigree information was analyzed by computing demographic parameters for WP, the RP as well as for each cohort using Endog 4.8 [Gutiérrez and Goyache, 2005] genetic software. POPREP program [Groeneveld et al., 2009] was used to illustrate the trends of the mean inbreeding across years.
Demographic parameters
To reveal the consequences of the applied random mating system and obtain critical information on the variation of the flock and its evolution over time, three demographic analyses were performed. First, the pedigree depth was assessed by computing the proportion of ancestors known per generation for each offspring [MacCluer et al., 1983]. Second, the equivalent complete generation parameter, called also the mean equivalent generation (ge) was calculated as defined by [Maignel et al., 1996] as the sum of all known ancestors 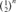 where, n is the number of the
where, n is the number of the 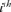 generation separating the individual to each known ancestor, i.e, parents = 1, grandparents = 2, great-grandparents = 3…etc. Third, the evaluation of Houbara generation interval, defined as the mean age of parents when their progeny is selected to be parent, was characterized along four pathways: Mother-Daughter, Mother-Son, Father-Daughter, and Father-Son [James, 1977].
generation separating the individual to each known ancestor, i.e, parents = 1, grandparents = 2, great-grandparents = 3…etc. Third, the evaluation of Houbara generation interval, defined as the mean age of parents when their progeny is selected to be parent, was characterized along four pathways: Mother-Daughter, Mother-Son, Father-Daughter, and Father-Son [James, 1977].
The probability of gene origin
The probability of transmission of a neutral gene from a parent to its offspring is ½, from a grandparent to its progeny is ¼, from a great-grandparent to its descendant is ⅛, and so on. The pedigree of an individual could be traced back to calculate the probability of the contribution of its eventual founders and/or ancestors to its genome. By definition, ancestors refer to the first two reproductive and unrelated parents at generation 0 whereas founders refer to ancestors with unknown parents. Thus the ancestors could be founders or not. The probability of gene origin allows the study of population genetic structure and the assessment of the contribution of ancestors and founders to the global genetic make up.
Houbara genetic diversity was characterized by computing the total effective number of founders, fe [Lacy, 1989] and the total effective number of ancestors, fa [Boichard et al., 1997]. The parameter fe is the number of founders that, if contributing in a balanced way, would be expected to produce the same genetic diversity as in the current population. This parameter is computed following the expression 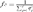 where, qj is the probability of genes contributed by the
where, qj is the probability of genes contributed by the 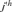 founder and f is the initial genetic stock of founders. The sum of the probabilities of gene origin
founder and f is the initial genetic stock of founders. The sum of the probabilities of gene origin 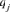 over all founders is equal to 1. It is important to mention that the initial number of founder genes f is often not completely transmitted to the current population because considerable portions are lost by genetic drift. When all founders equally contribute to the population, f is equal to fe.
over all founders is equal to 1. It is important to mention that the initial number of founder genes f is often not completely transmitted to the current population because considerable portions are lost by genetic drift. When all founders equally contribute to the population, f is equal to fe.
Parameter fa refers to the minimum number of ancestors, not necessarily founders, whose contribution to the reference subpopulation is higher than that of their ascendants, thus making allowances for bottlenecks in the pedigree. fa is calculated using the formula 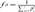 where, piis the probability of genes contributed by the
where, piis the probability of genes contributed by the 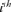 ancestor and f is the total initial genetic stock of the founders. Sometimes, the application of intensive AI programs within populations could lead to sudden reduction in
ancestor and f is the total initial genetic stock of the founders. Sometimes, the application of intensive AI programs within populations could lead to sudden reduction in 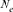 , in this case, the effective number of ancestors becomes lower than the effective number of founders (fa < fe). Furthermore, in order to determine the most significant ancestors with the major genetic marginal contributions within a population or cohort (i.e, all selected individuals in a particular year or breeding season), we applied Boichard's et al. [1997] algorithm. For each ancestor i, the computation of the marginal contribution
, in this case, the effective number of ancestors becomes lower than the effective number of founders (fa < fe). Furthermore, in order to determine the most significant ancestors with the major genetic marginal contributions within a population or cohort (i.e, all selected individuals in a particular year or breeding season), we applied Boichard's et al. [1997] algorithm. For each ancestor i, the computation of the marginal contribution 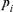 , defined as the contribution not yet explained by the other already selected ancestors, was performed in an iterative way by subtracting the contribution of the already considered ancestor
, defined as the contribution not yet explained by the other already selected ancestors, was performed in an iterative way by subtracting the contribution of the already considered ancestor 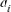 from the probabilities of gene origin
from the probabilities of gene origin 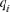 following the equation:
following the equation: 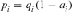 . The probabilities of gene origin were then divided by the total number of individuals with the gene of interest so that the ancestor contributions sum to 1. Finally, by ordering the ancestors based on their genetic contributions from the biggest to the smallest, the computation of the most contributing ancestors explaining a desired percentage of genetic diversity in a particular cohort was possible (e.g., 50%).
. The probabilities of gene origin were then divided by the total number of individuals with the gene of interest so that the ancestor contributions sum to 1. Finally, by ordering the ancestors based on their genetic contributions from the biggest to the smallest, the computation of the most contributing ancestors explaining a desired percentage of genetic diversity in a particular cohort was possible (e.g., 50%).
The concentration of gene origin was also assessed by calculating the number of founder genome equivalents (fge) [Lacy, 1989], defined as the number of founders that still exist in the actual population and would be expected to produce the same genetic diversity as in the population under study if the founders were equally represented and no loss of alleles occurred. The parameter fge was computed as: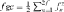 , where
, where 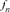 is the gene frequency of the
is the gene frequency of the 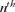 founder and f is the initial genetic stock of the founders. The fge takes into account all causes of genetic drift.
founder and f is the initial genetic stock of the founders. The fge takes into account all causes of genetic drift.
To calculate the loss of genetic diversity per generation in a particular RP, i.e, the expected heterozygosity originated by limited numbers of founders and its balanced contribution, we used the 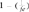 equation. A similar formula was applied on the founder genome equivalent parameter
equation. A similar formula was applied on the founder genome equivalent parameter 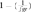 as it is directly related to the present coancestry.
as it is directly related to the present coancestry.
Inbreeding, coancestry, and Ne
By definition, the inbreeding coefficient (F) is the probability that an individual carries two alleles identical by descent (IBD) [Wright, 1931]. F was computed following Meuwissen and Luo [1992] and the mean F for each cohort from 1998 to 2004 was obtained by averaging F of the total individuals n. The coancestry coefficient between two individuals is the probability that two alleles at a locus taken at random are IBD [Malécot, 1948]. The mean coancestry and inbreeding coefficient of the entire metapopulation and the mean coancestry of subpopulations were used to obtain Wright's [1978] F-statistics (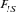 ).
).
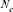 ). This population estimator defined by Wright [1931], as the number of breeding individuals of an idealized population that would lead to the same calculated inbreeding coefficient, loss of heterozygosity or variance in allele frequency under random genetic drift, is found to be sensitive to inbreeding effect and to selection [Crow and Kimura, 1970; Tallmon et al., 2004]. The (
). This population estimator defined by Wright [1931], as the number of breeding individuals of an idealized population that would lead to the same calculated inbreeding coefficient, loss of heterozygosity or variance in allele frequency under random genetic drift, is found to be sensitive to inbreeding effect and to selection [Crow and Kimura, 1970; Tallmon et al., 2004]. The (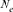 ) parameter was computed by comparing three different genetic methodologies and one demographic approach. First, via the increase in inbreeding per generation ΔF (
) parameter was computed by comparing three different genetic methodologies and one demographic approach. First, via the increase in inbreeding per generation ΔF (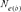 ) [Meuwissen and Luo, 1992]. Ne was obtained by computing the regression coefficient (b) of the individual inbreeding coefficient over the equivalent complete generations, and considering the corresponding regression coefficient as the increase in inbreeding between two generations and consequently,
) [Meuwissen and Luo, 1992]. Ne was obtained by computing the regression coefficient (b) of the individual inbreeding coefficient over the equivalent complete generations, and considering the corresponding regression coefficient as the increase in inbreeding between two generations and consequently, 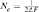 . Second, based on individual increase in inbreeding coefficient (
. Second, based on individual increase in inbreeding coefficient (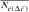 ) of Gutiérrez et al. [2009] computed as:
) of Gutiérrez et al. [2009] computed as: 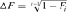 where,
where,  is the individual F coefficient and t the equivalent complete generation. Effective population size (
is the individual F coefficient and t the equivalent complete generation. Effective population size (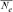 ), named “realized effective size” by Cervantes et al. [2008], was computed from
), named “realized effective size” by Cervantes et al. [2008], was computed from 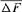 as
as 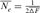 by averaging the ∆Fis of the n individuals in a given reference subpopulation. In this study, only individuals with at least two equivalent generations known were used. Third, using the paired increase in coancestry (
by averaging the ∆Fis of the n individuals in a given reference subpopulation. In this study, only individuals with at least two equivalent generations known were used. Third, using the paired increase in coancestry (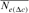 ) proposed by Cervantes et al. [2011] as
) proposed by Cervantes et al. [2011] as 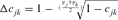 where,
where, 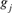 and
and 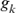 are the equivalent discrete generations of the parents j and k and
are the equivalent discrete generations of the parents j and k and 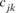 is the inbreeding F of the j and k's progeny. For idealized populations under random mating, a realized effective population size based on coancestry is computed as
is the inbreeding F of the j and k's progeny. For idealized populations under random mating, a realized effective population size based on coancestry is computed as 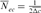 by averaging the increase in coancestry for all pairs of individuals in a reference subpopulation. In this study, only individuals with at least one equivalent generation known were used. Finally, Ne estimator was inferred, using a demographic approach, from the variance family size as proposed by Hill's [1979] equation as:
by averaging the increase in coancestry for all pairs of individuals in a reference subpopulation. In this study, only individuals with at least one equivalent generation known were used. Finally, Ne estimator was inferred, using a demographic approach, from the variance family size as proposed by Hill's [1979] equation as:
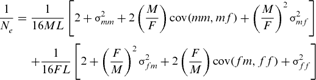
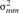 and
and 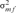 are the variances of the male and female offspring of a male,
are the variances of the male and female offspring of a male, 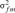 and
and 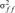 are the variances of the male and female offspring of a female, and
are the variances of the male and female offspring of a female, and 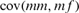 and
and 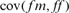 the respective covariances.
the respective covariances.RESULTS
Demographic Parameters
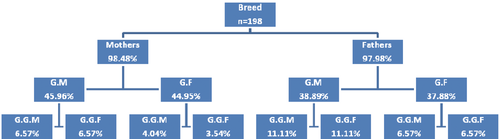
In Figure 1, the details of the pedigree quality in Houbara RP are shown. The percentage of completeness was computed as 98.23% for the parental generation, 41.19% for the grandparent generation and 7.00% for the third-generation of the great-grandparents. Table 1 gives generation lengths for the four selection paths (parents/offspring) in the WP and RP. The mean generation interval for the RP was equal to 4.64 years and slightly higher than for the WP estimated to 3.97 years. Furthermore, for both populations, generation interval for the selection path between the father and its daughter is the longest (4.05 years in WP and 5.25 years in RP). Across the last 9 years, the mean equivalent generation has known a nonregular increase in its numbers and varied from 0.80 in 1995 to 2.05 in 2004. This could be justified by the irregular inclusions of wild animals, mainly during the 1996 and 1998 breeding seasons. The low values in 2002 are due to the low number of individuals so, to the slightest level of pedigree information (Table 2).
| WP | RP | |||||
|---|---|---|---|---|---|---|
| Parents-offspring | N | Years | SE | N | Years | SE |
| Mother-Daughter | 57 | 3.95 | 0.17 | 13 | 4.49 | 0.57 |
| Mother-Son | 26 | 3.83 | 0.26 | 10 | 4.34 | 0.42 |
| Father-Daughter | 55 | 4.05 | 0.20 | 13 | 5.26 | 0.59 |
| Father-Son | 24 | 3.96 | 0.31 | 9 | 4.30 | 0.62 |
| Total | 162 | 3.97 | 0.11 | 45 | 4.64 | 0.25 |
| WP | RP | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2004 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of individuals | 531 | 198 | 40 | 17 | 20 | 52 | 78 | 58 | 68 | 86 | 67 | 9 | 36 |
| Number of founders | 113 | 99 | — | — | 15 | 53 | 47 | 55 | 56 | 68 | 60 | 25 | 45 |
| Number of ancestors | 113 | 99 | — | — | 15 | 50 | 46 | 53 | 54 | 68 | 58 | 7 | 41 |
| Effective number of founders (fe) | 32 | 34 | — | — | 11 | 42 | 24 | 36 | 28 | 34 | 29 | 18 | 20 |
| Effective number of ancestors (fa) | 32 | 34 | — | — | 11 | 41 | 24 | 35 | 28 | 34 | 28 | 9 | 20 |
| No. Ancestors explaining 50% | 12 | 13 | 40 | 17 | 4 | 20 | 9 | 14 | 11 | 13 | 10 | 5 | 8 |
| Founder genome equivalent (fge) | — | 28 | — | — | 9 | 36 | 21 | 26 | 23 | 26 | 21 | 9 | 13 |
| Mean equivalent generation (ge) | 1.00 | 1.50 | — | — | 0.80 | 0.40 | 0.90 | 1.05 | 1.10 | 1.26 | 1.48 | 1.16 | 2.05 |
| Generation interval (GI) | 3.97 | 4.64 | — | — | 1.92 | 2.93 | 3.72 | 3.48 | 4.90 | 4.43 | 5.00 | 3.82 | 3.90 |
| Fis | −0.0110 | −0.0114 |
The Probability of Gene Origin
Table 2 describes the evolution of gene concentration in the WP and RP in addition to within each cohort. The WP and RP have roughly the same effective number of founders and ancestors (32/32 and 34/34), respectively indicating that no bottlenecks were detected as a combination of an almost nonrandom mating policy and a short pedigree depth. To explain 50% of the genetic variability, a total of 12 and 13 ancestors were enough, respectively in the WP and RP. For the patterns of genetic diversity in the current population, a total of 28 founder genome equivalents were found in the RP. The contribution of the main ancestors to the RP is reported in Table 3. The 12 wild birds explained more than half of the genetic variability within the breed. In terms of number of progeny, the most represented ancestors are the first four sires born in 1993 with 162 chicks and more than quarter of genetic variance. Also, more than 86% of the total founders have contributed to the RP.
| Ancestors | Sex | Year of birth | Genetic variance (%) | Progeny |
|---|---|---|---|---|
| 930019 | ♂ | 1993 | 8.72 | 55 |
| 930035 | ♂ | 1993 | 6.60 | 38 |
| 930041 | ♂ | 1993 | 6.42 | 29 |
| 930037 | ♂ | 1993 | 5.81 | 40 |
| 930021 | ♂ | 1993 | 4.70 | 25 |
| 930096 | ♀ | 1993 | 3.89 | 18 |
| 930001 | ♀ | 1993 | 3.35 | 14 |
| 940030 | ♂ | 1994 | 2.89 | 16 |
| 960100 | ♂ | 1996 | 2.48 | 17 |
| 940010 | ♂ | 1994 | 2.33 | 18 |
| 930079 | ♀ | 1993 | 1.85 | 14 |
| 940023 | ♂ | 1994 | 1.73 | 13 |
The lost genetic diversity using the effective number of founders was calculated to 97.05% per generation and using the founder genome equivalent to 96.42% per generation.
Inbreeding, coancestry, and 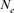
The evolution of the average inbreeding (F) in relation with the number of inbred animals across years is shown in Figure 2. The number of inbred individuals in 1998, 2000, 2001, and 2004 was 1, 3, 1, and 7, respectively. The total was 11 in RP. The average inbreeding coefficient curve fluctuated according to the number of inbred individuals in each cohort and ranged from 0.22% in 1998 to 1.61% in 2004. The realized increase in inbreeding (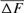 ) was concluded from Table 4 and was the same for 1998 and 2000 cohorts (6.525%), estimated to 0.547% for the 2004 season and to 1.125% for the RP. In the same way, paired increase in coancestry (
) was concluded from Table 4 and was the same for 1998 and 2000 cohorts (6.525%), estimated to 0.547% for the 2004 season and to 1.125% for the RP. In the same way, paired increase in coancestry (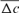 ) was calculated to be 1.113, 1.049, 1.149, 1.204, and 1.297% for 1998, 2000, 2001, 2004 cohorts, and RP, respectively. For inbreeding and coancestry calculations, only cohorts with inbred animal were included. Also, at least two equivalent generations were used in the computation of the
) was calculated to be 1.113, 1.049, 1.149, 1.204, and 1.297% for 1998, 2000, 2001, 2004 cohorts, and RP, respectively. For inbreeding and coancestry calculations, only cohorts with inbred animal were included. Also, at least two equivalent generations were used in the computation of the 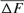 parameter otherwise there was no chance of having common ancestors of parents. In turn, if there was no inbred individual in the chosen cohort, the
parameter otherwise there was no chance of having common ancestors of parents. In turn, if there was no inbred individual in the chosen cohort, the 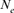 parameter becomes infinity. For the calculation of
parameter becomes infinity. For the calculation of 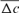 , ENDOG uses animals with at least 1 equivalent generation known as they can have common ancestors.
, ENDOG uses animals with at least 1 equivalent generation known as they can have common ancestors.
| Cohorts | n | 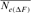 |
n | 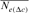 |
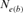 |
|---|---|---|---|---|---|
| 1998 | 2 | 8 | 53 | 44.92 | ∞ |
| 2000 | 6 | 8 | 86 | 47.65 | −1.06 |
| 2001 | 15 | — | 66 | 43.49 | ∞ |
| 2004 | 22 | 91.38 | 36 | 41.52 | 13.78 |
| RP | 44 | 44.41 | 194 | 38.54 | 51.79 |
- Estimates are based on individual increase in inbreeding (
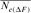 ), pairwise coancestry (
), pairwise coancestry (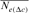 ), and regression on equivalent generations (
), and regression on equivalent generations (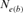 ).
). - n refers to the total number of individuals included in calculations.

Table 4 represents the effective population size estimates in four cohorts with the number of inbred individuals in RP and compares results following Gutiérrez's et al. [2008 and 2009] and Cervantes’ et al. [2011] approaches. The estimation of 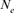 computed via regression on equivalent generations was calculated to 51.79 and to 44.41 based on realized
computed via regression on equivalent generations was calculated to 51.79 and to 44.41 based on realized 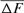 parameter. Within cohorts, the
parameter. Within cohorts, the 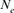 via individual increase in coancestry seemed to be the estimate the most stable and reliable and ranged from 41.52 in 2004 to 47.65 in 2000. The same parameter gives a value 38.54 in the RP. The assessment of
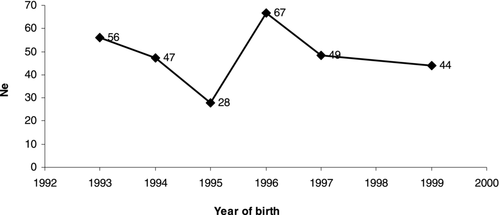
via individual increase in coancestry seemed to be the estimate the most stable and reliable and ranged from 41.52 in 2004 to 47.65 in 2000. The same parameter gives a value 38.54 in the RP. The assessment of 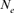 from the variance of the family size was presented in Figure 3. This methodology includes strictly individuals being grandparents, so issued from 1993 to 1999 cohorts only. The estimated
from the variance of the family size was presented in Figure 3. This methodology includes strictly individuals being grandparents, so issued from 1993 to 1999 cohorts only. The estimated 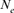 ranged from 28 to 67 and was pretty stable along the whole period. Though, the small
ranged from 28 to 67 and was pretty stable along the whole period. Though, the small 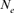 value of 28 in 1995 was most likely due to the low number of the breeding animals in this year with only eight females and three males for a
value of 28 in 1995 was most likely due to the low number of the breeding animals in this year with only eight females and three males for a 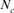 of 20 individuals (results not shown).
of 20 individuals (results not shown).
DISCUSSION
Moroccan Houbara population was formed from wild birds and eggs collected under license from Errachidia-Boudnib-Erfoud plateau in northeast Morocco. The Houbara bird has a very recent history and a genealogy that could be traced back to 1993. The low mean equivalent generations reflects further the shallowness of Houbara pedigree. The average generation interval of the Houbara population was estimated to 4.64 years and efforts provided in minimizing the inbreeding depression and kinship within the breed explained the increase in generation length parameter over years.
The IFCDW policy has respected the commonly minimum number of 20–30 contributing founders recommended at the foundation of any captive breeding program for the endangered species. Except for the 2002 cohort, the effective number of ancestors fa and founders fe were equals in general, and indicated the absence of bottlenecks in the Houbara breed. The founder genome equivalent fge parameter is fluctuating across generations and this instability is due to the genetic drift phenomenon within Houbara breeding flock. The founding operation was somehow, beneficial for the set up of the Houbara captive flock's genetic characteristics.
In the context of conservation, genetic diversity is inferred from the measure of gene diversity [Wright, 1951] called also Nei's expected heterozygosity [Nei, 1973] and/or from allelic richness [Foulley and Olliver, 2006; Leberg 2002; Petit et al., 1998]. As populations become endangered or size reduced, levels of genetic variation are most probably to be lost and result in a reduction of general fitness as well as in the apparition of inbreeding depression. Moreover, when dealing with finite and threatened species and after the establishment of any conservation system, the diminution of genetic diversity is not often unavoidable [Álvarez et al., 2008; Álvarez et al., 2010; Royo et al., 2007]. In fact, the genetic diversity decrease could be influenced by a multitude of factors such as: the short generation length, the homogenization effect due to the small 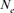 or the initial adaptation difficulties to captivity. The captive Houbara was, unfortunately, not an exception to this rule.
or the initial adaptation difficulties to captivity. The captive Houbara was, unfortunately, not an exception to this rule.
To characterize inbreeding depression, the coancestry rate in addition to the inbreeding rate, might constitute the alternative choice [González-Recio et al., 2007]. However, the former two parameters, when working with genealogies, are pedigree (knowledge and deepness) dependant. With regard to heterozygosity also, minimizing coancestry is strongly recommended to maximize the retention of genetic variation of threatened species in captivity [Frankham, 2002]. Álvarez et al. [2008], while working on the loss of genetic variability of the rare Xalda sheep breed, confirmed that for species with shallow pedigrees, coancestry is a more suitable parameter to monitor losses of genetic polymorphism than expected homozygosity and inbreeding especially during the first generations just after the foundation phase of the in situ preservation program. This could be of a great utility for the Houbara species as it would help in a better prediction of the future genetic variability loss within the captive breed.
The average increase in inbreeding was estimated to be 0.235% per generation for the WP and 1.125% for the RP. Even if the latter value is in the top range of the acceptable level of 0.5–1% recommended by the FAO [1998] guidelines for the livestock populations [Bijma, 2000; Nicholas, 1989], the inbreeding tendency is, however, believed to be low and reflects the management strategy efficiency based on migration. The 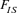 parameter deviated from Hardy Weinberg equilibrium and was negative for the (WP = −0.01018) and for the (RP = −0.01432). This small departure from the equilibrium could be interpreted by an outbreeding effect on the resulting offspring. Therefore, it is obvious that in our breeding scheme, the AI procedure have enhanced genetic flux within the Houbara population, thereby limiting inbreeding depression in the population.
parameter deviated from Hardy Weinberg equilibrium and was negative for the (WP = −0.01018) and for the (RP = −0.01432). This small departure from the equilibrium could be interpreted by an outbreeding effect on the resulting offspring. Therefore, it is obvious that in our breeding scheme, the AI procedure have enhanced genetic flux within the Houbara population, thereby limiting inbreeding depression in the population.
The effective population size reveals losses in fitness as well as in genetic variability and is considered as one of the most fundamental parameters that strongly influence the nature and the rate of genetic information transmission across generations, population viability, conservation strategies and wildlife management [Luikart et al., 2010; Waples, 2002]. Different approaches have been employed to calculate the effective population size estimator [Beaumont, 2003; Crow and Kimura, 1970; Hayes et al., 2003; MacLeod et al., 2009; Peel et al., 2004; Tallmon et al., 2008; Wang, 2009; Wright, 1931]. However, the 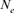 parameter remains difficult to assess and there is no particular good or magical approach for its calculation [Cervantes et al., 2008; Groeneveld et al., 2009; Luikart et al., 2010].
parameter remains difficult to assess and there is no particular good or magical approach for its calculation [Cervantes et al., 2008; Groeneveld et al., 2009; Luikart et al., 2010].
Our computations of 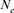 based on regression of inbreeding on equivalent generations (
based on regression of inbreeding on equivalent generations (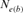 ) generated a negative value in the 2000 season, indicating that inbreeding in the involved period is not constant and is decreasing. This could happen when the mating policy aims to lower the coancestry after a period in which the crossings between close relative individuals was favored [Cervantes et al., 2008; Gutiérrez et al., 2008].
) generated a negative value in the 2000 season, indicating that inbreeding in the involved period is not constant and is decreasing. This could happen when the mating policy aims to lower the coancestry after a period in which the crossings between close relative individuals was favored [Cervantes et al., 2008; Gutiérrez et al., 2008].
The plot of 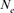 based on family size variance follows the same classical curve as for the captive breeding process with its three major stages: foundation, growth, and maintenance. For Houbara Bustard, the foundation phase corresponded to the 1993–1995 period, the growth stage coincided with 1996 and the maintenance stage started at the end of the 1997 breeding season. In managed small populations, inbreeding and loss of reproductive performance and fitness are inevitable during the foundation stage. Also, as
based on family size variance follows the same classical curve as for the captive breeding process with its three major stages: foundation, growth, and maintenance. For Houbara Bustard, the foundation phase corresponded to the 1993–1995 period, the growth stage coincided with 1996 and the maintenance stage started at the end of the 1997 breeding season. In managed small populations, inbreeding and loss of reproductive performance and fitness are inevitable during the foundation stage. Also, as 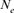 measures genetic diversity within populations, the decrease of
measures genetic diversity within populations, the decrease of 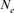 based on family size variance after the beginning of the conservation program is most in accord with the decrease in genetic diversity during the same period. Our methodologies showed that in the case of nonstructured populations like the Houbara, the
based on family size variance after the beginning of the conservation program is most in accord with the decrease in genetic diversity during the same period. Our methodologies showed that in the case of nonstructured populations like the Houbara, the  estimation from the variance of progeny as well as from the realized coancestry worked well and provided roughly the same
estimation from the variance of progeny as well as from the realized coancestry worked well and provided roughly the same 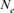 value of 45 individuals.
value of 45 individuals.
Small populations are more prone to genetic diversity loss. The breeding and conservation policies consist habitually, in maintaining high the genetic diversity of the stock and minimizing or avoiding inbreeding depression of their future generations. Sometimes, the genealogical information is not sufficient to ascertain genetic variability within small and finite populations with shallow pedigrees. Moreover, the logistic, technical, and financial difficulties and demands encountered when registering pedigrees, suggest the exploration and implementation of tools based on breeding techniques (e.g, cryopreservation) and molecular information both to describe and manage them. In other words, when special breeding strategies are a condition for the financial support of endangered breeds, a critical judgment of the mating system becomes more important [Baumung and Sölkner, 2003]. Indeed, rendering threatened local breeds profitable is, the most likely, the best conservation practice for their survival as it could act independently from the continuous financial assistance and support [Meuwissen, 2009].
CONCLUSION
To our knowledge, there have been no genetic studies on pedigree analysis of the Houbara avian species and this is the first time genetic parameters needed for conservation are computed in bustards. The application of genealogical parameters to characterize the Moroccan captive Houbara breed during 11 years was of great conservation relevance. Actually, despite the strong gene flow signal within the Houbara captive flock, the genetic evidence presented herein, revealed some deficiencies in the breeding strategies during the 2004 breeding season mainly. The increased values in inbreed individuals, coancestry, and inbreeding could indeed reflect the low expertise in the breeding operation. This also could be interpreted as a direct consequence of the arbitrary overuse of the artificial insemination technique as well as an absence of a particular vision toward the breed conservation. Since loss of genetic diversity is influenced by the average increase in inbreeding in outbred populations, and in order to achieve a balanced and sustained exploitation of the animal breeders and their gene origins, we do stress on the necessity of regular assessments of the annual and generational inbreeding levels and the set up of a pertinent selection program in parallel besides the routine control of genetic variability, breed characteristics and its specific tendencies under captivity conditions.
ACKNOWLEDGMENTS
The authors are grateful to the late Crown Prince, His Royal Highness Prince Sultan Bin Abdul Aziz Al Saud, sponsor and patron of the IFCDW, for His dedication, leadership, and generosity to the environment and protection of Moroccan natural resources and wildlife. We would like also to extend our gratitude to Sheikh Mohamed Bin Khalid Bin Hethlain and to Dr. S. Jadallah for their support and continuous encouragement. We are indebted to Dr. F. Chbel for her early contribution to the pedigree establishment and to two anonymous referees of this manuscript for their highly valuable comments and remarks. Thanks go also to all the persons and former staff from the IFCDW who had participated from near or far in this work. This study forms a part of the doctoral thesis of the author A. Korrida on Houbara Bustard genetics.




