Observability of the ambient conditions in model-based estimation for wind farm control: A focus on static models
Abstract
Wind farm control (WFC) algorithms rely on an estimate of the ambient wind speed, wind direction, and turbulence intensity in the determination of the optimal control setpoints. However, the measurements available in a commercial wind farm do not always carry sufficient information to estimate these atmospheric quantities. In this paper, a novel measure (“observability”) is introduced that quantifies how well the ambient conditions can be estimated with the measurements at hand through a model inversion approach. The usefulness of this measure is shown through several case studies. While the turbine power signals and the inter-turbine wake interactions provide information on the wind direction, the case studies presented in this article show that there is a strong need for wind direction measurements for WFC to sufficiently cover observability for any ambient condition. Further, generally, more wake interaction leads to a higher observability. Also, the mathematical framework presented in this article supports the straightforward notion that turbine power measurements provide no additional information compared with local wind speed measurements, implying that power measurements are superfluous. Irregular farm layouts result in a higher observability due to the increase in unique wake interaction. The findings in this paper may be used in WFC to predict which ambient quantities can (theoretically) be estimated. The authors envision that this will assist in the estimation of the ambient conditions in WFC algorithms and can lead to an improvement in the performance of WFC algorithms over the complete envelope of wind farm operation.
1 INTRODUCTION
The European Wind Energy Association (EWEA) predicts the amount of installed wind energy to increase from 106 GW in 2012 to 735 GW in 2050, which at that point should provide for about
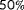 of the European Union's electricity demand.1 The success of wind energy largely relies on its financial competitiveness with other renewable and nonrenewable sources. Control plays an invaluable role in this matter. In the past, the focus of control research has been on wind turbine control. Recently, the interest has largely shifted towards wind farm control (WFC), in which multiple turbines inside a wind farm are coordinated together to improve their combined energy yield.2 WFC addresses the issue of wakes, which are slower and more turbulent pockets of air that form behind a wind turbine as energy is extracted. Wake formation has led up to an estimated
of the European Union's electricity demand.1 The success of wind energy largely relies on its financial competitiveness with other renewable and nonrenewable sources. Control plays an invaluable role in this matter. In the past, the focus of control research has been on wind turbine control. Recently, the interest has largely shifted towards wind farm control (WFC), in which multiple turbines inside a wind farm are coordinated together to improve their combined energy yield.2 WFC addresses the issue of wakes, which are slower and more turbulent pockets of air that form behind a wind turbine as energy is extracted. Wake formation has led up to an estimated
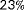 loss in the annual energy yield of the closely spaced Lillgrund offshore wind farm at the coast of Sweden compared WITH an idealized situation without wake formation.3 The underlying concept of WFC is to influence the wake such that it has a smaller impact on downstream turbines. A popular approach in the literature is yaw-based wake steering, in which the wake position is shifted laterally by purposely operating an upstream turbine at a yaw misalignment. Recent studies have shown the potential of yaw-based wake steering for wind farm power maximization in high-fidelity simulation,4 wind tunnel experiments,5 and field tests under dynamic inflow conditions.6-8 These publications suggest an increase in the annual energy yield in the order of 1% and situational increases of up to 20% for certain wind farms under particular inflow conditions that cause large wake losses.
loss in the annual energy yield of the closely spaced Lillgrund offshore wind farm at the coast of Sweden compared WITH an idealized situation without wake formation.3 The underlying concept of WFC is to influence the wake such that it has a smaller impact on downstream turbines. A popular approach in the literature is yaw-based wake steering, in which the wake position is shifted laterally by purposely operating an upstream turbine at a yaw misalignment. Recent studies have shown the potential of yaw-based wake steering for wind farm power maximization in high-fidelity simulation,4 wind tunnel experiments,5 and field tests under dynamic inflow conditions.6-8 These publications suggest an increase in the annual energy yield in the order of 1% and situational increases of up to 20% for certain wind farms under particular inflow conditions that cause large wake losses.
The wake losses and therefore the amount of yaw misalignment that maximizes the energy yield is highly dependent on the wind direction, wind speed, and turbulence intensity of the incoming wind field.3 As these atmospheric conditions constantly change, so do the optimal yaw angles. Typically, a simplified (“surrogate”) model of the flow and turbine dynamics is leveraged to calculate the optimal yaw angles.9 However, due to the complicated flow behavior at a range of temporal and spatial scales, no surrogate model exists that is accurate for all the different atmospheric conditions a wind farm may encounter. For this reason, closed-loop control solutions are becoming increasingly popular in the literature.2 The underlying idea of this closed-loop control framework is that the surrogate wind farm model is continuously adapted such that it accurately and consistently predicts the wind farm behavior.
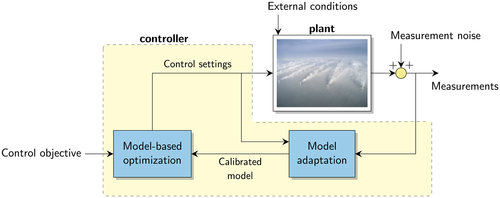
The closed-loop WFC framework is shown in Figure 1. This framework consists of three components, namely, (a) a surrogate wind farm model, (b) a model adaptation algorithm, and (c) a control setpoint optimization algorithm. Surrogate wind farm models can typically be separated into static and dynamic models. These model types attempt to predict the minute-averaged and the second-to-second flow and turbine behavior, respectively. The purpose of the model adaptation algorithm is to modify parameters inside the surrogate model such that it can accurately predict the wake interactions inside the wind farm, which includes the freestream wind speed and wind direction. Finally, an optimization algorithm is necessary to determine an optimal control policy such that a particular wind farm objective is achieved, eg, maximization of the wind farm power production. The focus in this article is on the model adaptation algorithm; the interested reader is referred to the survey by Boersma et al2 for more information on surrogate models and optimization algorithms.
The body of literature on real-time model adaptation for WFC is scarce. Most WFC literature has focused on setpoint optimization and model development.2 This goes paired with the fact that most WFC algorithms in the literature have been tested under quasi-steady ambient conditions, meaning that the mean wind speed, wind direction, and turbulence intensity were time invariant. This holds for both numerical simulations4 and real-world scaled experiments.5, 10 This limits the applicability of such algorithms, as the experiments do not sufficiently represent the real-world fluctations in the atmosphere.
A handful of articles in the literature is concerned with the estimation of atmospheric conditions and model adaptation for WFC. Annoni et al11 proposed a model-free algorithm to estimate the wind direction inside a wind farm using the wind vane measurements of different turbines and obtaining a consensus on the most probable value. Doekemeijer et al12 proposed a method to estimate the freestream conditions by a model inversion approach using the time-averaged turbine power measurements and a static surrogate model assuming the wind direction is known, which is comparable with the idea coined by Gebraad et al.4 Furthermore, Gebraad et al13 synthesized a Kalman filter for their dynamic surrogate model, which uses the turbine power measurements to estimate the flow field inside the wind farm. The adapted surrogate model was able to accurately predict the wind farm dynamics, though the wind direction was constant and assumed to be known. Similarly, Doekemeijer et al14 used a dynamic surrogate model with an ensemble Kalman filter to estimate the flow field and turbulence intensity using turbine power measurements. High-fidelity simulations showed that the algorithm was able to successfully reconstruct the dynamic wind field for a two-turbine and a nine-turbine wind farm. However, also in this work, the wind direction was assumed known. Further, Shapiro et al15 synthesized and evaluated a WFC solution assuming a constant wind direction. Besides the estimation of the ambient conditions, Bottasso and Schreiber16 attempt to estimate several model tuning parameters to improve the accuracy of the surrogate model.
- • Proposing a formal definition for a mathematical measure (henceforth referred to as observability) that quantifies how well the ambient conditions (ie, wind direction, wind speed, and turbulence intensity) can be reconstructed from the measurements available in the wind farm.
- • Comparing the effect of different wind farm topologies and sensor configurations on the observability for a large range of ambient conditions that a wind farm may encounter during operation.
- • Performing theoretical case studies with wind farms with DTU 10-MW wind turbines.
This article is organized as follows. The surrogate model used in this work is presented in Section 2. The issue of estimation and a novel quantitative measure of observability is presented in Section 3. Simulation results are shown in Section 4, and the article is concluded in Section 5.
2 SURROGATE MODEL: FLORIS
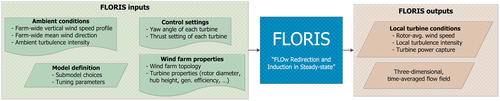
The surrogate model used in this work is referred to as the “FLOw Redirection and Induction in Steady-state” (FLORIS) model.9 This model predicts the time-averaged power capture of each turbine and the time-averaged three-dimensional flow field for a wind farm under a specified set of inflow conditions. The timescale of FLORIS is on the order of minutes. A schematic overview of the types of inputs and outputs to the FLORIS model is shown in Figure 2. Fundamentally, FLORIS combines several submodels from the literature. The main components of FLORIS used in this article are described in the remainder of this section.
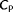 , as
, as
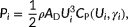 (1)
(1) is the air density,
is the air density,
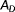 is the rotor swept area,
is the rotor swept area,
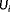 is the spatially averaged inflow wind speed at turbine
is the spatially averaged inflow wind speed at turbine
 , and
, and
 is the yaw angle of the turbine relative to the incoming wind. The nondimensional power and thrust coefficients,
is the yaw angle of the turbine relative to the incoming wind. The nondimensional power and thrust coefficients,
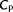 and
and
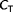 , can be derived using actuator disk theory for aligned inflow (
, can be derived using actuator disk theory for aligned inflow (
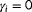 ). Alternatively, the nondimensional power and thrust coefficients can be calculated using an aero-elastic turbine simulation model for various wind speeds (and yaw misalignment angles) such as OpenFAST20 or Bladed. A common expression modeling the effect of a yaw misalignment on the turbine power production is4
). Alternatively, the nondimensional power and thrust coefficients can be calculated using an aero-elastic turbine simulation model for various wind speeds (and yaw misalignment angles) such as OpenFAST20 or Bladed. A common expression modeling the effect of a yaw misalignment on the turbine power production is4
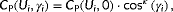 (2)
(2) has a typical value of
has a typical value of
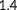 to
to
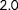 , depending on the wind turbine.
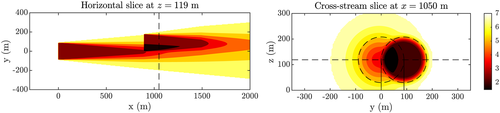
, depending on the wind turbine.The results of an arbitrary wind farm simulation with two 10-MW turbines21 is shown in Figure 3. The computational cost for a single FLORIS run is 10 millisecond to 1 second, depending on the number of turbines in the wind farm. FLORIS has shown a good match with results from high-fidelity simulations,12 wind tunnel experiments,22 and field tests.8, 23 Furthermore, the variant presented in this article has fewer tuning parameters than a comparable model proposed in Gebraad et al.4 For a more detailed, mathematical description of the model, the reader is referred to its related literature. Note that the results that will be presented in this article are not limited to FLORIS and can straightforwardly be reproduced with other static surrogate models.
3 METHODOLOGY: INTRODUCING A MEASURE OF OBSERVABILITY
The model adaptation solution of a WFC algorithm is not guaranteed to result in satisfactory performance. There has to be sufficient information in the wind farm measurements to correctly determine the ambient conditions. Hence, an observability analysis provides useful insight before the implementation of such a control algorithm. The traditional definition of observability refers to dynamical systems; a system is observable if the initial conditions and the time series of the system states can be reconstructed from a time series of the system output signals. As FLORIS is a static model, such a notion does not apply. Therefore, a static observability notion is defined as being true for a situation when the initial conditions can be reconstructed from the system output signals. In this section, a mathematical definition of this observability is introduced for the control framework presented in Figure 1.
3.1 Cost function in estimation
Generally, a simplistic, heuristic approach is used to determine the prevailing ambient conditions inside the wind farm. However, the reliability of such methods vary, the literature on them is scarce, and these methods are limited in their accuracy. Rather, in this work, a surrogate wind farm model is leveraged in a sensor fusion approach for the estimation of the ambient conditions.
 (3)
(3) the number of turbines, and
the number of turbines, and
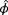 ,
,
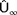 , and
, and
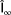 being the freestream wind direction, wind speed, and turbulence intensity as evaluated in FLORIS, respectively.
1Using this cost function for model adaptation, the idea is that values for
being the freestream wind direction, wind speed, and turbulence intensity as evaluated in FLORIS, respectively.
1Using this cost function for model adaptation, the idea is that values for
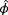 ,
,
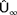 , and
, and
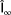 are found such that the error between the measured turbine power signals and what is predicted by FLORIS for these conditions is minimized. The cost function shown in Equation 3 was used for model adaptation in Doekemeijer et al12 assuming
are found such that the error between the measured turbine power signals and what is predicted by FLORIS for these conditions is minimized. The cost function shown in Equation 3 was used for model adaptation in Doekemeijer et al12 assuming
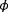 was known a priori, which allowed the successful estimation of
was known a priori, which allowed the successful estimation of
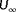 and
and
 . However, only using the turbine power measurements may lead to situations in which the true ambient conditions cannot be reconstructed accurately. For example, consider the case in which all turbines inside the wind farm are operating in above-rated conditions. All turbines are then generating their rated power, and one cannot distinguish different above-rated wind speeds from one another. To resolve this issue, one can include the wind speed estimates from a local turbine wind speed estimator24, 25 in the cost function. This term is denoted by
. However, only using the turbine power measurements may lead to situations in which the true ambient conditions cannot be reconstructed accurately. For example, consider the case in which all turbines inside the wind farm are operating in above-rated conditions. All turbines are then generating their rated power, and one cannot distinguish different above-rated wind speeds from one another. To resolve this issue, one can include the wind speed estimates from a local turbine wind speed estimator24, 25 in the cost function. This term is denoted by
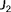 , given as
, given as
 (4)
(4) is the measurement of the local wind speed estimator of turbine
is the measurement of the local wind speed estimator of turbine
 , and
, and
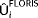 is what FLORIS predicts the local wind speed to be at turbine
is what FLORIS predicts the local wind speed to be at turbine
 for the hypothesized wind conditions
for the hypothesized wind conditions
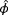 ,
,
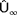 , and
, and
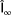 . Note that the inflow wind speed at a turbine in FLORIS, denoted by
. Note that the inflow wind speed at a turbine in FLORIS, denoted by
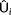 , is the freestream-equivalent wind speed at that turbine under zero yaw misalignment. Thus, the effects of a yaw misalignment of turbine
, is the freestream-equivalent wind speed at that turbine under zero yaw misalignment. Thus, the effects of a yaw misalignment of turbine
 are not accounted for in this signal. However, in practice, a typical local turbine wind speed estimator provides a freestream-equivalent wind speed using the turbine power signal under the assumption of zero yaw misalignment. To account for the situation in which a turbine is misaligned with the flow, one can model
are not accounted for in this signal. However, in practice, a typical local turbine wind speed estimator provides a freestream-equivalent wind speed using the turbine power signal under the assumption of zero yaw misalignment. To account for the situation in which a turbine is misaligned with the flow, one can model
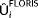 as
as
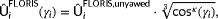 (5)
(5) . Finally, one can combine
. Finally, one can combine
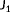 and
and
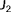 into cost function
into cost function
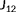 , as
, as
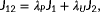 (6)
(6)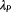 and
and
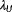 are weighing terms. Using the cost function defined in Equation 6, difficult situations may arise when trying to estimate
are weighing terms. Using the cost function defined in Equation 6, difficult situations may arise when trying to estimate
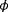 ,
,
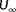 , and
, and
 . For example, if there is no wake interaction, one cannot estimate the freestream turbulence intensity, as the effects of
. For example, if there is no wake interaction, one cannot estimate the freestream turbulence intensity, as the effects of
 have no correlation with (ie, impact on) the measured signals. Moreover, issues may arise concerning the estimation of
have no correlation with (ie, impact on) the measured signals. Moreover, issues may arise concerning the estimation of
 , as demonstrated in Figure 4.
, as demonstrated in Figure 4.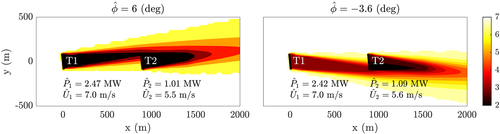
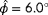 . The definitions are that
. The definitions are that
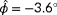 when the air moves from west to east (left to right) and is counterclockwise positive. The color bar depicts wind speed in meter per second. In this plot, it is seen that
when the air moves from west to east (left to right) and is counterclockwise positive. The color bar depicts wind speed in meter per second. In this plot, it is seen that
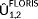 and
and
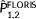 yield almost identical turbine power signals and local wind speeds, thus making them indistinguishable in the cost function of Equation 6. This leads to an unobservable situation [Colour figure can be viewed at wileyonlinelibrary.com]
yield almost identical turbine power signals and local wind speeds, thus making them indistinguishable in the cost function of Equation 6. This leads to an unobservable situation [Colour figure can be viewed at wileyonlinelibrary.com]In this situation,
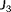 and
and
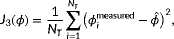 yield almost identical values for
yield almost identical values for
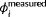 and
and
 , thereby making it impossible to distinguish these two situations using the measurements available.
, thereby making it impossible to distinguish these two situations using the measurements available.
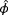 , given by
, given by
 (7)
(7) is the filtered wind vane measurement of turbine
is the filtered wind vane measurement of turbine
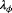 and
and
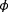 is the hypothesized wind direction in FLORIS. The complete cost function
is the hypothesized wind direction in FLORIS. The complete cost function
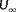 is now defined as
is now defined as
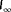 (8)
(8)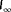 a weighing term for the local wind direction estimates. This weighing term is to be chosen according to the relative measurement noise and bias in the wind vane measurements, and could vary per turbine. The to-be-estimated quantities are
a weighing term for the local wind direction estimates. This weighing term is to be chosen according to the relative measurement noise and bias in the wind vane measurements, and could vary per turbine. The to-be-estimated quantities are
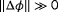 ,
,
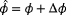 , and
, and
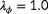 . Each of the three components includes a squared term to quadratically penalize mismatches between the surrogate model and sensor measurements. The situation of Figure 4 becomes increasingly better conditioned as the contribution of the wind vane measurements increases, as visualized in Figure 5.
. Each of the three components includes a squared term to quadratically penalize mismatches between the surrogate model and sensor measurements. The situation of Figure 4 becomes increasingly better conditioned as the contribution of the wind vane measurements increases, as visualized in Figure 5.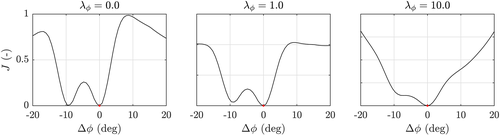
 (Equation 8), exemplified on the two-turbine case of Figure 4. In all subplots,
(Equation 8), exemplified on the two-turbine case of Figure 4. In all subplots,
 and
and
 (In this example case,
(In this example case,
 as it carries the same information as the power signals do. This statement will be proven in Section 4.1.1). In the left figure,
as it carries the same information as the power signals do. This statement will be proven in Section 4.1.1). In the left figure,
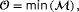 and thus exclusively power measurements are used. This leads to a critical point at
and thus exclusively power measurements are used. This leads to a critical point at
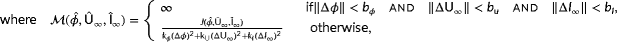 which has negligible cost, and thus, this point cannot be distinguished from the actual point
which has negligible cost, and thus, this point cannot be distinguished from the actual point
 , with
, with
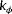 , leading to unobservability. This refers back to the situation shown in Figure 4. By including wind vane measurements (
, leading to unobservability. This refers back to the situation shown in Figure 4. By including wind vane measurements (
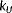 ), the cost function is better conditioned to uniquely estimate
), the cost function is better conditioned to uniquely estimate
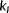 . Note that
. Note that
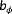 should be chosen in accordance with the vane's measurement reliability [Colour figure can be viewed at wileyonlinelibrary.com]
should be chosen in accordance with the vane's measurement reliability [Colour figure can be viewed at wileyonlinelibrary.com]Thus, it is clear that local wind speed measurements (to deal with above-rated wind speeds), wind direction measurements (to deal with situations as exemplified in Figure 4), and wake interaction (to enable correlation between
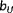 and the measurements) are required to promote observability of the freestream conditions over the full range of operation. When multiple minima exist at a notable distance from the true solution (in the example case of Figures 4 and 5, this would be
and the measurements) are required to promote observability of the freestream conditions over the full range of operation. When multiple minima exist at a notable distance from the true solution (in the example case of Figures 4 and 5, this would be
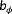 , with
, with
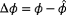 ), the ambient conditions cannot be reliably estimated, and the situation becomes unobservable.
2
), the ambient conditions cannot be reliably estimated, and the situation becomes unobservable.
2
However, while it is clear that particular situations are unobservable, a quantitative measure is still required to determine the degree of unobservability. For example, is the situation in Figure 5 with
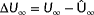 “observable enough” to uniquely determine the ambient conditions? To answer such questions, a quantitative measure of unobservability for static models is introduced in the next section.
“observable enough” to uniquely determine the ambient conditions? To answer such questions, a quantitative measure of unobservability for static models is introduced in the next section.
3.2 A quantitative measure for unobservability
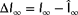 ,
,
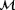 , and
, and
 . The main contribution of this paper is the introduction of such a mathematical notion for observability. The observability of a particular situation
. The main contribution of this paper is the introduction of such a mathematical notion for observability. The observability of a particular situation
 is defined as
is defined as
 (9)
(9)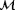 (10)
(10) as defined in Equation 8,
as defined in Equation 8,
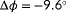 ,
,
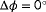 , and
, and
 denoting normalization terms, and
denoting normalization terms, and
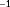 ,
,
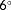 , and
, and
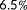 being thresholds. Further,
being thresholds. Further,
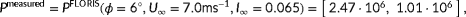 ,
,
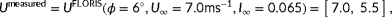 , and
, and
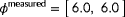 denote the difference between the true and hypothesized ambient conditions, respectively. In the remainder of this section, the working principle will be explained.
denote the difference between the true and hypothesized ambient conditions, respectively. In the remainder of this section, the working principle will be explained.The function
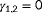 is defined such that critical points (low cost
is defined such that critical points (low cost
 , far away from the true solution) have a low value (less observable—hard to tell apart from the true solution), while situations in which the cost
, far away from the true solution) have a low value (less observable—hard to tell apart from the true solution), while situations in which the cost
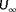 is high yields a high value (more observable—easier to distinguish from the true solution). Furthermore, the threshold terms are present to ensure that any value estimated close enough to the true optimum does not “endanger” the observability. A more elaborate discussion on these thresholds can be found in Appendix Appendix A.
is high yields a high value (more observable—easier to distinguish from the true solution). Furthermore, the threshold terms are present to ensure that any value estimated close enough to the true optimum does not “endanger” the observability. A more elaborate discussion on these thresholds can be found in Appendix Appendix A.
Figure 6 demonstrates how the observability
 is calculated for the example situation discussed in Section 3.1. Note that this is not necessarily a realistic scenario, but rather is discussed to provide insight into the method. The function
is calculated for the example situation discussed in Section 3.1. Note that this is not necessarily a realistic scenario, but rather is discussed to provide insight into the method. The function
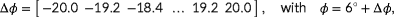 is derived from the cost function
is derived from the cost function
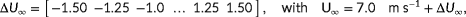 following Equation 10. The cost function has two minima: one at
following Equation 10. The cost function has two minima: one at
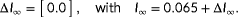 and one at
and one at
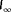 , indicating that there are two hypothetical wind directions that produce near-identical turbine power signals. This leads to a low observability.
, indicating that there are two hypothetical wind directions that produce near-identical turbine power signals. This leads to a low observability.
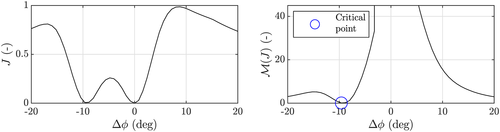
 is calculated. This is a continuation of the example shown in Figures 4 and 5. Firstly, the cost function
is calculated. This is a continuation of the example shown in Figures 4 and 5. Firstly, the cost function
 (left plot) is converted to a measure
(left plot) is converted to a measure
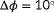 (right plot) which penalizes a low cost far away from the true solution (the true solution being
(right plot) which penalizes a low cost far away from the true solution (the true solution being
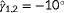 ). Secondly, the degree of observability
). Secondly, the degree of observability
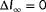 is the minimum value of
is the minimum value of
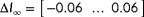 . In this example,
. In this example,
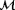 is small due to
is small due to
 at
at
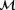 (referring back to
(referring back to
 and
and
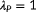 ), and the situation is thus poorly observable. This agrees with the qualitative discussion from Section 3.1 [Colour figure can be viewed at wileyonlinelibrary.com]
), and the situation is thus poorly observable. This agrees with the qualitative discussion from Section 3.1 [Colour figure can be viewed at wileyonlinelibrary.com]Note that the measured quantities in
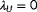 are taken as the values from the surrogate model (FLORIS) with the true ambient conditions, thus assuming a perfect model of the system. In reality, this will not hold, and the work herein presents an idealized case (theoretical upper bound) of observability.
are taken as the values from the surrogate model (FLORIS) with the true ambient conditions, thus assuming a perfect model of the system. In reality, this will not hold, and the work herein presents an idealized case (theoretical upper bound) of observability.
- Firstly, we evaluate the degree of observability of a single situation at a time. With a situation, we imply a wind farm subjected to a certain ambient inflow, giving us a certain set of measurements. For example, continuing the example two-turbine wind farm of Section 3.1, the observability for this wind farm is investigated at a true freestream wind speed of 7.0 m s
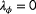 , a freestream wind direction of
, a freestream wind direction of
 , and a turbulence intensity of
, and a turbulence intensity of
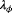 . Referring back to Figure 4, our measurements would be
. Referring back to Figure 4, our measurements would be
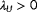 (11)
(11)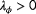 (12)The measurement vectors contain two entries, for turbines 1 and 2, respectively. In this simulation, the turbines are assumed to be aligned with the inflow wind direction;
(12)The measurement vectors contain two entries, for turbines 1 and 2, respectively. In this simulation, the turbines are assumed to be aligned with the inflow wind direction;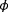 (13)
(13)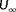 .
. - Secondly, we now assume that we do not know what the ambient conditions generated these measurements. This represents our estimation step. With this set of measurements, the cost function
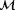 of Equation 8 is calculated for a range of hypothetical (tested) ambient conditions. For this example, the estimation algorithm is limited to the estimation of
of Equation 8 is calculated for a range of hypothetical (tested) ambient conditions. For this example, the estimation algorithm is limited to the estimation of
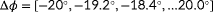 and
and
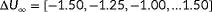 . The (two-dimensional) cost function is evaluated over the following ranges:
. The (two-dimensional) cost function is evaluated over the following ranges:
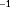 (14)
(14) (15)If
(15)If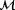 (16)
(16)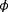 is additionally to be estimated, the (three-dimensional) cost function is also evaluated over the following range for
is additionally to be estimated, the (three-dimensional) cost function is also evaluated over the following range for
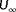 :
Furthermore, the turbine yaw angles are fixed in the inertial frame and assumed to be known a priori in the cost function evaluations. Thus, if the cost function is evaluated for
:
Furthermore, the turbine yaw angles are fixed in the inertial frame and assumed to be known a priori in the cost function evaluations. Thus, if the cost function is evaluated for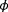 (17)
(17)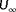 , then
, then
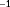 .
. - Finally, we check whether our estimation algorithm was successful. A two-dimensional (for
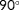 ) or three-dimensional (for
) or three-dimensional (for
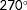 ) cost matrix is obtained following Equation 8, from which
) cost matrix is obtained following Equation 8, from which
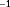 is calculated following Equation 10. The degree of observability
is calculated following Equation 10. The degree of observability
 is the minimum value of
is the minimum value of
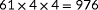 , being a positive real number.
, being a positive real number.
The degree of observability
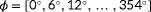 can be calculated for a range of true wind directions following the process described above and displayed in a single picture. The results of such an observability analysis assuming only power measurements are available (
can be calculated for a range of true wind directions following the process described above and displayed in a single picture. The results of such an observability analysis assuming only power measurements are available (
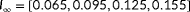 ,
,
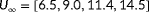 and
and
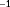 ) are shown in Figure 7 for a six-turbine wind farm. Note that
) are shown in Figure 7 for a six-turbine wind farm. Note that
 and
and
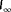 are zero to provide insight into the results. In a practical WFC implementation, one would opt for
are zero to provide insight into the results. In a practical WFC implementation, one would opt for
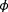 and
and
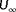 , if these measurements are available.
, if these measurements are available.
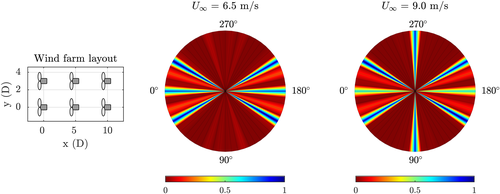
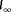 to
to
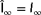 , plotted in 61 discrete points along the polar axis) and two true wind speeds (
, plotted in 61 discrete points along the polar axis) and two true wind speeds (
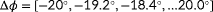 and
and
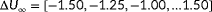 m s
m s
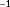 ). The true turbulence intensity is assumed to be known in the estimation problem, thus
). The true turbulence intensity is assumed to be known in the estimation problem, thus
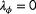 and
and
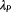 , where the estimability of
, where the estimability of
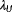 and
and
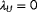 is assessed. Thus, for each of the
is assessed. Thus, for each of the
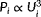 situations (a situation is defined as a particular true wind direction and wind speed for this six-turbine layout), the steps described earlier this section are followed. The results are normalized to a scale of
situations (a situation is defined as a particular true wind direction and wind speed for this six-turbine layout), the steps described earlier this section are followed. The results are normalized to a scale of
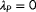 to
to
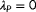 , with
, with
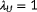 being unobservable and
being unobservable and
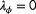 being to the best observable situation
being to the best observable situationEach of the two radial plots shown in Figure 7 represents the degrees of observability for 61 different wind directions. There is one degree of observability defined for each true wind direction, plotted as a particular color across the polar axis. This thus indicates the estimability of
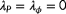 and
and
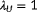 for this true wind direction. For each of the 61 true wind directions, a two-dimensional cost function
for this true wind direction. For each of the 61 true wind directions, a two-dimensional cost function
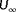 was calculated over the variables
was calculated over the variables
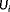 and
and
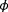 m s
m s
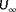 . Then,
. Then,
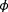 was taken to be the lowest value of
was taken to be the lowest value of
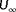 , being the degree of observability for this true wind direction, true wind speed, true turbulence intensity, wind farm layout, and with
, being the degree of observability for this true wind direction, true wind speed, true turbulence intensity, wind farm layout, and with
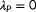 and
and
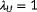 being the to-be-estimated parameters. We refer to this as the degree of observability for this particular situation.
being the to-be-estimated parameters. We refer to this as the degree of observability for this particular situation.
Figure 7 clearly shows that the
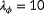 and
and
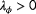 can only be estimated for a narrow range of true wind directions when only power measurements are available. This makes sense, since there is only wake interaction for a small range of wind directions. Without wake interaction, one cannot distinguish, for example, between the case where all turbines operate under a yaw misalignment and a higher inflow wind speed, from the case where all turbines operate without a yaw misalignment and a lower inflow wind speed. Furthermore, an interesting difference between the observability plot for a true wind speed of 6.5 and 9.0 m s
can only be estimated for a narrow range of true wind directions when only power measurements are available. This makes sense, since there is only wake interaction for a small range of wind directions. Without wake interaction, one cannot distinguish, for example, between the case where all turbines operate under a yaw misalignment and a higher inflow wind speed, from the case where all turbines operate without a yaw misalignment and a lower inflow wind speed. Furthermore, an interesting difference between the observability plot for a true wind speed of 6.5 and 9.0 m s
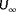 is the degree of observability at the true wind directions of
is the degree of observability at the true wind directions of
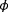 and
and
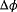 . This is because of the fact that the downstream turbines operate below cut-in wind speed for the 6.5 m s
. This is because of the fact that the downstream turbines operate below cut-in wind speed for the 6.5 m s
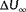 case at these wind directions due to the close spacing and the wake effects. As these downstream turbines do not generate any power, their signals hold little information. For the 9.0 m s
case at these wind directions due to the close spacing and the wake effects. As these downstream turbines do not generate any power, their signals hold little information. For the 9.0 m s
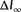 case, all turbines operate above cut-in wind speed, and thus, these power signals contain more information about the flow.
case, all turbines operate above cut-in wind speed, and thus, these power signals contain more information about the flow.
The methodology presented in this section serve for explanation purposes, and the cases becomes more interesting when considering more complicated farm layouts, various combinations of wind vane and wind speed measurements, and the inclusion of turbulence intensity estimation. This is the focus of the next section.
4 A COMPREHENSIVE OBSERVABILITY ANALYSIS FOR THREE WIND FARM LAYOUTS
The observability of the ambient conditions is investigated in this section for three different wind farm layouts, namely, two symmetrical wind farms and one asymmetrical wind farm. The layouts are shown in Figure 8. The asymmetrical eight-turbine wind farm is an interesting configuration, as there is more unique wake interaction situations in this layout. This reduces the issues with symmetry previously demonstrated in Figure 4 compared with symmetrical wind farm layouts.
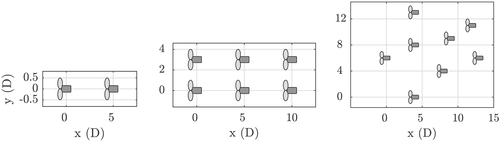
For each topology, the observability is calculated for
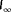 situations, namely, for 61 wind directions
situations, namely, for 61 wind directions
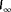 , 4 levels of turbulence intensity
, 4 levels of turbulence intensity
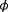 , and four wind speeds
, and four wind speeds
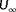 m s
m s
 , of which the latter wind speed is above rated. Thus, for each of these 976 conditions, a multidimensional cost function is set up, and the most critical situation is determined following Equation 10, upon which the observability for this situation is calculated using Equation 9. The parameters therein are shown in Table B1.
, of which the latter wind speed is above rated. Thus, for each of these 976 conditions, a multidimensional cost function is set up, and the most critical situation is determined following Equation 10, upon which the observability for this situation is calculated using Equation 9. The parameters therein are shown in Table B1.
This section is separated in two parts. In Section 4.1, the observability of the various situations is assessed under the assumption that the freestream turbulence intensity is known a priori. This simplifies the estimation problem and requires less information to be extracted from the measurements at hand. However, neglecting the estimation of
 is expected to significantly worsen the accuracy of the surrogate model in a practical WFC algorithm. Hence, the observability with the inclusion of
is expected to significantly worsen the accuracy of the surrogate model in a practical WFC algorithm. Hence, the observability with the inclusion of
 is presented in Section 4.2.
is presented in Section 4.2.
4.1 Estimating
 and
and
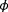 under perfect knowledge of
under perfect knowledge of
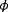
First, the observability of various situations under the assumption that the turbulence intensity is known,
 , is looked into. The range over which each particular cost function is calculated is
, is looked into. The range over which each particular cost function is calculated is
 and
and
 m s
m s
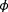 . The discretization of these parameters were tuned for convergence, such that the solutions no longer notably change at a higher precision. The range of these parameters is chosen to resemble the typical prior knowledge one has about the true ambient conditions in such an estimation problem.
. The discretization of these parameters were tuned for convergence, such that the solutions no longer notably change at a higher precision. The range of these parameters is chosen to resemble the typical prior knowledge one has about the true ambient conditions in such an estimation problem.
4.1.1 Redundancy in the cost function: Power and wind speed estimates
One important notion in the cost function shown in Equation 8 is that the local wind speed estimates and the turbine power signals carry duplicate information. Specifically, as the local wind speed estimators rely on the turbine power signal, the turbine power measurements theoretically add no information to the cost function that is not already included in the wind speed estimator signals. To validate this, an observability analysis is performed for the six-turbine wind farm under
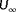 and various values for
and various values for
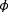 and
and
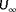 . The results are shown in Figure 9.
. The results are shown in Figure 9.
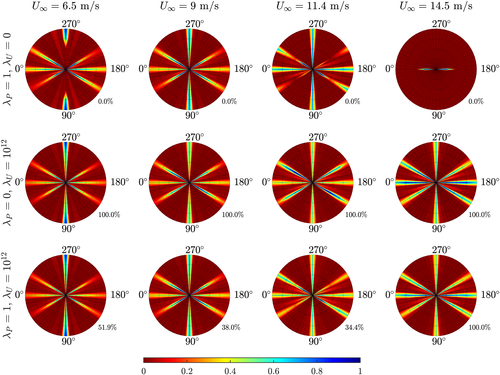
 is known, with
is known, with
 . The observability in each radial plot is normalized with respect to its highest value. The percentage on the bottom-right corner of each radial plot indicates to what degree the local wind speed measurements contribute to the observability. It can be seen that the power measurements provide no additional information compared with wind speed estimates and no information at all above rated wind speeds (top-right subplot) [Colour figure can be viewed at wileyonlinelibrary.com]
. The observability in each radial plot is normalized with respect to its highest value. The percentage on the bottom-right corner of each radial plot indicates to what degree the local wind speed measurements contribute to the observability. It can be seen that the power measurements provide no additional information compared with wind speed estimates and no information at all above rated wind speeds (top-right subplot) [Colour figure can be viewed at wileyonlinelibrary.com]From this figure, one can immediately see that situations in which all turbines are in above-rated operation are unobservable when
 (top-right subplot). This subplot shows some observability when the turbulence intensity is low and the wake interactions are deep, such that one or multiple downstream turbines are operating below rated conditions. Furthermore, turbine power measurements do not add anything to the observability compared with the wind speed estimates. Note that the observability plots are not identical for below-rated conditions as power is cubically related to the wind speed,
(top-right subplot). This subplot shows some observability when the turbulence intensity is low and the wake interactions are deep, such that one or multiple downstream turbines are operating below rated conditions. Furthermore, turbine power measurements do not add anything to the observability compared with the wind speed estimates. Note that the observability plots are not identical for below-rated conditions as power is cubically related to the wind speed,
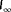 , and thus, the observability is spread slightly differently within the radial plots. Though, the trends are identical. Hence, in the remainder of this work,
, and thus, the observability is spread slightly differently within the radial plots. Though, the trends are identical. Hence, in the remainder of this work,
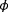 .
.
An important remark is that a different surrogate model, eg, one that directly correlates the upstream turbulence intensity with the upstream turbine power production, may provide a higher degree of observability from the same power measurements. Currently, such a correlation is not present in FLORIS.
4.1.2 Using exclusively wind speed estimator measurements (
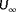 ,
,
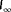 ,
,
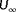 )
)
Here, the situation with solely wind speed measurements available is investigated;
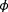 and
and
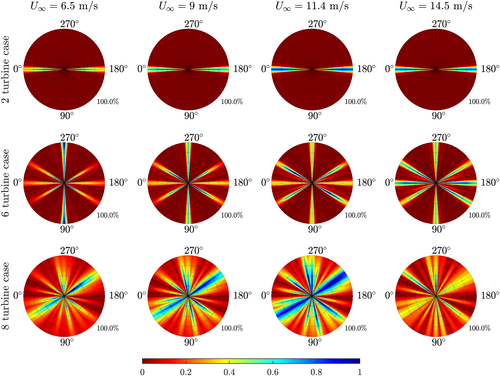
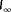 . This is comparable with the estimation framework applied in previous work,12 in which wind vane measurements were not assumed to be available. This is a particularly difficult problem, as previous results from Section 3 suggest. In the remainder of this section, all three wind farm layouts will be addressed. The observability roses are shown in Figure 10.
. This is comparable with the estimation framework applied in previous work,12 in which wind vane measurements were not assumed to be available. This is a particularly difficult problem, as previous results from Section 3 suggest. In the remainder of this section, all three wind farm layouts will be addressed. The observability roses are shown in Figure 10.
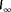 is known, with
is known, with
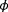 . The observability in each radial plot is normalized with respect to its highest value. The percentage on the bottom-right corner of each radial plot indicates to what degree the local wind speed measurements contribute to the observability, which in this situation is
. The observability in each radial plot is normalized with respect to its highest value. The percentage on the bottom-right corner of each radial plot indicates to what degree the local wind speed measurements contribute to the observability, which in this situation is
 [Colour figure can be viewed at wileyonlinelibrary.com]
[Colour figure can be viewed at wileyonlinelibrary.com]A number of observations can be made from Figure 10. Firstly, for the two-turbine wind farm, it is clear that the wind direction and wind speed can only be estimated accurately for a narrow range of wind directions—specifically, in which there is sufficient wake interaction. Theoretically, the
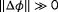 can always be reconstructed from the wind speed estimate of the upstream turbine, and the upstream turbine can be distinguished if there is wake interaction: it is the turbine with the highest power signal. The wind direction can then be estimated by looking at the quantity of wake losses at the downstream turbine. However, this may lead to situations in which two hypothesized wind directions lead to a near-identical inflow wind speed
can always be reconstructed from the wind speed estimate of the upstream turbine, and the upstream turbine can be distinguished if there is wake interaction: it is the turbine with the highest power signal. The wind direction can then be estimated by looking at the quantity of wake losses at the downstream turbine. However, this may lead to situations in which two hypothesized wind directions lead to a near-identical inflow wind speed
 , as was seen previously in Figure 4.
, as was seen previously in Figure 4.
Secondly, for the six-turbine wind farm, it can be seen that this topology has more wake interaction than the two-turbine wind farm and thus has an increased observability for many situations. However, there are still situations with little to no wake interaction which are unobservable. Note that the radial plots for both the two-turbine wind farm and the six-turbine wind farm are radially symmetrical, as the topologies are also radially symmetrical.
Thirdly, for the eight-turbine wind farm, one can directly see that observability greatly increases due to many more unique wake interaction between turbines. With all topologies, generally, it is noted that a higher atmospheric turbulence leads to a lower observability. Specifically, the turbulence intensity reduces the wake interaction with downstream turbines. The results from Figure 10 show that
 and
and
 can only be reconstructed for particular situations, and thus, care has to be taken in such estimation algorithms and related WFC algorithms. The next section shows the estimability of
can only be reconstructed for particular situations, and thus, care has to be taken in such estimation algorithms and related WFC algorithms. The next section shows the estimability of
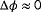 and
and
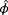 with the inclusion of wind vane measurements.
with the inclusion of wind vane measurements.
4.1.3 Using local wind speed and wind direction estimates (
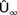 ,
,
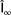 ,
,
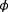 )
)
By including local estimates of the wind direction,
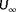 , one can attain observability for all situations, as shown in Figure 11. Now, one assumes both wind speed measurements and wind vane measurements to be available.
, one can attain observability for all situations, as shown in Figure 11. Now, one assumes both wind speed measurements and wind vane measurements to be available.
 is known, with
is known, with
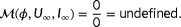 and
and
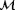 . The observability in each radial plot is normalized with respect to its highest value. The percentage on the bottom-right corner of each radial plot indicates to what degree the local wind speed measurements contribute to the observability, which provides an idea to the robustness of the solution [Colour figure can be viewed at wileyonlinelibrary.com]
. The observability in each radial plot is normalized with respect to its highest value. The percentage on the bottom-right corner of each radial plot indicates to what degree the local wind speed measurements contribute to the observability, which provides an idea to the robustness of the solution [Colour figure can be viewed at wileyonlinelibrary.com]It is clear to see that all the necessary information is contained in the measurements available for the estimation of
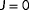 and
and
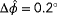 : all situations appear observable. Observability is guaranteed due to the availability of local wind speed and wind direction measurements, which are quantities directly derived from the ambient wind speed, ambient wind direction, and the wake interactions. Note that there are some variations within the radial circle, which are both due to physical effects such as more or less wake interaction and due to fact that the search space of the cost function (
: all situations appear observable. Observability is guaranteed due to the availability of local wind speed and wind direction measurements, which are quantities directly derived from the ambient wind speed, ambient wind direction, and the wake interactions. Note that there are some variations within the radial circle, which are both due to physical effects such as more or less wake interaction and due to fact that the search space of the cost function (
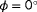 ,
,
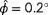 ,
,
 ) is discretized at a finite resolution.
) is discretized at a finite resolution.
The tools presented in this work may prove useful to find a balanced trade-off in the cost function between the contributions from various measurement sources. However, even with an accurate estimation of
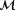 and
and
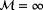 , significant model discrepancies may remain. The freestream turbulence intensity
, significant model discrepancies may remain. The freestream turbulence intensity
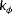 has a relatively large impact on the optimal turbine setpoints for wake steering, as it has a direct relationship to the degree of wake recovery. Hence, the estimation of
has a relatively large impact on the optimal turbine setpoints for wake steering, as it has a direct relationship to the degree of wake recovery. Hence, the estimation of
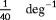 is a necessity in reliable WF algorithms. In the next section, the estimation of
is a necessity in reliable WF algorithms. In the next section, the estimation of
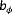 is incorporated into the observability analysis.
is incorporated into the observability analysis.
4.2 The full estimation problem: Estimating
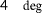 ,
,
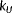 , and
, and
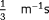
While observability for all situations was shown in Section 4.1.3, a compromising assumption was made that the freestream turbulence intensity
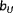 was known. In reality, this is not a realistic assumption and
was known. In reality, this is not a realistic assumption and
 must be estimated together with
must be estimated together with
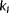 and
and
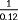 . The observability when estimating
. The observability when estimating
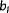 ,
,
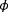 , and
, and
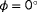 is shown in Figure 12, where
is shown in Figure 12, where
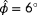 .
.
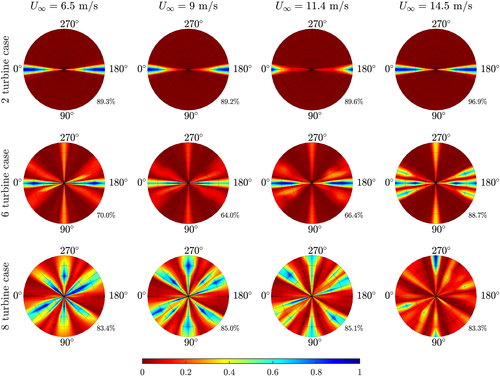
 and
and
 . The observability in each radial plot is normalized with respect to its highest value. The percentage on the bottom-right corner of each radial plot indicates to what degree the local wind speed measurements contribute to the observability, which provides an idea to the robustness of the solution [Colour figure can be viewed at wileyonlinelibrary.com]
. The observability in each radial plot is normalized with respect to its highest value. The percentage on the bottom-right corner of each radial plot indicates to what degree the local wind speed measurements contribute to the observability, which provides an idea to the robustness of the solution [Colour figure can be viewed at wileyonlinelibrary.com]Several observations can be made. Firstly, one can directly see that the observability significantly reduces for a large range of conditions compared with only the estimation of
 and
and
 . For the two-turbine case, observability only remains for the narrow window of wind directions in which there is wake interaction. This can be explained by the fact that the measurements provide direct information on
. For the two-turbine case, observability only remains for the narrow window of wind directions in which there is wake interaction. This can be explained by the fact that the measurements provide direct information on
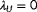 and
and
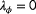 , while the estimation of
, while the estimation of
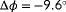 is enabled through inversion of the surrogate model and the usage of the local wind speed measurement at the downstream turbine. This only applies when wake interaction is present.
is enabled through inversion of the surrogate model and the usage of the local wind speed measurement at the downstream turbine. This only applies when wake interaction is present.
Secondly, observability is reduced in the six-turbine case compared with Figure 11, yet observability remains more widespread than the two-turbine case. More wake interaction and multiple-wake interaction leads to the fact that the turbine power signals are more sensitive to the freestream turbulence and thus yield a higher observability than the two-turbine case. Additionally, while a higher turbulence intensity leads to additional wake recovery, it also leads to wider wakes which can impact a downstream turbine where it would not for lower turbulence intensities. These two effects have an opposite effect on the observability, and hence observability does not uniformly decrease with an increase in the freestream turbulence intensity.
Thirdly, the eight-turbine wind farm has the most observable situations from the three topologies. Due to the many unique wake interactions, the solutions become relatively sensitive to the freestream turbulence intensity, and the ambient conditions can be estimated for most conditions. Though, also in this wind farm, one can find several situations in which the freestream conditions cannot uniquely be reconstructed from the measurements available.
An important remark to make is that all results presented in this section ignore the possibility of other measurement sources. While this framework allows the inclusion of turbulence intensity measurements, this was not pursued here. Additionally, one may argue that temporal correlation of measurements would allow for additional information on the ambient conditions. This would require a dynamic mathematical model that correlates the ambient conditions and the turbine measurements and a state estimation algorithm such as a Kalman filter. This is out of the scope of this article.
Finally, recall that these results present an idealized case, in which there is no measurement noise, and the surrogate model is used to generate the measurements, implying that the surrogate model perfectly represents reality. None of these assumptions are valid in practice, and thus, the observability roses presented in this section will further diminish. Though, the results presented in this section are an useful step towards the synthesis of an algorithm that estimates the ambient conditions in a robust manner. The observability roses from Figure 12 provide a theoretical upper limit on the relative estimatibility of the ambient conditions
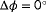 ,
,
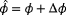 and
and
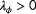 from the measurements available. This can provide guidance in C algorithms on when to estimate certain parameters. Since
from the measurements available. This can provide guidance in C algorithms on when to estimate certain parameters. Since
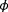 and
and
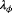 are always estimable according to Figure 11, the observability analysis presented in this section can be used to determine whether to estimate
are always estimable according to Figure 11, the observability analysis presented in this section can be used to determine whether to estimate
 in addition to
in addition to
 and
and
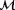 . If the situation is observable enough (which is to be selected experimentally), the measurements should contain sufficient information to reliably estimate
. If the situation is observable enough (which is to be selected experimentally), the measurements should contain sufficient information to reliably estimate
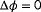 . If not, one can assume
. If not, one can assume
 to be equal to its past value (since the turbulence intensity also does not change very rapidly in the field) and exclusively estimate
to be equal to its past value (since the turbulence intensity also does not change very rapidly in the field) and exclusively estimate
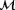 and
and
 . This approach is currently being explored and will be published in future work.
. This approach is currently being explored and will be published in future work.
5 CONCLUSIONS
Over the last years, the scientific community surrounding WFC has shown an increasing amount of interest towards the real-time estimation of the ambient conditions inside a wind farm. This ambient flow information is essential to the optimization of the turbine yaw angles for wake steering, which is currently the most popular methodology of WFC for power maximization. The degree of reconstructability of the ambient conditions highly depends on the meaurements available and the wind farm layout. For many situations, it is clear to see that the ambient conditions cannot be estimated. However, no quantitative measure exists to represent the degree of estimability of the ambient conditions. This paper addresses this scientific gap.
The main contribution of this paper is the introduction of a novel, mathematical definition for the observability of the ambient conditions. This measure describes how well the true ambient conditions can be distinguished from hypothesized ambient conditions through a model inversion approach for a particular set of measurements. This measure of observability is modular and can easily be extended with other measurement sources or other surrogate models. While a number of outcomes of this article may seem apparent, this theoretical framework provides the tools for extended analysis and a quantitative measure for the estimability of the inflow properties leveraging different measurement sources and surrogate models.
In several case studies, we show the usefulness of the proposed measure. Moreover, while information concerning the wind direction can be derived by looking at the turbine power signals and the inter-turbine wake interactions, the case studies presented show that there is a strong need for wind direction measurements for WFC to sufficiently cover observability for any topology and any ambient condition. Generally, situations in which there is sufficient wake interaction are observable, while situations with little to no wake interactions are unobservable. 3Furthermore, the mathematical framework supports the straightforward notion that local turbine power measurements provide no additional information compared with local wind speed estimates, implying that power measurements can be omitted from the cost function. 4Also, more complicated, unstructured wind farm layouts generally result in a higher observability as there are more unique wake interactions between turbines.
In general, even with local wind speed and wind direction information, one still cannot reconstruct the full set of ambient conditions (wind speed, wind direction, and turbulence intensity) for all conditions that a particular wind farm may encounter. Thus, before one may attempt to estimate the ambient conditions, one should consider whether the situation is observable in the first place. Using this information, one may condition their WFC algorithm to situations that are sufficiently observable. This aids in improving the reliability of WFC algorithms and thereby hopefully the willingness to adopt such algorithms by the industry.
ACKNOWLEDGEMENTS
This project has received funding from the European Union's Horizon 2020 Research and Innovation Programme under Grant Agreement No 727477 as part of the CL-Windcon project. The authors would like to thank Sebastiaan Mulders for his valuable insights in writing this document.
Financial disclosure
None reported.
Conflict of interest
The authors declare no potential conflict of interests.
Appendix A: ADDRESSING IRREGULAR BEHAVIOR, NUMERICAL ISSUES, AND SINGULARITIES IN THE CALCULATION OF THE DEGREE OF OBSERVABILITY
Equation 10 provides a clear measure for the degree of observability of a particular situation. With this formulation, evaluated ambient conditions far away from the true ambient conditions (eg,
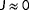 ) that yield a low estimation error
) that yield a low estimation error
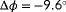 are penalized heavily. Namely, the nominator is small and the denominator is large, leading to a low value of
are penalized heavily. Namely, the nominator is small and the denominator is large, leading to a low value of
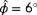 . In such a situation, it is unclear what the true ambient conditions are based on the measurements available. These situations result in a low degree of observability. Alternatively, situations with a high cost far away from the true ambient conditions result in a high degree of observability.
. In such a situation, it is unclear what the true ambient conditions are based on the measurements available. These situations result in a low degree of observability. Alternatively, situations with a high cost far away from the true ambient conditions result in a high degree of observability.
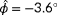 over the distance between the evaluated and true ambient conditions leads to undesired behaviour near the true ambient conditions (eg,
over the distance between the evaluated and true ambient conditions leads to undesired behaviour near the true ambient conditions (eg,
 ). For example, a singularity arises when the evaluated ambient conditions
). For example, a singularity arises when the evaluated ambient conditions
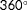 ,
,
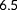 , and
, and
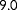 are exactly the true ambient conditions
are exactly the true ambient conditions
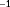 ,
,
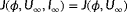 , and
, and
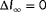 , respectively. Namely, then
, respectively. Namely, then
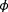
Similarly, when the evaluated conditions are very close to the true conditions, it becomes difficult to envision what the function of
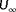 will look like. For example, if
will look like. For example, if
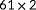 at
at
 , then the situation would turn out to be unobservable. This is because one cannot distinguish the true ambient condition (
, then the situation would turn out to be unobservable. This is because one cannot distinguish the true ambient condition (
 ) from a different evaluated condition (
) from a different evaluated condition (
 ). Clearly, this should not yield an unobservable situation, and a situation where
). Clearly, this should not yield an unobservable situation, and a situation where
 is very low “close enough” to the true conditions should not negatively impact the observability of the situation. To address this issue, a “deadzone” is introduced for
is very low “close enough” to the true conditions should not negatively impact the observability of the situation. To address this issue, a “deadzone” is introduced for
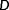 in proximity of the true ambient conditions. This deadzone enforces observability when the evaluated ambient conditions are close enough to the true ambient conditions. This can be seen as the upper formula in Equation 10, in which
in proximity of the true ambient conditions. This deadzone enforces observability when the evaluated ambient conditions are close enough to the true ambient conditions. This can be seen as the upper formula in Equation 10, in which
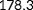 within the deadzone region. The effect of a deadzone is visualized in Figure A1. This deadzone resolves the issues related to singularities and numerical sensitivities.
within the deadzone region. The effect of a deadzone is visualized in Figure A1. This deadzone resolves the issues related to singularities and numerical sensitivities.
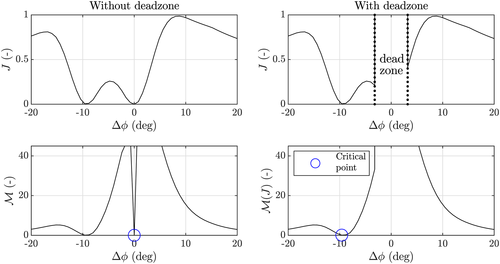
 for the calculation of
for the calculation of
 using Equation 10. The cost function shown here refers back to the two-turbine wind farm previously discussed in Section 3.1 with
using Equation 10. The cost function shown here refers back to the two-turbine wind farm previously discussed in Section 3.1 with
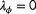 . In the top-left figure,
. In the top-left figure,
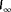 , the mean-squared error in turbine power signals, is plotted as a function of the hypothesized wind direction. Estimating the observability following Equation 9 leads to a singularity point at
, the mean-squared error in turbine power signals, is plotted as a function of the hypothesized wind direction. Estimating the observability following Equation 9 leads to a singularity point at
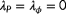 , while clearly
, while clearly
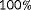 at the origin (true solution) should not lead to unobservability. This is corrected for by using a deadzone in proximity of
at the origin (true solution) should not lead to unobservability. This is corrected for by using a deadzone in proximity of
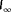 , as by Equation 10 [Colour figure can be viewed at wileyonlinelibrary.com]
, as by Equation 10 [Colour figure can be viewed at wileyonlinelibrary.com]Appendix B:
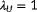 |
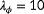 |
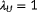 |
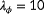 |
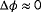 |
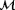 |
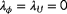 |
 |
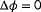 |
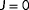 |
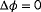 |
0.03 |
References
- 1 Note that the power measurements of different turbines can be weighted differently according to the amount of uncertainty in this measurement, as done in previous work.12 However, for the observability analysis at hand, this additional level of complexity does not sufficiently add to the theoretical foundation presented in this work.
- 2 Note that observability has a different notion in the field of control engineering for dynamical systems. In this article, an equivalent definition is defined for the static problem outlined in this section.
- 3 Here, the availability of other measurements than the local wind direction, wind speed, and turbine power capture were neglected. Additionally, the temporal evolution of measurement signals may provide insight into the current ambient conditions. This was outside of the scope of this article.
- 4 A promising research direction explored by the group of Professor Bottasso at the Technical University of Munich is to estimate missing model deficiencies over time through accumulative measurements of multiple measurement sources. Thus, one then does not discard duplicate information such as the turbine power signals, but rather estimates correction terms to improve the model fidelity through the integration of past data. This concept is not further explored here.



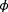 of
of
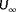 m and a hub height of
m and a hub height of
 m
m
