Dynamic event-triggered communication based distributed optimization
Corresponding Author
Zhiqiang Zhang
School of Mathematical Sciences, University of Jinan, Jinan, China
Correspondence Zhiqiang Zhang, School of Mathematical Sciences, University of Jinan, Jinan 250022, China.
Email: [email protected]
Search for more papers by this authorJan Lunze
Institute of Automation and Computer Control, Ruhr-University Bochum, Bochum, Germany
Search for more papers by this authorYuangong Sun
School of Mathematical Sciences, University of Jinan, Jinan, China
Search for more papers by this authorZehuan Lu
School of Mathematical Sciences, University of Jinan, Jinan, China
Search for more papers by this authorCorresponding Author
Zhiqiang Zhang
School of Mathematical Sciences, University of Jinan, Jinan, China
Correspondence Zhiqiang Zhang, School of Mathematical Sciences, University of Jinan, Jinan 250022, China.
Email: [email protected]
Search for more papers by this authorJan Lunze
Institute of Automation and Computer Control, Ruhr-University Bochum, Bochum, Germany
Search for more papers by this authorYuangong Sun
School of Mathematical Sciences, University of Jinan, Jinan, China
Search for more papers by this authorZehuan Lu
School of Mathematical Sciences, University of Jinan, Jinan, China
Search for more papers by this authorFunding information: National Natural Science Foundation of China, 61873110; 61903154; Natural Science Foundation of Shandong Province, ZR2018BF019
Abstract
This article presents distributed continuous-time algorithms with dynamic event-triggered communication, called the dynamic event-triggered algorithms, to solve a convex optimization problem in a multiagent network. Firstly, a new dynamic event-triggered communication scheme is introduced and it is shown that the optimization problem is solved and occurrence of Zeno behavior is prevented. Secondly, under the dynamic event-triggered communication implementations, both uniform and logarithmic quantized information algorithms are given to solve the optimization problem. Finally, numerical simulations are given to illustrate the effectiveness of the derived results.
CONFLICT OF INTEREST
The authors declare that there is no conflict of interest.
Open Research
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available from the corresponding author upon reasonable request.
REFERENCES
- 1Olfati-Saber R, Murray RM. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans Automat Contr. 2004; 49(9): 1520-1533.
- 2Xie G, Wang L. Consensus control for a class of networks of dynamic agent. Int J Robust Nonliner Control. 2007; 17(10–11): 941-959.
- 3Liu X, Ji Z. Controllability of multi-agent systems based on path and cycle graphs. Int J Robust Nonliner Control. 2018; 28(1): 296-309.
- 4Guan Y, Wang L. Target controllability of multiagent systems under fixed and switching topologies. Int J Robust Nonliner Control. 2019; 29(9): 2725-2741.
- 5Wei B, Xiao F, Shi Y. Fully distributed synchronization of dynamic networked systems with adaptive nonlinear couplings. IEEE Trans Cybern. 2019; 50(7): 2926-2934.
- 6 Lu Z, Ji Z, Zhang Z. Sampled-data based structural controllability of multi-agent systems with switching topology. J Frankl Inst. 2020; 357(15): 10886-10899.
- 7Ram SS, Veeravalli VV, Nedic A. Distributed and recursive parameter estimation in parametrized linear state-space models. IEEE Trans Automat Contr. 2010; 55(2): 488-492.
- 8Loia V, Vaccaro A. Decentralized economic dispatch in smart grids by self-organizing dynamic agents. IEEE Trans Syst Man Cybern Syst. 2014; 44(4): 397-408.
- 9Wang J, Elia N. A control perspective for centralized and distributed convex optimization. Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference; 2011; Orlando, FL.
- 10Gharesifard B, Cortés J. Distributed continuous-time convex optimization on weight-balanced digraphs. IEEE Trans Automat Contr. 2014; 59(3): 781-786.
- 11Kia SS, Corés J, Martínez S. Distributed convex optimization via continuous-time coordination algorithms with discrete-time communication. Automatica. 2015; 55: 254-264.
- 12Lu K, Jing G, Wang L. Distributed algorithms for solving convex inequalities. IEEE Trans Automat Contr. 2017; 63(8): 2670-2677.
- 13Lu K, Jing G, Wang L. Distributed algorithms for searching generalized Nash equilibrium of noncooperative games. IEEE Trans Cybern. 2018; 49(6): 2362-2371.
- 14
Miskowicz M. Event-Based Control and Signal Processing. CRC Press; 2015.
10.1201/b19013 Google Scholar
- 15Meng X, Chen T. Event based agreement protocols for multi-agent networks. Automatica. 2013; 49(7): 2125-2132.
- 16Zhu W, Li H, Jiang ZP. Consensus of multi-agent systems with time-varying topology: an event-based dynamic feedback scheme. Int J Robust Nonliner Control. 2017; 27(8): 1339-1350.
- 17Liu X, Du C, Lu P, Yang D. Distributed event-triggered feedback consensus control with state-dependent threshold for general linear multi-agent systems. Int J Robust Nonliner Control. 2017; 27(15): 2589-2609.
- 18Zhang Z, Wang L. Distributed integral-type event-triggered synchronization of multi-agent systems. Int J Robust Nonliner Control. 2018; 28(14): 4175-4187.
- 19Meng X, Xie L, Soh YC. Distributed event driven optimization for network utility maximization. Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC); 2016; Las Vegas.
- 20Tran NT, Wang YW, Liu XK, Xiao JW, Lei Y. Distributed optimization problem for second-order multi-agent systems with event-triggered and time-triggered communication. J Frankl Inst. 2019; 356(17): 10196-10215.
- 21 Ren L, Meng Z, Wang X, Zhang L, Yang LT. A data-driven approach of product quality prediction for complex production systems. IEEE Trans Ind Inform. 2020. https://doi.org/10.1109/TII.2020.3001054
- 22Li Y, Zhang H, Liang X, Huang B. Event-triggered-based distributed cooperative energy management for multienergy systems. IEEE Trans Ind Inform. 2019; 15(4): 2008-2022.
- 23Zhao T, Li Z, Ding Z. Consensus-based distributed optimal energy management with less communication in a microgrid. IEEE Trans Ind Inform. 2019; 15(6): 3356-3367.
- 24Girard A. Dynamic triggering mechanisms for event-triggered control. IEEE Trans Automat Contr. 2015; 60(7): 1992-1997.
- 25Dolk VS, Borgers DP, WPMH H. Output-based and decentralized dynamic event-triggered control with guaranteed
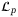-gain performance and zeno-freeness. IEEE Trans Automat Contr. 2017; 62(1): 34-49.
- 26Yi X, Liu K, Dimarogonas DV, Johansson KH. Distributed dynamic event-triggered control for multi-agent systems; 2017. arXiv preprint, arXiv:1704.05434.
- 27Yi X, Yao L, Yang T, George J, Johansson KH. Distributed optimization for second-order multi-agent systems with dynamic event-triggered communication; 2018. arXiv preprint, arXiv:1803.06380.
- 28Hu W, Yang C. Consensus of linear multi-agent systems by distributed dynamic event-triggered control. Proceedings of the International Workshop on Complex Systems and Networks; 2017; 284-289.
- 29Kashyap A, Basar T, Srikant R. Quantized consensus. Automatica. 2007; 43(7): 1192-1203.
- 30Ceragioli F, Persis CD, Frasca P. Discontinuities and hysteresis in quantized average consensus. Automatica. 2011; 47(9): 1916-1928.
- 31Zhang Z, Zhang L, Hao F, Wang L. Leader-following consensus for linear and Lipschitz nonlinear multiagent systems with quantized communication. IEEE Trans Cybern. 2017; 47(8): 1970-1982.
- 32Nedic A, Olshevsky A, Ozdaglar A, Tsitsiklis JN. On distributed averaging algorithms and quantization effects. IEEE Trans Automat Contr. 2009; 54(11): 2506-2517.
- 33Yuan D, Xu S, Zhao H, Rong L. Distributed dual averaging method for multi-agent optimization with quantized communication. Syst Control Lett. 2012; 61(11): 1053-1061.
- 34Li H, Liu S, Soh YC, Xie L. Event-triggered communication and data rate constraint for distributed optimization of multiagent systems. IEEE Trans Syst Man Cybern Syst. 2017; 48(11): 1908-1919.
- 35Liu S, Xie L, Quevedo DE. Event-triggered quantized communication based distributed convex optimization. IEEE Trans Control Netw Syst. 2016; 5(1): 167-178.
- 36 Khalil HK. Nonlinear Systems. 3rd ed. Prentice Hall; 2002.
Citing Literature
Special Issue:Emerging Approaches for Nonlinear Parameter Varying (NLPV) Systems
25 November 2021
Pages 8504-8522
