Strongly (J,J′)-lossless rational matrices and ℋ∞ problem
Corresponding Author
Jovan D. Stefanovski
Control & Informatics Division, JP Strezevo, Bitola, Republic of Macedonia
Correspondence
Jovan D. Stefanovski, Control & Informatics Division, JP Strezevo, Bitola, Republic of Macedonia.
Email: [email protected]
Search for more papers by this authorCorresponding Author
Jovan D. Stefanovski
Control & Informatics Division, JP Strezevo, Bitola, Republic of Macedonia
Correspondence
Jovan D. Stefanovski, Control & Informatics Division, JP Strezevo, Bitola, Republic of Macedonia.
Email: [email protected]
Search for more papers by this authorSummary
We strengthen the existing definition of (J,J′)-lossless rational matrices (RMs) and find an algebraic characterization of the newly defined class of strongly (J,J′)-lossless RMs. The algebraic characterization is given for possibly improper RMs. A connection is presented to a rational ℋ∞ problem, known as the Leech problem, which is elaborated on with necessary and sufficient conditions, given in terms of the strongly (J,J′)-lossless property, as an alternative of the Leech conditions, which can be expressed with positivity of a kernel. An algorithm for solving the Leech problem is given and illustrated by examples.
REFERENCES
- 1Hara S, Sugie T, Kondo R.
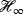control problem with jω-axis zeros. Automatica. 1992; 28(1): 55-70.
- 2Kimura H, Lu Y, Kawatani R. On the structure of
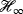control systems and related extensions. IEEE Trans Autom Control. 1991; 36(6): 653-667.
- 3Kimura H. Chain-scattering approach to
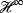control. Cambridge, MA: Birkhäuser; 1997.
10.1007/978-0-8176-8331-3 Google Scholar - 4Meinsma G, Kimura H. Corrections to “On the structure of
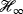control systems and related extensions”. IEEE Trans Autom Control. 1995; 40(11): 1921-1922.
10.1109/9.471216 Google Scholar - 5Genin Y, Van Dooren P, Kailath T, Delosme J-M, Morf M. On Σ-lossless transfer functions and related questions. Linear Algebra Appl. 1983; 50: 251-275.
- 6Leech RB. Factorization of analytic functions and operator inequalities. Integr Equ Oper Theory. 2014; 78: 71-73.
- 7Kaashoek MA, Rovnyak J. On the preceding paper of R. B. Leech. Integr Equ Oper Theory. 2014; 78: 75-77.
- 8Frazho AE, ter Horst S, Kaashoek MA. State space formulae for stable rational matrix solutions of a leech problem. Indag Math. 2014; 25: 250-274.
- 9Frazho AE, ter Horst S, Kaashoek MA. State space formulas for suboptimal rational Leech problem I: maximum entropy solution. Integr Equ Oper Theory. 2014; 79: 533-553.
- 10Saberi A, Stoorvogel AA, Sannuti P. Filtering Theory With Applications to Fault Detection, Isolation, and Estimation. Cambridge, MA: Birkhäuser; 2007.
- 11Lan J, Patton RJ. A new strategy for integration of fault estimation within fault-tolerant control. Automatica. 2016; 69: 48-59.
- 12Stefanovski J. Passive fault tolerant perfect tracking with additive faults. Automatica. 2017. https://doi.org/10.1016/j.automatica.2017.09.011
- 13Stefanovski J.
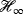control of descriptor systems possessing invariant zeros on the imaginary axis and infinity. IEEE Trans Autom Control. 2015; 60(12): 3127-3139.
- 14Wahls S, Boche H. Lower bounds on the infima in some H∞ optimization problems. IEEE Trans Autom Control. 2012; 57: 788-793.
- 15Wahls S, Boche H, Pohl V. Zero-forcing precoding for frequency selective MIMO channels with H∞ criterion and causality constraint. Signal Process. 2009; 89: 1754-1761.
- 16Li L, Gu G. Design of optimal zero-forcing precoders for MIMO channels via optimal full information control. IEEE Trans Signal Process. 2005; 53(8): 3238-3246.
- 17Molinari BP. Conditions for nonpositive solutions of the linear matrix inequality. IEEE Trans Autom Control. 1975; 20: 804-806.
- 18Trentelman HL, Rapisarda P. Pick matrix conditions for sign-definite solutions of the algebraic Riccati equation. SIAM J Control Opt. 2001; 40(3): 969-991.
- 19Glover K, Limebeer DJN, Doyle JC, Kasenally EM, Safonov MG. A characterization of all solutions to the four block general distance problem. SIAM J Control Optim. 1991; 29: 283-324.
- 20Stefanovski J.
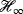problem with nonstrict inequality and all solutions: interpolation approach. SIAM J Contr Optim. 2015; 53(4): 1734-1767.
- 21Ishihara JY, Terra MH. Impulse controllability and observability of rectangular descriptor systems. IEEE Trans Autom Control. 2001; 46(6): 991-994.
- 22Willems JC. Dissipative dynamical systems - Part II: linear systems with quadratic supply rates. Archive Ration Mech Anal. 1972; 45: 352-393.
- 23Stefanovski J. Kalman-Yakubovich-Popov lemma for descriptor systems. Syst Control Lett. 2014; 74: 8-13.
- 24Stefanovski J. Numerical J-spectral factorization of general para-hermitian matrices. Syst Control Lett. 2008; 57: 1058-1066.
- 25Oara C, Varga A. Computation of general inner-outer and spectral factorizations. IEEE Trans Autom Control. 2000; 45: 2307-2325.
- 26Zhou K, Doyle JC, Glover K. Robust and Optimal Control. Upper Saddle River, NJ: Prentice Hall; 1996.
- 27Silverman LM, Payne HJ. Input-output structure of linear systems with applications to the decoupling problem. SIAM J Control. 1971; 9(2): 199-233.
- 28Gahinet P. Reliable computation of
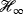central controllers near the optimum. Paper presented at: 1992 American Control Conference; 1992; Chicago, IL.
