Robust observer-based stabilization of Lipschitz nonlinear uncertain systems via LMIs - discussions and new design procedure

A. Zemouche,

Corresponding Author

A. Zemouche

[email protected]

University of Lorraine, CRAN UMR CNRS 7039, 54400 Cosnes et Romain, France

Correspondence to: Ali Zemouche, University of Lorraine, CRAN UMR CNRS 7039, 54400 Cosnes et Romain, France.

E-mail: [email protected]

Search for more papers by this author

R. Rajamani,

R. Rajamani

Laboratory for Innovations in Sensing, Estimation, and Control, Department of Mechanical Engineering, University of Minnesota, Minneapolis, MN, USA

Search for more papers by this author

H. Kheloufi,

H. Kheloufi

Department of Mathematics, Faculty of Sciences, University Mouloud Mammeri, Tizi-Ouzou, Algeria

Search for more papers by this author

F. Bedouhene,

F. Bedouhene

Department of Mathematics, Faculty of Sciences, University Mouloud Mammeri, Tizi-Ouzou, Algeria

Search for more papers by this author

A. Zemouche,

Corresponding Author

A. Zemouche

[email protected]

University of Lorraine, CRAN UMR CNRS 7039, 54400 Cosnes et Romain, France

Correspondence to: Ali Zemouche, University of Lorraine, CRAN UMR CNRS 7039, 54400 Cosnes et Romain, France.

E-mail: [email protected]

Search for more papers by this author

R. Rajamani,

R. Rajamani

Laboratory for Innovations in Sensing, Estimation, and Control, Department of Mechanical Engineering, University of Minnesota, Minneapolis, MN, USA

Search for more papers by this author

H. Kheloufi,

H. Kheloufi

Department of Mathematics, Faculty of Sciences, University Mouloud Mammeri, Tizi-Ouzou, Algeria

Search for more papers by this author

F. Bedouhene,

F. Bedouhene

Department of Mathematics, Faculty of Sciences, University Mouloud Mammeri, Tizi-Ouzou, Algeria

Search for more papers by this author

First published: 08 September 2016

https://doi.org/10.1002/rnc.3644

Citations: 62

Share a link

Email
Wechat
Bluesky

Summary

This paper presents a new observer-based controller design method for Lipschitz nonlinear systems with uncertain parameters and 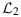$urn:x-wiley:rnc:media:rnc3644:rnc3644-math-0001$ -bounded disturbance inputs. In the presence of uncertain parameters, the separation principle is not applicable even in the case of linear time invariant systems. A state of the art review for uncertain linear systems is first presented to describe the shortcomings and conservatism of existing results for this problem. Then a new LMI-based design technique is developed to solve the problem for both linear and Lipschitz nonlinear systems. The features of the new technique are the use of a new matrix decomposition, the allowance of additional degrees of freedom in design of the observer and controller feedback gains, the elimination of any need to use equality constraints, the allowance of uncertainty in the input matrix and the encompassing of all previous results under one framework. An extensive portfolio of numerical case studies is presented to illustrate the superiority of the developed design technique to existing results for linear systems from literature and to illustrate application to Lipschitz nonlinear systems. Copyright © 2016 John Wiley & Sons, Ltd.

References

1Heemels WPMH, Daafouz J, Millerioux G. Observer-based control of discrete-time LPV systems with uncertain parameters. IEEE Transactions on Automatic Control 2010; 55(9): 2130–2135.
10.1109/TAC.2010.2051072
Web of Science® Google Scholar
2Lien CH. Robust observer-based control of systems with state perturbations via LMI approach. IEEE Transactions on Automatic Control 2004; 49(8): 1365–1370.
10.1109/TAC.2004.832660
Web of Science® Google Scholar
3Arcak M, Kokotovic P. Observer-based control of systems with slope-restricted nonlinearities. IEEE Transactions on Automatic Control 2001; 46(7): 1146–1150.
10.1109/9.935073
Web of Science® Google Scholar
4Ibrir S, Diopt S. Novel LMI conditions for observer-based stabilization of Lipschitzian nonlinear systems and uncertain linear systems in discrete-time. Applied Mathematics and Computation 2008; 206(2): 579–588.
10.1016/j.amc.2008.05.150
Web of Science® Google Scholar
5Gao H, Wang C, Zhao L. Comments on: an LMI-based approach for robust stabilization of uncertain stochastic systems with time-varying delays. IEEE Transactions on Automatic Control 2003; 48(11): 2073–2074.
10.1109/TAC.2003.819305
Web of Science® Google Scholar
6Atassi AN, Khalil HK. Separation results for the stabilization of nonlinear systems using different high-gain observer designs. Systems & Control Letters 2000; 39(3): 183–191.
10.1016/S0167-6911(99)00085-7
Web of Science® Google Scholar
7Hendricks E, Luther JB. Model and observer based control of internal combustion engines. Proceedings of the International Workshop on Modeling, Emissions and Control in Automotive Engines (MECA), Fisciano, Italy, 2001; 9–21.
Google Scholar
8Song B, Hedrick JK. Observer-based dynamic surface control for a class of nonlinear systems: an LMI approach. IEEE Transactions on Automatic Control 2004; 49(11): 1995–2001.
10.1109/TAC.2004.837562
Web of Science® Google Scholar
9Karafyllis I, Kravaris C. Robust output feedback stabilization and nonlinear observer design. Systems & Control Letters 2005; 54(10): 925–938.
10.1016/j.sysconle.2005.02.002
Web of Science® Google Scholar
10Pagilla PR, King EO, Dreinhoefer LH, Garimella SS. Robust observer-based control of an aluminum strip processing line. EEE Transactions on Industry Applications 2000; 36(3): 865–870.
10.1109/28.845063
Web of Science® Google Scholar
11Grip HF, Saberi A, Johansen TA. Observers for interconnected nonlinear and linear systems. Automatica 2012; 48(7): 1339–1346.
10.1016/j.automatica.2012.04.008
Web of Science® Google Scholar
12Zemouche A, Boutayeb M. On LMI conditions to design observers for Lipschitz nonlinear systems. Automatica 2013; 49(2): 585–591.
10.1016/j.automatica.2012.11.029
Web of Science® Google Scholar
13Zemouche A, Rajamani R, Boulkroune B, Rafaralahy H, Zasadzinski M. Convex optimization based dual gain observer design for Lipschitz nonlinear systems. IEEE American Control Conference, Boston, MA, USA, 2016.
Google Scholar
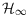14Zemouche A, Rajamani R, Boulkroune B, Rafaralahy H, Zasadzinski M. $urn:x-wiley:rnc:media:rnc3644:rnc3644-math-0395$ circle criterion observer design for Lipschitz nonlinear systems with enhanced LMI conditions. IEEE American Control Conference, Boston, MA, USA, 2016 July.
Google Scholar
15Ostertag E. An improved path-following method for mixed H₂/H_∞ controller design. IEEE Transactions on Automatic Control 2008; 53(8): 1967–1971.
10.1109/TAC.2008.928309
Web of Science® Google Scholar
16Lens H. Fast robust stabilization by saturating output feedback of uncertain linear systems with input constraints. 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference, Shanghai, P.R. China, 2009.
Google Scholar
17Toker O, Osbay H. On the NP-hardness of solving bilinear matrix inequalities and simultaneous stabilization with static output feedback, 1995.
Google Scholar
18Scherer C, Gahinet P, Chilali M. Multiobjective output-feedback control via lmi optimization. IEEE Transactions on Automatic Control 1997; 42(7): 896–911.
10.1109/9.599969
Web of Science® Google Scholar
19Swarnakar A, Marquez HJ, Chen T. A new scheme on robust observer-based control design for interconnected systems with application to an industrial utility boiler. IEEE Transactions on Control Systems Technology 2008; 16(3): 539–547.
10.1109/TCST.2007.908217
Web of Science® Google Scholar
20Kheloufi H, Zemouche A, Bedouhene F, Boutayeb M. On LMI conditions to design observer-based controllers for linear systems with parameter uncertainties. Automatica 2013; 49(12): 3700–3704.
10.1016/j.automatica.2013.09.046
Web of Science® Google Scholar
21Wang S, Jiang Y. Comment on “On LMI conditions to design observer-based controllers for linear systems with parameter uncertainties [Automatica 49 (2013) 3700-3704]”. Automatica 2014; 50(10): 2732–2733.
10.1016/j.automatica.2014.08.001
CAS Web of Science® Google Scholar
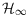22Kheloufi H, Zemouche A, Bedouhene F, Souley-Ali H. A robust $urn:x-wiley:rnc:media:rnc3644:rnc3644-math-0396$ observer-based stabilization method for systems with uncertain parameters and Lipschitz nonlinearities. International Journal of Robust and Nonlinear Control 2016; 26(9): 1962–1979.
10.1002/rnc.3391
Web of Science® Google Scholar
23Boyd S, El Ghaoui L, Feron E, Balakrishnan V. Linear matrix inequalities in system and control theory. In SIAM Studies in Applied Mathematics, vol. 15. Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, 1994.
10.1137/1.9781611970777
Google Scholar
24Ibrir S, Xie WF, Su CY. Observer-based control of discrete-time Lipschitzian non-linear systems: Application to one-link flexible joint robot. International Journal of Control 2005; 78(6): 385–395.
10.1080/00207170500101706
Web of Science® Google Scholar
25Ibrir S. Design of static and dynamic output feedback controllers through Euler approximate models: uncertain systems with norm-bounded uncertainties. IMA Journal of Mathematical Control and Information 2008; 25(3): 281–296.
10.1093/imamci/dnm023
Web of Science® Google Scholar
26Kheloufi H, Zemouche A, Bedouhene F, Boutayeb M. A new observer-based stabilization method for linear systems with uncertain parameters. 12th European Control Conference, ECC'13, Zurich, Switzerland, 2013.
Google Scholar
27Stankovic SS, Stipanovic DM, Siljak DD. Decentralized dynamic output feedback for robust stabilization of a class of nonlinear interconnected systems. Automatica 2007; 43(5): 861–867.
10.1016/j.automatica.2006.11.010
Web of Science® Google Scholar
28Jetto L, Orsini V. Efficient LMI-based quadratic stabilization of interval LPV systems with noisy parameter measures. IEEE Transactions on Automatic Control 2010; 55(4): 993–998.
10.1109/TAC.2010.2041617
Web of Science® Google Scholar
29Ibrir S. Static output feedback and guaranteed cost control of a class of discrete-time nonlinear systems with partial state measurements. Nonlinear Analysis 2008; 68(7): 1784–1792.
10.1016/j.na.2007.01.011
Web of Science® Google Scholar