Quantum machine learning with D-wave quantum computer
Summary
The new era of artificial intelligence (AI) aims to entangle the relationships among models (characterizations), algorithms, and implementations toward the high-level intelligence with general cognitive ability, strong robustness, and interpretability, which is intractable for machine learning (ML). Quantum computer provides a new computing paradigm for ML. Although universal quantum computers are still in infancy, special-purpose D-Wave machine hopefully becomes the breaking point of commercialized quantum computing. The core principle, quantum annealing (QA), enables the quantum system to naturally evolve toward the low-energy states. D-Wave's quantum computer has developed some applications of quantum ML based on quantum-assisted ML algorithms, quantum Boltzmann machine, etc. Additionally, working with CPUs, quantum processing units is likely to advance ML in a quantum-inspired way. Thus, a new advanced computing architecture, quantum-classical hybrid approach consisting of QA, classical computing, and brain-inspired cognitive science, is required to explore its superiority to universal quantum algorithms and classical ML algorithms. It is important to explore hybrid quantum/classical approaches to overcome the defects of ML such as high dependence on training data, low robustness to the noises, and cognitive impairment. The new framework is expected to gradually form a highly effective, accurate, and adaptive intelligent computing architecture for the next generation of AI.
1 INTRODUCTION
Artificial intelligence (AI), especially for machine learning (ML), including supervised learning and unsupervised learning, have been widely used in our daily life. Currently, ML mainly relies on enormous training data (like corpus data, image tags, and unlabeled data sets) and high-performance computing (HPC) platform,1 focusing on classification, regression, and more.
Deep learning (DL), as a key research area of ML, has been viewed as one of 10 breakthrough technologies in 2013 (MIT Technology Review) that massive amounts of computational power, instead of new algorithms, activated the practical machine intelligence. However, DL may ignore the classical sampling theorem,2 that is, generalization, robustness, and interpretability cannot be well guaranteed.
Furthermore, classical ML algorithms can hardly directly extract the high-level features of data sets without labels that is susceptible to the noises with low robustness and cognitive impairment.2, 3 For example, the initial cluster core in K-Means algorithm greatly limits the practical performance4 that is susceptible to the random initializations and outliners.
Thus, new computing paradigm and architecture should be considered to overcome the aforementioned problems.
1.1 Ignoring classical sampling theorem
The ML (or DL) currently tangles the models (characterizations), algorithms, and implementations so that it cannot get the high-level semantics and deep-level information, whereas the human can learn quickly based on intuitive reasoning, causal knowledge, and intelligent decision.5
Although DL can recognize cats in some cases,6 the cognitive ability shown by the machines is completely different from human intelligence that machine does not know what a “cat” is.
For example, modern cellular neural networks would give completely different outputs as there are few pixels change in the input. It suggests that DL essentially ignores the classical sampling theorem2 that the robustness and generalization are not guaranteed. Thus, there is still a long way before AI achieves human intelligence.
1.2 Cognitive impairment
The White House claimed in 2016 that it is unlikely that machines will exhibit broadly-applicable intelligence comparable to or exceeding that of humans in the next 20 years.7 Additionally, Professor Yoshua Bengio agreed (“Challenges for DL toward Human-Level AI”) that AI cannot realize the causality with the rules and common-sense knowledge for the moment, and new ML algorithms are required for constructing casual models to grasp high-level abstraction.
Briefly speaking, the machine intelligence is completely different from the human intelligence that the superiority of machine to human actually lies in a very limited regions (like image recognition). For example, human can easily distinguish whether it is a bottle or not, whereas the machine usually requires enormous training with a large labeled data sets and HPC platform.8 It partly suggests the human intelligence is of high robustness and versatility, whereas the cognitive impairment of machine requires another way to “approximate” the “human-like cognitive ability” on certain tasks.
1.3 “Dangerous” AI decision making
For the moment, the amount of human-constructed data sets provide the labels for machine to learn how to approximate the cognitive patterns given by human.9 However, to define the patterns actually partly ignores the real potentials of machines to characterize data sets. Additionally, the interpretability is also a problem.10 Thus, to achieve interpretability, as the bottleneck of advancing general AI in the field of security, ethics, and morality, is challenging.
Professor Fei-fei Li, the retired chief scientist of AI/ML and vice president of Google Cloud, aiming at constructing the ImageNet data sets before, utilized the labeling data sets to help machine classifier images. However, bias existing in the human-constructed data sets leads to machine bias, which may violate ethics and even common-sense knowledge.
In 2016, Microsoft, Google, Amazons, IBM, and Facebook jointly established the Partnership on AI (Apple joined in 2017) devoting to construct a good future of AI by correcting the errors or bias given by the machines.
As for supervised learning, the growth of computational power with high dependence on labeled training data sets may fail in real cognition and reasoning,11 which are also important for unsupervised learning with unlabeled data sets. Thus, how to construct a new way toward general AI with generalization, robustness, and interpretability is an open and important problem.
1.4 Quantum ML with new advanced computing architecture
For the moment, countries and companies are fighting for quantum supremacy and commercialized quantum computing applications, where quantum computing provides a completely different way from classical computing with the potential of native parallel computing capacity.12 As for ML, quantum computing may provide a new insight.
As in the report “High Performance Quantum Computing”, Professor Matthias Troyer reported that identifying killer-apps for quantum computing is challenging and listed four potential areas, namely, factoring and code breaking (limited use), quantum chemistry and material simulations (enormous potential), solving linear system, and ML.
Furthermore, quantum ML (QML) is one of the most promising areas from the aspect of quantum computing that quantum computing can generalize certain patterns, which the classical computers cannot generalize.13, 14 There are two types of quantum computer: universal quantum computer and special-purpose quantum computer.
Currently, the developments of universal quantum computers are still in infancy and cannot be practical in near term due to the slow progress of the quantum-system scalability, quantum-manipulating precision, system robustness, quantum error corrections, and quantum coherence. Professor John Martinis (UC Santa Barbara, joining Google since 2014) and Professor Matthias Troyer (now as the principal researcher of Microsoft's quantum computing program) pointed out15-17 that it will be many years18, 19 before the universal quantum computer achieves the practical quantum applications, including code-cracking.
On the other hand, D-Wave's quantum computer, as a special-purpose quantum machine, has developed more than 100 early applications for problems20-23 spanning quantum chemistry simulation, automotive design, traffic optimization, combinational optimization, ML, and more (“Press Releases” of D-Wave). D-Wave machine hopefully becomes the breaking point of commercialized quantum computing.
The first version of D-Wave commercialized quantum computer, D-Wave One (128 Qubits) purchased by Lockheed Martin, has implemented quantum effects and worked based on superconducting circuits near the absolute zero. The working unit, quantum processing unit (QPU), is constructed by niobium working in quantum states in low temperature that can activate the quantum tunneling effects. The most advanced version has come to D-Wave 2000Q with total 2048 qubits embedded in a limited Chimera graph that showed more powerful quantum computing capacity for different problems.
As the core algorithm, quantum annealing (QA) can utilize the quantum tunneling effects based on the adiabatic computing theorem24, 25 as a natural evolution toward low-energy states with the potential to approximate, or even achieve, the global optimum.26 It is the core advantage of QA compared to the classical methods that may easily get trapped in the local optimum in large-scale cases.
On the other hand, QA can be seen as a self-organizing and adaptive evolutionary algorithm, suitable for solving combinational optimizations and searching problems. From the aspect of intelligent computing, the intrinsic evolutionary property of QA toward the low-energy states is expected to show strong robustness and versatility in ML problems.
That is, the typical special-purpose quantum computer, D-Wave quantum system, can be regarded as the accelerator for ML. Furthermore, QA can be combined with brain-inspired cognitive techniques as a new advanced computing architecture, which is expected to show the subversive potential for ML.
Furthermore, inspired by perceptive and cognitive mechanism derived from the cognitive science and neuroscience, constructing a new advanced computing architecture, quantum-classical hybrid approach consisting of QA, classical computing, and brain-inspired cognitive science, is a novel proposal for gradually generating a highly effective, accurate, and adaptive intelligent computing architecture. In this way, QPUs can be embedded into the classical ML architecture as an accelerator, which is completely different from known algorithms for characterization, memory, and processing. The quantum-assisted framework is expected to better analyze the unstructured pattern and show subversive potential on classical ML.
In Section 2, we analyze the potential of QML with D-Wave machine based on the principle and quantum computing models of the quantum computer. Section 3 gives the theoretical analysis of QML with the annealer in two ways, ie, the feasibility of mapping ML problems to quantum spin models and the QA-based quantum Boltzmann machine (QBM). Section 4 briefly introduces the applications of QML by the quantum annealer and further analyzes the prospects of quantum-classical framework with the preliminary experiments and analysis for problems in cryptography and intelligent transportation. The last section summarizes our work.
2 POTENTIALS OF QML WITH D-WAVE'S QUANTUM COMPUTER
This part first introduces the procedure of QA for better understanding the QML applications by D-Wave machines, and it can be given as follows.
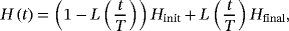 (1)
(1)However, the aforementioned evolutionary procedure is given in an ideal condition. In the real annealing environment, the quantum states tunnel toward the low energy state in certain time, whereas the noise in the hardware and from the annealing environment may lead to a suboptimal energy states. Therefore, although the D-Wave machine cannot always implement ideal QA, it can sometimes provide the (approximating) optimal solutions given in quantum states.
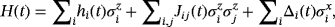 (2)
(2)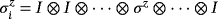 (the σz is in the ith position), similar for
(the σz is in the ith position), similar for
 and
and
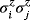 . Here, I is a 2 × 2 identity matrix, whereas σz and σx are the Pauli matrices.
. Here, I is a 2 × 2 identity matrix, whereas σz and σx are the Pauli matrices.Obviously,
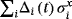 is given as Hinit, whereas
is given as Hinit, whereas
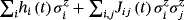 as Hfinal. Thus, adiabatic computing theorem can guarantee that the QA evolves toward the ground state of Hfinal. The feasible mapping from the ML problems to the Ising (or its equivalent model, ie, quadratic unconstrained binary optimization (QUBO)) paves the theoretical basis of QML with D-Wave quantum machine. In this way, finding the optimal solutions (or combinations) for ML problems can be mapped to the problems for searching ground state in the Ising models.
as Hfinal. Thus, adiabatic computing theorem can guarantee that the QA evolves toward the ground state of Hfinal. The feasible mapping from the ML problems to the Ising (or its equivalent model, ie, quadratic unconstrained binary optimization (QUBO)) paves the theoretical basis of QML with D-Wave quantum machine. In this way, finding the optimal solutions (or combinations) for ML problems can be mapped to the problems for searching ground state in the Ising models.
Additionally, the ground state not only characterizes the lowest energy corresponding the optimal solutions of ML problem but can also be seen as a new pattern or unique feature given based on the QA for further explorations, which can hardly be achieved by classical computing.
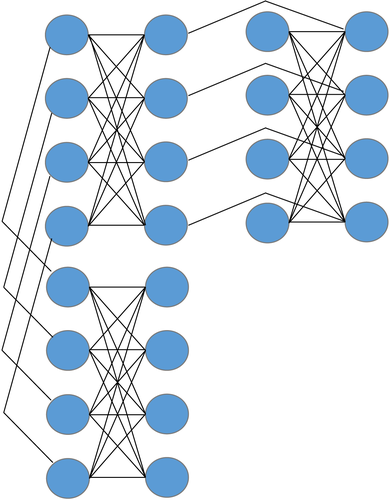
As for the physical realizations of quantum annealer, the Chimera graph is given as in Figure 1. We can directly note the limitations that one qubits can only connect up to 6 qubits simultaneously. Although the scalability and generalization can be partly guaranteed by minor-embedding,27 the machine itself may merely be used in small cases in near term.
Therefore, to identify the way of QPU to be embedded into the classical ML is important. Other than direct mapping from ML problems into Ising model, the quantum spin models can also be used for constructing QBM, which is inspired by Boltzmann machine (BM).28 It is a new way of QML so that the quantum sampling may replace the classical sampling algorithm with the potential of characterizing the data sets in a quantum-inspired way.29
As for supervised learning, the natural property of QA may help reduce, or even eliminate, the high dependence of ML on the labeled data sets, and search for the hidden characterizations that classical computers cannot find. It may help solve small cases with small data sets.22
As for unsupervised learning, QA is expected to find the special pattern different from the ones obtained by classical computers and provide a new learning paradigm. For example, there exist certain advantages from the comparison between QBM and classical BM, where QBM give a different Boltzmann distributions from the BM's.29
From the aspect of cognitive science, although QA can evolve toward the optimum, the cognitive ability depends on different tasks that should be defined by human. Thus, QA itself actually suffers from the lack of interpretability to some extent that cannot tell the differences among variety of ground states. Thus, to consider the combination of brain-inspired cognitive capabilities and D-Wave's quantum computer is required as a new but promising research area, which is expected to implement the human-like mechanism of intuitive reasoning, causal knowledge, and intelligent decision.
Additionally, the new pattern of “QPUs + CPUs” for D-Wave machine hopefully helps advance QML with D-Wave's quantum computer in near term. Actually, this type of hybrid quantum-classical framework is likely to maximize the advantage of classical and quantum computing.
On the one hand, compared to the exhaustive searching, QA has the potential speedup from the aspect of searching accuracy, coverage, and efficiency, and overcomes the defects of ML such as high dependence on enormous training data, low robustness to the noises, and lack of cognitive ability. On the other hand, although classical ML can solve enormous data simultaneous that the D-Wave machine cannot, the new features or patterns given in the quantum-inspired way are expected to provide a new learning paradigm to be combined with classical computing toward general AI.
3 THE THEORETICAL ANALYSIS OF QML BY D-WAVE
This part is to analyze the feasibility of D-Wave's quantum computer for quantum (assisted) ML based on QBM (Section 3.1) and the Ising models (Section 3.2).
3.1 Quantum Boltzmann machine
The BM30 is introduced based on energy function, where the distributions of different energy levels represent their equilibrium distributions, and is important for generative models. However, to approach the equilibrium distributions is difficult with limited computing accuracy.31
Thus, many scientists focused on approximating the Boltzmann distribution with physical quantum annealer.28, 32, 33 Inspired by BM, the scheme of realizing QBM based on the Ising model with transverse field has been proposed by introducing bounds on the quantum probabilities.28 Then, quantum sampling can estimate the gradients of the log-likelihood and QBM learned the data distribution better than BM in small cases.
Additionally, Korenkevych et al34 further analyzed that the fundamental support for a better QMB than the classical one is the capacity of sampling low-energy configurations, which has been proposed as “pause” and “quench” by D-Wave system.35 That is, D-Wave's quantum computer can effectively gather midanneal samples for the further applications of QBM.
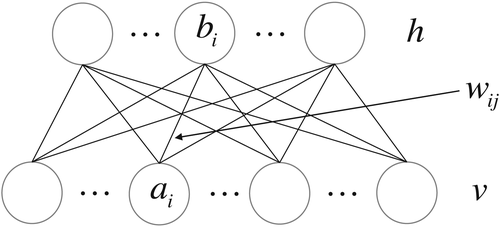
Here, this paper first briefly introduces the typical version of BM, ie, restricted BM (RBM). RBM is a generative stochastic artificial neural network that generally consists of visible layer v and hidden layer h. The layout can be seen in Figure 2. Obviously, the connections between h and v are similar to the D-Wave Chimera graph, a part of which can be seen in Figure 1. That is, the D-Wave can be used for realizing RBM with the similar structure, ie,
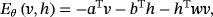 (3)
(3)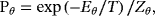 (4)
(4)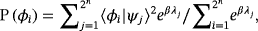 (5)
(5)The quantum Boltzmann distribution becomes identical to the Boltzmann distribution in the classical limit when ψj correspond to ϕi. In real annealing, the quantum Boltzmann distributions can be derived from the transverse expectations.36 Additionally, even if the final distributions deviate from the Boltzmann distributions due to ergodicity breaking, the estimates can also be used for data analysis.37
What should be pointed out is that D-Wave quantum machine not only can be a QBM for QML but also can be a QML components embedded into classical ML algorithm, like discrete variational autoencoders (VAEs)38 and quantum VAE.39 For example, Khoshaman et al39 employed the QBM in the latent generative process of a VAE and can get the state-of-the-art performance on the MINIST data sets.
In this way, QPUs can be widely used in different ML architectures so that the potentials provided by the quantum sampling contribute to the further combination of QPU with classical implementations to establish new and promising architecture for QML in future.
3.2 QML by quantum spin models
Other than QBM or its variant, D-Wave quantum spin models can directly be used for discrete optimization problems,40 which can search for the optimal combination of various weak classifiers. It is a different way from QBM to transform some mathematical constructions of ML to the procedure of evolutionary optimizations that (a part of) ML problems can be characterized by quantum spin models to be solved by D-Wave's quantum computer.
Theoretically, to solve ML problems by quantum spin models mainly depends on the capacity of D-Wave machine to solve two kinds of spin models: Ising model and its equivalent model, ie, QBUO model, which is of great importance to characterize many problems, including discrete optimization problems.
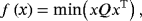 (6)
(6)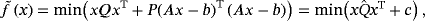 (7)
(7)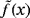 is equivalent to f (x), as a new QUBO model with a new coefficient matrix
is equivalent to f (x), as a new QUBO model with a new coefficient matrix
 .
.(2) x1 + x2 ≤ 1: Since xi can take 0 or 1, the condition is equivalent to the case that only one element of {x1, x2} takes 1, whereas the other one takes 0. Thus, a penalty term Px1x2 satisfies this condition where P is positive.
These two cases and the equivalent cases are involved in many problems that provide the second basis for D-Wave quantum machine to implement QML for small cases. For example, Neven et al40 constructed a QUBO model for selecting the optimal voting set of weak classifiers to help detect cars in digital images. Quantum-assisted optimization showed the potential of superiority to AdaBoost with fewer weak classifiers.
Currently, there are several limitations existing in the D-Wave's quantum computer, including limit-connection hardware graph, programmability, robustness to the environment, and QA accuracy. All the aforementioned factors cause the difficulty of implementing large-scale and effective QML solely by D-Wave machine. Thus, to see the QPU as a kind of low-power, high-performance coprocessor for assisting ML with the natural evolutionary property of QA is of great importance.
4 D-WAVE APPLICATION DEVELOPMENT
Section 4 first briefly analyzes the small-case experiments (Section 4.1) and successful QML applications (Section 4.2) with two aforesaid ways. Then, the new hybrid quantum-classical framework (Section 4.3) has been given for the preliminary experiments on specific tasks with potential advantages to improve system robustness and overcome cognitive impairments to some extent.
4.1 Feasibility of QML with D-Wave's quantum computer on small cases
The developments of QML by the D-Wave system are still at the beginning stage to be used for problems spanning chemistry,20, 21 materials, and biology.42 The limit-connection quantum hardware can hardly solve large-scale problems although it can achieve the comparable performance to classical ML in small cases.
For example, Professor Daniel Lidar (University of Southern) et al solved a Higgs-signal-versus-background ML optimization problem by the Ising models and showed the comparable performance to the state-of-the-art ML methods23 used in particle physics with clear physical meaning. Daniel Lidar et al first constructed weak classifiers from the distributions of kinematic variables, and then provided a carefully designed Ising model for quantum and classical annealing-based systems. Furthermore, the models provide clear meaning with certain robustness that would enable a substantial reduction in the level of human intervention and high accuracy of particle-collision data analysis.
O'Malley D. (LANL) et al applied the D-Wave chip for nonnegative/binary matrix factorization, showing the potentials of D-Wave machine as part of unsupervised learning methods for large-scale cases.43
To sum up, the problems, like training strong classifier and matrix factorization, are suited to the quantum annealer so that QA can help solve these problems involved in the classical ML algorithms. It not only can provide clear physical meaning as in the quantum spin model, but also have the potential to save computing resources to accelerate ML framework.
4.2 Quantum-assisted ML
Due to limitations of D-Wave quantum hardware, it is of great importance to consider the research works of quantum-assisted ML in future for large-scale applications. This framework is expected to maximize the potentials of quantum samplings and quantum characterizations to assist the classical computer for data analysis.
For example, Volkswagen's group provided a global optimizations for the traffic flow from the Beijing center to the airport to be solved by D-Wave machine.22 In this work, a suitable model for D-Wave machine has been given as an Ising model, similar to the evaluation function in ML, for characterizing the traffic flows. That is, D-Wave machine can provide a new characterization (more suitable for D-Wave) different from the classical ML to be learned with the natural evolutionary criterion of QA.
Essentially, some classical ML problems can be (partly) reformulated as discrete optimizations and mathematical problems suitable for the D-Wave machine that the optimal assignments of the theoretical spin models correspond to the ground state of the Hamiltonian.
Thus, we find that “problem + feasibility of characterizations + small-scale cases/large-scale architecture” is the key for QML toward breaking points of ML in near term. Adachi. S. H. et al proposed a QBM-assisted way for improving the efficiency of generative training in deep neural network,44 where the quantum sampling-based training approach can replace Gibbs sampling with comparable or better accuracy tested on the MINIST data sets.
As for feature selection, Alejandro Perdomo-Ortiz (NASA) et al proposed a quantum-classical DL framework, quantum-assisted Helmholtz machine.45 It consists of two networks. The recognition network utilized the quantum computer as the deepest hidden layers to extract the features while generating network reconstructed data sets based on the quantum distributions. In this work, they utilized the quantum sampling to abstract low-dimension features of MNIST handwritten digit data set as an unsupervised generative model to generate new digit data.
As another QML methods based on QBMs, quantum sampling not only can have the potential of replacing classical sampling for specific cases, like BMs, but also be used for low-dimensions feature selection in a way different from the classical ones. It has the potentials to realize high-accuracy characterization in small cases, which is important for generative models.
4.3 Hybrid quantum-classical framework with brain-inspired cognition
As discussed before, similar to classical ML, quantum spin models can be viewed as evaluation functions that estimates the performance of the learning procedure. Additionally, the way that QA evolves toward the ground state of Hamiltonian can be viewed as a learning paradigm of machine with multiple iterations. In this way, finding the ground states of system can be seen as a kind of unsupervised learning deigned for certain ML problems given in mathematical constructions.
In 2018, Feng Hu et al have utilized the D-Wave 2000Q system for designing cryptographic components with multiple criteria,46 as the first principle-of-proof experiments for the quantum cryptography by D-Wave machine. Meanwhile, Chao Wang et al showed optimistic potentials of QA algorithm and D-Wave's quantum computer for deciphering the RSA cryptosystem47, 48 with superiority to the latest IBM Q System One™ (20 Qubits, January 8, 2019).
Both cryptography design and analysis are presented in mathematic constructions that can be solved by the annealing rule. Then, the machine can find the optimal solutions most suited to the rule (like evaluation functions). Thus, the procedures of cryptography design, analysis, and more problems like that are equivalent to the procedure of searching for the hidden patterns in ML, where the final patterns are given in the Ising model with clear meaning.
However, these kinds of tasks require enormous classical/quantum computing resources and high-accuracy quantum annealer. Therefore, new learning mechanism of hybrid quantum/classical approaches with brain-inspired cognition is required, as a new potential way for advancing ML with stronger robustness and more reliable generalization.
Potok T. E. et al (ORNL) tested three different computing architectures (quantum platform, HPC, and neuromorphic computing) individually on the MNIST data set.49 They proposed the promising and feasible working pattern of combining the three architectures in tandem to solve DL limitations that may exceed beyond Neuman architecture based on different complex networks.
Thus, combined with the selective attention and knowledge extraction, the new evolutionary procedure has the potential to implement a quantum-inspired directional search. In this way, QA can work as an evolutionary and searching procedure with feedbacks from the natural rule, which is expected to provide a new way for surpassing ML toward general AI with strong robustness and interpretability.
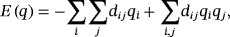 (8)
(8)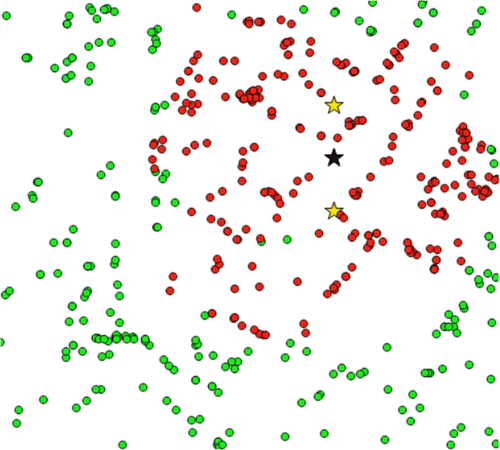
It can be seen that the black pentagram can effectively represent the center point of the red cluster. As a kind of quantum spectral clustering algorithm, our model is suited to different data distributions so that the initial points given for the second optimization can show certain robustness. It is a direct way to introduce brain-inspired model into the quantum spin models for QML. Compared to some classical algorithms, like K-Means, it is expected to give a better quantum initializations to overcome the susceptibility of classical algorithms to the random data distributions and noises. That is, robustness and generalization can be guaranteed with the introduction of quantum-inspired cognitive capacity embedded in the quantum spin models under the real traffic conditions.
Thus, although the research works about hybrid computing architectures are still at the beginning stage, hybrid quantum/classical approaches, as one of the key optimizations, will hopefully bring new lights to the next generation of ML with promising future and near-term applications by quantum-assisted ML. More attentions should also be paid on the special D-Wave's quantum computer as an accelerator for QML in the near future.
5 DISCUSSION
Classical ML, especially DL, ignores the classical sampling theorem, and they greatly depend on the training data and HPC for the moment. Thus, new advanced computing architectures are required to meet the demands of general AI on cognition, reasoning, and decision making. Moreover, QML, as a new paradigm for ML, sheds new lights on the next generation of AI.
Although the universal quantum computers are still in its infancy, the D-Wave machine, as the most advanced special-purpose quantum computer widely used in enormous areas, hopefully becomes the breaking point of commercialized quantum computing. Furthermore, due to the physical limitations given by the quantum Chimera graph, the QPU embedded in the D-Wave device can be regarded as the accelerators for ML to combine QA with brain-inspired cognitive algorithms to form a new hybrid computing system. It may help overcome the defects of classical ML algorithms, including the dependence on training data, low robustness to the noises, and cognitive impairment, which is to be expected to show subversive potential on classical ML.
On the one hand, quantum spin models, QUBO (or Ising) model, can be used to characterize the problems that the quantum tunneling effects, different from known learning algorithms in ML, can provide a new characterization suitable for pattern mining. On the other hand, QBM has the potentials to replace the classical sampling where the native evolutionary property of quantum is likely to find patterns that the classical ones cannot generalize. It is expected to show better robustness than classical ML, ie, the adaptive evolutionary criterion can, to some extent, eliminate the effects of human-guided and empirical searching, as a completely different way from the heuristic computing, advancing QML in many aspects, including training process, feature selection, and generative model.
Note that the current D-Wave quantum annealer cannot realize perfect QA yet due to temperature control defects and hardware restrictions. Thus, exploring the potential of new computing architecture and early validating experiments based on the D-Wave platform are of great important to the universal AI based on the D-Wave machine and others in future. The preliminary results of new framework on traffic optimizations also suggest that the new hybrid-augmented intelligence computing pattern can be used for various QML problems and the new era of “quantum (assisted) ML” is coming.
ACKNOWLEDGEMENTS
We acknowledge support from the National Natural Science Foundation of China (Grants 61332019, 61572304, and 61272096).
ADDITIONAL INFORMATION
Competing Interests: The author declares no competing interests.




