1 INTRODUCTION

The α-helix is the most common secondary structure found in proteins. It is a helical structure consisting of 3.6 residues per turn, and the main chain amide group of one residue is hydrogen bonded to the carbonyl group of four residues ahead. It was first described in 1951 by Pauling et al. (1951), and its presence in the protein structure was evidenced when the crystal structure of myoglobin was determined by Kendrew et al. (1960). The helix-coil transition was observed for synthetic polypeptides (Doty et al., 1954), and the helix formation was formulated by the Zimm–Bragg theory (Zimm & Bragg, 1959) or the Lifson–Roig theory (Lifson & Roig, 1961). Both theories define two parameters: nucleation and propagation parameters. For nucleation, three consecutive residues must take a helical φ–ψ angle to form the first hydrogen bond between the ith and i + 4th residues. Therefore, the nucleation of the helix is generally difficult. Only one residue is needed to form an additional hydrogen bond for propagation, and once nucleation has taken place, subsequent propagation is relatively easy. The nucleation and propagation parameters for individual amino acids have been evaluated with tremendous effort (Chakrabartty & Baldwin, 1995; Scheraga et al., 2002). Furthermore, statistical and experimental studies have revealed various factors that stabilized helices, such as capping interactions (Doig & Baldwin, 1995; Presta & Rose, 1988; Richardson & Richardson, 1988), charge-helix dipole interactions (Hol, 1985; Shoemaker et al., 1987; Wada, 1976), and side-chain interactions (Chakrabartty & Baldwin, 1995; Stapley et al., 1995). These helix-stabilizing factors known so far are the short-range interactions that occur within the helix and its flanking regions. In proteins, helices may interact with each other or with other secondary structural units, such as a β-sheet. In the case of disulfide-containing proteins, the helices may connect by disulfide bonds. Such long-range interactions frequently create a specific tertiary structure, and the contribution of individual interactions is difficult to analyze owing to the cooperativity of the tertiary structure. However, the effect of long-range interactions on helix stability can be analyzed in the folding intermediate or the partially unfolded state. Proteins, except for small proteins with less than 100 residues, assume a partially folded state during the early folding stages (Arai & Kuwajima, 2000; Chamberlain & Marqusee, 2000). Similar partially folded/unfolded states are observed under mild unfolding conditions such as at acidic or alkaline pH, at high temperature, and transiently under physiological conditions. These states are called “molten globule states” and have common characteristics. They have secondary structures that are similar to but not identical to the native secondary structure, their molecular sizes are compact like the native structures, they lose the side-chain packing, and they show diffuse unfolding transition (Ptitsyn, 1995). In this study, we address how the loop formed by a disulfide bond affects the stability of the helix. Although many studies report that the disulfide bond stabilizes or destabilizes the secondary structure in the folding intermediates (Horng et al., 2003; Ikeguchi et al., 1992; Ikeguchi & Sugai, 1989; Moriarty et al., 2000; Peng et al., 1995; Yamada et al., 2006), the effect of the disulfide bond on the specific secondary structural unit has not been investigated.

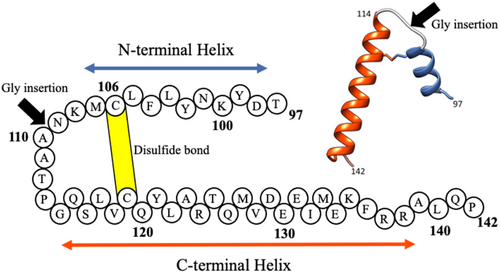
Previous studies have shown that equine β-lactoglobulin (ELG) forms a molten globule state at acidic pH (Ikeguchi et al., 1997). ELG is a 162-residue globular protein with eight antiparallel β-strands (labeled A–H) and a C-terminal helix downstream of the H-strand. In the molten globule state (A state), the region corresponding to the H-strand and C-terminal helix assumes a non-native helix in addition to a β-hairpin of F and G strands (Nakagawa et al., 2006). At lower temperatures, the molten globule is transformed to the cold-denatured state (C state), which has an expanded conformation, and the FG-hairpin is converted to the helix (Nakagawa et al., 2006, 2007; Yamada et al., 2005). The secondary structures in the C state can be mimicked in a fragment of ELG (residue: 88–142), which was named CHIBL (the core of the helical intermediate of β-lactoglobulin) (Nakagawa et al., 2007). Yamamoto et al. (2011) analyzed the detailed structure of the F strand-truncated CHIBL (CHIBLΔF) using nuclear magnetic resonance (NMR) and revealed that α-helices are formed around residues 98–107 (corresponding to G-strand region of the full length protein) and 114–135 (corresponding to H-strand and C-terminal helix regions of the full length protein). In this paper, we call these two helices the N-terminal helix and the C-terminal helix, respectively. These two helices are linked by the disulfide bond between Cys106 and Cys119 (Figure 1). Note that the structure is not persistent. At ambient temperatures, the structure of CHIBLΔF is considered to be the ensemble of various conformations, including a conformation in which only the N-terminal helix is formed, a conformation in which only the C-terminal helix is formed, and a conformation in which both helices are formed. Furthermore, the lengths of the helices would be various. Circular dichroism (CD) spectra show that the α-helical content of CHIBLΔF is reduced when the disulfide bond is cleaved. Short peptide fragments (97–110 and 111–138) do not form stable helices, and the sum of the spectra of these two peptides is similar to that of reduced CHIBLΔF (Yamamoto et al., 2011). These results show that α-helices in CHIBLΔF are stabilized by the disulfide bond. The authors suggested that the helices are stabilized because the helix nucleation is enhanced when the closed loop is formed by disulfide bond formation (Yamamoto et al., 2011). The aim of the present study was to verify this hypothesis.

2 RESULTS

2.1 Absence of tertiary interactions in CHIBLΔF

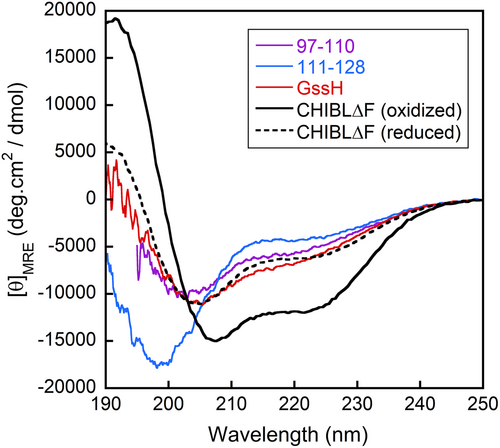
A possible mechanism by which the disulfide bond stabilizes the α-helices is that the disulfide bond increases the effective concentration of interacting side chains for stabilization of α-helices. If residues neighboring Cys106 and Cys119 interact with each other so that α-helices are stabilized, the interresidue nuclear Overhauser effects (NOEs) may be observed between such pairs of interacting residues. Although we previously investigated ¹⁵N-edited NOESY spectra of CHIBLΔF, we could find no long-range NOEs (Yamamoto et al., 2011). Therefore, the two helical regions do not pack together tightly. To further confirm the absence of interactions between residues in the two helical regions, we synthesized peptide GssH in which the peptide 97–110 (hereafter called the G-peptide) and H-peptide (corresponding to residue 111–128) were linked by the disulfide bond between Cys106 and Cys119. Figure 2 shows the CD spectrum of GssH compared with the spectra of G-peptide and H-peptide alone. The spectrum shows that the helical content of GssH is comparable with that of disulfide-reduced CHIBLΔF. Therefore, the helix promotion by the disulfide bond is not caused by the increased effective concentration of interacting side chains.

2.2 Closed loop effect on helix stabilization

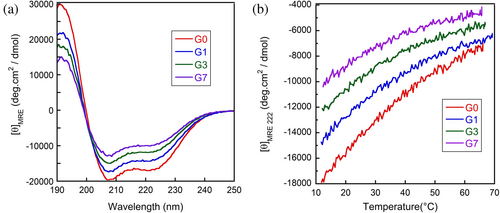
As an alternative mechanism of helix stabilization by the disulfide bond, Yamamoto et al. (2011) proposed the mechanism in which the helix nucleation is enhanced in the closed loop because of the restricted conformational freedom. If their assumption is correct, we can expect that the population of α-helices would be reduced if the loop were elongated by inserting several glycine residues in the middle. To confirm this, we made CHIBLΔF variants in which one, three, and seven glycine residue(s) were inserted into the loop region, and their helical fraction was compared with CHIBLΔF. Hereafter, CHIBLΔF is called G0, and one-, three-, and seven-glycine-inserted variants are called G1, G3, and G7, respectively.

The CD spectra of G0, G1, G3, and G7 in 0.1 M phosphoric acid are shown in Figure 3a, indicating that all protein fragments have α-helical structures. As the number of inserted glycine residues increased, the mean residue ellipticity ([θ]_MRE) at 222 nm increased, indicating that elongating the loop destabilizes the helix. The temperature dependence of the [θ]_MRE at 222 nm is shown in Figure 3b. For all fragments, the [θ]_MRE at 222 nm gradually increased with temperature. It is known for the molten globule states (Griko & Privalov, 1994; Ikeguchi & Sugai, 1989; Yamada et al., 2005; Yutani et al., 1992) and short peptides (Richardson & Makhatadze, 2004; Scholtz et al., 1991) that thermal helix–coil transitions are too broad to observe the entire transition within the experimentally accessible temperature range. Therefore, the temperature dependence of [θ]_MRE shown in Figure 3b is interpreted as a part of a broad thermal unfolding transition. Because the nearly identical [θ]_MRE values of the fully helical state and of the unfolded state are expected for G0–G7, Figure 3b shows that the glycine insertion (Gly-insertion) destabilizes the helix. However, it is unclear whether it destabilizes only the N-terminal helix or only the C-terminal helix or both helices. To clarify this, we measured the chemical shifts of individual residues using heteronuclear multidimensional NMR spectroscopy.

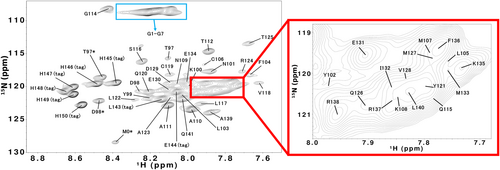
The ¹H–¹⁵N HSQC spectra of G1, G3, and G7 at 12°C are shown in Figure 4 and Supplementary Figure S1. The peak assignment is presented as the residue number in the whole polypeptide of ELG. Backbone ¹HN, ¹Hα, ¹³CO, ¹⁵N, ¹³Cα, and ¹³Cβ assignments were obtained for all residues (Table S1–S4 in the Supporting Information). Chemical shifts are derived from primary shifts (chemical shifts specific to individual amino acids) and secondary shifts (chemical shifts derived from the three-dimensional structure). The secondary shift is often used as an indicator of secondary structures. In general, when forming α-helices, the ¹Hα and ¹³Cβ chemical shifts are shifted lower than the random coil values, while the ¹³Cα and ¹³CO chemical shifts are shifted higher than the random coil values. The shift is usually opposite to the aforementioned shifts when forming β-sheets. In this study, the chemical shifts of linear peptides of six residues (Wishart, Bigam, Holm, et al., 1995) were used for the first-order shifts, and the second-order shifts of ¹Hα, ¹³Cβ, ¹³Cα, and ¹³CO for G0–G7 were calculated and are shown in Figure 5. The secondary shifts of ¹³Cα and ¹³CO showed low field shifts at residue numbers 98–107 and 114–135. A high field shift was observed in the same region for the secondary shift of ¹Hα. This was similar for all helix regions of G0–G7, but the shift amount decreased as the number of inserted glycine residues increased. These results show that the helical regions are essentially the same for all G0–G7 and the helical population of each residue decreases with the elongation of the loop.

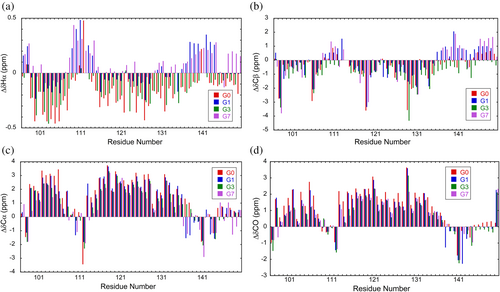
Unfolded proteins are heterogeneous in solution and cannot be described as a single structure. Therefore, they need to be characterized as a probability distribution. Camilloni et al. (2012) have developed a method called δ2D, which determines the populations of secondary structures (α-helix, β-strand, random coil, and polyproline II) for each residue. The helical fractions of individual residues in G0–G7 were calculated using δ2D from the ¹Hα, ¹³Cβ, ¹³Cα, ¹³CO, N, and HN chemical shifts (Figure 6). Figure 6 shows that the helical regions were essentially the same for all fragments and that the Gly-insertion reduced helical fractions in the entire region. The average helical fraction was 56%, 45%, 40%, and 25% for G0, G1, G3, and G7, respectively. A plot of CD values ([θ]_MRE) at 222 nm against the average helical fractions shows a straight line (Supplementary Figure S2), indicating that the helical fraction estimated by δ2D is consistent with the CD result. The line indicates that [θ]_MRE at 0% helical fraction is −3900deg∙cm²∙dmol⁻¹, which is consistent with [θ]_MRE of G7 at high temperatures (Figure 3b). [θ]_MRE at 100% helical fraction is −26,200deg∙cm²∙dmol⁻¹. Although this value is larger than the value proposed for 100% helix (e.g., −38,800deg∙cm²∙dmol⁻¹ at 12°C (Scholtz et al., 1991)), the value is reasonable because not all residues can assume the helical structure due to the loop formation. Furthermore, the experimental result showed that the residues beyond 140 do not assume the helix, irrespective of the number of inserted glycine residues.

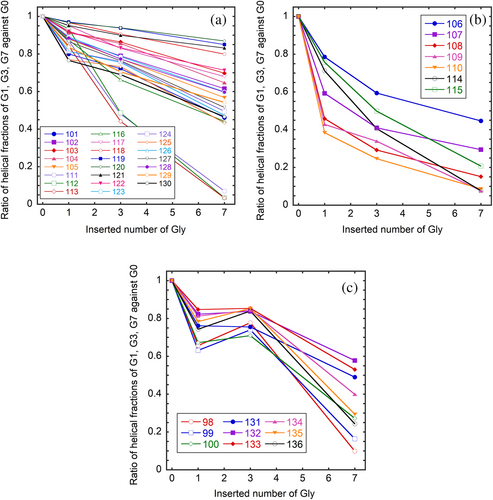
To investigate the effect of Gly-insertion on the helical fractions of individual residues, the ratios of helical fractions of G1, G3, and G7 against that of G0 were plotted against the number of inserted glycine residues (Figure 7). For clarity of Figure, we categorized the residues into three groups. Most residues (group 1) show a linear decrease in the helical fraction with the number of inserted glycine residues. Within this group, residues 111–113 are remarkable, and their helical fractions diminish in G7. The second group consists of the residues just ahead of the inserted position (106–110) and the residues 114 and 115, which show a significant decrease in the helical fractions when only one glycine residue is inserted. The third group consists of residues 98–100 and 132–136, that is, the residues located at the end of the helix far away from the Gly-inserted position. Their helical fractions do not significantly decrease in G1 and G3 but show an abrupt decrease in G7.

3 DISCUSSION

The cross-links, such as disulfide bonds, stabilize the native state by destabilizing the unfolded state (Betz, 1993; Zhang et al., 1994). The stability of the native conformation is evaluated through the free energy difference between the native and unfolded states. When cross-links are introduced into the random coil polypeptide, which is an ideal model of the unfolded state, the number of possible conformations is reduced so that the entropy of the unfolded state is decreased (Lin et al., 1984; Poland & Scheraga, 1965). Therefore, the free energy level of the unfolded state increases. If the cross-link does not significantly affect the native conformation, the free energy level of the native state is unchanged (the enthalpy change for making a cross-link is not included in this consideration because it is the same for both the native and unfolded states). As a result, the free energy difference between the native and unfolded states increases, making the native state more stable. Is this mechanism of structural stabilization applicable to flexible conformations such as CHIBLΔF? The answer is clearly no. In contrast to the native protein conformations, the structure of CHIBLΔF is so flexible that the number of possible conformations is reduced when a cross-link is introduced. Yamamoto et al. (2011) have proposed that the nucleation of α-helix is enhanced in the closed loop. The helix formation was formulated by the Zimm–Bragg theory (Zimm & Bragg, 1959) or the Lifson–Roig theory (Lifson & Roig, 1961). Both theories define two parameters: nucleation and propagation parameters. For nucleation, three consecutive residues must adopt a helical φ–ψ angle to form the first hydrogen bond between the ith and i + 4th residues. Therefore, the nucleation of the helix is generally laborious. Only one residue must be fixed to form an additional hydrogen bond for propagation once nucleation occurs. This makes propagation easier than nucleation. Yamamoto et al. (2011) have suggested that the entropy cost of nucleation is smaller in the closed loop than in the open chain. To support their suggestion, we estimated the possibility to take a helical φ–ψ angle as follows. The probability of taking a certain φ–ψ angle is assumed to obey the Boltzmann distribution based on the intrinsic potential energy of a residue depending on the φ–ψ angle. As the potential energy, we used the single amino acid potential calculated for a formyl alanine amide in water using a quantum chemical calculation based on a self-consistent isodensity polarizable continuum model for solute–solvent interactions (Iwaoka et al., 2006). The potential energy was calculated for each 15° of φ and ψ angles. If the population of the lowest energy angles (φ = −90°and ψ = −15°) is defined as unity, the summation of relative populations of all φ–ψ angles is 20.4 (Supplementary Figure S3). Of this number, 1.84 (9%) are compatible with α-helix (see Supplementary Figures S3 and S4). If the disulfide cross-link restricts the total number of conformations, how is the number of conformations defined by a certain φ–ψ angle changed? A theoretical study has shown that the number of independent variables reduces by six when forming a closed loop (Go & Scheraga, 1970; Wedemeyer & Scheraga, 1999). However, it is currently not known how reducing the degree of freedom corresponds to restricting the freedom of individual residues. We assumed that high-energy conformations are selectively excluded, leading to an increase in the probability of the helical φ and ψ angles because the energy of helical φ and ψ angles is relatively low. As a result, the helix nucleation in the loop closed by the disulfide cross-link (106–119) would be promoted. This nucleation promotion effect should be significant when the loop is small (the residue included in the loop is few). Therefore, the decrease in the helical fractions of the residues 106–119 with the increasing number of inserted glycine (Figure 6) is probably due to the reduced probability of the helix nucleation. The low helix propensity of the inserted glycine may affect the helical fractions of neighboring residues. To minimize this effect, the Gly-insertion point was selected between positions 109 and 110, where G0 inherently shows low helical propensity (Figure 6). The low helical fraction in this region is probably due to the strong helix breaker proline at 113. The influence of Gly-insertion can be clearly observed in the dependence of the helical fractions of individual residues (Figure 7). The many residues within the loop closed by the disulfide bond 106–119 show responses classified in group 2. The residues close to the inserted position (108, 109, and 110) in group 2 show large responses to the Gly-insertion (Figure 7b). Although we classified residues 111, 112, and 113 into group 1, they show characteristic large responses to the Gly-insertion (Figure 7a). At least part of these responses may be due to the low helix propensity of glycine. Although residues 114 and 115 are far from the insertion position, they show responses comparable to 108–110. Rather than the distance in sequence from the insertion position, the distance from Cys106 or Cys119 seems to be related to the response against the number of inserted glycine residues.

Once the helix is nucleated in the loop, it propagates to the N- and C-terminus directions beyond residues 106 and 119, respectively. Therefore, the helical fractions of residues 98–105 and 120–139 also decrease with the inserted glycine numbers (Figures 6 and 7). The effect of glycine insertion disappears around residue 140 due to the existence of Pro142. In contrast, the effect continues to the N-terminus. The residues located at the end of the helix (group 3) show the largest responses when seven glycine residues are inserted (Figure 7c). The entropic effect on helix nucleation is expected to be greater when a larger number of residues are inserted than when only one glycine residue is inserted. The fact that the responses of the residues in group 3 are observed at the residues close to the N- and C-terminus of the protein fragment suggests that the helices are mainly nucleated in the loop closed by the disulfide bond and propagated to the N- and C-terminus.

4 CONCLUSIONS

This study is the first to address the effect of cross-links on the conformational properties of individual residues in a flexible polypeptide. It was shown that the helices are destabilized with an increase in the number of residues within the loop formed by the disulfide bond. The results can be interpreted as follows. As the residue number forming the loop increases, the number of conformations within the loop increases. As a result, the entropy cost for assuming the helical φ and ψ angles increases, so that the helix nucleation is suppressed. This interpretation is supported by the fact that the helical fractions of the residues outside of the loop are changed depending on the number of glycine residues inserted. These findings are important for understanding the disulfide folding of proteins (Wedemeyer et al., 2000).

5 MATERIALS AND METHODS

AUTHOR CONTRIBUTIONS

Yuuki Yanagida: Investigation; writing – original draft; visualization; validation; funding acquisition. Kiyomi Yoshida: Investigation; writing – review and editing. Mio Ohtomo: Investigation; writing – review and editing. Kazuo Fujiwara: Writing – review and editing; resources; formal analysis. Masamichi Ikeguchi: Writing – review and editing; supervision; resources; conceptualization; project administration.

FUNDING INFORMATION

This work was supported in part by Japan Science and Technology Agency Support for Pioneering Research Initiated by the Next Generation, Japan Grant Number JPMJSP2143 to YY.