Protein Science
Volume 34, Issue 6 e70131
RESEARCH ARTICLE
Full Access

Exploring Abeta42 monomer diffusion dynamics on fibril surfaces through molecular simulations

Yuan-Wei Ma, 

Yuan-Wei Ma

Institute of Bioinformatics and Structural Biology, National Tsing-Hua University, Hsinchu, Taiwan

Department of Chemistry and Biochemistry, National Chung Cheng University, Chiayi, Taiwan

Contribution: ​Investigation, Data curation, Visualization, Writing - original draft, Formal analysis, Methodology, Validation, Software

Search for more papers by this author
Guan-Fang Wang, 

Guan-Fang Wang

Department of Chemistry and Biochemistry, National Chung Cheng University, Chiayi, Taiwan

Contribution: ​Investigation, Writing - original draft, Visualization, Formal analysis, Data curation, Methodology, Validation, Software

Search for more papers by this author
Hong-Yi Chen, 

Hong-Yi Chen

Department of Chemistry and Biochemistry, National Chung Cheng University, Chiayi, Taiwan

Contribution: Visualization, Formal analysis

Search for more papers by this author
Min-Yeh Tsai, 

Corresponding Author

Min-Yeh Tsai

Department of Chemistry and Biochemistry, National Chung Cheng University, Chiayi, Taiwan

Center for Nano Bio-Detection, National Chung Cheng University, Chiayi, Taiwan

Division of Physics, National Center for Theoretical Sciences, National Taiwan University, Taipei, Taiwan

Correspondence

Min-Yeh Tsai, Department of Chemistry and Biochemistry, National Chung Cheng University, Minhsiung, Chiayi, Taiwan.

Email: [email protected]

Contribution: Writing - review & editing, Writing - original draft, Conceptualization, ​Investigation, Funding acquisition, Resources, Supervision, Methodology, Validation, Formal analysis, Software

Search for more papers by this author
First published: 15 May 2025
https://doi.org/10.1002/pro.70131

Yuan-Wei Ma and Guan-Fang Wang contributed equally to this work.

Review Editor: Lynn Kamerlin

Abstract

This study provides critical insights into the role of surface-mediated processes in Alzheimer's disease, with implications for the aggregation of Abeta42 peptides. Employing coarse-grained molecular dynamics simulations, we focus on elucidating the molecular intricacies of these processes beyond primary nucleation. Central to our investigation is the analysis of a freely diffusing Abeta42 monomer on preformed fibril structures. We conduct detailed calculations of the monomer's diffusion coefficient on fibril surfaces (as a one-dimensional case), along with various monomer orientations. Our findings reveal a strong and consistent correlation between the monomer's diffusion coefficient and its orientation on the surface. Further analysis differentiates the effects of parallel and perpendicular alignments with respect to the fibril axis. Additionally, we explore how different fibril surfaces influence monomer dynamics by comparing the C-terminal and N-terminal surfaces. We find that the monomer exhibits faster diffusion coefficients on the C-terminal surface. Differences in surface roughness (SR), quantified using root-mean-square distances, significantly affect monomer dynamics, thereby influencing its diffusion on the surface. Importantly, this study underscores that fibril twisting acts as a regulatory niche, selectively influencing these orientations and their diffusion properties necessary for facilitating fibril growth within biologically relevant time scales. This discovery opens new avenues for targeted therapeutic strategies aimed at manipulating fibril dynamics to mitigate the progression of Alzheimer's disease.

1 INTRODUCTION

Protein aggregation plays a pivotal role in diseases such as Alzheimer's, especially in the context of the Amyloid Hypothesis (Hardy & Selkoe, 2002). Understanding this process, which includes nucleation, fibril growth, and breakage, is crucial for developing potential therapeutic interventions (Knopman et al., 2021). Despite this, the treatment landscape for Alzheimer's faces significant challenges. This is evident in the case of FDA-approved drugs like Aducanumab (Aduhelm), which are limited by usage constraints and safety issues (Center for Drug Evaluation, Research, 2023; Piller, 2022).

Recent studies have put forward the ‘oligomer hypothesis,’ which posits that while amyloid fibers might represent stable thermodynamic end-products, the toxic elements predominantly emerge from oligomers formed during protein aggregation (Bucciantini et al., 2002; Kayed et al., 2003; Walsh et al., 2002) (see a recent comprehensive review (Nguyen et al., 2021)). Understanding of primary nucleation mechanisms in amyloid fibers is robust (Lee et al., 2011; Oosawa & Asakura, 1975; Oosawa & Kasai, 1962); however, the dynamic complexity of protein fibril growth, particularly at lower concentrations (less than 10 μM), continues to present challenges (Xu et al., 2019). Insights from examining the morphologies and shapes of Abeta oligomers have deepened our understanding of how these oligomers, especially those with lateral branching, are formed (Yuan et al., 2022). Nonetheless, secondary processes such as filament breakage and secondary nucleation introduce additional complexity, substantially affecting the progression of neurodegenerative diseases (Cohen et al., 2013; Knowles et al., 2009).

Fibril growth and secondary processes are intricately linked to interactions at fibril surfaces and subsequent catalytic properties. Despite pioneering experiments elucidating surface-mediated nucleation (e.g., sickle hemoglobin (Bishop & Ferrone, 1984; Ferrone et al., 1985) and amyloid proteins (Cohen et al., 2013; Ruschak & Miranker, 2007)), a significant knowledge gap persists in understanding the molecular mechanisms underpinning these processes. These processes are crucial as they significantly influence the formation of toxic oligomers (Arosio et al., 2015; Cohen et al., 2015; Cohen et al., 2018), reflect reactive surface binding sites (Cohen et al., 2015; Scheidt et al., 2019), and modulate the macroscopic “lag time” (Arosio et al., 2015). This gap is particularly evident in the limited experimental data available for visualizing these interactions in real time or at atomic resolution, as emphasized in recent reviews (Cao et al., 2020). Interestingly, Xu et al. employed time-resolved in situ scanning probe microscopy, revealing that the monomer's association rate to the fibril end is significantly below the diffusion limit, indicating a high free energy barrier for new monomer incorporation into fibrils (Xu et al., 2019). The finding suggests that other rate-limiting processes, potentially involving surface-mediated interactions, could be influencing the monomer binding dynamics. Computational simulations can bridge this gap by providing a detailed understanding of these molecular interactions, which are challenging to capture directly through experimental methods (Cao et al., 2020; Törnquist et al., 2018). Full-atom simulations have shed light on early structural changes in aggregation, particularly hydrophobic and electrostatic forces influencing peptide adsorption on surfaces (Wang et al., 2011; Zhao et al., 2011). Additionally, extended atomistic simulations in explicit solvent (and implicit solvent) have also been employed to explore fibril surface-mediated nucleation and fibril growth (Barz & Strodel, 2016), enhancing our grasp of peptide docking pathways (Jalali et al., 2023). Coarse-grained models better explore longer timescales and biological contexts, revealing multiple aggregation pathways influenced by peptide-surface interactions and rigidity (Auer et al., 2009; Do et al., 2016; Morriss-Andrews & Shea, 2012; Vácha et al., 2014; Vácha & Frenkel, 2011). A recent review discussing the historical development of amyloid aggregation simulations provides further context to these computational efforts, illustrating how simulation strategies have evolved to tackle the complex phenomenon of protein aggregation (Fatafta et al., 2024). These computational insights have proven invaluable in identifying key features of protein aggregation that are difficult to observe experimentally, especially when considering the scale and complexity of biological systems.

Studies emphasize protein monomer mobility and lateral diffusion on surfaces in surface-mediated protein aggregation (Lin et al., 2018; Radic et al., 2015; Shen et al., 2012; Shezad et al., 2016). A crucial aspect of this is the intricate balance in the energy of protein monomer-surface interactions, which lies within a very narrow range and fulfills the energy requirement for secondary nucleation (Šarić et al., 2016). However, our understanding of monomer conformations and their diffusion behavior at the microdynamic level is still incomplete. For instance, the relationship between a protein's conformation and its diffusion dynamics on fibril surfaces remains an intriguing question. Gaining a comprehensive insight into these aspects is essential for effectively controlling monomer dynamics on surfaces.

Understanding the dynamics of protein monomers on fibril surfaces is not just crucial for surface-mediated aggregation, but also connects to broader principles in physical science. This leads us to consider the fundamental role of diffusion in natural processes, a concept central to the fluctuation–dissipation theorem. Diffusion, a key driver of atomic and molecular Brownian motion, manifests across various states of matter, including gases, liquids, solids, and glasses. Within biological contexts, such as in protein behavior, we observe significant variability in diffusion rates contingent on the environment. For example, protein diffusion is markedly slower in the crowded cytoplasm compared to dilute solutions (10 μm2/s vs. 100 μm2/s) (Milo & Phillips, 2015). Specifically, when proteins are attached to fibril surfaces, advanced techniques like total internal reflection fluorescence microscopy (TIRFM) and atomic fluorescence microscopy (AFM) have been instrumental in estimating diffusion coefficients, which range between 0.5 and 2.4 μm2/s (Shezad et al., 2016).

Our study therefore focuses on the “Oligomer Cascade Hypothesis,” which asserts that the mechanisms of seeded polymerization and surface-mediated nucleation are crucial for the formation and neurotoxic effects of soluble amyloid oligomers, key agents in the progression of neurodegenerative diseases (Hayden & Teplow, 2013; Selkoe & Hardy, 2016). These processes suggest that secondary processes on fibril surfaces depend on the dynamics and structure of newly attached protein monomers. Heterogeneous fibril surfaces, including assembly defects and specific amino acid binding sites, facilitate monomer diffusion, sliding, collisions, secondary nucleation, fibril elongation, and breakage, possibly leading to toxic aggregates. To explore this, we employ the openAWSEM simulation platform (Lu et al., 2021), known for its accuracy in physicochemical information, biological self-assembly, and fibril aggregation studies (Chen et al., 2021, 2022; Jin et al., 2022; Ma et al., 2021). openAWSEM excels in biophysical mesoscale kinetic analysis, capturing relevant time scales and molecular details, making it ideal for investigating the mesoscopic diffusion dynamics of amyloid-like peptides on fibril surfaces, a pioneering endeavor in this field.

By leveraging extensive simulations guided by the energy landscape theory (Zheng et al., 2016, 2017), the goal is to unravel the role of surface interactions in governing fibril growth, potentially offering innovative insights for neurodegenerative disease treatment and management. This research aims to enrich theoretical understanding and guide experimental approaches in this vital field.

2 METHODS

2.1 Open associative-memory, water-mediated, structure and energy model (OpenAWSEM)

In this study, openAWSEM is employed—a python implementation of the AWSEM protein coarse-grained force field devised by Wolynes and colleagues, as outlined by Lu et al (Lu et al., 2021). This innovative simulation framework is constructed on openMM (Eastman et al., 2017) to fulfill a rapid (GPU-enabled), adaptable, and user-friendly purpose. OpenAWSEM follows the legacy of the associative-memory, water-mediated, structure and energy model (AWSEM) for molecular dynamics (MD) simulation, as introduced by Davtyan et al. (2012), enabling precise and efficient modeling of protein dynamics.

To facilitate understanding for all readers, within the AWSEM framework, each amino acid residue is represented by three atoms: Cα, Cβ, and O, with glycine as the sole exception. The physicochemical characteristics of diverse side chains manifest in the Cβ atoms. The AWSEM-MD simulation protocol has been applied across a spectrum of biological studies, from protein structure prediction (Chen et al., 2018; Davtyan et al., 2012; Sirovetz et al., 2017; Tsai, Zheng, et al., 2016), prognostication of protein binding events (Tsai, Zheng, et al., 2016), investigations of protein aggregation phenomena (Zheng et al., 2016, 2017), to the exploration of intricate protein-DNA assemblies and remodeling processes (Potoyan et al., 2016; Tsai et al., 2019; Tsai, Zhang, et al., 2016; Zhang et al., 2016). For further details, the AWSEM-Suite web server offers additional resources for protein structure prediction (Jin et al., 2020).

In the simulations described, openAWSEM utilizes a coarse-grained scheme where each integration step is precisely 5 femtoseconds (fs). This fine temporal resolution strikes a balance between computational efficiency and the capability to capture essential dynamics crucial for our study of diffusion processes on fibril surfaces. This time step is standard within coarse-grained MDs, particularly with the AWSEM model, allowing us to bypass the fast dynamics of hydrogen bonds and side-chain interactions typical in all-atom models. Simulation trajectories were generated using the Langevin dynamics method, with the thermostat set to 300 K.

To estimate the effective time covered by the simulation, the output frequency and the stride length are key factors. For example, if the output frequency is set to 1000 steps and the stride for analysis is similarly 1000 steps, this implies that data is recorded and analyzed at these intervals. In a scenario where the x-axis in Figure 2b spans 106 (Walsh et al., 2002) steps, and considering the simulation scale, the effective time for this output is calculated by multiplying the number of steps (100) by the time per step, resulting in a total of 0.5 microseconds (μs). This calculation is based on 100 × 5 × 10−3 μs per step, effectively summing up to 0.5 μs for detailed analysis. This detailed temporal mapping is essential for a thorough understanding of the dynamics at play, providing critical insights for accurately modeling complex molecular behaviors over time.

Additionally, a limited set of all-atom simulations was carried out to validate the fibril stability observed from the AWSEM simulation (See Figure S3 in the Supporting Information for details).

2.2 Structural preparation and simulation protocol for Abeta monomer attaching to fibrils

We used the CreateFibril2.5 tool (Smaoui et al., 2013) to construct the fibril model of 62 chains. The program was used to replicate and extend selected protein chains from a specified PDB ID: 2MXU (Xiao et al., 2015). This process involves setting various parameters to control the replication, rotation, and placement of monomers along the fibril axis. We used this tool to generate fibril models with various morphological features, for example, straight, twisting. Figure 1 presents the filamentous models generated using the tool. See Supporting Information in Figure S1 for additional examples.

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Schematic diagram of Abeta monomer diffusion simulation on fibril surfaces. This diagram illustrates a fibril filament consisting of 62 chains in a gray cartoon representation, alongside an Abeta monomer depicted in three scenarios: (1) Initially detached and freely diffusing with a relaxed structure, shown in transparent blue. (2) At the initial attachment point, r(0), highlighted in blue. (3) At its subsequent position, r(t), at time t, shown in red. The position vector, r, is defined from the center of mass (COM) of chain A, which is the leftmost chain in the fibril marked by a solid yellow circle, to the projected COM of the monomer along the fibril's main axis (indicated by a thick arrow).

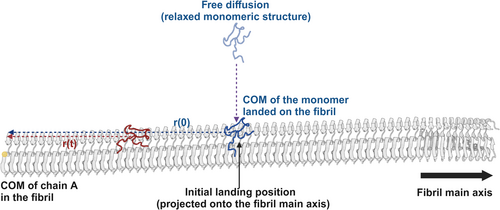
In constructing our fibril models from the 2MXU structure for this study, we primarily focused on examining the generic dynamic behaviors of monomers on fibril surfaces. Due to limitations in the available structural data and the scope of our computational model, we did not differentiate between interfacial and exposed surfaces in our analyses. The arrangement of protofilaments within the fibril, and specifically the amino acid sequences at the intrafibril interfaces, could not be precisely determined.

In the simulation setup for this study, the monomer structure for Abeta was generated to freely interact with the fibril, rather than being pre-positioned. Our simulation protocol was divided into two distinct stages to capture the dynamic adsorption process and subsequent surface diffusion:
  1. Free diffusion (3D): During the initial stage, the Abeta monomer was allowed to undergo structural relaxation and random three-dimensional diffusion. This stage was designed to simulate the monomer's natural movement in the environment above the fibril surface. The monomer was initially positioned at a distance of 24.2 Å from the fibril, specifically between the 40th chain of the fibril and the 11th residue of the monomer. Multiple independent simulation trajectories were conducted to ensure a variety of interaction outcomes, capturing successful adsorption events of the monomer onto the fibril.
  2. Surface-mediated Diffusion (2D to 1D): Following a successful adsorption during the first stage, the relaxed monomer's diffusion along the fibril surface was analyzed in the second stage. This part of the simulation focused on the two-dimensional to one-dimensional (1D) transition of the diffusion process once the monomer was absorbed on the fibril.

This methodological approach allows us to investigate how the Abeta monomer independently approaches and interacts with the fibril, highlighting the influence of dynamic and stochastic processes on the monomer's behavior and its subsequent impact on fibril surface properties.

2.3 Nematic order parameter

To delineate the distinction in structure among fibril polymorphs, we utilized the nematic order parameter (P2 value) to quantify the structured arrangement on the surface of fibrils. Initially devised for delineating structural order in liquid crystals, the nematic order parameter was introduced in the investigation of protein aggregation by Caflisch and colleagues (Cecchini et al., 2004). Subsequently, this parameter was employed to elucidate the aggregation of Amyloid peptides (Lin et al., 2023; Ma et al., 2021; Schwierz et al., 2017) and has recently undergone comparison with order parameters acquired through neural network learning, as demonstrated by Charest et al. (2020). All these demonstrate its growing importance in the study of protein aggregation.
P 2 = 1 N ∑ i = 1 N 3 2 z ̂ i ⋅ d ̂ 2 − 1 2 , $$ {P}_2=\frac{1}{N}\sum \limits_{i=1}^N\frac{3}{2}{\left({\hat{z}}_i\cdot \hat{d}\right)}^2-\frac{1}{2}, $$ ()
where d ̂ $$ \hat{d} $$ (the director) is a unit vector representing the preferred direction of the fibril surface (defined using residue 24 and 25 from each chain in the fibril), z i ̂ $$ \hat{z_i} $$ is the defined molecular vector (derived from residue 8–13 of the monomer), and N refers to the number of molecules considered in the calculation. Equation (1) outputs a value between −0.5 and 1, where 1 indicates perfect alignment along the reference axis, 0 indicates a random orientation, and −0.5 indicates perfect perpendicular alignment. Values within this range reflect varying degrees of alignment. This method enables precise quantification of orientation differences by measuring the extent to which monomers align with or diverge from the fibril axis. It clearly distinguishes between various orientations and their impact on the diffusion process.

2.4 Mean square displacement

We use the mean square displacement (MSD) formula to calculate the diffusion coefficient (D) in a 1D case, as shown below.
MSD t = r t − r 0 2 = 1 N ∑ i = 1 N r i t − r i 0 2 , $$ \mathrm{MSD}(t)=\left\langle {\left|\boldsymbol{r}(t)-\boldsymbol{r}(0)\right|}^2\right\rangle =\frac{1}{N}\sum \limits_{i=1}^N{\left|{\boldsymbol{r}}_i(t)-{\boldsymbol{r}}_i(0)\right|}^2, $$ ()
lim t → ∞ r t − r 0 2 = 2 Dt , $$ \underset{t\to \infty }{\lim}\left\langle {\left|\boldsymbol{r}(t)-\boldsymbol{r}(0)\right|}^2\right\rangle =2 Dt, $$ ()
where t refers to time; r(0) represents the initial center-of-mass (COM) distance between the monomer (at t = 0) and chain A (reference) in the fibril; r(t) indicates how the COM distance between the monomer and chain A in the fibril changes over time at t; N refers to the number of trajectories. To maintain accuracy and minimize deviation in vector calculations, the position vector r is defined as the distance from the COM of chain A (the leftmost chain in the fibril as the reference) to the projected COM of the monomer along the fibril's main axis. By applying Equation (2) to individual trajectories and then averaging the results, we can derive the diffusion coefficient as specified in Equation (3), utilizing what is termed “trajectory-based” approach for our analysis.
In scenarios where simulations capture monomer conformational or orientational changes, the diffusion dynamics can exhibit significant variability and may transition among different diffusion states. To accurately assess these dynamics, we segment each trajectory into smaller sections according to their orientations. These segments are then analyzed separately to calculate the diffusion coefficients specific to each orientation, employing what we refer to as a “segment-based” approach. The modified diffusion coefficient is thus calculated as
D ¯ = 1 T tot Δ t 1 ⋅ D 1 Δ t 1 + Δ t 2 ⋅ D 2 Δ t 2 + ⋯ + Δ t n ⋅ D n Δ t n , $$ \overline{D}=\frac{1}{T_{\mathrm{tot}}}\left[\varDelta {t}_1\cdot {D}_1\left(\varDelta {t}_1\right)+\varDelta {t}_2\cdot {D}_2\left(\varDelta {t}_2\right)+\cdots +\varDelta {t}_n\cdot {D}_n\left(\varDelta {t}_n\right)\right], $$ ()
where Ttot = ∑ i = 1 n Δ t i $$ {\sum}_{i=1}^n{\Delta t}_i $$ represents the sum of total time duration of trajectory segments; D ¯ $$ \overline{D} $$  is the overall diffusion coefficient; Dn is the diffusion coefficient for n-th segment; Δtn is the corresponding time duration. Equation (4) provides a precise measure of how monomer's conformation and orientation influence molecular mobility. Consequently, when calculating the diffusion coefficient, we account for the transitions between different monomer orientations within a single trajectory. By separating the trajectory based on each orientation and calculating the diffusion coefficient for each segment individually, we then apply a weighted average based on the frequency of each orientation. This approach ensures that the resulting average diffusion coefficient accurately represents the monomer's true diffusion behavior.

As a control for diffusion studies, we conducted simulations of a freely diffusing monomer and calculated its diffusion coefficient for benchmarking purposes. The baseline diffusion coefficient of the monomer was determined to be 430 μm2/s, which aligns well with the experimentally observed value of approximately 100 μm2/s for peptide diffusion (within the same order of magnitude, data not shown).

2.5 Free energy profile for Abeta monomer diffusion on fibril surfaces

To understand the kinetics of the monomer diffusion, we computed the free energy of protein moving along fibril surfaces, specifically the potential of mean force (PMF), using the umbrella sampling technique from the pyEMMA Python package, developed by Noe and collaborators (Scherer et al., 2015). Calculating PMFs requires selecting a specific progress coordinate for sampling. Due to the difficulty of accessing high-energy configuration spaces through thermal activation alone, we employed a biasing force, a technique known as “importance sampling,” to steer the sampling toward the desired configurational space. Our goal was to extensively sample the monomer distribution at various positions along the fibril's main axis and to reweight these distributions to map the free energy landscape of protein diffusion accurately. This approach allows us to explore how spatial variations along the fibril affect energy barriers and stability.

For practical implementation, similar to previous studies, we conducted all sampling tasks using MDs simulations on the openAWSEM platform (Ma et al., 2021). To monitor the trajectory of a monomer as it diffuses toward a specific position on the fibril's surface, we established numerous sampling windows. We applied a series of harmonic biasing restraints between the centers of mass of the monomer and the even end of the fibril. These restraints were set at intervals of approximately 2.2 Å, ranging from 20 to 230 Å from the even end (chain A) of the fibril, positioning the monomer on the surface. This setup resulted in 110 independent simulations.

The biasing coordinate was defined as the center of mass distance between the monomer and chain A of the fibril, with a biasing force constant of 6 kcal/mol (~25 kJ/mol) applied across all 110 simulations. Each simulation ran for 5 million time steps, outputting 5000 frames for analysis at every 1000 time steps. To manage data efficiently, we used a stride of 100, reducing the number of frames from 5000 to 50 for each simulation window. The collected data from these simulation trajectories, spanning 110 sampling windows, were then reweighted using the WHAM technique (Kumar et al., 1992), as implemented in the pyEMMA package (thermo.wham) (Scherer et al., 2015). The distribution across all sampling windows is detailed in the Supporting Information Figure S2.

2.6 Surface roughness (SR value)

To assess the roughness of the fiber surface, we defined a reference plane that minimizes the vertical distance deviations of selected residues' Cα atoms from it. First, we gather the 3D coordinates of all Cα atoms and calculate their centroid, which serves as the central reference point. The centroid represents the geometric center of the Cα atoms: residues 1–16 for the N-terminal surface and residues 36–42 for the C-terminal surface. Using this centroid, we compute the covariance matrix based on the positions of each atom relative to the centroid. This captures how the atoms are distributed in the x, y, and z directions. Specifically, we start with the coordinate matrix of full atoms, X
X = x 1 y 1 z 1 x 2 y 2 z 2 ⋮ ⋮ ⋮ x n y n z n , $$ X=\left[\begin{array}{ccc}{x}_1& {y}_1& {z}_1\\ {}{x}_2& {y}_2& {z}_2\\ {}\vdots & \vdots & \vdots \\ {}{x}_n& {y}_n& {z}_n\end{array}\right], $$ ()
where n = 992, and the 3D coordinates of each atom are listed sequentially. The centroid of the atoms of the plane, C, is thus given by
C = 1 n ∑ i = 1 n x i = x ¯ y ¯ z ¯ = 1 n ∑ i = 1 n x i ∑ i = 1 n y i ∑ i = 1 n z i , $$ C=\frac{1}{n}\sum \limits_{i=1}^n{x}_i=\left[\begin{array}{c}\overline{x}\\ {}\overline{y}\\ {}\overline{z}\end{array}\right]=\frac{1}{n}\left[\begin{array}{c}\sum \limits_{i=1}^n{x}_i\\ {}\sum \limits_{i=1}^n{y}_i\\ {}\sum \limits_{i=1}^n{z}_i\end{array}\right], $$ ()
where xi = [xi, yi, zi] are the coordinates of the i-th atom. At this step, we obtain the centroid as C = [ x ¯ $$ \overline{x} $$ , y ¯ $$ \overline{y} $$ , z ¯ $$ \overline{z} $$ ]. For the N-terminal surface, the calculated centroid is CN = [−2.801, 0.040, 1.042], and for the C-terminal surface, the centroid is CC = [10.205, −1.949, −3.695]. Using the definition, we proceed to formulate the covariance matrix, accordingly
A = Cov x , y z = 1 n − 1 ∑ i = 1 n x i − x ¯ 2 ∑ i = 1 n x i − x ¯ y i − y ¯ ∑ i = 1 n x i − x ¯ z i − z ¯ ∑ i = 1 n y i − y ¯ x i − x ¯ ∑ i = 1 n y i − y ¯ 2 ∑ i = 1 n y i − y ¯ z i − z ¯ ∑ i = 1 n z i − z ¯ x i − x ¯ ∑ i = 1 n z i − z ¯ y i − y ¯ ∑ i = 1 n z i − z ¯ 2 $$ A\kern0.5em =\kern0.5em \mathrm{Cov}\left(x,y,z\right)=\frac{1}{n-1}\left[\begin{array}{ccc}\sum \limits_{i=1}^n{\left({x}_i-\overline{x}\right)}^2& \sum \limits_{i=1}^n\left({x}_i-\overline{x}\right)\left({y}_i-\overline{y}\right)& \sum \limits_{i=1}^n\left({x}_i-\overline{x}\right)\left({z}_i-\overline{z}\right)\\ {}\sum \limits_{i=1}^n\left({y}_i-\overline{y}\right)\left({x}_i-\overline{x}\right)& \sum \limits_{i=1}^n{\left({y}_i-\overline{y}\right)}^2& \sum \limits_{i=1}^n\left({y}_i-\overline{y}\right)\left({z}_i-\overline{z}\right)\\ {}\sum \limits_{i=1}^n\left({z}_i-\overline{z}\right)\left({x}_i-\overline{x}\right)& \sum \limits_{i=1}^n\left({z}_i-\overline{z}\right)\left({y}_i-\overline{y}\right)& \sum \limits_{i=1}^n{\left({z}_i-\overline{z}\right)}^2\end{array}\right] $$ ()
where A equals Cov(x, y, z) represents the covariance matrix of the plane.
We then perform eigenvalue decomposition on the covariance matrix and obtain both eigenvalues and their corresponding eigenvectors.
Aν = λν , $$ A\nu =\lambda \nu, $$ ()
where A is the covariance matrix, ν is eigenvector, and λ is the corresponding eigenvalue. The eigenvector associated with the smallest eigenvalue indicates the direction of least variation in the data—essentially the normal (perpendicular) direction to the plane we want to define (used to derive the coefficients of a plane equation, ax + by + cz + d = 0). We obtain the normal vector as n = a , b , c $$ n=\left[a,b,c\right] $$ . By positioning this normal vector to pass through the centroid, we obtain the optimized plane
a x − x ¯ + b y − y ¯ + c z − z ¯ + d = 0 , $$ a\left(x-\overline{x}\right)+b\left(y-\overline{y}\right)+c\left(z-\overline{z}\right)+d=0, $$ ()
where d = −( a x ¯ $$ a\overline{x} $$ + b y ¯ $$ b\overline{y} $$ + c z ¯ $$ c\overline{z} $$ ). Equation (9) ensures that the calculated normal vector passes through the centroid. For the N-terminal surface, the values are aN = −0.876, bN = 0.229, cN = 0.425, and dN = −2.905. For the C-terminal surface, the values are aC = 0.435, bC = 0.806, cC = 0.402, and dC = −1.385. Figure 6a illustrates a schematic of this optimized plane intersecting the fibril surface structure. The root mean square (RMS) distances are calculated from the Cα atoms of residues 1–16 (N-terminal surface) or 36–42 (C-terminal surface) to this plane. It provides a quantitative measure of the structural deviation, which we define as surface roughness (SR value).

3 RESULTS

3.1 Differential diffusion behaviors of Abeta monomers based on orientation on fibril surfaces

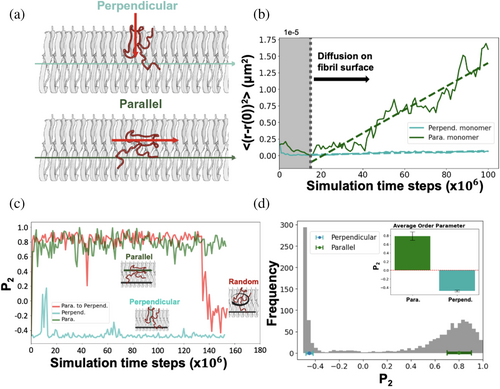
In our study of Abeta monomers on fibril surfaces, we have identified significant variations in diffusion behaviors that are directly influenced by the monomers' molecular orientation. To probe these variations more thoroughly, we conducted extensive simulations that illuminate the complex interplay between molecular structure and diffusion kinetics.

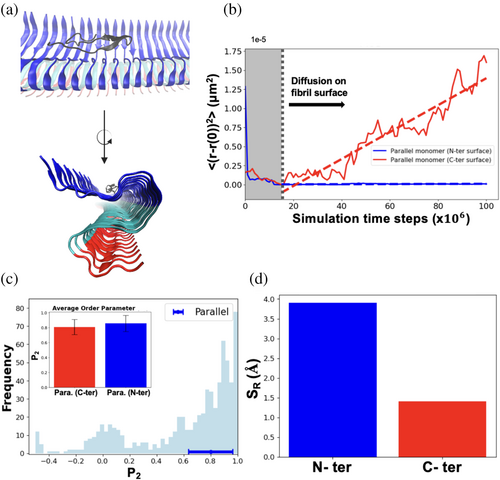
Expanding our understanding of these dynamics, Figure 2 provides a crucial observation: it shows that a monomer on the C-terminal fibril surface can adopt two distinct orientations—parallel and perpendicular, as illustrated in Figure 2a. The mean squared displacement (MSD) graph, plotted over time, furnishes vital insights into this diffusion phenomenon. By analyzing the slope of this graph, we determine the monomer's diffusion coefficient in a 1D case. The diffusion coefficient analysis reveals that the orientation of the monomer significantly influences its diffusion dynamics on the surface. Specifically, our results indicate that monomers oriented parallel to the fibril main axis diffuse faster, exhibiting a larger diffusion coefficient (D (para.) = 19.9 μm2/s), compared to those oriented perpendicularly (D (perpend.) = 0.88 μm2/s) (illustrated in Figure 2b). To more comprehensively analyze the effect of monomer orientation on diffusion, we employed the P2 order parameter. This quantitative measure represents the degree of alignment of monomers relative to the fibril's main axis (see “Methods” for details). This method precisely quantifies orientation differences by assessing the alignment of monomers relative to the fibril main axis. It clearly distinguishes their effects on the diffusion process. Figure 2c presents P2 values across simulation time steps for three example trajectories. One trajectory with parallel orientation (in dark green) shows P2 values ranging from 0.6 to 1.0 (mean ~0.8), while another in perpendicular orientation (in light green) ranges from −0.3 to −0.5 (mean ~ −0.4). These trajectories exemplify the distinct orientations maintained throughout the simulation (See Supporting Information Figures S4, S5 for details). Notably, a significant orientational switching event is observed in a selected trajectory (in red), where P2 dramatically shifts from 0.8 to −0.3 at later simulation time steps (~130 × 106). Our simulations highlight several transitions from parallel to perpendicular orientations (see Table 1), indicating dynamic switching in monomer alignment that merits further exploration. Figure 2d offers a detailed analysis of the orientation distribution across all trajectories as the monomer diffuses along the fibril surface. Two predominant distributions emerge, corresponding to parallel and perpendicular orientations, centered around P2 = 0.8 and P2 = −0.4, respectively. The average P2 values for these orientations, along with their associated error bars, are clearly depicted in the inset of Figure 2d. This analysis demonstrates that parallel-oriented monomers diffuse up to 1–2 orders of magnitude faster than their perpendicular counterparts, aligning with previously recorded experimental rates of 0.5–2.4 μm2/s, obtained via single-particle tracking with AFM on synthetic fibril surfaces.

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Analysis of an Abeta42 monomer's orientation and its diffusion dynamics on the C-terminal fibril surface is presented. (a) A schematic diagram shows the monomer's two main orientations—parallel and perpendicular—on the fibril surface. (b) Mean-squared displacement (MSD) over time of the entire trajectories (trajectory-based), with the diffusion coefficient calculated from the MSD using Equation (2). The diffusion coefficients are calculated: D ¯ $$ \overline{D} $$ (para.) = 19.9 μm2/s and D ¯ $$ \overline{D} $$ (perpend.) = 0.88 μm2/s). The early trajectory, shaded in gray (frame 0–15), is excluded from analysis due to the monomer's unclear attachment to the fibril. (c) Changes in the order parameter (P2) for monomers with different orientations over simulation time steps. P2 values of “1,” “0,” and “−0.5” correspond to “parallel,” “random,” and “perpendicular” orientations, respectively, as illustrated in the inset. Three example trajectories are shown: 1. Parallel trajectory in dark green 2. Perpendicular in light green 3. Parallel-to-perpendicular trajectory in red. (d) Distribution of monomer orientation on the fibril in terms of P2. Inset: Comparison of the average order parameter P2 (Parallel vs. Perpendicular); the perpendicular monomer is indicated in light green and the parallel monomer in dark green.
TABLE 1. Summary of simulation data collection and analysis across diverse trajectories.
Trajectory based 0 1 2 3 4 5 6 7 8 9
Para. ☑ ☑ ☑ ☑ ☑ ☑ ☑
Perpend. ☑ ☑ ☑
# of orientation change 1 — — — 1 — — — — 1
Segment based
Order parameter (P2) Para. 0–138 (frame) — — 0–153 0–90 0–100 — 0–100 0–100 —
Perpend. 139–154 0–152 0–154 — 91–152 — — — — 0–50
Diffusion coefficient Para. 85–137 (frame) — — 15–153 55–106 15–100 — 55–100 15–100 —
Perpend. 140–154 15–152 15–154 (87–106) — 107–152 — — — — 35–60
  • a Checked box represents the primary orientation of the monomer during diffusion on the fibril surface.
  • b (m–n) represents the calculation performed on frame “m” to frame “n.”
  • c (m–n) represents the second trajectory exhibiting unusual P2 values between frame m and frame n; therefore, its diffusion coefficient was calculated separately.

Crucially, this research presents the first computational work to successfully compute orientation-dependent peptide diffusion coefficients on fibril surfaces, with findings that align closely with experimental observations. This breakthrough enhances our understanding of peptide behavior on fibrillar substrates and provides a robust framework for future experimental validation.

3.2 Monomer displays diverse diffusion states

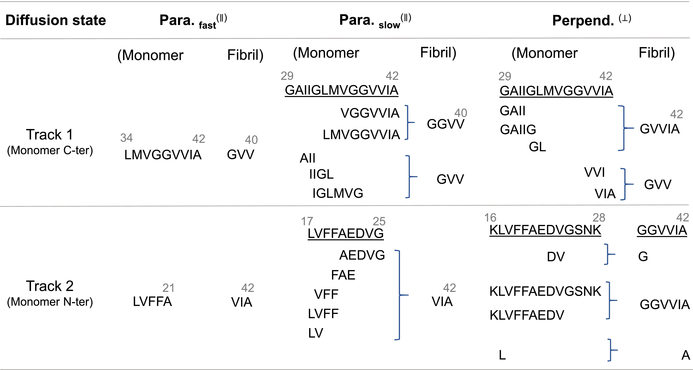
Monomers can undergo orientation changes while diffusing on the fibril surface. To accurately quantify their 1D diffusion coefficients, we meticulously analyze all simulation trajectories, categorizing them by the monomers' orientations—either perpendicular or parallel. This process involves segmenting the trajectories into distinct sections based on orientation, resulting in numerous well-defined segments. We then calculate the diffusion coefficients for each segmented trajectory. In other words, the “segment-based” analysis isolates the effects of orientation from those caused by orientation-switching events and conformational changes during monomer diffusion on the fibril. Figure 3a illustrates our findings that even within the “parallel” orientation, significant variations exist. We identified “fast” and “slow” diffusion states, with diffusion coefficients of 68.8 and 7.66 μm2/s, respectively. This differentiation highlights the complexity of monomer dynamics on fibril surfaces (See Supporting Information Figures S6–S8 for details). Table 2 provides a summary and comparison of the diffusion coefficients determined by both the trajectory-based and segment-based approaches.

Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
Further investigation of Abeta42 monomer's multiple diffusion states on the C-terminal fibril surface is shown. (a) The diffusion coefficients calculated from 11 trajectory segments are represented by solid dots and are categorized into three distinct groups based on their diffusion dynamics and orientation, with blue dots indicating parallel orientation (two subgroups: Light blue and regular blue) and red dots indicating perpendicular orientation. Monomers aligned parallel (140–170°) to the fibril, in general, diffuse faster ( D ¯ $$ \overline{D} $$ fast(∥) = 68.8 μm2/s; D ¯ $$ \overline{D} $$ slow(∥) = 7.66 μm2/s) compared to those aligned perpendicularly (80–120°), which show slower diffusion rates (D(⊥ = 0.88 μm2/s). The correlation between a monomer's orientation and its diffusion coefficient on the fibril surface is clearly demonstrated, revealing two distinct diffusion states within the parallel-oriented monomers. (b)–(d) Probability contact maps (made using Contact Map Explorer) for the monomer in different diffusion states, with representative structures displayed below each map. (b) Parallel (fast), (c) Parallel (slow), (d) Perpendicular. The horizontal axis represents the accumulated residue index for the repeated C-terminal sequence segment 36VGGVVIA42 across various fibril chains. The vertical axis indicates the residue index of the monomer, with a diagram of the secondary structure presented to the left. Blue dotted lines delineate different secondary structure elements along the monomer sequence. Pink boxes on the maps highlight regions that form significant contacts with the fibril surface, which are correspondingly marked in pink in the cartoon diagrams below each map.
TABLE 2. Summary of diffusion coefficients calculated.
Trajectory-based approach Para.(∥) Perpend.(⊥)
Diffusion coefficient ( D ¯ $$ \overline{D} $$ ) C-ter 19.9 ± $$ \pm $$ 30 (μm2/s) 0.88 ± $$ \pm $$ 3
N-ter 0.35 —
Periodic length (free energy profile) C-ter 100 (Å) 84
Segment-based approach Para.fast(∥) Para.slow(II) Perpend. (⊥)
Diffusion coefficient ( D ¯ $$ \overline{D} $$ ) C-ter 68.8 ± $$ \pm $$ 14 (μm2/s) 7.66 ± $$ \pm $$ 5 0.88 ± $$ \pm $$ 3
  • Note: Error analysis represents standard deviations calculated from multiple trajectories: for the trajectory-based approach, 6 trajectories were used for both Para.(‖) and Perpend.(⊥) orientations. For the segment-based approach, 2 trajectory segments were used for Para.fast(‖), 4 trajectory segments for Para.slow(‖), and 6 trajectory segments for the Perpend.(⊥) orientation.

To enhance our understanding of the molecular mechanisms underlying diffusion, we have analyzed the conformation of the monomer on fibril surfaces and its relationship to various diffusion states. Figure 3b through 3d displays probability contact maps that detail the conformation of the monomer in different orientations on the fibril surface, specifying the actual physical contacts between the monomer and the fibril. Figure 3b illustrates the contact profile for the “parallel (fast)” diffusion state, where the monomer forms contacts through two continuous sequence segments—17LVFFA21 and 34LMVGGVVIA42—with the C-terminal surface residues 40VIA42 and 38GVV40, respectively, (see Table 3). These interactions, primarily hydrophobic, create two virtual “tracks” of dynamic contacts that guide the monomer as it moves along the fibril. A representative structure is shown below, where the monomer's contact residues are highlighted in pink, providing a clear contrast to the complete monomer depicted in a red cartoon diagram. Figure 3c demonstrates the diverse contact profile for the “parallel (slow)” diffusion state, where the monomer primarily utilizes two sequences, 17LVFFAEDVG25 and 29GAIIGLMVGGVVIA42, while switching interchangeably between shorter segments within the sequence. These segments engage in hydrophobic interactions with the C-terminal surface residues 40VIA42 and GGVV40/GVV40, respectively. Unlike the fast mode, this contact profile exhibits a fish scale-like pattern, indicating multiple contact points across chains within the fibril. This increased number of hydrophobic interactions raises the dynamic friction of movement, as depicted in the cartoon diagram below. Figure 3d illustrates the contact profile for the “perpendicular” diffusion state, where the monomer predominantly interacts through the segments 16KLVFFAEDVGSNK28 and 29GAIIGLMVGGVVIA42. These interactions are primarily hydrophobic as well, with partial charged residues, involving residues on the C-terminal surface (GVV40/GVVIA42/GGVVIA42/37G/A42) of the fibril. The contact profile displays several non-sporadic, continuous tracks, leading to a restricted diffusion pattern, as depicted in the cartoon diagram below. Table 3 provides a comprehensive summary of the specific interactions between the monomer and the C-terminal surface of the fibril across various diffusion states. All other probability contact maps can be found in Figure S10 in the Supporting Information.

TABLE 3. Overview of specific interactions between the monomer and the C-terminal fibril surface across different diffusion states.
image

Additionally, the influence of monomer structure on diffusion dynamics, along with changes in its conformational dynamics, is detailed in Figure S9 in the Supporting Information.

3.3 Unveiling asymmetry in surface diffusion along the fibril: Computational insight into surface-mediated fibril growth

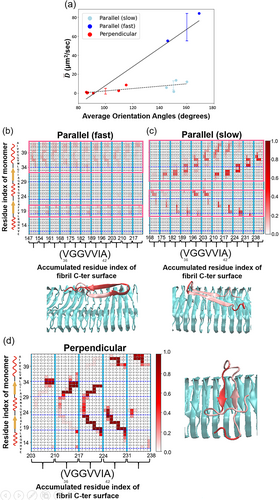
Our study explores the binding affinities of fibril surfaces and their position-dependent characteristics to better understand the mechanism of fibril growth kinetics. Using umbrella sampling, we explored the free energy landscape of an Abeta monomer on the C-terminal surface (see “Methods” for details). We observed a notable decrease in free energy as the monomer approached a specific fibril end, indicating a preference for binding to the even end over the odd end. Figure 4 illustrates the binding free energy of a monomer as a function of its position along the C-terminal fibril surface. The graph compares the “parallel” and “perpendicular” monomers with the odd end set as the energy reference point. We note that the overall free energies for both orientations (either parallel or perpendicular) declined toward the even end (left-hand side), punctuated by oscillatory fluctuations (will be discussed later). Notably, the even end of the simulated fibril system, approximately 25 nm away from the odd end, demonstrates a binding energy advantage of about 3–6 kcal/mol over the odd end. This observation aligns with the findings of a recent experimental study by Dev Thacker et al. (refer to Figure 5 in their publication) (Thacker et al., 2023), which reported asymmetric growth at the fiber endpoints. Our computational results support the experimental evidence of fibril asymmetry and offer deeper insight by showing that the even end has a lower free energy.

Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
The diffusion free energy profiles of an Abeta42 monomer with “parallel” and “perpendicular” orientations on the C-terminal fibril surface are shown. This profile is plotted as a function of the monomer's position along the fibril surface, extending from the even end to the odd end. Two orientations of the monomer are examined: Dark green dots represent the free energy of monomers oriented parallel to the surface. In contrast, light green dots indicate the free energy of monomers oriented perpendicularly. The solid curves are the corresponding fit curves with their periodic length indicated by λ(∥) (parallel) and λ(⊥) (perpendicular). The accompanying diagram of the fibril structure, shown above, clearly marks the even end on the left and the odd end on the right.
Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
The variations in diffusion behaviors across different types of fibril surfaces (N-terminal vs. C-terminal) are shown. (a) Structural diagram of a protofibril filament, where the N-terminal (N-ter) surface is depicted in blue, and the C-terminal (C-ter) surface is shown in red. A monomer in a “parallel” orientation is depicted on the N-ter surface in black. Panel (b) compares the mean squared displacement (MSD) analysis of the monomer in “parallel” orientation on the C-ter surface, represented by the red line (diffusion coefficient D ¯ $$ \overline{D} $$ = 19.9 μm2/s), to the MSD on the N-ter surface, represented by the blue line (diffusion coefficient D ¯ $$ \overline{D} $$ = 0.35 μm2/s). The early trajectory, shaded in gray (frame 0–15), is excluded from analysis due to the monomer's unclear attachment to the fibril. Panel (c) features the distribution of the P2 value across the entire set of simulation trajectories. It highlights a major population exhibiting “parallel” orientation at approximately P2 = 0.8, with its error bar indicated using blue color. The inset in this panel provides a comparison of the average P2 values of the monomer on the N-ter and C-ter surfaces, shown with blue and red bars, respectively, including error bars. Panel (d) displays a bar chart that compares the surface roughness (SR) of the N-ter and C-ter surfaces. It illustrates that the surface roughness of the N-ter (shown in blue) is greater than that of the C-ter (shown in red).

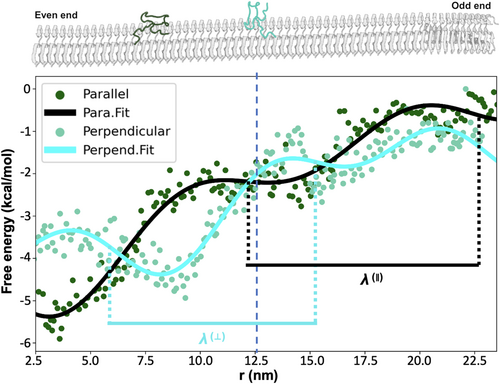
Additionally, our simulation uncovers a previously unreported oscillatory behavior in free energy, as evidenced by the fitted curves of the data. This oscillation enables monomers aligned parallel to the fibril axis to exhibit additional stabilization or destabilization energy, ranging ±2 kcal/mol, compared to those in perpendicular orientations. The magnitude of this energy variation is contingent upon the monomer's position along the fibril. For instance, at the 4 nm position, a monomer in a parallel orientation displays a free energy that is approximately 2 kcal/mol more stable than a monomer in a perpendicular orientation. Conversely, at the 9 nm position—just 5 nm away—the same parallel monomer becomes about 2 kcal/mol less stable compared to its perpendicular counterpart. Furthermore, we analyzed the oscillatory behavior of free energy and computed the periodic length for both parallel and perpendicular orientations. Our findings reveal that the parallel orientation exhibits a periodicity of approximately 100 Å, roughly equivalent to the length of 24 Abeta chains in the fibril, with each chain spanning an interval of about 4.2 Å. In contrast, the perpendicular orientation shows a periodic length of about 84 Å, which corresponds to the length of 20 Abeta chains (See Supporting Information for details). This discovery is pivotal as it illuminates the complex mechanics of surface-mediated fibril growth, providing a more comprehensive understanding of the processes that govern this phenomenon (see “Discussion” below).

3.4 Quantitative surface roughness analysis clarifies differences between N-terminal and C-terminal surfaces

Up to this point, our results have demonstrated that the diffusion dynamics of the Abeta monomer depend on its orientation, particularly on the C-terminal (C-ter) fibril surface. To expand our understanding and explore the effects of different fibril surface types, we conducted a comparative analysis, focusing particularly on the N-terminal (N-ter) surfaces, as depicted in Figure 5. The N-ter surface of the fibril structure exhibits an inward curved, groove-like shape. The groove provides an environment that enhances the formation of physical contacts with the monomer. As shown in Figure 5a, this unique geometry causes the monomer to reposition its orientation to align parallel within the groove, affecting its diffusion dynamics. Consequently, as illustrated in Figure 5b, the diffusion coefficient (D) of the monomer on the N-ter surface tends to be lower compared to that on the C-ter surface, indicating a slower diffusion rate. (See Supporting Information Figure S11 for details.)

Figure 5c presents the distribution of the P2 values across all simulation trajectories on the N-ter surface, where a significant population aligns around P2 = 0.8, indicative of a “parallel” orientation (see Supporting Information Figure  S5 for details). This result aligns with observations on both the N-ter and C-ter surfaces, confirming consistent orientation across different fibril regions, as illustrated in the inset in the figure. Interestingly, despite the monomers displaying similar parallel orientations, notable differences in their diffusion properties are observed. We hypothesize that these variations are due to the distinct geometric shapes of the N-ter and C-ter surfaces, which significantly influence their diffusion behaviors.

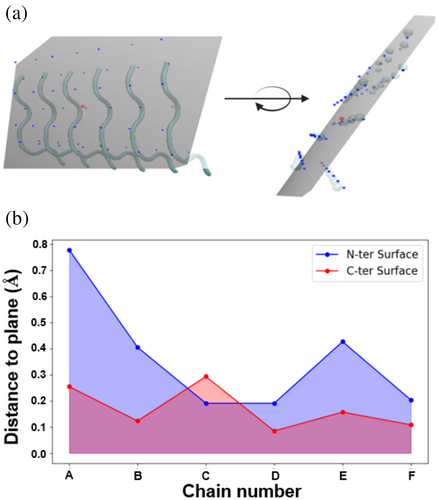
Our analysis extended beyond the P2 properties of the monomers to a deeper examination of the structural differences between the N-ter and C-ter surfaces. Structurally, the C-ter surface is smoother, offering a more favorable landing area for monomers, whereas the N-ter surface is comparatively rougher. To quantify this, we employ the average Root Mean Square (RMS) Distance, measuring the fluctuations in distance between Cα atoms and the best-fit plane. This optimized plane is defined by a normal vector corresponding to the smallest eigenvalue (termed as the surface roughness (SR) value). Conceptually, a higher RMS Distance indicates greater surface roughness due to increased fluctuations. Our RMS distance analysis confirms that the N-ter surface is indeed rougher than the C-ter surface, as illustrated in Figure 5d. Figure 6a illustrates the generation of an optimized plane and how to calculate the surface roughness accordingly (see “Methods” for details). Figure 6b compares the SR value of N-terminal and C-terminal surfaces and shows the N-terminal surface's higher SR value. In conclusion, our findings suggest that the surface shape not only influences the monomer's orientation but also entraps it in a state of reduced diffusive dynamics.

Details are in the caption following the image
FIGURE 6
Open in figure viewerPowerPoint
A schematic of the surface roughness calculation is presented. (a) An optimized plane (in gray) intersecting the fibril structure is used to calculate the RMS distances of the Cα atoms (solid blue circles) to the plane. The cartoon diagram represents the backbone structure of the peptides in the fibril; the C-terminal surface is used as the example. The solid red circle refers to the geometric center of the Cα atoms where the optimized plane intersects. A rotation angle is used to guide the visualization from different angle perspectives. (b) The surface roughness is shown as a function of the chain number in the fibril (chain A–F).

While our current methodology primarily quantifies surface roughness through RMS distance, recognizing the influence of surface chemistry—specifically the distribution and interaction of hydrophobic and hydrophilic residues—could significantly impact diffusion behaviors. The electrostatic interactions, influenced by the amino acid side chains, can either facilitate or hinder the movement of monomers across the fibril surface, depending on their charge and polarity. These interactions, while not explicitly considered in our current calculations, play a crucial role in the physical chemistry of protein–protein interactions and could provide deeper insights into the mechanistic aspects of protein aggregation on fibril surfaces. By integrating these chemical properties into our future calculations, we aim to achieve a more comprehensive understanding of the factors governing monomer dynamics and their implications for fibril growth and stability.

4 DISCUSSION

4.1 Monomer orientation's active role in fibril growth

It is suggested that the fibril surface contributes actively to fibril growth, rather than serving merely as a passive scaffold (Jean et al., 2012; Thacker et al., 2023). This perspective offers a nuanced understanding of amyloid protein dynamics on pre-existing fibrils, an area critical for advancing our approach to neurodegenerative diseases (Cao et al., 2020). Investigations employing MD simulations (Schwierz et al., 2016, 2017) and high-speed atomic force microscopy (HS-AFM) (Watanabe-Nakayama et al., 2020) have revealed how alterations in protein dynamics on fibrils correlate with protein misfolding, aggregation, and disease progression. These methods allow for detailed observation and analysis of the structural and dynamic changes in amyloid proteins, providing insights into their role in disease mechanisms. Deviations in these dynamic processes could lead to abnormal fibril growth and morphology, potentially culminating in cellular toxicity (Cohen et al., 2015). A recent integrated theoretical study highlighted the role of diffusion dynamics of Abeta monomers on fibril surfaces, introducing “Bulk-docking” and “Surface-docking” as key pathways (Zhang et al., 2024). This analysis reinforces the significance of their mechanisms in modulating the growth kinetics of amyloid-like fibrils.

In this study, we have identified three distinct states of monomer diffusion, influenced by their orientation, conformational changes, and interactions at the surface interface. These findings highlight how the orientation of the monomer affects its diffusion dynamics on the fibril surface. Specifically, monomers in a perpendicular orientation demonstrate slower diffusion rates (Dslow(⊥)), while monomers in a parallel orientation exhibit both slower (Dslow(∥)) and faster (Dfast(∥)) diffusion states. The subscript in our notation specifies the diffusion rate as “slow” or “fast,” and the superscript indicates the orientation—“perpendicular” (⊥) or “parallel” (∥). Furthermore, we have observed transitions between these diffusion states. This finding underscores the importance of orientation and dynamic states in controlling diffusion mechanisms.

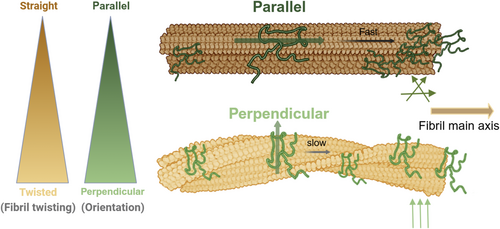
Various polymorphic fibril types may exhibit distinct diffusion dynamics, influenced by surface heterogeneity (Bouchard et al., 2000; Kurouski et al., 2012; Usov et al., 2013). For instance, “helical” fibrils could regulate diffusion rates by altering the orientation of monomers on their surface, such as by modulating sliding speeds, as observed from this work. These micro-level changes might have significant implications at the macroscopic level, possibly affecting the overall rate of fibril growth. A scenario where monomers slide excessively rapidly might be less favorable. That being said, nature avoids straight filamentous fibrils for biological use. To date, there are no experimental studies specifically showing how changes in monomer orientation on fibrils can alter the overall growth rate of the fibrils. However, our results suggest that fibrillar twisting can facilitate slower protein diffusion along the fibril surfaces (see Supporting Information in Figure S12), which favors elongation at rates compatible with biological timescales, as illustrated in Figure 7. Such a hypothesis is compatible with the view of fibril surface-mediated growth kinetics, as evidenced by both theoretical and computational studies (Ma et al., 2021; Zhang et al., 2024). Our finding suggests that the physical structure and surface properties of fibrils are not just passive elements but actively influence the behavior and movement of amyloid proteins in fibril growth. Recent computational analyses reveal a complex ensemble structure at fibril tips, characterized by the collective motions of several peptide chains. These motions, rate-limiting for fibril elongation, involve overcoming significant non-native contacts (Xu et al., 2021). This indicates a critical interaction between the molecular-scale dynamics and the larger-scale structural behaviors, linking the diffusion of individual peptides on fibril surfaces to the emergent properties at fibril tips. Specifically, the collective behavior of peptides at the fibril tips, involving complex and coordinated movements, could be key to understanding how the physical and chemical characteristics of the fibril itself control fibril elongation (e.g., exploring the kinetics of unidirectional fibril growth (Han & Schulten, 2014)). Such insights could be pivotal in understanding the mechanistic pathways involved in the progression of neurodegenerative diseases.

Details are in the caption following the image
FIGURE 7
Open in figure viewerPowerPoint
Schematic illustrating the influence of straight and twisted fibril structures on the preferred orientation of monomers. This figure illustrates the pivotal role of fibrillar twisting in controlling monomer diffusion dynamics through orientation modulation. The top schematic depicts rapid monomer diffusion toward one fibril end, leading to a disordered assembly of many monomers. This configuration may impact fibril growth. In contrast, the bottom schematic shows slower monomer diffusion, where accumulated monomers form an ordered assembly that facilitates efficient fibril growth within biological conditions. The color-coded bars on the left schematically represent the degree of fibril twisting and the population of monomer orientations, respectively. The gradient in colors illustrates a gradual and continuous change in both the twist of the fibril and the distribution of orientations. This representation emphasizes the general trend rather than a specific orientation correlated to a particular degree of fibril twist. It is important to note that the fibril formation discussed here does not necessarily relate to neurotoxicity, but rather to the type of fibril assembly that does not generate toxic oligomers.

4.2 Hypothesis on the kinetic stages of fibril growth via surface-mediated processes

While traditional views on fibril elongation primarily focus on monomers bulk-docking at fibril tips, recent insights highlight the significant role of surface-mediated processes. Unlike the restricted, rod-like areas at the fibril tips, fibril surfaces provide extensive interaction zones, making surface-docking more advantageous than bulk-docking. This understanding is framed by a hypothesis that fibril growth involves a sequential three-stage process: 3D bulk-diffusional attachment of monomers to the fibril surface, 1D surface-mediated diffusion along the surface, and finally, a conformational conversion into the fibril structure.

Stage One: 3D bulk-diffusional attachment—Initially, monomers move from the bulk solution to the fibril surface. At low protein concentrations, the infrequent arrival of monomers on the surface may slow down the growth, potentially becoming the rate-determining step.

Stage Two: 1D surface-mediated diffusion—After attachment, monomers traverse along the fibril surface seeking optimal sites for integration into the fibril structure. The efficiency of this process becomes increasingly critical as protein concentrations rise, influencing the rate of fibril elongation.

Stage Three: Conformational conversion into the fibril structure—The final stage involves the monomers undergoing conformational changes to integrate into the fibril. The rate of this stage is influenced by local conditions and could become more significant at higher protein concentrations.

This comprehensive model suggests that at lower concentrations, bulk-diffusional attachment dominates the rate-determining process. However, as concentrations increase, the critical step may shift to surface-mediated diffusion or conformational conversion, depending on monomer availability and specific surface conditions. The extensive surface area of fibrils facilitates the attachment of multiple monomers, supporting a concentration-dependent elongation rate as observed at low Abeta concentrations (1–3 μM). This framework provides a mechanistic basis for the observed “stop-go” elongation behavior, underscoring the complex interplay between kinetics and protein concentration in fibril growth (Zimmermann et al., 2021).

Our study further underscores the vital role of monomer orientation and the dynamic interplay between molecular and surface properties, enhancing dock-and-lock-based microkinetic models with surface-mediated perspectives (Shayesteh Zadeh & Peters, 2021). The existence of multiple orientational configurations of monomers on these surfaces indicates a more complex energy landscape, critical for understanding secondary nucleation processes and fibril growth. Whether these surface-enhanced events occur rarely or frequently, they are essential for a comprehensive understanding of the evolving length distribution and aggregation kinetics within an ensemble of growing fibrils.

4.3 Asymmetric fibril ends: Influencing monomer's 1D diffusion and growth dynamics

In studying amyloid fibrils, it is crucial to understand the asymmetric effects at the fibril ends due to their substantial influence on fibril growth and stability. Each end of the fibril displays unique kinetic and structural characteristics that dictate monomer addition and affect the rate of fibril elongation. Insights into these variations are critical for the development of targeted therapies that could selectively interact with the more reactive fibril end to potentially halt fibril extension.

Fibril growth demonstrates distinctive behaviors at the even and odd ends, driven by structural differences. At the even end, the Aβ peptide tends to adopt a closed conformation where the β1 and β2 sheets are closely juxtaposed, leading to minimal fluctuations. This stability is linked to the robust β-sheet interactions facilitated by the β1 sheet exposed at the even end (Okumura & Itoh, 2016). In contrast, at the odd end, the Aβ peptide is more variable, often adopting an open conformation with more widely spaced β-sheets. This is attributed to weaker β-sheet interactions due to the exposure of the β2 sheet at this end (Okumura & Itoh, 2016). These structural differences explain why fibril extension predominantly occurs from the odd end, which exhibits more dynamic structural states (Heldt et al., 2011; Okumura & Itoh, 2016).

While previous studies primarily observed fibril elongation at the odd end, indicating a kinetic preference for growth in this region, our research introduces a contrasting perspective by revealing a distinct sliding preference toward the even end based on energetic analyses. This suggests a thermodynamic favorability at the even end, offering a new viewpoint on fibril elongation dynamics that contrasts with earlier kinetic-focused studies. This divergence invites further investigation into the conditions under which thermodynamic versus kinetic factors dominate fibril growth, enhancing our understanding of amyloid fibril mechanics and providing novel targets for therapeutic intervention.

Our findings show that the binding free energy of a monomer varies along the fibril surface depending on its orientation—parallel or perpendicular—with the odd end serving as the reference. The free energy generally decreases toward the even end, accompanied by oscillatory profiles. Notably, the even end of our ~25 nm fibril system demonstrates a binding energy advantage of 3–6 kcal/mol over the odd end. Monomers aligned parallel to the fibril axis additionally benefit from a stabilization/destabilization energy of about ±2 kcal/mol compared to those in a perpendicular orientation. These results, when scaled per chain in the fibril, translate to 0.05–0.1 kcal/mol per amino acid for even over odd ends, and ± 0.03 kcal/mol per amino acid for parallel over perpendicular alignments.

4.4 Origins of periodic free energy barriers in monomer diffusion on fibril surfaces

The origins of periodic free energy barriers observed in our simulations are not definitively known; however, we suggest two potential explanations. First, the periodicity may be influenced by the geometric properties of the fibril's structure, notably if the fibril exhibits twisting. As the monomer progresses along the fibril's axis, it could encounter energy barriers when aligning with half-twists relative to the fibril's full helical pitch. Nonetheless, our fibril models are primarily straight or exhibit minimal twisting, which does not account for the observed periodic lengths. Second, these periodic barriers could stem from dynamic interactions at the monomer-fibril interface as the monomer moves along the surface. Variations in the number of contact points, proportional to the monomer's size and the contact area, may elucidate the noted energy oscillations.

As a simple validation step, we have examined the oscillatory behaviors in free energy linked to surface properties at the monomer-fibril interfaces. Remarkably, the monomer sizes measured in both parallel and perpendicular orientations along the fibril axis—35.5 and 24.0 Å, respectively—show a definitive monotonic correlation with their respective free energy periods of 100 and 84 Å (see Supporting Information for details). This relationship suggests that these periodicities are intrinsically linked to the physical dimensions of the monomer. This supports the second scenario as shown in the previous paragraph. Our analysis indicates that the diffusion dynamics are influenced by periodic potentials, similar to those experienced by a Brownian particle undergoing a random walk with a global bias toward the fibril's even end. This analogy is further supported by the visualization of consecutive barrier-crossing events within these biased effective potentials, which mimic random walk dynamics and enhance our understanding of monomer diffusion on fibril surfaces.

Oscillations in the free energy profile likely result from a blend of structural heterogeneity and dynamic interactions between the monomer and the fibril. These oscillations showcase variations in the energetic favorability of different positions along the fibril surface, arising from periodic structural features of the fibril itself and the inherent properties of the Abeta monomer, such as its size and shape, and how these features align with the fibril's topography.

A similar oscillatory free energy behavior has been observed in systems such as DNA allostery, where oscillatory behaviors often stem from the elastic properties of the DNA molecule and allosteric effects mediated by protein binding (Kim et al., 2013). These effects alter the physical state of DNA, such as tension or bending, which can propagate along the molecule, affecting binding affinity at distant sites, often resulting in periodic patterns of binding affinity (Kim et al., 2013).

While DNA allostery involves changes propagated through a flexible, yet uniform, polymer backbone, the oscillatory behavior in Abeta diffusion is likely more influenced by localized interactions within a structurally and chemically complex substrate—the fibril surface. Unlike DNA, where oscillatory behavior is about the propagation of physical changes along a continuous medium, in Abeta diffusion, the oscillations are linked to discrete interactions with varying energy landscapes.

In summary, the most plausible explanation for the oscillatory behavior in Abeta diffusion involves the combined structural and chemical heterogeneity of the fibril surface, creating a periodic or quasi-periodic energy landscape. As the Abeta monomer navigates the surface, it encounters regions with differing binding affinities due to variations in surface roughness, chemical composition, and the structural fit between the monomer and the fibril. A model incorporating dynamic interactions as the monomer diffuses may elucidate how different fibril regions could variably stabilize or destabilize the monomer, resulting in an oscillatory free energy pattern.

5 CONCLUSIONS

This study provides critical insights into the role of surface-mediated secondary processes in Alzheimer's disease, particularly in the context of Abeta42 peptide aggregation. Through the use of coarse-grained MD simulations, we focused on elucidating the molecular intricacies of these surface-mediated processes, distinct from primary nucleation.

Central to our investigation was the analysis of a freely diffusing Abeta42 monomer in proximity to preformed fibril structures. We meticulously calculated the diffusion coefficient (D) of the monomer as it interacted with both straight and twisted fibril surfaces, taking into account different monomer orientations. Our research reveals a strong and consistent correlation between the monomer's diffusion coefficient and its orientation on the fibril surface. This finding is crucial, as it remains valid across different degrees of fibrillar twisting, emphasizing the significance of monomer orientation in surface-mediated secondary aggregation processes. This is the first simulation work to reveal the roles of orientation-dependent monomer dynamics in determining the kinetic behaviors of its diffusion on fibril surfaces.

Additionally, our study explored the differential effects of fibril surfaces on monomer dynamics. We conducted a comparative analysis of the C-terminal and N-terminal surfaces, observing that monomers exhibit faster diffusion coefficients on the C-terminal surface. This variation in diffusion dynamics is largely attributable to differences in surface roughness, quantified using the surface roughness (SR). Such disparities in shape and roughness of the fibril surfaces are pivotal in shaping the monomer dynamics, thereby influencing the secondary aggregation process.

In conclusion, our findings highlight the complex and nuanced role of surface characteristics in the secondary aggregation processes of Abeta42 peptides in Alzheimer's disease. By shedding light on the molecular dynamics of these processes, our study opens new avenues for understanding and potentially intervening in the progression of Alzheimer's disease, focusing on the manipulation of surface-mediated aggregation mechanisms.

AUTHOR CONTRIBUTIONS

Yuan-Wei Ma: Investigation; data curation; visualization; writing – original draft; formal analysis; methodology; validation; software. Guan-Fang Wang: Investigation; writing – original draft; visualization; formal analysis; data curation; methodology; validation; software. Hong-Yi Chen: Visualization; formal analysis. Min-Yeh Tsai: Writing – review and editing; writing – original draft; conceptualization; investigation; funding acquisition; resources; supervision; methodology; validation; formal analysis; software.

ACKNOWLEDGMENTS

This work was supported by the National Science and Technology Council (NSTC), Taiwan, Grant No. NSTC 112-2113-M-194-012 and NSTC 113-2628-M-194-001-MY3. We thank the National Center for High-performance Computing (NCHC) of National Applied Research Laboratories (NARLabs) in Taiwan for providing computational and storage resources.

    DATA AVAILABILITY STATEMENT

    The data that support the findings of this study are openly available in pyAggreg at https://github.com/MYTLab/pyAggreg.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.