CHARMING: Harmonizing synonymous codon usage to replicate a desired codon usage pattern
Funding information: National Institute of General Medical Sciences, Grant/Award Number: DP1 GM146256; National Institutes of Health, Grant/Award Number: R01 GM120733; W. M. Keck Foundation
Abstract
There is a growing appreciation that synonymous codon usage, although historically regarded as phenotypically silent, can instead alter a wide range of mechanisms related to functional protein production, a term we use here to describe the net effect of transcription (mRNA synthesis), mRNA half-life, translation (protein synthesis) and the probability of a protein folding correctly to its active, functional structure. In particular, recent discoveries have highlighted the important role that sub-optimal codons can play in modifying co-translational protein folding. These results have drawn increased attention to the patterns of synonymous codon usage within coding sequences, particularly in light of the discovery that these patterns can be conserved across evolution for homologous proteins. Because synonymous codon usage differs between organisms, for heterologous gene expression it can be desirable to make synonymous codon substitutions to match the codon usage pattern from the original organism in the heterologous expression host. Here we present CHARMING (for Codon HARMonizING), a robust and versatile algorithm to design mRNA sequences for heterologous gene expression and other related codon harmonization tasks. CHARMING can be run as a downloadable Python script or via a web portal at http://www.codons.org.
1 INTRODUCTION
Synonymous codon substitutions alter an mRNA sequence but not its encoded amino acid sequence. For this reason, synonymous substitutions were historically considered to be phenotypically silent. In recent years, however, it has become clear that substitutions between synonymous codons can lead to a variety of effects on functional protein production, a term we use here to describe the net effect of transcription (mRNA synthesis), mRNA half-life, translation (protein synthesis) and the probability of a protein folding correctly to its active, functional structure, versus alternative outcomes like aggregation or degradation. Although a comprehensive understanding of the precise mechanisms and their interplay is still emerging, synonymous codon substitutions have been shown to affect each step of functional protein production.
A well-studied example of the effects of codon usage on functional protein production is the impact of synonymous substitutions amongst codons with different codon usage frequencies. Although the genetic code is (essentially) universal, synonymous codons tend to be used with different frequencies in different organisms. A particularly striking difference in codon usage is the arginine codon AGA, which is rarely used in Escherichia coli but the most common of all six arginine codons in human coding sequences. The tRNA that decodes AGA is present at very low abundance in E. coli, which leads to slow translation of AGA by the ribosome, which can lead to mistranslation.1 Recombinant expression of human coding sequences in E. coli can therefore be increased by substituting AGA with a synonymous arginine codon used more frequently in E. coli. These and other related observations led to the widespread practice of “codon optimization,” which involves systematically substituting all or most codons in a coding sequence with the synonymous codon most commonly used in the heterologous expression host.2-6 However, codon optimization is not always successful: although these negative results are rarely reported, it is widely acknowledged that codon “optimization” can instead be detrimental to functional protein production.7 Codon optimization can fail for a variety of reasons, including changing the rate of rate of synthesis of the nascent peptide chain. Changes to protein synthesis rate can alter co-translational folding mechanisms, which can lead to misfolding, aggregation and/or degradation of the encoded protein (Figure 1).8-12
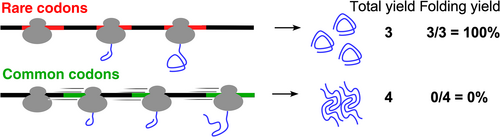
Source: This figure was modified from Reference 8
The limitations of codon optimization as a universal approach for producing high levels of functional protein have sparked an appreciation of the importance of patterns of synonymous codon usage in coding sequences. For example, even many highly expressed genes include significant clusters of rare or otherwise sub-optimal codons,13 the locations of which are often conserved between homologous coding sequences.14, 15 Disrupting local patterns of synonymous codon usage can lead to altered folding of the encoded protein,9, 10, 16, 17 even when gene-wide average codon usage metrics are preserved.11, 12, 18 These results have led to an alternative approach for maximizing recombinant gene expression called “codon harmonization.” Harmonization involves substituting synonymous codons with the goal of closely replicating the codon usage pattern (e.g., rare vs. common) in the original gene/organism (Figure 2a, b).8, 11, 19-21
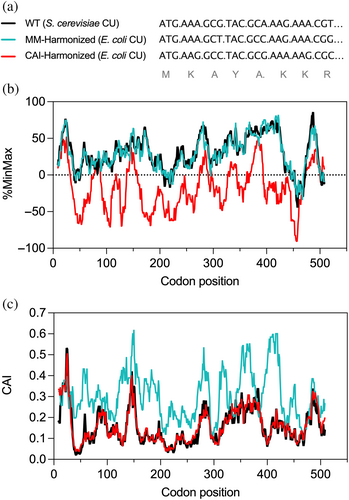
Harmonizing the codon usage values of a sequence of interest from one organism to another requires an algorithm that can take an mRNA sequence and the codon usage values from both the origin organism and a proposed destination (heterologous host) organism, analyze the values in the sequence using a measure of interest, and then harmonize the synonymous codon usage pattern in the heterologous host to match the pattern in the origin organism by systematically altering the mRNA coding sequence (Figure 2). Here we present such an algorithm, called CHARMING, for “Codon HARMonizING”, a major expansion and refinement of a simple codon harmonizing procedure we previously developed.8 CHARMING can be run as a Python script or via a web-based portal at http://www.codons.org. Included with the script and the web-based portal are options to analyze coding sequences using two commonly used codon measures: (a) ORFeome-wide codon usage frequency (calculated using %MinMax)8, 13 for E. coli, yeast, human and several other common organisms, or (b) CAI values22 for E. coli and yeast codons, which are calculated as a geometric mean. Both can be analyzed using a sliding window of adjustable size. Users can also use either of these two calculations to harmonize to values other than those provided, by uploading their own tables of codon usage values. Below we describe the structure and operations of CHARMING and its applications.
2 GENERAL CONSIDERATIONS
The codon usage patterns described in the introduction to this article arise due to differences in global codon usage frequencies across all coding sequences. However, it is important to note that codon usage can instead be evaluated using a variety of other measures, including those based on tRNA abundance (tAI),23 tRNA supply versus codon demand (nTE)24 and the codon usage in only highly expressed genes (Codon Adaptive Index, CAI).22, 25 Although all of these codon usage measures are somewhat correlated with one another, the underlying differences, as well as mathematical differences between how the most common codon calculators compare values to one another (see Box 1), can lead to distinct codon usage patterns within a coding sequence (Figure 2). Currently, there is no broad consensus regarding which codon usage measure is most predictive of translation rate or functional protein production.26, 27 Hence it can be useful to compare codon patterns generated by different codon usage measures. Here, we focus primarily on CAI, as it is one of the earliest and most widely used codon usage measures, and %MinMax, which has been shown to be predictive of the effect of local ribosome elongation rate on co-translational protein folding in E. coli.16 Of note, calculating %MinMax for a gene of interest requires knowing only genome-wide codon usage frequencies,13 which are readily available for many organisms.28, 29
BOX 1. Common codon calculators measure different things and scale values differently
When evaluating codon usage, it is important to appreciate that distinctions between codon usage measures and their underlying scaling calculations mean that, depending on the specific harmonization application, one calculation may be more well-suited than another. Key differences include: (a) the biological consideration that defines codon optimality and subsequent codon value assignment, (b) the strategy used to normalize codon values relative to each other, (c) the strategy used to scale codon usage values relative to each other, and (d) whether usage bias is summarized using a geometric mean or average, across either the entire gene or as a sliding window (gene profile).
-
Assigning codon values
As outlined in the main text, different codon usage measures evaluate distinct codon features when defining a synonymous codon to be optimal or non-optimal for translational efficiency, which is defined here as the amount of protein synthesized from an mRNA transcript per unit time. For example, CAI defines as optimal the synonymous codon with the highest usage frequency in only highly expressed genes,22, 25 whereas tAI defines as optimal the synonymous codon with the highest cognate tRNA concentration (typically estimated from tRNA gene copy number).23 Similarly, nTE defines as optimal the codon with the highest ratio of tRNA supply (estimated concentration) to the cognate codon abundance in the transcriptome,24 whereas %MinMax considers the most optimal synonymous codon to be the one used most frequently in the ORFeome.8, 13 Each codon measure assigns a value to each codon, based on its optimality considerations.
-
Normalizing codon values: Absolute versus relative comparisons
After individual codon values are assigned, there is an additional distinction between how values are normalized. This normalization step has important implications for interpreting synonymous codon patterns in gene sequences. Broadly speaking, codon usage values can be normalized either (a) in an absolute sense, as compared to all 61 sense (non-stop) codons (this approach is used by tAI and nTE), or (b) in a relative sense, versus only the synonymous codons that encode the same amino acid (used by CAI) or amino acid sequence window (%MinMax). This distinction means that codon usage measures that use absolute normalization include in their codon values contributions from amino acid usage bias. For example, the amino acid cysteine is rarely used in proteins, whereas the amino acid leucine is abundant. Hence in an absolute comparison, both cysteine codons will have a lower normalized value than most (if not all) of the six codons that encode leucine. In contrast, when normalized relative to only the codons within the same synonymous codon group, the more commonly used cysteine codon will be ranked as more optimal than the rarest leucine codon.
-
Scaling relative-normalized codon values
There is an additional distinction between how the two most commonly-used relative codon calculators, CAI and %MinMax, scale normalized codon values. CAI scales the highest codon value within each synonymous codon group to 1, whereas %MinMax scales the highest value as +100 and the lowest as −100, relative to an average value of zero in a codon window. The consequence of this difference is that, by virtue of the differences in scaling alone, %MM gives equal weight to differences between usage frequencies that are below average as those that are above average. In contrast, scaling from 1 to 0 (as CAI does) compresses the percentage difference between values that are below average.
As a simple example, imagine there are four codons in a codon usage group (A, B, C, and D) with usage frequencies of 50, 25, 10, and 5 codons per 1,000 total codons, respectively. If we assume the usage frequencies of A, B, C, and D are identical in the ORFeome and highly expressed genes and a window size of one, usage frequency values for CAI and %MinMax are equal:
| Scaled value | |||
|---|---|---|---|
| Codon name | Usage frequency value | CAI | %MinMax |
| A | 50 | 1 | +100 |
| B | 25 | 0.5 | +9 |
| C | 10 | 0.2 | −71 |
| D | 5 | 0.1 | −100 |
- 4.
Summarizing usage bias: geometric mean versus average, and single value versus sliding window
Historically, some codon measures (most notably CAI and tAI) calculated a geometric mean of individual codon values to generate for each coding sequence a single value, with a higher value describing a sequence that is more optimal (higher translational efficiency, defined above):
where Cj is the corresponding codon usage value of the jth codon in the sequence, and n is the total number of codons in the sequence. More recently, as interest in intra-gene codon usage patterns has increased, these codon usage measures have been adapted to generate for each coding sequence a codon usage profile, by calculating the geometric mean of a sliding window of codons along the coding sequence. %MinMax does not use a geometric mean calculation; instead, %MinMax calculates the average value of a sliding window of adjustable length. Describing synonymous codon usage with a single value can be useful for making correlations in large datasets. Describing codon usage bias with a sliding window profile is useful for identifying regions within a sequence with the largest contributions to translational efficiency or for comparing codon usage across orthologs or a library of synonymous mutants.
We previously developed a simple three-step algorithm for harmonizing the codon usage of a coding sequence from one organism to another.8 This simple algorithm, which we refer to here as “Rodriguez initialization,” operates by first ranking each codon in order of usage frequency relative to its synonyms in each of the two organisms, then mapping the ranked codons from one organism to the other, and finally, where necessary, substituting the codons in a coding sequence with the usage frequency-ranked match in the destination organism. This extremely simple harmonization procedure alone can do a remarkably good job of matching the general trends of codon usage frequency patterns,8 as can other, related codon-ranking procedures.20 However, for many applications a more robust and versatile algorithm is necessary, to outperform frequency-ranked matching alone and/or to explore the vastness of synonymous codon space. CHARMING addresses this need, providing the first (to our knowledge) open-source algorithm of its kind for versatile and robust codon harmonization. Together, Rodriguez initialization and CHARMING provide a powerful tool to design well-harmonized synonymous coding sequences.
3 EXPLORING THE VASTNESS OF SYNONYMOUS CODON SPACE
Codon harmonization is a computationally difficult problem. Because the length of the average coding sequence in E. coli is ~300 codons and the average number of codons used to encode each amino acid is 3.05 (61/20), the resulting potential solution space (roughly 3.05300, or 2 × 10145, synonymous sequences per gene) is simply too large for a brute-force search through all options to find the globally optimum (most-closely harmonized) sequence. Moreover, results of a codon calculation are typically averaged over a sliding window of codons, which vastly increases the number of synonymous sequence solutions that are equally well-harmonized to a desired codon usage pattern. CHARMING provides a computationally inexpensive solution to the intractable brute-force problem of identifying synonymous sequences with closely harmonized codon patterns.
4 THE CHARMING WORKFLOW
At its core, the CHARMING algorithm is a nested series of iterative steps that systematically substitute codons in a wild type (WT) coding sequence to recapitulate in a destination organism (typically, a heterologous expression host) the general pattern of high and low codon values experienced when the WT coding sequence is expressed in its origin organism (Figure 3). In doing so, CHARMING recapitulates a codon usage pattern for a desired codon usage measure from one organism (with one set of values) in a different organism with different values, as in the example shown in Figure 4. CHARMING therefore fulfills a key task of codon harmonization for heterologous gene expression.
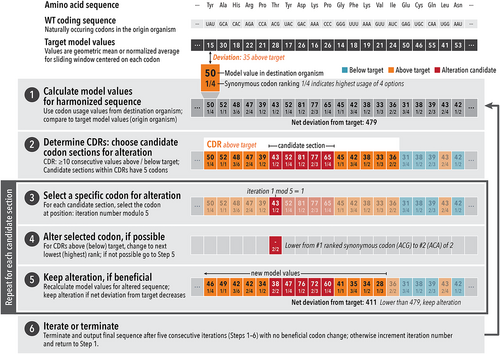
CHARMING is a deterministic algorithm, meaning that for a given input coding sequence it will always return the same harmonized coding sequence. However, because synonymous sequence space for even a single sequence is astronomically vast (see previous section), and because most codon usage patterns are analyzed as a sliding window average across multiple codons, there are potentially many synonymous sequences that will harmonize equally well to the desired codon usage pattern. For users interested in sampling the vastness of possible synonymous sequence-space solutions for a specific harmonization task, CHARMING includes an option to generate a set of N (where N is defined by the user) harmonized synonymous sequences. This set is produced by first generating a set of random synonymous starting sequences to use as input into the algorithm, which in turn generates distinct sequences harmonized to the same sequence feature pattern. See the Section 5.1 for more details.
CHARMING can be used either online (at codons.org) or as a Python script (downloadable from github.com/wrightgs/CHARMIING). In both versions, the user must specify parameters before CHARMING is run. These parameters include the sequence to be harmonized, which codon usage measure to use, the window size for the codon usage measure, how many harmonized mutants to generate as output, and the codon usage tables for the origin and destination species (if applicable—see Section 5.1).
After the user specifies their desired parameters, CHARMING then is run. There are seven steps to CHARMING (shown schematically in Figure 3), including the initial Rodriguez initialization step:
4.1 Step 0: Initialization (optional)
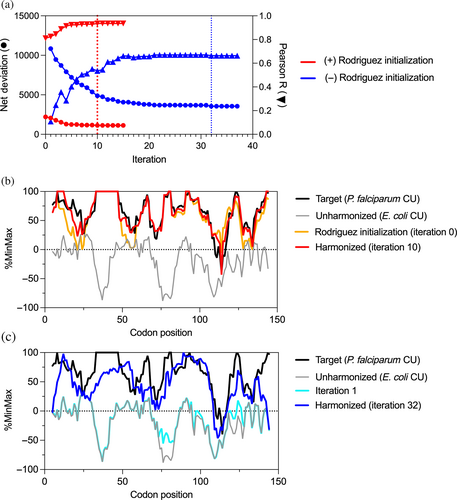
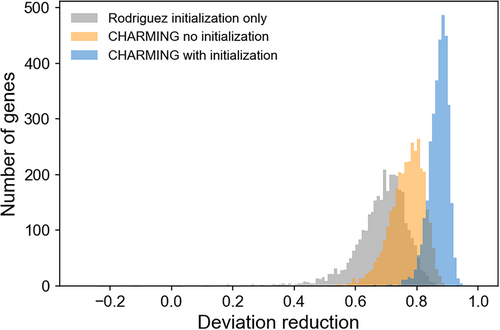
We found that the performance of CHARMING improves when it begins with Rodriguez initialization, the simplified harmonization procedure we previously developed8 (see General considerations, above). Step 1 of CHARMING (below) then uses this initial harmonized sequence as the “current synonymous mutant.” We found that including Rodriguez initialization improves CHARMING harmonization by an average of 10.5%, as detailed in the harmonization case study (below) (see also Figures 4 and 5). Despite this improvement, there are some codon harmonization applications that are incompatible with Rodriguez initialization, hence it is only used by the algorithm when the user specifies parameters that benefit from initialization. Two examples of applications not suitable for initialization are described in a later section (Section 5.1).
4.2 Step 1: Calculate the codon usage pattern for the synonymous mutant sequence
For the desired codon usage measure, CHARMING analyzes the current synonymous mutant sequence using codon usage values from the destination species (e.g., a heterologous expression host like E. coli). Each codon usage measure analyzes per-codon usage values over a sliding window of M codons, where M is set by the user. In the examples shown here (Figures 1 and 4), window sizes of 17 and 9 codons were used; note that a window size of 10 codons was found to correlate most closely with ribosome footprint counts.27, 30 CHARMING then assigns the resulting value for a particular sliding window to the middle codon in the sliding window (or, in the case of even-sized windows, the right-most center codon), creating per-codon output values. These per-codon values are then compared to the target values (i.e., the per-codon values of the WT sequence when analyzed with the same measure, using codon usage values from the origin species). If this is the first iteration of the algorithm and the optional initialization step was not used, the “current synonymous mutant” is the WT coding sequence or a randomly generated synonymous mutant (as described before).
4.3 Step 2: Choose candidate codon positions for alteration
CHARMING next marks each sequence region of ≥10 consecutive codon positions where the output values for the current synonymous mutant are consistently above or below the target values as a consecutive deviation region (CDR). A minimum CDR length of 10 codons was chosen because larger values generally resulted in less well-correlated harmonized outputs, while smaller values led to only incremental reductions in the harmonization deviation at the cost of increased runtimes. The example sequence shown in Figure 3 has one CDR of length = 15 (colored orange). Next, CHARMING selects candidate sections for codon alteration within each CDR. CHARMING calculates the number of candidate sections for each CDR as (CDR length)/10, rounded down to the nearest integer. Each candidate section consists of five consecutive codon positions, spaced evenly within each CDR. In Figure 3 example, the CDR of length 15 generates one candidate section (colored red), placed at the middle five codon positions of the CDR.
4.4 Step 3: Choose a specific codon for alteration
Based on the algorithm's current iteration, CHARMING then selects one of the five positions within each candidate section for possible alteration. Specifically, the codon selected is the remainder of the iteration number divided by the number of candidate positions (i.e., the iteration number modulo 5). In Figure 3 example, the first codon is chosen because the algorithm is in its first iteration.
4.5 Step 4: Alter the selected codon, if possible
For CDRs above the corresponding target values, CHARMING changes the codon at the selected position to the synonymous codon with the next lowest rank for the codon measure of interest. Likewise, for CDRs below the corresponding target values CHARMING selects the synonymous codon with the next highest value to replace the selected codon. This step “pulls” sequence regions with consistent deviations closer to the target values. If the codon position cannot be altered in the desired direction (i.e., if the codon occupying the selected position is already the extreme value in the desired direction), then CHARMING makes no change and the algorithm advances to Step 5. In Figure 3 example, the selected codon is lowered from the highest ranked synonymous codon under the given measure to the second highest ranked synonymous codon (which is also the lowest ranked synonymous codon for the corresponding amino acid). If instead the codon at the selected position was already the lowest ranked of its synonyms, no change would be made.
4.6 Step 5: If the codon alteration reduces net deviation, keep it
If a CDR is long enough to contain multiple candidate sections or there are multiple CDRs in the current synonymous mutant sequence (or both), the sequence will have multiple selected codons during each iteration. In this case, CHARMING repeats Steps 3–5 independently for each set of candidate positions.
4.7 Step 6: Iterate or terminate (output the final harmonized sequence)
After each set of candidate positions has been processed through Steps 3–5, CHARMING increments the iteration number by one and a new iteration of the algorithm begins at Step 1. Alternatively, the algorithm terminates (i.e., the synonymous sequence is output as the final harmonized sequence) after five consecutive iterations where no beneficial codon change is found. This stopping condition implies that all five candidate positions of each CDR have been chosen for alteration, and no beneficial alteration could be found.
5 CASE STUDY: HARMONIZING RELATIVE CODON USAGE FREQUENCIES FROM YEAST TO E. COLI
To computationally evaluate the performance of CHARMING, we created synonymous mutants for 3,358 E. coli coding sequences, harmonized to closely match Saccharomyces cerevisiae ORFeome-wide relative codon usage frequencies, as calculated by %MinMax8, 13 using codon usage frequency tables from KazUSA28 (tables “Escherichia coli O157:H7 EDL933 [gbbct]” and “Saccharomyces cerevisiae [gbpln]”, respectively). Harmonizing from E. coli to S. cerevisiae is a good test of CHARMING as these two organisms have similar but distinct codon usage frequencies, exemplified by their difference in %GC base composition: 51.5% for E. coli versus 39.8% for S. cerevisiae.
- only Rodriguez initialization8
- only CHARMING (no initialization)
- Rodriguez initialization prior to CHARMING harmonization
5.1 Beyond heterologous expression
In addition to heterologous gene expression, there are other applications where codon harmonization can be a useful tool. However, it is important to note that some alternative applications, including the two described below, are incompatible with Rodriguez initialization (Step 0, above). In these cases, CHARMING skips the initialization step.
First, a user may desire to sample—albeit very sparsely—the vastness of synonymous codon space by designing not just one well-harmonized codon sequence but a small set of distinct synonymous sequences that harmonize equally well (or closely so) to the target sequence. Such a set could be useful, for example, to ensure that a harmonized sequence is not cross-correlated with another measure under consideration, and/or to ensure the generation of a harmonized sequence that avoids undesirable features, such as nuclease recognition sequences. To accomplish this, CHARMING includes an option to generate a set of synonymous sequences harmonized to the same sequence feature pattern. However, because CHARMING is deterministic, it will always output the same harmonized sequence for a given input sequence (assuming all other parameters remain unchanged). Therefore, when a user requests multiple harmonized synonymous mutant sequences, Rodriguez initialization is used as input to CHARMING for one sequence and the WT sequence is used as input to CHARMING for another. Any additional remaining output harmonized sequences are created by CHARMING first generating random synonymous sequences [technically, unweighted random reverse translations (RRTs)13, 14] to serve as the input for Step 1 of CHARMING.
In other applications, a user may wish to design an alternative, equally-well harmonized synonymous sequence for use in the origin species. Because Rodriguez initialization chooses codons of equal rank based on usage rankings in the native and the host species, initialization will always return the WT sequence when the origin species is also the destination. To overcome this limitation, a random synonymous sequence is generated to first artificially create areas of “deviation” for harmonization, akin to the procedure described above for generating multiple harmonized mutants.
ACKNOWLEDGEMENTS
We thank the members of our laboratories for helpful input on the development of the CHARMING algorithm. We are grateful to Kristina Davis for her assistance with Figure 3. This project was supported by grants from the National Institutes of Health (R01 GM120733 to T.M., P.L.C., S.J.E. and J.L. and DP1 GM146256 to P.L.C.) and the W. M. Keck Foundation (to P.L.C.).
AUTHOR CONTRIBUTIONS
Gabriel Wright: Conceptualization (lead); formal analysis (equal); investigation (equal); methodology (lead); software (lead); visualization (supporting); writing – original draft (supporting); writing – review and editing (supporting). Anabel Rodriguez: Conceptualization (supporting); formal analysis (equal); investigation (equal); methodology (supporting); software (supporting); visualization (lead); writing – original draft (supporting); writing – review and editing (supporting). Jun Li: Funding acquisition (equal); methodology (supporting); supervision (supporting). Tijana Milenkovic: Funding acquisition (equal); methodology (supporting); supervision (lead). Patricia L. Clark: Funding acquisition (equal); project administration (equal); supervision (lead); writing – original draft (lead); writing – review and editing (lead).
CONFLICT OF INTEREST
The authors declare no conflicts of interest.




