Network representation of protein interactions: Theory of graph description and analysis
Understanding the interactions of proteins with their natural targets is one of the most important tasks of modern molecular biology. Here a method is presented that allows to determine intramolecular correlations between the amino acids involved in aprotein's interaction. This elucidates the functional constitution of the underlying interaction mechanism.
Abstract
A methodological framework is presented for the graph theoretical interpretation of NMR data of protein interactions. The proposed analysis generalizes the idea of network representations of protein structures by expanding it to protein interactions. This approach is based on regularization of residue-resolved NMR relaxation times and chemical shift data and subsequent construction of an adjacency matrix that represents the underlying protein interaction as a graph or network. The network nodes represent protein residues. Two nodes are connected if two residues are functionally correlated during the protein interaction event. The analysis of the resulting network enables the quantification of the importance of each amino acid of a protein for its interactions. Furthermore, the determination of the pattern of correlations between residues yields insights into the functional architecture of an interaction. This is of special interest for intrinsically disordered proteins, since the structural (three-dimensional) architecture of these proteins and their complexes is difficult to determine. The power of the proposed methodology is demonstrated at the example of the interaction between the intrinsically disordered protein osteopontin and its natural ligand heparin.
Introduction
The study of protein interactions represents one of the most important aspects of modern molecular biology. The development of medicinal therapeutics as well as prevention of various diseases can benefit from a comprehensive knowledge of structural dynamics, binding sites or affinities of the relevant proteins. In the past decades, nuclear magnetic resonance (NMR) spectroscopy has become a widespread tool for the investigation of structural and kinetic aspects of protein interactions at atomic resolution.1-4 Especially, for the study of structural dynamics of intrinsically disordered proteins (IDPs), NMR provides an irreplaceable method as crystallography is not applicable.5-8 However, NMR data is frequently not easy to interpret. Allosteric restructuring, folding-upon-binding, etc., often lead to complicated effects along the entire primary sequence of the protein making it difficult to understand the usually residue-resolved NMR-observations.9, 10 Here we present a methodology to quantitatively analyze residue-resolved NMR data of protein interactions based on graph theory. The latter has already found numerous successful applications not only in the analysis of protein structure11 and dynamics,12 but also in fields of science like biological interaction networks,13 social network analysis14 or artificial neural networks.15 Here graph theory is employed for the precise determination of interaction sites and functional particularities of protein–ligand binding events. A graph representing the network of residue–residue correlations in a protein interaction provides means to quantify the functional connectivity between amino acids as well as the centrality of each single residue. This analysis is related to network representations of proteins,11 since a graph can be regarded as a representation of a network with a certain number of nodes and a particular distribution of edges connecting these nodes. In other words, we present a method based on prototypical NMR data of proteins to unravel and analyze the complicated pattern of correlations between residues by depicting these correlations as connections between nodes, which represent protein residues in a network.11, 16, 17 A plethora of information can be obtained from the graph representation of protein interactions concerning residue collectivity, centrality, edge density, etc.
The proposed method combines data from different NMR experiments on a protein interaction into a unified representation. The latter exhibits an improved apparent signal-to-noise ratio, which significantly enhances the sensitivity for weak effects. Thus, the functional interplay between multiple interactions sites can readily be revealed and analyzed, even for very weak binders. The graph analysis is facilely applied to routinely detected NMR data as it does not require any chemical or biological modification of the investigated sample nor any specific experimental hardware. Yet, it yields a substantial amount of information that might remain undiscovered by conventional means of data analysis.
In the following, we develop the theory of the network representation of a protein interaction and describe in detail the construction of the associated graph. We demonstrate the graph analysis, its advantages and its properties at the example of the well-documented osteopontin–heparin interaction. In part two of this contributions we investigate in detail five further examples of protein interactions to validate and test the here presented methodology. At these examples we highlight the advantages gained by our methods in more detail. We show how the proposed graph analysis allows for precise determination of binding sites from data sets that are complicated to understand by means of conventional analysis as they contain multiple binding sites and diffuse interaction patterns. These examples involve three folded proteins YqcA,18 calmodulin (CaM)19, 20 and the cold shock protein A (CspA);21 as well as two IDPs: Myc22, 23 and the brain acid soluble protein 1 (BASP1).24
Results
Data normalization
For the present study, we investigate residue-resolved data from different two-dimensional NMR experiments. Each experiment yields an independent NMR parameter, P, for each amino acid of a protein's primary sequence. Typically, NMR monitors protein interactions via changes in parameters like chemical shift (CS), transverse relaxation rates (R2) or heteronuclear 15N{1H} Overhauser enhancements (NOE, η).4, 25 We focus on differential values of these parameters, denoted here as ΔP. The latter is defined as the value of a parameter found for the holo-form (ligand bound) of a protein minus the value corresponding to its apo-form (ligand free). The various abovementioned differential NMR parameters report on different aspects of a protein interaction: Changes in CS (i.e., ΔCS) due to the binding of a ligand to a protein depend on variations of the chemical environment of the typically observed amide 15N-nitrogens and protons, 1HN, of the protein backbone. For proteins changes in 15N transverse relaxation rates, ΔR2, typically report on variations of the average amplitude of backbone motions on the nanosecond timescale. The differential NOE, Δη, reports complementarily on alterations in mobility on the picosecond timescale.
Note that we generally analyze ΔCS values separately for amide protons, 1HN, and backbone amide, 15N, nitrogens. Such, for a single protein interaction one may readily obtain four independent residue-resolved data sets of differential values ΔCS(1HN), ΔCS(15N), ΔR2, and Δη.
To quantitatively relate ΔCS(1HN), ΔCS(15N), ΔR2, and Δη to each other we have to normalize these independent parameters in a common way. (We will focus on the four abovementioned parameters throughout this contribution, although further parameters might be available in many cases.) This means, the data originating from different experiments must be simultaneously referenced to a universal scale. Hence, normalization must not be applied individually for each experiment, but must include some common scaling. This is complicated by the fact that one wants to compare values that span different ranges and that have different units. For example, a change of 5 s1 in R2 may not be very large, but a change of 5 ppm in CS would be quite drastic for an 1HN nucleus. To compare different NMR parameters we propose a two-step solution. In a first step, each NMR parameter is normalized by dividing it by a “global” standard deviation denoted σglobal. Here, “global” indicates that this standard deviation corresponds to the width of a hypothetical probability distribution of all possible values that an NMR parameter can adopt—independent of a particular experimental context. The four individual σglobal values that “globally” normalize the four NMR parameters (CS(1HN), CS(15N), R2, and η) are obtained through computation of the standard deviation from all measured values found in the Biological Magnetic Resonance Data Bank (BMRB) database26 for each of these observables.
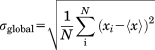 (1)
(1)Here N is the number of values found for a particular observable and magnetic field strength in the BMRB. xi denotes one of these values and <x> the mean over these values. As an example, in the case of R2 measured at 14 T experimental field strength we would take all values found in the BMRB for 15N–R2 values of protein amides at 14 T and compute the standard deviation of the obtained distribution of values. σglobal provides a “global” estimate of the distribution or span of possible values of R2. The same argument holds for η. Hence, we can conclude that σglobal of R2 and η constitutes a global average of the corresponding differential values ΔR2 and Δη since the latter denote shifts inside the range of possible values of R2 and η, which in return is approximated by σglobal. This range constitutes the desired universal scale for the normalization of ΔR2 and Δη.
In principle, an equivalent argumentation holds for ΔCS(1HN) and ΔCS(15N). However, it has to be taken into account that the σglobal parameter needed for normalization of ΔCS depends on the type of amino acid under investigation. Hence, the primary sequence of the protein has to be taken into account for normalization. The standard deviations, σglobal, of chemical shifts for each amino acid type are directly provided by the BMRB26 for 15N as well as for 1HN. We individually normalize the data for both nuclei to bring them to a common scale. For a residue-resolved data set of chemical shift changes of either 1HN or 15N we divide every entry by σglobal found in the BMRB for the underlying amino acid. Through this, a combination of chemical shifts into chemical shift perturbation is not necessary.
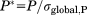 (2)
(2)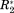 found for a given amide in a ligand–protein binding event indicates in both cases a similarly strong influence of the ligand on CS(1HN)* and
found for a given amide in a ligand–protein binding event indicates in both cases a similarly strong influence of the ligand on CS(1HN)* and
 of the protein amide. This is not the case for the non-normalized parameters ΔCS(1HN) and ΔR2. Here a value of 5 ppm or 5 Hz, respectively, cannot be numerically compared. The normalization via σglobal makes NMR parameters from different experiments comparable in terms of their significance. ΔCS* and Δ
of the protein amide. This is not the case for the non-normalized parameters ΔCS(1HN) and ΔR2. Here a value of 5 ppm or 5 Hz, respectively, cannot be numerically compared. The normalization via σglobal makes NMR parameters from different experiments comparable in terms of their significance. ΔCS* and Δ
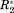 still have different meanings, since they report on different aspects of a protein interaction, but the significance of their values are all referenced to a unified scale.
still have different meanings, since they report on different aspects of a protein interaction, but the significance of their values are all referenced to a unified scale.In Figure 1, the distribution found for 15N–R2 and η in the BMRB are exemplarily shown for 600 and 800 MHz proton Lamor frequency (ωH). The standard deviations of these distributions yield σglobal,R2 and σglobal,η. To derive σglobal, more than 14,000 values of R2 and η were obtained. For ωH = 600 MHz we find σglobal,R2 = 5.41 Hz and σglobal,η = 0.24. For ωH = 800 MHz we find σglobal,R2 = 14.02 Hz and σglobal,η = 0.18.
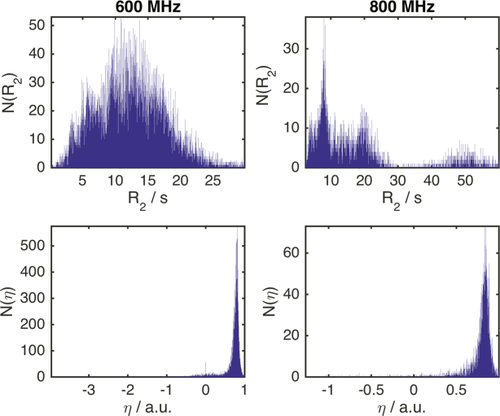
Histograms of 15N-R2 and η values of protein backbone amides found in the BMRB at 600 (left) and 800 MHz proton Lamor frequency (right). Note that the distributions are not scaled to correlation times or protein sizes. This might transform the distributions into monomodal functions and will be treated elsewhere. For the present purpose, the unscaled distributions yield the desired information.
In Figure 2, ΔCS(1HN), ΔCS(15N), ΔR2, and Δη are exemplarily shown for the well-studied osteopontin (OPN)/heparin interaction [adopted from Ref. 9]. OPN is an intrinsically disordered protein (IDP) involved in metastasis and several kinds of cancer. Its regulatory function involves binding to CD44 receptors employing heparin as a cofactor.27-29 Characterized as an IDP, this protein does not have a rigid three-dimensional structure. Instead, it can be described as a flexible coil comprising a more compact patch between amino acid (aa) 100 and 190 of its primary sequence.9 Earlier studies on the OPN–heparin interaction localized a heparin binding site between aa 140 and aa 160 of OPN. During the binding event aa 100–140 (containing two RGD motifs that are central to CD44 receptor binding27-29) are dispatched from the compacted patch of the IDP leading to a thermodynamic compensation of the loss in configurational entropy due to the protein–heparin association.9 In Figure 2(A) one can clearly see that the binding site and the compensatory site show changes in ΔCS(1HN) and ΔCS(15N) indicating changes in chemical environment of the affected residues due to the presence of the ligand. Furthermore, aa 140–160 display increased R2 values. This indicates reduced microsecond dynamics due to the presence of bound heparin, which restricts the motional freedom at the binding site. In contrast, aa 100–140 exhibit increased picosecond dynamics as reported by a negative Δη. This augmented mobility entails the entropic compensation of the binding event. Employing the σglobal-based referencing introduced above [see 1), (2)] we arrive at the normalized NMR parameters ΔCS(1HN)*, ΔCS(15N)*, Δ
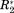 and Δη* shown in Figure 2(B). Note that Δ
and Δη* shown in Figure 2(B). Note that Δ
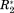 and Δη* are larger than ΔCS(1HN)* and ΔCS(15N)*. This is in agreement with the experimental observation that, on the one hand, the chemical shift of the detected resonances does not change strongly since the protein remains disordered also in the presence of Heparin, while, on the other hand, the relaxation parameters display more drastic changes due to the inherent flexibility of OPN, which allows for significant changes in local backbone dynamics.
and Δη* are larger than ΔCS(1HN)* and ΔCS(15N)*. This is in agreement with the experimental observation that, on the one hand, the chemical shift of the detected resonances does not change strongly since the protein remains disordered also in the presence of Heparin, while, on the other hand, the relaxation parameters display more drastic changes due to the inherent flexibility of OPN, which allows for significant changes in local backbone dynamics.
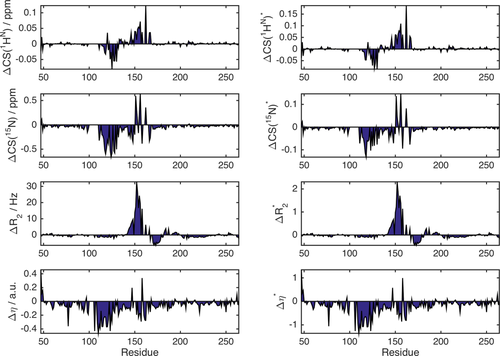
NMR observables ΔCS(1HN), ΔCS(15N), ΔR2, and Δη as a function of residue position for the OPN–heparin interaction (left) and normalized NMR observables parameters ΔCS(1HN)*, ΔCS(15N)*, Δ
 , and Δη* derived according to Eqs. (1), and (2) (right).
, and Δη* derived according to Eqs. (1), and (2) (right).
Construction of the graph representation
The argument of equivalent reference scales for ΔCS(1HN)*, ΔCS(15N)*, Δ
 , and Δη* is only valid in an ideal case. In a real system, the σglobal-normalized data from different experiments will not have an exactly similar significance. The relative scales of the different normalized observables will still be slightly unequal since the relevant reference ranges—as approximated by σglobal—do not constitute rigid thresholds. Contrary, CS(1HN), CS(15N), R2 and η values depend on factors like sample temperature, pH, or protein concentration. Additionally, R2 and η depend on the molecular size and correlation times. Hence, σglobal—which approximates the range of possible values over all data found in the BMRB for a given parameter—may constitute a rather unprecise normalization factor for a particular protein interaction, as it neither takes protein sizes and dynamics into account nor experimental conditions. This problem induces a bias of the σglobal-normalized ΔP* values. Thus, the ΔP* values found for the different NMR parameters as well as for different protein interactions cannot be compared quantitatively. To eliminate the resulting uncertainties in the ΔP* values we employ a regularization procedure in the next step.30 This embraces conversion of the normalized differential NMR data into a single covariance matrix, Cov. This n × n matrix has the dimension of the number of residues in the primary sequence of the protein under investigation. The diagonal elements of this matrix are ordered in the sense of the primary sequence meaning that the first diagonal element corresponds to the variance over the four NMR parameters observed for residue one the primary sequence, the second diagonal element analogously corresponds to the second residue of the primary sequence, etc. Subsequently, this matrix will be “digitized” in a second step.
, and Δη* is only valid in an ideal case. In a real system, the σglobal-normalized data from different experiments will not have an exactly similar significance. The relative scales of the different normalized observables will still be slightly unequal since the relevant reference ranges—as approximated by σglobal—do not constitute rigid thresholds. Contrary, CS(1HN), CS(15N), R2 and η values depend on factors like sample temperature, pH, or protein concentration. Additionally, R2 and η depend on the molecular size and correlation times. Hence, σglobal—which approximates the range of possible values over all data found in the BMRB for a given parameter—may constitute a rather unprecise normalization factor for a particular protein interaction, as it neither takes protein sizes and dynamics into account nor experimental conditions. This problem induces a bias of the σglobal-normalized ΔP* values. Thus, the ΔP* values found for the different NMR parameters as well as for different protein interactions cannot be compared quantitatively. To eliminate the resulting uncertainties in the ΔP* values we employ a regularization procedure in the next step.30 This embraces conversion of the normalized differential NMR data into a single covariance matrix, Cov. This n × n matrix has the dimension of the number of residues in the primary sequence of the protein under investigation. The diagonal elements of this matrix are ordered in the sense of the primary sequence meaning that the first diagonal element corresponds to the variance over the four NMR parameters observed for residue one the primary sequence, the second diagonal element analogously corresponds to the second residue of the primary sequence, etc. Subsequently, this matrix will be “digitized” in a second step.
This unification approach is predicated on the intuition that the different NMR parameters detected for a particular protein interaction are based on a single conformational ensemble of protein structures although they might report on different aspects of the ensemble.
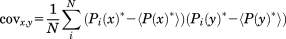 (3)
(3)Here, i runs over the four normalized NMR parameters, P*. x and y indicate residues of the primary protein sequence. N denotes the number of data sets (different NMR experiments), that is, here N = 4. <P(x)*> denotes the average over all four NMR parameters for residue x. The diagonal elements of Cov indicate for each single residue the variance between the four NMR observables. The off-diagonal elements, covx,y, with x ≠ y, indicate covariance between the two residues x and y. This means, if x and y show the same deviation of ΔCS(1HN)*, ΔCS(15N)*, Δ
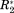 , and Δη* from their mean value the associated covariance element covx,y will be positive. If the deviation from average is negative for x and positive for y (or vice versa) the element covx,y will be negative. Hence, if two residues are strongly affected by a protein interaction and their associated NMR parameters vary the connecting matrix element covx,y will indicate a significant nonzero (positive or negative) covariance between these two residues. (Note that correlation coefficients are not applicable in the present case due to the residue specific normalization, which would entail large correlation coefficients between idle residues. Moreover, one could also add further data sets like R1 to the covariance matrix. Yet, changes in R1 are less pronounced than changes in R2 and report on a similar timescale. Thus, if R2 is available it should be preferred over R1.)
, and Δη* from their mean value the associated covariance element covx,y will be positive. If the deviation from average is negative for x and positive for y (or vice versa) the element covx,y will be negative. Hence, if two residues are strongly affected by a protein interaction and their associated NMR parameters vary the connecting matrix element covx,y will indicate a significant nonzero (positive or negative) covariance between these two residues. (Note that correlation coefficients are not applicable in the present case due to the residue specific normalization, which would entail large correlation coefficients between idle residues. Moreover, one could also add further data sets like R1 to the covariance matrix. Yet, changes in R1 are less pronounced than changes in R2 and report on a similar timescale. Thus, if R2 is available it should be preferred over R1.)
In order to eliminate the abovementioned uncertainties in ΔP* values that propagate into the covariance matrix it is transformed into a matrix A. A has the same order as Cov, but all elements with values larger than the noise level of the covariance matrix are set to 1 and all other entries to 0. Variations of the elements of the covariance matrix due to imperfect referencing of the four NMR parameters are eliminated through this operation. In other words, the uncertainties introduced by the σglobal normalization (as it does not take into account the particularities of each individual protein) propagate into uncertainties in the elements covx,y. However, these uncertainties are eliminated as all values are “digitized” by the transformation into A. Thus, after this regularization the entries of the adjacency matrix are reliable despite a possibly biased ΔP*. In this context, the normalization via σglobal is required to roughly match the noise levels of the different ΔP* sets. This prevents that a particular value for an NMR parameter drops below the noise level of any other NMR parameter set. This would lead to the loss of the information contained in this value as the corresponding covariance element would drop below the noise level of the covariance matrix and would be cut off during the normalization procedure. Note that the signal-to-noise ratio of the covariance matrix is generally quite high (as will be shown below). Through this, differences between the noise levels of the different ΔP* parameters (introduced by a biased σglobal) are compensated and a reliable digitization of the covariance matrix is guaranteed (see the Supporting Information for details).
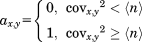 (4)
(4)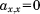
A is a matrix that combines all NMR parameters—as determined for each residue of a protein—into a representation of connections between these residues based on correlated functional activity in a molecular interaction. In this context, the first step of our procedure (the normalization of the four NMR parameters via σglobal) guarantees a comparable noise level of each NMR parameter. This ensure that important and significant observation of large values of ΔCS(1HN)*, ΔCS(15N)*, Δ
 , or Δη* always entail large off-diagonal Cov-elements. Thus, no significant observation is excluded from the analysis through the transformation of Cov into A. In other words, if the scales of ΔCS*, Δ
, or Δη* always entail large off-diagonal Cov-elements. Thus, no significant observation is excluded from the analysis through the transformation of Cov into A. In other words, if the scales of ΔCS*, Δ
 , Δ
, Δ
 , and Δη* are roughly equivalent it is guaranteed that the noise level of the matrix Cov represents an equal threshold of significance for each NMR parameter. (Note that the diagonal elements of the adjacency matrix are set to zero, which excludes autocorrelation of residues from the graph representation.) Through the transformation of Cov into A, we “digitize” all elements of the covariance matrix. Thus, we avoid the subtle problem of correctly weighting the different observations of relaxation parameters and chemical shifts. For a perfectly weighted normalization factor one would need to take into account the particularities of each individual sample and parameter. In contrast, the here proposed adjacency matrix takes all significant ΔP* values similarly into account eliminating all deficiencies of the covariance matrix.
, and Δη* are roughly equivalent it is guaranteed that the noise level of the matrix Cov represents an equal threshold of significance for each NMR parameter. (Note that the diagonal elements of the adjacency matrix are set to zero, which excludes autocorrelation of residues from the graph representation.) Through the transformation of Cov into A, we “digitize” all elements of the covariance matrix. Thus, we avoid the subtle problem of correctly weighting the different observations of relaxation parameters and chemical shifts. For a perfectly weighted normalization factor one would need to take into account the particularities of each individual sample and parameter. In contrast, the here proposed adjacency matrix takes all significant ΔP* values similarly into account eliminating all deficiencies of the covariance matrix.
Figure 3(A) shows the covariance matrix [cf. Eq. (3)] derived from the data presented in Figure 2. Both axes correspond to the residue index of OPN. Strong covariance can be observed between residues in the heparin binding site (aa 140–160) and the compensatory site (aa 100–140), which are both subject to pronounced ΔCS(1HN)*, ΔCS(15N)*, Δ
 , and Δη* values [see Fig. 2(B)]. The two sites are correlated among each other, as can be deduced from the large covx,y2 values connecting them. Residues located in the “hotspot” (around aa 150) of the heparin binding site exhibit a particularly large covariance among themselves.
, and Δη* values [see Fig. 2(B)]. The two sites are correlated among each other, as can be deduced from the large covx,y2 values connecting them. Residues located in the “hotspot” (around aa 150) of the heparin binding site exhibit a particularly large covariance among themselves.
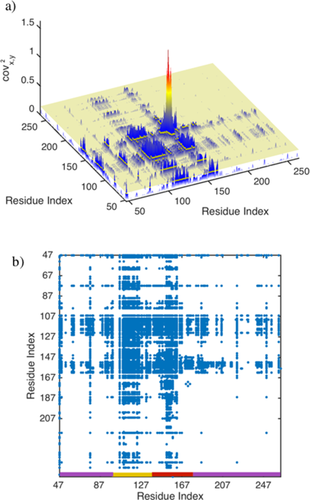
(a) Graphical display of the covariance matrix (squared values) corresponding to the OPN/heparin interaction. The yellow plain depicts the noise level, <n>, found for the covariance matrix (see text). (b) Adjacency matrix derived for the OPN/heparin interaction if all values smaller than <n> in (a) are set to 0 and all other values to 1 [blue dots, cf. Eqs. (3), (4)]. The adjacency matrix can be grouped into three clusters of residues as indicated at the bottom of the figure (red: heparin binding site, yellow: compensatory site, purple: residual affected residues).
The average noise level, <n>, of the covariance matrix is represented as yellow plain in Figure 3(A). It divides the covariance matrix in two parts. One part with matrix elements larger than <n> and another part with matrix element smaller than <n>. These two parts define the zero and nonzero elements of the matrix A according to Eqs. (3) and (4). The matrix A derived from the matrix in Figure 3(A) is shown in Figure 3(B).
Note that we combine four different NMR data sets into a unified representation, that is, the covariance matrix. Through this, the signal-to-noise ratio of the covariance matrix (SNRCOV) exceeds the SNR of the individual ΔP* data sets (SNRNMR). The magnitude of this gain depends on many factors like the number of residues affected by the interaction, the distribution of affected sites along the primary sequence etc. Under optimal conditions, the SNRCOV exceeds SNRNMR by an order of magnitude. This renders the network representation of protein interactions a powerful tool for the analysis of weak protein–ligand complexes as their formation frequently entail very small ΔP* values. In this context, error propagation from NMR data to the covariance and adjacency matrices is negligible, too, as we digitize the covariance matrix (see Supporting Information for details). The main remaining source of error in our analyses is the experimental noise. This source of error is yet reduced by the unification of different data sets and the gain in SNR. A loss of information is excluded as the string separation of signals from noise guarantees a reliable construction of the adjacency matrix. (Details and simulations on the dependence of SNRCOV on SNRNMR can be found in Supporting Information.)
Significance of the adjacency matrix
The matrix A can be regarded as an adjacency matrix if we picture the covariances/correlations among the residues of OPN as connections in a network: Each diagonal element of A represents a node of this network. Each node is associated with a residue in the backbone of the protein that was investigated by NMR. Two nodes, x and y, are connected by an edge if the matrix element ax,y that connects the two nodes equals 1. If ax,y = 0, x and y are not directly connected. In other words, A represents the NMR data in a unified manner by relating residues that display significant changes (covariance) in the different NMR parameters due to the ligand binding. Thus, A constitutes a graph or network of covariance/correlations among residues in a protein interaction. It can be regarded as a functional representation of the protein interaction as it depicts the “correlated implication” of two (functional) residues in the binding event.
This representation allows to determine the “connectivity” between different functional sites of a protein—an important piece of information for the understanding of protein interactions. (More examples are given in part two of this contribution.)
Note that the transformation of the covariance matrix into the adjacency matrix [cf. Eq. (4)] becomes more and more unprecise as the number of signals in the ΔP* residue plots increases (see Supporting Information for details). It has to be taken into account that the variance of the covariance matrix is increasing with the number elevated ΔP* values. This might lead to a possible loss of information during the regularization procedure as weak signals might drop below the cut off level of the covariance matrix, Var(Cov). However, as the SNR of the covariance matrix is typically quite high this risk can be neglected in most cases. Several examples are given in part two that show that the adjacency matrix can reliably be constructed also for very complicated protein–ligand interaction patterns.
In the context of “digitized” covariance matrices it should be mentioned that Selvaratnam et al. have already shown how to combine covariance analyses of different NMR CS data sets from different ligands and cluster analysis to identify several allosterically active patches along a protein backbone.31, 32 In this approach residue-resolved correlation coefficients (covx,y/σxσy, where σx denotes the standard deviation for residue x) are calculated from sets of chemical shifts obtained from different complexes of the same protein with different ligands. In contrast to covariance matrix elements correlation coefficients tend to correlate spectral noise. Thus, Selvaratnam et al. introduce a cutoff at a very large correlation coefficient of 0.98 and set all values below this threshold to zero.
The here proposed method has the advantage that it uses a covariance matrix that is digitized on the basis of its own noise level. This minimizes the probability to lose significant data points through the cut off procedure. Furthermore, one does not need different ligands, which are frequently not available. We here use data sets that stem exclusively from a single interaction. Thus, while the method of Selvaratnam et al. is superior for the analysis allosterically active epitopes, the here proposed method is superior to observe features that are unique to an interaction with a certain ligand.
A further possibility to obtain different NMR data sets and to combine them mathematically into a unified representation is the monitoring of pH-dependent chemical shift changes and a subsequent principle component analysis of the different CS sets. This method, as introduced by Sakurai and Goto33 allows to identify structural changes of a protein under varying the buffer (pH) conditions.
Brüschweiler and co-workers as well as Karplus and co-workers34 applied a covariance analysis to molecular dynamics simulations of proteins to yield covariance matrices that correlate the dynamics of the different residues. This method identifies intramolecular dynamics.35 In contrast, we here focus on intermolecular phenomena. In general one should differentiate between the well-established intramolecular contact maps between protein residues that give rise to a network representation of a protein structure,36 and the here presented connectivity-based representation of intermolecular interactions. Examples for successful application of intramolecular contact maps are the work by Nussinov and co-workers who developed a way to use the intramolecular network representation of protein structures to classify structural disorder11 or the work by Konrat and co-workers who showed how to use the network representation of proteins to predict pH-dependent conformational changes.37
Analysis of the functional network of the OPN/heparin interaction
The adjacency matrix A represents a network of residues that are involved in the interaction of a protein. The adjacency matrix can be regarded as a representation of the graph or network indicating the functional particularities—i.e., correlations among residues—of protein–ligand interactions. A schematic display of the network structure corresponding to the OPN/heparin interaction is shown in Figure 4.
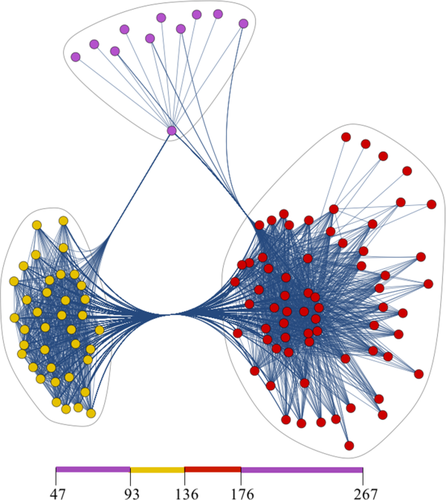
Display of the correlation network of the OPN/heparin interaction. It is represented with three pronounced hubs as indicated by the blue loops. These hubs correspond to the binding site, the affected site and residual correlated residues Isolated nodes are ignored. Every spot corresponds to a node, that is, to a diagonal element of the adjacency matrix and every line indicates an edge between two nodes, that is, a nonzero off-diagonal matrix elements of A. The residue patches of the primary sequence corresponding to the nodes are indicated at the bottom; see Figure 3 for the corresponding nodes in the adjacency matrix. The clustering was performed by means of binary hierarchical clustering using an Euclidean distance norm and a predefined number of three clusters. The graphical visualization was done using Mathematica 10's spring electrical embedding method.
The three hubs or clusters of the network correspond to the binding site (red), the affected site (yellow) and residual connected residues of OPN (purple). Note that an edge here stems from pronounced covariance between any two residues, which are represented by the nodes in Figure 4. Hence, the edges indicate a functional correlation between two residues. In Figure 4(a), strong correlation between the two clusters can be observed that represent the binding and the affected sites. This indicates that these two sites are functionality coupled in the Heparin binding event. This is in agreement with earlier studies based on computational metastructure analysis, electron paramagnetic resonance (EPR), NMR, and isothermal titration calorimetry (ITC).5, 9, 38 These studies show that the apo-form of OPN samples cooperatively folded, compacted states that base on electrostatic as they dissolve under high salt conditions.9 The electrostatic interaction that stabilizes these states is constituted by clusters of negatively charged residues in the compensatory site and positively charged residues in the binding epitope. The mutual attraction between these two sites leads to the observed compaction of OPNs core. When the negatively charged Heparin binds to OPN it is attracted by the positively charged binding site and at the same time repels the negatively charged compensatory site. This leads to a compensation of the configurational entropy loss due to the binding event. The depicted network in Figure 4 may, thus, be regarded as a display of this functional correlation between the binding epitope and the compensatory sites in the OPN–heparin interaction.
Since the adjacency matrix, A, can be regarded as a description of a graph it can be analyzed on a graph theoretical basis, which is a well-established branch of mathematics.39 Parameters such as the degree, δ, local clustering coefficient, C, and eigenvalue centrality, W, of any node/residue, x, of can be defined.39 In the case at hand, these paramters corrspond to the functional connectivity of the different amino acids of a protein.
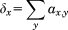 (6)
(6)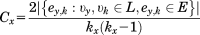 (7)
(7)Here kx is the number of neighbors of node υx. The denominator in Eq. (6) corresponds to the number of possible edges between the neighbors of a particular node, while the numerator indicates the number of actually realized edges between the neighbors of this node. Equation (6) can further be graphically explained. In Figure 5(A), a graph is depicted with 4 nodes and 4 edges.
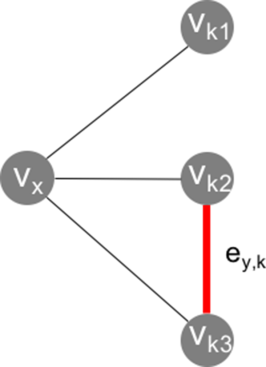
A graph with four nodes and four edges. For the node υx, δx = 3, and Cx = 1/3 [cf. Eqs. (5), (6)].
The node of interest, υx, is connected to three other nodes via three separate edges. Hence, the number of neighboring edges is three. The degree of node υx is, thus, δx = 3. The number of edges between these three neighboring edges is 1 (highlighted as edge ey,k in Fig. 5). Thus, the local cluster coefficient for υx amounts to Cx = 1/3.
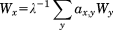 (8)
(8)Here λ denotes the lead eigenvalue of A, which is the largest eigenvalue of the adjacency matrix. The associated lead eigenvector W has only positive entries. Wx can be regarded as the average eigenvector centrality of all residues that are connected by an edge to residue x. Hence, its definition is in a sense recursive.
The node centrality can be regarded as a measure of the importance of a node for a network. This means, if a node with high centrality is deleted form the graph, its constitution will change significantly. Contrary, if a residue with Wx = 0 is deleted the architecture of the network described by the graph does not change at all. This means for a protein interaction that if a residue corresponding to a high Wx is altered or deleted, for example, due to a point mutation, the interaction of the protein with its ligand is likely to be influenced or even suppressed.
Note that the study of eigenvector centralities is based on the extraction of eigenvalues/modes of the correlation network. In the context of the analysis of biomacromolecules Brüschweiler and co-workers as well as Karplus and co-workers34 spearheaded the analysis of eigenmodes in the context of NMR to unravel collective motions in proteins. These methods yet base on molecular dynamics simulations, while the here proposed method identifies regions of importance (high eigenvector centrality) for an interaction with a ligand without the need for computational input.
In the context of protein interactions, it should be mentioned that graph theoretical approaches to the analysis and derivation of protein structures and dynamics have already been successfully applied in the past.40 For example, Kaptein and co-workers apply graph theory to assign intramolecular NOEs.41 Wüthrich and co-workers use graph theoretical concepts for the sequential resonance assignment in multidimensional protein spectra.42 Jacobs et al. apply graph theory to predict the flexibility of proteins.12 We here expand the application of this branch of mathematics to the analysis of intermolecular phenomena.
Graph analysis at the example of the OPN–heparin interaction
Figure 6 displays the eigenvector centrality, W, local clustering coefficient, C, and local node degree, δ, derived from the adjacency matrix shown in Figure 3(B) for the OPN/heparin interaction. All three measures show increased values around the binding site (aa 140–160) and the compensatory site (aa 100–140). For these residues a high eigenvector centrality, W, means a central function in the interaction with heparin. Their deletion would likely alter the interaction. A large local clustering coefficient, C, means that these residues are embedded in a densely connected graph neighborhood (cf. Eq. (6) and Fig. 5); that is, a large number of correlated residues is neighboring each of them. This can be expected for the directly affected sites, where the presence of the ligand simultaneously affects different (correlated) residues. The large degree, δ, of the residues in the binding and compensatory site means that each of them is functionally correlated with many other residues [cf. Eq. (6)]. Thus, the important residues for the interaction can be distinguished from the others through higher values of W, C, and δ. The binding site shows especially high measures in C, and δ. Hence, it can be distinguished from the compensatory site. Its “hotspot” can be precisely localized to residues 159–166. These results are in agreement with the above mentioned earlier biochemical studies based on EPR, NMR, and ITC9 which indicate that the primary binding epitope is located between residue 160 and 180, while the compensatory site is located between residues 100 and 140. The electrostatic interaction between these two sites is modulated by the heavily charged heparin ligand leading to pronounced changes in the observed NMR parameters. Our method precisely locates these two sites in agreement with the earlier studies and additionally allows to distinguish the binding epitope from the expelled site via the local clustering coefficient, C, as shown in Figure 6.
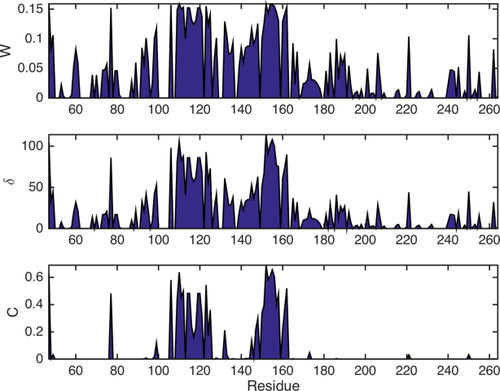
Residue plots of connectivity and centrality measures W, C, and δ corresponding to the matrix in Figure 3(B) [cf. Eqs. (5)–(7)]. All three parameters show increased values around the heparin binding site (aa 140–160) and the compensatory site (aa 100–140).
Note that the local clustering coefficient only displays large values upon pronounced changes in an all NMR parameters of a particular residue, since the local clustering coefficient is based on the connectivity of neighboring nodes (see Fig. 5). This connectivity will only be high if the residue of interest is embedded in a dense network of correlations. This in return requires that the site containing the residue is strongly affected by the ligand, which will result in changes in all observable NMR parameters. In contrast, W and δ are dependent on the direct functional connections of a residue, that is, the number of its edges. Since the adjacency matrix already exhibits an edge if only one of the input data sets is affected by the interaction, W and δ show elevated values as soon as one NMR parameter of a residue deviates significantly from zero. One might say that these two measures are more sensitive to changes in dynamics and structure of the observed protein, while C is more reliable in distinguishing the important sites of the interaction.
Note that none of the three used metrics, W, δ, and C, is creating false positive values nor are they differently insensitive to the NMR data as they are all based on the same adjacency matrix. The different aspects of the NMR data highlighted by the three different measures reflect the particularities of the adjacency matrix that in return reflects the functional structure of the input data.
In part two of this contribution the power of the graph analysis will be demonstrated at further examples. It will be shown how the three different measures, W, δ, and C allow for the identification of binding patterns that are only complicated to determine by conventional means.
Discussion
The methodology presented here is centered around the idea that all information about a protein interaction is based on a unique conformational ensemble. Hence, all data sets concerning this interaction reflect certain aspects of the protein's conformational space. The functional architecture of this space is represented (at least in parts) by our adjacency matrices. The combination of all four NMR parameters into one single graph, thus, aims at a partial reconstruction of the functional residue correlations in the conformational ensemble of a protein in one of its interactions.
The method may readily be applied to standard NMR data sets gained from conventional samples. A widespread application might, hence, be anticipated.
The here proposed analysis generalizes the idea of network representations of protein structures by expanding it to protein interactions. This enables the definition of mathematical precise means for the quantification of residue activity in a protein interaction going beyond the established means of data interpretation. The network representation of a protein interaction yields a universally tool that might help to quantitatively compare the importance of residues as well as the functional connectivity between residues in a protein.
Acknowledgments
The author thanks the Professors Robert Konrat and Geoffrey Bodenhausen for their support and meaningful discussions.




