A large strain thermoplasticity model including recovery, recrystallisation and grain size effects
Abstract
In manufacturing, thermomechanical processes such as static annealing and hot working are commonly used to tailor the microstructure of metals to achieve favourable macroscopic material properties that meet specific application requirements. To improve sequential manufacturing processes and to accurately predict the microstructural changes of the material along the process chain, physically motivated constitutive models are required that simultaneously account for the effects of recovery and recrystallisation, as well as grain size dependencies. To this end, Cho et al. [Int. J. Plasticity 112, 123–157 (2019)] proposed a macroscopic hypo-elasticity based large strain thermoplasticity model that aims at the unification of the effects of static and dynamic recovery and recrystallisation, as well as grain growth and refinement. In the present contribution, the hypo-elasticity based large strain recrystallisation formulation proposed by Cho et al. is transferred to a hyper-elasticity based large strain thermoplasticity framework to overcome the limitations typically accompanied with hypo-elasticity based formulations. For this purpose, an isotropic temperature dependent hyper-elastic Hencky type formulation defined in logarithmic strains is combined with a temperature dependent von Mises yield criterion. The recrystallisation modelling approach by Cho et al. is adopted, assuming a non-associated temperature dependent proportional hardening rate in the form of an Armstrong-Frederick type hardening minus recovery format, wherein the proportional hardening related internal variable is interpreted as a measure of dislocation density. It is shown that the hyper-elasticity based format results in a thermodynamical consistency condition that effectively constrains the physically motivated evolutions of recrystallised volume fraction and average grain size. To investigate the capability of the model to predict the material response of unified recrystallisation thermodynamically consistently, representative thermomechanical sequential loading conditions including static annealing and hot working are studied.
1 INTRODUCTION
In a plastically deforming material, the generation of new dislocations by work hardening leads to the accumulation of hardening related energy contributions represented by an increased dislocation density. At elevated temperatures, the dislocation density acts as a driving force for the initiation of microstructural processes of recovery, recrystallisation and grain size evolution [1, 2]. Recovery, the predecessor to recrystallisation, reduces the dislocation density by annihilation and rearrangement of dislocations, resulting in the formation of low angle grain boundaries. With increasing temperature, plastically deformed grains are replaced with new high angle dislocation free grains by recrystallisation. Both processes of recovery and recrystallisation effectively release the hardening related energy contributions, resulting in a decrease in strength and a simultaneous increase in ductility observed in the macroscopic material response, which will be referred to as the softening effect in the following. Grain growth, the successor to recrystallisation, is driven by grain boundary energy and influences the macroscopic material behaviour in terms of the Hall-Petch effect [3, 4].
In this work, following Cho et al. [5], the two primary underlying recrystallisation mechanisms of subgrain rotation recrystallisation and grain boundary migration recrystallisation are considered, which are both driven by hardening related energy contributions. Subgrain rotation recrystallisation occurs exclusively during plastic loading, that is hot working processes, where new high angle grains form in plastically deformed grains from dislocation walls generated by dynamic recovery [6]. In turn, grain boundary migration recrystallisation is a time dependent recrystallisation mechanism that is observed during both, static annealing and hot working processes. It involves the nucleation and growth of new high angle grains at the grain boundaries, consuming plastically deformed grains [7].
In the literature, several recrystallisation models can be found that are typically limited to specific thermomechanical conditions, focusing on simulating either static recrystallisation, see for example [8, 9], or dynamic recrystallisation, see for example [10-13]. These models commonly adopt a purely phenomenological Avrami type formulation [14, 15] or are based on a physically motivated recrystallised volume fraction evolution that is coupled to hardening related energy contributions. They may depend on a critical value for the onset of recrystallisation or are missing a grain size evolution equation. Other models aim at the unification of the effects of work hardening, recovery, recrystallisation and grain size evolution, see for example [5, 16-18]. However, these models may lack certain model features, such as a coupling to plasticity including the grain size related Hall-Petch effect [3, 4] or are following a hypo-elasticity based formulation.
The unified recrystallisation framework proposed by Cho et al. [5] is based on a hypo-elasticity based large strain thermoplasticity formulation and features physically motivated evolution equations of newly introduced internal state variables of recrystallised dislocation free volume fraction and average grain size. By incorporating a plasticity formulation with the proportional hardening internal variable interpreted as a measure of dislocation density, the evolutions of these internal variables are accurately modelled based on their true physical driving forces of hardening related energy contributions and grain boundary energy. By entering a proportional hardening rate in the form of a hardening minus recovery format by Armstrong and Frederick [19], the recrystallised volume fraction and average grain size internal variables model the microstructure dependent softening and grain size related Hall-Petch effect [3, 4]. In addition, the proposed recrystallisation formulation avoids a critical value for the onset of recrystallisation by employing Arrhenius type functions for the activation of recovery, recrystallisation and grain size evolutions.
As this work proceeds, the hypo-elasticity based thermoplasticity recrystallisation model proposed by Cho et al. [5] is transferred to an isotropic Hencky type hyper-elasticity based thermoplasticity framework to overcome the limitations typically accompanied with hypo-elasticity based formulations. Such hypo-elastic formulations do not define a thermodynamic potential and therefore cannot be proven to adhere to the second law of thermodynamics. As a result, they may lead to unphysical dissipation in the simulation of only elastic processes. Following a hyper-elasticity based framework, a temperature dependent Helmholtz energy function defined in logarithmic strains is introduced as the thermodynamic potential for the underlying constitutive model. Based on a temperature dependent von Mises plasticity, an associated plastic flow rule and a non-associated proportional hardening rate are employed by introducing additional recrystallisation related plastic potentials that follow the hardening minus recovery recrystallisation formulation proposed by Cho et al. [5]. It is shown that the thermodynamical consistent framework results in a thermodynamical consistency condition which gives rise to the thermodynamical intercorrelation between the internal variables of recrystallised volume fraction and average grain size.
2 A HYPER-ELASTICITY BASED UNIFIED RECRYSTALLISATION MODEL
In a large strain setting, let the motion of a deformable continuum body be defined by 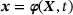 , which is a nonlinear mapping of referential material point placements
, which is a nonlinear mapping of referential material point placements 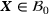 to their spatial counterparts
to their spatial counterparts 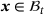 at time
at time 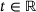 . The related deformation gradient
. The related deformation gradient 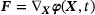 , with
, with 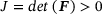 , transforms infinitesimal referential line elements dX to their spatial counterparts dx. By introducing a locally incompatible and stress-free intermediate configuration, the deformation gradient is assumed to multiplicatively decompose into an elastic part Fe and a plasticity related internal state variable contribution Fp, so that
, transforms infinitesimal referential line elements dX to their spatial counterparts dx. By introducing a locally incompatible and stress-free intermediate configuration, the deformation gradient is assumed to multiplicatively decompose into an elastic part Fe and a plasticity related internal state variable contribution Fp, so that 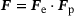 , with
, with 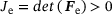 .
.
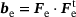 is introduced, wherein •t denotes transposition. It gives raise to the elastic logarithmic strain tensor, that is the elastic Hencky strain tensor [20], defined as
is introduced, wherein •t denotes transposition. It gives raise to the elastic logarithmic strain tensor, that is the elastic Hencky strain tensor [20], defined as
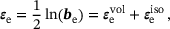 (1)
(1)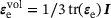 the volumetric elastic logarithmic strains and I the second-order identity tensor.
the volumetric elastic logarithmic strains and I the second-order identity tensor.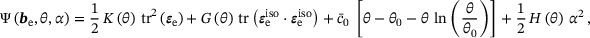 (2)
(2)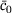 a heat capacity parameter,
a heat capacity parameter, 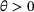 the absolute temperature, θ0 the reference temperature and H the temperature dependent proportional hardening modulus.
the absolute temperature, θ0 the reference temperature and H the temperature dependent proportional hardening modulus.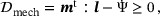 (3)
(3)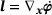 is the spatial velocity gradient and
is the spatial velocity gradient and 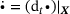 denotes the material time derivative. The spatial Mandel type stresses mt are related to the Kirchhoff stresses τ via
denotes the material time derivative. The spatial Mandel type stresses mt are related to the Kirchhoff stresses τ via 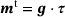 , with g the spatial co-variant metric tensor.
, with g the spatial co-variant metric tensor.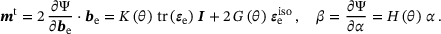 (4)
(4)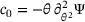 . Inserting the above constraints into the dissipation inequality (3) together with the additive split of
. Inserting the above constraints into the dissipation inequality (3) together with the additive split of 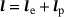 with
with 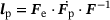 , results in the reduced mechanical dissipation inequality
, results in the reduced mechanical dissipation inequality
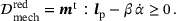 (5)
(5)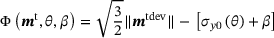 (6)
(6)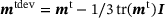 the deviatoric Mandel type stresses,
the deviatoric Mandel type stresses, 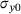 the temperature dependent initial yield limit and
the temperature dependent initial yield limit and 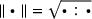 denoting the Frobenius norm.
denoting the Frobenius norm.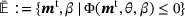 , so that
, so that
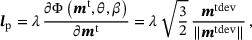 (7)
(7) ,
, 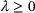 and
and 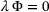 .
.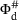 and
and 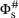 is assumed to take the form
is assumed to take the form
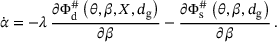 (8)
(8) , and average grain size dg, representing the microstructure of the material. The proportional hardening evolution equation reads
, and average grain size dg, representing the microstructure of the material. The proportional hardening evolution equation reads
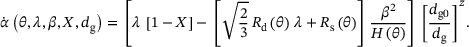 (9)
(9)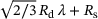 . It is driven by the hardening stress squared divided by the proportional hardening modulus, that is
. It is driven by the hardening stress squared divided by the proportional hardening modulus, that is 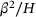 , representing hardening related energy contributions. Temperature dependent Arrhenius type activation functions Rd and Rs of the form
, representing hardening related energy contributions. Temperature dependent Arrhenius type activation functions Rd and Rs of the form
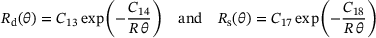 (10)
(10)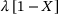 . Based on the precursor of recovery, recrystallisation further increases the softening effect by reducing the work hardening related contribution.
. Based on the precursor of recovery, recrystallisation further increases the softening effect by reducing the work hardening related contribution.To account for the grain size related Hall-Petch effect [3, 4], the hardening relation (9) is additionally weighted by a factor of 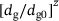 , where dg0 is the initial average grain size and z is a grain size material parameter. In the case of cold working with approximately vanishing activation functions
, where dg0 is the initial average grain size and z is a grain size material parameter. In the case of cold working with approximately vanishing activation functions 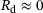 and
and 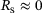 , the hardening relation (9) reduces to a work hardening related contribution weighted by recrystallised volume fraction and the grain size factor. In that way, the influence of the microstructural evolution on cold working processes resulting from preceded, for example, thermal steps is taken into account.
, the hardening relation (9) reduces to a work hardening related contribution weighted by recrystallised volume fraction and the grain size factor. In that way, the influence of the microstructural evolution on cold working processes resulting from preceded, for example, thermal steps is taken into account.
Due to this nonlinear hardening formulation, cf. (9), it is ensured that the proportional hardening variable itself cannot become negative, that is 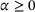 , assuming an initial value of
, assuming an initial value of  , although negative evolutions
, although negative evolutions  are possible for a non-vanishing proportional hardening variable.
are possible for a non-vanishing proportional hardening variable.
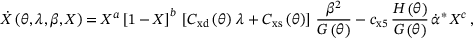 (11)
(11)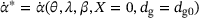 is the proportional hardening rate for a virgin material, cf. (9), and cx5 and c are reduction rate material parameters.
is the proportional hardening rate for a virgin material, cf. (9), and cx5 and c are reduction rate material parameters.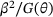 . A nonlinear sigmoidal form [2] is employed that is in agreement with experimental results. The Lagrange multiplier distinguishes between plastic loading and time dependent recrystallisation mechanisms related to subgrain rotation recrystallisation and grain boundary migration recrystallisation. The related Arrhenius type activation functions Cxd and Cxs are defined as
. A nonlinear sigmoidal form [2] is employed that is in agreement with experimental results. The Lagrange multiplier distinguishes between plastic loading and time dependent recrystallisation mechanisms related to subgrain rotation recrystallisation and grain boundary migration recrystallisation. The related Arrhenius type activation functions Cxd and Cxs are defined as
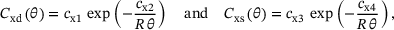 (12)
(12)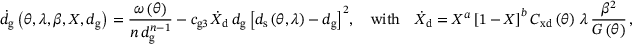 (13)
(13)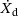 is the plastic loading related recrystallised volume fraction increase rate extracted from (11), and ds is the steady state average grain size. The average grain size growth rate is driven by the grain boundary energy and is temperature activated by an Arrhenius type function
is the plastic loading related recrystallised volume fraction increase rate extracted from (11), and ds is the steady state average grain size. The average grain size growth rate is driven by the grain boundary energy and is temperature activated by an Arrhenius type function 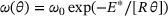 with ω0 the grain size growth rate material parameter and
with ω0 the grain size growth rate material parameter and 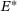 the activation energy for grain size growth. An average grain size growth driven by hardening related energy contributions is not included in Cho et al. [5] and remains for future work.
the activation energy for grain size growth. An average grain size growth driven by hardening related energy contributions is not included in Cho et al. [5] and remains for future work.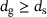 with the temperature dependent steady state average grain size defined as
with the temperature dependent steady state average grain size defined as
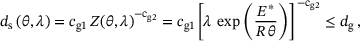 (14)
(14)3 THERMODYNAMICAL CONSISTENCY
 (15)
(15)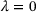 . Inserting this condition into the above inequality results in the static contribution to the reduced mechanical dissipation inequality in the form
. Inserting this condition into the above inequality results in the static contribution to the reduced mechanical dissipation inequality in the form
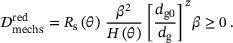 (16)
(16)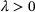 , the initial form of (15) reduces to the dynamic contribution to the reduced mechanical dissipation inequality of the form
, the initial form of (15) reduces to the dynamic contribution to the reduced mechanical dissipation inequality of the form
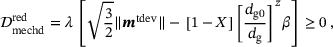 (17)
(17) , together with assuming
, together with assuming  and inserting the yield criterion
and inserting the yield criterion  , cf. (6), into the above inequality results in
, cf. (6), into the above inequality results in
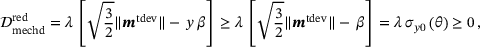 (18)
(18)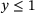 holds. Therefore, thermodynamical consistency is directly obtained for grain size growth controlled hot working processes. For grain size reduction controlled hot working processes, due to
holds. Therefore, thermodynamical consistency is directly obtained for grain size growth controlled hot working processes. For grain size reduction controlled hot working processes, due to 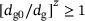 , thermodynamical consistency must be verified manually in terms of showing that
, thermodynamical consistency must be verified manually in terms of showing that 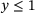 which gives rise to the thermodynamical intercorrelation between the internal variables of recrystallised volume fraction and average grain size. Note that thermodynamical consistency can still be achieved even if the condition
which gives rise to the thermodynamical intercorrelation between the internal variables of recrystallised volume fraction and average grain size. Note that thermodynamical consistency can still be achieved even if the condition  is violated, due the second term in (15) including Rd and Rs potentially compensating negative values of
is violated, due the second term in (15) including Rd and Rs potentially compensating negative values of  in (17). If thermodynamical consistency is obtained, the resulting reduced mechanical dissipations of the form (15) and (16) can be considered as a heat source in hot working and static annealing processes, respectively, which is motivated by the release of hardening related energy contributions.
in (17). If thermodynamical consistency is obtained, the resulting reduced mechanical dissipations of the form (15) and (16) can be considered as a heat source in hot working and static annealing processes, respectively, which is motivated by the release of hardening related energy contributions.4 NUMERICAL EXAMPLES
Based on the proposed hyper-elasticity based recrystallisation formulation and the derived constraint condition for grain size refinement controlled hot working processes, thermodynamical consistency can be verified by analysing representative thermomechanical sequential loading conditions including static annealing and hot working. An algorithmic formulation of the underlying model is obtained by employing an implicit backward Euler time integration for the evolutions of the proportional hardening variable, recrystallised volume fraction and average grain size. For the evolution of the plastic deformation gradient, an implicit exponential time integration scheme is applied that preserves plastic incompressibility and an initial recrystallised volume fraction of 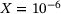 is adopted to ensure numerical stability, cf. (11). For static annealing processes, the coupling between recrystallisation and the proportional hardening rate is achieved by introducing a modified backward Euler time integration scheme, as proposed by Cho et al. [5], of type
is adopted to ensure numerical stability, cf. (11). For static annealing processes, the coupling between recrystallisation and the proportional hardening rate is achieved by introducing a modified backward Euler time integration scheme, as proposed by Cho et al. [5], of type 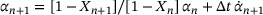 if
if 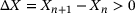 . This formulation accounts for the consumption of original grains during recrystallisation. The resulting effect under hot working conditions on thermodynamical consistency remains for future work.
. This formulation accounts for the consumption of original grains during recrystallisation. The resulting effect under hot working conditions on thermodynamical consistency remains for future work.
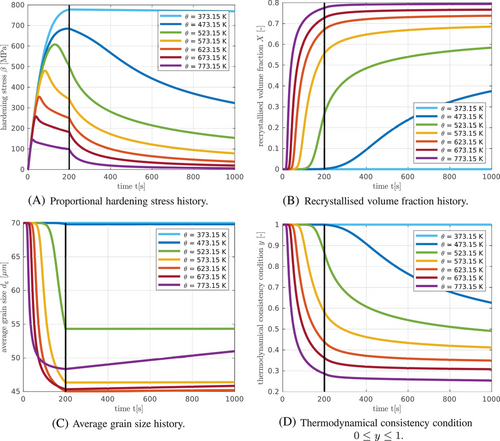
Figure 1 shows the results obtained for a sequential load-unload-hold test using the material parameters listed in Table 1. During a first hot working step, homogeneous states of deformation under uniaxial tension are enforced, followed by an unloading and holding at various temperatures in a second step. The deformation gradient takes the form 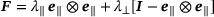 such that a uniaxial tension stress state
such that a uniaxial tension stress state 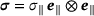 is obtained. The results show a softening effect in the evolution of the hardening stress, see Figure 1A, a sigmoidal evolution of recrystallised volume fraction, see Figure 1B, a grain size reduction followed by grain size growth in Figure 1C and ultimately a thermodynamical consistent response, where the thermodynamical consistency condition is fulfilled during the grain size refinement controlled hot working process, see Figure 1D.
is obtained. The results show a softening effect in the evolution of the hardening stress, see Figure 1A, a sigmoidal evolution of recrystallised volume fraction, see Figure 1B, a grain size reduction followed by grain size growth in Figure 1C and ultimately a thermodynamical consistent response, where the thermodynamical consistency condition is fulfilled during the grain size refinement controlled hot working process, see Figure 1D.
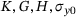 are set constant).
are set constant).| K0 | 135.417 GPa | C13 | 5.098 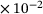 1/MPa 1/MPa |
cx1 | 1.780 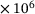 1/MPa 1/MPa |
cg1 | 7.410 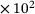 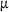 m s m s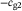 |
a | 8.052 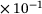 |
| G0 | 48.508 GPa | C14 | 3.963 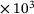 J/mol J/mol |
cx2 | 6.490 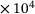 J/mol J/mol |
cg2 | 8.826 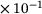 |
b | 3.680 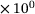 |
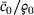 |
0.385 J/[g K] | C17 | 2.487 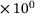 1/[MPa s] 1/[MPa s] |
cx3 | 5.401 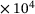 1/[MPa s] 1/[MPa s] |
cg3 | 1.185 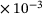 1/ 1/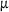 m2 m2 |
c | 4.485 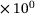 |
| H0 | 8000.0 MPa | C18 | 6.328 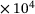 J/mol J/mol |
cx4 | 7.436 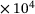 J/mol J/mol |
ω0 | 8.600  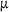 mn/s mn/s |
z | 0.650 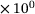 |
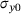 |
200.0 MPa | ϱ0 | 8.96 g/cm3 | cx5 | 5.000 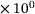 |
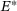 |
8.200 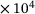 kJ/mol kJ/mol |
n | 2.000 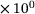 |
5 SUMMARY AND OUTLOOK
The hyper-elasticity based formulation proposed in this work, which builds upon the hypo-elasticity based model by Cho et al. [5], allows for the derivation of a thermodynamical consistency condition. It is shown that this condition effectively constrains the evolution of internal variables, namely the recrystallised dislocation-free volume fraction and average grain size, and gives rise to the thermodynamical intercorrelation between them. When applied to static annealing and grain size growth controlled hot working processes, the model produces thermodynamically consistent and physically sound results, adhering to the second law of thermodynamics. The thermodynamical consistency condition is further investigated under thermomechanical sequential loading conditions for grain size refinement controlled hot working processes. The results demonstrate the capability of the proposed model to thermodynamically accurately predict the microstructural evolution, including the associated recrystallisation effects. The fundamental developments presented in this contribution provide a basis for future research, including potential extensions such as incorporating a Perzyna type ansatz [23] to account for strain rate dependency in the plasticity formulation. In addition, the current framework is to be extended to include a damage formulation [24], where ensuring thermodynamic consistency within the framework will be crucial, particularly when modelling self-healing during recrystallisation.
ACKNOWLEDGMENTS
Financial support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), Project-ID 278868966, TRR 188, is gratefully acknowledged.
Open access funding enabled and organized by Projekt DEAL.




