Fast contact detection for ellipsoids using optimization approaches
Abstract
The paper is concerned with fast and robust contact detection methods for arbitrary ellipsoids. An iterative procedure, namely the Levenberg-Marquardt method, based on the common normal concept for parametric ellipsoids, is employed together with an implementation of the widely used GJK algorithm for comparison. The performance and accuracy of both are analysed and compared to each other on the basis of two test sets, each containing a total of 70 000 pairs of prolates or oblates. Emphasis is placed on the specific error measure relating the iterative solution to the exact one, which was chosen to be the maximum angle between the normal vector and the distance vector between two ellipsoids. The results indicate increased performance when using the Levenberg-Marquardt method over the GJK algorithm with no loss of accuracy.
1 INTRODUCTION
The transport of particles in fluid flow plays an extensive role in both industrial [1] and environmental [2] processes. Spatially resolved simulations of particle-laden flows, considering the interactions between the particles and the fluid as well as among the particles themselves, allow the physics underlying these processes to be studied. Recent simulations of this kind considering sediment transport with ellipsoidal particles indicate a significant influence of the particle shape on the characteristics of the flow [3] as well as on the motion of the particles themselves [4]. These findings were obtained using direct numerical simulations of a channel flow with different ellipsoidal shapes, with the phase-resolved particles being coupled to the fluid using the immersed boundary method (IBM) [5]. While the IBM was employed for fluid-particle coupling, the inter-particle forces were computed using an impulse-based collision model [6] that relies on the knowledge of the points of contact, which were determined using an iterative procedure. It accounts for both, forces created by direct contact between the particle surfaces, as well as lubrication forces. In fact, the latter are highly relevant in such a situation and require the distance between the particle surfaces to be known, even if these do not touch, as this is the input for the lubrication model. A similar approach shall be used in future simulations as well, with a substantially larger number of particles. Hence, an efficient and robust contact detection method for ellipsoids has to be available.
Contact detection methods for ellipsoids can be classified by the definition of the contact points and by the their surface descriptions. Regarding the contact point, either the common normal concept or the geometric potential concept can be applied [7]. The former aims to minimise the Euclidean distance between the two ellipsoids, while the latter minimises the geometric potential. These approaches can be combined with either an implicit or a parametric surface description to generate root-finding or optimisation problems of varying dimension and complexity [8]. It is understood that such a contact detection is employed in cases where particle surfaces are in direct contact, as well as for the situation that the surfaces are still apart but close. In this case the method has to determine the shortest distance between the surfaces, as well as two points, one on each surface, constituting the anchor of the segment realising the closest distance. These points are called contact points here. Ellipsoids are strictly convex, so that a unique set of contact points exists.
It has to be recognised that the multiphase-flow community of researchers has long employed relatively simple algorithms for contact detection, while in the computer graphics community other methods are being used. One of the algorithms widespread in the latter is the Gilbert-Johnson-Keerthi (GJK) algorithm [9]. While generally devised for piecewise linear surfaces it has recently been applied to analytically defined ellipsoids with promising results [10]. For this reason it has been implemented during the present study as well in the same computational framework, so as to allow a comparison of execution times.
In the present contribution, the common normal concept together with a parametric surface description is discussed, with the GJK algorithm as a reference. The methods are tested and compared on large sets of prolate and oblate ellipsoids, providing essential insights into the performance and accuracy of both.
2 METHOD
2.1 Statement of contact problem
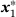 and
and 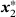 on the surfaces of two ellipsoids
on the surfaces of two ellipsoids 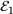 and
and 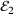 the distance
the distance 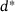 of which is minimal. This requirement can be formulated in terms of the constrained optimization problem as
of which is minimal. This requirement can be formulated in terms of the constrained optimization problem as
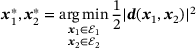 (1)
(1)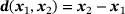 is the vector connecting the two points and
is the vector connecting the two points and 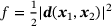 is the objective function to be minimized. The two constraints ensure that the points are located on the surfaces of the respective ellipsoids. To fulfill these conditions, the parametric surface description for ellipsoids
is the objective function to be minimized. The two constraints ensure that the points are located on the surfaces of the respective ellipsoids. To fulfill these conditions, the parametric surface description for ellipsoids 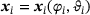 is introduced, with
is introduced, with 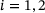 referring to one of the two ellipsoids. This allows transforming the constrained optimization problem into an unconstrained one, that is
referring to one of the two ellipsoids. This allows transforming the constrained optimization problem into an unconstrained one, that is
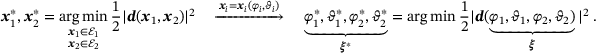 (2)
(2)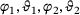 are summarized by the vector
are summarized by the vector 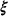 . A necessary condition for an optimal solution to (2) is a vanishing gradient of the objective function. This yields
. A necessary condition for an optimal solution to (2) is a vanishing gradient of the objective function. This yields
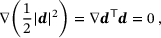 (3)
(3)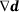 comprises the derivatives of the two points
comprises the derivatives of the two points 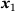 and
and 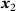 , and the scalar product of each of them with the distance vector
, and the scalar product of each of them with the distance vector 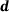 must vanish. This states that the tangent vectors
must vanish. This states that the tangent vectors
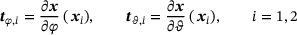 (4)
(4)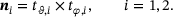 (5)
(5)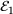 and
and  .
.
 and
and 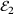 together with the exact contact points in the context of the common normal concept. Both contact points have to share the same normal vector, apart from orientation, resulting in the requirement that each normal vector has to be co-linear to the distance vector.
together with the exact contact points in the context of the common normal concept. Both contact points have to share the same normal vector, apart from orientation, resulting in the requirement that each normal vector has to be co-linear to the distance vector.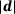 , indeed, assumes a minimum and not a maximum can be rephrased into restrictions on the direction of the vector d with respect to the normal vectors n1 and n2 at the two contact points that is
, indeed, assumes a minimum and not a maximum can be rephrased into restrictions on the direction of the vector d with respect to the normal vectors n1 and n2 at the two contact points that is
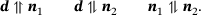 (6)
(6)2.2 Solution procedure
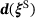 , successive positions
, successive positions 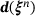 are determined, using the step
are determined, using the step 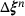 to decrease f. For the present study, this was achieved by employing the Levenberg-Marquardt algorithm [11], resulting in
to decrease f. For the present study, this was achieved by employing the Levenberg-Marquardt algorithm [11], resulting in
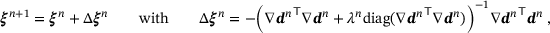 (7)
(7)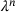 . The latter is updated in every step based on the model quality, which relates the actual change in the objective function
. The latter is updated in every step based on the model quality, which relates the actual change in the objective function 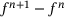 to the predicted change. The initial condition of the iterations is obtained from connecting the centers of the two ellipsoids and taking the intersection points of the two ellipsoids and the vector connecting their centers.
to the predicted change. The initial condition of the iterations is obtained from connecting the centers of the two ellipsoids and taking the intersection points of the two ellipsoids and the vector connecting their centers.2.3 Convergence criterion
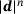 between the two ellipsoids is sufficiently close to the exact distance
between the two ellipsoids is sufficiently close to the exact distance 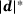 , such that
, such that 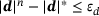 . Since
. Since 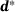 is not known for an arbitrary arrangement of two ellipsoids, the difference must be estimated. This estimation is realized using quantities which are readily given in each iteration of the solution procedure. Considering condition (6), the maximum angle between one of the two normal vectors and the distance vector
is not known for an arbitrary arrangement of two ellipsoids, the difference must be estimated. This estimation is realized using quantities which are readily given in each iteration of the solution procedure. Considering condition (6), the maximum angle between one of the two normal vectors and the distance vector 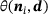 was chosen as the convergence criterion, such that the solution procedure is terminated if
was chosen as the convergence criterion, such that the solution procedure is terminated if
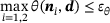 (8)
(8)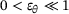 , and the final iteration called N.
, and the final iteration called N.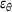 are considered. One is based on the scalar product
are considered. One is based on the scalar product
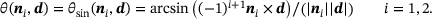 (9)
(9)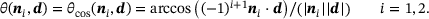 (10)
(10)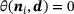 .
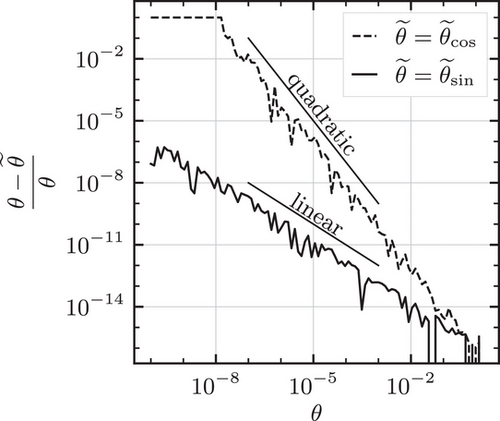
.The two possible implementations were evaluated in terms of their accuracy. For this reason, a test setup was constructed, as shown in Figure 2, and the relative error for the two implementations analysed for decreasing angles θ. To make the test more difficult, the parameter k was introduced making one of the vectors very short in all tests reported, with 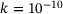 . It turned out, however, that the results did not change when
. It turned out, however, that the results did not change when 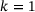 was employed.
was employed.
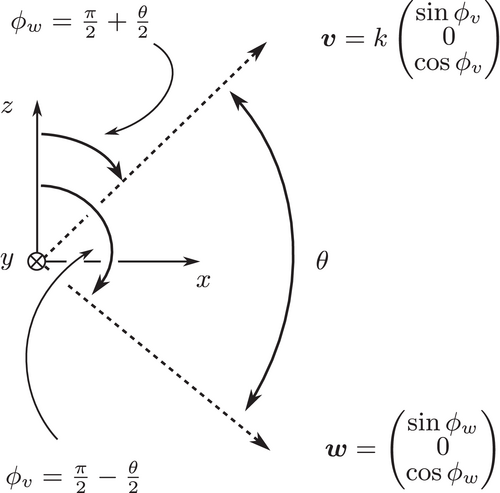
 and
and 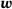 with the length of the former multiplied by k.
with the length of the former multiplied by k.The diagram in Figure 3 shows a linear increase in the relative error for decreasing angle when using (9). With (10), quadratic behaviour is observed. For very small angles, the relative error might be considered too large for being used in a complex multiphase computation. It is therefore necessary to assess whether this effect has an actual impact on the overall performance and accuracy of the contact detection method.
 , where
, where  and
and  refer to the vector product and the scalar product computation, respectively.
refer to the vector product and the scalar product computation, respectively.3 SETUP
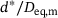 , each containing a total of 104 pairs of ellipsoids. The sphericity
, each containing a total of 104 pairs of ellipsoids. The sphericity 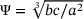 according to Krumbein [13] of the ellipsoids was fixed at
according to Krumbein [13] of the ellipsoids was fixed at 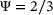 to agree with the simulations of Jain et al. [3]. This leads to two cases, a case of oblate ellipsoids and a case of prolate ellipsoids. For each individual pair, the mean equivalent diameter
to agree with the simulations of Jain et al. [3]. This leads to two cases, a case of oblate ellipsoids and a case of prolate ellipsoids. For each individual pair, the mean equivalent diameter 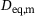 and the ratio of equivalent diameters
and the ratio of equivalent diameters 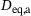 were drawn from a logarithmic uniform distribution. Then the three semi-axes
were drawn from a logarithmic uniform distribution. Then the three semi-axes 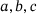 of the two ellipsoids were constructed based on Ψ,
of the two ellipsoids were constructed based on Ψ, 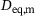 ,
, 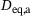 , resulting in ellipsoids of different size and shape. In addition to the computed distance
, resulting in ellipsoids of different size and shape. In addition to the computed distance 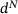 and the contact points
and the contact points 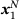 and
and 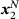 after the final iteration, different error measures were determined to evaluate the accuracy of the procedure. Since the contact points are exactly known by construction, it is straightforward to compare these exact quantities with the solutions of the iterative procedure. The following measures were determined:
after the final iteration, different error measures were determined to evaluate the accuracy of the procedure. Since the contact points are exactly known by construction, it is straightforward to compare these exact quantities with the solutions of the iterative procedure. The following measures were determined:
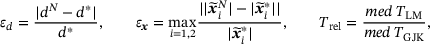 (11)
(11)4 RESULTS
4.1 Prolate-prolate contact
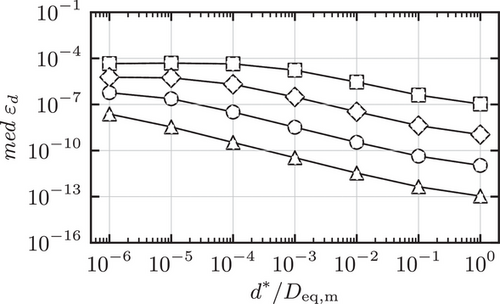
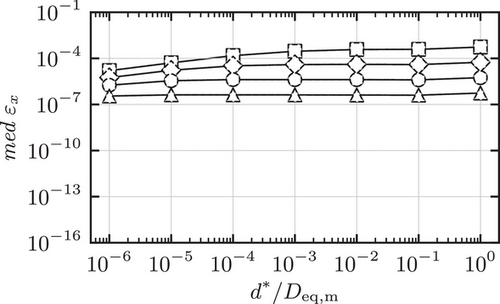
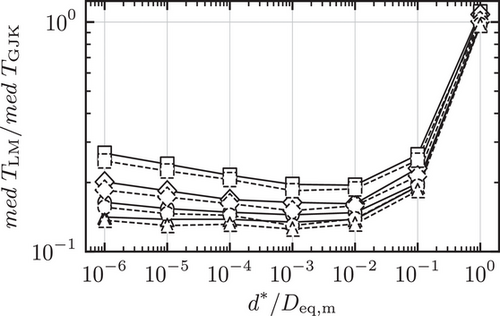
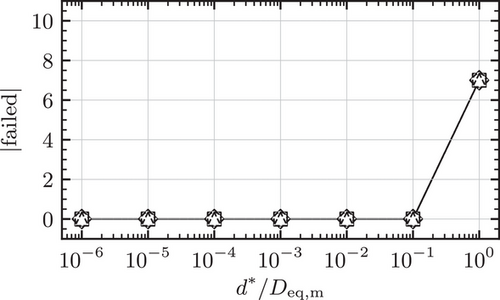
The results for the medians of the measures (11) for the pairs of prolates are shown in Figure 4, 5 and 6 together with an evaluation of the robustness in Figure 7. In some of the figures only a single curve can be discerned, since continuous and broken lines strictly overlap.

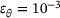 ,
, 
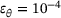 , ◯
, ◯ 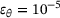 , △
, △ 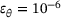 and
and 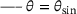 and
and 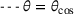 .
.

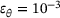 ,
, 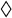
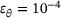 , ◯
, ◯ 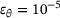 , △
, △ 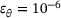 and
and 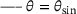 and
and 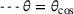 .
.

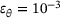 ,
, 
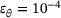 , ◯
, ◯ 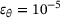 , △
, △ 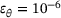 and
and 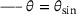 and
and 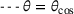 .
.

 ,
, 
 , ◯
, ◯ 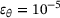 , △
, △ 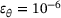 and
and 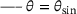 and
and 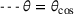 .
.The findings justify the utilization of the angle 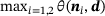 as the error measure for the iterative procedure, which can be observed in Figure 4 and 5. In the calculations performed, the medians of the maximum angles correspond to both the error in the distance
as the error measure for the iterative procedure, which can be observed in Figure 4 and 5. In the calculations performed, the medians of the maximum angles correspond to both the error in the distance 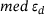 and the error in the contact points
and the error in the contact points 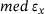 . Moreover,
. Moreover, 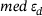 decreases monotonically as the distance
decreases monotonically as the distance 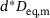 increases, while
increases, while 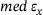 remains approximately constant. This is due to the definition of
remains approximately constant. This is due to the definition of 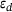 , given in (11). In addition, Figure 6 reveals that the Levenberg-Marquardt algorithm converges significantly faster than the GJK algorithm for small distances
, given in (11). In addition, Figure 6 reveals that the Levenberg-Marquardt algorithm converges significantly faster than the GJK algorithm for small distances 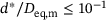 , while the opposite behavior is observed for distances
, while the opposite behavior is observed for distances 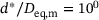 . Such cases, however, are not of interest, since the distances are too large to be needed in a true simulation with ellipsoids of this sphericity. The robustness of the Levenberg-Marquardt algorithm is illustrated in Figure 7. It is in accordance to the evaluation of the computation time since it reveals a guaranteed convergence for distances
. Such cases, however, are not of interest, since the distances are too large to be needed in a true simulation with ellipsoids of this sphericity. The robustness of the Levenberg-Marquardt algorithm is illustrated in Figure 7. It is in accordance to the evaluation of the computation time since it reveals a guaranteed convergence for distances 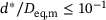 . Finally, the algorithm failed to converge in 9 out of 10000 cases for which
. Finally, the algorithm failed to converge in 9 out of 10000 cases for which 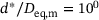 , corresponding to a percentage of 0.09%. If this should occur in an application appropriate measures can be taken, such as an under-relaxation of the increment, etc.
, corresponding to a percentage of 0.09%. If this should occur in an application appropriate measures can be taken, such as an under-relaxation of the increment, etc.
4.2 Oblate-oblate contact
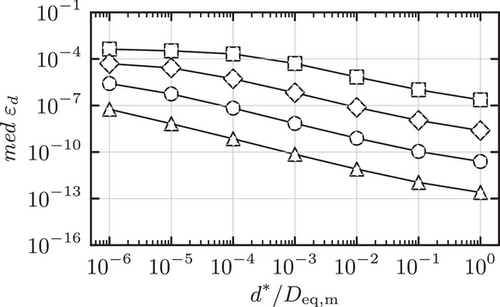
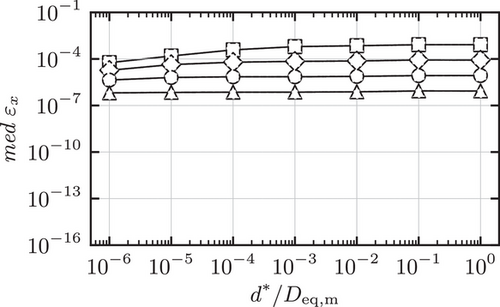
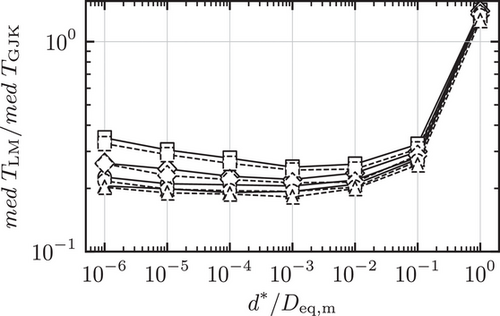
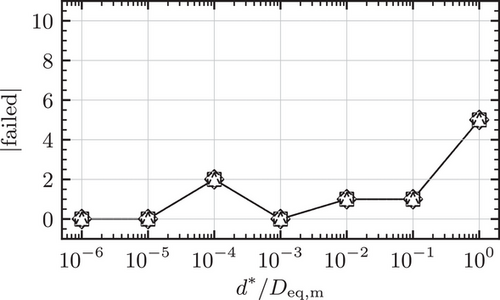
The results for the medians of the measures (11) for the oblates are presented in the same way as the results of the prolates. This is shown in Figure 8, 9 and 10 together with the assessment of the robustness in Figure 11.

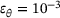 ,
, 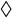
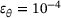 , ◯
, ◯ 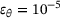 , △
, △ 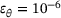 and
and 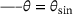 and
and  .
.

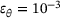 ,
, 
 , ◯
, ◯ 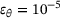 , △
, △ 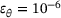 and
and  and
and 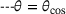 .
.

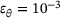 ,
, 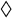
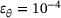 , ◯
, ◯ 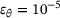 , △
, △ 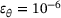 and
and 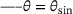 and
and 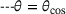 .
.

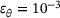 ,
, 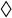
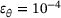 , ◯
, ◯ 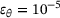 , △
, △ 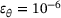 and
and 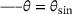 and
and 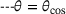 .
.A very similar pattern to the above case can be observed as well, with the Levenberg-Marquardt algorithm failing to converge to the contact points in only 4 cases for 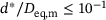 . These cases can be addressed as indicated above. Hence, it can be concluded that the medians of the relative performance and accuracy of the algorithms are independent of the specific configuration of the ellipsoids with the given shapes, for the given sphericity.
. These cases can be addressed as indicated above. Hence, it can be concluded that the medians of the relative performance and accuracy of the algorithms are independent of the specific configuration of the ellipsoids with the given shapes, for the given sphericity.
5 CONCLUSIONS
Two contact detection methods, namely a parametric common normal concept solved with the Levenberg-Marquardt algorithm as well as the GJK algorithm, have been employed. Two test sets, each containing a total of 70 000 pairs of prolates or oblates, respectively, were constructed with varying distance, orientation and volume. These were used to compare the two contact detection methods in terms of performance and accuracy.
The Levenberg-Marquardt algorithm converged to the contact points in over 99.9% of the test cases.
The results indicate increased performance of the Levenberg-Marquardt algorithm over the GJK algorithm. The accuracy exhibits no significant differences, since the same convergence criterion was used for both algorithms and the iterations pursued until this criterion was met. The computation time, however, was shorter by a factor of 3 to 6 for distances around and below a tenth of the mean equivalent diameter. For larger distances the algorithm is still faster than GJK, until the order of magnitude of the equivalent diameter is reached, a situation not of interest in a multiphase flow simulation, since lubrication forces, for example, vanish at such a distance. The present results are being extended to further cases and further algorithms in ongoing work.
ACKNOWLEDGMENTS
The authors thank the Center for Information Services and High Performance Computing (ZIH), TU Dresden, Germany, for providing the computational resources and support. RR gratefully acknowledges the scholarship provided by the Free State of Saxony, No. L-202214 as well as the financial support from the TU Dresden Graduate Academy, financed by federal and state funds.
Open access funding enabled and organized by Projekt DEAL.




