SLEQP: An open-source package for nonlinear programming
Abstract
We present SLEQP, an open source C-package consisting of an active-set method capable of solving large-scale nonlinear programming (NLP) problems based on successive linear programming and equality constrained quadratic programming techniques. The method includes a feasibility restoration phase and second-order corrections (SOCs), achieving robust practical performance. It has also been adapted for the special cases of unconstrained optimization, box-constrained problems, and nonlinear least squares problems and contains interfaces to both Python and MATLAB. To demonstrate the performance of the package, we perform a computational study based on the well-known CUTest suite of NLP problems.
1 INTRODUCTION
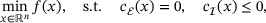 (NLP)
(NLP)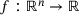 and the constraints
and the constraints 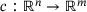 are twice differentiable functions and
are twice differentiable functions and 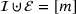 . Our goal is to find a point
. Our goal is to find a point 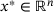 satisfying first-order optimality conditions with suitable multipliers
satisfying first-order optimality conditions with suitable multipliers 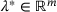 , that is,
, that is,
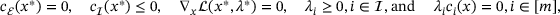 (1)
(1)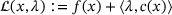 denotes the Lagrangian of (NLP). We begin in Section 2 by describing the algorithm and proceed to provide details of the implementation in Section 3. We conduct numerical experiments in Section 4 and conclude in Section 5.
denotes the Lagrangian of (NLP). We begin in Section 2 by describing the algorithm and proceed to provide details of the implementation in Section 3. We conduct numerical experiments in Section 4 and conclude in Section 5.2 ALGORITHM
To solve (NLP), we employ the algorithmic framework introduced in ref. [9]. The approach is iterative, generating a sequence  based on an initial point
based on an initial point 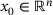 . It uses the (exact) penalty function
. It uses the (exact) penalty function 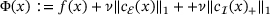 , where
, where 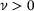 is a penalty parameter and
is a penalty parameter and 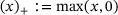 . An iteration consist of multiple phases, used to compute a step leading to the next iterate as well as an estimate of the required multipliers for the Lagrangian.
. An iteration consist of multiple phases, used to compute a step leading to the next iterate as well as an estimate of the required multipliers for the Lagrangian.
LP phase
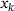 is computed by minimizing the piecewise linear approximation
is computed by minimizing the piecewise linear approximation
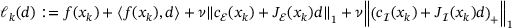 (2)
(2)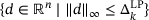 . This optimization problem can be reformulated into a linear program (LP) to be solved by state-of-the-art LP solvers:
. This optimization problem can be reformulated into a linear program (LP) to be solved by state-of-the-art LP solvers:
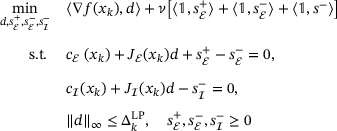 (LP)
(LP) and
and 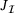 are the matrices composed of the gradients of the equality and inequality constraints respectively. Note that this program is always feasible and bounded, and therefore guaranteed to have an optimal solution. What is more, the solution of (LP) is connected to first-order optimality conditions (see ref. [11]): Iterate
are the matrices composed of the gradients of the equality and inequality constraints respectively. Note that this program is always feasible and bounded, and therefore guaranteed to have an optimal solution. What is more, the solution of (LP) is connected to first-order optimality conditions (see ref. [11]): Iterate 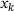 is first-order optimal iff the criticality
is first-order optimal iff the criticality 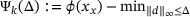 is zero for some
is zero for some 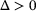 . Indeed, it can be shown [12] that the series of iterates
. Indeed, it can be shown [12] that the series of iterates 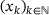 satisfies
satisfies 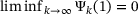 , implying the existence of a first-order optimal accumulation point
, implying the existence of a first-order optimal accumulation point 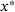 .
.Working set identification
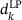 but also a row basis
but also a row basis 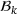 , that is, a subset of
, that is, a subset of 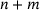 of the constraints of (LP) such that
of the constraints of (LP) such that  is the unique solution of the system of rows in
is the unique solution of the system of rows in 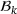 against the corresponding right hand side. Due to the structure of the constraints of (LP) the basis
against the corresponding right hand side. Due to the structure of the constraints of (LP) the basis 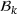 must contain at least one of the two rows involving each of the variables in
must contain at least one of the two rows involving each of the variables in 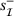 and two involving each pair of variables in
and two involving each pair of variables in 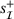 and
and 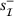 respectively. A working set
respectively. A working set  is constructed from the basis, which includes
is constructed from the basis, which includes
- 1.
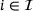 iff both of the rows
iff both of the rows 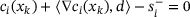 and
and 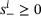 are contained in
are contained in 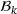 , and
, and - 2.
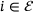 iff all three of the rows
iff all three of the rows 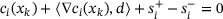 ,
, 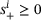 , and
, and  are contained in
are contained in 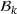 .
.
Simple linear algebra shows that the rows of the constraint Jacobian, 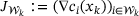 , defined in terms of the rows associated with
, defined in terms of the rows associated with 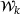 , has full (row) rank of
, has full (row) rank of 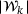 . As we will see later, this identification of the working set makes the subsequent identification of the multipliers substantially easier.
. As we will see later, this identification of the working set makes the subsequent identification of the multipliers substantially easier.
Cauchy direction
The Cauchy direction is obtained by optimizing a quadratic model of Φ, given by 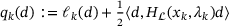 along the interval
along the interval 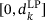 . Here, the Hessian
. Here, the Hessian 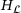 of the Lagrangian can be either exact or a quasi Newton approximation, while the multipliers
of the Lagrangian can be either exact or a quasi Newton approximation, while the multipliers  will be introduced later. This one-dimensional optimization problem can be solved exactly, given that
will be introduced later. This one-dimensional optimization problem can be solved exactly, given that 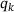 is known to be piecewise quadratic, or based on an inexact Armijo-type line search, yielding the Cauchy direction
is known to be piecewise quadratic, or based on an inexact Armijo-type line search, yielding the Cauchy direction 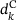 . Recall that a trust-region method based on Cauchy steps alone is already convergent [5, Chapter 6].
. Recall that a trust-region method based on Cauchy steps alone is already convergent [5, Chapter 6].
Dual estimation
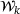 can be formulated as a quadratic problem:
can be formulated as a quadratic problem:
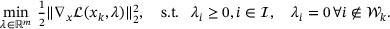 (3)
(3)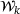 , whereas the inequality constraint makes the estimation significantly more complicated. We can simplify the problem by disregarding the constraints, leading to a linear least squares problem, which can be optimized by solving the system
, whereas the inequality constraint makes the estimation significantly more complicated. We can simplify the problem by disregarding the constraints, leading to a linear least squares problem, which can be optimized by solving the system
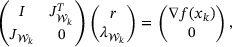 (4)
(4)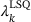 of inequality constraints to zero. Note that due to
of inequality constraints to zero. Note that due to 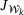 having full rank, the linear system in (4) is regular.
having full rank, the linear system in (4) is regular.EQP phase
In order to enable locally quadratic convergence, an equality-constrained quadratic programming (EQP) phase can be added to the algorithm, yielding an EQP step 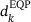 used to augment the Cauchy step. Its goal is two-fold: For one, we aim at finding a stationary point of the Lagrangian, for another, we want to decrease the violation of the nonlinear constraints. The classical trust-region subproblem [5, Chapter 7] is concerned with the optimization of quadratic problems subject to a trust-region constraint of the form
used to augment the Cauchy step. Its goal is two-fold: For one, we aim at finding a stationary point of the Lagrangian, for another, we want to decrease the violation of the nonlinear constraints. The classical trust-region subproblem [5, Chapter 7] is concerned with the optimization of quadratic problems subject to a trust-region constraint of the form 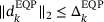 . The subproblem, having been studied extensively, has a rich structure which can be exploited to yield highly efficient and readily available algorithms such as refs. [13, 14], based on Krylov methods.
. The subproblem, having been studied extensively, has a rich structure which can be exploited to yield highly efficient and readily available algorithms such as refs. [13, 14], based on Krylov methods.
An obvious choice regarding the objective is the function 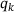 introduced above. It is however necessary to deal with the non-smoothness of
introduced above. It is however necessary to deal with the non-smoothness of 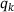 . In particular,
. In particular, 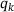 has kinks whenever any
has kinks whenever any 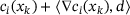 passes zero. To alleviate this problem, we fix the variables in
passes zero. To alleviate this problem, we fix the variables in 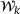 to their respective bounds by requiring that
to their respective bounds by requiring that 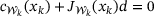 . We can decompose
. We can decompose 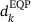 into
into 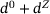 , where d0 is the orthogonal projection of the zero vector onto the set feasible set and
, where d0 is the orthogonal projection of the zero vector onto the set feasible set and 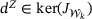 .
.
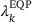 based on the dual estimation with additional penalties added for the constraints violated at d0. Specifically, we let
based on the dual estimation with additional penalties added for the constraints violated at d0. Specifically, we let
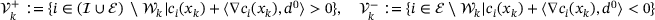
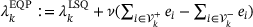 . To compute the initial solution, the projection onto the feasible set can be computed by optimizing another least squares problem, which reduces to solving (4) against a different right hand side. To ensure that
. To compute the initial solution, the projection onto the feasible set can be computed by optimizing another least squares problem, which reduces to solving (4) against a different right hand side. To ensure that 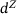 remains in the kernel of
remains in the kernel of 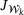 , if is sufficient to project the steps in the respective Krylov spaces back onto the kernel, which once more involves the solution of (4).
, if is sufficient to project the steps in the respective Krylov spaces back onto the kernel, which once more involves the solution of (4).Finally, special care must be taken when the initial projection d0 is not feasible with respect to the trust region constraint. In this case the trust-region subproblem as formulated above is infeasible itself. A simple workaround is to relax the linear feasibility requirements.
Step acceptance
The step 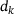 to be ultimately used is computed based on the Cauchy and EQP steps
to be ultimately used is computed based on the Cauchy and EQP steps 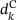 and
and 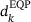 using a line search as before. The step is tested against the original model, yielding the reduction ratio
using a line search as before. The step is tested against the original model, yielding the reduction ratio 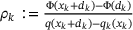 . The step is accepted iff
. The step is accepted iff 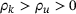 and rejected otherwise. In the former case, we set
and rejected otherwise. In the former case, we set 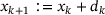 , in the latter we keep
, in the latter we keep 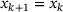 . Optionally, a second-order correction (SOC) is computed based on the system (4) to avoid the Maratos effect [15]. Next, the trust-region radii
. Optionally, a second-order correction (SOC) is computed based on the system (4) to avoid the Maratos effect [15]. Next, the trust-region radii  and
and 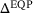 are updated (see ref. [9] for details). In terms of the LP trust radius, any update needs to satisfy certain conditions to ensure convergence [5, Chapter 6], while the EQP trust radius can be chosen more liberally. Similarly, the penalty parameter ν can be periodically updated in order to improve convergence speed.
are updated (see ref. [9] for details). In terms of the LP trust radius, any update needs to satisfy certain conditions to ensure convergence [5, Chapter 6], while the EQP trust radius can be chosen more liberally. Similarly, the penalty parameter ν can be periodically updated in order to improve convergence speed.
3 IMPLEMENTATION
The SLEQP package1 has been implemented in the C programming language. To solve the subproblems introduced above, several dependent packages are used. Specifically, linear programs are solved using an LP solver (such as HiGHS [16], Gurobi [17], or SoPlex [18]), and the systems (4) are factorized using codes such as UMFPACK [19], MUMPS [20], or others. To solve the EQP, we use either the TRLIB [14] code or an implementation of Steihaug's truncated conjugate gradient algorithm [21]. Since both approaches are iterative, we only require the map 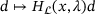 , that is, products with the Hessian of the Lagrangian rather than the entire matrix.
, that is, products with the Hessian of the Lagrangian rather than the entire matrix.
In the following, we examine certain aspects of the implementation, including both those being challenges to be overcome and algorithmic improvements result in benefits with respect to running time and robustness.
Working set identification
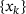 is guaranteed, the working sets
is guaranteed, the working sets 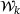 and the resulting multipliers
and the resulting multipliers 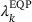 are not guaranteed to result in correct residuals that is,
are not guaranteed to result in correct residuals that is, 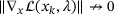 in general. The problem is particularly pronounced in problems without constraint qualification. Consider for example, the problem
in general. The problem is particularly pronounced in problems without constraint qualification. Consider for example, the problem
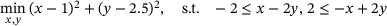
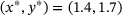 , which does not satisfy qualifications such as the Linear Independence (LICQ) / Mangasarian-Fromovitz (MFCQ) constraint qualifications. The resulting (LP) at the optimal solution with a suitable trust region of say
, which does not satisfy qualifications such as the Linear Independence (LICQ) / Mangasarian-Fromovitz (MFCQ) constraint qualifications. The resulting (LP) at the optimal solution with a suitable trust region of say 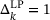 and a sufficiently large penalty parameter ν has two optimal bases, containing one of the two respective linear constraints, yielding two different working sets. The multipliers obtained from (3) are 0.8 and 0 respectively. While the former choice ensures a vanishing Lagrangian gradient, the latter does not. Since termination criteria are often based on this gradient, the solver never terminates, even though it has reached an optimum. What is more, the incorrect multipliers may also impede the effectiveness of the EQP phase, leading to poor convergence. If an LP has multiple optimal bases, it is generally considered an implementation detail which of these bases is returned by an LP solver. Therefore, the behavior of our algorithm attempting to solve (LP) can change significantly, even between different versions of an underlying LP solver.
and a sufficiently large penalty parameter ν has two optimal bases, containing one of the two respective linear constraints, yielding two different working sets. The multipliers obtained from (3) are 0.8 and 0 respectively. While the former choice ensures a vanishing Lagrangian gradient, the latter does not. Since termination criteria are often based on this gradient, the solver never terminates, even though it has reached an optimum. What is more, the incorrect multipliers may also impede the effectiveness of the EQP phase, leading to poor convergence. If an LP has multiple optimal bases, it is generally considered an implementation detail which of these bases is returned by an LP solver. Therefore, the behavior of our algorithm attempting to solve (LP) can change significantly, even between different versions of an underlying LP solver.The problem of identifying an active set has been examined and can be solved exactly using an integer program [22]. Of course, such an approach is intractable in general. A simpler enhancement of the original approach, implemented in SLEQP, consists of fixing the variables 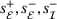 to their solutions in (LP), and to resolve the LP for the remaining variables d in order to obtain a row basis in
to their solutions in (LP), and to resolve the LP for the remaining variables d in order to obtain a row basis in 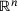 which can be directly turned into a working set. Of course, such a resolve is often unnecessary. An indicator for a problem such as introduced above to occur is that LP rows which are active, that is, having nonzero multipliers in the LP, are excluded during the standard working set identification.
which can be directly turned into a working set. Of course, such a resolve is often unnecessary. An indicator for a problem such as introduced above to occur is that LP rows which are active, that is, having nonzero multipliers in the LP, are excluded during the standard working set identification.
Local infeasibility
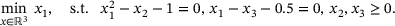
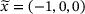 , at which point the solution step
, at which point the solution step 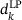 of (LP) becomes the zero vector, indicating a local optimum of Φ. Following this, no further progress is made. Recall that this is not a theoretical contradiction: First-order optimal points of (NLP) are local minima of the penalty function Φ, but not all local optima of Φ need to be feasible.
of (LP) becomes the zero vector, indicating a local optimum of Φ. Following this, no further progress is made. Recall that this is not a theoretical contradiction: First-order optimal points of (NLP) are local minima of the penalty function Φ, but not all local optima of Φ need to be feasible.One attempt to escape such points is to include a so-called restoration phase, used in filter–SQP algorithms [6], in which the original objective is discarded in favor of a term designed to solely reduce a measure of infeasibility, such as 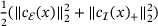 . Switching between restoration and optimization phases ensures convergence to a local optimum for the particular instance introduced above.
. Switching between restoration and optimization phases ensures convergence to a local optimum for the particular instance introduced above.
Preprocessing
Preprocessing techniques have been widely studied in the context of linear or quadratic programming problems [24], where the richer problem structure enables significant speed ups. For general nonlinear programs of type (NLP), there is less structure to be exploited during preprocessing. The general constraints c do however often include bound constraints of the type 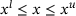 for
for 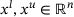 as well as linear constraints of the form
as well as linear constraints of the form 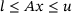 for
for  ,
, 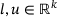 . If the presence of these types of constraints are made available to the solver, some forms of preprocessing, such as discarding redundant linear constraints or removing fixed variables, are possible. The test suite used in the numerical experiments in Section 4 contains several instances where a significant portion of variables is fixed, such as the A0ENDNDL instance, where 35 000 of the about 60 000 variables are fixed. Removing the fixed variables during preprocessing about halves the required solution time. Similar effects are likely to occur on computer-generated instances.
. If the presence of these types of constraints are made available to the solver, some forms of preprocessing, such as discarding redundant linear constraints or removing fixed variables, are possible. The test suite used in the numerical experiments in Section 4 contains several instances where a significant portion of variables is fixed, such as the A0ENDNDL instance, where 35 000 of the about 60 000 variables are fixed. Removing the fixed variables during preprocessing about halves the required solution time. Similar effects are likely to occur on computer-generated instances.
Least-squares problems
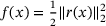 . Clearly, its gradient is given by
. Clearly, its gradient is given by 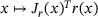 and its Hessian may be approximated using the Gauss-Newton term
and its Hessian may be approximated using the Gauss-Newton term 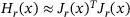 , which becomes increasingly accurate when approaching a critical point with a small objective, that is, a small residual. We make algorithmic use of this particular structure by using the Gauss-Newton approximation in the EQP phase instead of the Lagrangian of the Hessian. Due to the iterative nature of our trust region solvers, we only require callbacks to compute the residuals
, which becomes increasingly accurate when approaching a critical point with a small objective, that is, a small residual. We make algorithmic use of this particular structure by using the Gauss-Newton approximation in the EQP phase instead of the Lagrangian of the Hessian. Due to the iterative nature of our trust region solvers, we only require callbacks to compute the residuals 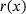 as well as forward and adjoint sweeps with respect to the Jacobian
as well as forward and adjoint sweeps with respect to the Jacobian 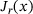 . As an alternative to the standard EQP objective, we offer the computation of a step d obtained by solving the following linear least-squares problem
. As an alternative to the standard EQP objective, we offer the computation of a step d obtained by solving the following linear least-squares problem
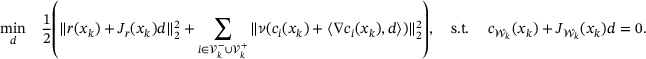
 using LSQR iterations.
using LSQR iterations.4 NUMERICAL EXPERIMENTS
We evaluate our implementation based on the CUTEst [26] suite of 1 156 optimization problems. All experiments were ran on an AMD EPYC 7742 workstation clocked at up to 3.4 GHz. We compare our implementation against Ipopt 3.11, an open-source interior point method, and Knitro 13.20, a commercial solver, using interior point or quadratic programming algorithms depending on problem structure. In our implementation, we use Gurobi 9.0.0 as LP solver and UMFPACK 5.7.8 to factorize the systems (4).
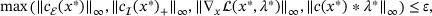
 . The results, depicted in Figure 1, show the cumulative sum of instances solved over time. As can be seen, SLEQP performs reasonably well, even though it still seems to lack some stability compared to the more established packages, solving a total of 869 instances, compared to the 1 003 solved by Ipopt and the 967 solved by Knitro. The results are broken down in Table 1, where we see that, compared to Knitro, our implementation so far mainly struggles with larger instances: where the percentage of instances solved is virtually identical for the very small instances, that percentage differs by about 40 percentage points for the large instances. On the other hand, some improvements may be within reach when considering the small instances, with a difference of more than 10 percentage points. While a successful solution of the large instances may require advances in computing factorizations and solving linear programs, the lower performance of our implementation on the small instances suggest that improvements with respect to numerical robustness are possible.
. The results, depicted in Figure 1, show the cumulative sum of instances solved over time. As can be seen, SLEQP performs reasonably well, even though it still seems to lack some stability compared to the more established packages, solving a total of 869 instances, compared to the 1 003 solved by Ipopt and the 967 solved by Knitro. The results are broken down in Table 1, where we see that, compared to Knitro, our implementation so far mainly struggles with larger instances: where the percentage of instances solved is virtually identical for the very small instances, that percentage differs by about 40 percentage points for the large instances. On the other hand, some improvements may be within reach when considering the small instances, with a difference of more than 10 percentage points. While a successful solution of the large instances may require advances in computing factorizations and solving linear programs, the lower performance of our implementation on the small instances suggest that improvements with respect to numerical robustness are possible.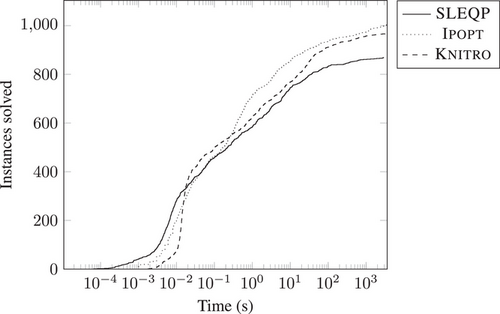
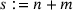 .
.| Size | #Instances | % Solved | ||
|---|---|---|---|---|
| SLEQP | Knitro | |||
| VS | (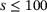 ) ) |
453 | 93.59823399558499 | 93.81898454746137 |
| S | (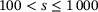 ) ) |
134 | 67.16417910447761 | 79.1044776119403 |
| M | (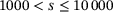 ) ) |
354 | 69.49152542372882 | 74.85875706214689 |
| L | (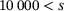 ) ) |
215 | 50.697674418604656 | 79.53488372093022 |
Notably however, some improvements are more difficult to achieve for an NLP solver. For example, we observe on several CUTEst instances that it is not possible to evaluate the objective f or the constraints c, or their respective derivatives at certain iterates 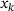 . Specifically, the CUTEst library returns values of
. Specifically, the CUTEst library returns values of 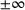 or produces floating point errors during evaluations. Since we do not know the actual domain where objective and constraints can be successfully evaluated, our code terminates once any such errors occur.
or produces floating point errors during evaluations. Since we do not know the actual domain where objective and constraints can be successfully evaluated, our code terminates once any such errors occur.
5 CONCLUSION AND FUTURE WORK
We have presented an open-source implementation of an existing, well-known active-set based NLP algorithm. We have addressed some of the practical problems appearing in real-world problems of the CUTEst suite as well as possible solutions to increase the robustness of our code even in the absence of usual regularity assumptions. The numerical results of the implementation are promising, even though they are not quite on par with Ipopt and Knitro.
Regarding future work, we expect that significant improvements particularly with respect to robustness can be made by examining the small instances of the CUTEst suite and making suitable algorithmic adjustments. In regards to improving the performance, we plan to follow similar approaches as laid out in ref. [9]. In particular, a closer integration with existing LP solvers could significantly increase performance. In early iterations for example, solving the LP to optimality is likely unnecessary. What is more, it may be beneficial to maintain a factorization of the linear system over several iterations when iterates approach a stationary point and derivatives and active sets stabilize. Lastly, we are confident that the dual estimation presented above can be improved by computing iterative improvements to the unconstrained estimation problem rather than simply clipping the resulting multipliers to be consistent with the working set.
ACKNOWLEDGMENTS
Open access funding enabled and organized by Projekt DEAL.




