PAMM
Volume 23, Issue 4 e202300203
RESEARCH ARTICLE
Open Access

Shape-optimization of extrusion-dies via parameterized physics-informed neural networks

Steffen Tillmann, 

Corresponding Author

Steffen Tillmann

Chair for Computational Analysis of Technical Systems, RWTH Aachen University, Aachen, Germany

Correspondence

Steffen Tillmann, Chair for Computational Analysis of Technical Systems, RWTH Aachen University, Schinkelstr. 2, 52062 Aachen, Germany.

Email: [email protected]

Search for more papers by this author
Daniel Hilger, 

Daniel Hilger

Chair for Computational Analysis of Technical Systems, RWTH Aachen University, Aachen, Germany

Search for more papers by this author
Norbert Hosters, 

Norbert Hosters

Chair for Computational Analysis of Technical Systems, RWTH Aachen University, Aachen, Germany

Search for more papers by this author
Stefanie Elgeti, 

Stefanie Elgeti

Chair for Computational Analysis of Technical Systems, RWTH Aachen University, Aachen, Germany

Institute for Lightweight Design and Structural Biomechanics, Tu Wien, Vienna, Austria

Search for more papers by this author
First published: 20 November 2023
https://doi.org/10.1002/pamm.202300203

Abstract

In this paper, we present an approach to efficiently optimize the design of extrusion dies. Extrusion dies, which are relevant to the manufacturing process of plastics profile extrusion, traditionally require time-consuming iterations between manual testing and die adjustments. As an alternative, numerical optimization can be used to obtain a high quality initial design and thereby reduce the number of adjustments to the actual die. However, numerical optimization can be computationally expensive, so the use of surrogate models can be helpful to improve efficiency. The latter is the goal of this work. Our method uses physics-informed neural networks (PINNs) that directly incorporate a free-form deformation (FFD) approach to allow for geometric variations. The FFD approach allows for a wide range of domain deformations, while the fully trained PINN ensures fast evaluation of the objective function. Using a two-dimensional model of an extrusion die for demonstration, we detail the integration of the FFD method into the PINN model and discuss its potential in the three-dimensional context.

1 INTRODUCTION

The design and manufacturing process of extrusion dies for plastic profile extrusion currently requires many iterations between manual testing and reworking of the die. These iterations tie up both highly skilled labor and material, are time consuming, and are often limited in their ability to explore complex design spaces. For this reason, the initial design of the extrusion die should be as close as possible to the final part to minimize the number of iterations required. To identify the optimal design of a die geometry, numerical analysis is a useful tool. While numerical analysis can provide insight into complex processes, it quickly becomes costly when used in a multiquery context like optimization. Given the high computational cost of optimization problems, two strategies can be used to minimize this cost: First, keep the number of optimization parameters to a minimum, and second, reduce the cost of a model evaluation.

In shape optimization, the optimization parameters are geometric parameters. The type of geometric parameters ranges from a few simple parameters—for example, the width and height of an object—to thousands of parameters—for example, when the computational mesh is also used as a geometry parameterization [1]. In terms of the relationship between the number of parameters and design flexibility, spline-based approaches are a convenient compromise between these two extremes. For example, one can represent the boundary of the geometry using splines [2], or one can embed the entire geometry in a box spline and perform free-form deformation (FFD). FFD originates from the field of computer graphics [3], but has also been intensively used in shape optimization [4, 5]. It is easily applicable to complex shapes, since it only requires a box spline and a connection of each node in the mesh to a local coordinate of the spline. Subsequently, any deformation of the spline is automatically transferred to the mesh.

As mentioned above, the second way to reduce the computational cost of optimization problems is to reduce the cost of each simulation. The research area covering this topic is the field of model order reduction (MOR) or reduced order modeling (ROM). ROM encompasses a variety of very different strategies. In the literature, these strategies are typically grouped into three categories: (1) hierarchical ROM, (2) projection-based ROM, and (3) data-driven ROM [6, 7]. The ROM we use in the context of this work are physics-informed neural networks (PINNs), which do not fully fit into any of the above categories. Although PINNs can be trained with data, it is not required. PINNs use prior knowledge in the form of partial differential equations (PDEs) in the model.

The first publications on PINNs date back to the 1990s, where first Psichogios and Ungar [8] and later Lagaris et al. [9] used PDEs to improve the prediction and training process of neural networks (NNs). However, the rise of PINNs began almost two decades later with the publication of Raissi et al. [10]. Subsequently, the PINN concept has been applied to various areas of computational analysis. The works on PINNs that are strongly connected to the modeling of the physics present in plastic extrusion processes involve the modeling of the Navier–Stokes equation [10, 11] and non-Newtonian fluids [12, 13], as well as works on PINNs that involve geometry variation. For example, in Refs. [14, 15], the positioning of individual edges is parameterized and integrated into the PINN model. Further, Refs. [14, 16] combined PINNs with the variational autoencoders to place objects of different shapes in a flow field.

In this work, we present a novel PINN approach that allows geometric variations through an integrated FFD approach. In the presented method, the shape of the computational domain is to be varied by a minimum number of parameters. We demonstrate and discuss the method using a two-dimensional representation of an extrusion die as an example and provide an outlook on the method applied to three-dimensional domains.

The paper is structured as follows: In a first step, we summarize the governing equations used to model the flow inside extrusion dies. Subsequently, we present the underlying PINN and the embedded FFD method in detail. The method is then discussed in the context of a case study of the aforementioned two-dimensional extrusion die. Finally, we conclude with a brief discussion of the performance of the method and possible limitations in the context of shape optimization.

2 GOVERNING EQUATIONS

The modeling of the plastic melt flow follows the assumptions of Hopmann and Michaeli [17]. Furthermore, the Reynolds number is low and the flow can be described using the Stokes equations. This yields the following flow equations:
∇ · v = 0 , $$\begin{equation} \nabla \cdot \mathbf {v}=0\;, \end{equation}$$ (1)
∇ · τ = 0 , with τ = − p I + η ( ∇ v + ( ∇ v ) T ) , and p = − t r ( τ ) · 1 n . $$\begin{equation} \nabla \cdot \bm{\tau }=0\;,\nobreakspace \text{with}\nobreakspace \bm{\tau }=-p\bm{I}+\eta (\nabla \mathbf {v}+(\nabla \mathbf {v})^T)\;,\nobreakspace \text{and}\nobreakspace p=-tr(\bm{\tau })\cdot \frac{1}{n}\;. \end{equation}$$ (2)
Here, v $\mathbf {v}$ is the velocity, τ the stress tensor, and p the pressure. The viscosity η is not constant here and depends on the shear rate, as plastic melt expresses non-Newtonian material behavior [17]. The material model is covered in the following paragraph and the boundary conditions (BCs) are explained in Chapter 4.1. The equation for the pressure p is an additional equation that can be derived with our applied simplifications of the flow equations, by taking the trace of the stress tensor. This equation will be used in the training of the PINN.
Additionally to these simplifications, the equations are also nondimensionalized, as this is advantageous for the implementation of PINNs. The nondimensionalization is done with the addition of reference scales for length, velocity, pressure, stress tensor, and viscosity:
x ∗ = 1 L r e f · x , v ∗ = 1 V r e f · v , p ∗ = 1 ρ V r e f 2 · p , τ ∗ = 1 ρ V r e f 2 · τ , η ∗ = 1 η r e f · η , ∇ ∗ = L r e f · ∇ . $$\begin{equation} \mathbf {x}^{*}=\frac{1}{L_{ref}}\cdot \mathbf {x}\;, \mathbf {v}^{*}=\frac{1}{V_{ref}}\cdot \mathbf {v}\;, p^{*}=\frac{1}{\rho V_{ref}^{2}}\cdot p\;, \bm{\tau }^{*}=\frac{1}{\rho V_{ref}^{2}}\cdot \bm{\tau }\;, \eta ^{*}=\frac{1}{\eta _{ref}}\cdot \eta \;, \nabla ^{*}=L_{ref}\cdot \nabla \;. \end{equation}$$ (3)
Here, x are the coordinates, L r e f $L_{ref}$ is the reference length, V r e f $V_{ref}$ is the reference velocity, and η r e f $\eta _{ref}$ is the reference viscosity. These nondimensional variables are then inserted into Equations (1) and (2).
Plastic melts show shear thinning behavior, meaning that the viscosity decreases for high shear-stresses. In the literature exist multiple material models for shear thinning fluids. One popular model is the Carreau–Yasuda model, which was first proposed by Carreau [18] and then modified by Yasuda [19]. There exist different formulations of the model, we use the following formulation [17]:
η ( γ ̇ ) = A ( 1 + B γ ̇ ) C , γ ̇ = ∇ v + ( ∇ v ) T , γ ̇ = 1 2 ∑ i ∑ j γ ̇ i j γ ̇ j i . $$\begin{equation} \eta (\dot{\gamma })=\frac{A}{(1+B\dot{\gamma })^{C}}\;, \bm{\dot{\gamma }}=\nabla \mathbf {v}+(\nabla \mathbf {v})^{T}\;, \dot{\gamma }=\sqrt {\frac{1}{2}\sum _{i}\sum _{j}\dot{\gamma }_{ij}\dot{\gamma }_{ji}}\;. \end{equation}$$ (4)
with γ ̇ $\dot{\gamma }$ as the shear rate and the material specific parameters A, B, and C, where A acts as the viscosity when no shear stress is applied and it is also used as the reference viscosity η r e f $\eta _{ref}$ . This model states the dependence of the viscosity on the shear rate of the fluid. The shear rate tensor γ ̇ $\bm{\dot{\gamma }}$ depends on the velocity gradients in the fluid. To calculate the viscosity, a scalar value measuring the magnitude of the shear rate is necessary. The magnitude of the shear rate is computed by taking the square root of one half of the second invariant of the shear rate tensor.

Additionally to the shear rate, the viscosity depends on the temperature of the fluid as well [20]. However, in this work, the temperature in the extruder die is assumed to be constant and thus the temperature dependence is omitted.

3 NUMERICAL METHODS

We are using a PINN to solve the fluid flow equations stated above. The PINN contains the flow equations and then acts as a reduced order model to quickly evaluate the flow field for a range of parameterized domains. To validate the PINN, its predictions are compared to a computational fluid dynamics (CFD) solution. The CFD solution is generated with the inhouse finite element flow simulation program XNS developed by the Chair for Computational Analysis of Technical Systems at RWTH Aachen University.

3.1 Parameterized physics-informed neural networks

The choice of the PINN architecture has an important influence on the quality of the results. Here, we adhere to the structure proposed by Rao et al. [11], which has also been used in Heger et al. [15]. The advantage of this approach is that no longer second derivatives of the velocity are required and that the continuity equation is enforced automatically, for details please refer to Rao et al. [11]. For the present work, the main task of the PINN is to predict the flow field inside a deformed 2D or 3D domain for the case of steady, incompressible flows at high viscosities considering a non-Newtonian material model. Each shape of the computational domain can be described uniquely by a set of deformation parameters. How the deformation is implemented is explained in Section 3.3.

Consequently, for a given location in space with given deformation parameters, the PINN should predict the velocity and pressure of the fluid. Hence, the input layer needs the coordinates and the deformation parameters as inputs. The hidden layers consist of a varying number of layers and neurons per layer. The layers are fully connected and the hyperbolic tangent is used as activation function. Only for the last layer, a linear activation function is used to scale the output variables to the correct dimension.

Furthermore, due to the high viscosity, an additional scaling factor f p $f_{p}$ is required for the pressure and stress tensor, so that the output of the PINN can be of the order of one to avoid vanishing gradients during training. The pressure scale factor f p $f_{p}$ has to be tuned for each flow problem to the magnitude of the maximum pressure.

As suggested in Rao et al. [11], the first output variable is the stream function Ψ $\mathbf {\Psi }$ . The functional relationship between the stream function and the velocity is shown in the following formula for the 2D and 3D cases, respectively [15]:
v = ∂ Ψ ∂ y , − ∂ Ψ ∂ x T , and v = ∂ Ψ 3 ∂ y − ∂ Ψ 2 ∂ z , ∂ Ψ 1 ∂ z − ∂ Ψ 3 ∂ x , ∂ Ψ 2 ∂ x − ∂ Ψ 1 ∂ y T . $$\begin{equation} \mathbf {v} = {\left[ \frac{\partial \Psi }{\partial y}, -\frac{\partial \Psi }{\partial x}\right]}^T,\nobreakspace \text{and}\; \mathbf {v}={\left[ \frac{\partial \Psi _{3}}{\partial y}-\frac{\partial \Psi _{2}}{\partial z} , \frac{\partial \Psi _{1}}{\partial z}-\frac{\partial \Psi _{3}}{\partial x} , \frac{\partial \Psi _{2}}{\partial x}-\frac{\partial \Psi _{1}}{\partial y}\right]}^T. \end{equation}$$ (5)
Note that due to the symmetry of the second derivatives, it follows that the mass conservation equation (Equation 1) is automatically satisfied and, consequently, is no longer needed in the loss function. However, at least one additional variable is required to compute the velocity and the pressure. Preliminary experiments using the stress tensor τ showed the best results in terms of memory consumption and accuracy. From the output variables Ψ $\mathbf {\Psi }$ and τ, the velocity field and the pressure can be computed using Equations (5) and (2), respectively. The next section describes how to compute the loss function from the flow field minimized during training.

3.2 Loss function formulation

The loss function of PINNs evaluates how accurately the system of PDEs—including the BCs and initial conditions (ICs)—is fulfilled by its predictions. In this work, for BCs, only Dirichlet BCs are used, which are weakly enforced by adding the mean square error of their residuals to the loss function.

As we consider a steady flow problem, ICs are not needed. The total loss function L consists of a sum of the PDE loss and the BC loss. The latter is scaled with a factor f B C $f_{BC}$ in order to equalize the order of magnitude of both loss terms. Without scaling, it is difficult to reduce all individual loss functions during the training. In practice, the BC loss has to be weighted higher than the PDE loss to prevent a solution that satisfies the PDEs to a high degree but not the BCs. We write
L = L P D E + f B C · L B C . $$\begin{equation} L=L_{PDE}+f_{BC}\cdot L_{BC}\;. \end{equation}$$ (6)
The loss of the PDEs is a sum of the loss values of the governing fluid equations. The loss of each of the fluid flow equations is computed with the mean square error of the residuals, normalized with the number of collocation points. The residuals of the nondimensionalized equations (1)–(2) are computed as follows:
R 1 = ∇ ∗ · τ ∗ ( x ∗ , k ) , R 2 = 1 Re · η ∗ ( γ ̇ ) · ( ∇ ∗ v ∗ ( x ∗ , k ) + ( ∇ ∗ v ∗ ( x ∗ , k ) ) T ) − p ∗ I − τ ∗ ( x ∗ , k ) . $$\begin{align} R_{1}=\nabla ^{*} \cdot \bm{\tau }^{*}(\mathbf {x}^{*},\mathbf {k})\;,\, R_{2}=\frac{1}{\textrm {Re}}\cdot \eta ^{*}(\dot{\gamma }) \cdot (\nabla ^{*}\mathbf {v}^{*}(\mathbf {x}^{*},\mathbf {k})+(\nabla ^{*}\mathbf {v}^{*}(\mathbf {x}^{*},\mathbf {k}))^T)-p^{*}\bm{I}-\bm{\tau }^{*}(\mathbf {x}^{*},\mathbf {k})\;. \end{align}$$ (7)

The stress tensor τ ∗ $\bm{\tau }^{*}$ and the velocity v ∗ $\mathbf {v}^{*}$ directly depend on the inputs of the NN, which are the coordinates x ∗ $\mathbf {x}^{*}$ and the deformation parameters k $\mathbf {k}$ . The Reynolds number is calculated with the reference values used in Equation (3) and the shear-rate-dependent viscosity η ∗ ( γ ̇ ) $\eta ^{*}(\dot{\gamma })$ is calculated using Equation (4).

3.3 Spline-based free-form deformation

The option of domain variations is integrated into the PINN via the concept of FFD.

In FFD, a simple to generate B-spline, such as a cube or a cylinder, is defined around the complex, to be deformed geometry. In context of this work, the surrounding B-spline is a square in 2D or a cube in 3D. B-splines are parametric functions that describe n-dimensional objects. The shape of the spline objects is determined by the positioning of control points and associated shape-functions. Thereby, B-splines provide a parametric relation between a spatial coordinates vector x $\mathbf {x}$ and its associated position on the spline object [21].

In the FFD approach employed in this work, the initial geometry is deformed by applying the following steps, which are also visualized in Figure 1. First, the coordinates of the geometry are scaled to the range of the parameter space of the B-spline. This implicitly establishes a relationship between the coordinates of the geometry and their corresponding points on the spline object. Second, the spline object can be deformed by moving its control points. If the spline object is now evaluated at the parametric coordinates previously associated with the scaled geometry points, one obtains the displaced spatial coordinates of the scaled geometry. In a final step, the deformed geometry is obtained in its original domain by applying the inverse scaling of the first step.

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Visualization of FFD concept.

The strategy described above for representing domain variations is now incorporated into the PINN model. To do this, the PINN is extended in two places: First, the input vector is extended by the deformation vector describing the displacement of the spline control points, and second, the training set is adapted accordingly. Each point of the training set is now patched with the vector of deformation parameters k $\mathbf {k}$ related to the displacement of the spline control points. Furthermore, the coordinates of the training vectors are updated according to the corresponding displacement using the FFD procedure.

4 NUMERICAL RESULTS

In this section, we evaluate the proposed PINN based on a numerical experiment. The evaluation includes a comparison of the model prediction with results computed using the finite element method, as well as a discussion of model tuning and scaling of loss terms.

4.1 2D geometry

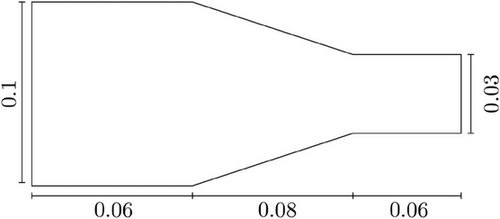
We apply our method to a simple 2D geometry, which is a pipe with decreasing diameter from the inlet to the outlet (Figure 2). As BC, a parabolic velocity profile is enforced at the inlet, and a no-slip condition is enforced at the wall. At the outlet, the pressure is set to zero. All material parameters used are listed in Table 1.

TABLE 1. Material and boundary condition specification.
Material parameters
ρ Density 900 [ kg · m − 3 ] $[\mathrm{kg}\cdot \mathrm{m}^{-3}]$
A Carreau A 9146.6 [Pa · s]
B Carreau B 0.296 [s]
C Carreau C 0.0941 [ − ]
u i n l e t − m a x $u_{inlet-max}$ Max velocity inlet 0.005 [ m · s − 1 ] $[\mathrm{m}\cdot \mathrm{s}^{-1}]$
L r e f $L_{ref}$ Reference length 0.015 [m]
V r e f $V_{ref}$ Reference velocity 0.005 [ m · s − 1 ] $[\mathrm{m}\cdot \mathrm{s}^{-1}]$
Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Sketch showing the dimension of the computational domain in [m].

For a detailed validation of the PINN implementation, the velocity in x-direction u, the velocity in y-direction v, and the pressure p are evaluated. The hyperparameters of the PINN are chosen based on preliminary experiments to deliver the best results and are listed in Table 2. The collocation points are distributed evenly inside the domain. The prediction of the flow field of the PINN inside the domain is shown in Figure 3. One observes that the velocity in x-direction (Figure 3A) at the inlet has a parabolic profile and with decreasing pipe diameter, the velocity increases. The maximum velocity at the outlet reaches a value of 1.67 e- 02 $1.67\text{e-}02$ m· s−1. The velocity in y-direction (Figure 3B) has its maximal magnitude near the end of the decreasing diameter, which is small compared to the velocity in the x-direction. The pressure (Figure 3C) decreases from the inlet to the outlet with the majority of the pressure drop occurring inside the section with the smallest diameter near the outlet. We conclude that qualitatively, the prediction is conforming with the expectations.

TABLE 2. Chosen PINN hyperparameters for the undeformed 2D pipe geometry.
Parameter Value
BC scale factor f B C $f_{BC}$ 1e+12
Pressure scale factor f p $f_{p}$ 1e+06
Learning rate 0.1
Number of hidden layers 6
Number of nodes per layer 60
Number of collocation points 3272
Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
PINN prediction of the velocity field in x-direction (A), in y-direction (B) and the pressure (C) inside the 2D pipe geometry.

In order for the PINN to be suitable for shape optimization, it must be trained on a number of deformed domains. As described in Section 3.3, the deformation is realized by control points of splines that can be moved to a specific position in space. For the 2D pipe case, the outline of the geometry is defined by third-order splines with four control points in the x-direction and second-order splines with three control points in the y-direction. In this test case, only the two middle points at the top and bottom are modified. The maximum deformation for each moved spline point is set to k = 0.4 $k=0.4$ units in both directions of the y-axis on the unit square.

In order for the PINN to handle the deformation, intermediate deformations between the maximum deformations must also be generated. Therefore, it is necessary to define a distance between the intermediate deformations, which must be chosen carefully. Otherwise, this can lead to problems regarding memory consumption and computation time, since the number of deformation combinations of possible deformations increases exponentially. Even with only four movable spline points, with the chosen amplitude, the total number of deformations can be high. Tests have shown that a deformation spacing of Δ k = 0.1 $\Delta k= 0.1$ is sufficient for PINN to handle the deformations of the 2D pipe test case.

In general, only deformations that are symmetric about the y-axis are considered in this test case, otherwise the total number of deformations would be too large. The symmetry reduces the number of independent spline points even further, that is, from four to two. This means that the deformation vector only consists of two independent parameters: k1 and k2. For the large training set generated, a minibatch gradient descent is required with the batch size set to the maximum value supported by the amount of video memory. The training is structured as follows: First, a random selection is made from the input set with the size of the specified batch size, then this batch of inputs is trained for a specified number of iterations before a new batch is generated. This process is repeated until the training converges.

All hyperparameters tuned for the training with deformations are shown in Table 3. In the case with deformations, a higher pressure scale factor of 1 e+ 07 $1\text{e+}07$ is required compared to the case without deformations to account for the higher pressure values of the deformed pipe with reduced diameter. Consequently, the BC scale factor must also be adjusted.

TABLE 3. Chosen PINN hyperparameters for the 2D pipe geometry with deformation.
Parameter Value
BC scale factor f B C $f_{BC}$ 1e+13
Pressure scale factor f p $f_{p}$ 1e+07
Learning rate 0.1
Number of hidden layers 6
Number of nodes per layer 60
Deformation parameters range of k1, k2 −0.4 to 0.4
Number of collocation points 3272

To validate the PINN also for the deforming domain scenario, the PINN prediction is compared to a CFD solution. The difference between each solution is normalized with the respective maximum velocity. This normalized difference between the PINN prediction and a CFD solution of the velocity in x-direction are examined for three cases with maximal deformation (Figure 4). It is assumed that the cases of maximal deformation will have the largest errors, and all intermediate deformations have roughly the same or smaller errors. The maximum normalized error of the three tested deformations is low with only 0.086, but higher than in the undeformed case. Note that for all three cases, the maximum normalized error is located at the outlet. Possible reasons for this are discussed in the remark at the end of this section. High normalized differences also occur in the cases with deformation parameters k 1 = 0.4 $k_{1}=0.4$ and k 2 = 0.4 $k_{2}=0.4$ , shown in Figure 4A. Here, at the smallest diameter, the shear rate and velocity are the highest, resulting in an overall higher pressure. Because of the increase in maximum pressure, it is possible that the pressure scale factors are not optimally tuned for this particular deformation case.

Remark.As one can observe from Figure 4, the PINN prediction and the CFD solution differ significantly at the outlet of the pipe. This is due to a difference in the imposed outlet boundary condition. In the finite element CFD solution, zero normal stress is imposed at the boundary. This is a result of the partial integration performed on the weak form during the finite element discretization. This condition is not enforced by the PINN, where only ambient pressure is enforced at the outlet.

Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
Normalized difference of velocity in x-direction between the PINN prediction and a CFD solution of the deformed 2D pipe case. The deformations of the pipe are a reduced diameter in the front and back (A), enlarged diameter in the front and reduced diameter in the back (B) and enlarged diameter in the front and back (C).

4.2 3D geometry

Our method has also been applied to a 3D geometry, here a rotationally symmetric version of the 2D pipe geometry. The results from the 3D case are not shown here, as this would go beyond the scope of this paper. The method still works, but the training time and memory consumption of the PINN increase significantly, making hyperparameter tuning more difficult. This problem is exacerbated when more complex geometries are used.

5 DISCUSSION

In this paper, we have demonstrated the novel approach of combining PINNs with FFD. We have shown that PINNs are capable of accurately predicting the flow field in a parameterized domain that can be deformed with FFD. The PINN implementation was adapted to the high-viscosity flow of plastic melt, including non-Newtonian material behavior. The PINN was then trained on a set of FFD deformed domains to predict the flow field inside different shapes of a domain. After the initial training stage, the prediction of the flow field from the PINN is fast. Consequently, PINNs can be used for shape optimization of an initial design, which was our goal. In the 2D case, the time required for hyperparameter tuning and training the PINN is reasonable. In the case of more complex geometries in 3D, the training time of the PINN increases significantly. Thus, it needs to be investigated whether the PINN approach is useful in a shape optimization context in terms of computational effort compared to standard shape optimization approaches.

ACKNOWLEDGMENTS

The work was funded by the Deutsche Forschungsgemeinschaft e.V. (DFG, German Research Foundation) under the Collaborative Research Centre SFB1120-236616214 “Bauteilpräzision durch Beherrschung von Schmelze und Erstarrung in Produktionsprozessen” at RWTH Aachen University and funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy EXC-2023 Internet of Production - 390621612. The sponsorship and support are gratefully acknowledged. The computations were conducted on computing clusters provided by the RWTH Aachen University.

Open access funding enabled and organized by Projekt DEAL.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.