Extension of a shell-like RVE model to represent transverse shear effects in textile reinforced composites
Abstract
Textile reinforcements have long been used in shell-like components like tires, belts, hoses and, in particular, air spring bellows. These bellows consist of a certain number of cords embedded in soft rubber, resulting in high membrane stiffness to absorb tensile forces and low resistance to changes in curvature. The embedded cords are produced by twisting multifilament yarns. Modelling and simulation of bellows is a challenging task. Thereby, the complex internal geometry, large deformations as well as the strongly anisotropic and nonlinear material behavior have to be taken into account in a computationally efficient manner. One approach is the application of multiscale analyses in conjunction with representative volume elements (RVE). Within this study, a through-thickness RVE based on in-plane periodic microstructures is applied. The local behavior of the cords is represented by an anisotropic constitutive model that regards directions and mechanical properties of filaments, which result from previous cord twisting simulations. In this contribution, an extension of the classical periodic boundary conditions (PBC) is presented, which considers curvature, pressure load, and, in particular, transverse shear. The RVE is used to simulate the stresses and strains in cord-rubber composites under realistic load conditions. Moreover, it is employed for homogenizing the mechanical behavior and, thus, for developing a suitable constitutive model for shells.
1 INTRODUCTION
Air spring bellows feature a highly complex internal geometry and are characterized by strong anisotropic, nonlinear material behavior, generally large deformations, and contact. The main objective is to provide novel high-resolution models that account for these characteristics for the structural mechanical simulation of air springs. Consequently, the models have to be both efficient and realistic. Figure 1 illustrates a cross-ply reinforced bellows. The rubber matrix contains two layers of textile cords, which are oriented at the angle α relative to the axial direction and are significantly stiffer than the cord matrix. However, the cord owns a complex geometry and filament structure. The filament structure plays an important role in determining the stiffness properties of the cord and, consequently, the resulting stiffness properties of the composite. This composite structure allows for the absorption of significant membrane forces, which are crucial for the load-carrying capacity of the air spring. Due to the dominant influence of the rubber matrix, the composite remains highly flexible against bending. Over the past years, many finite element models have been developed for cord-rubber composites. Frequently, these models use simplifications to deal with the complex structure of the cord, its anisotropic behavior, significant large deformations, or the challenging discretization of the composite [1]. For instance, shell elements or rebar models are often employed to analyze the overall behavior of the component. However, these models are not capable of accurately determining local results such as stresses or strains. For such an evaluation, microstructural modelling is required, considering a representative volume element (RVE). These models have the advantage of providing a larger number of elements to resolve the large gradients near the interface. The challenge with these models lies in formulating the macroscopic boundary conditions in such a way that an efficient analysis of real loads on shell-like structures is enabled, while minimizing disruptions caused by boundary effects. Typical loadings on those structures are curvatures, membrane deformations, transversal shear, and pressure loads. The shell-like RVE can capture important features such as microscopic geometric structures and material properties that influence the overall behavior of the system. By analyzing such an RVE, valuable insights into the behavior of the larger system can be gained without the need to model the entire structure or material. Thus, the RVE can be replaced by a shell element of the same physical properties. This procedure is called homogenization. With the aid of a submodel, which is surrounded by an elastomer layer, the results in the interface region can be further enhanced. The boundary conditions of the submodel are derived from the macroscopic simulation of the RVE.

2 HOMOGENIZATION
Homogenization is efficiently applied in multiscale modelling when the complexity of the geometric and mechanical microstructure is too challenging to be handled by other conventional modelling techniques. In order to describe the behavior of composite materials, there are three methods of homogenization. The first method is analytical homogenization, followed by numerical homogenization techniques, such as fast Fourier transformation (FFT)-based homogenization for obtaining effective properties in linear elasticity and conductivity problems. Thus, this method is not suitable for arbitrary microscale material behavior, including physically nonlinear and time dependent behavior [3]. The last method is computational homogenization, which represents an effective method for incorporating multiscale hierarchies into computational models. The basic idea behind computational homogenization is to couple two finite element models () by solving a microscale boundary value problem at the integration points of the macroscale model. However, the main challenge of this approach is the high computational cost, which requires additional efforts to explore strategies for reducing the computational costs. The theory of shell computation homogenization is proposed by [4] and [5]. The aim of this paper is to develop a shell-like RVE for highly loaded thin cord-elastomer composites that is capable of simulating not only membrane deformations, large curvatures, and internal pressure but also transverse shear. Two homogenization techniques are implemented and compared in order to identify the optimal approach for defining the periodic boundary conditions (PBC). The first technique, proposed by [4], represents a second-order computational homogenization framework of thin shells, as an extension of the classical first-order computational homogenization framework introduced by [6]. This technique is presented in detail in Section 2.2 of the paper. The second technique, proposed by [1], extends the classical first-order PBC to allow for rigid body rotation of the material line elements at the periodic surfaces of the RVE. In the context of this work, the second technique is further extended to incorporate transverse shear deformation. This technique is explained in Section 2.3.
2.1 Macroscale mindlin-reissner kinematics
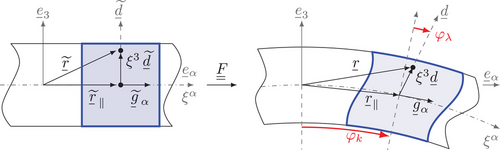
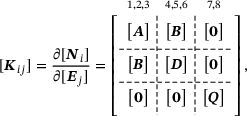 (6)
(6)2.2 Microscale projection: Second-order homogenization

The displacements of the cross-section are linearly approximated, which leads to deviations when the cross-section undergoes large rotations.
2.3 Microscale projection: Rotation-based homogenization
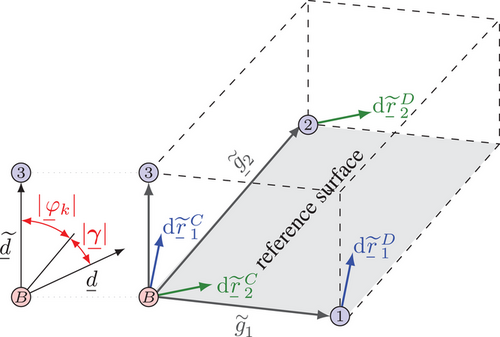
It is important to emphasize that only surfaces with a Gaussian curvature are considered as so-called developable surfaces. This means that the curved surface can be flattened without distortion. Please note that the sphere is the only closed surface with a constant Gaussian curvature. In general, undesired surface effects increase with increasing Gaussian curvature. Therefore, either small RVEs of highly curved surfaces or large RVEs of slightly curved surfaces can be analyzed with negligible surface effects. In the case of an air spring, the curvature of the rolling lobe is large compared to the curvature in the circumferential direction. Hence, the highly loaded areas can be modeled as a parabolic RVE.
2.4 Implementation
3 NUMERICAL RESULTS
3.1 Verification of surface effects and validation
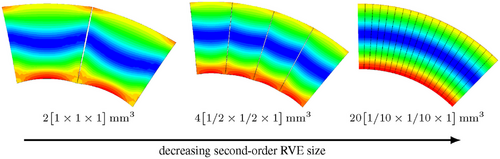
To verify the surface effects, multiple homogeneous second-order RVEs are connected in series. These RVEs are defined by dimensions specified as , with the number of these RVEs denoted as N, and each having defined length (l), width (w), and thickness (h). These RVEs are loaded with a high curvature of . The surface effects refer to disturbances in the peripheral regions of the RVE. On the left side of the illustration 5 (the first image from the left), it is clearly evident that changes in the von Mises stress distribution occur not only in the thickness direction but also in other coordinate directions, indicating disturbances in the peripheral areas. When the RVE is reduced in size (as seen in the third image from the left), the disturbances in the peripheral region decrease despite constant curvature. This becomes particularly evident when the stress distribution changes exclusively in the thickness direction. From this, the following conclusion can be drawn: When analyzing a small RVE with significant curvature, the curvature is indeed significant, but the RVEs are small enough to assume that surface effects are relatively negligible. The smaller the RVE, the more the surface effect is reduced until it converges to a free surface effect. In contrast, when examining large RVEs with minimal curvature, the curvature is less pronounced, but the RVEs are large enough to justify the assumption that surface effects are negligible. In the case of a rotation-based RVE, the stress distribution is only free from thickness any surface effects in the parabolic scenario, regardless of the size of the RVE, as depicted in Figure 6 on the left. This is due to the strict constraints in Equation (8). This emphasizes the statements of the theorems by Minding and Liebmann, which explain the surface effects in elliptical and hyperbolic structures. Only surfaces with a Gaussian curvature of zero are considered “developable”, meaning that the curved surface can be flattened without distortion.
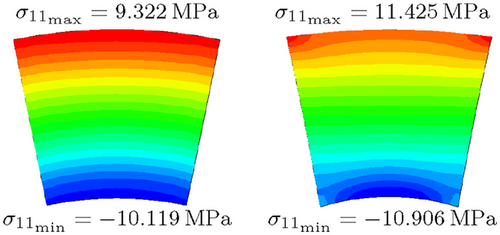
In order to prove the correct implementation of the constraints and the validity of the homogenization, a homogeneous FE-plate made of elastomer is considered. Initially, a FE-plate with dimensions of for length, width, and thickness is modeled, using volume elements (5 elements in the thickness direction). The plate is assigned a soft isotropic material with Hooke's parameters , and a curvature of is applied. The results of the macroscopic simulation show at a specific location the maximum normal stress in the tensile region of (on the upper surface) and the minimum normal stress of in the compressive region (on the lower surface). At the same location, an RVE with dimensions of is extracted, and the same material and boundary condition parameters are applied. The results of the microscopic simulation of the RVE using both methods are presented in Figure 6. It is shown that the rotation-based RVE provides more accurate results, and the small differences observed are due to numerical differentiation and can be disregarded when using a fine mesh. Instead, the second-order RVE exhibits some deviation, which diminishes as the size is reduced. It is shown that the rotation-based RVE provides more accurate results, and the small deviation in results between the FE plate and the RVE is attributed to numerical differentiation and can be disregarded when using a fine mesh. Instead, the second-order RVE exhibits some deviation, which diminishes as the size of RVE is reduced.
3.2 Cross-layer reinforced composites of an air spring
In this section, shell-like rotation-based RVEs for cord-elastomer composites with two intersecting reinforcement layers are considered. The objective is to analyze the locale stresses (localization) in the composite under realistic loading conditions that occur in a component such as an air spring. This aims to enable efficient optimization of cord-elastomer composites, including their durability, under realistic conditions. Figure 7 (left) shows the geometry of an undeformed air spring bellows with its dimensions in a top view. The RVEs represent sections of the bellows with different periodicity and loading directions. Although the initial geometry of many air spring bellows is cylindrical, the RVEs are assumed to be initially straight due to the large radius compared to the bellows thickness and the high number of cords n. The parameters of the cross-layer reinforced composite are cord angle , the thickness of the composite h, the spacing of the cords , and the relative position of the cords in the thickness direction. The RVE features a structured mesh with C3D8H hybrid elements, and the material model assigned to each integration point is assumed to be influenced by its corresponding material region. A hyperelastic model is chosen for the rubber matrix. In particular, the strain energy potential of Neo-Hookean type is used, which is split into deviatoric and volumetric contributions. The second material region that needs to be considered is the cord, which has a filament structure. The cord bundle is considered to possess transversely isotropic behavior with the preferred direction represented by . The total strain energy potential is composed of an anisotropic part and an isotropic part that accounts for shear and volumetric deformations [1]. The next step involves developing a global FE model in ABAQUS using the rebar formulation. In this context, the global model refers to an FE model of the air spring that does not rely on any assumed symmetries. The aim of the global model is to accurately capture all typical macroscopic deformation modes present in the air spring bellows, enabling their transfer to the RVE.
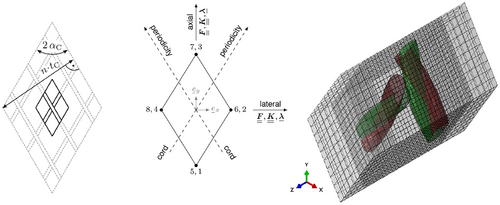
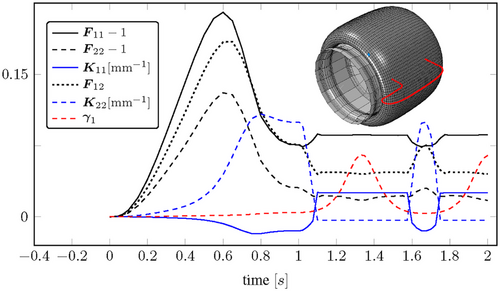
These deformation modes specifically include membrane deformation, curvatures, and transverse shear effects occurring within the matrix between two cord layers (see, ref. [8]), as illustrated in Figure 8. A transfer of the macroscopic deformations to the RVE as PBC allows for a more precise analysis of the local stress distribution. However, the use of multiphase elements inevitably entails a loss of information concerning the interface. Since the interface between the cords and the elastomer often represents preferred locations for crack initiation and, consequently, for later component failure, the analysis of stress in this region is of particular interest. One way to significantly improve the quality of results near the interface is through the application of submodeling techniques. Figure 9 illustrates the distribution of maximum logarithmic strain in both the RVE and the submodel. Based on the simulations, it has been observed that the primary influence in changing the cord angle is a result of the combined effects of curvature and transverse shear. This interaction leads to a significant shearing of the elastomer layer located between the cord layers. The subsequent step involves calculating an effective shell stiffness using a second-order RVE, as depicted in Figure 9. This calculation is necessary for homogenization the effective mechanical behavior of the corresponding shell element and, thus, developing an appropriate constitutive model.
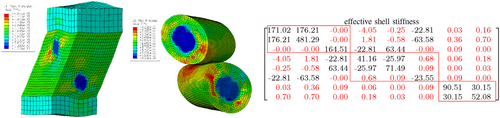
Additionally, all contributions highlighted in red appear as discretization errors. Besides the tension-torsion coupling, the coupling between bending and shearing is particularly interesting. Due to the curvature of the RVE, tension and compression sides are formed. Instead of simply stretching or compressing, the cords can also change their angle in response.
4 SUMMARY
The rotation-based RVE is expanded to incorporate transverse shear and is highly suitable for localization and accurately analyzing the local stress in cord-elastomer composites. Its effectiveness lies in its ability to simulate significant curvature effects at different sizes without violating the periodicity conditions. For its discretization, a simple structured meshing approach was used, combined with an integration point-wise assignment of material properties, resulting in a suitable FE model for cord-elastomer composites. The loss of information due to the implicitly modeled interface between the materials was compensated for by conducting a subsequent analysis of a submodel of a cord, which is coated with an elastomer layer. However, the rotation-based RVE is unable to simulate arbitrary curvatures in different directions. The curvature tensor must satisfy certain conditions, such as having zero Gaussian curvature, in order to avoid surface effects. In case of non-zero Gaussian curvature, like in air springs, the second-order RVE is perfectly suited for homogenizing the effective properties and coupling with shell elements in analyses. However, it is important to choose an appropriate size to minimize surface effects.
ACKNOWLEDGMENTS
Open access funding enabled and organized by Projekt DEAL.




