Multi-level Bézier extraction of truncated hierarchical B-splines for isogeometric analysis
Abstract
Multivariate basis splines (B-splines) and Non-uniform rational B-splines (NURBS) lack adaptivity due to their tensor product structure. Truncated hierarchical B-splines (THB-splines) provide a solution for this. THB-splines organize the parameter space into a hierarchical structure, which enables efficient approximation and representation of functions with different levels of detail. The truncation mechanism ensures the partition of unity property of B-splines and defines a more scattered set of basis functions without overlapping on the multi-level spline space. Transferring these multi-level splines into Bézier elements representation facilitates straightforward incorporation into existing finite element (FE) codes. By separating the multi-level extraction of the THB-splines from the standard Bézier extraction, a more general independent framework applicable to any sequence of nested spaces is created. The operators for the multi-level structure of THB-splines and the operators of Bézier extraction are constructed in a local approach. Adjusting the operators for the multi-level structure from an element point of view and multiplying with the Bézier extraction operators of those elements, a direct map between Bézier elements and a hierarchical structure is obtained. The presented implementation involves the use of an open-source Octave/MATLAB isogeometric analysis (IGA) code called GeoPDEs. A basic Poisson problem is presented to investigate the performance of multi-level Bézier extraction compared to a standard THB-spline approach.
1 INTRODUCTION
Isogeometric analysis (IGA) [1-3] is a numerical method for solving partial differential equations (PDEs) by using a unified representation for both the analysis and design of structures. IGA is promising to close the gap between analysis and computer-aided design (CAD) geometries of the structures. Traditionally, engineers have used separate methods for modeling the geometry of a structure and analyzing its behavior. However, IGA breaks through this limitation by employing non-uniform rational B-splines (NURBS) functions, a standard technology employed in CAD systems. The isoparametric philosophy is invoked, and the solution space for dependent variables is represented in terms of the same functions that represent the geometry.
Refinement techniques for NURBS functions are inherently simple and do not require further communication with the CAD system. Order elevation and knot insertion are refinement techniques analogous to standard FE methods like h- and p-, and a new, higher-order methodology emerges, k-refinement, which combines order elevation followed by knot insertion. All subsequent meshes retain the exact geometry of the initial CAD structure.
Due to the tensor product structure of the B-spline and NURBS functions, local refinement can not be achieved. Various approaches have been developed to overcome this limitation of tensor product structures, such as T-splines [4], locally refined B-spline (LR-splines) [5], and hierarchical B-splines (HB-splines) [6]. HB-splines are based on a multi-level structure with different levels of detail and appear promising to implement local refinement. Those splines can also be applied to T-splines indicating hierarchical T-splines [7]. The hierarchical B-splines recently extended with the truncation mechanism, namely, THB-splines [8]. This work presents an adaptive IGA framework based on THB-splines. This type of function preserves all the essential mathematical properties of standard B-splines and retains the partition of unity property in a hierarchical structure. Despite the good properties of THB-splines and their simplicity, implementing the hierarchical definition of shape functions into existing finite element (FE) solvers can be rather challenging. The proposed approach for this implementation is based on a generalization of the classical Bézier extraction [9], extended into a hierarchical concept [10, 11]. In fact, the multi-level Bézier extraction maps the multi-level hierarchical functions, and the corresponding knot spans, into a sequence of elements being equipped with a standard single-level basis.
2 PRELIMINARIES
In this section, some preliminary concepts need to be discussed in order to give a summarized overview of the work steps. In particular, B-splines and NURBS, the idea of Bézier extraction, and hierarchical splines, together with the truncation mechanism, are presented.
2.1 B-splines and NURBS
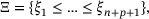 (1)
(1)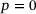 , up to the prescribed degree,
, up to the prescribed degree,
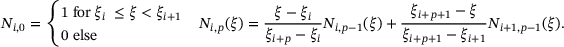 (2)
(2) . In the case of open knot vectors, the first and the last knot values have multiplicity
. In the case of open knot vectors, the first and the last knot values have multiplicity 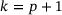 , and the basis is interpolatory at the ends of its definition domain. A B-spline curve can be constructed as the linear combination of the basis functions.
, and the basis is interpolatory at the ends of its definition domain. A B-spline curve can be constructed as the linear combination of the basis functions.
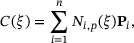 (3)
(3) are the control points and equal the number of basis functions. Figure 1, shows a representation of a B-spline with knot vector
are the control points and equal the number of basis functions. Figure 1, shows a representation of a B-spline with knot vector  and degree
and degree  .
.
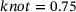 .
. , the degrees p and q and knot vectors
, the degrees p and q and knot vectors  and
and  , define each dimension of a surface. Thus, two sets of basis functions along with the control net Pi, j with
, define each dimension of a surface. Thus, two sets of basis functions along with the control net Pi, j with  ,
, 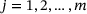 , describe the surface:
, describe the surface:
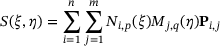 (4)
(4)2.2 Standard Bézier extraction
This section provides a short introduction to Bézier extraction [9]. Unlike the standard FE approaches, B-spline basis functions are defined globally (see Figure 1). Bézier extraction provides a mapping between the smooth spline space and a C0 representation of Bézier elements. Those elements are defined by Bernstein polynomials, which are local, that is, their support is non-zero only in a single element. Thus, conventional element-based FE routines can be enriched by splines in a straightforward manner.
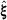 into Ξ, so
into Ξ, so 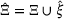 , where
, where 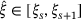 . This procedure continues until the desired multiplicity of the internal knots is achieved, resulting a new set of basis functions and a new set of control points that retain the geometry of the curve. Further details for knot insertion techniques can be found in ref. [2]. The B-spline curve C is described by a set of Bernstein polynomials
. This procedure continues until the desired multiplicity of the internal knots is achieved, resulting a new set of basis functions and a new set of control points that retain the geometry of the curve. Further details for knot insertion techniques can be found in ref. [2]. The B-spline curve C is described by a set of Bernstein polynomials 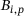 and the Bernstein control points
and the Bernstein control points 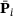
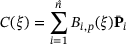 (5)
(5)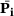 can be computed as a linear combination of the original control points
can be computed as a linear combination of the original control points 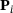 , which are represented by a matrix operator
, which are represented by a matrix operator  , the Bézier extraction operator. The same operator is used for the translation of the basis functions
, the Bézier extraction operator. The same operator is used for the translation of the basis functions 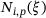 to the Bernstein polynomials
to the Bernstein polynomials 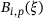 . The basis functions can be written in a vector format with
. The basis functions can be written in a vector format with 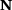 and
and 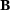 , respectively. So, globally defined B-splines transformed into a basis of Bézier elements reads
, respectively. So, globally defined B-splines transformed into a basis of Bézier elements reads
 (6)
(6)2.3 Truncated hierarchical B-splines
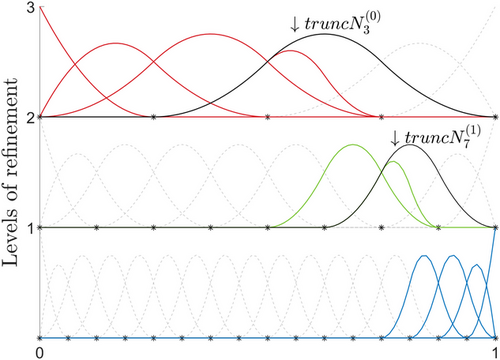
In this section, the hierarchical B-splines are presented, which are used to achieve local refinement and overcome the limitation of adaptivity due to the tensor product structure of splines. Then, the extension with the truncation mechanism is added to retain the partition of unity property [8, 10].
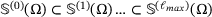 with the same polynomial degree, where
with the same polynomial degree, where 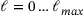 are the levels of refinement. In this contribution, the different levels are constructed with the dyadic refinement technique, where each new level has
are the levels of refinement. In this contribution, the different levels are constructed with the dyadic refinement technique, where each new level has 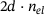 elements (d is the dimension and
elements (d is the dimension and 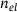 number of elements in
number of elements in 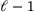 ). In Figure 2, a univariate quadratic B-spline with two additional levels of refinement is depicted. The geometry and the parametric representation do not change under the refinement process, but the relation between the levels is happening by an operator called, subdivision matrix
). In Figure 2, a univariate quadratic B-spline with two additional levels of refinement is depicted. The geometry and the parametric representation do not change under the refinement process, but the relation between the levels is happening by an operator called, subdivision matrix 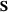 . The parent functions of the level ℓ are a linear combination of fine-scale functions (children functions) of level
. The parent functions of the level ℓ are a linear combination of fine-scale functions (children functions) of level 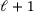
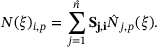 (7)
(7)
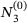 and
and 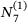 are truncated functions.
are truncated functions. defines a new set of B-spline basis functions
defines a new set of B-spline basis functions 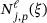 . So, the multi-level spline space is defined as in ref. [14]
. So, the multi-level spline space is defined as in ref. [14]
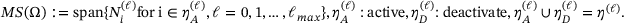 (8)
(8)Therefore, the refinement process starts by deactivating parent functions of the corresponding element from the coarse level ℓ and activating their children on level  , until the desired adaptivity is achieved, see Figure 2. The selection of the coarse and fine elements results from error estimator algorithms or manual selection of the preferred elements. This information is stored in the subdivision matrices [14, 15].
, until the desired adaptivity is achieved, see Figure 2. The selection of the coarse and fine elements results from error estimator algorithms or manual selection of the preferred elements. This information is stored in the subdivision matrices [14, 15].
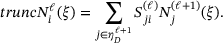 (9)
(9)In general, it is straightforward to identify the truncated B-spline functions. Let us assume an evaluation of an element on the finest level 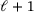 . The basis functions that describe the element are
. The basis functions that describe the element are 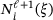 , with
, with  , where the
, where the 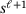 is the knot span of the element in that level. This element holds truncated B-splines on the previous level, ℓ, only if at least one of its
is the knot span of the element in that level. This element holds truncated B-splines on the previous level, ℓ, only if at least one of its 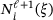 is inactive (see Figure 2).
is inactive (see Figure 2).
3 MULTI-LEVEL BÉZIER EXTRACTION
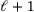 , with the subdivision matrix (7). The global multi-level extraction operator,
, with the subdivision matrix (7). The global multi-level extraction operator, 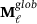 , can be defined by applying a sequence of nested spline spaces, where the goal is to extract the hierarchical functions supporting an element at a specific level. For levels
, can be defined by applying a sequence of nested spline spaces, where the goal is to extract the hierarchical functions supporting an element at a specific level. For levels 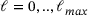 the
the 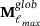 can be obtained by joining the rows, corresponding to the active basis, of the refinement operators
can be obtained by joining the rows, corresponding to the active basis, of the refinement operators 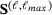 . More details for constructing the global multi-level extraction operator can be found in ref. [11]. Next, localization of the global multi-level extraction to each element of the domain leads to a local element-by-element approach. By selecting the appropriate columns and rows associated with the basis functions of the element, the extraction operator effectively captures the hierarchical functions. The multi-level extraction operator is always of the same level as the element. All the different matrices,
. More details for constructing the global multi-level extraction operator can be found in ref. [11]. Next, localization of the global multi-level extraction to each element of the domain leads to a local element-by-element approach. By selecting the appropriate columns and rows associated with the basis functions of the element, the extraction operator effectively captures the hierarchical functions. The multi-level extraction operator is always of the same level as the element. All the different matrices, 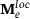 , correspond to each element of the hierarchical spline space,
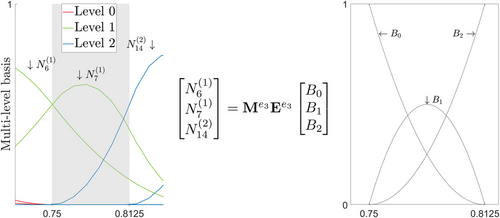
, correspond to each element of the hierarchical spline space, 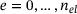 . They can be combined directly with the Bézier extraction operator, resulting the multi-level Bézier extraction technique (see Figure 3). This creates a direct map
. They can be combined directly with the Bézier extraction operator, resulting the multi-level Bézier extraction technique (see Figure 3). This creates a direct map 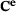 from a standard set of reference basis functions equal for each element (Bernstein basis,
from a standard set of reference basis functions equal for each element (Bernstein basis, 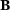 ) to the multi-level local basis (hierarchical basis).
) to the multi-level local basis (hierarchical basis).
 (10)
(10)
As the hierarchical basis functions are mapped into a local approach with elements with a standard set of basis functions, the calculations into the Bézier elements are performed. This can happen using the existing FE algorithms, and there is no need for separate algorithms to handle the globally defined spline basis functions.
4 NUMERICAL EXAMPLE
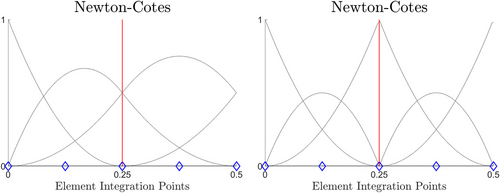
This contribution uses GeoPDEs [1, 16], an open-source FE solver for IGA, based on Matlab/Octave. Let us first highlight an advantage of Bézier extraction over the direct use of B-splines basis functions. The problem refers to the evaluation of points at the boundaries of the elements. Due to the Cox-de Boor formula (2), boundary points are generally associated with the right element of the domain, which can lead to misinterpretations. Consider the numerical integration of an element using a Newton-Cotes quadrature rule. These rules contain the boundary points, and based on (2), the contribution of the last point would be associated with the next element instead of the current one. This can be easily overcome with the use of Bézier extraction. An example to illustrate the problem is in Figure 4, where the Newton-Cotes quadrature rule is applied for the integration of the elements in a univariate problem, instead of the Gaussian quadrature method. Bézier extraction should be applied to evaluate accurately. In this case, improving the results is not the goal of Newton-Cotes, but to verify the problem of spline-based algorithms using Cox-de Boor formula.
4.1 Unit square boundary value problem
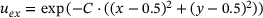 , where C is constant.
, where C is constant.
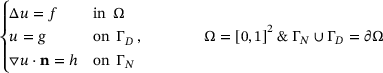 (11)
(11) , as described in Section 3, and then calculating the stiffness matrix of a single Bézier element, the stiffness matrix of an element in the hierarchical structure can be derived.
, as described in Section 3, and then calculating the stiffness matrix of a single Bézier element, the stiffness matrix of an element in the hierarchical structure can be derived.
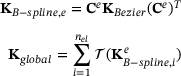 (12)
(12)

Gathering all the element-wise stiffness matrices, the stiffness matrix for the whole multi-level spline space is obtained. Figure 7 shows the convergence of the multi-level Bézier extraction and the local refinement of GeoPDEs.
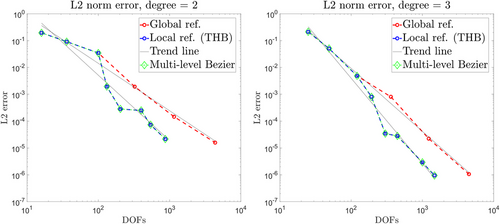
When comparing the values of the graphs in both cases, the results of multi-level Bézier extraction fit the IGA-based algorithm. This verifies that by just evaluating a single Bézier element, the stiffness matrix can be directly mapped into a hierarchical structure and evaluate multi-level spline spaces.
5 CONCLUSION
This study demonstrates that Bézier extraction can be extended into a multi-level structure of THB-splines, resulting the multi-level Bézier extraction. The calculation over Bézier elements is sufficient to extract results for hierarchical spline spaces which perform local refinement. The only calculation that needs to be derived is the multi-level Bézier extraction operators for each element of the domain and the standard Bézier extraction operator. Then those operators are applied to Bézier elements. The implementation of the IGA concept into existing FE solvers can be employed. Additionally, this general approach is not restricted to THB-splines but can be compatible with any nested space.




