Approximate postbuckling analysis of shear deformable laminates
Abstract
In the lightweight design of aircraft, spacecraft and marine vessels, often advanced materials are utilised. Advanced materials such as laminated composites made of fibre-reinforced plastics show transverse shear deformations if they are considered “thick” or possess little transverse shear stiffness. In most cases, the effect of the shear deformations is neglected, and few computational models exist that consider the closed-form approximate analysis of the postbuckling behaviour. Thus, a new computational model based on high-order shear deformation theories is introduced. The solution is derived based on the principle of the minimum of the total elastic potential and is evaluated in comparison to finite element analyses. The highly efficient approximate computational model is developed to offer a valuable tool for the preliminary design of lightweight structures utilising shear deformable advanced materials.
1 INTRODUCTION
Composite laminates made of fibre-reinforced plastics are frequently used for example in the aerospace, marine and civil engineering industry. Here, they are important for the lightweight design of structures because of their advantageous material properties that offer high specific strength and stiffness. However, the transverse shear stiffness is low compared to other commonly used materials. Typically, laminated plates are analysed using the classical laminated plate theory (CLPT), which does not model shear deformation effects. For thick laminated plates or plates with very low transverse shear stiffness, this simplification leads to an overestimation of the load-carrying capabilities, that is, critical buckling loads are overestimated [1]. Consequently, also the postbuckling behaviour is affected.
For the analysis of shear deformable laminates, shear deformation theories (SDT), such as the first-order shear deformation (FSDT) and third-order shear deformation theory (TSDT), are required. The description of the constitutive behaviour in the present work is based on the TSDT as formulated by Reddy [2], as it does not require a shear correction factor and fulfills the boundary condition of vanishing transverse shear stresses at the top and bottom surface of the laminate. This is contrary to the FSDT. The utilisation of the TSDT leads to two additional degrees of freedom, which are the independent rotations of the transverse cross-sections 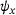 and
and 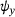 .
.
A crucial factor in the lightweight design of structures is the stability behaviour. In general, this behaviour can be analysed using various analytical and numerical methods, such as the finite-element method, the finite strip method, the semi-analytical Ritz method and closed-from analytical solutions. For the preliminary design, when for example, an optimisation is performed to fully exploit the lightweight potential, computational efficiency is a vital criterion for the selection of appropriate analysis tools. Due to the high number of function evaluations, the utilisation of closed-form analytical models is preferred. This is despite their often approximate character. Consequently, the present work is focused on the development of closed-form analytical solutions.
In the literature, the problem of buckling and postbuckling is addressed by numerous authors. Thus, the review of relevant literature is presented focused on closed-form modelling approaches for on the one-hand postbuckling of laminates based on CLPT and on the other-hand buckling of shear deformable laminates based on SDT. In most closed-form analytical models, the postbuckling analysis considers single laminated plates with varying boundary conditions [3-9]. This includes the modelling of uniaxially compressed cross-ply laminates with elastically restraint longitudinal edges [3], infinitely long panels under combined biaxial and shear loading including bending-twisting coupling [5], modelling of imperfect fully simply-supported (SSSS) and combined simply-supported and clamped (SSCC) panels [8], and other combinations of the listed boundary and loading conditions. However, also more complex structures are investigated in a closed-form analytical fashion. Models for the postbuckling analysis are available for blade-stiffened [10] and omega-stringer-stiffened [11] composite panels. For a more extensive review of previous works regarding the postbuckling of laminated structures based on the CLPT, the reader is referred to Ref. [11]. For closed-form analytical analysis models based on FSDT or TSDT, no works are known to the authors that consider postbuckling. However, for the buckling analysis, several relevant works exist that investigate individual laminated panels with various boundary conditions. This includes next to the classical Navier solutions, for example, presented in Ref. [2], the consideration of SRSR panels based on FSDT [12] and based on TSDT [13-15]. A more detailed literature review is available in Ref. [16], where closed-form modelling approaches are presented for unsymmetrically laminated shear deformable laminates. From the review of relevant literature, a clear lack of computationally highly efficient analysis models for the postbuckling of shear deformable laminates is identified and addressed in the present work by extending the postbuckling models based on CLPT to the TSDT employing the insights gained by the modelling approaches for the buckling analyses.
The lack of fast analytical models is addressed in the present work by establishing a novel closed-form analytical postbuckling analysis model for a shear deformable panel with simply supported boundary conditions. The panel is depicted in Figure 1A. The approximate solution is derived based on the principle of the minimum of the total elastic potential. Therefore, the total elastic potential energy is derived based on the TSDT and von Kármán strains, including initial imperfections of the panel. The equilibrium conditions are reduced by using a suitable Airy stress function. First, a linear buckling solution is derived and used as the starting point for a consecutively derived nonlinear postbuckling solution. The results of the novel approach are successfully verified against finite-element analyses and show promising potential for their future application in preliminary design.
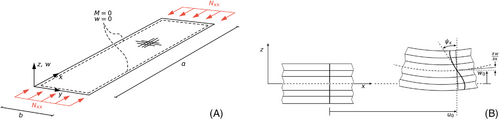
 -plane with the mid-plane deflection w0, the in-plane displacement u0, the slope
-plane with the mid-plane deflection w0, the in-plane displacement u0, the slope 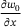 and the rotation
and the rotation 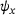 .
.2 METHODS
2.1 Introduction
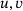 and w are described by the laminate's mid-plane displacements
and w are described by the laminate's mid-plane displacements  and w0. The displacement field is given in Equation (1).
and w0. The displacement field is given in Equation (1).
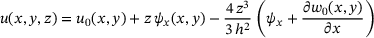 (1)
(1)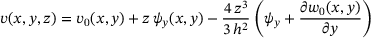 (2)
(2)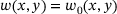 (3)
(3)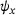 and
and 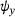 are included in the formulation. The deformation is additionally graphically represented in Figure 1B. Inserting the displacement field into the von Kármán strains leads to the strain formulation in Equations (4-5) based on the TSDT required for the computation of the total elastic potential. However, to include imperfections in the formulation the deflection w is substituted with
are included in the formulation. The deformation is additionally graphically represented in Figure 1B. Inserting the displacement field into the von Kármán strains leads to the strain formulation in Equations (4-5) based on the TSDT required for the computation of the total elastic potential. However, to include imperfections in the formulation the deflection w is substituted with 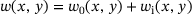 .
.
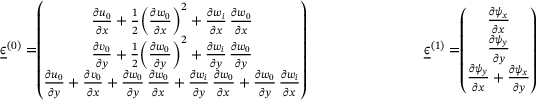 (4)
(4)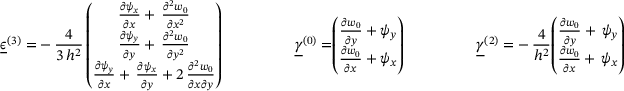 (5)
(5)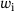 are neglected:
are neglected:
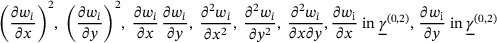
 (6)
(6)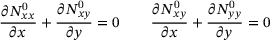 (7)
(7)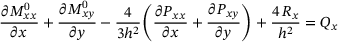 (8)
(8)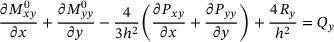 (9)
(9)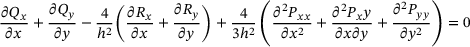 (10)
(10)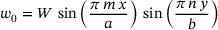 (11)
(11) (12)
(12)2.2 Airy stress function
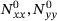 and
and 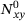 to fulfil the equilibrium conditions (7). This leads to the formulation given in Equation (13).
to fulfil the equilibrium conditions (7). This leads to the formulation given in Equation (13).
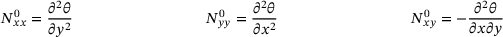 (13)
(13) .
.
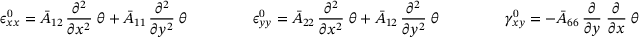 (14)
(14)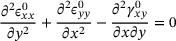 (15)
(15)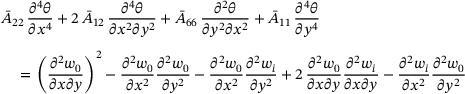 (16)
(16)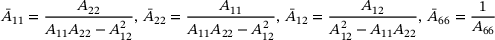
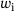 are included in the given representation. The compatibility equation is solved, obtaining a particular and homogeneous solution for the Airy stress function. Using a suitable ansatz, the particular solution
are included in the given representation. The compatibility equation is solved, obtaining a particular and homogeneous solution for the Airy stress function. Using a suitable ansatz, the particular solution 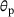 is obtained after inserting the buckling shape function w0 and imperfection
is obtained after inserting the buckling shape function w0 and imperfection 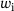 by comparison of coefficients. The resulting expression is given in Equation (17).
by comparison of coefficients. The resulting expression is given in Equation (17).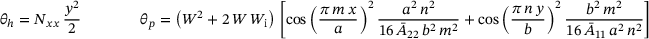 (17)
(17)2.3 Total elastic potential
 , the bending behaviour
, the bending behaviour  and the external forces
and the external forces 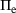 which are formulated in Equations (18-19)
which are formulated in Equations (18-19)
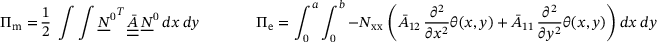 (18)
(18)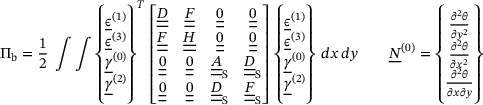 (19)
(19)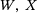 and Y as shown in Equation (20)
and Y as shown in Equation (20)
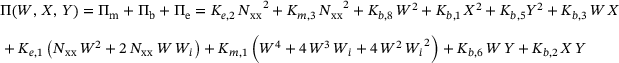 (20)
(20)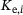 ,
, 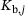 and
and 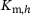 are computed based on the buckling shape functions, the dimensions, and the material properties of the panel. Based on the total elastic potential, a solution for the linear buckling analysis and the postbuckling analysis is derived in the next subsections. Both utilise the principle of the minimum of the total elastic potential that leads to the formulation of three Ritz-equations (21).
are computed based on the buckling shape functions, the dimensions, and the material properties of the panel. Based on the total elastic potential, a solution for the linear buckling analysis and the postbuckling analysis is derived in the next subsections. Both utilise the principle of the minimum of the total elastic potential that leads to the formulation of three Ritz-equations (21).
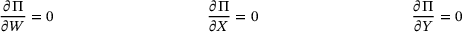 (21)
(21)2.4 Buckling analysis
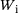 . This leads to the simplified expression in Equation (22).
. This leads to the simplified expression in Equation (22).
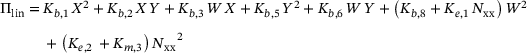 (22)
(22) (23)
(23)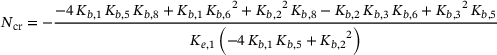 (24)
(24)2.5 Postbuckling analysis
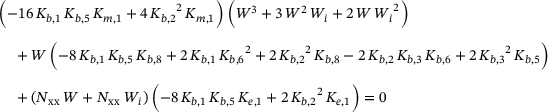 (25)
(25)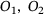 and O3, the nonlinear equation is expressed in a simplified form in Equation (26).
and O3, the nonlinear equation is expressed in a simplified form in Equation (26).
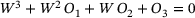 (26)
(26)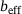 . The quality of the novel approximate solution is assessed in the next section in comparison with finite element analyses.
. The quality of the novel approximate solution is assessed in the next section in comparison with finite element analyses.3 RESULTS AND DISCUSSION
The simply supported plate investigated in the present work is a cross-ply square laminate with four layers. The laminate configuration is proposed by Reddy [2] for the comparison of the different laminated plate theories (CLPT, FSDT, TSDT) and for this reason, adopted in the following investigation. The material of the single layer is defined with the ratio between the two elastic moduli E1 and E2, which is set to 40. The Poisson's ratio is 0.25. The shear moduli are assumed as 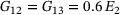 and
and 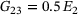 . The elastic modulus E2 is set to 1. The thickness aspect ratio is
. The elastic modulus E2 is set to 1. The thickness aspect ratio is 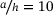 , if not stated otherwise.
, if not stated otherwise.
Before the postbuckling behaviour is analysed, the buckling behaviour is investigated. The presented results clearly motivate the necessity of the utilisation of SDT for shear deformable laminates.
In Figure 2A, the nondimensional critical buckling load is plotted based on the CLPT, FSDT, and TSDT versus the thickness aspect ratio 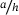 . It depicts the decrease of the critical buckling load due to the increasing thickness of the plate. Thus, the influence of shear deformation is not negligible. Because of this influence, also the postbuckling behaviour is affected, as illustrated in Figure 2B, where two exemplary load deflection curves are plotted for the thickness aspect ratios of
. It depicts the decrease of the critical buckling load due to the increasing thickness of the plate. Thus, the influence of shear deformation is not negligible. Because of this influence, also the postbuckling behaviour is affected, as illustrated in Figure 2B, where two exemplary load deflection curves are plotted for the thickness aspect ratios of 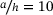 and
and 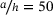 . Considering the results in the two figures, the motivation to investigate shear deformable laminates is affirmed, as the influence on the buckling and postbuckling behaviour is clear.
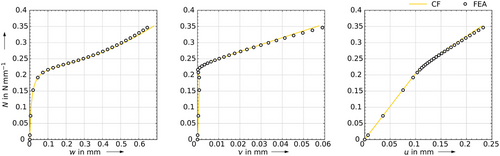
To assess the quality of the closed-form analytical solution, first, the behaviour of the displacements depending on the applied compressive loading is compared to finite element analysis in Figure 3. The load is evaluated for up to 1.5 times the critical buckling load. Consequently, the analysis considers only the early postbuckling regime. The agreement between the finite element analyses and the novel closed-form analytical model is very good for all three investigated displacements. The deviations become visible only for higher loads. It must be noted that also the initial imperfection is captured correctly by the analytical model. This is confirmed in Figure 4A, where the magnitude of the initial imperfection is varied from 0 to 0.02. The increasing imperfection results in increasing deflections in the area of the critical buckling load and significant deflections even before the bifurcation point of the perfect plate is reached. With increasing compression, the influence of the imperfection diminishes and the different curves converge.
. Considering the results in the two figures, the motivation to investigate shear deformable laminates is affirmed, as the influence on the buckling and postbuckling behaviour is clear.
To assess the quality of the closed-form analytical solution, first, the behaviour of the displacements depending on the applied compressive loading is compared to finite element analysis in Figure 3. The load is evaluated for up to 1.5 times the critical buckling load. Consequently, the analysis considers only the early postbuckling regime. The agreement between the finite element analyses and the novel closed-form analytical model is very good for all three investigated displacements. The deviations become visible only for higher loads. It must be noted that also the initial imperfection is captured correctly by the analytical model. This is confirmed in Figure 4A, where the magnitude of the initial imperfection is varied from 0 to 0.02. The increasing imperfection results in increasing deflections in the area of the critical buckling load and significant deflections even before the bifurcation point of the perfect plate is reached. With increasing compression, the influence of the imperfection diminishes and the different curves converge.

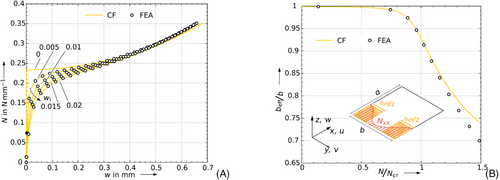
 by investigating the load deflection behaviour; (B) the behaviour of the effective width with increasing compression.
by investigating the load deflection behaviour; (B) the behaviour of the effective width with increasing compression.In Figure 4B, the behaviour of the effective width computed based on the internal load distribution is illustrated taking an initial imperfection of 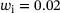 into account. It can be noted that the results of the present solution show good agreement, which is very suitable for approximate methods with a deviation of only approx. 6%.
into account. It can be noted that the results of the present solution show good agreement, which is very suitable for approximate methods with a deviation of only approx. 6%.
The present work proposes a novel simple closed-form analytical approximate solution for the postbuckling of shear deformable laminates. The discussed results show, that the analysis method is a computationally efficient alternative to numerical methods when the early postbuckling regime is considered. The quality of the new method is very suitable for preliminary design, where the number of function evaluations is high in the framework, for example, of an optimisation.
ACKNOWLEDGMENTS
The financial support of the German Research Foundation DFG [project number 426146527] is acknowledged with gratitude.
Open access funding enabled and organized by Projekt DEAL.




