The proximal map of the weighted mean absolute error
Abstract
We investigate the proximal map for the weighted mean absolute error function. An algorithm for its efficient and vectorized evaluation is presented. As a demonstration, this algorithm is applied to a nonsmooth energy minimization problem.
1 INTRODUCTION
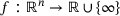 , the proximal map
, the proximal map 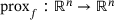 is defined as the solution of the problem
is defined as the solution of the problem
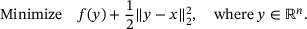 (1)
(1)Under the mild condition that f is proper, lower semicontinuous and convex, 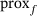 , is well defined. We refer the reader to [4, Ch. 12.4] for details and further properties. We also mention http://proximity-operator.net/
, where formulas and implementations of the proximal map for various functions have been collected.
, is well defined. We refer the reader to [4, Ch. 12.4] for details and further properties. We also mention http://proximity-operator.net/
, where formulas and implementations of the proximal map for various functions have been collected.
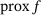 , where
, where 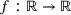 is defined as
is defined as
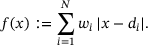 (2)
(2)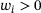 are given, positive weights and
are given, positive weights and 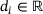 are given data,
are given data,  for some
for some 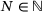 . We refer to (2) as the weighted mean absolute error. Any of its minimizers is known as a weighted median of the data
. We refer to (2) as the weighted mean absolute error. Any of its minimizers is known as a weighted median of the data 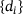 . Clearly, f is proper, continuous, and convex, and so is
. Clearly, f is proper, continuous, and convex, and so is 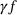 for any
for any 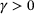 .
.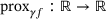 for f as in (2) is given by
for f as in (2) is given by
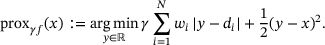 (3)
(3)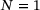 ), problem (3) reduces to the well-known problem
), problem (3) reduces to the well-known problem
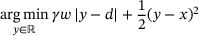 (4)
(4)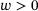 and
and 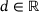 , whose unique solution is explicitly given in terms of the soft-thresholding operator
, whose unique solution is explicitly given in terms of the soft-thresholding operator 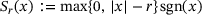 . In this case, we have
. In this case, we have
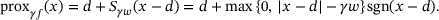 (5)
(5)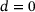 , arises in many iterative schemes for the solution of problems involving the 1-norm; see, for instance, [5, 6]. We can therefore view (3) as a multithresholding operation.
, arises in many iterative schemes for the solution of problems involving the 1-norm; see, for instance, [5, 6]. We can therefore view (3) as a multithresholding operation.
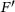 bijective. The prototypical examples are functions
bijective. The prototypical examples are functions 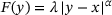 with
with 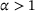 . We concentrate on the case
. We concentrate on the case 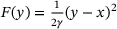 , which agrees with (3). The algorithm in [7] computes the solution of (3) by finding the median in the union of two sorted lists of cardinality N. By contrast, our implementation in1 finds an index in a single sorted list of cardinality N. In contrast to [7], we provide a vectorized, open-source implementation of (3) in [8].
, which agrees with (3). The algorithm in [7] computes the solution of (3) by finding the median in the union of two sorted lists of cardinality N. By contrast, our implementation in1 finds an index in a single sorted list of cardinality N. In contrast to [7], we provide a vectorized, open-source implementation of (3) in [8].This paper is structured as follows: We establish an algorithm for the evaluation of the proximal map of the weighted mean absolute error (3) in Section 2 and prove its correctness in Theorem 2.1. In Section 3, we briefly discuss the structural properties of the proximal map. We conclude by showing an application of the proposed algorithm to a nonsmooth energy minimization problem.
2 ALGORITHM FOR THE EVALUATION OF THE PROXIMAL MAP
In this section, we derive an efficient algorithm for the evaluation of the proximal map 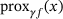 (3) and prove its correctness in Theorem 2.1. To this end, we assume that the points
(3) and prove its correctness in Theorem 2.1. To this end, we assume that the points 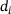 have been sorted and duplicates have been removed and their weights added. As a result, we can assume
have been sorted and duplicates have been removed and their weights added. As a result, we can assume 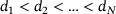 . Moreover, we assume
. Moreover, we assume 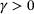 ,
,  and
and 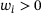 for all
for all 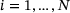 . Summands with
. Summands with 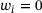 can obviously be dropped from the sum in (3).
can obviously be dropped from the sum in (3).
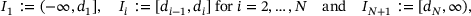 (6)
(6) and
and 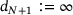 . We further introduce the forward and reverse cumulative weights as
. We further introduce the forward and reverse cumulative weights as
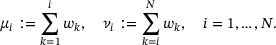
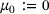 ,
, 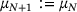 and
and 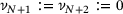 . We therefore have
. We therefore have 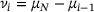 for all
for all 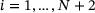 . Using this notation, we can rewrite the derivative of f as
. Using this notation, we can rewrite the derivative of f as
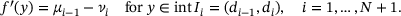
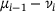 is monotonically increasing with i. Moreover,
is monotonically increasing with i. Moreover, 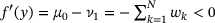 holds for all
holds for all 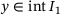 (points to the left of smallest data point d1), and
(points to the left of smallest data point d1), and 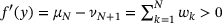 holds for all
holds for all 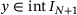 (points to the right of the largest data point
(points to the right of the largest data point 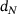 ). At
). At 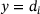 ,
, 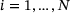 , f is nondifferentiable but we can specify its subdifferential, which is
, f is nondifferentiable but we can specify its subdifferential, which is

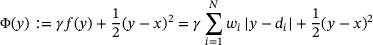 (7)
(7)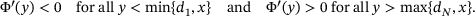
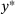 of (7) is to locate the smallest index
of (7) is to locate the smallest index 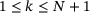 such that
such that 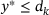 holds, that is, the nearest data point to the right of
holds, that is, the nearest data point to the right of 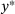 . In other words, we need to find
. In other words, we need to find 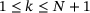 such that
such that
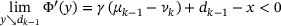 (8a)
(8a) (8b)
(8b)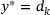 and
and 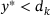 . The first case applies if and only if
. The first case applies if and only if
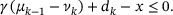
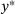 lies in
lies in 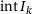 , and thus, it is the unique minimizer
, and thus, it is the unique minimizer 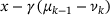 of the locally quadratic objective Φ. In either case, once the index
of the locally quadratic objective Φ. In either case, once the index 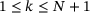 has been identified,
has been identified, 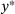 is given by
is given by
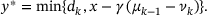 (9)
(9)The considerations above lead to Algorithm 1. In our implementation, we evaluate (10) for all k simultaneously and benefit from the quantities being monotone increasing with k when finding the first nonnegative entry.
ALGORITHM 1. Evaluation of (3), the proximal map of the weighted mean absolute error.
| Require: | data points 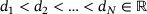 , ,  , and , and 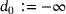 , , 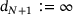 |
| Require: | weight vector  with entries with entries 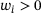 |
| Require: | prox parameter 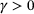 and point of evaluation and point of evaluation 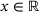 |
| Ensure: | 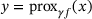 , the unique solution of (3) , the unique solution of (3) |
| 1: | Find the smallest index 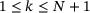 that satisfies that satisfies
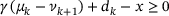 (10) (10) |
| 2: | return 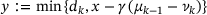 |
Let us prove the correctness of Algorithm 1.
Proof.Let 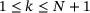 be the index found in Algorithm 1. First, suppose
be the index found in Algorithm 1. First, suppose 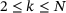 . Then
. Then 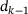 and
and 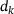 are both finite, and (8) and (10) imply
are both finite, and (8) and (10) imply
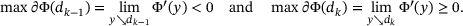
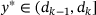 such that
such that 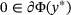 , that is,
, that is, 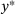 is the unique minimizer of (3). This point either belongs to
is the unique minimizer of (3). This point either belongs to 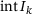 , or else
, or else 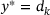 holds. In the first case, Φ is differentiable, so that
holds. In the first case, Φ is differentiable, so that 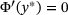 holds, yielding
holds, yielding
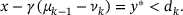
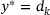 , and
, and 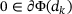 implies
implies
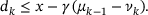
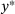 of (3) is determined by
of (3) is determined by 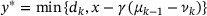 , which is the quantity returned in Algorithm 1.
, which is the quantity returned in Algorithm 1.It remains to verify the marginal cases 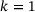 and
and 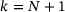 . In case
. In case 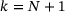 , we have
, we have 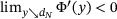 due to the minimality of k. Hence,
due to the minimality of k. Hence, 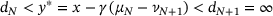 . A similar reasoning applies in the case
. A similar reasoning applies in the case 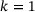 .
.
We provide an efficient and vectorized open-source Python implementation of Algorithm 1 in [8]. It allows the simultaneous evaluation of (3) for multiple values of x, provided that each instance of (3) has the same number N of data points. The weights 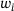 and data points
and data points 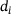 as well as the prox parameter γ may vary between instances. The discussion so far assumed positive weights for simplicity, but the case
as well as the prox parameter γ may vary between instances. The discussion so far assumed positive weights for simplicity, but the case 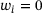 is a simple extension and it is allowed in our implementation. This is convenient in order to simultaneously solve problem instances that differ with respect to the number of data points N. In this case, we can easily pad all instances to the same number of data points using zero weights. In addition, data points are allowed to be duplicate, that is, we only require
is a simple extension and it is allowed in our implementation. This is convenient in order to simultaneously solve problem instances that differ with respect to the number of data points N. In this case, we can easily pad all instances to the same number of data points using zero weights. In addition, data points are allowed to be duplicate, that is, we only require 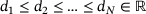 ,
,  . Notice that since the data points are assumed to be sorted, finding the index in Algorithm 1 is of complexity
. Notice that since the data points are assumed to be sorted, finding the index in Algorithm 1 is of complexity 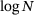 .
.
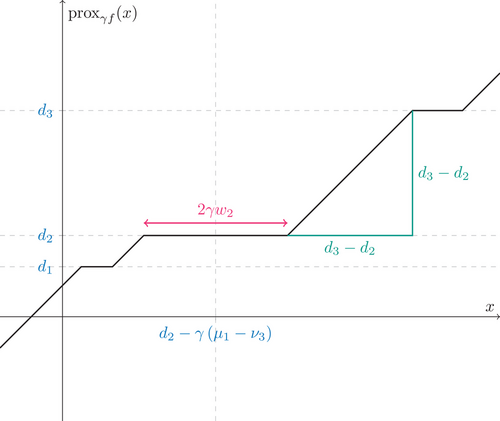
3 STRUCTURE OF 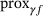
In this section, we briefly discuss the structure of the map 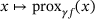 . Since it generalizes the soft-thresholding operation (5), it is not surprising that we obtain a graph that features a staircase pattern. An illustrative plot for certain choices of weights
. Since it generalizes the soft-thresholding operation (5), it is not surprising that we obtain a graph that features a staircase pattern. An illustrative plot for certain choices of weights 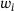 , data points
, data points  , and prox parameter
, and prox parameter 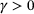 is shown in Figure 1. Each of the N distinct data points provides one plateau in the graph.
is shown in Figure 1. Each of the N distinct data points provides one plateau in the graph.
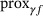 in case
in case 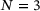 data points.
data points.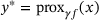 , as x ranges over
, as x ranges over 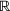 . First, when
. First, when 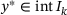 holds, then (9) implies that
holds, then (9) implies that 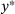 is an affine function of x with slope 1. This is the case for x whose associated index k is constant, that is,
is an affine function of x with slope 1. This is the case for x whose associated index k is constant, that is,
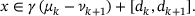
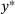 enters a constant regime that applies to
enters a constant regime that applies to
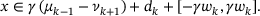
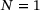 reduces to the soft-thresholding map (5) with only one plateau.
reduces to the soft-thresholding map (5) with only one plateau.4 APPLICATION TO A DEFLECTION ENERGY MINIMIZATION PROBLEM
In this section, we consider the minimization of the nonsmooth energy 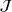 of a deflected membrane. We apply an alternating direction method of multiplier (ADMM) scheme that requires the parallel evaluation of the proximal map Algorithm 1 in each inner loop of the scheme.
of a deflected membrane. We apply an alternating direction method of multiplier (ADMM) scheme that requires the parallel evaluation of the proximal map Algorithm 1 in each inner loop of the scheme.
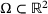 occupied by a thin membrane. In our model, the energy of this membrane is given in terms of its unknown deflection (displacement) function
occupied by a thin membrane. In our model, the energy of this membrane is given in terms of its unknown deflection (displacement) function 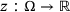 and it takes the following form:
and it takes the following form:
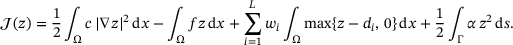 (11)
(11)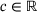 is the stiffness constant. The second term accounts for an external area force density f, which we assume to be a nonnegative function on Ω. Consequently, the deflection will be nonnegative as well. The specialty of our model is the third term, which can be interpreted as follows. The nonnegative constants
is the stiffness constant. The second term accounts for an external area force density f, which we assume to be a nonnegative function on Ω. Consequently, the deflection will be nonnegative as well. The specialty of our model is the third term, which can be interpreted as follows. The nonnegative constants 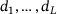 serve as thresholds.1
Once the deflection z at a point in Ω exceeds any of these thresholds
serve as thresholds.1
Once the deflection z at a point in Ω exceeds any of these thresholds 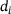 , an additional downward force of size
, an additional downward force of size 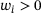 times the excess deflection activates. Finally, the fourth term models an additional potential energy due to springs along the boundary Γ of the domain with stiffness constant α. A related problem has been studied in [9] with an emphasis on a posteriori error analysis and adaptive solution.
times the excess deflection activates. Finally, the fourth term models an additional potential energy due to springs along the boundary Γ of the domain with stiffness constant α. A related problem has been studied in [9] with an emphasis on a posteriori error analysis and adaptive solution.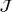 among all displacements
among all displacements 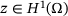 corresponds to the weak form of a partial differential equation (PDE), or rather a variational inequality. In fact, the necessary and sufficient optimality conditions for the minimization of (11) amount to
corresponds to the weak form of a partial differential equation (PDE), or rather a variational inequality. In fact, the necessary and sufficient optimality conditions for the minimization of (11) amount to
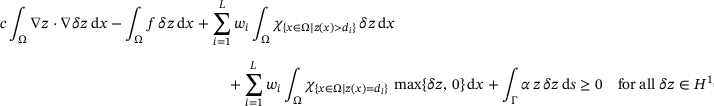 (12)
(12)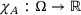 is the characteristic function of the set A with values in
is the characteristic function of the set A with values in 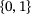 . Provided that the set
. Provided that the set 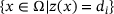 is of Lebesgue measure zero, the variational inequality (12) becomes an equation, whose strong form—using integration by parts—can be seen to be
is of Lebesgue measure zero, the variational inequality (12) becomes an equation, whose strong form—using integration by parts—can be seen to be
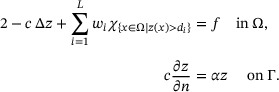
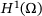 by some finite-dimensional subspace of piecewise linear, globally continuous finite element functions defined over a triangulation of Ω. Denoting the associated nodal basis by
by some finite-dimensional subspace of piecewise linear, globally continuous finite element functions defined over a triangulation of Ω. Denoting the associated nodal basis by 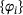 , we define the stiffness matrix
, we define the stiffness matrix
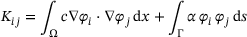
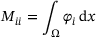
 when
when 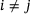 . The reason for using mass lumping to approximate all area integrals in (11) that do not involve derivatives is to translate the pointwise maximum operator into a coefficientwise one. This technique is crucial for an efficient numerical realization and has been used before, for example, in [10, 11].
. The reason for using mass lumping to approximate all area integrals in (11) that do not involve derivatives is to translate the pointwise maximum operator into a coefficientwise one. This technique is crucial for an efficient numerical realization and has been used before, for example, in [10, 11].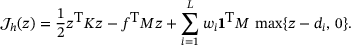 (13)
(13)The minimization of the convex but nonsmooth energy (13) is not straightforward. Our method of choice here is an ADMM scheme, which moves the nonsmooth terms into a separate subproblem, which can then be efficiently solved using Algorithm 1. We refer the reader to [12] and the references therein for an overview on ADMM.
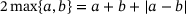 and arrive at
and arrive at
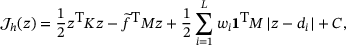 (14)
(14)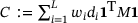 is a constant and
is a constant and  is a modification of the force vector. Moreover, the absolute value
is a modification of the force vector. Moreover, the absolute value  is understood coefficientwise. Dropping the constant C, introducing a second variable y, the constraint
is understood coefficientwise. Dropping the constant C, introducing a second variable y, the constraint 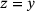 , and associated (scaled) Lagrange multiplier μ gives rise to the augmented Lagrangian
, and associated (scaled) Lagrange multiplier μ gives rise to the augmented Lagrangian
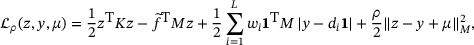 (15)
(15)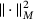 is the squared norm induced by the positive diagonal matrix M.
is the squared norm induced by the positive diagonal matrix M.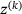 ,
, 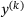 ,
,  according to the following update scheme;
according to the following update scheme;
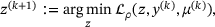 (16a)
(16a)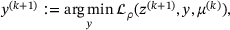 (16b)
(16b)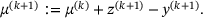 (16c)
(16c)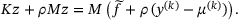
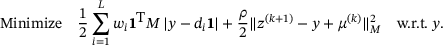 (17)
(17)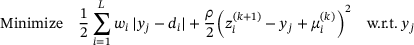 (18)
(18)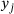 of y. This problem fits into the pattern of (3), and thus, can be solved efficiently and simultaneously for all components
of y. This problem fits into the pattern of (3), and thus, can be solved efficiently and simultaneously for all components 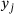 by Algorithm 1.
by Algorithm 1.
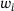 , and threshold deflections
, and threshold deflections 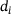 to be constant over the domains in each case, as
to be constant over the domains in each case, as
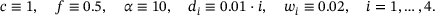 (19)
(19)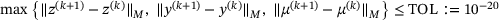 (20)
(20)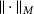 denotes the norm induced by the lumped mass matrix M. With this setup and
denotes the norm induced by the lumped mass matrix M. With this setup and 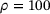 , the ADMM algorithm required 186 iterations for the problem on Ω1 and 278 iterations in case of Ω2. The resulting solutions z are shown in Figure 2.
, the ADMM algorithm required 186 iterations for the problem on Ω1 and 278 iterations in case of Ω2. The resulting solutions z are shown in Figure 2.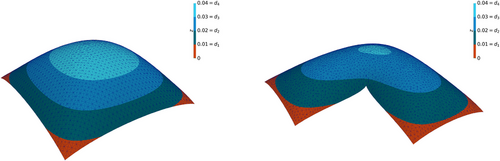
ACKNOWLEDGMENTS
This work was supported by DFG grants HE 6077/10–2 and SCHM 3248/2–2 within the Priority Program SPP 1962 (Nonsmooth and Complementarity-based Distributed Parameter Systems: Simulation and Hierarchical Optimization), which is gratefully acknowledged.
Open access funding enabled and organized by Projekt DEAL.
REFERENCES
- 1 We could also allow
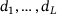 to be nonnegative functions on Ω, with minor modifications in what follows.
to be nonnegative functions on Ω, with minor modifications in what follows.



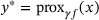 , the unique solution of (
, the unique solution of (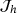 defined in (
defined in ( in (
in (
