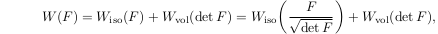Volume 22, Issue 1 e202200185

Section 14

Open Access

Remarks on rank-one convexity and quasiconvexity for planar functions with an additive volumetric–isochoric split

Robert J. Martin,

Robert J. Martin

[email protected]

Chair for Nonlinear Analysis and Modeling, University of Duisburg-Essen, Thea-Leymann-Str. 9, 45127 Essen, Germany

Institute for Technologies of Metals, University of Duisburg-Essen, Friedrich-Ebert-Str. 12,47119 Duisburg, Germany

Search for more papers by this author

Jendrik Voss,

Corresponding Author

Jendrik Voss

[email protected]

Chair for Nonlinear Analysis and Modeling, University of Duisburg-Essen, Thea-Leymann-Str. 9, 45127 Essen, Germany

Institute for Structural Mechanics and Dynamics, Technical University Dortmund, August-Schmidt-Str. 8, 44227 Dortmund, Germany

Jendrik Voss

Chair for Nonlinear Analysis and Modeling, University of Duisburg-Essen, Thea-Leymann-Str. 9, 45127 Essen, Germany

Institute for Structural Mechanics and Dynamics, Technical University Dortmund, August-Schmidt-Str. 8, 44227 Dortmund, Germany

Email: [email protected]

Search for more papers by this author

Oliver Sander,

Oliver Sander

[email protected]

Institute of Numerical Mathematics, Technische Universität Dresden, Zellescher Weg 12–14, 01069 Dresden, Germany

Search for more papers by this author

Patrizio Neff,

Patrizio Neff

[email protected]

Chair for Nonlinear Analysis and Modeling, University of Duisburg-Essen, Thea-Leymann-Str. 9, 45127 Essen, Germany

Search for more papers by this author

Robert J. Martin,

Robert J. Martin

[email protected]

Chair for Nonlinear Analysis and Modeling, University of Duisburg-Essen, Thea-Leymann-Str. 9, 45127 Essen, Germany

Institute for Technologies of Metals, University of Duisburg-Essen, Friedrich-Ebert-Str. 12,47119 Duisburg, Germany

Search for more papers by this author

Jendrik Voss,

Corresponding Author

Jendrik Voss

[email protected]

Chair for Nonlinear Analysis and Modeling, University of Duisburg-Essen, Thea-Leymann-Str. 9, 45127 Essen, Germany

Institute for Structural Mechanics and Dynamics, Technical University Dortmund, August-Schmidt-Str. 8, 44227 Dortmund, Germany

Jendrik Voss

Chair for Nonlinear Analysis and Modeling, University of Duisburg-Essen, Thea-Leymann-Str. 9, 45127 Essen, Germany

Institute for Structural Mechanics and Dynamics, Technical University Dortmund, August-Schmidt-Str. 8, 44227 Dortmund, Germany

Email: [email protected]

Search for more papers by this author

Oliver Sander,

Oliver Sander

[email protected]

Institute of Numerical Mathematics, Technische Universität Dresden, Zellescher Weg 12–14, 01069 Dresden, Germany

Search for more papers by this author

Patrizio Neff,

Patrizio Neff

[email protected]

Chair for Nonlinear Analysis and Modeling, University of Duisburg-Essen, Thea-Leymann-Str. 9, 45127 Essen, Germany

Search for more papers by this author

First published: 24 March 2023

https://doi.org/10.1002/pamm.202200185

About

PDF

Tools

Share a link

Email
Wechat
Bluesky

Abstract

We study convexity properties of isotropic energy functions in planar nonlinear elasticity in the context of Morrey's conjecture, which states that rank-one convexity does not imply quasiconvexity in the two-dimensional case. Recently, it has been shown that for the special case of isochoric energy functions on GL⁺(2) = {F ∈ ℝ^2×2 | det F > 0}, i.e. for any isotropic function W : GL⁺(2) → ℝ with W(aF) = W(F) for all a > 0, these two notions of generalized convexity are, in fact, equivalent. Here, we consider the more general case of functions on GL⁺(2) with an additive volumetric–isochoric split of the form

$urn:x-wiley:16177061:media:PAMM202200185:pamm202200185-math-0001$

with an isochoric function W_iso on GL⁺(2) and a function W_vol on (0, ∞). In particular, we investigate the importance of the function

$urn:x-wiley:16177061:media:PAMM202200185:pamm202200185-math-0002$

and its convexity properties; here, λ_max ≥ λ_min > 0 are the ordered singular values of the deformation gradient F ∈ GL⁺(2). This function arises naturally as an “extremal” case in the class of volumetric–isochorically split energies with respect to rank-one convexity.

References

1 J. M. Ball. “Convexity conditions and existence theorems in nonlinear elasticity”. Archive for Rational Mechanics and Analysis 63.4 (1976). Pp. 337–403.
Google Scholar
2 B. Dacorogna. Direct Methods in the Calculus of Variations. 2nd edition. Vol. 78. Applied Mathematical Sciences. Berlin: Springer, 2008.
Google Scholar
3 W. Fenchel and D. W. Blackett. Convex Cones, Sets, and Functions. Princeton University, Department of Mathematics, Logistics Research Project, 1953.
Google Scholar
4 J. K. Knowles and E. Sternberg. “On the failure of ellipticity of the equations for finite elastostatic plane strain”. Archive for Rational Mechanics and Analysis 63.4 (1976). Pp. 321–336.
Google Scholar
5 J. K. Knowles and E. Sternberg. “On the failure of ellipticity and the emergence of discontinuous deformation gradients in plane finite elastostatics”. Journal of Elasticity 8.4 (1978). Pp. 329–379.
Google Scholar
6 R. J. Martin, J. Voss, I.-D. Ghiba, O. Sander, and P. Neff. “The quasiconvex envelope of conformally invariant planar energy functions in isotropic hyperelasticity”. Journal of Nonlinear Science 30.6 (2020). Pp. 2885–2923.
Google Scholar
7 R. J. Martin, I.-D. Ghiba, and P. Neff. “Rank-one convexity implies polyconvexity for isotropic, objective and isochoric elastic energies in the two-dimensional case”. Proceedings of the Royal Society Edinburgh A 147A (2017). Pp. 571–597, available at arXiv:1507.00266
Google Scholar
8 R. J. Martin, J. Voss, I.-D. Ghiba, and P. Neff. “Quasiconvex relaxation of isotropic functions in incompressible planar hyperelasticity”. Proceedings of the Royal Society of Edinburgh Section A: Mathematics 150.5 (2020). Pp. 2620–2631.
Google Scholar
9 A. Mielke. “Necessary and sufficient conditions for polyconvexity of isotropic functions”. Journal of Convex Analysis 12.2 (2005). P. 291.
Google Scholar
10 C. B. Morrey. “Quasi-convexity and the lower semicontinuity of multiple integrals.” Pacific Journal of Mathematics 2.1 (1952). Pp. 25–53.
Google Scholar
11 C. B. Morrey. Multiple Integrals in the Calculus of Variations. Springer Science & Business Media, 2009.
Google Scholar
12 M. Šilhavỳ. The Mechanics and Thermodynamics of Continuous Media. Texts and Monographs in Physics. Springer, 1997.
Google Scholar
13 V. Šverák. “New examples of quasiconvex functions”. Archive for Rational Mechanics and Analysis 119.4 (1992). Pp. 293–300.
Google Scholar
14 V. Šverák. “Rank-one convexity does not imply quasiconvexity”. Proceedings of the Royal Society of Edinburgh Section A: Mathematics 120.1-2 (1992). Pp. 185–189.
Google Scholar
15 J. Voss, I.-D. Ghiba, R. J. Martin, and P. Neff. “Sharp rank-one convexity conditions in planar isotropic elasticity for the additive volumetric-isochoric split”. Journal of Elasticity 143.2 (2021). Pp. 301–335, available at arXiv:2008.04188
Google Scholar
16 J. Voss, R. J. Martin, I.-D. Ghiba, and P. Neff. “Morrey's conjecture for the planar volumetric-isochoric split: Least rank-one convex energy functions”. Journal of Nonlinear Science 32.76 (2022). Pp. 1–49.
Google Scholar
17 J. Voss, R. J. Martin, O. Sander, S. Kumar, D. M. Kochman, and P. Neff. “Numerical approaches for investigating quasiconvexity in the context of Morrey's conjecture”. Journal of Nonlinear Science 32.77 (2022). Pp. 1–41.
Google Scholar