Poiseuille-Type Fluid Transport in Poro-Elastic Solids at Fracture

Hydraulic fracturing has led to controversial public debates about its risks due to environmental issues, such as increased seismic activity or drinking water contamination. The technique is primarily used to gain crude oil or natural gas from unconventional wells. To this end, a high pressurized fracking fluid is injected into a wellbore to fracture deep-rock formations, leading to growing cracks, a subsequent increase of permeability in these formations and thus to an increased flow of natural gas and crude oil. To weight the risks and the perspectives of hydraulic fracturing a profound understanding of the involved processes is crucial. Numerical simulations are the most cost efficient way for the required studies, but demand a reliable model with a stable implementation.

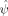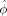We propose a canonical minimization principle for the Biot-type fluid transport in porous media based on only two constitutive functions, that is the free energy function , and a dissipation potential , [1]. This formulation is coupled to a phase-field approach for fracture which characterizes an intuitive and descriptive regularization of a crack surface that converges for vanishing length-scale parameter to a sharp crack. The crack phase-field allows for a distinct incorporation of an extra fluid flow within cracked regimes of the solid [2]. This extra fluid flow is modeled according to Poiseuille law for laminar flow, yielding an implementation via a change of the permeability tensor, i. e., making it a function of the crack opening width, formulated itself in terms of the strain and the gradient of the crack phase field. © 2016 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim)