Networks
Volume 84, Issue 4 pp. 481-490
RESEARCH ARTICLE
Open Access

A dynamic programming algorithm for order picking in robotic mobile fulfillment systems

Jan-Erik Justkowiak, 

Corresponding Author

Jan-Erik Justkowiak

Institute of Information Systems, Faculty III, University of Siegen, Siegen, Germany

Correspondence

Jan-Erik Justkowiak, Institute of Information Systems, Faculty III, University of Siegen, 57068, Siegen, Germany.

Email: [email protected]

Search for more papers by this author
Mikhail Y. Kovalyov, 

Mikhail Y. Kovalyov

United Institute of Informatics Problems, National Academy of Sciences of Belarus, Minsk, Belarus

Search for more papers by this author
Erwin Pesch, 

Erwin Pesch

Institute of Information Systems, Faculty III, University of Siegen, Siegen, Germany

Search for more papers by this author
First published: 28 July 2024
https://doi.org/10.1002/net.22245
Citations: 3

Abstract

The order scheduling and rack sequencing problem deals with the order picking process in robotic mobile fulfillment systems: automated guided vehicles lift and transport movable storage racks to picking stations to supply items requested by customer orders which are put together in cardboard boxes on a workbench of limited capacity. To efficiently operate the station, the sequence in which racks visit the station one after another and the intervals at which customer orders are scheduled must be coordinated. We present a dynamic programming algorithm for the order scheduling and rack sequencing problem at a single picking station minimizing the number of rack visits. Despite monolithic mixed integer linear programming formulations, our approach appears to be the first combinatorial solution method for the problem in literature. A computational study demonstrates the effectiveness of the approach.

1 INTRODUCTION

Order picking in robotic mobile fulfillment systems (a type of semiautomatic warehouse) is driven by automated guided vehicles that are equipped with a lifting mechanism to hoist movable racks containing items in their storage locations. The racks are transported to stationary picking stations, each of which is operated by a warehouse employee, to supply requested items to picked orders. This way, robotic mobile fulfillment systems put the so-called parts-to-picker paradigm into practice and operate at a higher pick rate than traditional picker-to-parts systems [8, 16]. Installations of such systems are increasingly found in the e-commerce sector and in business-to-customer supply chains with tight delivery deadlines [1, 5].

The workflow in a robotic mobile fulfillment system can be outlined as follows: incoming items enter the warehouse through inbound docks and the stock levels of racks are refilled at the nearby replenishment stations. The order picking takes place at stationary picking stations, and completed customer orders are forwarded to the outbound docks for final shipping. Automated guided vehicles perform transportation tasks, that is, moving racks from the storage area to replenishment or picking stations. Racks that are currently unused are parked in the rack storage area.

We are particularly interested in the customer order handling at a single picking station according to the problem description of [4]. There is a service area with a workbench to place a limited number of bins or cardboard boxes at a time, each of which corresponds to a customer order and intended for the items purchased by the customer. Racks queue up at the station to supply the requested items which are picked from the racks by a warehouse employee and put into the relevant bin, but only the front rack of the queue is available to the picker. If the front rack cannot provide any items for the orders currently on the workbench, then the rack is released either to the storage area or it is moved to some subsequent position in the rack queue to revisit the station and the next rack is presented to the picker. Once a customer bin contains all requested items, it is moved to the outbound area and the bin of the next scheduled order takes its place.

As the total number of orders allocated to the picking station usually exceeds the number of bins the service area can handle simultaneously, operators must synchronize the sequence in which racks are presented to the picker and the intervals at which customer orders are scheduled to efficiently operate the station. In this regard, minimizing the number of rack visits (that is, each time a rack is presented to the picker) shortens the order picking makespan and allows to reduce the fleet size of automated guided vehicles [4].

1.1 Literature

Decision planning in robotic mobile fulfillment systems has attracted many research efforts in the recent years [2]. Here we solely consider research specifically addressing the order scheduling and rack sequencing problem. For the upstream order allocation to picking stations we refer the reader to [9, 13, 17, 18].

Boysen et al. [4] introduce the order scheduling and rack sequencing problem at a single picking station with rack visit minimization and prove that it is strongly NP-hard. The authors propose a mixed integer linear programming (MILP) formulation as well as several heuristics, with two of them including dynamic programming to either solve the problem for a given rack sequence or for a given order schedule. Valle and Beasley [13] and Justkowiak and Pesch [11] propose MILP formulations as well, the former investigating a slightly different problem setting (stock levels are observed exactly and for a fixed predefined number of rack visits a feasible solution is determined). Justkowiak and Pesch [10, 11] present several heuristics, including preprocessing techniques, and a special-case analysis. A generalization of the problem with multiple picking stations is considered in [14, 19, 20]. The authors propose MILP formulations and heuristic solution approaches. Boysen et al. [6] review and structure various synchronization problems arising in the order picking process of parts-to-picker systems. They apply a classification scheme to systematically analyze computational complexity and derive exact solution procedures for problems shown to be solvable in polynomial time.

1.2 Contribution

There are several heuristics and decision-rule based real-world policies for the order scheduling and rack sequencing problem, but despite MILP formulations there is a lack of exact solution approaches in literature [10]. We develop a dynamic programming approach to optimally solve the problem and evaluate its performance on a broad set of instances in a comparative computational study.

The solution process is accelerated by lower bounds to prune suboptimal states during the search, though computing the bounds requires a mathematical optimization solver. Bringing together the latter with dynamic programming, we refer to the methodology of our approach as dynamath (similar to e.g., dynasearch [7] and matheuristics [12]), a combination that, to the best of our knowledge, has not been proposed in literature.

2 PROBLEM DEFINITION

In the order scheduling and rack sequencing problem with rack visit minimization at a single picking station according to [4], we are given a set O $$ O $$ of customer orders, a set R $$ R $$ of racks solely available to this station, a set I $$ I $$ of items and the capacity B ∈ ℕ $$ B\in \mathbb{N} $$ of the service area, that is, the number of orders that can be handled on the workbench simultaneously. The given set of items requested by the customer of order o ∈ O $$ o\in O $$ is denoted as I o ⊆ I $$ {I}_o\subseteq I $$ . Similarly, the given set of items supplied by rack r ∈ R $$ r\in R $$ is referred to as I r ⊆ I $$ {I}_r\subseteq I $$ . It is assumed that there is an unlimited stock of item i ∈ I r $$ i\in {I}_r $$ on rack r $$ r $$ , r ∈ R $$ r\in R $$ .

The problem description closely follows the formalization introduced by [10]: with σ $$ \sigma $$ we refer to the sequence in which the racks are presented to the picker one after another, | σ | $$ \mid \sigma \mid $$ is the length of the rack sequence (i.e., the number of rack visits), and σ ( p ) ∈ R $$ \sigma (p)\in R $$ denotes the rack that is assigned to position p ∈ { 1 , … , | σ | } $$ p\in \left\{1,\dots, |\sigma |\right\} $$ in the sequence. The order processing schedule is defined by intervals ( b o , c o ) $$ \left({b}_o,{c}_o\right) $$ , ∀ o ∈ O $$ \forall o\in O $$ , with b o , c o ∈ { 1 , … , | σ | } $$ {b}_o,{c}_o\in \left\{1,\dots, |\sigma |\right\} $$ and b o ≤ c o $$ {b}_o\le {c}_o $$ , indicating that o $$ o $$ is moved to the service area while the rack at position b o $$ {b}_o $$ is with the picker (i.e., the processing of o $$ o $$ starts and o $$ o $$ occupies a bin position until its completion), and passed from the service area to the outbound docks while the rack at position c o $$ {c}_o $$ is with the picker (the processing of o $$ o $$ completes). A feasible rack sequence σ $$ \sigma $$ and an order processing schedule ( b o , c o ) , ∀ o ∈ O $$ \left({b}_o,{c}_o\right),\forall o\in O $$ , have to meet the following conditions:
  1. The items I o $$ {I}_o $$ requested by the customer of order o ∈ O $$ o\in O $$ must be taken exclusively from (some of) the racks assigned to positions between b o $$ {b}_o $$ and c o $$ {c}_o $$ , both inclusive. Formally, I o ⊆ ⋃ p = b o c o I σ ( p ) $$ {I}_o{\subseteq \bigcup}_{p={b}_o}^{c_o}{I}_{\sigma (p)} $$ , ∀ o ∈ O $$ \forall o\in O $$ .
  2. The number of started but uncompleted orders in the service area while the rack assigned to position p ∈ P $$ p\in P $$ is accessible to the picker, must not exceed B $$ B $$ . More precisely, ∀ p ∈ P : | { o ∈ O | b o ≤ p < c o } | ≤ B $$ \forall p\in P:\mid \left\{o\in O|{b}_o\le p<{c}_o\right\}\mid \le B $$ . Note that this condition concerns orders each of which is serviced by at least two racks. It does not restrict the number of orders o ∈ O $$ o\in O $$ with b o = p = c o $$ {b}_o=p={c}_o $$ .
  3. If there are B $$ B $$ orders in the service area when the rack at position p ∈ P $$ p\in P $$ becomes available to the picker, and none of these orders currently in the service area can be completed by the rack σ ( p ) $$ \sigma (p) $$ , then no order can be started and completed during σ ( p ) $$ \sigma (p) $$ 's current accessibility. In particular, if for position p ∈ P $$ p\in P $$ holds | { o ∈ O | b o < p < c o } | = B $$ \mid \left\{o\in O|{b}_o<p<{c}_o\right\}\mid =B $$ , then we require | { o ∈ O | b o = p = c o } | = 0 $$ \mid \left\{o\in O|{b}_o=p={c}_o\right\}\mid =0 $$ . Observe that the number of orders o ∈ O $$ o\in O $$ with b o = p = c o $$ {b}_o=p={c}_o $$ is not limited if | { o ∈ O | b o < p < c o } | < B $$ \mid \left\{o\in O|{b}_o<p<{c}_o\right\}\mid <B $$ .

We require a feasible order schedule and rack sequence with minimal | σ | $$ \mid \sigma \mid $$ , thus minimizing the number of rack visits. We repeat that a single picking station case is considered with the racks solely available to this station.

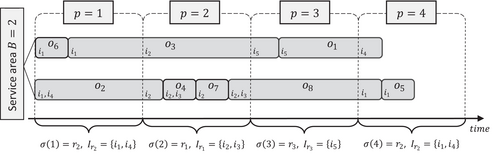
Example. (Optimal order schedule and rack sequence)Consider a picking station with B = 2 $$ B=2 $$ , orders O = { o 1 , … , o 8 } $$ O=\left\{{o}_1,\dots, {o}_8\right\} $$ with I o 1 = { i 4 , i 5 } $$ {I}_{o_1}=\left\{{i}_4,{i}_5\right\} $$ , I o 2 = { i 1 , i 2 , i 4 } $$ {I}_{o_2}=\left\{{i}_1,{i}_2,{i}_4\right\} $$ , I o 3 = { i 1 , i 2 , i 5 } $$ {I}_{o_3}=\left\{{i}_1,{i}_2,{i}_5\right\} $$ , I o 4 = { i 2 , i 3 } $$ {I}_{o_4}=\left\{{i}_2,{i}_3\right\} $$ , I o 5 = { i 1 } $$ {I}_{o_5}=\left\{{i}_1\right\} $$ , I o 6 = { i 1 } $$ {I}_{o_6}=\left\{{i}_1\right\} $$ , I o 7 = { i 2 } $$ {I}_{o_7}=\left\{{i}_2\right\} $$ , I o 8 = { i 1 , i 2 , i 3 } $$ {I}_{o_8}=\left\{{i}_1,{i}_2,{i}_3\right\} $$ , and racks R = { r 1 , r 2 , r 3 } $$ R=\left\{{r}_1,{r}_2,{r}_3\right\} $$ with I r 1 = { i 2 , i 3 } $$ {I}_{r_1}=\left\{{i}_2,{i}_3\right\} $$ , I r 2 = { i 1 , i 4 } $$ {I}_{r_2}=\left\{{i}_1,{i}_4\right\} $$ , and I r 3 = { i 5 } $$ {I}_{r_3}=\left\{{i}_5\right\} $$ .

Figure 1 shows an optimal order schedule and rack sequence with four rack visits. Using the notation introduced above, the order schedule of, for example, o 8 $$ {o}_8 $$ , is defined by ( 2 , 4 ) $$ \left(2,4\right) $$ . Let us describe the picking process at one of the bin positions in the service area in detail, for instance at the lower one where o 2 $$ {o}_2 $$ , o 4 $$ {o}_4 $$ , o 7 $$ {o}_7 $$ , o 8 $$ {o}_8 $$ , and o 5 $$ {o}_5 $$ are processed sequentially over time. Order o 2 $$ {o}_2 $$ is moved to the service area first and the requested items i 1 $$ {i}_1 $$ and i 4 $$ {i}_4 $$ are picked. The order is completed when the rack at the second position is with the picker, as it supplies the missing item i 2 $$ {i}_2 $$ . Then, the vacant bin position is taken by order o 4 $$ {o}_4 $$ , which is completed immediately as r 1 $$ {r}_1 $$ stores the requested items i 2 $$ {i}_2 $$ and i 3 $$ {i}_3 $$ , similar to o 7 $$ {o}_7 $$ followed by order o 8 $$ {o}_8 $$ , which is only partially processed (picking items i 2 $$ {i}_2 $$ and i 3 $$ {i}_3 $$ ) by the rack at the second position. Eventually, o 8 $$ {o}_8 $$ 's missing item i 1 $$ {i}_1 $$ is available at position four to complete the order. Then o 5 $$ {o}_5 $$ is moved to the service area and completed by the rack assigned to the fourth position as well. In the example above the optimal solution is not unique, for example, o 5 $$ {o}_5 $$ can be processed at the first position before o 2 $$ {o}_2 $$ .

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Schematic order picking illustration.

3 DYNAMIC PROGRAMMING ALGORITHM

We propose a dynamic programming algorithm to solve the problem exactly. The general idea of the algorithm is described in Section 3.1, while Section 3.2 provides more technical details. In the latter subsection, we also introduce a problem specific pruning technique and sorting rules to reduce the search space and to accelerate the runtime of the algorithm in practice. The dynamic programming algorithm is referred to as DP in the following.

3.1 Overview

In the algorithm DP, partial solutions are constructed, each of which is characterized by a set of parameters called state. The state is represented by a triple ( X , Y , Z ) $$ \left(X,Y,Z\right) $$ , which consists of a set X ⊆ O $$ X\subseteq O $$ of completed orders (that have been immediately moved from the service area to the outbound docks for shipping), by a set Y ⊆ O ∖ X $$ Y\subseteq O\setminus X $$ of uncompleted orders in the service area with | Y | ≤ B $$ \mid Y\mid \le B $$ (currently occupying bin positions), and by a set of tuples Z ⊂ { ( o , i ) | o ∈ Y , i ∈ I o } $$ Z\subset \left\{\left(o,i\right)|o\in Y,i\in {I}_o\right\} $$ to track missing items i ∈ I o $$ i\in {I}_o $$ of order o ∈ Y $$ o\in Y $$ . In terms of the problem formalization introduced in Section 2, each triple ( X , Y , Z ) $$ \left(X,Y,Z\right) $$ is associated with a position p ∈ { 1 , … , | σ | } $$ p\in \left\{1,\dots, |\sigma |\right\} $$ in the rack sequence σ $$ \sigma $$ and defines the state of the picking station once the rack σ ( p ) $$ \sigma (p) $$ at position p $$ p $$ leaves the picker.

We call a state ( X 0 , Y 0 , Z 0 ) $$ \left({X}^0,{Y}^0,{Z}^0\right) $$ a predecessor of the state ( X , Y , Z ) $$ \left(X,Y,Z\right) $$ if ( X 0 , Y 0 , Z 0 ) $$ \left({X}^0,{Y}^0,{Z}^0\right) $$ can be translated into ( X , Y , Z ) $$ \left(X,Y,Z\right) $$ by a single rack. The so-called translation process depicts the three-stage workflow at a picking station when a rack r ∈ R $$ r\in R $$ is presented to the picker. The stages s = 1 , 2 , 3 $$ s=1,2,3 $$ are performed successively over time:
  • Stage 1

    (Process orders currently in the service area). Rack r $$ r $$ is presented to the picker and missing items of orders currently in the service area, which are supplied by r $$ r $$ , are retrieved from the rack. Completed orders are immediately removed from the service area (e.g., order o 6 $$ {o}_6 $$ at p = 1 $$ p=1 $$ or order o 2 $$ {o}_2 $$ at p = 2 $$ p=2 $$ in Figure 1), thus releasing bin positions. Partially completed orders remain in the service area (e.g., order o 2 $$ {o}_2 $$ at p = 1 $$ p=1 $$ or o 3 $$ {o}_3 $$ at p = 2 $$ p=2 $$ in Figure 1).

  • Stage 2

    (Add and complete orders). Given that there is a vacant bin position available after the first stage, all unprocessed orders from the set O r ′ : = { o ∈ O | I o ⊆ I r } $$ {O}_r^{\prime}:= \left\{o\in O|{I}_o\subseteq {I}_r\right\} $$ that can be taken from rack r $$ r $$ are completed and moved to the outbound area during the rack's current stop at the picker (e.g., order o 6 $$ {o}_6 $$ at p = 1 $$ p=1 $$ or orders o 4 $$ {o}_4 $$ and o 7 $$ {o}_7 $$ at p = 2 $$ p=2 $$ in Figure 1). Note that a single empty bin position is sufficient to process orders from O r ′ $$ {O}_r^{\prime } $$ one by one.

  • Stage 3

    (Add and partially complete orders). Denote by U r $$ {U}_r $$ a subset of yet unprocessed orders from the set O r : = { o ∈ O | I o ∩ I r ≠ ∅ ∧ o ∉ O r ′ } $$ {O}_r:= \left\{o\in O|{I}_o\cap {I}_r\ne \varnothing \wedge o\notin {O}_r^{\prime}\right\} $$ that can partially be completed by rack r $$ r $$ , including the case of U r = ∅ $$ {U}_r=\varnothing $$ . Assign orders from U r $$ {U}_r $$ to the service area. The cardinality of U r $$ {U}_r $$ is bounded from above by the number of empty bin positions available after the first stage and requested items that are supplied by r $$ r $$ are taken from the rack (e.g., order o 3 $$ {o}_3 $$ at p = 1 $$ p=1 $$ or order o 8 $$ {o}_8 $$ at p = 2 $$ p=2 $$ in Figure 1). Then, rack r $$ r $$ leaves the picker and the orders currently in the service area will be completed by some subsequent rack(s) in the queue later on.

In the workflow description we implicitly assume obvious properties of an optimal solution: there is no point of delaying orders in the first and second stage, and upon the decision of which orders are assigned to the service area in the third stage the requested items supplied by rack r $$ r $$ will be picked. Note, moving an order to the service area can be delayed until a rack is available that provides at least one item requested by the order.

In the following, we introduce sets X r ( s ) $$ {X}_r^{(s)} $$ , Y r ( s ) $$ {Y}_r^{(s)} $$ , and Z r ( s ) $$ {Z}_r^{(s)} $$ , for r ∈ R $$ r\in R $$ and s = 1 , 2 , 3 $$ s=1,2,3 $$ , to track changes of X 0 $$ {X}^0 $$ , Y 0 $$ {Y}^0 $$ , and Z 0 $$ {Z}^0 $$ induced by rack r $$ r $$ after the first ( s = 1 $$ s=1 $$ ), second ( s = 2 $$ s=2 $$ ), and third stage ( s = 3 $$ s=3 $$ ) according to the workflow description, that is, after stage s $$ s $$ has passed with rack r $$ r $$ presented to the picker, X r ( s ) $$ {X}_r^{(s)} $$ denotes the updated set of completed orders, Y r ( s ) $$ {Y}_r^{(s)} $$ denotes the uncompleted orders currently in the service area, and Z r ( s ) $$ {Z}_r^{(s)} $$ indicates the missing items of orders Y r ( s ) $$ {Y}_r^{(s)} $$ . Using this notation, we are now equipped to properly formalize the translation process outlined above. For any r ∈ R $$ r\in R $$ and s = 1 $$ s=1 $$ we define:
Z r ( 1 ) = { ( o , i ) ∈ Z 0 | i ∉ I r } , Y r ( 1 ) = { o ∈ Y 0 | ∃ i ∈ I o : ( o , i ) ∈ Z r ( 1 ) } , X r ( 1 ) = X 0 ∪ ( Y 0 ∖ Y r ( 1 ) ) . $$ {Z}_r^{(1)}=\left\{\left(o,i\right)\in {Z}^0|i\notin {I}_r\right\},\kern1.30em {Y}_r^{(1)}=\left\{o\in {Y}^0|\exists i\in {I}_o:\left(o,i\right)\in {Z}_r^{(1)}\right\},\kern1.30em {X}_r^{(1)}={X}^0\cup \left({Y}^0\setminus {Y}_r^{(1)}\right). $$ (1)
With respect to the second and third stage, we first determine the number B ′ = B − | Y r ( 1 ) | $$ {B}^{\prime }=B-\mid {Y}_r^{(1)}\mid $$ of vacant bin positions in the service area once the first stage has passed. Then, it holds
Z r ( 2 ) = Z r ( 1 ) , Y r ( 2 ) = Y r ( 1 ) , if B ′ > 0 then X r ( 2 ) = X r ( 1 ) ∪ O r ′ else X r ( 2 ) = X r ( 1 ) , $$ {Z}_r^{(2)}={Z}_r^{(1)},\kern1em {Y}_r^{(2)}={Y}_r^{(1)},\kern1em \mathrm{if}\kern0.3em {B}^{\prime }>0\kern0.3em \mathrm{then}\kern0.3em {X}_r^{(2)}={X}_r^{(1)}\cup {O}_r^{\prime}\kern1em \mathrm{else}\kern0.3em {X}_r^{(2)}={X}_r^{(1)}, $$ (2)
as the orders O r ′ $$ {O}_r^{\prime } $$ flow through a single vacant bin position one after another and are immediately assigned to the set X r ( 2 ) $$ {X}_r^{(2)} $$ of completed orders. Thus, there is no change in Z r ( 2 ) $$ {Z}_r^{(2)} $$ and Y r ( 2 ) $$ {Y}_r^{(2)} $$ .
No additional orders complete in the third stage, that is, X r ( 3 ) = X r ( 2 ) $$ {X}_r^{(3)}={X}_r^{(2)} $$ . Denote by U r $$ {U}_r $$ the set of orders in the third stage of the workflow description which are moved to the service area and are partially completed by the rack r $$ r $$ currently available for the picker. Then, we call a state ( X 0 , Y 0 , Z 0 ) $$ \left({X}^0,{Y}^0,{Z}^0\right) $$ a predecessor of state ( X , Y , Z ) $$ \left(X,Y,Z\right) $$ if and only if there is a rack r ∈ R $$ r\in R $$ and a set U r $$ {U}_r $$ with U r ⊆ O r ∖ ( X r ( 3 ) ∪ Y r ( 2 ) ) $$ {U}_r\subseteq {O}_r\setminus \left({X}_r^{(3)}\cup {Y}_r^{(2)}\right) $$ , | U r | ≤ B ′ $$ \mid {U}_r\mid \le {B}^{\prime } $$ , and
X = X r ( 3 ) , Y = Y r ( 2 ) ∪ U r ⏟ = Y r ( 3 ) , Z = Z r ( 2 ) ∪ { ( o , i ) | o ∈ U r , i ∈ I o ∖ I r } ⏟ = Z r ( 3 ) . $$ X={X}_r^{(3)},\kern1em Y=\underset{={Y}_r^{(3)}}{\underbrace{Y_r^{(2)}\cup {U}_r}},\kern1em Z=\underset{={Z}_r^{(3)}}{\underbrace{Z_r^{(2)}\cup \left\{\left(o,i\right)|o\in {U}_r,i\in {I}_o\setminus {I}_r\right\}}}. $$ (3)
Let 𝒱 ( X , Y , Z ) be the set of predecessors of state ( X , Y , Z ) $$ \left(X,Y,Z\right) $$ and denote by Γ ( X , Y , Z ) $$ \Gamma \left(X,Y,Z\right) $$ the minimum number of rack visits that lead to the state ( X , Y , Z ) $$ \left(X,Y,Z\right) $$ . The recursion of DP can then be written as
Γ ( X , Y , Z ) = min ( X 0 , Y 0 , Z 0 ) ∈ 𝒱 ( X , Y , Z ) { Γ ( X 0 , Y 0 , Z 0 ) } + 1 , (4)
with Γ ( ∅ , ∅ , ∅ ) = 0 $$ \Gamma \left(\varnothing, \varnothing, \varnothing \right)=0 $$ . The optimal solution value equals Γ ( O , ∅ , ∅ ) $$ \Gamma \left(O,\varnothing, \varnothing \right) $$ .

3.2 State pruning (dynamath)

It is convenient to generate states in a forward fashion starting from ( ∅ , ∅ , ∅ ) $$ \left(\varnothing, \varnothing, \varnothing \right) $$ , especially in light of the pruning technique and sorting rules that are introduced in this subsection to reduce the state space. For each current state ( X 0 , Y 0 , Z 0 ) $$ \left({X}^0,{Y}^0,{Z}^0\right) $$ , only those successor states ( X , Y , Z ) $$ \left(X,Y,Z\right) $$ are generated that can be derived according to the translation process, that is, ( X 0 , Y 0 , Z 0 ) ∈ 𝒱 ( X , Y , Z ) . Generated states are added to the set 𝒮 of states.

Denote by Γ ^ ( X , Y , Z ) $$ \hat{\Gamma}\left(X,Y,Z\right) $$ the currently best known upper bound on Γ ( X , Y , Z ) $$ \Gamma \left(X,Y,Z\right) $$ for a state ( X , Y , Z ) $$ \left(X,Y,Z\right) $$ . We define Γ ^ ( X , Y , Z ) : = ∞ $$ \hat{\Gamma}\left(X,Y,Z\right):= \infty $$ if the state ( X , Y , Z ) $$ \left(X,Y,Z\right) $$ has not (yet) been generated (i.e., ( X , Y , Z ) ∉ 𝒮 ). The value Γ ^ ( X , Y , Z ) $$ \hat{\Gamma}\left(X,Y,Z\right) $$ is successively improved when generating states in a forward fashion, particularly, if a state ( X , Y , Z ) $$ \left(X,Y,Z\right) $$ is generated multiple times (called copies), then we keep only a single copy with minimal Γ ^ ( X , Y , Z ) $$ \hat{\Gamma}\left(X,Y,Z\right) $$ to meet Equation (4) and store the corresponding predecessor and the translating rack to track the (partial) best solution. The incumbent solution value Γ ^ ( O , ∅ , ∅ ) $$ \hat{\Gamma}\left(O,\varnothing, \varnothing \right) $$ is referred to as γ ^ $$ \hat{\gamma} $$ in the following.

To prune suboptimal states we evaluate if a non-final state ( X 0 , Y 0 , Z 0 ) ≠ ( O , ∅ , ∅ ) $$ \left({X}^0,{Y}^0,{Z}^0\right)\ne \left(O,\varnothing, \varnothing \right) $$ with γ 0 $$ {\gamma}^0 $$ rack visits cannot lead to a solution with a smaller value than γ ^ $$ \hat{\gamma} $$ . Therefore, we calculate a lower bound on the number of rack visits required to translate ( X 0 , Y 0 , Z 0 ) $$ \left({X}^0,{Y}^0,{Z}^0\right) $$ to the final state ( O , ∅ , ∅ ) $$ \left(O,\varnothing, \varnothing \right) $$ , which equals the minimum number of racks to cover the set I res : = ∪ o ∈ O ∖ ( X 0 ∪ Y 0 ) I o ∪ { i ∈ I | ∃ o ∈ Y 0 : ( o , i ) ∈ Z 0 } $$ {I}^{\mathrm{res}}:= {\cup}_{o\in O\setminus \left({X}^0\cup {Y}^0\right)}{I}_o\kern0.3em \cup \kern0.3em \left\{i\in I|\exists o\in {Y}^0:\left(o,i\right)\in {Z}^0\right\} $$ of missing items. We denote this lower bound for a given I res $$ {I}^{\mathrm{res}} $$ as γ _ ( I res ) $$ \underset{\_}{\gamma}\left({I}^{\mathrm{res}}\right) $$ and prune the state ( X 0 , Y 0 , Z 0 ) $$ \left({X}^0,{Y}^0,{Z}^0\right) $$ if γ 0 + γ _ ( I res ) $$ {\gamma}^0+\underset{\_}{\gamma}\left({I}^{\mathrm{res}}\right) $$ is greater than or equal to the current value of γ ^ $$ \hat{\gamma} $$ . The lower bound can be calculated by employing a MILP solver for a set cover problem, which is to cover a given set of items (set I res $$ {I}^{\mathrm{res}} $$ ) with a minimum number of racks containing these missing items. Thus, it is reasonable to store and memorize lower bounds that have already been calculated to prevent expensive solver calls triggered by states with identical I res $$ {I}^{\mathrm{res}} $$ .

The lower bound can easier be obtained for a special case in which, for any items i $$ i $$ , there is a unique rack storing this item i $$ i $$ . If there is a unique rack for each item i ∈ I res $$ i\in {I}^{\mathrm{res}} $$ , then γ _ ( I res ) $$ \underset{\_}{\gamma}\left({I}^{\mathrm{res}}\right) $$ is equal to the number of racks storing items from I res $$ {I}^{\mathrm{res}} $$ , and using the solver can be avoided to accelerate the overall algorithm. Instances of such a special case occur in the data sets from literature and are first investigated in [11]. The special case becomes more likely if DP is embedded in a sequential approach that first solves the upstream order and rack allocation to picking stations, as we only observe a smaller set of racks in the sequencing problem thereafter compared to the whole inventory.

Algorithm 1 below describes the call of a routine D P ( X 0 , Y 0 , Z 0 , γ 0 ) $$ DP\left({X}^0,{Y}^0,{Z}^0,{\gamma}^0\right) $$ that explores states in a forward fashion starting from a state ( X 0 , Y 0 , Z 0 ) $$ \left({X}^0,{Y}^0,{Z}^0\right) $$ with γ 0 $$ {\gamma}^0 $$ rack visits. The initial call is D P ( ∅ , ∅ , ∅ , 0 ) $$ DP\left(\varnothing, \varnothing, \varnothing, 0\right) $$ . We initialize 𝒮 = ∅ and γ _ ( I res ) = − ∞ , ∀ I res ⊆ I $$ \underset{\_}{\gamma}\left({I}^{\mathrm{res}}\right)=-\infty, \kern0.3em \forall {I}^{\mathrm{res}}\subseteq I $$ , to indicate that the lower bound γ _ ( I res ) $$ \underset{\_}{\gamma}\left({I}^{\mathrm{res}}\right) $$ is yet unknown for I res ⊆ I $$ {I}^{\mathrm{res}}\subseteq I $$ . Note that several objects are not passed as call parameters explicitly, for example, the set 𝒮 or the map Γ ^ ( X , Y , Z ) $$ \hat{\Gamma}\left(X,Y,Z\right) $$ , to shorten the notation. These objects can also be considered as global variables being updated within the calls of D P $$ DP $$ during runtime.

Algorithm 1. DP( X 0 , Y 0 , Z 0 , γ 0 $$ {X}^0,{Y}^0,{Z}^0,{\gamma}^0 $$ ).

image

In the beginning of Algorithm 1 (lines 1–6), several tests are applied to evaluate if the state ( X 0 , Y 0 , Z 0 ) $$ \left({X}^0,{Y}^0,{Z}^0\right) $$ must be generated. Provided that the state is novel or superior (to its best generated copy), and that the state may lead to a better solution than γ ^ $$ \hat{\gamma} $$ , we update 𝒮 , Γ ^ ( X 0 , Y 0 , Z 0 ) $$ \hat{\Gamma}\left({X}^0,{Y}^0,{Z}^0\right) $$ , as well as γ ^ $$ \hat{\gamma} $$ in case ( X 0 , Y 0 , Z 0 ) $$ \left({X}^0,{Y}^0,{Z}^0\right) $$ is a final state (lines 7–12). The predecessor state s 0 $$ {s}^0 $$ of the state ( X 0 , Y 0 , Z 0 ) $$ \left({X}^0,{Y}^0,{Z}^0\right) $$ and the rack r 0 $$ {r}^0 $$ that translated s 0 $$ {s}^0 $$ to ( X 0 , Y 0 , Z 0 ) $$ \left({X}^0,{Y}^0,{Z}^0\right) $$ are stored as well to track the (partial) solution. Then, successors of ( X 0 , Y 0 , Z 0 ) $$ \left({X}^0,{Y}^0,{Z}^0\right) $$ (that have been constructed according to the translation process implemented in lines 14–28) are passed to the routine D P $$ DP $$ and the procedure repeats. Specifically, lines 15–17 correspond to the first stage of the workflow description outlined in the previous subsection, lines 18–23 correspond to the second stage and the inner for loop depicts the third stage (lines 24–28). The algorithm explores states in a depth-first manner to take advantage from quick improvements in γ ^ $$ \hat{\gamma} $$ in combination with lower bounds when pruning search states. Finally, we introduce dominance and sorting rules to avoid suboptimal states and to generate more promising states earlier on:
  • -

    Algorithm 1, line 14: In case of Z 0 ≠ ∅ $$ {Z}^0\ne \varnothing $$ it is sufficient to iterate over racks r ∈ R $$ r\in R $$ with I r ∩ { i ∈ I | ∃ o ∈ Y : ( o , i ) ∈ Z 0 } ≠ ∅ ∨ O r ∖ ( X 0 ∪ Y 0 ) ≠ ∅ $$ {I}_r\cap \left\{i\in I|\exists o\in Y:\left(o,i\right)\in {Z}^0\right\}\ne \varnothing \kern0.3em \vee \kern0.3em {O}_r\setminus \left({X}^0\cup {Y}^0\right)\ne \varnothing $$ . A rack r ∈ R $$ r\in R $$ that only has items with orders in O r ′ ∖ ( X 0 ∪ Y 0 ) $$ {O}_r^{\prime}\setminus \left({X}^0\cup {Y}^0\right) $$ in common can always be moved to the end of the rack sequence (in case it is scheduled at all). If Z 0 = ∅ $$ {Z}^0=\varnothing $$ , and it holds O ∖ X 0 ⊈ ∪ r ∈ R O r ′ $$ O\setminus {X}^0\nsubseteq {\cup}_{r\in R}{O}_r^{\prime } $$ , then there is an optimal solution with a rack r ∈ R : O r ∖ X 0 ≠ ∅ $$ r\in R:{O}_r\setminus {X}^0\ne \varnothing $$ assigned to the subsequent position in the rack queue.

  • -

    Algorithm 1, line 14: Racks are sorted in descending order of the number of picks a rack can contribute to the uncompleted customer orders currently under processing in the service area (first priority). We resolve ties according to the number of picks a rack can contribute to the customer orders that are yet unprocessed (second priority). If there are still ties afterwards, a random order of the respective racks is used.

  • -

    Algorithm 1, line 25: Subsets U r $$ {U}_r $$ are sorted in descending order of | U r | $$ \mid {U}_r\mid $$ , thus exploring states with a more filled service area earlier.

  • -

    Algorithm 1, line 25: Let 𝒟 be a family of subsets of O $$ O $$ , such that for any D ∈ 𝒟 and for all o , o ′ ∈ D $$ o,{o}^{\prime}\in D $$ it holds I o = I o ′ $$ {I}_o={I}_{o^{\prime }} $$ , that is, all customer orders of any set D ∈ 𝒟 are equal and we denote D $$ D $$ as duplicate group. The customer orders of a duplicate group D ∈ 𝒟 can be considered as interchangeable and we implement a strict but arbitrary processing-order for the elements of a duplicate group, that is to say, given two orders o , o ′ ∈ D $$ o,{o}^{\prime}\in D $$ with o < o ′ $$ o<{o}^{\prime } $$ , order o ′ $$ {o}^{\prime } $$ cannot be started before order o $$ o $$ and all states violating the predecessor relationship are discarded.

4 COMPUTATIONAL STUDY

We compare DP with the strongest standalone MILP formulation for the problem at hand from literature (referred to as SMF [11]). SMF is solved with Cplex 20.1.0.0. For the computational experiments we use an Intel(R) Core(TM) i7-8665U CPU @1.90 GHz (8 CPUs), 2.1 GHz with 32 GB RAM. Both approaches are implemented with Python 3.8. The maximum runtime per instance is 600 seconds.

Next we briefly highlight the characteristics of the benchmark data from literature:
  • -

    benchmark set 1 from [4], consisting of 360 instances,

  • -

    benchmark sets 2 and 3 from [11], consisting of 240 and 720 instances, respectively, and

  • -

    benchmark set 4 from [20], consisting of 105 instances.

Each set consists of several classes, which are identified by triples ( | O | , | R | , B ) $$ \left(|O|,|R|,B\right) $$ that define the number of orders and racks as well as the capacity of the service area for each instance within a class. In case of the first benchmark set triples are denoted as ( | O | , | R | , ξ ) $$ \left(|O|,|R|,\xi \right) $$ , with the latter entry ξ $$ \xi $$ being a parameter that was used in the data generation (here, B $$ B $$ is a random integer between two and ten and varies between instances of a class). For the largest benchmark set three we bundle instances with B ∈ { 2 , 3 , 4 , 5 , 6 } $$ B\in \left\{2,3,4,5,6\right\} $$ and B ∈ { 7 , 8 , 9 , 10 } $$ B\in \left\{7,8,9,10\right\} $$ into two groups denoted as ( | O | , | R | , s ) $$ \left(|O|,|R|,s\right) $$ (small-sized service area) and ( | O | , | R | , l ) $$ \left(|O|,|R|,l\right) $$ (large-sized service area) to shorten the presentation of computational results.

The generated instances simulate real world data of robotic mobile fulfillment systems operating in the e-commerce and business to customer market, for example, the majority of the customers request one or two items at most with 1.6 items per order on average [5, 15], and some items are requested with a higher frequency than others [3]. For a more detailed description we refer to the aforementioned literature.

4.1 Computational results

In Tables 1–4 each row corresponds to a benchmark class, with n $$ n $$ indicating the number of instances within a class. The computational results include the number of rack visits (obj) and the runtime in seconds (time), as well as the optimality gap in case of SMF (gap). For the dynamic programming algorithm we count the number of instances within a benchmark class that have not been solved to (proven) optimality as the time limit was hit before (t/o). Except for the latter performance indicator, all values are arithmetic means across a benchmark class (“—” indicates a missing value as the time limit was hit in several instances before obtaining feasible solutions).

TABLE 1. Comparison of exact solution approaches on benchmark set 1.
SMF DP
| O | $$ \mid O\mid $$ | R | $$ \mid R\mid $$ ξ $$ \xi $$ n $$ n $$ obj gap time obj t/o time
10 5 0.005 20 2.65 0.00 0.14 2.65 0.00 0.08
0.05 20 2.80 0.00 0.13 2.80 0.00 0.08
0.2 20 2.65 0.00 0.13 2.65 0.00 0.07
10 100 0.005 20 8.80 0.00 4.09 8.80 0.00 3.20
0.05 20 7.40 0.00 5.27 7.40 0.00 1.18
0.2 20 3.50 0.00 0.37 3.50 0.00 0.21
50 5 0.005 20 3.60 0.00 0.53 3.60 0.00 0.42
0.05 20 3.95 0.00 0.51 3.95 0.00 0.40
0.2 20 3.45 0.00 0.51 3.45 0.00 0.40
50 100 0.005 20 — — — 39.25 20.00 600.00
0.05 20 33.85 0.64 600.00 31.00 20.00 600.00
0.2 20 13.60 0.38 455.96 11.50 19.00 572.82
100 5 0.005 20 3.85 0.00 1.52 3.85 0.00 0.81
0.05 20 4.35 0.00 1.09 4.35 0.00 0.77
0.2 20 3.85 0.00 1.09 3.85 0.00 0.80
100 100 0.005 20 — — — 95.60 20.00 600.00
0.05 20 — — — 72.30 20.00 600.00
0.2 20 — — — 21.40 20.00 600.00
TABLE 2. Comparison of exact solution approaches on benchmark set 2.
SMF DP
| O | $$ \mid O\mid $$ | R | $$ \mid R\mid $$ B $$ B $$ n $$ n $$ obj gap time obj t/o time
25 25 2 20 4.65 0.00 0.73 4.65 0.00 0.68
5 20 4.30 0.00 0.46 4.30 0.00 0.55
10 20 4.30 0.00 0.50 4.30 0.00 0.47
50 50 2 20 11.45 0.11 394.48 11.05 6.00 219.87
5 20 9.50 0.00 49.96 9.50 0.00 5.14
10 20 9.45 0.00 10.29 9.45 0.00 3.10
75 75 2 20 25.70 0.49 600.00 21.70 20.00 600.00
5 20 18.05 0.22 495.78 15.00 4.00 164.62
10 20 16.05 0.15 301.29 14.55 0.00 15.71
100 100 2 20 — — — 34.75 20.00 600.00
5 20 — — — 22.35 15.00 489.65
10 20 — — — 19.35 2.00 129.32
TABLE 3. Comparison of exact solution approaches on benchmark set 3.
SMF DP
| O | $$ \mid O\mid $$ | R | $$ \mid R\mid $$ B $$ B $$ n $$ n $$ obj gap time obj t/o time
25 25 s $$ s $$ 100 13.30 0.01 141.59 13.25 0.00 0.52
l $$ l $$ 80 12.70 0.00 1.45 12.70 0.00 0.20
50 50 s $$ s $$ 100 31.17 0.15 534.26 27.26 7.00 85.28
l $$ l $$ 80 26.45 0.02 204.00 25.65 0.00 0.45
75 75 s $$ s $$ 100 51.69 0.66 600.00 43.57 43.00 296.01
l $$ l $$ 80 46.48 0.55 595.46 39.46 5.00 45.06
100 100 s $$ s $$ 100 73.16 0.92 600.00 62.86 81.00 498.15
l $$ l $$ 80 66.00 0.92 600.00 54.51 25.00 192.78
TABLE 4. Comparison of exact solution approaches on benchmark set 4.
SMF DP
| O | $$ \mid O\mid $$ | R | $$ \mid R\mid $$ B $$ B $$ n $$ n $$ obj gap time obj t/o time
10 5 3 15 3.20 0.00 0.23 3.20 0.00 0.10
2 15 3.33 0.00 0.21 3.33 0.00 0.10
20 5 2 15 3.40 0.00 0.38 3.40 0.00 0.17
40 10 6 15 8.33 0.01 50.81 8.33 1.00 44.03
50 10 6 15 9.33 0.01 84.64 9.33 0.00 8.30
50 30 6 15 13.40 0.10 249.62 12.60 4.00 184.33
3 15 18.33 0.16 491.87 16.00 4.00 225.49

The results for the first benchmark set in Table 1 are ambivalent: all instances of twelve out of eighteen benchmark classes are solved to optimality by any exact method within a handful of seconds on average, but it becomes apparent that the remaining benchmark classes with ( | O | , | R | ) ∈ { ( 50 , 100 ) , ( 100 , 100 ) } $$ \left(|O|,|R|\right)\in \left\{\left(50,100\right),\left(100,100\right)\right\} $$ are far too challenging for the approaches under consideration (this is due to an increase of up to 2.86 items per order on average). Nevertheless, DP performs better than SMF on these difficult classes in terms of rack visits, especially as SMF is unable to obtain feasible solutions within the time limit on most instances. It should be noted that heuristics in [4, 10] provide significantly better solutions in less time here.

Almost all instances of the second benchmark set (Table 2) with at most fifty orders are solved to optimality regardless of the approach and the capacity of the service area, with DP being slightly faster on average. On larger instances with | O | ∈ { 75 , 100 } $$ \mid O\mid \in \left\{75,100\right\} $$ , DP outperforms SMF decisively, for example, DP solves instances with | O | = 75 $$ \mid O\mid =75 $$ and B = 10 $$ B=10 $$ in contrast to SMF to optimality in only 15 s on average, thus being at least twenty times as fast as SMF. Moreover, SMF fails to obtain feasible solutions for many instances with | O | = 100 $$ \mid O\mid =100 $$ and | B | ∈ { 2 , 5 , 10 } $$ \mid B\mid \in \left\{2,5,10\right\} $$ , while DP is even able to optimally solve instances with | O | = 100 $$ \mid O\mid =100 $$ and B ∈ { 5 , 10 } $$ B\in \left\{5,10\right\} $$ . In summary, most instances that are either small- or medium-sized ( | O | ∈ { 25 , 50 } $$ \mid O\mid \in \left\{25,50\right\} $$ ) or with a large capacity of the service area ( B = 10 $$ B=10 $$ ) are solved by DP in quite a short time, while large instances in terms of | O | $$ \mid O\mid $$ with a small-sized workbench remain challenging. The incumbent solutions of SMF when hitting the time limit often require more rack visits than DP's, for example, 25.70 compared to 21.70 in row seven.

DP performs particularly well compared to the MILP formulation on the third benchmark set (Table 3), both with respect to the runtime and number of rack visits. Often, DP is at least two orders of magnitude faster than the solver. In addition, and in accordance with previous results, solutions obtained with SMF are significantly worse when running out of time, for example, 66.00 rack visits on average compared to 54.51 in the last row.

The results of both approaches are more similar in Table 4, but some of the previous observations apply here as well (e.g., with respect to the solution quality in the last two rows, and DP is always faster). In total, only 9 out of 105 instances could not be solved to optimality with DP, while Cplex runs out of time in 19 cases.

We complete the computational study with some short comments on the effectiveness of the solver-driven pruning technique (dynamath) applied in DP: in 95.61% of function calls (Algorithm 1) the current state is pruned. However, this plain number does not take into account the cost of exploring (suboptimal) successors if the parent state is not pruned. Therefore, we run DP without lower bounds on a sample of instances (in particular, benchmark class ( 25 , 25 , 2 ) $$ \left(25,25,2\right) $$ in Table 2) to estimate the actual impact. The average ratio without/with lower bounds in terms of function calls (states explored), unique states (states generated), and runtime equals 727.28, 1389.41, and 157.33, respectively. Thus, there is a significant improvement if lower bounds are applied, compensating the additional runtime consumed by the solver, which accounts for approximately 10% of the total runtime on average across all benchmark sets. Indeed, 97.71% of solver calls are avoided by memorizing previous results, that is, the set cover lower bound γ _ ( I res ) $$ \underset{\_}{\gamma}\left({I}^{\mathrm{res}}\right) $$ has already been determined for I res $$ {I}^{\mathrm{res}} $$ before.

5 CONCLUSIONS

In this article, we describe a dynamic programming algorithm to optimize the order picking process in robotic mobile fulfillment systems. In particular, the order scheduling and rack sequencing problem at a single picking station with rack visit minimization is solved to optimality. Except for monolithic MILP formulations, the dynamic programming algorithm is the first combinatorial method for the problem at hand, outperforming an academic version of a commercial MILP solver on the strongest formulation from literature. Instances with up to one-hundred orders can often be solved to proven optimality in about ten minutes of runtime, given that the service area is rather large-sized with around ten bin positions.

Also, we have coined the term dynamath regarding the methodology of the approach, that is, a mathematical optimization solver is used at each state in the search process to determine lower bounds. While it seems quite expensive to invoke solver calls frequently during the search process of a dynamic programming algorithm, computational results have shown that a large percentage of lower bounds is memorized in our case and that determining lower bounds overcompensates for exploring many suboptimal states.

Little is known about the structure and properties of optimal solutions, which might be a promising direction when designing faster combinatorial methods in future research. Also, stronger lower bounds are of importance to accelerate exact algorithms like the proposed dynamic programming approach. For practitioners, exact methods observing stock levels and multiple picking stations might be of interest, too.

ENDNOTE

  • 1 The gap reported by Cplex is defined as | z _ − z ∗ | 1 e − 10 + | z ∗ | $$ \frac{\mid \underset{\_}{z}-{z}^{\ast}\mid }{1{e}^{-10}+\mid {z}^{\ast}\mid } $$ , with z _ $$ \underset{\_}{z} $$ denoting the best lower bound and z ∗ $$ {z}^{\ast } $$ denoting the best upper bound (best feasible solution value) obtained from the solver.

    • DATA AVAILABILITY STATEMENT

    The data that support the findings of this study are available from the corresponding author upon reasonable request.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.