Multiperiod transshipment location–allocation problem with flow synchronization under stochastic handling operations
Abstract
The transshipment location–allocation problem consists of locating transshipment facilities (e.g., intermodal hubs) of a transportation network and allocating freight flows through them, from several origins to several destinations, to satisfy demand and supply constraints. The objective is to maximize the total net transportation utility given by the total shipping utility minus the total cost to locate the facilities. Moreover, flow synchronization at the facilities must also be ensured. Unfortunately, the flow synchronization depends on a broad set of unknown events, which could cause both unexpected reductions of the facility capacity and uncertain utility of handling operations. In this paper, we first want to evaluate how uncertainty on facility capacity and handling operations utility affects the transshipment location–allocation problem in terms of complexity, net gain, and optimal solutions. Moreover, we extend the problem from a single to a multi-period setting to have a wider view of future scenarios realizations and consequently synchronize the flows by using different facilities on different periods. We propose a two-stage stochastic programming formulation with recourse and analyze, over a ground set of instances, some well-known economic indicators to derive managerial insights on the importance of addressing uncertainty for the problem. Finally, given the computational burden of solving the deterministic equivalent problem, we propose several heuristics based on progressive hedging and test their performance.
1 INTRODUCTION
Recently, a new paradigm called synchromodality has emerged in the field of transportation and logistics. This paradigm has already shown its effectiveness in real implementations [28], European research projects [11, 12, 26], and it is also gaining increasing attraction from academic research. Synchromodality, among several other aspects, focuses on the importance of synchronizing operations to improve the efficiency and the sustainability of the supply chain. For its implementation in realistic settings, Pfoser et al. [27] identified two main critical success factors, namely, the development of sophisticated planning methods and the use of efficient physical infrastructures (which in turn implies planning a good network design). On the other hand, the increase of freight transportation, and e-commerce, in particular, is fostering the need to synchronize operations and modes better, as well as to address different sources of uncertainty.
In such complex logistic settings, the transshipment problem consists of minimizing the total transportation cost over a network by using transshipment facilities as intermediate points for shipping freight from origins to destinations [24]. In the literature, the utilization of transshipment facilities addresses several kinds of issues, such as consolidation, packing and unpacking operations, inter-modal or inter-vehicle changes, and so on. When considering transshipment problems combined with some settings of the well-known location–allocation problem [5], the main decisions to take are which intermediate hubs to place and how to manage the flows throughout the network. These are the main characteristics of the so-called transshipment location–allocation problem (TLAP).
However, as pointed out by Giusti et al. [13], dealing with unexpected events has a fundamental role in reducing the negative impact of disruptions in strategic/tactical planning of synchromodal networks. In fact, over a medium or long-term time horizon, a transshipment facility is subjected to events with unknown probability, such as lateness of the incoming/outgoing transportation modes, congestion, or unexpectedly slow execution of the handling operations. These events could cause significant stand-by time for vehicles in a facility and, in turn, loss of transshipment connections and reduction in the expected available capacity of the facilities.
In this work, we provide a stochastic programming (SP) formulation of the problem to evaluate the possible potentialities to consider uncertainty explicitly. More precisely, according to realistic decision-making processes in logistics, a two-stage SP model with recourse is proposed where the location of facilities is decided at the first stage. In contrast, the allocation of the freight flows is agreed at the second stage. To achieve a model that can be practically solved through mathematical programming techniques, a deterministic equivalent formulation of the stochastic model is derived by assuming certain probability distributions for the random variables and discretizing them through the use of a finite (although significant) set of scenarios. The number of scenarios required to discretize the random variables with a good approximation is experimentally found by performing stability analysis. Then, several standard SP indicators (VSS, EVPI, LUSS, and LUDS) are calculated and analyzed to show that the problem is worth to be studied since an explicit consideration of the stochasticity can lead to conspicuous gains. Finally, to overcome the computational burden of solving the problem by state-of-the-art commercial solvers, we introduce several matheuristic procedures based on the well-known progressive hedging (PH) approach of Rockafellar and Wets [30]. The accuracy and efficiency of the proposed algorithms are tested over a broad set of representative instances.
The rest of the paper is organized as follows. In Section 2, we discuss the state-of-the-art regarding problems with similar characteristics to the TLAP. In Section 3, we introduce the problem and present its stochastic (a two-stage model with recourse) and deterministic equivalent formulations. In Section 4, we analyze the effects of introducing stochasticity in the problem through the calculation of insightful SP indicators. The generation of the test instances and the stability analysis are also described there. In Section 5, we present the scenario decomposition required to implement the PH, the steps of the algorithm, the initialization, and the update of PH parameters. Section 6 provides the description of two PH variants and a primal heuristic to improve computational performances. In Section 7, we discuss the results of the computational experiments regarding the PH-based heuristic algorithms. Section 8 proposes conclusions of the work and future developments.
2 LITERATURE REVIEW
Location–allocation problems that make use of intermediate hubs for shipping goods from origins to destinations have been primarily addressed in the literature to deal with modern global freight logistics. For instance, Di Francesco et al. [8] studied the problem of a forwarder that needs to ship containers filled with pallets to intermediate depots of a two echelon-network where pallets are unpacked and sent to different destinations. Instead, Zhao et al. [37] approached the location of consolidation centers in China as transshipment facilities to ship freight by rail routes from China to Europe.
Moreover, as for other practices, our TLAP requires a strategic/tactical planning of facilities location beforehand as well as more operational flow management. A similar decision process is typical, for example, when implementing the well-known cross-docking procedure, which consists of processing the shipments as quickly as possible to minimize storage and handling operations [14]. To achieve an effective cross-docking, it is crucial to choose distribution centers capable of managing the continuous flow of shipments with handling operations, mainly consisting of moving goods from the inbound vehicles to the outbound vehicles by consolidating the cargo based on the location of the customers [10].
Synchronization, which plays an essential role in our work, can be found in several papers. For example, Jin et al. [16] pointed out that unsynchronized shipping services at hub ports generate operation issues and high costs. To improve synchronization, they designed feeder vessel services to pick up and deliver containers between neighboring local ports, working like transshipment facilities, and synchronize them with long-haul services improving the efficiency of container transshipment. Other benefits of the synchronization in transshipment facilities are studied in Neves-Moreira et al. [23]. The authors developed a method to provide long-haul services using short-haul jobs, over a logistics network of freight transportation in which trucks are allowed to exchange semi-trailers through several transshipment points. In this case, the synchronization helps to reduce the empty truck journeys drastically and finds applications in a decision support system of a Portuguese logistics operator. In addition, cross-docking procedures require a reliable synchronization between the incoming and outgoing flows (see, e.g., Luo et al. [19] who considered the synchronization between production and warehouse operations). On the other hand, synchronization cannot be activated without a wise tactical facility location. Very recently, Qu et al. [29] considered synchronization of transshipment flows at intermediate terminals, pointing out that, in some cases, overloaded terminals could cause delays and delay propagation. Hence, locating the right facilities in advance and synchronizing flows can have a significant impact on limiting this issue.
Another essential characteristic of our setting is the presence of uncertainty, which could disrupt optimal plans if not treated correctly. Tadei et al. [33] proposed a model to maximize the total net utility, calculated by subtracting the total fixed cost of the located facilities from the total shipping utility. The shipping utility is given by a deterministic utility for shipping freight from origins to destinations via transshipment facilities plus a stochastic handling utility at the facilities. Eventually, a deterministic approximation of the problem was provided by using some results from the theory of extreme values [31, 34]. Instead, the model proposed in Baldi et al. [2] aimed to minimize the total cost by finding an optimal location of the transshipment facilities for which the cost of their throughput in terms of freight are random variables with an unknown probability distribution. Here, the total cost is given by a deterministic fixed cost plus the expected cost of the total freight flow. Lastly, Wang et al. [36] proposed different types of belief degree constrained programming models (optimistic value, pessimistic value, and Hurwicz criterion), in which costs and demands are studied as uncertain variables. They also addressed a problem that takes into account sustainability issues by fixing the maximal CO2 emissions that cannot be exceeded by the whole transportation system.
Similarly to Tadei et al. [33], our goal is to find a usage plan of a set of transshipment facilities that maximizes the total net transportation utility (i.e., the total shipping utility minus the total cost to locate the facilities). While classical transshipment problems only consider the allocation of flows to the existing facilities, our variant consists of finding transshipment facility locations and allocating flows through them to satisfy customers' demand. This involves both a network design problem (facility location) and a network flow planning one (flow allocation), which are part of the strategic and tactical planning, respectively [32]. A crucial focus is put on the consequences (in terms of transshipment capacity and loss) of possible unforeseen events in the transshipment synchronization. For this reason, we consider for the first time in the literature, the uncertainty coming from the capacity of the facilities and the handling utilities simultaneously. The uncertainty regarding the loss of capacity is explicitly considered to model possible leftovers at the facilities due to non correctly synchronized operations.
Furthermore, we consider a multi-period setting instead of a single-period one. In fact, in strategic/tactical planning, decisions must be taken on the long/medium-term horizon, which implies having a more comprehensive view of the problem and not only on the next imminent set of operations. Considering only one period would possibly lead to design a network that can perform well in many cases, but then having catastrophic losses of revenue in other situations. Hence, having more periods allows us to have a more accurate view of the possible realization of the uncertainty and to avoid as much as possible the worst consequences. In conclusion, we want to locate facilities to enable synchronization mechanism, so to provide a good trade-off between locating capacities that remain unused and the risk of leftovers.
3 PROBLEM DEFINITION AND MATHEMATICAL MODELS
This section is dedicated to the formal definition of the TLAP. We propose a two-stage Stochastic Programming formulation for the problem in Section 3.1 and its deterministic equivalent version in Section 3.2.
- I: set of origins;
- J: set of destinations;
- K: set of potential transshipment locations;
- T: set of periods representing the optimization horizon (say, a week); and the following parameters
- pi: the flow of freight supplied by origin i ∈ I;
- qj: the demand required by destination j ∈ J;
- fk: fixed cost (e.g., contract cost) of using a facility k ∈ K;
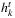 : utilization cost to use a facility k ∈ K in a time period t ∈ T;
: utilization cost to use a facility k ∈ K in a time period t ∈ T;- cijk: the unitary cost to use an external carrier to ship a freight unit from origin i ∈ I to destination j ∈ J via transshipment location k ∈ K;
- Ck: maximum deterministic capacity of a facility k ∈ K;
- vijk(ξ) = uijk + θ(ξ): stochastic utility of a unit of freight shipped from origin i ∈ I to destination j ∈ J via transshipment location k ∈ K, subject to a random variable ξ. Without loss of generality, we consider such utility made by a deterministic part uijk and a fluctuation θ(ξ);
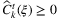 : loss of capacity that reduce the maximum capacity of a certain facility k ∈ K in a specific period t ∈ T, subject to a random variable ξ. The capacity fluctuations implicitly model the freight leftover in a facility because of possible nonsynchronization or handling delays in previous periods.
: loss of capacity that reduce the maximum capacity of a certain facility k ∈ K in a specific period t ∈ T, subject to a random variable ξ. The capacity fluctuations implicitly model the freight leftover in a facility because of possible nonsynchronization or handling delays in previous periods.
Then, our stochastic multi-period TLAP aims at finding a facility location and flow allocation plan that maximizes the total net transportation utility, given by the total shipping utility minus the total contract and handling costs of the located facilities, subject to capacity constraints. Without loss of generality, we will assume throughout the paper that the transportation system is balanced in terms of supply and demand, that is, ∑i ∈ Ipi = ∑j ∈ Jqj (standard methods for balancing a network can be found in [1]). An exemplification of the network underlying our problem is shown in Figure 1, where two origins, three transshipment facilities, and four destinations are considered.

3.1 Two-stage SP formulation
In this section, we provide a two-stage SP formulation of the problem. Readers are referred to Birge and Louveaux [4] and King and Wallace [18] for an overview of this modeling paradigm. According to a realistic decision-making process, the first stage is about deciding which facilities should be used (strategic planning), while the second-stage recourse actions are about how to manage the flows at the transshipment hubs (tactical planning). Moreover, to always maintain the feasibility of the problem concerning the supply/demand constraints, the transportation company is also allowed to pay for an external cost to ship the freight.
- xk: first-stage boolean variables taking value 1 if facility k ∈ K is used for transshipment in any period, and 0 otherwise;
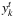 : first-stage boolean variables taking the value 1 if facility k ∈ K is used for a transshipment in time period t ∈ T, and 0 otherwise;
: first-stage boolean variables taking the value 1 if facility k ∈ K is used for a transshipment in time period t ∈ T, and 0 otherwise;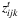 : second-stage continuous variables representing the freight from origin i ∈ I to destination j ∈ J transshipped via facility k ∈ K in time period t ∈ T;
: second-stage continuous variables representing the freight from origin i ∈ I to destination j ∈ J transshipped via facility k ∈ K in time period t ∈ T;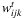 : second-stage continuous variables, representing the freight shipped from origin i ∈ I to destination j ∈ J transshipped via facility k ∈ K in time period t ∈ T by an external transportation company.
: second-stage continuous variables, representing the freight shipped from origin i ∈ I to destination j ∈ J transshipped via facility k ∈ K in time period t ∈ T by an external transportation company.
 (1)
(1) (2)
(2) (3)
(3) (4)
(4) represents the expected total shipping utility over the whole time horizon, depending on the first-stage variables y and the random variable ξ.
represents the expected total shipping utility over the whole time horizon, depending on the first-stage variables y and the random variable ξ. (5)
(5) (6)
(6) (7)
(7) (8)
(8) (9)
(9) (10)
(10) (11)
(11)The objective function (5) aims at maximizing the total shipping utility given by the freight correctly transshipped at the facilities over the time horizon minus the cost to use external shipments. Constraints (6) and (7) ensure that supplies in all origins are collected and that all demands in all destinations are satisfied, respectively. Constraints (8) ensure that, in each period and for each located facility, freight flow does not exceed the available capacity. Constraints (9) ensure that, in each period, flows pass only through the facility that we decided to use. Constraints (10) ensure that the external shipments (i.e., flows leftovers) never exceed the total freight. Finally, constraints (11) are nonnegative conditions on variables.
3.2 Deterministic equivalent problem
- S: set of scenarios representing the possible realization of the uncertainty;
- πs: probability of a scenario s ∈ S to occur (note that such probabilities are derived so to ensure the standard axiom ∑s ∈ Sπs = 1).
 (12)
(12) (13)
(13) (14)
(14) (15)
(15) (16)
(16) (17)
(17) (18)
(18) (19)
(19) (20)
(20) (21)
(21) ,
,  ,
,  , and
, and  have the same meaning of
have the same meaning of  ,
,  , vijk(ξ), and
, vijk(ξ), and  for a particular scenario s ∈ S.
for a particular scenario s ∈ S.The constraints 13-21) correspond to the constraints of the stochastic model 2-4) and (6-11) exploded by scenarios when depending by stochastic parameters. The objective function (12) maximizes the expected value over all possible realizations of the scenarios of the total net transportation utility given by the total shipping utility minus the total contract and handling costs of the located facilities.
Note that, given the discretization in scenarios, we can calculate the expected value in the objective function as a linear expression. Hence, our DEP belongs to the class of mixed-integer linear problems (MILP), which are, in general, difficult to solve for real-life instances. Moreover, the complexity of the problem also grows with the cardinality of S, namely the number of scenarios used to discretize the probability distributions of the random variables.
4 IMPACT OF THE UNCERTAINTY
In this section, we want to analyze the economic impact of explicitly consider the uncertainty in our multiperiod TLAP instead of using classical deterministic estimators (such as the expected value) for approximating the stochastic parameters. Since our problem incorporates two main sources of uncertainty (transshipment capacity and handling utility), we also assess the impact of each source separately. Moreover, we consider some properties of the solutions obtained by the deterministic estimation to derive useful algorithmic insights for the efficient solution of the stochastic problem. In Section 4.1, we describe how deterministic instances are generated and stochastic parameters are modeled. In Section 4.2, we present the results of the stability analysis, which helped us to define the number of scenarios needed to calculate the SP indicators presented in Section 4.3.
4.1 Instances generation
To be consistent with the literature, we adapt our generation procedure from Tadei et al. [33], in which a similar problem is studied. However, we propose some modifications to take into account the multi-periodic structure of the problem.
 to represent a Uniform distribution in the range [a, b])
to represent a Uniform distribution in the range [a, b])
- the flow supply pi, i ∈ I, is drawn from
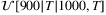 ;
; - the flow demand qj, j ∈ J, is drawn from
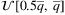 , where
, where 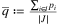 . Note that, in order to guarantee a balanced system, the demand of the last destination is adjusted afterward;
. Note that, in order to guarantee a balanced system, the demand of the last destination is adjusted afterward; - the maximum deterministic capacity Ck, k ∈ K is drawn from different distribution ranges to create three different types of facilities (small-, medium-, and large-sized). For each size, about
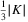 facilities are generated. The distributions used for small-, medium-, and large-sized facilities are
facilities are generated. The distributions used for small-, medium-, and large-sized facilities are 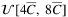 ,
, 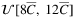 , and
, and 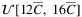 , respectively, where
, respectively, where 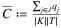 ;
; - the deterministic part uijk of the utility, i ∈ I, j ∈ J, k ∈ K, is drawn from
 ;
; - the contract cost fk, k ∈ K, and the handling cost
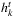 , k ∈ K, t ∈ T, are equal to
, k ∈ K, t ∈ T, are equal to 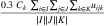 ;
; - the unitary cost cijk of using an external transportation company, i ∈ I, j ∈ J, k ∈ K, is equal to
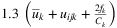 , where
, where 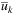 is the average utility for each facility k ∈ K, that is
is the average utility for each facility k ∈ K, that is 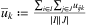 . Note that such a generation avoids pathological situations in which it would be more convenient to use an external carrier instead of the planned transportation services.
. Note that such a generation avoids pathological situations in which it would be more convenient to use an external carrier instead of the planned transportation services.
- the realized utility
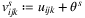 for each i ∈ I, j ∈ J, k ∈ K where θs is drawn from a Gumbel distribution having a location parameter
for each i ∈ I, j ∈ J, k ∈ K where θs is drawn from a Gumbel distribution having a location parameter 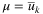 and a scale parameter
and a scale parameter 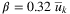 truncated in the range [1, 20].
truncated in the range [1, 20]. - the realized loss of capacity
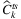 , for each k ∈ K, t ∈ T, is drawn from a Normal distribution having a mean value μ = 0.3Ck and a standard deviation σ = 2Ck truncated in the range [0, Ck]. Basically, we are simulating that, on average, the whole capacity of the facility will not be available and the probability of having almost all the capacity is higher than having no space at all.
, for each k ∈ K, t ∈ T, is drawn from a Normal distribution having a mean value μ = 0.3Ck and a standard deviation σ = 2Ck truncated in the range [0, Ck]. Basically, we are simulating that, on average, the whole capacity of the facility will not be available and the probability of having almost all the capacity is higher than having no space at all.
Eventually, we decided to consider 30 different and reasonable combinations of number of origins |I | ∈ {2,3,5}, number of destinations |J | ∈ {15,20,25,30,40}, number of transshipment facilities |K | ∈ {10,12,15,17,20}, and periods |T | ∈ {7,14,31}.
4.2 Stability analysis
We performed an in-sample stability analysis on instances corresponding to 10 out of the 30 combinations of |I|, |J|, |K|, and |T| described above. For each combination, uniquely defined by the label |I|–|J|–|K|–|T|, we calculated the value of the recourse problem (RP) by solving the DEP (see Section 3.2). Then we computed the percentage ratio between the standard deviation and the mean of the RP over 10 random generations of the stochastic parameters, that is, using different random seeds (see, e.g., [22]). We repeated this calculation for increasing number of scenarios, that is, for |S | ∈ {5,10,25,50,75,100}.
The RP solutions are obtained by applying the CPLEX solver on the plain DEP formulation, with a MIP gap of 0.5% [15]. The results of this analysis are presented in Figure 2 and can help us to determine the number of scenarios needed to have RP solutions stable enough. To make this decision, we must consider that we used a MIP gap of 0.5% that can cause small errors in calculating the ratios. So, even if 50 and 75 scenarios already show good stability (under 1%), we preferred to use 100 scenarios to ensure stability that guarantees a ratio under 0.5%.

4.3 Stochastic programming indicators
In this section, we present the analysis of several SP indicators for three different versions of our stochastic problem: the first one considering both stochastic utilities and losses of capacity (TLAP-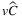 ), the second one considering only stochastic utilities (TLAP-v), and the last one considering only stochastic losses of capacity (TLAP-
), the second one considering only stochastic utilities (TLAP-v), and the last one considering only stochastic losses of capacity (TLAP-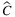 ). Before discussing the results, we briefly describe the indicators computed.
). Before discussing the results, we briefly describe the indicators computed.
The value of the stochastic solution (VSS), introduced by Birge [3], is an SP indicator largely used in the analysis of stochastic models, representing the value of studying the stochastic model versus the deterministic one. The VSS is calculated as VSS ≔ RP − EEV, where the expectation of the expected value problem (EEV) is computed by solving the DEP in which the first-stage variables are fixed to the values given by the so-called expected value problem (EV) solution, that is, the solution to the problem in which their mean values simply substitute random variables. In particular, we will calculate a percentage VSS with respect to the RP solution, that is, VSS % ≔ 100 (RP − EEV) / RP.
Another largely studied SP indicator, presented by Dempster [7], is the expected value of the perfect information (EVPI), representing the maximum value of profitable investments to forecast uncertainties. The EVPI is calculated as EVPI ≔ WS − RP, where the wait-and-see (WS) solution value corresponds to the mean of the DEP solved separately for each scenario. In particular, we will calculate a percentage EVPI with respect to the RP solution, that is, EVPI % = 100 (WS − RP) / RP.
We also present the loss of using the skeleton solution (LUSS) and the loss of upgrading the deterministic solution (LUDS), presented Maggioni and Wallace [20]. These indicators are not used frequently in the literature, but they can provide additional insights about the EV solution and the characteristics of the problem. The LUSS is calculated as LUSS ≔ RP − ESSV, where the expected skeleton solution value (ESSV) is computed by solving the DEP in which the first-stage variables are fixed to the values given by the EV solution only if they take the value of their lower bound. Instead, the LUDS is calculated as LUDS ≔ RP − EIV, where the expected input value (EIV) is computed by solving the DEP in which the lower bounds of the first-stage variables are fixed to the values given by the EV solution. In particular, we will calculate a percentage LUSS and LUDS with respect to the RP solution, that is, LUSS % = 100 (RP − ESSV) / RP and LUDS % = 100 (RP − EIV) / RP. Note that, since all our first-stage variables are binary, the ESSV can be calculated by excluding all the facilities not selected in the EV. In contrast, the EIV can be calculated by ensuring the utilization of all the facilities selected in the EV solution.
Table 1 presents all the indicators, for all the TLAP variants, calculated for 30 instances corresponding to all the considered combinations of parameters |I|, |J|, |K|, and |T|. First, we analyze the results concerning the TLAP-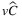 , in which the two stochastic parameters are studied together. The high values of VSS% show that the deterministic solution does not perform well, whereas explicitly considering the uncertainty can lead to an increase on revenues. In fact, the EV solution tends to be more conservative by using the least number of facilities to ship all the demand, thus causing a great amount of leftovers when stochastic losses of capacity are considered. Instead, the values of EVPI% clearly show that we could increase a lot our profit if we knew the exact realization of random parameters in the future. Then, we can notice that LUSS% and VSS% are always the same, which implies that EEV = ESSV. To avoid recourse costs, the ESSV solution selects the same facilities of the EV solution, since forced not to open new facilities. Finally, even if the EV solution does not perform well, LUDS% tends to 0, indicating that the deterministic solution can be used as a good lower bound for the stochastic one. The EIV solution can open new facilities besides those already selected in the EV solution to find the right balance between facility cost and the risk of having leftovers. Note that the behavior of LUSS and LUDS remains the same for TLAP-v and TLAP-
, in which the two stochastic parameters are studied together. The high values of VSS% show that the deterministic solution does not perform well, whereas explicitly considering the uncertainty can lead to an increase on revenues. In fact, the EV solution tends to be more conservative by using the least number of facilities to ship all the demand, thus causing a great amount of leftovers when stochastic losses of capacity are considered. Instead, the values of EVPI% clearly show that we could increase a lot our profit if we knew the exact realization of random parameters in the future. Then, we can notice that LUSS% and VSS% are always the same, which implies that EEV = ESSV. To avoid recourse costs, the ESSV solution selects the same facilities of the EV solution, since forced not to open new facilities. Finally, even if the EV solution does not perform well, LUDS% tends to 0, indicating that the deterministic solution can be used as a good lower bound for the stochastic one. The EIV solution can open new facilities besides those already selected in the EV solution to find the right balance between facility cost and the risk of having leftovers. Note that the behavior of LUSS and LUDS remains the same for TLAP-v and TLAP-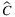 .
.
| Instance | TLAP-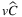 |
TLAP-v | TLAP-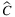 |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |I| | |J| | |K| | |T| | VSS% | LUSS% | LUDS% | EVPI% | VSS% | LUSS% | LUDS% | EVPI% | VSS% | LUSS% | LUDS% | EVPI% |
| 2 | 15 | 10 | 7 | 8.59 | 8.59 | 0.64 | 23.82 | 0.04 | 0.04 | 0.04 | 9.32 | 5.23 | 5.23 | 0.08 | 8.54 |
| 2 | 15 | 10 | 14 | 7.26 | 7.26 | 1.30 | 22.29 | 0.18 | 0.18 | 0.14 | 11.21 | 5.09 | 5.09 | 0.83 | 10.67 |
| 2 | 15 | 10 | 31 | 6.21 | 6.21 | 1.56 | 20.49 | 0.42 | 0.42 | 0.42 | 10.26 | 3.52 | 3.52 | 0.90 | 6.38 |
| 2 | 15 | 12 | 7 | 5.07 | 5.07 | 0.00 | 19.87 | 0.07 | 0.07 | 0.07 | 8.18 | 7.45 | 7.45 | 0.24 | 10.60 |
| 2 | 15 | 12 | 14 | 6.18 | 6.18 | 1.02 | 21.42 | 0.94 | 0.94 | 0.90 | 11.35 | 5.39 | 5.39 | 0.24 | 7.80 |
| 2 | 15 | 15 | 7 | 6.98 | 6.98 | 0.49 | 19.60 | 0.33 | 0.33 | 0.33 | 9.70 | 4.78 | 4.78 | 0.28 | 9.40 |
| 2 | 20 | 10 | 7 | 9.28 | 9.28 | 0.13 | 23.62 | 1.55 | 1.55 | 1.55 | 13.68 | 7.41 | 7.41 | 0.76 | 12.77 |
| 2 | 20 | 10 | 14 | 6.73 | 6.73 | 0.75 | 23.99 | 0.24 | 0.24 | 0.24 | 11.07 | 3.67 | 3.67 | 0.30 | 9.37 |
| 2 | 20 | 10 | 31 | 5.56 | 5.56 | 0.83 | 18.22 | 0.52 | 0.52 | 0.52 | 10.10 | 4.41 | 4.41 | 0.62 | 8.82 |
| 2 | 20 | 12 | 7 | 8.55 | 8.55 | 0.71 | 22.27 | 0.01 | 0.01 | 0.01 | 9.65 | 4.17 | 4.17 | 0.00 | 10.06 |
| 2 | 20 | 12 | 14 | 5.97 | 5.97 | 0.65 | 21.28 | 0.44 | 0.44 | 0.44 | 11.19 | 3.71 | 3.71 | 0.29 | 9.28 |
| 2 | 20 | 15 | 7 | 7.73 | 7.73 | 1.24 | 24.04 | 1.28 | 1.28 | 1.28 | 12.45 | 6.10 | 6.10 | 0.10 | 9.23 |
| 2 | 25 | 12 | 7 | 7.91 | 7.91 | 0.34 | 24.89 | 0.52 | 0.52 | 0.52 | 13.41 | 5.18 | 5.18 | 0.11 | 9.21 |
| 2 | 25 | 15 | 7 | 8.04 | 8.04 | 0.24 | 20.57 | 0.00 | 0.00 | 0.00 | 12.82 | 6.30 | 6.30 | 1.07 | 10.39 |
| 2 | 25 | 17 | 7 | 8.04 | 8.04 | 0.00 | 23.25 | 0.36 | 0.36 | 0.36 | 12.16 | 4.91 | 4.91 | 0.53 | 6.91 |
| 3 | 15 | 10 | 7 | 7.85 | 7.85 | 3.08 | 22.58 | 0.22 | 0.22 | 0.22 | 10.82 | 7.14 | 7.14 | 0.50 | 8.97 |
| 3 | 15 | 12 | 7 | 6.43 | 6.43 | 0.66 | 24.59 | 0.09 | 0.09 | 0.09 | 13.81 | 3.28 | 3.28 | 0.07 | 9.12 |
| 3 | 15 | 15 | 7 | 6.08 | 6.08 | 0.67 | 21.80 | 0.00 | 0.00 | 0.00 | 10.96 | 3.57 | 3.57 | 0.00 | 7.87 |
| 3 | 20 | 10 | 7 | 7.50 | 7.50 | 0.77 | 21.27 | 0.00 | 0.00 | 0.00 | 12.46 | 8.19 | 8.19 | 0.65 | 12.45 |
| 3 | 20 | 12 | 7 | 8.98 | 8.98 | 1.37 | 25.76 | 1.40 | 1.40 | 1.40 | 12.06 | 5.98 | 5.98 | 0.43 | 11.12 |
| 3 | 25 | 15 | 7 | 7.92 | 7.92 | 0.56 | 23.75 | 0.08 | 0.08 | 0.08 | 13.28 | 3.45 | 3.45 | 0.00 | 6.98 |
| 3 | 25 | 15 | 31 | 3.66 | 3.66 | 0.88 | 19.18 | 0.09 | 0.09 | 0.09 | 10.55 | 2.97 | 2.97 | 0.48 | 6.08 |
| 3 | 30 | 12 | 31 | 4.88 | 4.88 | 0.69 | 21.17 | 1.24 | 1.24 | 0.94 | 11.29 | 1.88 | 1.88 | 0.35 | 4.73 |
| 3 | 30 | 20 | 7 | 5.64 | 5.64 | 0.24 | 24.03 | 0.51 | 0.51 | 0.51 | 14.94 | 5.10 | 5.10 | 0.54 | 8.78 |
| 3 | 40 | 20 | 7 | 6.87 | 6.87 | 0.97 | 26.53 | 0.35 | 0.35 | 0.35 | 14.26 | 4.78 | 4.78 | 0.55 | 7.49 |
| 5 | 15 | 10 | 14 | 6.47 | 6.47 | 1.24 | 21.85 | 0.46 | 0.46 | 0.46 | 12.47 | 4.63 | 4.63 | 0.11 | 8.10 |
| 5 | 25 | 17 | 7 | 6.18 | 6.18 | 0.16 | 28.29 | 0.04 | 0.04 | 0.04 | 14.63 | 4.73 | 4.73 | 0.24 | 8.43 |
| 5 | 30 | 15 | 7 | 7.94 | 7.94 | 1.13 | 27.66 | 0.12 | 0.12 | 0.12 | 16.52 | 5.64 | 5.64 | 0.34 | 10.20 |
| 5 | 30 | 17 | 7 | 7.34 | 7.34 | 0.89 | 28.07 | 0.24 | 0.24 | 0.24 | 16.73 | 3.92 | 3.92 | 0.00 | 7.03 |
| 5 | 40 | 17 | 7 | 7.32 | 7.32 | 0.43 | 26.23 | 0.44 | 0.44 | 0.44 | 15.64 | 3.42 | 3.42 | 0.00 | 6.87 |
| Average | 6.97 | 6.97 | 0.79 | 23.08 | 0.41 | 0.41 | 0.39 | 12.23 | 4.87 | 4.87 | 0.35 | 8.79 | |||
| Min | 3.66 | 3.66 | 0.00 | 18.22 | 0.00 | 0.00 | 0.00 | 8.18 | 1.88 | 1.88 | 0.00 | 4.73 | |||
| Max | 9.28 | 9.28 | 3.08 | 28.29 | 1.55 | 1.55 | 1.55 | 16.73 | 8.19 | 8.19 | 1.07 | 12.77 | |||
Concerning TLAP-v, we can see that the percentage of the VSS tends to 0, and this seems reasonable because leftovers have a more significant negative impact on revenues. The recourse function adds costs if we are exceeding the available capacity. Hence, by considering losses of capacity as deterministic parameters is sufficient to use the EEV results to avoid leftovers. This implies that considering only the stochastic utilities does not bring significant economic benefits in comparison to the average utilities. Moreover, we can see that also, LUDS and VSS are almost the same for all instances, indicating that the deterministic solution cannot be upgraded. Since the EV solution already selected enough capacity, it does not seem convenient to open more facilities, even if they have better utilities in a stochastic environment.
Instead, concerning TLAP-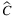 , it results in clear that losses of capacity have a more significant impact on VSS. We can notice how the VSS% for TLAP-
, it results in clear that losses of capacity have a more significant impact on VSS. We can notice how the VSS% for TLAP-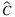 represents, on average, about 70% of the VSS% for the whole problem. The values of the EVPI% for TLAP-v and TLAP-
represents, on average, about 70% of the VSS% for the whole problem. The values of the EVPI% for TLAP-v and TLAP-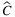 are more or less half of the ones in TLAP-
are more or less half of the ones in TLAP-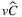 , showing that both stochastic parameters have an impact on that indicator. The results for TLAP-
, showing that both stochastic parameters have an impact on that indicator. The results for TLAP-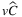 are sort of a combination of the results for TLAP-
are sort of a combination of the results for TLAP-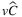 and TLAP-
and TLAP-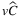 . More precisely, it seems that considering both the stochastic parameters together leads to indicators, which are always, on average, higher than the sum of the relative indicators for the other two variants.
. More precisely, it seems that considering both the stochastic parameters together leads to indicators, which are always, on average, higher than the sum of the relative indicators for the other two variants.
In conclusion, this analysis shows that the stochastic problem with both stochastic utilities and losses of capacity is the most interesting to be studied and can bring to great economic benefits. Moreover, the analysis of LUDS showed that it is possible, in some cases, to derive first-stage solutions very close to the optimal ones. Based on this insight, we will propose a variant of the PH algorithm firmly based on the EIV solution (see Section 6.2) in order to provide better lower bounds.
5 PROGRESSIVE HEDGING-BASED HEURISTIC ALGORITHM
Given the complexity of the stochastic problem, CPLEX and other commercial solvers do not perform well in terms of computational time to solve the DEP model, especially against large instances. Hence, we decided to develop a PH approach to overcome this limit.
The basic PH algorithm has been introduced by Rockafellar and Wets [30]. It is based on the decomposition of the problem by scenario, after having relaxed the nonanticipativity constraints, and on a subgradient method to converge to the first-stage decision consensus. Variants of this algorithm have been used in recent studies with excellent results in terms of approximation of the exact solution and computational time on various kinds of problems. For instance, the PH has been used to solve problems regarding the social engagement paradigm [9], scheduling and planning in industry [25], suppliers selection [21], expansion plans for electric vehicle charging station [17], and fixed-charge capacitated multicommodity network design [6]. Therefore, we decided to implement a generic version of the PH and to propose some interesting variants to improve its performance in several ways.
The section is organized as follows. In Section 5.1, we propose a decomposition of the problem, suitable to the PH algorithm. Section 5.2 summarizes the general framework of the algorithm, while Section 5.3 discuss the initialization and updating of the PH parameters.
5.1 Scenario decomposition
To implement the PH approach we need to make our DEP decomposable by scenario.
 , and
, and  , to represent the copy of xk and
, to represent the copy of xk and  variables, respectively, for a specific scenario s ∈ S. Then, the DEP can be rewritten as follows
variables, respectively, for a specific scenario s ∈ S. Then, the DEP can be rewritten as follows
 (22)
(22) (23)
(23) (24)
(24) (25)
(25) (26)
(26) (27)
(27) (28)
(28) (29)
(29) (30)
(30) (31)
(31) (32)
(32) (33)
(33) are first-stage decisions on the selection of each facility k ∈ K, whereas
are first-stage decisions on the selection of each facility k ∈ K, whereas  are first-stage decisions on the usage of each facility k ∈ K in any time period t ∈ T.
are first-stage decisions on the usage of each facility k ∈ K in any time period t ∈ T. and
and  and the penalty factors ρ1 ≥ 0 and ρ2 ≥ 0. Hence, the scenario-separable model for each scenario s ∈ S can be rewritten as follows
and the penalty factors ρ1 ≥ 0 and ρ2 ≥ 0. Hence, the scenario-separable model for each scenario s ∈ S can be rewritten as follows
 (34)
(34) (35)
(35) (36)
(36) (37)
(37) (38)
(38) (39)
(39) (40)
(40) (41)
(41) (42)
(42) (43)
(43)5.2 PH main framework
Our PH algorithm (see pseudocode in Algorithm 1) can be subdivided into three phases: initialization, consensus, and finalization. In the description of the algorithm, we will use the symbol τ to indicate the iteration number.
In the initialization phase, we calculate the EV solution (Step 2), and the solution found is used to assign a value to 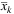 and
and 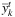 , which represent the so-called temporary global solution (TGS). Then, we initialize the Lagrangian multipliers and the penalties (Step 3). After the initialization phase, we move to the consensus phase (Steps 4–16), which can be executed for a maximum of τmax iterations (Step 5). In each iteration, we solve all the scenario dependent subproblems (Steps 6–8), and we use the obtained results to update the TGS (Step 9). Then, if the consensus is met (Step 10) we terminate the iterations (Step 11), otherwise, we update the Lagrangian multipliers and penalties (Step 13). After the consensus phase, we move to the finalization phase, in which we fix the first-stage variables that reached the consensus during the second phase, and we solve the simplified MILP problem (Step 17).
, which represent the so-called temporary global solution (TGS). Then, we initialize the Lagrangian multipliers and the penalties (Step 3). After the initialization phase, we move to the consensus phase (Steps 4–16), which can be executed for a maximum of τmax iterations (Step 5). In each iteration, we solve all the scenario dependent subproblems (Steps 6–8), and we use the obtained results to update the TGS (Step 9). Then, if the consensus is met (Step 10) we terminate the iterations (Step 11), otherwise, we update the Lagrangian multipliers and penalties (Step 13). After the consensus phase, we move to the finalization phase, in which we fix the first-stage variables that reached the consensus during the second phase, and we solve the simplified MILP problem (Step 17).
Algorithm 1. PH algorithm
1: τ = 0
2: Solve the EV problem to find the initial 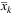 and
and 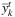
3: Initialize all the Lagrangian multipliers and penalties (Section 5.3)
4: τ = 1
5: while τ ≤ τmax do
6: for each scenario s ∈ S do
7: Solve the corresponding sub-problem
8: end for
9: Update 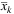 and
and 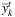
10: if full consensus is met then
11: break
12: else
13: Update the Lagrangian multipliers and penalties (Section 5.3)
14: end if
15: τ = τ + 1
16: end while
17: Fix the first-stage variables for which the consensus is met and solve the model
5.3 Initialize and update PH parameters
The PH parameters (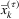 ,
, 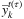 ,
, 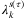 ,
, 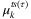 ,
, 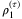 ,
, 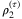 ) must be initially set and then updated at each iteration τ. The choice of such parameters value can be used to tune the algorithm.
) must be initially set and then updated at each iteration τ. The choice of such parameters value can be used to tune the algorithm.
Initially (for τ = 0), we set the TGS by using the result values of the EV solution, hence 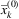 and
and 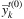 can be either 0 or 1. All the Lagrangian multipliers start with a value equal to 0, more precisely
can be either 0 or 1. All the Lagrangian multipliers start with a value equal to 0, more precisely 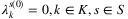 and
and 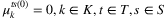 . Finally, since the starting values for penalties ρ1 and ρ2 must be small and positive.
. Finally, since the starting values for penalties ρ1 and ρ2 must be small and positive.
 (44)
(44) (45)
(45) (46)
(46) (47)
(47) (48)
(48) (49)
(49)6 PH VARIANTS AND PRIMAL HEURISTIC
In this section, we discuss two PH variants (Sections 6.1 and 6.2) and a primal LP-based heuristic (Section 6.3).
6.1 PH-Bounds
To improve the performance of the PH algorithm we implemented a variant named PH-Bounds (see Algorithm 2).
Algorithm 2. PH-Bounds algorithm
1: τ = 0
2: Solve the EV problem to find the initial 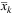 and
and 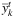
3: Initialize all the Lagrangian multipliers and penalties (Section 5.3)
4: Initialize LB and UB
5: τ = 1
6: while τ ≤ τmax do
7: for each scenario s ∈ S do
8: Solve the corresponding sub-problem
9: end for
10: Update 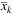 and
and 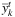
11: if full consensus is met then
12: break
13: else
14: Update the Lagrangian multipliers and penalties (Section 5.3)
15: Fix to 1 all x and y with 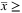 UB and
UB and 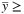 UB
UB
16: Fix to 0 all x and y with 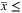 LB and
LB and 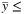 LB
LB
17: Increase LB and decrease UB
18: end if
19: τ = τ + 1
20: end while
21: Fix the first-stage variables for which the consensus is met and solve the model
Compared to the classical PH presented in Section 5.2, PH-Bounds forces the consensus at each iteration by fixing to 0 or 1 those variables of TGS with a value outside a range defined by a specific upper and lower bound (UB and LB, respectively). The rationale behind this variant of the algorithm is to simplify, iteration by iteration, the underlying model to solve. More precisely, both bounds are initialized to a value representing a percentage of the consensus (Step 4). During the iterations, every time the consensus is evaluated and is not reached, we fix to 1 the variables whose value is not less than UB (Step 15) and to 0 the ones that do not exceed LB (Step 16). To speed up the variables fixing process, LB is increased, and UB is decreased at each iteration (Step 17).
6.2 PH-LUDS
Since in Section 4.3 we recognized that the values of LUDS tend to the perfect upgradability, we decided to implement a PH variant (PH-LUDS) based on the concept of expected input value (EIV). In practice, we initialize the TGS with the EIV solution. Using the EIV solution ensures to start from a solution with a good approximation, especially in the case that the termination criterion of the PH leads to solutions far from the optimal.
6.3 Primal LP-based heuristic
To achieve intermediate feasible solutions during the PH, and not just at the very end, we implemented an LP-based heuristic that is executed at the end of each iteration (i.e., after Step 14 of Algorithm 1) if the consensus is not met.
The primal heuristic works as follows. First, we sort the variables 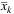 and
and 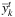 in decreasing order of value currently shown in the TGS. Then, we scan the ordered list of
in decreasing order of value currently shown in the TGS. Then, we scan the ordered list of 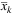 and fix a variable to 1 if its value is greater than or equal to 0.5 or until we do not obtain at least the same number of facilities opened (
and fix a variable to 1 if its value is greater than or equal to 0.5 or until we do not obtain at least the same number of facilities opened ( ) as in the EV solution (
) as in the EV solution (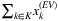 ). We execute a similar fixing procedure for
). We execute a similar fixing procedure for 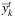 , but we will ensure that, for a certain k ∈ K, a variable
, but we will ensure that, for a certain k ∈ K, a variable 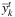 , t ∈ T, can be fixed to 1 only if the corresponding
, t ∈ T, can be fixed to 1 only if the corresponding 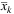 has been already fixed to 1. Therefore, we scan the ordered list of
has been already fixed to 1. Therefore, we scan the ordered list of 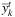 and fix a variable to 1 if its value is greater than or equal to 0.5 or until we do not obtain a number of facilities opened in any period (
and fix a variable to 1 if its value is greater than or equal to 0.5 or until we do not obtain a number of facilities opened in any period (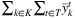 ) that is at least equal to that in the EIV solution (
) that is at least equal to that in the EIV solution ( ) for the PH-LUDS variant, whereas is at least the 20% more than that in the EV solution (
) for the PH-LUDS variant, whereas is at least the 20% more than that in the EV solution (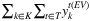 ) in all the other PH variants. The last choice depends on the fact that, in general, the EV solution tends to open fewer facilities and, particularly, in fewer periods with respect to the RP solution. In contrast, the EIV solution tends to select a correct number of facilities. Finally, we fix to 0 all the first-stage variables that have not been fixed by the above procedure and simply solve the remaining LP problem.
) in all the other PH variants. The last choice depends on the fact that, in general, the EV solution tends to open fewer facilities and, particularly, in fewer periods with respect to the RP solution. In contrast, the EIV solution tends to select a correct number of facilities. Finally, we fix to 0 all the first-stage variables that have not been fixed by the above procedure and simply solve the remaining LP problem.
Note that this heuristic has a low cost in terms of computational time since we fix all the binary variables and thus solve an LP problem. Therefore, we have implemented this improvement in all the PH variants presented.
7 COMPUTATIONAL EXPERIMENTS
We test the computational performance of the different PH variants by solving five different instances (generated with random seeds) for all the 30 combinations of some origins |I|, destinations |J|, facilities |K|, and periods |T|, for a total of 150 instances. All the tests have been done on an Intel(R) Core(TM) i7-5930K [email protected] GHz machine with 64 GB RAM and running Windows 7 64-bit operating system. The algorithms have been implemented in Java. We also implemented a parallel execution to solve the decomposed problems in the consensus phase to speed up even further the computation performance of our heuristics.
- τmax = 15 (see Section 5.2);
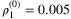 ,
, 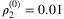 , α1 = 1.5, and α2 = 3 (see Section 5.3). We decided to have smaller penalties for the parameters related to x variables, since excluding a facility makes impossible its utilization for any time period;
, α1 = 1.5, and α2 = 3 (see Section 5.3). We decided to have smaller penalties for the parameters related to x variables, since excluding a facility makes impossible its utilization for any time period;- starting value of UB and LB equal to 1 and 0, respectively. Moreover, at each iteration τ, UB(τ) = UB(τ − 1) − 0.02 and LB(τ) = LB(τ − 1) + 0.02 (see Section 6.1).
In Table 2, we present the results regarding the accuracy of CPLEX and our methods. In particular, the first four columns denote the instance, column five reports the average percentage MIP gap achieved by CPLEX. In comparison, the remaining three columns present the percentage deviation (Δ%avg) of each specific PH solution with respect to the CPLEX one. A positive deviation indicates that CPLEX performs better, whereas a negative value indicates that the PH achieves a better solution. Note that the lines of the table have been divided into two groups. We have noticed that in some instances, the MIP gap is not too large (less than 10%), indicating that CPLEX can find solutions close to the optimum (which provide reasonable benchmarks for the PH variants). Instead, for other instances, MIP gaps tend to increase a lot to enormous values, thus making the CPLEX solver not suitable anymore. This division allows us to better describe the relative statistics.
| Instance | CPLEX | PH | PH-Bounds | PH-LUDS | |||
|---|---|---|---|---|---|---|---|
| |I| | |J| | |K| | |T| | MIP gap%avg | Δ%avg | Δ%avg | Δ%avg |
| 2 | 15 | 10 | 7 | 0,63 | 2,37 | 2,70 | 1,06 |
| 2 | 15 | 12 | 14 | 1,61 | 1,95 | 2,24 | 0,47 |
| 2 | 15 | 10 | 14 | 2,31 | 1,08 | 2,01 | 0,51 |
| 2 | 15 | 10 | 31 | 1,35 | 0,51 | 1,38 | 0,21 |
| 2 | 15 | 12 | 7 | 0,85 | 2,83 | 2,89 | 0,81 |
| 2 | 15 | 15 | 7 | 1,09 | 2,13 | 1,47 | 0,48 |
| 2 | 20 | 10 | 7 | 2,71 | 1,04 | 1,50 | 0,03 |
| 2 | 20 | 10 | 14 | 3,75 | -0,07 | 0,76 | -0,49 |
| 2 | 20 | 12 | 7 | 1,55 | 1,48 | 2,29 | 0,53 |
| 2 | 20 | 15 | 7 | 3,00 | 0,74 | 0,88 | 0,24 |
| 2 | 20 | 12 | 14 | 7,09 | −4,16 | −3,85 | −5,06 |
| 2 | 25 | 12 | 7 | 2,44 | 1,70 | 1,60 | 0,66 |
| 2 | 25 | 15 | 7 | 3,60 | 1,35 | 1,05 | 0,13 |
| 2 | 25 | 17 | 7 | 3,39 | 1,32 | 1,40 | −0,21 |
| 3 | 15 | 10 | 7 | 1,19 | 1,08 | 1,85 | 0,45 |
| 3 | 15 | 12 | 7 | 2,93 | 0,15 | 1,16 | 0,03 |
| 3 | 15 | 15 | 7 | 2,54 | 1,44 | 1,00 | 0,31 |
| 3 | 20 | 10 | 7 | 3,86 | 0,31 | 0,76 | 0,06 |
| 3 | 20 | 12 | 7 | 2,84 | 1,01 | 1,36 | 0,50 |
| 3 | 25 | 15 | 7 | 3,05 | 0,22 | 0,27 | −0,03 |
| 3 | 40 | 20 | 7 | 4,13 | −0,60 | −0,81 | −1,17 |
| 5 | 25 | 17 | 7 | 7,12 | −4,52 | −3,90 | −4,41 |
| Average | 2,86 | 0,61 | 0,91 | −0,22 | |||
| Best | 0,63 | −4,52 | −3,90 | −5,06 | |||
| Worst | 7,12 | 2,83 | 2,89 | 1,06 | |||
| 2 | 20 | 10 | 31 | 120,56 | −115,28 | −114,27 | −116,26 |
| 2 | 25 | 15 | 31 | 99 052,14 | −185,46 | −183,28 | −186,71 |
| 3 | 30 | 12 | 31 | 357 932,73 | −447,76 | −441,46 | −449,45 |
| 3 | 30 | 20 | 7 | 860,54 | −811,75 | −814,08 | −829,59 |
| 5 | 15 | 10 | 14 | 75,35 | −72,41 | −70,91 | −72,41 |
| 5 | 30 | 15 | 7 | 150,09 | −140,34 | −137,07 | −140,52 |
| 5 | 30 | 17 | 7 | 182,39 | −173,15 | −172,95 | −174,56 |
| 5 | 40 | 17 | 7 | 242 291,95 | −1264,36 | −1269,13 | −1274,79 |
| Average | 87 583,22 | −401,31 | −400,39 | −405,54 | |||
| Best | 75,35 | −1264,36 | −1269,13 | −1274,79 | |||
| Worst | 357 932,73 | −72,41 | −70,91 | −72,41 | |||
In general, all the three heuristics have a good approximation with respect to the CPLEX solution. First, it is clear that the PH variants solutions are mostly better than CPLEX ones for the second part of the table, showing an average Δ%avg about −400% with some extreme cases where the deviation are less than −1000%. However, it is more interesting to focus on those results in which CPLEX provides reasonable benchmarks (first part of the table). Here, we can see that our PH variants have deviations often close to 0 and, in several cases, even below. In particular, on average, the classical PH method achieves a deviation of about 0.6%, PH-Bounds performs slightly worse with a deviation of about 0.9%, whereas PH-LUDS outperforms all the methods providing a deviation of about −0.2%. So, the most precise method results to be the PH-LUDS, which takes advantage of using the upgradability of the deterministic solution. Note that this variant, except for the combination 2-15–10-7, always shows a Δ%avg below 1%, with a best-case of about −5%. For the other two PH variants, the worst-case combination shows a Δ%avg of about 2.8%.
In Table 3, instead, we compare the computational times of the methods. In particular, the first four columns denote the instance, while the remaining columns report, for CPLEX and the different PH variants, the average computational time (tavg) and the average time-to-best (ttbavg), that is, the time to reach the best solution.
| Instance | CPLEX | PH | PH-Bounds | PH-LUDS | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| |I| | |J| | |K| | |T| | tavg | ttbavg | tavg | ttbavg | tavg | ttbavg | tavg | ttbavg |
| 2 | 15 | 10 | 7 | 7165 | 5901 | 182 | 146 | 128 | 62 | 221 | 89 |
| 2 | 15 | 12 | 14 | 10 800 | 8964 | 309 | 196 | 204 | 124 | 417 | 138 |
| 2 | 15 | 10 | 14 | 10 800 | 9962 | 420 | 398 | 281 | 175 | 499 | 87 |
| 2 | 15 | 10 | 31 | 10 800 | 10 510 | 573 | 573 | 367 | 235 | 702 | 473 |
| 2 | 15 | 12 | 7 | 8296 | 6613 | 255 | 146 | 162 | 98 | 311 | 63 |
| 2 | 15 | 15 | 7 | 9649 | 9053 | 275 | 114 | 197 | 147 | 370 | 98 |
| 2 | 20 | 10 | 7 | 10 800 | 9549 | 355 | 222 | 196 | 109 | 410 | 63 |
| 2 | 20 | 10 | 14 | 10 800 | 10 800 | 375 | 308 | 231 | 169 | 519 | 294 |
| 2 | 20 | 10 | 31 | 10 800 | 10 800 | 1567 | 1458 | 956 | 778 | 1944 | 952 |
| 2 | 20 | 12 | 7 | 9279 | 7443 | 375 | 211 | 218 | 113 | 470 | 159 |
| 2 | 20 | 15 | 7 | 10 800 | 10 747 | 230 | 132 | 168 | 105 | 308 | 108 |
| 2 | 20 | 12 | 14 | 10 800 | 10 012 | 836 | 313 | 480 | 228 | 1060 | 243 |
| 2 | 25 | 12 | 7 | 10 800 | 9488 | 418 | 180 | 287 | 215 | 515 | 142 |
| 2 | 25 | 15 | 7 | 10 800 | 10 409 | 553 | 443 | 362 | 232 | 676 | 154 |
| 2 | 25 | 17 | 7 | 10 800 | 10 476 | 603 | 265 | 404 | 204 | 746 | 175 |
| 3 | 15 | 10 | 7 | 10 020 | 8944 | 337 | 277 | 193 | 141 | 424 | 173 |
| 3 | 15 | 12 | 7 | 10 800 | 9635 | 424 | 335 | 263 | 174 | 585 | 364 |
| 3 | 15 | 15 | 7 | 10 800 | 9503 | 432 | 211 | 302 | 172 | 598 | 216 |
| 3 | 20 | 10 | 7 | 10 800 | 8828 | 663 | 387 | 310 | 228 | 786 | 489 |
| 3 | 20 | 12 | 7 | 10 800 | 9580 | 550 | 339 | 355 | 217 | 701 | 213 |
| 3 | 25 | 15 | 7 | 10 800 | 9040 | 1091 | 770 | 597 | 203 | 1344 | 397 |
| 3 | 25 | 15 | 31 | 10 800 | 10 559 | 5007 | 4001 | 2900 | 1776 | 6236 | 2450 |
| 3 | 30 | 12 | 31 | 10 800 | 10 800 | 4705 | 4705 | 2594 | 1607 | 6294 | 3804 |
| 3 | 30 | 20 | 7 | 10 800 | 8167 | 1650 | 824 | 883 | 613 | 1951 | 584 |
| 3 | 40 | 20 | 7 | 10 800 | 9679 | 1914 | 770 | 1081 | 508 | 2289 | 627 |
| 5 | 15 | 10 | 14 | 10 800 | 8808 | 1521 | 1521 | 628 | 458 | 1951 | 1951 |
| 5 | 25 | 17 | 7 | 10 800 | 9880 | 2110 | 981 | 1024 | 519 | 2662 | 1209 |
| 5 | 30 | 15 | 7 | 10 800 | 10 123 | 3521 | 3521 | 1209 | 786 | 4128 | 2801 |
| 5 | 30 | 17 | 7 | 10 800 | 10 415 | 3897 | 3309 | 1504 | 1012 | 4473 | 1532 |
| 5 | 40 | 17 | 7 | 10 800 | 10 800 | 6207 | 5455 | 2231 | 1905 | 7345 | 2610 |
| Average | 10 480 | 9516 | 1378 | 1084 | 691 | 444 | 1698 | 755 | |||
| Best | 7165 | 5901 | 182 | 114 | 128 | 62 | 221 | 63 | |||
| Worst | 10 800 | 10 800 | 6207 | 5455 | 2900 | 1905 | 7345 | 3804 | |||
From the table, we can see that PH-Bounds is (as expected) the fastest method, both in terms of total execution time and the time-to-best. In particular, PH-Bounds needs, on average, half the time with respect to the other PH variants to be completed without reducing too much the accuracy. For CPLEX, 3 h is often not enough to reach the optimum or even a good solution, making the solver not competitive in terms of computational time respect to the PH heuristics. By comparing the tavg of the classical PH, PH-Bounds, and PH-LUDS with the CPLEX one, we can see that our heuristics can find good solutions in 13%, 6%, and 16% of the CPLEX execution time. The best tavg among all the instances for the PH, PH-Bounds, and PH-LUDS are, respectively, 182, 128, and 221 s, whereas the best ttbavg are 114, 62, and 63 s. PH-LUDS requires additional computational effort to compute the EIV solution.
In general, we can say that the three PH variants have excellent performance in terms of both approximation and computational time. Some additional information about the heuristics can be found in Table A1 (see Appendix A) where, for the different PH variants, the best and the worst values of the percentage deviation and of the computational time are given. Note that our PH methods could be further improved by developing a tailored and more efficient algorithm to solve the single-scenario problems during the consensus phase. We have noticed that using CPLEX as an internal solver is not very efficient. To speed up the process, we had to set a MIP gap of 5%, with bad consequences on the quality of the solutions.
8 CONCLUSIONS AND FUTURE DEVELOPMENTS
In this paper, we presented a TLAP by considering a synchromodal network in which flows are synchronized at intermediate facilities under the uncertainty of transshipment capacities and utilities. The SP indicators studied in the paper pointed out that optimizing a stochastic version of the problem provides better revenues by avoiding leftovers as much as possible. The deterministic solution was always underestimating the number of facilities needed to reduce the impact of the worst scenario realizations, that is, those with the highest losses of capacity. Given the computational burden of solving the stochastic problem by commercial solvers, we developed three Progressive Hedging-based heuristic methods. Since studying the LUDS we discovered that a good subset of facilities could be pre-selected by solving the deterministic problem. We used this insight to develop a PH variant (PH-LUDS) and also to implement a primal LP-based heuristic. For the future, it will be interesting to study how other sources of uncertainty (e.g., demand and costs), distributions, and constraints impact on the problem. For example, we would like to understand if the almost perfect upgradability of the deterministic solution is related to the problem itself or this stochastic setting only.
Regarding computational experiments, the PH methods perform far better than CPLEX for hard-to-solve instances in much lower computational time, but also provide solutions very close to the CPLEX one for the other instances. The limit of the PH methods mainly concerns the solution time of the single-scenario problem during the consensus phase, which sometimes leads to high total computational time. Implementing a faster approach, exact or even heuristic, to solve the single-scenario problem could be of primary importance to improve the PH performance further. Lastly, the PH-Bounds showed that strategies for fixing variables could speed up the algorithm with a small loss of accuracy. Hence, exploring new criteria to perform the fixing procedure might be of interest for future work.
ACKNOWLEDGMENTS
The authors would like to thank two anonymous referees for their valuable suggestions. Computational resources for the stability analysis were provided by HPC@POLITO, a project of Academic Computing within the Department of Control and Computer Engineering at the Politecnico di Torino (http://www.hpc.polito.it).
Appendix A: ADDITIONAL PH RESULTS
| Instance | PH | PH-Bounds | PH-LUDS | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |I| | |J| | |K| | |T| | tbest | tworst | ttbbest | ttbworst | Δ%best | Δ%worst | tbest | tworst | ttbbest | ttbworst | Δ%best | Δ%worst | tbest | tworst | ttbbest | ttbworst | Δ%best | Δ%worst |
| 2 | 15 | 10 | 7 | 128 | 240 | 39 | 240 | 0.83 | 3.39 | 89 | 156 | 9 | 106 | 1.08 | 4.32 | 162 | 276 | 22 | 216 | 0.37 | 1.91 |
| 2 | 15 | 12 | 14 | 278 | 340 | 71 | 317 | 1.31 | 2.59 | 194 | 212 | 84 | 183 | 1.12 | 3.26 | 379 | 467 | 85 | 222 | 0.19 | 0.75 |
| 2 | 15 | 10 | 14 | 262 | 509 | 155 | 509 | −0.55 | 1.99 | 184 | 354 | 59 | 266 | 0.60 | 2.85 | 354 | 613 | 61 | 105 | −0.58 | 1.20 |
| 2 | 15 | 10 | 31 | 462 | 673 | 462 | 673 | −0.74 | 1.05 | 348 | 411 | 42 | 328 | 0.04 | 3.05 | 578 | 787 | 114 | 787 | −1.32 | 1.05 |
| 2 | 15 | 12 | 7 | 148 | 323 | 12 | 323 | 1.18 | 4.53 | 102 | 194 | 42 | 194 | 0.42 | 5.71 | 183 | 374 | 47 | 102 | 0.40 | 1.22 |
| 2 | 15 | 15 | 7 | 163 | 341 | 14 | 307 | 1.11 | 3.07 | 114 | 232 | 54 | 232 | 0.54 | 2.48 | 195 | 461 | 38 | 138 | 0.09 | 0.98 |
| 2 | 20 | 10 | 7 | 210 | 559 | 39 | 559 | 0.00 | 1.84 | 122 | 225 | 54 | 159 | −0.51 | 3.15 | 265 | 634 | 48 | 88 | −0.63 | 0.87 |
| 2 | 20 | 10 | 14 | 339 | 400 | 48 | 400 | −0.83 | 1.05 | 211 | 250 | 126 | 211 | −0.09 | 2.31 | 508 | 540 | 128 | 511 | −1.67 | 0.35 |
| 2 | 20 | 10 | 31 | 987 | 1931 | 987 | 1931 | −458.93 | 1.08 | 624 | 1209 | 495 | 1072 | −459.58 | 2.03 | 1212 | 2650 | 225 | 2650 | −463.07 | 1.08 |
| 2 | 20 | 12 | 7 | 219 | 456 | 29 | 441 | 0.32 | 2.15 | 158 | 283 | 30 | 283 | 0.31 | 4.09 | 279 | 551 | 74 | 358 | 0.03 | 1.01 |
| 2 | 20 | 15 | 7 | 212 | 240 | 50 | 212 | 0.29 | 1.08 | 159 | 182 | 37 | 148 | 0.35 | 1.31 | 267 | 374 | 71 | 204 | −0.55 | 0.88 |
| 2 | 20 | 12 | 14 | 503 | 1438 | 41 | 717 | −23.93 | 1.04 | 329 | 633 | 91 | 378 | −23.93 | 1.55 | 641 | 1806 | 144 | 378 | −25.63 | 0.26 |
| 2 | 25 | 12 | 7 | 251 | 530 | 33 | 394 | 1.31 | 2.60 | 194 | 352 | 172 | 282 | 0.70 | 2.29 | 319 | 596 | 66 | 297 | 0.30 | 1.27 |
| 2 | 25 | 15 | 7 | 284 | 720 | 75 | 671 | 0.03 | 3.50 | 216 | 490 | 121 | 320 | 0.13 | 2.14 | 423 | 847 | 101 | 179 | −0.89 | 1.27 |
| 2 | 25 | 17 | 7 | 369 | 862 | 53 | 440 | 0.41 | 2.33 | 255 | 560 | 66 | 326 | 0.51 | 2.37 | 419 | 1074 | 69 | 267 | −0.59 | 0.43 |
| 3 | 15 | 10 | 7 | 184 | 428 | 21 | 428 | −0.37 | 1.96 | 127 | 250 | 22 | 195 | −0.37 | 3.76 | 232 | 535 | 45 | 535 | −0.71 | 1.21 |
| 3 | 15 | 12 | 7 | 209 | 642 | 35 | 642 | −0.92 | 0.88 | 154 | 354 | 35 | 354 | 0.52 | 1.58 | 306 | 911 | 70 | 911 | −0.92 | 0.71 |
| 3 | 15 | 15 | 7 | 270 | 562 | 46 | 488 | −0.29 | 3.79 | 202 | 386 | 60 | 291 | −0.28 | 2.85 | 365 | 776 | 145 | 363 | −0.50 | 1.06 |
| 3 | 20 | 10 | 7 | 358 | 1135 | 56 | 1135 | −2.34 | 1.65 | 204 | 402 | 58 | 402 | −0.22 | 1.55 | 454 | 1324 | 102 | 1324 | −2.34 | 1.23 |
| 3 | 20 | 12 | 7 | 362 | 797 | 34 | 797 | 0.41 | 1.45 | 255 | 465 | 109 | 465 | 0.49 | 2.96 | 467 | 1033 | 126 | 323 | 0.02 | 0.99 |
| 3 | 25 | 15 | 7 | 637 | 1388 | 76 | 1388 | −0.44 | 0.98 | 377 | 741 | 46 | 478 | −0.90 | 0.98 | 883 | 1728 | 244 | 571 | −0.68 | 0.98 |
| 3 | 25 | 15 | 31 | 3665 | 5998 | 894 | 5559 | −309.37 | 0.02 | 2114 | 3717 | 471 | 2892 | −303.55 | 1.29 | 5075 | 7444 | 1502 | 6062 | −309.51 | 0.02 |
| 3 | 30 | 12 | 31 | 3766 | 6958 | 3766 | 6958 | −674.28 | −319.46 | 2138 | 3768 | 81 | 2539 | −662.76 | −314.85 | 4636 | 9238 | 989 | 9238 | −674.28 | −320.81 |
| 3 | 30 | 20 | 7 | 1202 | 2920 | 146 | 1452 | −3005.09 | 1.11 | 718 | 1332 | 134 | 1044 | −3005.09 | −0.52 | 1372 | 2997 | 454 | 691 | −3066.15 | −1.12 |
| 3 | 40 | 20 | 7 | 1366 | 3044 | 195 | 1724 | −4.04 | 1.41 | 902 | 1280 | 244 | 866 | −4.04 | 0.93 | 1849 | 3199 | 336 | 1108 | −4.89 | 0.51 |
| 5 | 15 | 10 | 14 | 786 | 2065 | 786 | 2065 | −351.90 | 0.58 | 510 | 861 | 192 | 861 | −347.99 | 1.13 | 1169 | 2477 | 1169 | 2477 | −351.90 | 0.58 |
| 5 | 25 | 17 | 7 | 1633 | 2901 | 112 | 2050 | −22.76 | 0.74 | 788 | 1320 | 108 | 1087 | −21.51 | 1.20 | 2051 | 3434 | 454 | 3038 | −22.97 | 0.78 |
| 5 | 30 | 15 | 7 | 2892 | 4275 | 2892 | 4275 | −564.96 | −0.44 | 980 | 1420 | 139 | 1196 | −553.91 | 1.02 | 3288 | 4939 | 513 | 4939 | −565.56 | −0.44 |
| 5 | 30 | 17 | 7 | 3111 | 4997 | 435 | 4997 | −823.15 | 1.44 | 1309 | 1796 | 133 | 1796 | −822.81 | 1.24 | 3626 | 5596 | 562 | 3626 | −826.37 | −0.05 |
| 5 | 40 | 17 | 7 | 4332 | 6998 | 571 | 6998 | −2490.95 | −8.73 | 1991 | 2464 | 1114 | 2464 | −2502.01 | −8.78 | 5124 | 8415 | 817 | 8340 | −2516.83 | −9.02 |
| Best | 128 | 240 | 12 | 212 | −3005.09 | −319.46 | 89 | 156 | 9 | 106 | −3005.09 | −314.85 | 162 | 276 | 22 | 88 | −3066.15 | −320.81 | |||
| Worst | 4332 | 6998 | 3766 | 6998 | 1.31 | 4.53 | 2138 | 3768 | 1114 | 2892 | 1.12 | 5.71 | 5124 | 9238 | 1502 | 9238 | 0.40 | 1.91 | |||




