Magnetic resonance fingerprinting: a technical review
Abstract
Multiparametric quantitative imaging is gaining increasing interest due to its widespread advantages in clinical applications. Magnetic resonance fingerprinting is a recently introduced approach of fast multiparametric quantitative imaging. In this article, magnetic resonance fingerprinting acquisition, dictionary generation, reconstruction, and validation are reviewed.
1 INTRODUCTION
In recent years, there has been increased interest in quantitative MRI methods to measure physical properties such as T1, T2, and diffusion coefficients. Quantitative methods provide the advantage of reduced subjectivity, which could aid in diagnosis, tissue characterization, follow-up, and therapeutic assessment. Moreover, characterization of pathologies is often dependent not only on a single tissue property, but on a combination of properties evaluated together.1-4 Ideally, all property maps should be registered to one another.
Most quantitative MRI approaches allow for the measurement of tissue properties but are relatively slow and generally provide only a single property at a time. Approaches to quantify a single property involve measuring signal changes after varying a single acquisition parameter, keeping others constant. Within each image or data point used to obtain the map of interest, the signal is kept constant to avoid errors in property estimation due to deleterious effects from undesired fluctuations. Thus, the magnetization must recover to the same initial state for every cycle, to limit the signal variation caused by changing the acquisition parameter. This requirement of retaining the same conditions is one of the primary reasons for the relatively long scan time of these approaches. Faster alternative techniques have been developed, including some of the commonly used techniques,5-9 but these are often affected by other undesired tissue or system properties10-12 such as B1, diffusion, and magnetization transfer, thereby resulting in errors for the estimation of target property. To improve this situation, techniques have been proposed to acquire multiple tissue proprieties at the same time.13-15 However, none of these methods has achieved widespread clinical adoption.
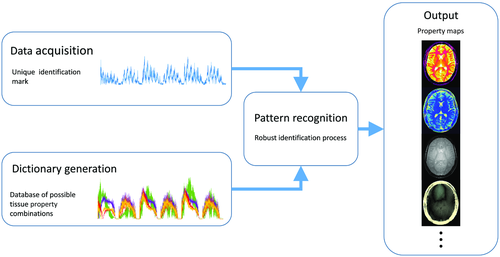
Magnetic resonance fingerprinting (MRF)16 is a framework (Figure 1) in which a different formalism is used to achieve the goal of fast multiproperty quantitative imaging. In this framework, instead of sequentially acquiring information of desired multiple tissue properties, the idea is to simultaneously probe for information on all of the desired tissue properties with the goal of improving SNR and scan efficiency of the entire experiment. The acquisition is made sensitive to multiple tissue properties by simultaneously varying multiple sequence parameters throughout the acquisition, providing fingerprint-like signal evolutions for combinations of desired tissue properties. Separately, a dictionary of simulated signal time courses is generated for anticipated combinations of tissue properties using an appropriate signal model. Pattern recognition is used to compare each voxel’s fingerprint with the dictionary to identify the best matching entry from the dictionary for each voxel. The property values associated with the best dictionary match are assigned as the measured properties for that voxel. It has been demonstrated that the matching process allows identification of tissue properties even in the presence of undersampling artifacts, allowing for high acceleration factors to be used for individual time points, enabling high efficiency17, 18 in the MRF acquisition. Magnetic resonance fingerprinting therefore presents a relatively generalized framework with the potential to measure a wide variety of tissue properties. The initial applications of MRF focused on T1, T2, B0, and proton density mapping.16 However, recent work has shown the feasibility to measure B1+, T2*, perfusion,19, 20 and hemodynamic21, 22 related properties. The relatively open framework of MRF presents many options for each component of the acquisition and reconstruction process. In this review, we will cover each of the primary components of an MRF method: acquisition, dictionary generation, and reconstruction.
2 ACQUISITION
The MRF framework does not impose constraints on the sequence design so long as the primary goals of conducting an efficient (based on SNR and scan time) experiment and ensuring the desired tissue properties are separable enough to be extracted with sufficient precision. Because of this flexibility, nearly any sequence can be used in an MRF acquisition, and multiple sequence types can be combined in a single acquisition. The design of the sequence determines the acquisition efficiency, the properties that can be estimated and their accuracy, and the corresponding clinical application.
2.1 General approaches
2.1.1 Balanced SSFP
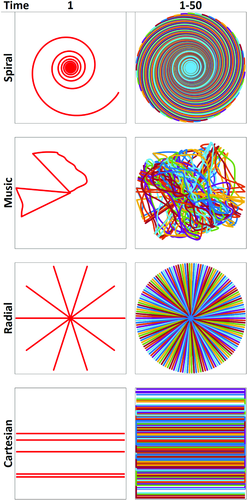
In the proof-of-principle implementation of MRF by Ma et al,16 an inversion recovery–prepared balanced SSFP (bSSFP) based approach (Figure 2) was used, as the bSSFP sequence has been extensively studied.23-31 The properties of retaining spin history, high SNR, high scan efficiency, and high sensitivity to T1, T2, and off-resonance frequencies make bSSFP highly suitable for MRF. Results from 2 different flip angle (FA) and TR variations were presented. For k-space sampling, a variable density spiral trajectory was used with uniform rotation (360º/48) at each time point (Figure 3 and Figure S1), which allows the undersampling artifacts to have sufficient spatio-temporal incoherence.

The accuracy of bSSFP-MRF was compared with DESPOT1 and DESPOT22 in phantoms with reference measurements performed using spin-echo (SE) based techniques. The results obtained from MRF were in good agreement with the SE measurements and the associated concordance correlation coefficients were higher compared with the DESPOT approach. The T1 and T2 values of brain tissues obtained using bSSFP-MRF in vivo were shown to be in agreement with literature values (Table 1). Additionally, the MRF efficiency in phantoms was superior to the DESPOT efficiency by an average factor of 1.87 (DESPOT1) and 1.85 (DESPOT2).
|
bSSFP (1.5 T) |
FISP (3 T) |
pSSFP (3 T) |
Music (3 T) |
QUEST (3 T) |
||||
|---|---|---|---|---|---|---|---|---|
|
Literature (1.5 T) |
Literature (3 T) |
|||||||
| WM | T1 (ms) | 685 ± 33 | 781 ± 61 | 1090 ± 75 | 847 ± 49 | 744-809 | 608-756 | 788-898 |
| 1084 ± 45 1084 ± 79 | ||||||||
| T2 (ms) | 65 ± 4 | 65 ± 6 | 61.9 ± 6.4 | 48 ± 6.3 | 44-55 | 54-81 |
78-80 69 ± 3 63-80 |
|
| GM | T1 (ms) | 1180 ± 104 | 1193 ± 65 | 1616 ± 78 | 1223 ± 65 | 1008-1493 | 998-1304 | 1286-1393 |
| 1820 ± 110 1703 ± 53 | ||||||||
| T2 (ms) | 97 ± 5.9 | 109 ± 11 | 94.4 ± 5.4 | 64 ± 5.2 | 64-71 | 78-98 |
99-117 99 ± 7 78-117 |
|
| CSF | T1 (ms) | 4880 ± 379 | 2000-3800 | 4103-5400 | — | |||
| T2 (ms) | 550 ± 251 | 115-160 | 1800-2460 | — |
- a Abbreviations: GM, gray matter; pSSFP, pseudo-SSFP; WM, white matter.
- b Note: For each approach, the estimated values are shown as well as the literature values used to validate the technique.
The bSSFP sequence presents many favorable properties, one of which is the ability to refocus spins of different off-resonance frequencies at TE = TR/2 in the steady state.27 However, the use of transient state, variable FA, and variable TR in MRF may lead to a loss of this SE-like refocusing characteristic. The work presented by Assländer et al33 aimed to reduce the sensitivity of the bSSFP-MRF acquisition to static magnetic field inhomogeneities. They proposed to estimate TE and TR patterns based on the variable FA pattern, which maintains the SE-like refocusing characteristic of bSSFP.
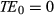 is assumed and TE and TR were updated by the following equations:
is assumed and TE and TR were updated by the following equations:
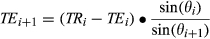 (1)
(1)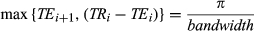 (2)
(2)where bandwidth is the desired bSSFP-based bandwidth in radians/second. Equation 1 exploits the property of the RF pulse to retain the Euclidean distance between the tips of the magnetization vectors of different isochromats. Additionally, this neglects relaxation and uses the small dispersion angle approximation.33 This algorithm provides a series of TRs that will produce a SE-like refocusing at the corresponding set of TEs for a given set of FA series (Figure 4 and Figure S2).

It was shown in a phantom that the pseudo-SSFP-MRF design is less sensitive than bSSFP-MRF in the presence of B0 variation, resulting in an accurate signal description even without including off-resonance and intravoxel dephasing in the dictionary. This makes the pseudo-SSFP pattern dependent on fewer degrees of freedom, thereby reducing the complexity and size of the dictionary; however, it precludes the mapping of B0. Reported results for a brain scan in a healthy subject were in agreement with literature values (Table 1).
2.1.2 Fast imaging with steady-state precision
Balanced SSFP–based acquisitions provide sensitivity to off-resonance and a relatively high SNR but suffer from banding artifacts when a wide range of off-resonant spins are present within the FOV. To compensate for this, an MRF approach was proposed based on the unbalanced SSFP (fast imaging with steady-state precision [FISP], fast field echo, gradient-recalled acquisition in steady state, gradient field echo, field echo, first postcontrast acquisition subtracted, and SSFP34) acquisition.35 This acquisition strategy adds an unbalancing gradient moment at the end of each TR, which produces a phase twist within each voxel, thereby retaining signal coherence and reducing the sequence sensitivity to off-resonance. Thus, the FISP-MRF approach eliminates the banding artifacts; however, it has reduced SNR and is unable to quantify off-resonance. Sample results illustrating FISP-MRF’s insensitivity to off-resonance are shown in Figure 5 and Figure S3. The FA varies smoothly using half-sine waves, similar to the bSSFP-MRF approach, though no additional oscillations are added (Figure 4 and Figure S2). The TR variations (Figure 4 and Figure S2), the inversion recovery pulse, and the readout trajectory were the same as that used in the bSSFP-MRF approach.
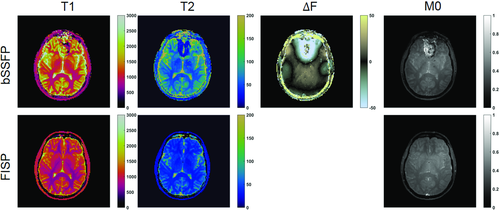
The accuracy of the FISP-MRF35 approach was evaluated in phantoms. The authors reported a good agreement between FISP-MRF and SE measurements for both T1 and T2. The agreement was retained even when the shim settings were changed, demonstrating the robustness of the FISP-based approach to B0 inhomogeneity. The FISP-MRF approach also showed good agreement with literature values in healthy volunteers for white and gray matter (Table 1). This same approach was also successfully translated to small animal imaging at 7 T.36
2.1.3 Radiofrequency-spoiled gradient echo
Recently, a new method was proposed by Rieger et al37 for simultaneous measurement of T1 and T2*. In this approach, a RF-spoiled gradient echo (GRE) based acquisition strategy, in which gradient and RF spoiling were used with an empirically chosen smooth variation of TE (range: 14-75 ms) and the FA variation based on the FISP-MRF sequence.35 The authors proposed to use a single-shot EPI readout. For acceleration, they used partial Fourier (factor 6/8) and GRAPPA38-based parallel imaging (factor = 3). A total of 160 frames were acquired for a scan time of 10 seconds for a 2D acquisition. The method was validated in phantoms and in healthy subjects, in whom close agreement with reference values over various regions of interest was seen.
2.1.4 Quick-echo splitting NMR
Imaging patient populations such as those with deep brain stimulators or metallic implants require strict constraints on specific absorption rate, thereby imposing restrictions on the RF duty cycle and RF pulse shapes. Jiang et al39 proposed an approach for these applications, using a quick echo splitting NMR (QUEST) based MRF sequence to overcome these constraints. The sequence used subsequent “acquisition blocks” of QUEST (Figure 6). Each block consisted of 4 aperiodic RF excitations to acquire a total of 11 higher-order echoes. Acquiring also the FID after each pulse, a total of 15 MRF time points were obtained from only 4 RF excitations. This QUEST block was repeated 15 times, leading to a total of 225 time points acquired through 60 RF pulses. The FA of each RF excitation was randomly selected between 1° and 60°, and the time interval between the first and second RF pulse of each QUEST block was randomly changed between 10 ms and 13 ms (Figure 4 and Figure S2). This entire acquisition was repeated 12 times to acquire the 12 interleaves needed to fully sample the center of k-space for each time point.
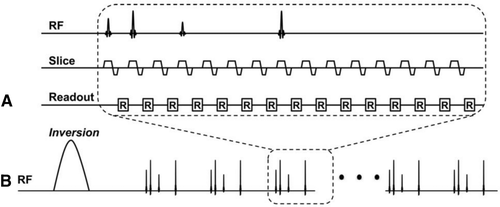
The MRF-QUEST framework allowed significant reduction of the number of RF pulses used during the acquisition and thereby the energy deposition into the subject. In vitro and in vivo tests showed that the accuracy of MRF-QUEST is in line with the standard SE-based methods and literature values for brain tissues except for white matter T2 (Table 1), at lower specific absorption rate than GRE or turbo SE methods (MRF-QUEST = 0.03 W/kg, GRE = 0.1 W/kg, and turbo SE = 0.3 W/kg).39
2.2 Approaches designed for specific applications
2.2.1 Perfusion and vascular properties
Microvascular structure
The MRF framework has also been extended to characterize the properties associated with the microvascular network. In the study performed by Christen et al,21 the authors developed a new approach to measure the cerebral blood volume, the mean vessel radius and the blood oxygenation saturation. The acquisition sequence was based on a GRE sampling of the FID and SE sequence. In this acquisition, 40 time points were sampled for each TR, with a ΔTE of 3 ms, and 14 echoes acquired before the SE-associated 180º pulse. No undersampling was used for this acquisition. A total of 12 slices were acquired to cover the entire brain in 4 minutes. The acquisition was performed before and 2 minutes after injection of the contrast agent (ferumoxytol). Unlike the other methods, the signal variation in this approach is caused by the change in contrast concentration and variations in echo type and TE. Furthermore, the ratio of the precontrast and postcontrast signal evolutions were used as the fingerprint, which reduced the effect of B0 inhomogeneities and T2. In vivo results showed good contrast of cerebral blood volume between white matter and gray matter, whereas the mean radius and blood oxygenation saturation were found to be homogeneous. The cerebral blood volume values obtained agreed with the literature values obtained from PET and alternative MRI approaches as well as with a steady-state susceptibility approach.
Arterial spin labeling
The feasibility of performing arterial spin labeling (ASL) based on MRF has recently been investigated. Su et al19 modified an ASL sequence by using a variable labeling duration time for each TR, removing the postlabeling delay and ordering the labeling-control pairing in a pseudorandom fashion. The acquisition was performed using an EPI readout for 3D volumetric coverage for each time point and a total of 3 minutes of scan time. Different properties can be extracted depending on the model applied. The authors used 2 different tissue models. A single-compartment model (tissue and microvasculature) was used to estimate cerebral blood flow, bolus arrival time (BAT), T1, and B1+. A 2-compartment model was also used, in which pass-through blood was introduced as a second compartment, which additionally provided pass-through arterial bolus arrival time, pass-through blood volume (vblood), and pass-through blood travel time.
The MRF-ASL method was compared with Look-Locker–based pulsed ASL and pseudo-continuous ASL techniques in healthy subjects. The cerebral blood flow and bolus arrival time values measured using MRF-ASL were correlated with corresponding measurements using Look-Locker–based pulsed ASL. Additionally, the reproducibility of MRF-ASL was also evaluated in these subjects, whose results provided a coefficient of variation under 10% for all of the estimated properties. The sensitivity of MRF-ASL to hemodynamic variation was tested through a hypercapnic challenge on volunteers in whom an increased perfusion was found to be concomitant with the CO2 inhalation of the volunteers. The sequence was applied on Moyamoya patients, in whom bolus arrival time measurements obtained with MRF-ASL were in concordance with CT-based measurements.
2.2.2 Cardiac MRF
To translate the MRF framework to cardiac imaging, a FISP-based design was used because of its insensitivity to off-resonance artifacts (Figure 4 and Figure S2), and electrocardiogram triggering40 was used to reduce the effects of cardiac motion. Figure 7 shows examples illustrating the advantages of electrocardiogram triggering. The acquisition was performed over 16 heartbeats, acquiring a total of 768 time points. The FAs used in this design ranged from 4° to 15° (Figure 4 and Figure S2). To enhance the T1 and T2 sensitivity of the sequence, inversion pulses or T2 preparation modules were played out before each acquisition window. The combined use of adiabatic preparation pulses and low FA values makes the cardiac MRF approach less sensitive to B1+ variations over the FOV. The electrocardiogram triggering also affects the timings and weightings in the signal time courses, and thus must be dynamically accounted for in dictionary computation, as described subsequently in the dictionary generation section.
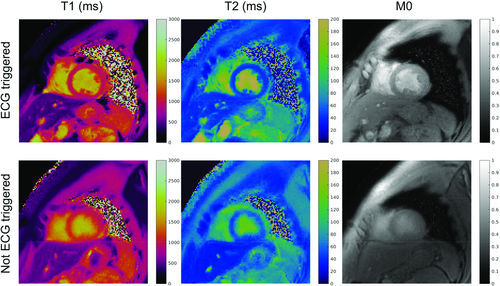
Cardiac MRF measurements in phantoms were in good agreement with SE measurements even for acquisitions with different simulated electrocardiogram heart rates, demonstrating robustness to variations in heart rate. The reported tests on volunteers also showed good agreement with reference sequences and literature (Table 2) for all myocardial tissues except for left-ventricular blood T2. This mismatch can be attributed to the 2D nature of the approach, which allows spins to enter and leave the acquisition plane and experience an excitation history that cannot easily be simulated in the dictionary.
|
Abdomen (3 T) |
PnP (3 T) |
Cardiac (3 T) |
|||
|---|---|---|---|---|---|
| Literature | |||||
| Liver | T1 (ms) | 745 ± 65 |
809 ± 71 824 ± 61 |
||
| T2 (ms) | 31 ± 6 | 34 ± 4 | |||
| Spleen | T1 (ms) | 1232 ± 92 | 1328 ± 31 1251 ± 95 | ||
| T2 (ms) | 60 ± 19 | 61 ± 9 | |||
|
Kidney medulla |
T1 (ms) | 1702 ± 205 | 1545 ± 142 1610 ± 55 | ||
| T2 (ms) | 60 ± 21 | 81 ± 8 | |||
|
Kidney cortex |
T1 (ms) | 1314 ± 77 | 1142 ± 154 1194 ± 88 | ||
| T2 (ms) | 47 ± 10 | 76 ± 7 | |||
| Skeletal muscle | T1 (ms) | 1100 ± 59 | 1499 ± 56 |
898 ± 33 1017 ± 78 1420 ± 38 |
|
| T2 (ms) | 44 ± 9 | 26 ± 1 |
29 ± 4 32 ± 2 |
||
| Fat | T1 (ms) | 253 ± 42 | 323 ± 57 |
343 ± 37 307 ± 37 371 ± 8 |
|
| T2 (ms) | 77 ± 16 | 126 ± 10 |
68 ± 4 133 ± 4 |
||
| Myocardium | T1 (ms) | 1199-1316 | 1080-1500 | ||
| T2 (ms) | 34-43 | 38-50 | |||
| Oxygenated blood | T1 (ms) | 1701-1931 | 1550-1932 | ||
| T2 (ms) | 76-107 | 175-275 |
- a Note: For each approach, the estimated values are shown, compared with the literature values used to validate the technique.
2.2.3 Abdominal MRF
Chen et al41 proposed an approach to apply the MRF framework to the abdomen. Large variations in B0 and RF transmit (B1+) fields present challenges in abdominal imaging; therefore, the authors chose the FISP-based acquisition to overcome the B0 inhomogeneity. To compensate for variations in B1+, a 1.8-second long Bloch-Siegert–based scan42 was used to estimate B1+ map, acquired within the same breath-hold as the MRF scan. B1+ was used as an additional property for dictionary simulation, as described subsequently.
The authors tested this approach in phantoms and in healthy subjects (Table 2) and concluded that incorrect B1+ estimation led primarily to errors in T2, which were corrected after the incorporation of the measured B1+ maps. The results from the healthy subjects were compared with literature values (Table 2) for multiple organs. When applied to patients, the FISP-MRF sequence exhibited a significant increase in T1 and T2 values (1673 ± 331 ms and 43 ± 13 ms, respectively) within metastatic adenocarcinoma lesions compared with the values from lesion-free liver tissue (840 ± 113 ms and 28 ± 3 ms, respectively) as well as compared with the values from healthy subjects (Table 2).
2.3 Approaches to overcome specific limitations
2.3.1 B1+ inhomogeneity
Integrated B1+
An alternative approach to mitigate the effects of B1+ inhomogeneities was proposed by Buonincontri et al43 This design included B1+ as an additional measurement property along with T1, T2, and M0. Because the authors noticed B1+ variations primarily affect T2, their approach used a B1+ sensitizing segment, which is less sensitive to T2,44 at the end of a FISP-based MRF sequence. This B1+ sensitizing segment consisted of alternating blocks (15 time points) of 90° and waiting periods with 0° FA (Figure 4 and Figure S2). The authors showed with phantom tests that their approach allowed for compensation of B1+ inhomogeneities when combined with 3D imaging or when a simulation of the slice profile36, 45 is included in the dictionary. The results were also confirmed in an ex vivo study in a rat using a 4.7T animal scanner (Figure 8 and Figure S4). This approach cannot overcome large variations in B1+ due to signal voids. Because the B1+ information is heavily reliant on the final segment of the acquisition, any kind of acquisition errors in the latter stages, such as subject motion, would result in errors in estimated B1+ values, which in turn would affect other estimated tissue properties.
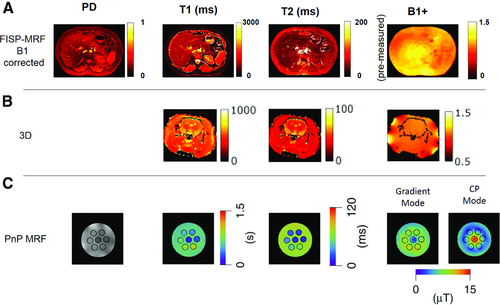
Plug-and-play MRF
The approaches described so far account for B1+ variations in dictionary simulations using dedicated41 or integrated43 B1+ estimates to reduce the effects of B1+ on the estimated properties. However, in applications presenting large variations in B1+, it becomes extremely difficult to extract viable information in certain regions due to destructive interference of the RF field. The B1+ variations can be extremely problematic, especially for applications such as high field imaging or imaging near orthopedic implants. Cloos et al46 proposed an approach in which the MRF framework is used to convert B1+ heterogeneities as a means to probe information. The key idea was to use 2 or more spatially complementary transmit coil modes to generate temporal variations in illumination (excitation profile) over different parts of the acquisition sequence. In this way, the method does not require a homogeneous B1+ field, but only sufficient signal from each spatial location for at least some part of the acquisition. This is a significant relaxation of constraints, especially at high fields. The MRF framework was then used to estimate the B1+ values in the different modes and to reduce the sensitivity of estimated tissue properties to B1+ variations. The authors termed this approach “plug-and-play MRF” (PnP-MRF).
The PnP-MRF sequence as initially proposed consisted of 4 acquisition segments, each containing 120 time points. The TR ranged from 4.8 ms to 8 ms, and the FA variations were expressed with the voltage amplitude used to drive the different coil modes (Figure 4 and Figure S2). The odd-numbered segments were designed using a RF-spoiled GRE-based acquisition and the complementary coil modes were circularly rotated from time point to time point. The even-numbered segments were based on a FISP acquisition. The coil mode was switched from segment to segment and all time points within a segment used the same coil mode. The interleaving of the complementary coil modes avoids destructive interference between RF sources, and avoids local heating of conductive tissues by minimizing constructive interference of electric fields. Radial sampling was used and each radial spoke was rotated by an angle equal to 84º/(total number of spokes per time point) from TR to TR, to improve sampling incoherence across the temporal dimension (Figure 3).
The authors tested the approach on a phantom at 7 T, showing that alternating different coil modes leads to a suppression of the B1+ artifacts on the tissue property maps (Figure 8 and Figure S4). Additionally, the PnP-MRF was applied in a patient with a prosthetic metal implant and compared with a turbo-SE acquisition. The corresponding results showed that the PnP-MRF approach provides unbiased property maps despite the strong heterogeneities in B1+ due to the metallic implant.
2.3.2 Music MRF
The sound generated by MRI hardware during an acquisition can not only be unpleasant, but may also be deleterious, especially in sensitive patient populations such as children, the elderly, those with claustrophobia, and patients with psychiatric disorders.47 These sounds may increase patient anxiety.48, 49 Ma et al50 proposed an approach that exploits the freedom in encoding found in the MRF framework to convert a long-existing disadvantage (gradient noise) into an advantage (music). The proposed acquisition was named “MRF-Music” and used the waveform of audio files to design the acquisition timing and gradients.
The authors noted that the sound quality of the generated music was highly dependent on the retention of the basic timing and the zero crossings of the music waveform. Therefore, the acquisition was split into segments using criteria based on zero-crossings of music and timing constraints of acquisition, which allows one to independently design gradients for each segment. An example TR is shown in Figure 9, and an example trajectory is shown in Figure 3. Finally, variable-rate selective-excitation RF pulses were designed for each time point to adjust for the modification of the corresponding slice-selection gradient to maintain consistency with respect to the excitation slice profile.
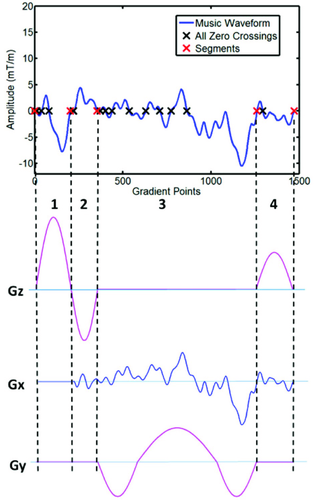
When the authors tested the subject comfort level of the MRF-Music approach, they found it to be significantly better than a turbo SE and a diffusion-weighted EPI acquisition, although periods of no scanning were rated the most comfortable. The accuracy of MRF-Music was in agreement with the reference SE-based acquisition, but the efficiency was lower than the standard bSSFP-MRF, although still fast enough for clinical applications.
2.3.3 Volumetric coverage
Simultaneous multislice
The simultaneous multislice (SMS) imaging technique was applied to MRF for achieving accelerated multislice multiparametric imaging.51, 52 The gradient-based approach was based on “blipped-CAIPI,” which uses an additional z-gradient blip to achieve phase modulation across slices, allowing for simultaneous acquisition of multiple slices with different phase encodings. The moments of the Gz blips were varied at each time point to create controlled aliasing of simultaneously acquired slices. This method was termed “t-blipped SMS-MRF.” As a proof-of-principle implementation, the bSSFP-based MRF16 sequence was modified to incorporate multiband variable-rate selective-excitation RF pulses53 and additional Gz blips before and after readout. It was shown that using t-blipped SMS-MRF, a multiband factor of 2 can be achieved using a reconstruction algorithm based on slice-SENSE,51 and a multiband factor of 3 can be achieved using a reconstruction algorithm based on slice-GRAPPA.54 In both of these methods, the SMS decoding was performed through both phase cycling and parallel imaging. The coil sensitivities for slice-SENSE were estimated through a modified adaptive combination method,51, 55 whereas for slice-GRAPPA the kernel was estimated using a separate training data set (1 second/slice). Additionally, an RF-based phase-cycling approach was used52 to achieve a multiband factor of 2. In this method, the SMS decoding was performed through pattern matching to a slice-specific dictionary.
Simultaneous multislice t-blipped with multiband = 2 showed high concordance correlation coefficients in Monte Carlo simulations compared with the MRF acquisition. In addition, the reported results of an in vivo scan showed good agreement of the SMS-MRF maps with the bSSFP-MRF when a smooth off-resonance prior is used. When the multiband factor was increased to 3, the slice-SENSE reconstruction51 was significantly worse than the slice-GRAPPA54-based reconstruction. These SMS-based approaches provide multiple slices without increasing the acquisition time, which increases the scan efficiency per slice. However, these techniques increase the specific absorption rate due to the use of multiband pulses and are limited to noncontiguous volumetric coverage.
Three-dimensional MRF
For many clinical applications, contiguous volumetric coverage is crucial. Ma et al56 extended the MRF approach to provide contiguous volumetric coverage using stack-of-spirals–based 3D k-space coverage. To maintain the signal across different slice-encoding values, the MRF signal evolution cycle was repeated multiple times to ensure adequate k-space coverage for each time frame. The acquisition used an undersampling factor of up to 48 along the in-plane direction and an acceleration rate of 3 along the slice-encoding direction. The uniform rotation (7.5º)–based spiral ordering was used, while the slice encoding was stepped from TR to TR to generate a sheared-grid–based undersampling in the kz-t space. The study used a FISP-based MRF sequence pattern with each cycle consisting of 14 seconds of MRF data acquisition and 3 seconds of signal recovery. The method was evaluated in phantoms and in vivo, with full 3D coverage in the brain with a resolution of 1.2  1.2
1.2  3 mm3 and acquisition time of 4.6 minutes.
3 mm3 and acquisition time of 4.6 minutes.
Liao et al57 also presented an approach that also used stack-of-spirals–based 3D MRF acquisition. The acquisition used an undersampling factor of up to 30 along the in-plane direction and a uniform acceleration rate of 3 along the slice-encoding direction. The study used a FISP-based MRF acquisition with each partition encoding cycle consisting of 5 seconds of MRF data acquisition and 2 seconds of signal recovery. For reconstruction, the authors used a sliding window approach along the temporal dimension to reduce the in-plane aliasing artifacts, followed by a GRAPPA reconstruction to eliminate aliasing from through-plane acceleration, and finally a voxel-wise pattern matching reconstruction. The kernel weights were estimated from separate training data, which were acquired during the 2-second signal recovery phase of the acquisition. The method was evaluated in phantoms and in vivo brain imaging with 1-mm isotropic resolution whole brain data acquired in 7.5 minutes.
3 DICTIONARY GENERATION
The MRF dictionary contains simulated signal evolutions using a predefined range of tissue-property combinations. Because the dictionary is used to assign the tissue properties to each pixel, the accuracy of MRF is governed by the accuracy of the signal model. The dictionary should cover the broadest possible range of physiologically relevant combinations of tissue properties. However, in a straight-forward implementation of pattern matching, the dictionary size presents a trade-off between precision35 and reconstruction speed. For a given sequence pattern, the dictionary needs to be generated only once except for experiment designs in which the dictionary must be dynamically adapted to the subject, such as cardiac or vascular fingerprinting.
The dictionary is generated by modeling the spin behavior during the acquisition. The dictionary for the bSSFP-based MRF approach proposed by Ma et al16 was generated using the Bloch equations, which modeled the effects of the RF pulses and timing of the sequence on a single isochromat resonating at a given frequency.16 This was performed under the assumption that each voxel consists of a single isochromat. The application of the same Bloch equation model can also be applied to the FISP-based MRF acquisition,35, 40, 41 but with increased computation time. Because a dephasing gradient was used in the FISP-based sequence, the signal within each voxel was modeled as an average from multiple isochromats. As an efficient alternative for FISP simulations, several authors35, 39, 46, 50 have used the extended phase graph formalism.58, 59 This approach describes the spin system within a voxel as a discrete set of dephasing states, and is an efficient way to represent the evolution of spins affected by unbalanced gradients.
For the abdominal MRF approach by Chen et al,41 the dictionary also included the effect of B1+, simulating it as the ratio of the effective FA compared with the nominal one. This dimension was not used directly in the matching process; rather, the B1+ was measured with a separate scan prior to the MRF acquisition and the measured values of B1+ are enforced in the dictionary during the matching process. The approaches of Buonincontri et al43 and Cloos et al46 instead quantified B1+ directly with the pattern matching, although at the expense of higher computation time for dictionary generation and pattern matching.
Generally, the dictionary is computed once and stored; however, there are some techniques for which the dictionary must be computed for each acquisition. One example is the cardiac adaptation of MRF from Hamilton et al,40 in which the patient-specific sequence time affected by heart rate variations must be included in the dictionary, requiring the dictionary to be computed for each patient. However, only 12 seconds were needed to generate the dictionary due to the relatively few number of properties needed for the FISP acquisition and the use of the extended phase graph formalism.
In the work by Christen et al,21 the signal evolutions for a given set of microvasculature properties before and after the contrast injections were predicted using numerical simulations incorporating diffusion effects and models described in Pannetier et al.60 In these simulations, each vessel was assumed to have free water exchange across the walls. The approach modeled the effects of water diffusion, approximated as a discrete Gaussian kernel, perturbations in local magnetic fields, and application of RF pulses.
A 2-compartment model was explored by Su et al19 for MRF-ASL. The model had a pass-through arterial compartment representing arterial blood that did not perfuse to the tissue. A conventional perfusion kinetic model was used to estimate the evolution of the tissue magnetization. Multiple factors, such as tissue bolus arrival time, history of label/control state and blood T1, were used to model the TR-to-TR variation of arterial input function. Additionally, the effects of nonsaturating RF pulse and B1+ on the initial condition of the tissue magnetization were also incorporated in the model. Finally, the sum of the magnetization of blood spins in the pass-through artery was used as an estimate of the blood magnetization.
4 RECONSTRUCTION
4.1 Pattern recognition
The final step after the acquisition and dictionary generation is pattern matching to identify the dictionary entry that best represents the tissue present in each voxel. The accuracy and efficiency of MRF is dependent on this pattern matching being robust to noise and artifacts due to undersampling. Several reconstruction algorithms have been proposed, from the simplest template matching to more advanced nonlinear reconstructions. Some of these aim at speeding up the matching process,61, 62 whereas others instead aim to reduce the aliasing artifacts, which can result in reduced acquisition time and higher accuracy in the estimated tissue properties.33, 63-67
4.1.1 Template matching
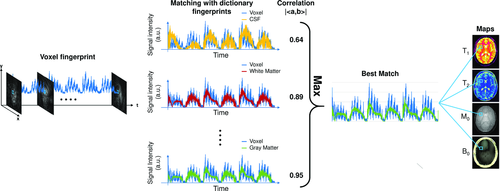
In the proof-of-principle implementation of MRF,16 the pattern recognition algorithm was based on template matching, which uses a correlation-based metric to identify the best match (Figure 10). For this method, the complex inner product between the normalized voxel fingerprint and each dictionary entry is computed to find the maximum (in absolute value); proton density is then computed as the scaling factor between the voxel fingerprint and the corresponding unnormalized dictionary match.
4.1.2 Error tolerance in fingerprint identification
The pattern recognition step can be made to be tolerant to errors; however, the properties and the level of error tolerance depends on the metric and the algorithm used for the recognition. For example, the inner product–based template matching approach has been shown to be tolerant to undersampling artifacts16, 35 that are spatio-temporally incoherent and incoherent with the fingerprint time course. The spatio-temporal incoherence of the undersampling pattern as measured by the mutual coherence of the sensing matrix68-70 ensures that the signal from pixel A is not consistently bleeding to pixel B, thus avoiding potential biases. However, the incoherence with the fingerprint time course as measured by correlation with the temporal subspace of the dictionary ensures that the combined interference from multiple locations does not appear like a tissue fingerprint. As was noted in Ref 16, errors that do not prevent the correct simulated fingerprint from being the best match based on the matching algorithm are tolerable, even if the matching metric is globally reduced or the gap in the metric between the first and second best match is reduced. In other words, it is the relative position that matters as opposed to the absolute value of the metric. Thus, template matching will be tolerant to any errors that lie in the temporal null-space of the dictionary. Taking advantage of these concepts, Ma et al16 showed that using a single interleaf of a variable-density spiral trajectory for a single frame and rotating this interleaf by 7.5° from time frame to time frame was adequate in generating undersampling artifacts that are sufficiently spatio-temporally incoherent with each other and temporally incoherent with the signal time courses. This sampling strategy can yield accurate maps with each frame having an acceleration factor of 48 at the edge of the k-space and 1 at the center of the k-space.16 The template matching has also been shown to be tolerant to subject motion during the latter part of the acquisition, and the matching process is still able to properly identify the underlying tissues. However, if the motion is severe and occurs in the early or the middle stage of the acquisition, then the conventional pattern matching fails to reconstruct artifact-free property maps. 71-73 However, improvement of motion insensitivity is an active area of research.71-76
4.2 Approaches to reduce matching time
For clinical applications, tissue property maps must be generated rapidly. Although template matching using the inner product is accurate, it can take several minutes to compute for a single slice, depending on dictionary size and the number of pixels.61 Finding ways to speed up the matching process is therefore important for the clinical application of MRF.
McGivney et al61 proposed a method to reduce the computation time of the pattern recognition step by projecting the dictionary and voxel fingerprints to a lower-dimensional subspace along the time domain and performing the pattern matching in this lower-dimensional subspace. The subspace was determined by applying singular value decomposition (SVD) to the dictionary and using the k singular vectors associated with the largest singular values as the basis for the subspace. The selection of the subspace dimension, k, determines the tradeoff between loss of accuracy in estimated properties and reduction in computational time. The steps associated with this method are as follows: (1) SVD of the original dictionary was computed to find the singular vectors and singular values; (2) the transformation matrix was generated using the k largest temporal singular vectors; (3) dictionary compression was performed through the transformation matrix (only once); (4) acquired data (either from the Fourier domain or from the spatial domain) were projected to the lower-dimensional subspace using the transformation matrix; and (5) pattern matching was performed on the projected data and dictionary to estimate the tissue property maps. This method showed a reduction of template matching time by a factor of 3.4 for a bSSFP-based MRF acquisition (k = 200) and a factor of 4.8 for a FISP-based MRF acquisition (k = 25) with the mean error in estimated properties under 2%.
Recently, Yang et al77 proposed using randomized SVD to directly estimate low-dimensional dictionary subspace without the need for simulating all of the atoms of the original dictionary, thereby reducing the computation time and the storage size of the dictionary. Additionally, they proposed to exploit the smoothness of the tissue property dimension in the randomized SVD space to further reduce the size and computation time of the dictionary. First, the tissue-property dimension of the randomized SVD space of the coarse dictionary was fitted to a polynomial hypersurface. Second, the polynomial hypersurface was used to estimate the tissue properties at finer resolution. These methods were illustrated to provide memory savings during dictionary computation and illustrated accurate T1 and T2 maps even from a dictionary with a 4-times coarser step size for each tissue property.
The fast group-matching algorithm62 is another method that can be used to speed up the matching time. In this method, dictionary entries were grouped based on correlation, and a representative fingerprint signal for each group was calculated based on the mean of all the atoms within the group. Once the dictionary has been separated into groups, the following steps were performed: (1) The correlation between the voxel fingerprint and each group's representative fingerprint was computed (2) groups were pruned, based on relative or absolute correlation threshold; and (3) SVD compression–based matching61 was applied on the atoms from the remaining groups to identify the voxel properties. The number of groups and pruning criteria can be adjusted based on the dictionary to achieve optimal reduction in computation time with minimal loss in accuracy. For a bSSFP-based MRF acquisition, the computation time for the group-matching algorithm (2.5 seconds) was smaller by a factor greater than 10 compared with SVD compression method (27 seconds) and by a factor greater than 70 compared with template matching (178 seconds) with a mean relative error of the estimated tissue properties under 2%. The speed-up factors are dependent on the MRF data, the dictionary size, and the reconstruction parameters; thus, they can vary across different studies.
4.3 Compressed sensing–based approaches using prior knowledge
Connections can be made between MRF and the CS framework.68, 69, 78 Recent advances in compressed sensing and prior-information–based reconstruction algorithms can be used to improve the pattern recognition–based MRF reconstruction. These methods additionally rely on assumptions associated with convergence theory for the nonconvex optimization problems.
In the Bloch response recovery in the iterated projection (BLIP)64 work, the MRF problem is formulated within a standard CS framework. This method uses a Bloch response manifold–based approach with a recovery algorithm based on the projected Landweber algorithm.79 The authors treated the Bloch response manifold as a continuous signal and applied subsampling to this manifold. Cline et al80 proposed an approach termed “accelerated iterative reconstruction MRF,” which improved on the work done by Davies et al.64 The authors performed the CS-based iterative reconstruction79 in a low-dimensional subspace determined by the dictionary and used spatial regularization on the M0 map. Additionally, Cline et al80 presented a k-dimensional tree-based dictionary matching approach to speed up the computation time for template matching.
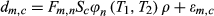 (3)
(3)where 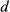 represents the k-space measurements,
represents the k-space measurements, 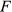 is the undersampled Fourier transform operator,
is the undersampled Fourier transform operator, 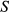 represents the receive coil sensitivities,
represents the receive coil sensitivities, 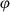 is the signal evolution for given T1 and T2 using Bloch equations,
is the signal evolution for given T1 and T2 using Bloch equations, 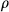 is the proton density, and
is the proton density, and  is additive complex white Gaussian noise. The recovery algorithm was based on variable splitting strategy, alternating direction method of multipliers,81, 82 and the variable projection method. The accuracy of the algorithm is highly dependent on the initialization because of the nonconvexity of the cost function. The authors note that initialization using gridding-based reconstructed time frames have consistently yielded accurate results.
is additive complex white Gaussian noise. The recovery algorithm was based on variable splitting strategy, alternating direction method of multipliers,81, 82 and the variable projection method. The accuracy of the algorithm is highly dependent on the initialization because of the nonconvexity of the cost function. The authors note that initialization using gridding-based reconstructed time frames have consistently yielded accurate results.
Pierre et al developed an iterative reconstruction approach called iterative multiscale MRF.63 This method incorporated the prior knowledge of the k-space sampling density by taking advantage of the higher sampling density in the center of the k-space. Their method iterated between data consistency and pattern recognition. The data consistency was performed using windowed k-space measurements in which the kernel width gradually increased as a function of iteration number to include higher-resolution measurements. The study showed in vivo brain results using bSSFP-MRF, illustrating reduction of scan time (factor = 6; time frames = 500) with accuracy similar to original MRF.
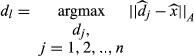
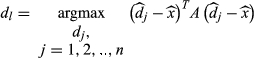 (4)
(4)where 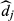 are the normalized dictionary fingerprints,
are the normalized dictionary fingerprints, 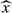 is the normalized voxel fingerprint,
is the normalized voxel fingerprint, 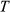 is the transpose operation, A is the learned positive semidefinite matrix, and
is the transpose operation, A is the learned positive semidefinite matrix, and 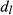 is the correct match. The method was evaluated using numerical phantoms and acquisition simulations to illustrate improvement in scan time and accuracy of estimated properties compared with the conventional approach.
is the correct match. The method was evaluated using numerical phantoms and acquisition simulations to illustrate improvement in scan time and accuracy of estimated properties compared with the conventional approach.
To reconstruct the data of the pseudo-SSFP acquisition, Assländer et al33 designed an algorithm that uses a spatial smoothness prior in addition to the common prior of consistency with Bloch equations. The image-based smoothness prior was incorporated using a sparsity constraint in the wavelet domain across the spatial dimensions and was jointly applied along time. Their algorithm was designed based on the variable splitting strategy and alternating direction method of multipliers methods. There are several factors that determine the appropriateness of the spatial-smoothness constraint, such as the type of acquisition, the constraints in the reconstruction problem, and the reconstruction algorithm. There have been several studies that demonstrate the advantages of the spatial smoothness prior, whereas other studies have shown no major improvement. Therefore, it may be beneficial to include a smoothness prior when possible, with one drawback being increased computation time.
Due to the nature of the Bloch equations and the design of the acquisitions, the signal evolutions for property mapping have shown high spatio-temporal correlation.83-87 This prior knowledge has been exploited by multiple approaches to achieve high acceleration for traditional property mapping. For example, Pederson et al83 proposed an approach that used constraints on the support of the data in a hybrid space consisting of phase-encode k-space dimension and temporal principal component dimension. This approach was applied to accelerate (factor = 8) multiproperty mapping (T1, T2, and M0) in brain using inversion recovery–TrueFISP acquisition.13, 88 Doneva et al89 presented an approach to linearize the exponential signal models of relaxation properties using an overcomplete dictionary, which is formed using the K-SVD algorithm.90 For reconstruction, they exploit the sparsity in the dictionary coefficient space (i.e., the signal at each pixel can be represented by a linear combination of a few dictionary atoms). Using this approach, they present acceleration up to 6 for T1 mapping in brain and up to 4 for T2 mapping in brain. Lingala et al84 and Zhao et al87, 91 presented approaches that exploit the low rank of the spatio-temporal data matrix and the sparsity of data in a transform domain. These approaches have been applied widely for accelerating parameter mapping.91-93
Because MRF also shares the property of having high spatio-temporal correlation, multiple groups have exploited this prior knowledge to further accelerate the MRF acquisition. Zhao et al94 presented an approach in which they used a low-rank model through matrix factorization85 and dictionary-based temporal subspace61 to reconstruct artifact-free time frames, which were then used to estimate properties through template matching.16 The authors showed improvement in accuracy compared with template matching in accelerated (700 time frames) in vivo FISP-MRF brain data, at the expense of increased computation time. Assländer et al95 also presented an approach using low-rank approximation through a dictionary-based subspace. The reconstruction problem was solved using the alternating direction method of multipliers algorithm. The authors showed improvement in the precision of estimated tissue properties in accelerated (850 time frame equivalent to 4.1 seconds of acquisition time) in vivo pseudo-SSFP-MRF brain data acquired using radial trajectory. Doneva et al96 presented a matrix completion–based method in which the low-rank prior is applied in k-space instead of image space, thereby significantly reducing the computation burden by eliminating the need for forward and backward Fourier transformations. However, this restricts the algorithm by using additional priors such as sparsity in transform domains, which is not the case for the other approaches mentioned previously. Additionally, the computation time is further reduced by calculating a low-dimensional temporal subspace from a subset of low spatial-frequency k-space data points, which were sampled for all of the time points, as opposed to using SVD of the dictionary itself. In general, this approximation reduces the computation time and improves the image quality, however, at the expense of potentially biasing the results against a high-frequency component such as an isolated small tumor or edge.
4.4 Partial volume effect
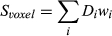 (5)
(5)where  is the measured signal time course of the voxel,
is the measured signal time course of the voxel, 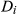 is the signal evolution of the
is the signal evolution of the  th basis tissue component (generally 3 or 4 components), and
th basis tissue component (generally 3 or 4 components), and 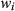 is the corresponding weight. One approach to estimate the weights for each tissue component is by solving Equation 5 using the pseudoinverse to calculate for the weights.16 Another approach is to generate a new partial volume dictionary in which the atoms consist of various volume fraction combinations of signal evolutions of the basis tissue components. In this way, the volume fractions for the basis tissue components are treated as the unknown “tissue properties” instead of the underlying T1 and T2.97 Pattern recognition was used to match the measured voxel signal with atoms of the partial volume dictionary to estimate unknown volume fractions.97 The validation of both the approaches were performed using numerical phantom simulations to evaluate the effects of noise, undersamlping, tissue variation, and model error.97-99 An alternative approach is not to assume that the basis tissue components are known a priori; thus,
is the corresponding weight. One approach to estimate the weights for each tissue component is by solving Equation 5 using the pseudoinverse to calculate for the weights.16 Another approach is to generate a new partial volume dictionary in which the atoms consist of various volume fraction combinations of signal evolutions of the basis tissue components. In this way, the volume fractions for the basis tissue components are treated as the unknown “tissue properties” instead of the underlying T1 and T2.97 Pattern recognition was used to match the measured voxel signal with atoms of the partial volume dictionary to estimate unknown volume fractions.97 The validation of both the approaches were performed using numerical phantom simulations to evaluate the effects of noise, undersamlping, tissue variation, and model error.97-99 An alternative approach is not to assume that the basis tissue components are known a priori; thus, 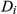 in Equation 5 represents the full dictionary. McGivney et al100, 101 have proposed an approach to solve this highly underdetermined and ill-conditioned inverse problem using a Bayesian statistical framework with a sparsity-inducing prior. The approach was evaluated using numerical simulations97, 99-101 and in vivo data.99, 101, 102 Recently, Tang et al103 also presented an approach to solve the same inverse problem using a sparsity-inducing penalty function through an approach based on iterative reweighted
in Equation 5 represents the full dictionary. McGivney et al100, 101 have proposed an approach to solve this highly underdetermined and ill-conditioned inverse problem using a Bayesian statistical framework with a sparsity-inducing prior. The approach was evaluated using numerical simulations97, 99-101 and in vivo data.99, 101, 102 Recently, Tang et al103 also presented an approach to solve the same inverse problem using a sparsity-inducing penalty function through an approach based on iterative reweighted 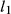 norm regularization of the weights (
norm regularization of the weights ( ). The approach was evaluated in phantoms and in vivo brain data.
). The approach was evaluated in phantoms and in vivo brain data.
5 DISCUSSION
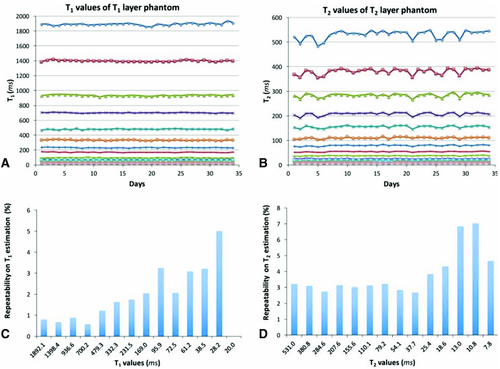
Reproducibility is an important aspect for quantitative imaging. The reproducibility of MRF has been thoroughly validated in the work by Jiang et al.104 In this study, the authors applied the FISP-MRF sequence to repeatedly quantify T1 and T2 of a reference phantom. The measurements were repeated for 34 consecutive days and compared with the values obtained through SE-based standard methods. For this study, the National Institute of Standard Technologies/International Society for Magnetic Resonance in Medicine MRI system phantom was used, which was specifically designed for quantitative imaging with several layers of varying T1 and T2 values.105 It was shown that variation in the measured MRF values throughout the 34 days was below 5%, except for in spheres with very short T2 values (below 13 ms) in which the variation was below 8% (Figure 11). Additionally, other evaluations of repeatability such as test-retest, intrascanner, interscanner, variability across different scanner types, and variability across different sites is ongoing work. The authors firmly believe that measurements such as these should be a key part of any future MRF work. Without consistent results across multiple days and even multiple scanners, these methods will fail to make any significant impact on clinical medicine.
The MRF framework provides many degrees of freedom and a large amount of flexibility in the design of acquisition and sequence parameters, making the design and optimization of these parameters a challenging problem. Most of the methods described in this paper were heuristically optimized. Optimization of acquisition and sequence parameters is an open question and active area of research with multiple groups focusing on the problem. Recent works have explored optimization through improvement in incoherence of simulated dictionary fingerprints,106, 107 Cramer-Rao bound,108-110 genetic algorithm,111 and Monte Carlo–based sequence simulations107, 111 based approaches.
Another aspect that is flexible in the MRF framework is the k-space sampling pattern. In general, the design and selection of the sampling trajectory is performed based on factors such as sampling efficiency, sensitivity to systemic effects and imperfections, and the spatial incoherence of undersampling artifacts. Non-Cartesian trajectories such as spirals provide high k-space sampling efficiency and present spatially incoherent undersampling artifacts; however, they are highly sensitive to gradient nonlinearities and physical effects such as eddy currents, which affect the k-space position of the sampled data. In practice, the trajectories are either separately measured112 or anticipated based on model and scanner specific parameters.113 Additionally, these effects constrain the flexibility of the sequence with respect to variation in FOV and spatial resolution. The radial trajectory design also presents incoherent undersampling artifacts and is less sensitive to errors due to systemic imperfections as compared with spiral trajectory. However, the radial trajectory has lower k-space sampling efficiency compared with spiral trajectory; thus, it requires multiple repetitions of the MRF acquisition cycle or temporal averaging through k-space view sharing. The Cartesian trajectory is the most stable with respect to errors due to system imperfection; however, it presents the lowest spatial incoherence of undersampling artifacts and low sampling efficiency. Echo planar imaging can present an alternative option19, 37 that improves upon Cartesian with relatively higher sampling efficiency, although at the expense of increased sensitivity to errors due to system imperfections. The temporal reordering of the sampling trajectory is designed such that the undersampling artifacts are spatio-temporally incoherent. Additionally, the undersampling artifacts should also be temporally incoherent to the temporal subspace spanned by the dictionary fingerprints. For example, a golden angle–based reordering might be a more suitable acquisition for smoothly varying signal evolutions such as seen in FISP-MRF, whereas a linear reordering is more suitable for acquisitions with fast varying signal evolutions, such as bSSFP-MRF. Finally, applications in which measured properties present low signal sensitivity, such as perfusion19 or vascular properties,21 have used no undersampling as a means of simplification and out of the concern of propagation of errors.
Although MRF presents a new framework, it shares similarities with other quantitative MR approaches. Some of the components of MRF have been previously used independently across different frameworks. For example, an overcomplete dictionary was used by Doneva et al89 for acceleration of property mapping through a CS framework. Pseudo-randomness and incoherence are both key components of the CS framework. Multiple other methods13-15, 32 have looked at simultaneous estimation of multiple properties. A few of the differences and key innovations of the MRF framework are variation of multiple acquisition parameters to simultaneously probe multiple tissue properties, pattern recognition, and combination of all of the subcomponents to formulate a complete framework. However, the MRF framework may not be the ideal option if the specific clinical question needs either estimation of a single property or a qualitative evaluation, as there are existing techniques that have been thoroughly optimized and validated to address these questions.
6 CONCLUSIONS
In summary, MRF is a general and flexible framework that allows measuring several tissue properties with a single, time-efficient acquisition. The framework is compatible with a wide variety of acquisition strategies (3), such as bSSFP, FISP, RF-spoiled GRE, GRE sampling of the FID and SE sequence, QUEST, or their combinations. Additionally, it is also compatible to a wide variety of readout strategies such as spiral, radial, and EPI. This flexibility has enabled the application of MRF for imaging brain, heart, musculoskeletal system, and abdomen. Magnetic resonance fingerprinting has also shown feasibility of probing and achieving simultaneous measurement of a wide variety of properties such as T1, T2, T2*, B0, perfusion, and cerebral blood volume. The reconstruction aspect of the MRF framework allows for high acceleration and is not limited to template matching or conventional pattern recognition. Several other approaches have been proposed to speed up the dictionary matching or to improve the acceleration. The repeatability studies also show that the MRF framework provides robust results through time and within different scans.
| Approaches | Primary advantage | Primary disadvantage |
|---|---|---|
| bSSFP | Simultaneous estimation of T1, T2, M0, and off-resonance frequency with high scan efficiency | Susceptible to B0 field inhomogeneity |
| pSSFP | Provides spin-echo effect within the acquisition bandwidth | Restricted TR and TE and loss of sensitivity to off-resonance frequency |
| FISP | Insensitive to B0 field inhomogeneity | Loss of information related to ΔB0 field and relatively low scan efficiency |
| Gradient echo | Simultaneous estimation of T1, T2*, and M0 | Loss of T2 sensitivity |
| QUEST | Low specific absorption rate | Relatively low scan efficiency |
| Integrated B1+ | Partial insensitivity to B1+ field variations | Unable to overcome B1+ voids due to destructive interference of the RF field |
| PnP-MRF | Insensitivity to large B1+ field variations | Requires control of complementary RF coil modes |
| Music | Gradient music resulting in improved patient comfort and reduced anxiety | Constrained sampling pattern |
CONFLICTS OF INTEREST
The authors receive research support from Siemens.




