A method for unwrapping highly wrapped multi-echo phase images at very high field: UMPIRE
Abstract
Purpose
To develop a method of unwrapping phase images from multi-echo scans that works even where there are several wraps between echoes, and which generates unwrapped phase images in addition to phase difference (PD) images.
Theory
The difference between the echo spacings in an acquisition with three unevenly spaced echoes (an imposed delay) can be selected such that the phase evolution in that time is in the range −π to +π in all voxels of interest. Under this condition, an image of the difference between the phase evolutions in the two inter-echo periods, an estimate of ΔB0, is free of wraps. This ΔB0 estimate can be used to identify and remove receiver phase offsets and wraps in phase images.
Methods
The approach was tested on simulated data and high-resolution in vivo brain data acquired from six subjects at 7 Tesla.
Results
The method generated wrap-free phase images. It was able to remove more wraps than is possible with PD imaging and was faster and more reliable than spatial unwrapping.
Conclusion
Unwrapping Multi-echo Phase Images with iRregular Echo spacings (UMPIRE) is conceptually simple, fast, reliable, and requires no fitting, thresholds, or operator intervention. Magn Reson Med 72:80–92, 2014. © 2013 Wiley Periodicals, Inc.
INTRODUCTION
Enhanced susceptibility effects at high field have led to the rapid development of methods which use the phase of the MR signal, particularly in neuroimaging. These include mapping local deviations from the static magnetic field (ΔB0) 1, 2, high-resolution phase imaging 3, 4, susceptibility-weighted imaging (SWI) 5, 6 and quantitative susceptibility mapping 7-9. ΔB0 mapping is widely used to correct distortions in echo-planar imaging 1, and high-resolution gradient-echo (GE) phase imaging has been applied in the assessment of vascular malformations such as cavernomas 10 and iron stores in pathologies including dementia 11, Huntington's, and Alzheimer's disease 12.
The phase of the MR signal has both time-independent and time-dependent components. The time-independent components, frequently referred to cumulatively as the “receiver phase offset” comprise contributions arising from the path length of the MR signal from a particular location in the object to the receiver coil in question given a finite MR wavelength 13, 14, a linear phase gradient in the readout direction introduced by the readout gradient 15, the cable length from the coil to the receiver and artifacts in the receiver chain including frequency synthesizer drift and imperfectly centered k-space 16. The time-dependent component is dominated by deviation from the static magnetic field, ΔB0, which evolves linearly over time. This contribution reflects physiologically interesting tissue properties such as local iron content.
Because the range of phase values which can be measured in MRI is limited to 2π, phase aliasing occurs, leading to discontinuities in phase images which are known as “wraps.” Well-behaved wraps are isocontours that either form closed loops within the object or begin and terminate at the object boundary. A wrap which ends within the object is known as a “non-terminating fringe line,” and indicates a nonphysical infinite gradient in the phase, and generally belies a point at which there is no signal in the corresponding magnitude image. Wraps obscure interesting phase features in the object and, in most applications, need to be removed.
In this study, we classify unwrapping methods as either “spatial” or “temporal.” Spatial methods are image-based, and use some regional characteristics of phase or complex values at a single echo time, usually abrupt change, to identify wraps. Temporal methods, on the other hand, are based on identifying wraps by means of the evolution of the phase in each voxel at two or more echo times. Temporal phase unwrapping should not be confused with the unwrapping of a time-series of data (as in, e.g., 17). Spatial methods usually use region-growing algorithms which begin in a region of stable phase (as defined, e.g., by local phase coherence 18 and proceed either in two dimensions (2D) or 3D, identifying a wrap when the phase difference (PD) between adjacent voxels exceeds π. The main disadvantages of spatial unwrapping are that it tends to be computationally intensive and, in most implementations, needs to distinguish the object (which should be unwrapped) from the background (which should not be unwrapped). This requires a threshold relating to the local phase coherence 19 or signal level in the corresponding magnitude image 19, 20 to be set, which generally entails operater intervention. Spatial unwrapping also leaves an integer number of 2π phase jumps between slices (in 2D unwrapping) and echoes 2, if applied to multi-echo data. As a result of these problems, spatial methods have proven too slow and fragile to be implemented on the scanner console. Instead, homodyne filtering 21—complex division by a low-pass filtered version of the data—is often used. This fails if images are highly wrapped, and modifies phase values so they cannot be used quantitatively 19.
Temporal methods require phase images acquired at two or more echo times. Where the phase evolution between two measurements is between +π and −π, a wrap-free image can be created by calculating the difference between the two images from the angle of the complex difference, by means of a conditional phase difference or using the Hermitian inner product method 19. This is a simple and robust approach. At high field, however, with ΔB0 values up to approximately 1300 rad s−1 at 3 Tesla (T) and 3000 rad s−1 at 7T in the head (2) (down to a level of z = −14 in the ICBM152 template of the Montreal Neurological Institute (MNI) 22), echo spacings would have to be approximately 2.4 ms at 3T and 1 ms at 7T to avoid wraps developing in the inter-echo period. While using such a short echo spacing has been demonstrated to be feasible for SWI at 3T 15, dB/dt limitations mean that this cannot be achieved in a high-resolution multi-echo acquisition at 7T or higher field strengths. A very recent method by Dagher et al has shown one way in which this limit may be overcome in a triple-echo acquisition with unevenly spaced echoes 23, although this involves calculating and comparing several feasible wrap scenarios. The second problem with temporal methods is that most have been developed to yield unwrapped PD images and not unwrapped individual phase images. This limitation arises as receiver offset contributions to the phase, which can also cause wraps, have generally not been isolated and resolved. PD images have lower gray–white matter contrast than phase images 14.
The aim of this study was to develop a fast and simple method of unwrapping phase images from multi-echo acquisitions with widely spaced echoes, corresponding to low bandwidth, high signal to noise ratio (SNR) scans, at ultra-high field, in which several wraps occur between echoes, and to generate unwrapped phase images rather than PD images. The method we present 24, 25 achieves this by using unequal echo spacings, chosen such that no wraps occur in the time difference between the echo spacings, and by calculating and removing receiver phase offsets.
THEORY
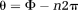 (1)
(1)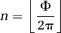 (2)
(2)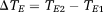 (3)
(3)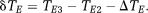 (4)
(4)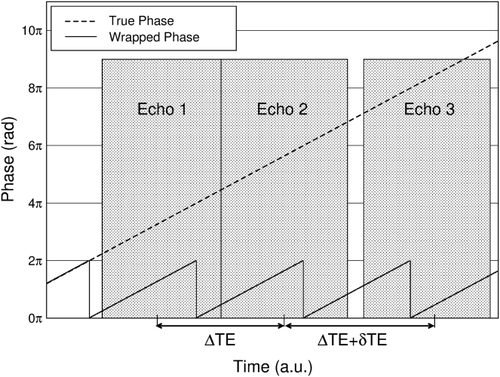
No wraps occur in the time δTE, which can be chosen at will, for
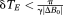 . δTE can be selected on the basis of knowledge of the typical range of ΔB0 values encountered at the field strength in question, or can be set on the basis of ΔB0 values measured in the subject under study in a prior fast, low-resolution field map. Steps in the following description correspond to the images in Figure 2. Calculations are carried out on all voxels in images; voxel indices are omitted for simplicity.
. δTE can be selected on the basis of knowledge of the typical range of ΔB0 values encountered at the field strength in question, or can be set on the basis of ΔB0 values measured in the subject under study in a prior fast, low-resolution field map. Steps in the following description correspond to the images in Figure 2. Calculations are carried out on all voxels in images; voxel indices are omitted for simplicity.
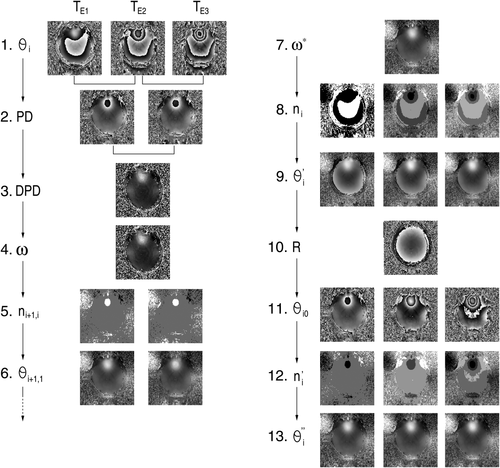
Step 1: Phase images θi are reconstructed for each echo time TEi.
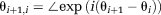 (5)
(5) denotes the angle (the four-quadrant inverse tangent) of the complex vector, (b) the Hermitian inner product 19
denotes the angle (the four-quadrant inverse tangent) of the complex vector, (b) the Hermitian inner product 19
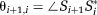 (6)
(6)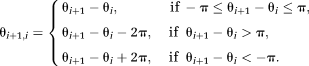 (7)
(7)PD images reflect phase changes that evolve in the echo spacings ΔTEi. They contain values in the range −π to π, and are subject to residual wraps if
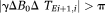 , where γ is the gyromagnetic ratio. This is frequently the case in high-resolution measurements at very high field.
, where γ is the gyromagnetic ratio. This is frequently the case in high-resolution measurements at very high field.
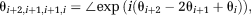 (8)
(8)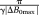 , where ΔB0max is the highest value occurring in the object for which the phase should be unwrapped. For this value of δTE (and all lower values), the DPD image contains no wraps.
, where ΔB0max is the highest value occurring in the object for which the phase should be unwrapped. For this value of δTE (and all lower values), the DPD image contains no wraps.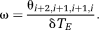 (9)
(9)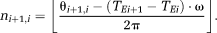 (10)
(10)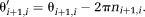 (11)
(11)The original phase images are unwrapped in the following steps.
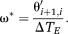 (12)
(12)A magnitude-weighted average of
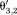 and
and
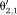 could be used here.
could be used here.
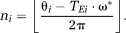 (13)
(13)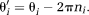 (14)
(14)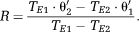 (15)
(15)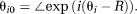 (16)
(16)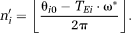 (17)
(17)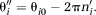 (18)
(18)This approach can be extended to more echoes, which may be separated by several different echo spacings, and the additional delay can be inserted between any pair of echoes. Modest smoothing of the DPD image can lead to a reduction of errors in the calculation of n. Steps 10–13 are not needed if receiver offsets are removed in combining the phase images from the individual channels in a phased array 14. In that case, the images are fully unwrapped after step 9.
METHODS
The characteristics and performance of UMPIRE were investigated in unwrapping simulated data and in vivo MR data acquired at 7 Tesla. UMPIRE was compared with conventional temporal phase unwrapping and the most commonly used spatial unwrapping implementations PRELUDE 20 (in both 2D and 3D mode) and PHUN 19.
Simulated data, created with MATLAB (Mathworks Inc, Natick, MA), allowed the features of UMPIRE to be explored and the performance of all unwrapping methods to be compared against the ground truth.
Simulated Data 1: Linear Gradients in ΔB0 and Receiver Phase Offset
These data were simulated to illustrate the properties of UMPIRE compared with conventional temporal phase unwrapping. Simulated phase images consisted of a time-dependent gradient in the x direction
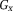 (simulating a range of ΔB0 values) and a time-independent linear gradient in phase offset in the y direction,
(simulating a range of ΔB0 values) and a time-independent linear gradient in phase offset in the y direction,
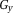 (simulating a range of receiver phase offsets).
(simulating a range of receiver phase offsets).
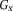 varied from −π to +π rad ms−1 and
varied from −π to +π rad ms−1 and
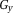 from 0 to 6π. Phase images were generated at TE = 5, 10, and 16 ms. The simulated phase Φ was given by
from 0 to 6π. Phase images were generated at TE = 5, 10, and 16 ms. The simulated phase Φ was given by
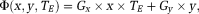 (column A in Fig. 3). Wrapped phase images θ(x,y,TE) were generated according to Eqs. 1 and 2 (column B in Fig. 3).
(column A in Fig. 3). Wrapped phase images θ(x,y,TE) were generated according to Eqs. 1 and 2 (column B in Fig. 3).
Simulated Data 2: Complex Topographies
The accuracy and processing time of UMPIRE was compared with spatial methods in unwrapping complex topographies. These were 256 × 256 × 256 voxels in size and were labeled Complexity 1–6, with 6 being the most difficult to unwrap. Complexity 1 consisted of a single 3D Gaussian distribution, centered in the centre of the matrix, with a full width half maximum (FWHM) (W1) of 128 voxels. Complexity 2 was the sum of the Complexity 1 topography and a second 3D matrix of the same dimensions which was formed from the 2 × 2 × 2 arrangement of eight narrower Gaussian distributions (width W2 = 64 voxels) each occupying a matrix of 128 × 128 × 128 voxels. Each more complex topography was formed by adding (Complexity 3) Gaussian distributions occupying a matrix of size 256/(2Complexity-3), of width W1/(2Complexity-3) to the previous one (first column in Fig. 4). The wrapping operator (Eqs. 1 and 2) was applied to generate wrapped phase images (second column in Fig. 4).

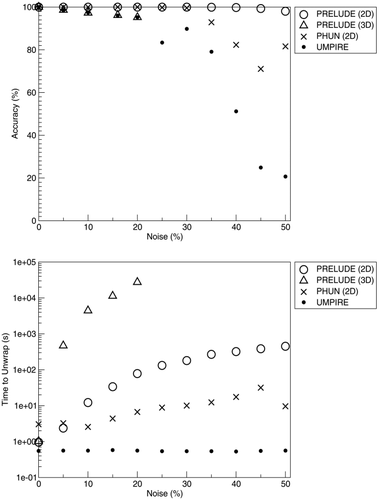
Simulated Data 3: Noisy Objects
The accuracy and processing time of UMPIRE in unwrapping in the context of noise was compared with spatial methods. The data set was 128 × 128 × 128 voxels in size, and the object to unwrap was a sphere 90 voxels in diameter, which contained a 3D Gaussian distribution with FWHM of 128 voxels. The phase distribution was such that there were four wraps to remove at the third echo time. Magnitude data are required by the spatial methods. The magnitude signal was taken to decay with a T2* time of 20 ms, and data were simulated at echo time = 5, 10, and 16 ms. Gaussian distributed white noise of between 0 and 60% of the value at time zero (in 5% increment), was added to both the magnitude and phase before applying the wrapping operator to the phase.
Measurements
Measurements were made with a 7T MR whole-body system (Magnetom, Siemens Healthcare, Erlangen, Germany) using a 32-channel head coil (Nova Medical, Wilmington, MA) consisting of a birdcage transceiver coil and 32 receive-only elements. The study was approved by the Ethics Committee of the Medical University of Vienna. Six healthy subjects (two females), aged 33.9 ± 7.8 years, participated in the study with written, informed consent. A high-resolution 3D multi-echo GE (NE = 3) scan was acquired with a matrix size of 320 × 320 × 160 (isometric voxels of 0.65 mm side length), monopolar readout, and TE = [3.9, 9.0, 15.1] ms, i.e., with an additional delay (δTE) of 1 ms between the second and third echo. The bandwidth (BW) was 240 Hz/pixel and the total acquisition time (TA) was 10 min 57 s. The first echo was flow compensated in all directions. To allow the performance of UMPIRE to be assessed in very inferior regions, the same sequence was acquired with more extensive coverage in the head–foot direction (17.2 cm) in an acquisition with 320 × 320 × 265 voxels in one subject (TA = 22 min 27 s). A low-resolution 2D dual-echo GE scan was also acquired for all subjects for the purpose of phase combination 14), with TE/TR = (4.6, 9.3)/606 ms, GRAPPA factor 4, TA = 42 s, with a 128 × 128 matrix, 50 slices of 3.0-mm thickness, and a 230 × 230 field of view.
Analysis
The steps in UMPIRE, which are outlined in Figure 2 and Eqs. 3-18, were implemented in C using standard NIfTI libraries (http://nifti.nimh.nih.gov/). When applied to Simulated Data 3 and for in vivo data, DPD images were median filtered using a 3 × 3 × 3 voxel kernel to reduce noise.
Analysis of Simulated Data
Simulated Data 1 were unwrapped with UMPIRE, including steps for removing receiver phase offsets. Conventional temporal phase unwrapping was also used both to create PD images and to attempt to unwrap individual phase images, using the PD between the images at 5 ms and 10 ms to extrapolate and identify wraps that had occurred between TE = 0 and each echo time. Simulated Data 2 and 3 were unwrapped with UMPIRE, PRELUDE (in 2D and 3D mode), and PHUN. For Simulated Data 2 (complex topographies) threshold values in PRELUDE and PHUN were set so as to unwrap all voxels (in PRELUDE, by setting t, the intensity threshold for masking, to 0, and in PHUN, using the -phaseOnly option). For Simulated Data 3 (noisy objects) PRELUDE and PHUN were set to unwrap only the object by fixing the intensity threshold for masking to 5 in PRELUDE, and in PHUN, setting -tqmin, the lower limit for pixel quality 19), to 0.05, where these values were determined empirically. There were residual inter-slice and inter-echo phase jumps of n2π (where n is an integer) in PRELUDE and PHUN, arising from the fact that seed voxels can be located on different sides of isophase contours in different slices and/or echoes. These jumps were identified and removed using a MATLAB program that compared the mean in-brain phase in adjacent slices 2. Unwrapped phase values in all the methods were compared with simulated values. For each method, the percentage accuracy was calculated as the mean over all voxels of
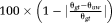 , where θgt is the ground truth phase (the simulation value) and θuw the unwrapped phase value.
, where θgt is the ground truth phase (the simulation value) and θuw the unwrapped phase value.
Analysis of In Vivo Data
In vivo phase data from the 32 surface coils were combined using MCPC-3D-II 14), in the process of which receiver phase offsets are calculated and removed from the phase information from each channel. In unwrapping with UMPIRE, steps for the subtraction of receiver phase offsets (steps 10–13 in Fig. 2) were, therefore, omitted as redundant. Average processing times for all methods were calculated from six executions on a desktop computer with a quad-core 2.67 GHz Intel Xeon processor and 12 GB RAM, running Ubuntu 12.04. In the spatial methods, the additional time required to remove inter-slice and inter-echo phase jumps was not included in the calculation time.
To allow methods to be compared in data with spatially variable SNR, in vivo phase images from individual radiofrequency (RF) coils were also unwrapped with UMPIRE (including the removal of receiver phase offsets), PRELUDE, and PHUN.
RESULTS
Simulated Data 1
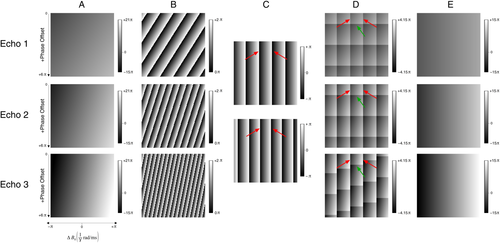
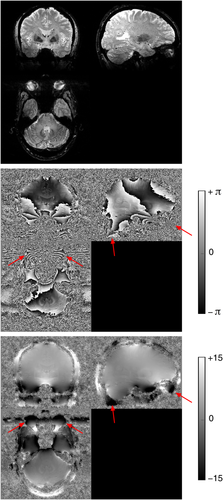
The characteristics of conventional temporal phase unwrapping were compared with those of UMPIRE over a range of simulated local field deviations (x direction in “A”) and phase offsets (y direction in “A”) (Fig. 3). Conventional temporal phase unwrapping, or PD imaging, failed when the magnitude of the phase change in the time interval ΔTE exceeded π (Fig. 3C). This corresponds to the vertical wraps, the first of which are indicated by red arrows. If unwrapping of individual phase images was attempted with the conventional method, these phase images also contain phase wraps due to phase offsets (Fig. 3D). The first of these is indicated by green arrows. As a result of these deficits, phase values are only correct in the region bounded by arrows. The range of phase values over which UMPIRE can unwrap was limited only by δTE, which was 1 ms in this simulation, and phase offsets were removed in a separate step. The resulting images (Fig. 3E), therefore, contained no wraps and only phase arising from ΔB0 [note the lack of phase variation in the y direction, and the reduced phase range of −15π → +15π compared with −15π → +21π in the original images (Fig. 3A)].
Simulated Data 2
PRELUDE and PHUN both made errors in unwrapping complex topographies. PHUN made errors in unwrapping difficulty levels 4, 5, and 6 and PRELUDE (2D) in unwrapping difficulty levels 5 and 6 (see examples in Fig. 4). These unwrapping errors are quantified in Figure 5 (top). UMPIRE made no unwrapping errors in any difficulty levels. The time taken by UMPIRE to unwrap complex topographies was independent of the complexity, and was approximately 10 times faster than the fastest spatial unwrapping method, PHUN, which was approximately 50 times faster than PRELUDE 2D. PRELUDE 3D only completed difficulty level 1 (in 11.6 days), with more complex topographies not completing in under 20 days. Unwrapping times are plotted in Figure 5 (bottom).
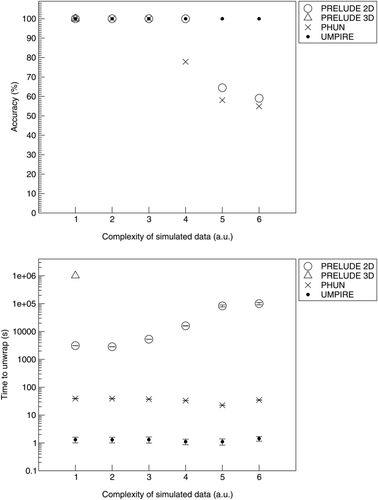
Simulated Data 3
The accuracy and time taken to unwrap noisy spheres are shown in Figure 6. Prelude (2D) showed the best performance, maintaining an accuracy of 98% up to 50% noise fraction. Prelude (3D) performed well at low noise levels, but no assessment was performed above 20%, where unwrapping times exceeded 36 h. The performance of PHUN reduced sharply at 35%. UMPIRE performed similarly to the spatial methods up to 20% noise, after which the accuracy dropped sharply. A comparison of SNR between in vivo and simulated data indicates that typical in vivo data correspond with 10% noise in simulations. Unwrapping times in UMPIRE were independent of noise and were the shortest of all methods tested (at 0.5 s). UMPIRE was 5–10 times faster than PHUN and 3–600 times faster than PRELUDE 2D (where the unwrapping time was more strongly dependent on noise). Unwrapping times in PRELUDE 3D were heavily dependent on noise, with the unwrapping time for no noise being 1 s and over 5 h for 20% noise, with higher noise levels not completing.
In Vivo Results
Conventional temporal phase unwrapping showed residual wraps where
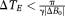 (Fig. 7, red arrows). PRELUDE (2D) failed to unwrap phase in a large vein (Fig. 7, red arrow) but otherwise yielded good results within the brain. There were phase jumps between disconnected regions of scalp signal. PRELUDE (3D) did not complete processing, although the threshold was appropriate. PHUN made the same error in the large vein as PRELUDE 2D, and additionally showed several “tear” artifacts: regions beginning at a voxel with a large difference in phase to the surrounding region, which propagated over a region to the image periphery. UMPIRE showed no phase errors and yielded plausible results for the skull and eyeballs as well as brain. Results from all six subjects (Fig. 8) demonstrate UMPIRE's ability to unwrap highly wrapped phase images consistently over subjects, generating phase images with circa 60 rad phase range.
(Fig. 7, red arrows). PRELUDE (2D) failed to unwrap phase in a large vein (Fig. 7, red arrow) but otherwise yielded good results within the brain. There were phase jumps between disconnected regions of scalp signal. PRELUDE (3D) did not complete processing, although the threshold was appropriate. PHUN made the same error in the large vein as PRELUDE 2D, and additionally showed several “tear” artifacts: regions beginning at a voxel with a large difference in phase to the surrounding region, which propagated over a region to the image periphery. UMPIRE showed no phase errors and yielded plausible results for the skull and eyeballs as well as brain. Results from all six subjects (Fig. 8) demonstrate UMPIRE's ability to unwrap highly wrapped phase images consistently over subjects, generating phase images with circa 60 rad phase range.
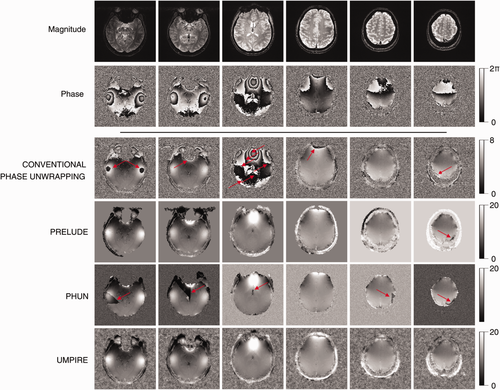
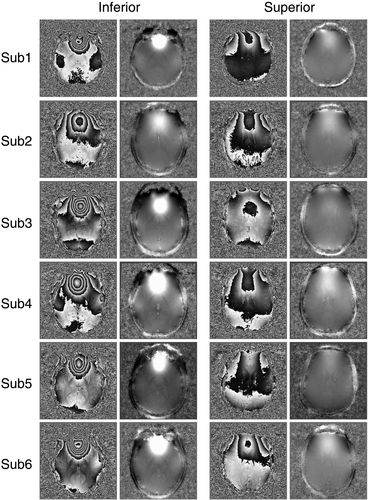
UMPIRE successfully unwrapped phase in highly wrapped ventral regions and cerebellum (Fig. 9), and even the eyes and scalp (Fig. 9, arrows).
In single-channel data, difficulty choosing a threshold level appropriate for the whole image in the spatial unwrapping methods led to unwrapping noise close to the coil (green arrows in Fig. 10) and neglecting brain regions distant from the coil (blue arrows in Fig. 10). There were also unwrapping errors with PHUN (red arrows in FIg. 10). UMPIRE unwrapped the entirety of the image without apparent errors.

The time taken for UMPIRE to unwrap all three echoes of the high resolution in vivo data (of 320 × 320 × 160 voxels, a total of circa 5 × 107 voxels) was 20.76 ± 0.04 s. The corresponding times for PHUN and PRELUDE (2D) were 103.3 ± 6.5 s and 2091.2 ± 1.7 s (approx. 35 min), respectively.
DISCUSSION
We have presented a method for unwrapping multi-echo GE phase images that is based on an acquisition with at least three unevenly spaced echoes. The timing and spacing of one pair of echoes is selected at will, according to SNR requirements, dB/dt limitations, and the desired T2* weighting. An additional delay δTE is added between the other pair of echoes such that
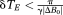 . Under this condition, the phase evolution in the time δTE is in the range −π → +π in all voxels of interest. Calculating the difference between the phase evolution in the two inter-echo periods allows a wrap-free field map to be calculated. This is used to unwrap PD images (by comparison) and ultimately, after receiver offsets have been calculated and removed, to unwrap the original phase images. The approach is conceptually simple, computationally fast, and works even when there are several wraps between pairs of echoes.
. Under this condition, the phase evolution in the time δTE is in the range −π → +π in all voxels of interest. Calculating the difference between the phase evolution in the two inter-echo periods allows a wrap-free field map to be calculated. This is used to unwrap PD images (by comparison) and ultimately, after receiver offsets have been calculated and removed, to unwrap the original phase images. The approach is conceptually simple, computationally fast, and works even when there are several wraps between pairs of echoes.
The dominant phase unwrapping approaches in current use are Homodyne filtering 10 and spatial phase unwrapping 26. Both require only one echo. Homodyne filtering is fast and simple, and removes many phase wraps. The fact that it also removes receiver phase offsets (as low-frequency features) means that, if it is applied to phase data from each channel, these data can be combined. The removal of low-frequency phase information makes it inappropriate for quantitative methods such as quantitative susceptibility mapping; however, and the ability of this approach to remove wraps is dependent on the filter width. As such, wraps in regions of high ΔB0 remain, and, if further processed in SWI, have the potential to be misconstrued as pathologies, such as microhemorrhages 27. Spatial unwrapping is capable of removing wraps more effectively than Homodyne filtering, but is inherently slow and subject, in both calculation time and unwrapping quality, to specification of the threshold that defines which parts of images to unwrap. In addition, there needs to be continuity of signal in the image and the approach works poorly where there is inhomogeneous SNR, such as in the single-channel phase images that need to be unwrapped in the unwrap-and-high-pass-filter phase combination method 2, 28. Problems also occur if there are rapid phase changes within images, as can occur in large veins such as the sagittal sinus. Phase jumps between echoes and slices (in the case of 2D spatial unwrapping) also need to be removed after unwrapping 2. These constraints make it unsuitable for implementation on the scanner console, and were evident in this study.
UMPIRE was 5 times faster than PHUN, which showed several gross unwrapping errors, and 100 times faster than PRELUDE (in the faster 2D mode). The voxel-by-voxel nature of UMPIRE would allow further speed improvement if parallelization to multiple processors were to be used 29. Both PHUN and PRELUDE performed poorly in unwrapping single-channel data in which there was inhomogeneous SNR. Thresholds had to be set carefully in the spatial methods, necessitating repeated executions. UMPIRE uses no thresholds or user-defined parameters.
Temporal phase unwrapping avoids many of the problems of spatial unwrapping by treating each voxel independently, meaning the object does not need to be defined by means of a threshold and there need not be continuity of signal between objects; an advantage in breast imaging, ophthalmological applications, and the assessment of in vitro samples. Temporal phase unwrapping has historically suffered from three significant disadvantages, however, which have seen it underused. First, images at more than one echo time are required. Second, the echo spacing must satisfy
 in order for phase wraps to be resolvable, and third, temporal approaches generally yield unwrapped PD images rather than phase images. We consider these problems in turn, particularly in relation to the inroads offered by UMPIRE.
in order for phase wraps to be resolvable, and third, temporal approaches generally yield unwrapped PD images rather than phase images. We consider these problems in turn, particularly in relation to the inroads offered by UMPIRE.
A minimum of two echoes are required for temporal phase unwrapping, although many temporal approaches require three 23, 30 or more echoes 15, 31. Acquiring echoes in separate or interleaved acquisitions is too time-consuming to be practical for high-resolution imaging, and is not considered further. Instead, we consider multi-echo approaches. An increasing number of phase-related applications use multi-echo sequences. In SWI, multi-echo acquisitions have been shown to offer increased contrast to noise ratio and SNR over single-echo acquisitions 32-34, as well as to improve the possibilities for noise reduction 33, 35. In imaging with multi-channel coils at high field, measurements of phase at two or more echo times can also be used to calculate the phase offsets for each channel, allowing phase images from several RF coils to be combined without a reference volume coil measurement 14. Multi-echo GE images also allow T2* mapping, and field maps derived from the series of echoes can be used to correct for macroscopic dephasing effects 36. Acquiring more than one echo within the desired TR is feasible even for high-resolution, low-bandwidth acquisition at ultra-high field. The advantages of multi-echo acquisitions and the additional information they provide demonstrate that the requirement that two or three echoes be acquired rarely constitutes a drawback of temporal phase unwrapping.
The usual restriction in temporal phase unwrapping is that
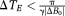 in all voxels to be unwrapped. In high-resolution phase imaging and SWI in the brain, the echo times will generally be chosen to achieve a set of desired T2* weightings, conditional on the minimum echo spacing. This is in turn determined, for a particular imaging resolution, by both the receiver BW (RBW) and gradient switching rate. RBW is inversely proportional to SNR squared, so phase images become noisy for high RBW. Ultimately, the limiting factor on ΔTE is not SNR, however, but the gradient switching rate. High dB/dt can cause peripheral nerve stimulation, gradient heating, high levels of acoustic noise, and image degradation due to eddy currents. Feng et al have shown that the echo spacing condition above can be met at 3T even in quite ventral brain regions and for a relatively high resolution of 0.5 mm in-plane (with an RBW of 465 Hz/pixel and echo spacings down to 2.63 ms) 15. It is not feasible with high-resolution measurements at 7T, however. Both UMPIRE and the method recently described by Dagher et al 23 overcome the echo spacing limitation. The method of Dagher et al also uses triple-echo scans with unequal echo spacings to calculate PD images over a range larger than the conventional limitation (γΔTEΔB0). This method is based on the principle that, if all feasible wrap possibilities are considered for each pair of echoes, then the best agreement between ΔB0 calculated from each scenario will be for the number of wraps that actually occurred. The authors demonstrated a dynamic unwrapping range in vivo of 91% more than would be expected from the shortest echo spacing, which is 1/TE (in Hz) 37. In UMPIRE, all echoes can be very widely spaced, and we demonstrate unwrapping corresponding to 510% of the range expected from the shortest echo spacing. Compared with the Dagher method, UMPIRE offers the advantages that an unwrapped map of ΔB0 is generated in a single step (step 3 in Fig. 2), without the need to calculate and compare alternative possibilities. Additionally, by calculating and subtracting receiver offsets, UMPIRE generates unwrapped phase images from each echo time in addition to field maps. In challenging SNR conditions, the echo times selected by means of the Dagher TE optimization procedure 23 will lead to the fewest unwrapping errors, whether unwrapping is undertaken by means of the authors' Closest L2-Distance Estimation or UMPIRE.
in all voxels to be unwrapped. In high-resolution phase imaging and SWI in the brain, the echo times will generally be chosen to achieve a set of desired T2* weightings, conditional on the minimum echo spacing. This is in turn determined, for a particular imaging resolution, by both the receiver BW (RBW) and gradient switching rate. RBW is inversely proportional to SNR squared, so phase images become noisy for high RBW. Ultimately, the limiting factor on ΔTE is not SNR, however, but the gradient switching rate. High dB/dt can cause peripheral nerve stimulation, gradient heating, high levels of acoustic noise, and image degradation due to eddy currents. Feng et al have shown that the echo spacing condition above can be met at 3T even in quite ventral brain regions and for a relatively high resolution of 0.5 mm in-plane (with an RBW of 465 Hz/pixel and echo spacings down to 2.63 ms) 15. It is not feasible with high-resolution measurements at 7T, however. Both UMPIRE and the method recently described by Dagher et al 23 overcome the echo spacing limitation. The method of Dagher et al also uses triple-echo scans with unequal echo spacings to calculate PD images over a range larger than the conventional limitation (γΔTEΔB0). This method is based on the principle that, if all feasible wrap possibilities are considered for each pair of echoes, then the best agreement between ΔB0 calculated from each scenario will be for the number of wraps that actually occurred. The authors demonstrated a dynamic unwrapping range in vivo of 91% more than would be expected from the shortest echo spacing, which is 1/TE (in Hz) 37. In UMPIRE, all echoes can be very widely spaced, and we demonstrate unwrapping corresponding to 510% of the range expected from the shortest echo spacing. Compared with the Dagher method, UMPIRE offers the advantages that an unwrapped map of ΔB0 is generated in a single step (step 3 in Fig. 2), without the need to calculate and compare alternative possibilities. Additionally, by calculating and subtracting receiver offsets, UMPIRE generates unwrapped phase images from each echo time in addition to field maps. In challenging SNR conditions, the echo times selected by means of the Dagher TE optimization procedure 23 will lead to the fewest unwrapping errors, whether unwrapping is undertaken by means of the authors' Closest L2-Distance Estimation or UMPIRE.
The final restriction of temporal unwrapping methods to date has been that they generally yield PD images rather than phase images. PD images are noisier and inferior in contrast to phase images 14. Temporal phase unwrapping methods are generally not able to generate phase images, because they calculate ΔB0 contributions to the phase but not other, temporally invariant, sources, which can also lead to wraps. As far as we are aware, the only other temporal phase unwrapping method that yields unwrapped phase images is the recent CAMPUS method of Feng et al 15. In this, the user defines a strip region of interest along the readout direction in a homogeneous background region, which is used to calculate the phase induced by the readout gradients, which is subtracted from the phase at each echo time. This was shown to be effective, although it has the disadvantage of requiring operator intervention. Also, other contributions to the receiver phase offset are assumed to be constant throughout the image in CAMPUS. The authors demonstrate that this does not lead to phase wraps in 3T phase images. At 7T, however, where the RF wavelength is shorter, and the variation in receiver phase offset exceeds 2π over the brain 14, it would be expected to lead to residual wraps. In UMPIRE, phase unwrapping can be applied to phase images in which the receiver phase offset has been subtracted in the reconstruction process or these can be calculated and subtracted from phase images in the steps outlined. This allows phase images to be reconstructed regardless of how large receiver phase offsets are. As such, it can be expected to work at higher field strength, with shorter RF wavelength.
UMPIRE isolates receiver phase offset information. Although this contribution to the phase has generally been viewed as uninteresting, recent work has shown that receiver phase offsets can be used to calculate tissue conductivity 38, a property which can be modified in pathologies including stroke 39 and brain tumors 40.
An appropriate value for the additional delay to be used, δTE, can be determined from measurements of the range of ΔB0 values encountered in a group of subjects at the field strength in question, or can be set on the basis of ΔB0 values measured in the subject under study in a prior fast, low-resolution field map. In the first approach, some margin should be left for outlier subjects, but this should be kept modest, as very short δTE values lead to low SNR in DPD images, which are the starting point of the unwrapping.
As a method based on the difference between phase images, UMPIRE is more sensitive to noise than spatial approaches. This was reflected in its relatively poor performance in simulations with high noise levels. With the SNR typical of in vivo images and the appropriate additional echo spacing, however, excellent results were achieved, even in the temporal poles, the cerebellum, the scalp, and eyes. Regarding noise, UMPIRE has the advantage over spatial methods that unwrapping time is independent of noise level (as well as topographical complexity), a feature that would be valuable in on-console use.
A limitation of the sequence used in this study was that only the first echo was fully flow-compensated. This leads to vessel displacement artifact in later echoes, and velocity-induced (rather than susceptibility-induced) phase changes 28, 41. This can be greatly reduced by using a bipolar flow compensation gradient before each echo 41.
Phase changes have been assumed to be linear over echo time in our approach. Phase has been shown to have a quadratic component in vessels with significant flow, however, even when bipolar flow compensation is used. This could lead to UMPIRE failing to correctly unwrap phase in large vessels, although that was not apparent in our results. Nonlinear behavior also arises in voxels containing multiple water compartments 42, an effect that has been used to image myelin. The frequency shifts involved are small, however. At less than 5 Hz at 7T 42, δTE would have to be exceed 100 ms for them to cause a phase wrap. As such, it is difficult to conceive of a situation in which they would jeopardize the approach outlined here.
In the current description, the steps in UMPIRE have been outlined for a multi-echo GE acquisition with three echoes. UMPIRE can be extended, without substantial modification to the method, to any number of echoes. In the simplest case, there would, as for three echoes, only be one additional delay between one pair of echoes, with all other echo spacings being equal. To optimize SNR in the DPD image, the starting point for unwrapping, the additional delay should be between either of the first two pairs of echoes, and the DPD image should be calculated from the first three echoes, to minimize T2* degradation of SNR.
CONCLUSIONS
The UMPIRE method allows phase images to be unwrapped even where the phase evolution between echo times is much greater than π. Only three, unequally spaced echoes are required. Phase images, rather than PD images, are generated by means of the calculation and subtraction of time-invariant contributions to the phase. As such, the method is suited to widely spaced, highly wrapped phase images acquired at very high field. The speed and simplicity of the approach make it ideally suited to implementation on the scanner console.
ACKNOWLEDGMENTS
This study was supported by the Austrian Science Fund (FWF) project KLI264.




