The goal of this paper is to investigate the dynamical behavior of a general nonlinear delayed viral infection model with cytotoxic T lymphocyte (CTL) immune response. The intrinsic growth rate of uninfected hepatocytes, incidence rate of infection, removal rate of infected hepatocytes and capsids, production and removal rate of viruses, activation rate of CTLs, and decay rate of CTLs are given by general nonlinear functions with a set of conditions on these general nonlinear functions, which make the analysis of the model more difficult. The global threshold dynamics with respect to the reproduction numbers for viral infection 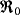$urn:x-wiley:mma:media:mma5392:mma5392-math-0001$ and for CTL immune response 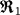$urn:x-wiley:mma:media:mma5392:mma5392-math-0002$ have been presented by constructing suitable Lyapunov functionals. Numerical simulations are carried out for a model with specific forms of the general functions to confirm the theoretical results and show that both the numerical and theoretical results are consistent.

REFERENCES

1Nowak MA, Bangham CRM. Population dynamics of immune responses to persistent viruses. Science. 1996; 272: 74-79.
10.1126/science.272.5258.74
CAS PubMed Web of Science® Google Scholar
2Nowak MA, Bonhoeffer S, Hill AM, et al. Viral dynamics in hepatitis B virus infection. Proc Natl Acad Sci. 1996; 93: 4398-4402.
10.1073/pnas.93.9.4398
CAS PubMed Web of Science® Google Scholar
3Murase A, Sasaki T, Kajiwara T. Stability analysis of pathogen-immune interaction dynamics. J Math Biol. 2005; 51: 247-267.
10.1007/s00285-005-0321-y
PubMed Web of Science® Google Scholar
4Manna K, Chakrabarty SP. Global stability of one and two discrete delay models for chronic hepatitis B infection with HBV DNA-containing capsids. Comput Appl Math. 2017; 36(1): 525-536.
10.1007/s40314-015-0242-3
Web of Science® Google Scholar
5Yang Y, Zou L, Ruan S. Global dynamics of a delayed within-host viral infection model with both virus-to-cell and cell-to-cell transmissions. Math Biosci. 2015; 270: 183-191.
10.1016/j.mbs.2015.05.001
PubMed Web of Science® Google Scholar
6Geng Y, Xu J, Hou J. Discretization and dynamic consistency of a delayed and diffusive viral infection model. Appl Math Comput. 2018; 316: 282-295.
Web of Science® Google Scholar
7Georgescu P, Hsieh YH. Global stability for a virus dynamics model with nonlinear incidence of infection and removal. SIAM J Appl Math. 2006; 67: 337-353.
10.1137/060654876
Web of Science® Google Scholar
8Korobeinikov A. Global properties of basic virus dynamics models. Bull Math Biol. 2004; 66: 879-883.
10.1016/j.bulm.2004.02.001
PubMed Web of Science® Google Scholar
9Buonomo B, Vargas-De-León C. Global stability for an HIV-1 infection model including an eclipse stage of infected cells. J Math Anal Appl. 2012; 385: 709-720.
10.1016/j.jmaa.2011.07.006
Web of Science® Google Scholar
10Manna K, Chakrabarty SP. Chronic hepatitis B infection and HBV DNA-containing capsids: Modeling and analysis. Commun Nonlinear Sci Numer Simul. 2015; 22: 383-395.
10.1016/j.cnsns.2014.08.036
Web of Science® Google Scholar
11Deeks SG, Kitchen CMR, Liu L, et al. Immune activation set point during early HIV infection predicts subsequent CD4⁺ T-cell changes independent of viral load. Blood. 2004; 104: 942-947.
10.1182/blood-2003-09-3333
CAS PubMed Web of Science® Google Scholar
12Bowen DG, Walker CM. Adaptive immune responses in acute and chronic hepatitis C virus infection. Nature. 2005; 436: 946-952.
10.1038/nature04079
CAS PubMed Web of Science® Google Scholar
13Kamp C, Wilke CO, Adami C, et al. Viral Evolution Under the Pressure of an Adaptive Immune System: Optimal Mutation Rates for Viral Escape. Complexity. 2002; 8: 28-33.
10.1002/cplx.10067
Google Scholar
14Wang K, Wang W, Pang H, et al. Complex dynamic behavior in a viral model with delayed immune response. Phys D. 2007; 226: 197-208.
10.1016/j.physd.2006.12.001
Web of Science® Google Scholar
15Xu J, Zhou Y. Bifurcation analysis of HIV-1 infection model with cell-to-cell transmission and immune response delay. Math Biosci Eng. 2016; 13: 343-367.
PubMed Web of Science® Google Scholar
16Wang T, Hu Z, Liao F, et al. Global stability analysis for delayed virus infection model with general incidence rate and humoral immunity. Math Comput Simulat. 2013; 89: 1-22.
10.1016/j.matcom.2013.03.004
CAS Web of Science® Google Scholar
17Elaiw AM, AlShamrani NH. Global stability of humoral immunity virus dynamics models with nonlinear infection rate and removal. Nonlinear Analysis: Real World Application. 2015; 26: 161-190.
10.1016/j.nonrwa.2015.05.007
Web of Science® Google Scholar
18Xu J, Geng Y. Dynamic consistent NSFD scheme for a delayed viral infection model with immune response and nonlinear incidence. Discrete Dyn Nature Soc. 2017; 2017: Article ID 3141736, 12.
Google Scholar
19Manna K. Global properties of a HBV infection model with HBV DNA-containing Capsids and CTL immune response. Int J Appl Comput Math. 2017; 3: 2323-2338.
10.1007/s40819-016-0205-4
Google Scholar
20Li MY, Wang L. Backward bifurcation in a mathematical model for HIV infection in vivo with anti-retroviral treatment. Nonlinear Analysis: Real World Application. 2014; 17: 147-160.
10.1016/j.nonrwa.2013.11.002
CAS PubMed Web of Science® Google Scholar
21Wang L, Li MY. Mathematical analysis of the global dynamics of a model for HIV infection of CD4⁺ T cells. Math Biosci. 2006; 200: 44-57.
10.1016/j.mbs.2005.12.026
CAS PubMed Web of Science® Google Scholar
22Elaiw AM. Global properties of a class of HIV models. Nonlinear Analysis: Real World Application. 2010; 11: 2253-2263.
10.1016/j.nonrwa.2009.07.001
Web of Science® Google Scholar
23Huang G, Takeuchi Y, Ma W. Lyapunov functionals for delay differential equations model of viral infections. SIAM J Appl Math. 2010; 70: 2693-2708.
10.1137/090780821
Web of Science® Google Scholar
24Wang Y, Zhou Y, Wu J, et al. Oscillatory viral dynamics in a delayed HIV pathogenesis model. Math Biosci. 2009; 219: 104-112.
10.1016/j.mbs.2009.03.003
CAS PubMed Web of Science® Google Scholar
25Yang X, Chen L, Chen J. Permanence and positive periodic solution for the single-species nonautonomous delay diffusive models. Comput Math Appl. 1996; 32: 109-116.
10.1016/0898-1221(96)00129-0
Web of Science® Google Scholar

Citing Literature

Volume42, Issue3

February 2019

Pages 892-906

Threshold dynamics of a delayed virus infection model with cellular immunity and general nonlinear incidence

Abstract

REFERENCES

Citing Literature

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Threshold dynamics of a delayed virus infection model with cellular immunity and general nonlinear incidence

Abstract

REFERENCES

Citing Literature

References

Related

Information